Meta-analytic framework for sparse K-means to identify disease subtypes in multiple transcriptomic studies

Abstract

Disease phenotyping by omics data has become a popular approach that potentially can lead to better personalized treatment. Identifying disease subtypes via unsupervised machine learning is the first step towards this goal. In this paper, we extend a sparse K-means method towards a meta-analytic framework to identify novel disease subtypes when expression profiles of multiple cohorts are available. The lasso regularization and meta-analysis identify a unique set of gene features for subtype characterization. An additional pattern matching reward function guarantees consistent subtype signatures across studies. The method was evaluated by simulations and leukemia and breast cancer data sets. The identified disease subtypes from meta-analysis were characterized with improved accuracy and stability compared to single study analysis. The breast cancer model was applied to an independent METABRIC dataset and generated improved survival difference between subtypes. These results provide a basis for diagnosis and development of targeted treatments for disease subgroups.

1. INTRODUCTION

Many complex diseases were once thought of as a single disease but modern transcriptomic studies have revealed their disease subtypes that contain different disease mechanisms, survival outcomes and treatment responses. Representative diseases include leukemia (Golub et al., 1999), lymphoma (Rosenwald et al., 2002), glioblastoma (Parsons et al., 2008; Verhaak et al., 2010), breast cancer (Lehmann et al., 2011; Parker et al., 2009), colorectal cancer (Sadanandam et al., 2013) and ovarian cancer (Tothill et al., 2008). Taking breast cancer as an example, Perou et al. (2000) was among the first to apply gene expression profile information to identify clinically meaningful subtypes of breast cancer, such as Luminal A, Luminal B, Her2-enriched and Basal-like. Many independent studies have followed the approach on different cohorts and identified similar breast cancer subtypes (Ivshina et al., 2006; Loi et al., 2007; Sørlie et al., 2001; van’t Veer et al., 2002; Wang et al., 2005). Although the breast cancer subtype classification models have been shown to cross-validate across studies with moderately satisfying consistency (Sørlie et al., 2003), each study claims a different intrinsic gene set (i.e. the list of genes used to define subtype classification) and a different characterization of cancer subtypes (Mackay et al., 2011), making it difficult to classify new patients with confidence in clinical applications. Parker et al. (2009) combined five transcriptomic studies using pre-existing subtype classifications from each study and identified 50 genes most reproducible in the subtype classification by Prediction Analysis of Microarray (PAM) (Tibshirani et al., 2002). These signature genes (often called PAM50) have been widely followed up and validated thereafter but, from a statistical point of view, the construction of PAM50 genes was an ad hoc framework and did not fully integrate information of multiple transcriptomic studies. In a parallel line, Wirapati et al. (2008) performed meta-analysis of breast cancer subtyping based on three pre-selected genes (ER, HER2 and ERBB2) and the consequential subtypes were associated with the prior gene selections.

As high-throughput experiments become affordable and prevalent, many data sets of the same omic type (e.g. transcriptome) and of a related disease hypothesis have often been collected and meta-analyzed. The meta-analysis to combine multiple studies has brought new statistical challenges. When multiple transcriptomic studies are combined, most methods have been developed to improve differential analysis (candidate marker detection) and pathway analysis. These methods mostly extend from traditional meta-analysis by combining effect sizes or p-values of multiple studies to a genome-wide scale (see review papers for microarray and GWAS meta-analysis by (Tseng et al., 2012; Begum et al., 2012) for details). But when it comes to disease subtype discovery, no integrative method for combining multiple transcriptomic studies is available, to the best of our knowledge. In the literature, hierarchical clustering (Eisen et al., 1998), K-means (Dudoit and Fridlyand, 2002) and variants of mixture model-based approaches (Xie et al., 2008; McLachlan et al., 2002) have been applied to disease subtype discovery of a single transcriptomic study. Many resampling and ensemble methods have been developed to improve stability of the cluster analysis (Kim et al., 2009; Swift et al., 2004) or to pursue tight clusters by leaving scattered samples without being clustered (Tseng, 2007; Tseng and Wong, 2005). Witten and Tibshirani (2010) proposed a sparse K-means algorithm that can effectively select gene features and perform sample clustering simultaneously. In this paper, we propose a Meta-analytic sparse K-means method (MetaSparseKmeans) for combining multiple transcriptomic studies, which identifies disease subtypes and associated gene signatures, and constructs prediction models to classify future new patients. The method contains embedded normalization and scaling to account for potential batch effects from different array platforms and a multi-class correlations (MCC) measure (Lu et al., 2010) to account for different sample proportions of the disease subtypes across studies. A pattern matching reward function is included in the objective function to guarantee consistency of subtype patterns across studies. We will demonstrate improved performance of MetaSparseKmeans by simulations and two real examples in leukemia and breast cancer studies.

The paper is structured as the following. In Section 2, we will demonstrate a motivating example to combine three large breast cancer transcriptomic studies for disease subtype discovery. We will describe the input data structure, problem setting and the biological goals to motivate the development of MetaSparseKmeans. In Section 3, introduction of classical K-means, sparse Kmeans and development of MetaSparseKmeans are presented. Section 4 contains simulation results and applications to real data in breast cancer and leukemia. Finally, conclusions and discussions are included in Section 5.

2. MOTIVATING EXAMPLE

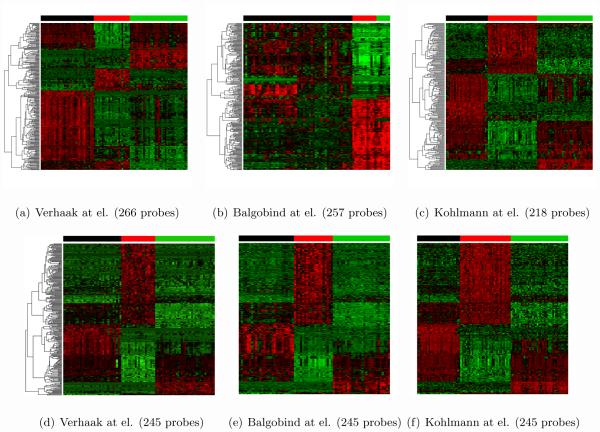
Table 1 shows a summary description of three breast cancer training transcriptomic studies: Wang (Wang et al., 2005), Desmedt (Desmedt et al., 2007) and TCGA (Network, 2012) as well as one testing study METABRIC (Curtis et al., 2012) with large sample size (n=1981) and survival information. In the training set, each study contains about 150-500 samples. Wang and Desmedt applied Affymetrix U133A chip that generated log-intensities ranging between 2.104 and 14.389, while TCGA adopted Agilent Custom 244K array that produced log-ratio intensities ranging between −13.816 and 14.207. All probes in three studies were matched to gene symbols before meta-analysis. When multiple probes matched to one gene symbol, the probe with the largest inter-quartile range (IQR) was used (Gentleman et al., 2005). 11,058 genes were matched across studies and three gene expression matrices (11,058×260, 11,058×164 and 11,058×533) were used as input data for disease subtype discovery. In such a meta-analysis framework of sample clustering analysis, we pursue two goals simultaneously: identification of a gene set (often called “intrinsic gene set”) for subtype characterization and clustering of samples in each study. Five major analytical issues (or procedures) have to be considered in the new meta-analytic framework: (A) combine information from multiple studies and perform feature (gene) selection; (B) use the combined information to perform clustering on each study; (C) accommodate potential batch effect across studies and the fact that each study contains different mixture proportions of the subtypes. (e.g. study 1 contains 20% of the first subtype while study 2 contains 35%); (D) guarantee that subtypes across studies can be matched with consistent gene signature and pattern; (E) construct a prediction model based on the combined analysis to predict future patients. In the following method section, we will develop a MetaSparseKmeans method to answer all five issues described above. Figures 1(d)-1(f) illustrate the heatmap result of our developed method on the motivating example (details will be discussed in the Result Section 4.3). 203 genes (on the rows of heatmaps) were simultaneously selected to characterize the disease subtypes. Clustering results were shown on the color bars above the heatmaps. The expression patterns of the five disease subtypes were matched well across studies from visual inspection in the heatmaps and a classification model was constructed to predict future patients. In contrast, Figures 1(a)-1(c) show sparse K-means clustering results when applied to each study separately. Each study generates different gene selection (220, 197, 239 genes respectively) and cluster patterns that are difficult to be integrated to predict a future patient. Throughout this paper, we will develop and illustrate the method for combining multiple transcriptomics studies, but the method is also applicable to meta-analysis of other types of omics data, such as miRNA, methylation or copy number variation.

Table 1.

Breast Cancer Data information

	Training			Testing
Study Name	TCGA	Wang at el.	Desmedt at el.	METABRIC
Platform	Agilent	Affymetrix	Affymetrix	Illumina
Number of genes	17,814	12,704	12,704	19,602
Number of patients	533	260	164	1,981
Range of intensity	[−13.816, 14.207]	[3.085, 14.389]	[2.104, 14.160]	[−1.262 16.618]
Mean intensity	0.003	6.797	5.523	6.954
Standard deviation	1.34	1.71	1.84	1.70

Figure 1.

Individual study clustering and MetaSparseKmeans result for 3 breast cancer datasets. Rows represent genes and columns represent samples. Red and green color represent higher and lower expression. In each study, the patients are divided into 5 clusters, represented by 5 unique colors in the color bar above the heatmaps. 1(a)-1(c): Sparse K-means result from three studies separately. 1(d)-1(f): MetaSparseKmeans result.

3. METHODS

3.1 K-means and sparse K-means

K-means algorithm (Hartigan and Wong, 1979) has been a popular clustering method due to its simplicity and fast computation. Consider X_jl the gene expression intensity of gene j and sample l. The method aims to minimize the within-cluster sum of squares (WCSS):

$$\underset{C}{\overset{\text{min}}{}}\sum _{j=1}^{p}WCS{S}_j\left(C\right)=\underset{C}{\overset{\text{min}}{}}\sum _{j=1}^p\sum _{k=1}^K\frac{1}{n_k}\sum _{l,m\in C_k}{d}_{lm,j}$$ (1)

where p is the number of genes (features), K is the number of clusters, C = (C₁, C₂, …, C_K) denotes the clustering result containing partitions of all samples into K clusters, n_k is the number of samples in cluster k and d_lm,j = (X_jl − X_jm)² denotes the squared Euclidean distance of gene j between sample l and m. Although the initial development of K-means was a heuristic algorithm, it was shown to be a special classification likelihood method in model-based clustering when data from each cluster come from Gaussian distribution with identical and spherical covariance structure (Tseng, 2007).

One major drawback of K-means is that it utilizes all p features with equal weights in the distance calculation. In genomic applications, p is usually high but biologically only a small subset of genes should contribute to the sample clustering. Witten and Tibshirani (2010) proposed a sparse K-means approach with lasso regularization on gene-specific weights to tackle this problem. One significant contribution of their sparse approach was the observation that direct application of lasso regularization to Equation 1 will result in a meaningless null solution. Instead, they utilized the fact that minimizing WCSS is equivalent to maximizing between-cluster sum of squares (BCSS) since WCSS and BCSS add up to a constant value of total sum of squares (TSS_j = BCSS_j (C) + WCSS_j (C)). The optimization in Equation 1 is equivalent to

$$\underset{C}{\overset{\text{max}}{}}\sum _{j=1}^{p}BCS{S}_j\left(C\right)=\underset{C}{\overset{\text{max}}{}}\sum _{j=1}^p\left[\frac{1}{n}\sum _{l,m}{d}_{lm,j}-\sum _{k=1}^K\frac{1}{n_k}\sum _{l,m\in C_k}{d}_{lm,j}\right]$$ (2)

The lasso regularization on gene-specific weights in Equation 2 gives the following sparse K-means objective function:

$$\begin{array}{cc}\hfill & \underset{C,\mathbf{w}}{\overset{\text{max}}{}}\sum _{j=1}^p{w}_{j}BCS{S}_j\left(C\right)\hfill \\ \hfill & \text{subject}\text{to}\parallel \mathbf{w}{\parallel }_2\le 1,\parallel \mathbf{w}{\parallel }_1\le \mu ,w_j\ge 0,\forall j,\hfill \end{array}$$ (3)

where w_j denotes weight for gene j, C = (C₁, …, C_K) is the clustering result, K is the pre-estimated number of clusters and ∥w∥₁ and ∥w∥₂ are the l₁ and l₂ norm of the weight vector w = (w₁, …, w_p). The regularization shrinks most gene weights to zero and μ is a tuning parameter to control the number of non-zero weights (i.e. the number of intrinsic genes for subtype characterization).

3.2 MetaSparseKmeans

Equation 3 identifies gene features and performs sample clustering simultaneously for a given transcriptomic study. To extend it for combining S(S ≥ 2) transciptomic studies, a naive solution is to consider optimization of the sum over S studies:

$$\begin{array}{cc}\hfill & \underset{C^{\left(s\right)},\mathbf{w}}{\overset{\text{arg}\text{max}}{}}\sum _{j=1}^p{w}_j\times \sum _{s=1}^{S}BCS{S}_j^{\left(s\right)}\left(C^{\left(s\right)}\right)\hfill \\ \hfill & \text{subjects}\text{to}\parallel \mathbf{w}{\parallel }_2\le 1,\parallel \mathbf{w}{\parallel }_1\le \mu ,w_j\ge 0,\forall j.\hfill \end{array}$$ (4)

where superscript of (s) in BCSS^(s) and C^(s) denotes the BCSS and clustering in study s (1 ≤ s ≤ S). A notable feature of Equation 4 is that the weights w_j are identical across all studies and thus it generates a common intrinsic gene set together with clustering of samples in each study $C^{\left(s\right)}=(C_1^{\left(s\right)},\cdots ,C_{K_s}^{\left(s\right)})$ (K_s is the number of clusters in study s). In this paper, K_s is assumed to be equal to K (equal number of clusters across studies) and its extension is discussed later. A downside for Equation 4 is that it treats all studies equally without considering that different studies may contain different sample sizes and intensity ranges as shown in Table 1. As a result, studies with larger sample sizes and higher intensity variability ranges will dominate the analysis in Equation 4. To fix this problem, we propose to standardize BCSS score by TSS below:

$$\begin{array}{cc}\hfill & \underset{C^{\left(s\right)},\mathbf{w}}{\overset{\text{arg}\text{max}}{}}\sum _{j=1}^p{w}_j\times \sum _{s=1}^S\frac{1}{S}\frac{BCS{S}_j^{\left(s\right)}\left(C^{\left(s\right)}\right)}{TS{S}_j^{\left(s\right)}}\hfill \\ \hfill & \text{subjects}\text{to}\parallel \mathbf{w}{\parallel }_2\le 1,\parallel \mathbf{w}{\parallel }_1\le \mu ,w_j\ge 0,\forall j.\hfill \end{array}$$ (5)

Note that the standardized BCSS score in each study is always bounded between 0 and 1. The formulation so far answers issues (A)-(C) in Section 2 by generating a common intrinsic gene set, clustering samples in each study and accommodating different sample sizes and intensity ranges among studies. In Equation 5, the contribution of BCSS/TSS is equal from each study and is not adjusted by sample size (denoted as equal weight or EW). Alternative option is to replace the 1/S term with $n_s∕{\sum }_s{n}_s$ (n_s is the sample size of study s) so that studies with larger sample size contribute greater in the clustering formation (denoted by unequal weight or UW). In the simulation section (Figure 4), EW and UW are compared. Conceptually, when studies are homogeneous, UW performs better by accounting for sample size. But when studies contain heterogeneous information, EW is expected to be more robust and will be recommended in real applications.

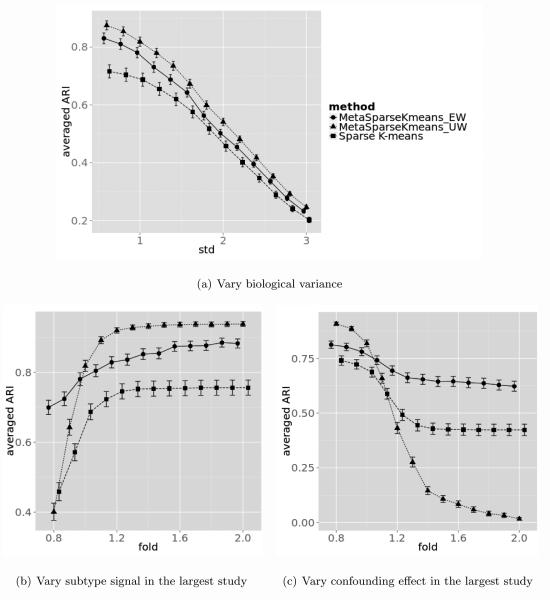
Figure 4.

Simulation result comparing MetaSparseKmeans (EW), MetaSparseKmeans (UW) and sparse K-means under different scenarios. Figure 4(a): varying biological variance. Figure 4(b): varying subtype predictive gene intensity in the first study with the largest sample size. Figure 4(c): varying confounding impacted gene intensity in the first study with the largest sample size.

A next issue in this meta-analytic framework is to match the cluster patterns obtained from different studies (issue (D) in Section 2). For example, samples of the light blue cluster in all three studies in Figure 1(d)-1(f) are up-regulated (red) in the upper part of genes and down-regulated (green) in the lower part of genes. Equation 5 guarantees to generate sample clusters with good separability in each study but does not warrant such subtype matching across studies. To achieve this purpose, we added pattern matching reward function $f_j^{match}\left(M\right)$ in the objective function:

$$\begin{array}{cc}\hfill & \underset{C^{\left(s\right)},\mathbf{w},M}{\overset{\text{max}}{}}\sum _{j=1}^p{w}_j\times \left[\frac{1}{S}\sum _{s=1}^S\frac{BCS{S}_j^{\left(s\right)}\left(C^{\left(s\right)}\left(K\right)\right)}{TS{S}_j^{\left(s\right)}}+\lambda \times f_j^{match}\left(M\right)\right]\hfill \\ \hfill & \text{subject}\text{to}\parallel \mathbf{w}{\parallel }_2\le 1,\parallel \mathbf{w}{\parallel }_1\le \mu ,w_j\ge 0,\forall j,\hfill \end{array}$$ (6)

where M is the cluster matching enumeration across S studies, $M=M(C^{\left(1\right)},\dots ,C^{\left(s\right)})$. For example, when S = 3 and K = 3, denote $(C_1^{\left(1\right)}-C_3^{\left(2\right)}-C_1^{\left(3\right)},C_2^{\left(1\right)}-C_2^{\left(2\right)}-C_3^{\left(3\right)},C_3^{\left(1\right)}-C_1^{\left(2\right)}-C_2^{\left(3\right)})$ as a possible matching function of M, where the first cluster in study 1, the third cluster in study 2 and the first cluster in study 3 are matched with similar gene expression pattern to represent the first disease subtype. Similarly, patients in the second clusters in study 1, second cluster in study 2 and third cluster in study 3 form the second disease subtype and so on. Under this notation, the total number of possible pattern matching of M is (K!)^(S−1). M can be regarded as a cluster label reordering operator for all S studies: M = (φ⁽¹⁾(C⁽¹⁾), φ⁽²⁾(C⁽²⁾), …, φ^(S)(C^(S))), where φ^(s)(C^(s)) maps the K clusters in the s^th study $C^{\left(s\right)}=(C_1^{\left(s\right)},C_2^{\left(s\right)},\dots ,C_K^{\left(s\right)})$ to disease subtype 1, 2, …, K. In the example above, the corresponding mapping is ${\varphi }^{\left(1\right)}(C_1^{\left(1\right)},C_2^{\left(1\right)},C_3^{\left(1\right)})=(1,2,3),{\varphi }^{\left(2\right)}(C_1^{\left(2\right)},C_2^{\left(2\right)},C_3^{\left(2\right)})=(3,2,1),{\varphi }^{\left(3\right)}(C_1^{\left(3\right)},C_2^{\left(3\right)},C_3^{\left(3\right)})=(1,3,2)$.

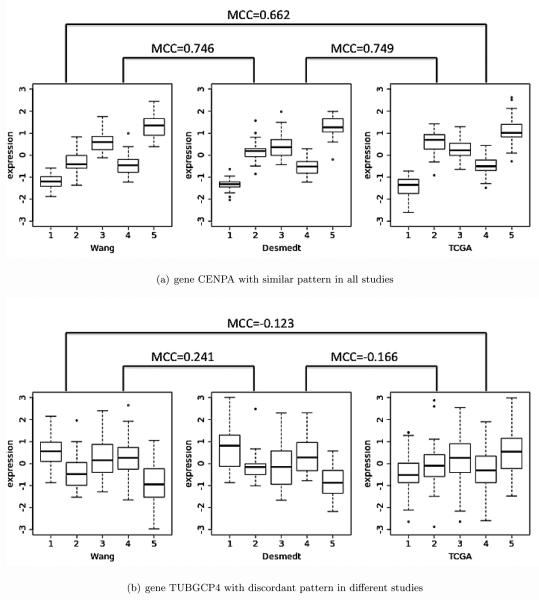
The pattern matching reward function $f_j^{match}\left(M\right)$ borrows the concept from multi-class correlation (MCC) (Lu et al., 2010) that was developed to quantify concordant multi-class (more than two classes) expression pattern for candidate marker detection in the meta-analysis of multiple transcriptomic studies. Traditionally, one can calculate the Pearson correlation of two vectors with equal lengths. However, our pattern matching score needs to consider the correlation of identical number of clusters with unequal number of samples in each cluster. For example, Figure 2(a) shows the expression pattern of a given gene CENPA in the three breast cancer studies, each with 5 clusters of samples. All studies have relatively high expression in cluster 5, intermediate expression level in cluster 2 and 3, and lower expression in cluster 1 and 4. This is our desired concordant pattern gene which would generate high total MCC scores. Figure 2(b) shows a gene with different cluster patterns in different studies. In Wang the pattern is higher expression in cluster 1, 3 and 4, and lower expression in cluster 2 and 5. The TCGA study, however, does not have a clear pattern. Desmedt is somewhat similar to Wang but very different from TCGA. Since the patterns are not consistent across studies, the total MCC scores in this case should be lower.

Figure 2.

Two real gene examples to show the idea of MCC. The x axis is the cluster index and y axis is the expression intensity. Gene CENPA shows similar patterns across studies and MCCs are large (Figure 2(a)). Gene TUBGCP4 shows discordant patterns across studies and MCCs are smaller (Figure 2(b)).

Below we describe the MCC score definition from the empirical distributions of each cluster in a pair of studies study (See Lu et al. (2010) for more details). Consider D_X = {x_ki} (1 ≤ k ≤ K, 1 ≤ i ≤ n_k) to represent expression intensity of class k and sample i for the first study and D_Y = {y_kj } (1 ≤ k ≤ K, 1 ≤ j ≤ m_k) for the second study, where n_k and m_k are the number of samples of class k in the first and second studies. We first define an imaginary bivariate distribution $(\mathbb{𝕏},\mathbb{𝕐})$ that is a mixture of the K independent bivariate distributions (X₁, Y₁), … , (X_K, Y_K) with equal probability where X_k and Y_k are empirical distributions from {x_k1, …, x_knk} and {y_k1, …, y_kmk} (i.e. the CDF of $(\mathbb{𝕏},\mathbb{𝕐})\text{is}{G}_{\mathbb{𝕏},\mathbb{𝕐}}(x,y)=\frac{1}{K}{\sum }_{k=1}^K{G}_{X_k,Y_k}(x,y)=\frac{1}{K}{\sum }_{k=1}^K{G}_{X_k}\left(x\right)G_{Y_k}\left(y\right)$). MCC score is defined as the Pearson correlation of X and Y as shown below

$$MCC(D_X,D_Y)=\text{cor}(\mathbb{𝕏},\mathbb{𝕐})=\frac{\left(\sum _{k=1}^K{\mu }_{X_k}{\mu }_{Y_k}\right)-K_{{\stackrel{‒}{\mu }}_X{\stackrel{‒}{\mu }}_Y}}{\sqrt{[\sum _{k=1}^K{\sigma }_{X_k}^2+\sum _{k=1}^K{({\mu }_{X_k}-{\stackrel{‒}{\mu }}_X)}^2][\sum _{k=1}^K{\sigma }_{Y_k}^2+\sum _{k=1}^K{({\mu }_{Y_k}-{\stackrel{‒}{\mu }}_Y)}^2]}}$$

,where $\mu X_k={\sum }_{i=1}^{n_k}{x}_{ki}∕n_k,\mu Y_k={\sum }_{j=1}^{m_k}{y}_{k_j}∕m_k,{\sigma }_{X_k}^2={\sum }_{i=1}^{n_k}{(x_{ki}-{\mu }_{X_k})}^2∕n_k,{\sigma }_{Y_k}^2={\sum }_{j=1}^{m_k}{(y{k}_j-{\mu }_{Y_k})}^2∕m_k,{\stackrel{‒}{\mu }}_X={\sum }_{k=1}^K{n}_k{\mu }_{X_k}∕{\sum }_{k=1}^K{n}_k,{\stackrel{‒}{\mu }}_Y={\sum }_{k=1}^K{m}_k{\mu }_{Y_k}∕{\sum }_{k=1}^K{m}_k$.

It is worth noting that MCC is defined from conventional Pearson correlation and is restricted between −1 and 1. When n₁ = … = n_k = n and m₁ = … = m_k = m, MCC reduces to

$$MCC=\frac{r_{{\overrightarrow{\mu }}_X{\overrightarrow{\mu }}_Y}}{\sqrt{\frac{1}{F_X}\cdot \frac{K}{K-1}+1}\sqrt{\frac{1}{F_Y}\cdot \frac{K}{K-1}+1}}$$

,where $r_{{\overrightarrow{\mu }}_X{\overrightarrow{\mu }}_Y}=\frac{{\sum }_k({\mu }_{X_k}-{\stackrel{‒}{\mu }}_X)({\mu }_{Y_k}-{\stackrel{‒}{\mu }}_Y)}{\sqrt{{\sum }_k{({\mu }_{X_k}-{\stackrel{‒}{\mu }}_X)}^2}\sqrt{{\sum }_k{({\mu }_{Y_k}-{\stackrel{‒}{\mu }}_Y)}^2}}$ is the sample correlation of ${\overrightarrow{\mu }}_X=({\mu }_{X_1},\dots ,{\mu }_{X_k})$ and ${\overrightarrow{\mu }}_Y=({\mu }_{Y_1},\dots ,{\mu }_{Y_k})$. $F_X=\frac{{\sum }_k{({\mu }_{X_k}-{\stackrel{‒}{\mu }}_X)}^2∕(K-1)}{{\sum }_k{\sum }_i{(x_{ki}-{\mu }_{X_k})}^2∕\left((n-1)K\right)}$ and $F_Y=\frac{{\sum }_k{({\mu }_{Y_k}-{\stackrel{‒}{\mu }}_Y)}^2∕(K-1)}{{\sum }_k{\sum }_j{(y_{k_j}-{\mu }_{Y_k})}^2∕\left((m-1)K\right)}$ are exactly the F-statistics in ANOVA for D_X and D_Y. When the within-class variation is much smaller than the between-class variation, F_X and F_Y become large. MCC converges to $r_{{\overrightarrow{\mu }}_X{\overrightarrow{\mu }}_Y}$ as expected.

Finally, the pattern matching reward function is defined as the average of MCC of all pairs of studies as below:

$$f_j^{match}\left(M\right)=\left(\frac{1}{\left(\begin{array}{c}\hfill S\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{s,s^{\prime }\in S}MC{C}_j({\varphi }^{\left(s\right)}\left(C^{\left(s\right)}\right),{\varphi }^{\left(s^{\prime }\right)}\left(C^{\left(s^{\prime }\right)}\right))+1\right)∕2$$

where s and s^′ denote any two studies from all S studies and φ^(s)(C^(s)) was previously defined for cluster matching function M. Note that the pattern matching reward function is transformed to guarantee taking values between 0 and 1.

In summary, the objective function of MetaSparseKmeans in Equation 6 generates a common feature set from the non-zero estimated weights and sample clustering in each study. The first term in Equation 6 ensures good cluster separation in each study, the second term guarantees the consistent patterns of identified disease subtypes across studies and the l₁ penalty generates sparsity on gene weights to facilitate feature selection.

3.3 Implementation of MetaSparseKmeans

In this subsection, we discuss the optimization procedure, parameter estimation and how the classification model from the clustering can predict a future patients cohort.

Optimization without pattern matching reward function

For clarity of demonstration, we first illustrate the optimization procedure without reward function as shown in Equation 5. The algorithm is a simple extension from Witten and Tibshirani (2010).

1. Initialize w such that $w_j=\frac{s{d}_j}{s{d}_1+\dots +s{d}_p}\times \mu$, where sd_j is the standard deviation of gene j.

2. Fix w, update C^(s) for study s (∀s ∈ S) by optimizing Equation 5 applying conventional weighted K-means.

3. Fix C^(s), update w by optimizing Equation 5 following Karush-Kuhn-Tucker (KKT) condition.

4. Iterate Step 2-3 until converge.

In Step 1, we apply unequal initialization weight that is proportional to the standard deviation of each gene. We have found better performance of this initialization compared to equal weight initialization suggested in (Witten and Tibshirani, 2010). In Step 2, since the weights are fixed and TSS^(s) is irrelevant to the clustering result, the optimization is essentially to repeat regular K-means algorithm with weighted gene structure for each study independently. In Step 3, fixing $a_j={\sum }_{s=1}^S\frac{BCS{S}_j^{\left(s\right)}\left(C^{\left(s\right)}\left(K\right)\right)}{TS{S}_j^{\left(s\right)}}$, optimization of weights w is a convex optimization problem that leads to $w_j=\frac{{\Gamma }_{\Delta }\left(a_j\right)}{\parallel {\Gamma }_{\Delta }\left(a_j\right){\parallel }_2}$ following KKT condition, where Γ is the soft-thresholding operator which is defined as Γ_Δ(x) = max(x − Δ, 0). Δ > 0 is chosen such that ∥w∥₁ = μ; otherwise Δ = 0 if ∥w∥₁ < μ. Readers may refer to (Boyd and Vandenberghe, 2004; Witten and Tibshirani, 2010) for more details.

Finally, Steps 2 and 3 are iterated until convergence of the weight estimate $\left(\text{i.e.}\frac{{\sum }_{j=1}^p\mid w_j^{\left(r\right)}-w_j^{(r-1)}\mid }{{\sum }_{j=1}^p\mid w_j^{(r-1)}\mid }<{10}^{-4}\right)$, where $w_j^{\left(r\right)}$ represents the w_j estimate in the r^th iteration. In our simulation and real data experiences, the algorithm usually converges within 20 iterations.

Optimization with pattern matching reward function

When the pattern matching reward function is added, the iterative optimization has an additional step to estimate the best clustering matching across studies M. In this case we split optimization of Equation 6 into 3 parts:

$$C^{\left(s\right)+}=\underset{C^{\left(s\right)}}{\overset{\text{arg}\text{max}}{}}\sum _{j=1}^p{w}_j\times \left[\frac{1}{S}\sum _{s=1}^S\frac{BCS{S}_j^{\left(s\right)}\left(C^{\left(s\right)}\right)}{TS{S}_j^{\left(s\right)}}\right]$$ (7a)

$$M^{+}=\underset{M}{\overset{\text{arg}\text{max}}{}}\sum _{j=1}^p{w}_j\times f_j^{match}\left(M\right)$$ (7b)

$$\begin{array}{cc}\hfill {\mathbf{w}}^{+}=\underset{\mathbf{w}}{\overset{\text{arg}\text{max}}{}}\sum _{j=1}^p{w}_j& \times \left[\frac{1}{S}\sum _{s=1}^S\frac{BCS{S}_j^{\left(s\right)}\left(C^{\left(s\right)}\right)}{TS{S}_j^{\left(s\right)}}+\lambda \times f_j^{match}\left(M\right)\right]\hfill \\ \hfill & \text{subject}\text{to}\parallel \mathbf{w}{\parallel }_2\le 1,\parallel \mathbf{w}{\parallel }_1\le \mu ,w_j\ge 0,\forall j,\hfill \end{array}$$ (7c)

where C^(s)+, M ⁺, w⁺ are the updating rule in the iteration. The optimization algorithm becomes:

1. Initialize w such that $w_j=\frac{s{d}_j}{s{d}_1+\dots +s{d}_p}\times \mu$, where sd_j is the standard deviation of gene j.

2. Fix w, for ∀s ∈ S, update C^(s) by weighted K-means according to Equation 7a.

3. Fix w and C^(s), update M by using exhaustive search or simulated annealing (see below) according to Equation 7b.

4. Fix C^(s) and M, update w by KKT condition according to Equation 7c.

5. Iterate Step 2-4 until converge.

One potential concern in Equation 7a is the lack of consideration of $f_j^{mathch}\left(M\right)$. Including $f_j^{mathch}\left(M\right)$ in Equation 7a will greatly complicate the optimization for C ^(s). We decided to remove this term so that C^(s) can be efficiently estimated in each study separately and then update M right after updating C^(s). The simplified algorithm performed well in all our applications.

When updating M in Equation 7b, exhaustive search requires evaluation of all possible (K!)^S−1 combinations. In our motivating example of K = 5 and S = 3, it takes 14,400 evaluations. The number of evaluations increases to 207.36 million when S increases to 5. As an alternative, we propose a linear stepwise search to reduce the computational burden. In the first step, we match the first two studies with the largest sample sizes. Then the third study is added to match with existing patterns and the procedure continues by adding one study at a time. This approach will reduce to (K!) × (S − 1) possible evaluations. The search space will reduce from exponential order to linear order of the number of studies. In the case of K = 5 and S = 5, the number of evaluations reduces from 207.36 million to 480. In case that the linear stepwise search may reach an undesirable suboptimal solution, we propose a third approach to apply stepwise search solution as an initial value to a simulated annealing algorithm (Kirkpatrick et al., 1983) (see Appendix for detailed algorithm). Simulated annealing is an MCMC-based stochastic optimization algorithm for non-convex function. We expect that the third approach will achieve the best balance for affordable computing time while maintaining high clustering accuracy (Table 6). The computing load and performance of these three matching approach will be evaluated in Section 4.4. In our software package, we suggest to perform exhaustive search when (K!)^S−1 ≤ 14, 400 and automatically switch to simulated annealing otherwise.

Table 6.

Computing time and accuracy. Table 6(a): computing time in minutes comparing different combination of S and K using a regular desktop computer. Table 6(b): performance comparing with the best matching score (percentage of agreement with optimal matching) and clustering accuracy by ARI (mean estimate± standard error) under different biological variances (σ = 2 and σ = 6).

(a) Computing time

	Algorithm	S=3	S=5	S=15
	Exhaustive	2.604	5.614	> 2.9 × 104
K=3	Stepwise	2.854	5.290	18.024
	MCMC	4.288	7.429	35.736
	Exhaustive	15.616	> 2.9 × 104	> 2.9 × 104
K=5	Stepwise	8.738	13.951	39.273
	MCMC	11.645	16.541	78.687

(b) Accuracy

	% of optimal		accuracy
Variance	σ = 2	σ = 6	σ = 2	σ = 6
Exhaustive	100%	100%	0.829 ± 0.031	0.020 ± 0.002
Stepwise	93.3%	92.8%	0.828 ± 0.031	0.020 ± 0.002
MCMC	100%	100%	0.828 ± 0.031	0.020 ± 0.002

Parameter selection

In the MetaSparseKmeans formulation above, the number of clusters K are assumed pre-specified. In practice, it has to be estimated from data. The issue of estimating the number of clusters has received wide attention in the literature (Milligan and Cooper, 1985; Kaufman and Rousseeuw, 2009; Sugar and James, 2003). Here, we suggest the numbers of clusters to be estimated in each study separately using conventional methods such as prediction strength (Tibshirani and Walther, 2005) or gap statistics (Tibshirani et al., 2001) and jointly compared across studies (such that the numbers of clusters are roughly the same for all studies) for a final decision before applying MetaSparseKmeans. Below we assume that a common K is pre-estimated for all studies.

Another important parameter to be estimated is μ that controls the number of non-zero weights in the lasso regularization. Larger μ results in larger number of non-zero weights (i.e. the number of intrinsic genes to characterize the subtypes). We follow and extend the gap statistic procedure in sparse K-means (Witten and Tibshirani, 2010) to estimate μ:

1. For each gene feature in each study, randomly permute the gene expression row vector (permute samples). This creates a permuted data set X⁽¹⁾. Repeat for B times to generate X⁽¹⁾, X⁽²⁾, …, X^(B).

2. For each potential tuning parameter μ, compute the gap statistics as below.

   $$\text{Gap}\left(\mu \right)=O\left(\mu \right)-\frac{1}{B}\sum _{b=1}^B{O}_b\left(\mu \right),$$ (8)

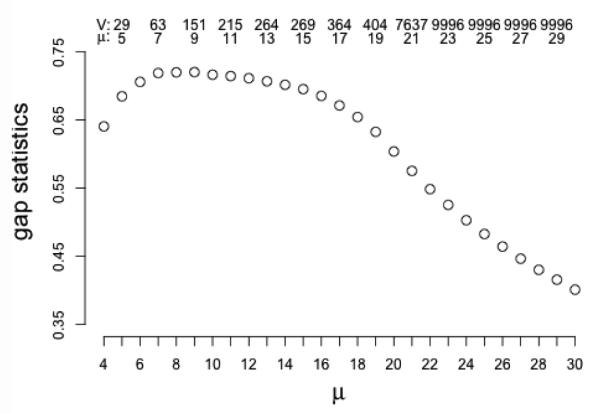
   where $O\left(\mu \right)={\sum }_{j=1}^p{w}_j^{\ast }[\frac{1}{S}\left({\sum }_{s=1}^S\frac{BCS{S}_j^{\left(s\right)}\left(C^{\left(s\right)\ast }\left(K\right)\right)}{TS{S}_j^{\left(s\right)}}\right)+\lambda \times f_j^{match}\left(M^{\ast }\right)]$ is from observed data, where w^∗, C^∗(K), M ^∗ are the maximizers of the objective function. O_b(μ) is similar to O(μ) but it is from permuted data X^(b)

3. For a range of selections of μ, select μ^∗ such that the gap statistics in Equation 8 is maximized. Figure 3 shows the candidate region and the corresponding gene numbers of different μ for a simulated dataset that will be discussed in Section 4.1.

Figure 3.

Gap statistics to select μ in simulated data with biological variance σ₁ = 1. X-axis: μ; y-axis: gap statistics. V and μ on top give the number of non-zero weight features and corresponding tuning parameter. Gap statistics is maximized at μ = 9, which is coresponding to 151 genes.

Our simulation has shown good performance of the gap statistics procedure but the performance may vary in real data. In practice, the users may test different selections of μ and examine the change of clustering assignment. In general, slight change of μ (or equivalently the number of selected genes) does not greatly change the clustering result. Another possibility is to use clinical or survival information to guide estimation of μ although we chose not to do so in the breast cancer example to avoid re-using the survival information in the evaluation.

Finally, the parameter λ controls the balance of the standardized BCSS and pattern matching rewards in Equation 6. The former term drives the optimization to seek for clear cluster separations while the latter term emphasizes on concordant pattern of disease subtypes across studies. We performed sensitivity analysis on λ in the applications and found that slightly changing λ had little impact on the final clustering result in most cases. Since considerations of both terms are biologically important, we suggest to use λ = 0.5 in general unless users have particular reasons to change. Note that the first and second terms in Equation 6 are standardized to range between 0 and 1 and are at comparable scales.

Data visualization

To generate heatmaps similar to Figure 1(a)-1(f), data normalization is necessary so genes at different expression scales can be presented simultaneously. Conventional wisdom in microarray analysis is to standardize each gene vector to have zero mean and unit variance in each study independently. This is, however, not applicable in our situation since the sample proportions of each disease subtype are not equal across studies. We instead applied a ratio-adjusted gene-wise normalization (Cheng et al., 2009) that accounts for differential subtype mixture proportions in the studies.

Classification of a future patient cohort

For a future dataset that possibly comes from a different experimental platform, models from MetaSparseKmeans can help cluster the new cohort and match the signature patterns to determine the subtypes. The algorithm goes with two steps:

1. The optimal weights w^∗ from MetaSparseKmeans algorithm on training data are used to cluster patients of the new cohort using conventional K-means with pre-specified weighted gene structure:

   $$C^{\left(new\right)}=\underset{C}{\overset{\text{arg}\text{min}}{}}\sum _{j=1}^p{w}_j^{\ast }\sum _{k=1}^K\frac{1}{n_k}\sum _{l,m\in C_k}{d}_{lm,j}$$
2. The generated clusters C^(new) are then matched back to disease subtypes determined by MetaSparseKmeans training results. Specifically, we ask for the best cluster pattern matching of the new clusters to the original subtypes. Since the matching in the training studies are fixed, the optimization only requires MCC calculation of new cohort clustering C^(new) with clustering of each training study C⁽¹⁾, …, C^(S).

   $$M^{(new\ast )}=\underset{M^{\left(new\right)}}{\overset{\text{arg}\text{max}}{}}\sum _{j=1}^p\sum _{s\in S}{w}_j^{\ast }MC{C}_j({\varphi }^{\left(s\right)}\left(C^{\left(s\right)}\right),{\varphi }^{\left(new\right)}\left(C^{\left(new\right)}\right))$$

Extensions for practical applications

Below we discuss two extensions for practical applications. Firstly, our framework has applied equal K in all studies. The question is whether and how to allow variable K across studies. Biologically, it is not reasonable to have wildly different number of disease subtypes across studies. Thus, we decided not to extend the algorithm for automatically searching variable K. Instead, we suggest the users to apply equal K and perform ad hoc analysis if evidence shows that some studies have almost no samples for a particular subtype or an additional subtype is needed (e.g. reduce from K=(5,5,5) to K = (5, 4, 5) in the second study). Secondly, the number of genes may reduce greatly in the gene matching step if one or two studies apply an old array platform with less comprehensive coverage of the genome. In this case, our framework can easily extend to allow missing genes in partial studies (by simply ignoring the terms of a specific missing gene in a study). We have included this function in the software package and suggest to include genes as long as they appear in > 70% of studies.

4. RESULT

We evaluated MetaSparseKmeans on simulation datasets as well as two real multi-center examples in leukemia and breast cancer. In the simulation datasets, we showed that MetaSparseKmeans could recover the underlying true clusters with higher accuracy than single study analysis. We also showed that MetaSparseKmeans using equal weight (EW) is superior than MetaSparseKmeans using unequal weight (UW) in the heterogenous scenario and reversely MetaSparseKmeans UW is superior than MetaSparseKmeans EW in the homogenous scenario. In the leukemia dataset, we demonstrated that MetaSparseKmeans obtained unified gene selection and stable cluster pattern while single study analysis by sparse K-means claimed different gene selections and unmatched cluster patterns in different studies. In the breast cancer dataset, we applied MetaSparseKmeans to 3 breast cancer studies and showed that MetaSparseKmeans had better performance than single study sparse K-means. The classification model was used to predict the fourth METABRIC dataset and the meta-analyzed model generated more significant survival differences than the prediction based on single study models. Lastly we evaluated the computation time and accuracy for MetaSparseKmeans using different matching algorithm. MCMC (with linear stepwise search initial) will balance the computing load and optimization performance.

4.1 Simulation

Simulation setting

To evaluate the performance of MetaSparseKmeans and compare with sparse K-means, we simulated S(S = 3) studies with K(K = 3) subtypes in each study. To best mimic the nature of microarray study, we will simulate confounding variables, gene correlation structure and noise genes (e.g. housekeeping genes or unexpressed genes). Below are the detailed generative steps to create subtype predictive genes, confounder impacted genes and noise genes.

(a) Subtype predictive genes

1. We simulate N_k1 ~ POI(400), N_k2 ~ POI(200), N_k3 ~ POI(100) samples for subtype k(1 ≤ k ≤ 3) in study s(1 ≤ s ≤ 3). The number of subjects in study s is N_s = Σk N_ks.

2. Sample M = 20 gene modules (1 ≤ m ≤ 20). In each module, sample n_m genes where n_m ~ POI(20). Therefore, there will be an average of 400 subtype predictive genes.

3. μ_sik is the template gene expression of study s(1 ≤ s ≤ S), subtype k(1 ≤ k ≤ 3) and module m(1 ≤ m ≤ M ). For the first study, sample the template gene expression μ_1km ~ UNIF(4, 10) with constrain max_p,q |μ_1pm − μ_1qm| ≥ 1, where p, q denote two subtypes. For the second and third study, set μ_2km = μ_3km = μ_1km, ∀k, m. This part define the subtype mean intensity for each module in all studies. To simulate the situation that the first study (with the largest sample size) containing stronger signal, we introduced a new parameter f (for fold) to recalculate the template gene expression for the first study μ_1km: ${\mu }_{1km}^{\ast }$ = (μ_1km − min_k,m{μ_1km}) × f + min_k,m{μ_1km}, We set f = 1 unless otherwise mentioned.

4. Add biological variation ${\sigma }_1^2$ to the template gene expression and simulate $X_{skmi}^{\prime }~\text{N}({\mu }_{skm},{\sigma }_1^2)$ for each module m, subject i(1 ≤ i ≤ N_ks) of subtype k and study s.

5. Sample the covariance matrix Σ_mks for genes in module m, subtype k and study s, where 1 ≤ m ≤ 20, 1 ≤ k ≤ 3 and 1 ≤ s ≤ 3. First sample ${\sum }_{mks}^{\prime }~{\text{W}}^{-1}(\Phi ,60)$, where $\Phi =0.5I_{n_m\times n_m}+0.5J_{n_m\times n_m},{\text{W}}^{-1}$ denotes the inverse Wishart distribution, I is the identity matrix and J is the matrix with all elements equal 1. Then Σ_mks is calculated by standardizing ${\sum }_{mks}^{\prime }$ that the diagonal elements are all 1’s.

6. Sample gene expression levels of genes in cluster m as ${(X_{1skmi},\dots ,X_{n_{m}skmi})}^{\mathrm{T}}~\text{MVN}(X_{skmi}^{\prime },{\sum }_{mks})$, where 1 ≤ i ≤ N_ks, 1 ≤ m ≤ M, 1 ≤ k ≤ 3 and 1 ≤ s ≤ 3.

(b) Confounder impacted genes

1. Sample 4 confounding variables. In practice, confounding variables can be gender, race, other demographic factors or disease stage etc. They will add heterogeneity to each study to complicate disease subtype discovery. For each confounding variable c, we will sample R = 15 modules. For each of these modules r_c(1 ≤ r_c ≤ R), sample number of genes n_rc ~ POI(20). These genes will be the same for all 3 studies. Therefore, there will be an average of 1,200 confounder impacted genes.

2. For each study s(1 ≤ s ≤ 3) and each confounding variable c, sample the number of confounder subclass h_sc ~ POI(3) with constraint h_sc > 1. The N_s samples in study s will be randomly divided into h_sc subclasses.

3. Sample confounding template gene expression μ_slrc ~ UNIF(4, 10) for confounder c, gene module r, subclass l(1 ≤ l ≤ h_sc) and study s. We recalculate ${\mu }_{1lrc}^{\ast }=({\mu }_{1lrc}-{\text{min}}_{lrc}\left\{{\mu }_{1lrc}\right\})\times f+{\text{min}}_{lrc}\left\{{\mu }_{1lrc}\right\}$ which is similar to Step a3. Add biological variation ${\sigma }_1^2$ to the confounding template gene expression $X_{scrli}^{\prime }~\text{N}({\mu }_{slrc},{\sigma }_1^2)$. Similar to Step a5 and a6, we simulate gene correlation structure within modules of confounder impacted genes.

(c) Noise genes

1. Sample 8,400 noise genes denoted by g(1 ≤ g ≤ 8, 400). For each study, we generate the mean template gene expression μ_sg ~ UNIF(4, 10). Then we add biological variation variance ${\sigma }_2^2=1$ to generate $X_{sgi}~N({\mu }_{sg},{\sigma }_2^2),1\le i\le N_s$. Gene expression level generated here will be relatively stable. Therefore these genes could be regarded as housekeeping genes if their expression are high, or un-expressed genes if their expression are low.

Simulation result

In this section we compared the performance of MetaSparseKmeans using equal weight (EW) and unequal weight (UW), and compared metaSparseKmeans with single study sparse K-means result. The tuning parameter for MetaSparseKmeans was selected from gap statistics. For a fair comparison, we selected the tuning parameter in single study such that the number of selected genes are similar to the number in MetaSparseKmeans. We compared the results by adjusted Rand index (Hubert and Arabie, 1985) (ARI) with the underlying truth in each study. The ARIs were averaged over 3 studies. Figure 4(a) shows the performance of three methods for B = 100 simulations and σ₁ = 0.6, 0.8 ~ 3 (error bars represent mean ± standard error). When the biological variation increases, performance of all three methods decreases. MetaSparseKmeans (both EW and UW) outperforms individual analysis. Figure 4(b) shows the performance of three methods when the subtype predictive gene fold change in the largest study f varies: f = 0.8, 0.9 ~ 2 (error bars represent mean ± standard error). When the largest study has stronger signal f > 1, performance of MetaSparseKmeans-UW is better than MetaSparseKmeans-EW. When the largest study has weaker signal f < 1, performance of MetaSparseKmeans-EW is better than MetaSparseKmeans-UW. Figure 4(c) shows a third simulation when the fold change of the confounding impacted genes in the largest study varies: f = 0.8, 0.9 ~ 2 (error bars represent mean ± standard error). When the largest study has strong confounding effect (i.e. heterogeneous compared to other studies) f > 1, MetaSparseKmeans-UW has worse performance than MetaSparseKmeans-EW and can be even worse than individual study clustering. When the studies are more homogeneous f < 1, performance of MetaSparseKmeans-UW is superior.

4.2 Leukemia example

Table 2 shows a summary description of three Leukemia transcriptomic studies: Verhaak (Verhaak et al., 2009), Balgobind (Balgobind et al., 2011), Kohlmann (Kohlmann et al., 2008). We only considered samples from acute myeloid leukemia (AML) with subtype inv(16)(inversions in chromosome 16), t(15;17)(translocations between chromosome 15 and 17), t(8;21)(translocations between chromosome 8 and 21). These three gene-translocation AML subtypes have been wellstudied with different survival, treatment response and prognosis outcomes. We treat these class labels as the underlying truth to evaluate the clustering performance. The expression data for Verhaak, Balgobind ranged from around [3.169, 15.132] while Kohlmann ranged in [0, 1]. All the datasets were downloaded directly from NCBI GEO website. Originally there were 54,613 probe sets and we filtered out probes with 0 standard deviation in any study. In the end 48,788 probes were remained matched across studies. Three gene expression matrices with sample size 89, 74 and 105 were used as input data for disease subtype discovery.

Table 2.

Leukemia dataset information

Study Name	Verhaak at el.	Balgobind at el.	Kohlmann at el.
Number of probes	48,788	48,788	48,788
Number of patients	89	74	105
True class label *	(33, 21, 35)	(27, 19, 28)	(28, 37, 40)
Data range	[4.907, 14.159]	[3.169, 15.132]	[0, 1]
Mean intensity	6.163	6.093	0.309
Standard deviation	1.543	1.334	0.196
Platform	Affymetrix human genome u133 plus 2.0 array

^*: true class labels are the number of samples for (inv(16), t(15:17), t(8,21))

To compare the performance between MetaSparseKmeans and single sparse K-means, we chose μ such that the number of selected probe sets was around 200-300 in each method. Figures 5(a)-5(c) show heatmap of clustering results from each single study sparse K-means. Each study generated three disease subtypes using different intrinsic gene sets, making it difficult to classify future patients with a unified classification rule. Figures 5(d)-5(f) demonstrate heatmap from MetaSparseKmeans clustering using 245 probe sets. We not only obtained a common intrinsic gene set, but also observed clear consistent patterns of the three disease subtypes across the three studies. Table 3 shows the ARI of each clustering result with the underlying leukemia subtype truth. Single study analysis in Verhaak and Kohlmann produced almost perfect clustering (ARI = 0.97 and 0.95) while Balgobind gave a poor ARI = 0.41. The MetaSparseKmeans generated improved ARIs in each study (ARI = 0.97, 1 and 0.95).

Figure 5.

The three figures on top are heatmaps of Leukemia dataset after sparse K-means. The three figures on bottom are results from MetaSparseKmeans.

Table 3.

Comparison between MetaSparseKmeans and sparse K-means on Leukemia dataset

	MSKM	Verhaak	Balgobind	Kohlmann
μ	12	10	10	10
Number of selected probes	245	266	257	218
ARI	0.97/1/0.95	0.97	0.41	0.95

4.3 Breast cancer example

Clustering result and survival association

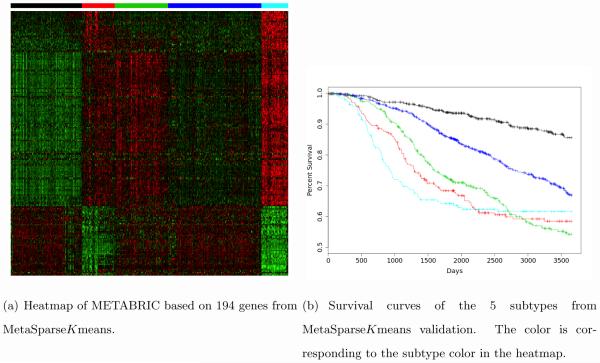
As shown in the motivating example in Figure 1(a)-1(c), single study sparse K-means generated different sets of intrinsic genes. MetaSparseKmeans obtained 203 common intrinsic genes to cluster the patients into five disease subtypes with consistent expression pattern across studies. Since the underlying true cancer subtypes are not available in this example, we applied the models from each method to classify an independent testing cohort METABRIC (Curtis et al., 2012), which contained 1,981 samples from Illumina HT12 arrays. This serves the purpose of extending the training model to a validating dataset. Figure 6(a) shows the subtype prediction patterns from MetaSparseKmeans method. We can clearly see that the resulting expression patterns are consistent with those from three training studies in Figure 1(d)-1(f). The Kaplan-Meier survival curves of the five disease subtypes are well-separated with p-value 3.79 × 10⁻²⁵ from log-rank test (Figure 6(b)). The survival separation demonstrates high potential of clinical utility of the discovered disease subtypes. Note that although only 194 out of 203 genes appeared in the METABRIC dataset, those genes still had enough power to separate the subtypes. Table 4 shows log-rank p-value of survival separation from each individual sparse K-means classification and PAM50. MetaSparseKmeans generated the best survival separation of the subtypes. PAM50 is currently the most well-accepted transcriptomic subtype definition of breast cancer. We have further compared the clustering results from MetaSparseKmeans and PAM50 in the Appendix and Supplement Table S1

Figure 6.

clinical result of METABRIC dataset

Table 4.

Survival analysis in METABRIC: classification models trained in each single study and combined meta-framework are applied to METABRIC. P-value of survival differences of identified subgroups were evaluated based on log-rank test. The previously published PAM50 model was also compared. The number in () indicates the actual number of genes used in the prediction model since a few genes were not observed in the METABRIC array platform.

Model	Number of Samples	number of selected genes	p value
Meta(TCGA+Wang+Desmedt)	533+260+164	203(194)	3.79 × 10−25
TCGA	533	239(233)	1.46 × 10−19
Wang	260	220(214)	3.31 × 10−14
Desmedt	164	197(193)	7.81 × 10−14
PAM50		50	1.01 × 10−20

Pathway Enrichment

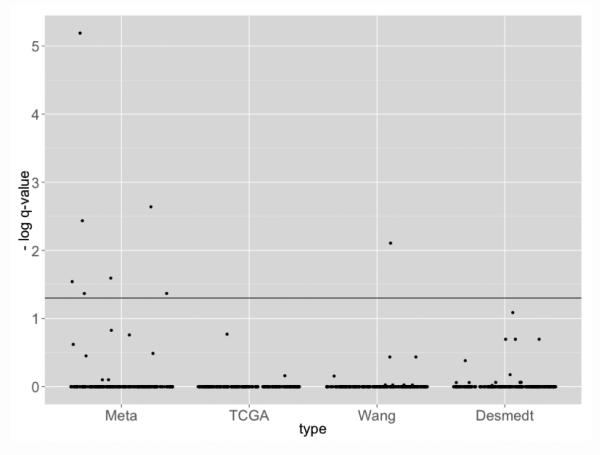
In order to evaluate whether the genes obtained from each model are bio-logically meaningful, pathway enrichment analysis was perform using Fisher’s exact test by testing association of selected intrinsic genes and genes in a particular pathway. We applied the BioCarta Database obtained from MSigDB (http://www.broadinstitute.org/gsea/msigdb/collections.jsp#C2). This database contains 217 curated cancer related pathways and is particularly suited to evaluate the breast cancer example. Figure 7 shows the jitter plot pathway enrichment q-values at log-scale (base 10). The horizontal solid line corresponds to the q = 0.05 significance level threshold. The pathway enrichment result from MetaSparseKmeans yielded more significant pathways than the individual models(7 significant pathway in MetaSparseKmeans versus 1 in individual sparse K-means). All 8 significant pathways are listed in Table 5.

Figure 7.

Pathway enrichment result from four different models (Meta, TCGA, Wang, Desmedt). Clustering from meta-analysis identified intrinsic genes more associated to cancer related pathways.

Table 5.

Eight significant BIOCARTA pathways. The p-values were obtained using Fisher’s exact test based on selected genes from MetaSparseKmeans or individual study clustering and Benjamini-Hochberg correction (Benjamini and Hochberg, 1995) was applied to generate q-values in the table.

Pathway name	MetaSparseKmeans	TCGA	Wang	Desmedt
BIOCARTA SRCRPTP PATHWAY	*0.0255	1	1	1
BIOCARTA MCM PATHWAY	*6.47 × 10−6	1	1	1
BIOCARTA G1 PATHWAY	*0.0427	1	1	1
BIOCARTA G2 PATHWAY	*0.0367	1	1	1
BIOCARTA P27 PATHWAY	*0.0472	1	1	1
BIOCARTA RANMS PATHWAY	*0.0229	1	1	1
BIOCARTA PTC1 PATHWAY	*0.0287	1	1	1
BIOCARTA HER2 PATHWAY	0.149	0.170	*0.0078	0.0817

^*: q-value smaller than 0.05 cutoff

Accuracy and stability analysis

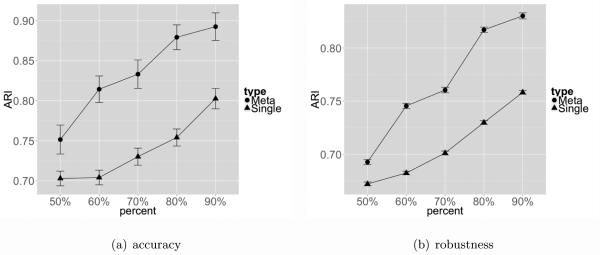
We have performed additional subsampling evaluation on breast cancers studies to evaluate the accuracy and stability of MetaSparseKmeans compared to single study analysis. For accuracy, since TCGA had larger sample size than the other two studies, we randomly subsampled 50%, 60%, 70%, 80%, 90% of samples in TCGA for evaluation. Sparse K-means was applied to the whole TCGA data (n=533) without considering Wang and Desmedt to generate sample clustering C_{T CGA,all} and this result was treated as a pseudo-gold standard. Sparse K-means was then similarly applied to 100 independently subsampled p%(p = 50, 60, 70, 80, 90) TCGA dataset to generate clustering result $C_{TCGA,p\%}^{\left(b\right)}(1\le b\le 100)$. The adjusted Rand index (ARI) was calculated between $C_{TCGA,p\%}^{\left(b\right)}$ and C_{T CGA,all} and the trajectories with error bar (standard error) are shown in Figure 8(a) (blue). Similar analysis was performed for MetaSparseKmeans when the TCGA subtype clustering results were combined with Wang and Desmedt for clustering and the ARI results were shown in red. In this analysis, we used the large sample size of TCGA data to generate the subtype clustering result and treated it as a pseudo-gold standard. The data subsampling represented the situation when sample size was not large and the ARI value represented an indirect evidence of the clustering accuracy. Figure 8(a) demonstrates a clearly better accuracy for MetaSparseKmeans than single study sparse K-means and the increased power evidently comes from the incorporated information from the other two studies, Wang and Desmedt.

Figure 8.

Figure 8(a) compares the accuracy of MetaSparseKmeans and sparse K-means. For sparse K-means we used the TCGA data (n=533) only and for MetaSparseKmeans we combined TCGA, Wang and Desmedt. At each sub-sampling point, ARI was calculated 100 times and averaged. Figure 8(b) compares the stability of MetaSparseKmeans and sparse K-means. At each sub-sampling point, ARI was calculated 4950 times and averaged.

For stability, we performed similar subsampling in TCGA data as before. But instead of comparing to the whole data clustering results, we restricted to all pair-wise comparison of subsampled data. For a given p% subsampling rate, B (B = 100) TCGA subsampled data were generated and sparse K-means were applied to each subsampled dataset. ARIs were calculated for each pair-wise comparison that generated $C_2^{100}=4950$ = 4950 ARIs and the trajectories with error bar (standard error) are shown in Figure 8(b) (blue). Similar analysis for MetaSparseKmeans was performed where Wang and Desmedt were combined with subsampled TCGA data in the subtype clustering (red in Figure 8(b)). The result showed that MetaSparseKmeans generated more stable disease subtype assignments than single study sparse K-means by incorporating information from the other two studies. Note that when comparing two p% subsampled clustering results, only overlapped samples were considered in the ARI calculation.

4.4 Computation time and matching accuracy

To evaluate computation time for the MetaSparseKmeans algorithm using different pattern matching algorithms, we will use the simulation scenario in Section 4.1 with different S, K and σ. We use two criteria to evaluate the accuracy for using different matching algorithms described in Section 3.3: percent of reaching global optimal based on Equation 7b, and the resulting cluster agreement with the underlying truth using ARI. Table 6(a) shows that stepwise and MCMC searching greatly reduced computing time for large S. Even in a large meta-analysis of S = 15 and K = 5, computing time was at 39 and 79 minutes without using any powerful machine or parallel programming. In Table 6(b), we fixed S = 3 and K = 3 and varied biological variance σ = 2, 6 and did 100 simulations for each σ. On the left, the performance of matching score is evaluated by comparing with exhaustive matching score. We observed that stepwise matching sometimes will deviate from the optimal matching, but MCMC (with stepwise initial) can increase the chance to the best matching. On the right, we evaluated the final cluster agreement. We observed that all of the three methods would achieved similar performance. The result demonstrates that MCMC achieves the best balance between computing load and optimization performance. Besides, in our real data examples, all three matching algorithms will yield the same clustering result.

5. DISCUSSION

Disease phenotyping and subtype discovery have received increasing attention since high-throughput experimental data have become more and more affordable and prevalent. In the literature, such modeling is usually performed in a single study and attempts have been made to validate in other studies. As more and more studies of the same disease are available, combining multiple studies for simultaneous subtype clustering is an appealing approach to identify a common set of intrinsic genes and a common model of subtype definition for future prediction. In this paper, we developed a MetaSparseKmeans framework that can achieve this goal. Simulations and applications to leukemia datasets and breast cancer datasets demonstrated improved performance by meta-analysis. We demonstrated a superior accuracy and stability of MetaSparseKmeans compared to individual analysis counterpart in the breast cancer example. We also performed a validation on a large independent METABRIC study which evaluated its potential clinical significance by survival analysis and demonstrated the better pathway association of the identified intrinsic genes with cancer related pathways.

Although MetaSparseKmeans was mainly applied to transcriptomic studies in this paper, it can also be applied to other high-throughput omics data such as methylation, copy number variation, miRNA and proteomics. There are a few potential extensions of MetaSparseKmeans. First of all, the feature selection in sparse K-means ignores prior knowledge or dependence structure between features. For example, if features contain both gene expression and methylation, the interrelationship between multi-omics data may be modeled to improve the analysis and interpretation. Secondly, the gap statistic usually leads to a candidate region with near optimal μ and we selected μ corresponding to less number of features. One may design a penalized gap statistics for which μ could be automatically selected. Thirdly, disease-related genes or pathways may be available in wellstudied diseases. Incorporating these prior biological information may generate more biologically relevant results and is a future direction. Finally, subtypes identified by MetaSparseKmeans do not necessarily guarantee association with clinical outcome (e.g. survival, tumor stage, tumor grade etc). It is possible that less obvious subtypes with important clinical association may be masked by strong subtypes with no clinical importance. A guided clustering approach incorporating prior clinical information may help identify clinically relevant disease subtypes.

MetaSparseKmeans inherits fast computation from K-means algorithms. The stepwise search algorithm and simulated annealing also provide a viable solution to the large searching space of cluster matching when the number of studies is large. In the breast cancer example (K = 5 and S = 3), MetaSparseKmeans took only about 8 minutes for exhaustive search using a regular laptop (CPU 2GHz and 4GB RAM). An R package MetaSparseKmeans is available to perform the analysis.

APPENDIX

Algorithms for simulated annealing

When the number of studies is large, the space to search for matching clusters across studies is not viable with exhaustive search. To maximize the matching objective Equation 7b, denoted as π(M), we applied simulated annealing, a stochastic optimization algorithm for non-convex function (Kirkpatrick et al., 1983). Our configuration space is defined as a matching matrix, where the columns correspond to the studies, and the rows correspond to the matched clusters. For example, if the first row of 3 studies is (1,2,1), that means the first cluster of 1^st study, second cluster of 2^nd study and first cluster of 3^rd study are matched as one disease subtype. Also denote 0 ≤ β ≤ 1 as the temperature cooling coefficient and α_i as the acceptance rate at temperature T_i, which is defined as:

$${\alpha }_i=\frac{\text{total}\text{number}\text{of}\text{acceptance}}{\text{total}\text{number}\text{of}\text{simulated}\text{annealing}\text{steps}}$$

at each temperature. β will decide how slow the temperature T decreases and balance between the accuracy of the result and computation speed. η is the acceptance threshold which decides when the algorithm stops.

The simulated annealing is conducted in the following steps:

1. Start with a high temperature T_i(i = 1).

2. At temperature T_i (one simulated annealing step), we perturb the configuration space by randomly choosing two elements in the cluster matching enumeration M from two studies and switch their positions, then calculate the new target value π(M ^new). Accept the new configuration with probability:

   $$P_{acc}=\text{min}\left(1,\text{exp}(-\frac{\pi \left(M^{new}\right)-\pi \left(M^{old}\right)}{T})\right)$$

   This procedure will be repeated N times (MC steps).

3. Set T_i+1 = T_i × β

4. Repeat Step 2-3 until α_i < η,

In our analysis, we used the MC steps N = 300 at each temperature T_i. The temperature decreasing rate β is 0.9. The simulated annealing stops when the acceptance ratio drops below η = 0.1 or the total simulated annealing steps exceed 10, 000. The initial temperature T₁ is set as the objective function value of the initial configuration. In case the initial temperature is too high which result in a high acceptance ratio, we multiply the temperature with β = 0.7 whenever the acceptance rate α_i > 0.5. This will accelerate the convergent rate at initial steps when the acceptance rate is high.

Comparing MetaSparseKmeans clusters and PAM50 clusters on METABRIC dataset

PAM50 is currently the most popular transcriptomic subtype definition of breast cancer. The model consists of 50 intrinsic genes to predict the five subtypes of breast cancer. Among these 50 genes, 42 appeared in the METABRIC dataset and among these 42 genes, 22 overlapped with 194 genes selected by our MetaSparseKmeans result (Fisher’s exact test p-value for overlap enrichment < 2.2× 10⁻¹⁶). Supplementary Table S1 shows a full comparison of the two clustering results by PAM50 and MetaSparseKmeans. There are significant similarity but also discrepancy between the two. Since no underlying truth is known in such a real application, it is difficult to judge which one is better (although MetaSparseKmeans generated smaller p-value of survival difference of the subtypes). Conceptually, PAM50 is a supervised machine learning result that utilizes class labels determines by many past studies with prior biological knowledge. On the other hand, MetaSparseKmeans is a pure in silico clustering approach.