Multi-site study of diffusion metric variability: effects of site, vendor, field strength, and echo time on regions-of-interest and histogram-bin analyses

Abstract

It is now common for magnetic-resonance-imaging (MRI) based multi-site trials to include diffusion-weighted imaging (DWI) as part of the protocol. It is also common for these sites to possess MR scanners of different manufacturers, different software and hardware, and different software licenses. These differences mean that scanners may not be able to acquire data with the same number of gradient amplitude values and number of available gradient directions. Variability can also occur in achievable b-values and minimum echo times. The challenge of a multi-site study then, is to create a common protocol by understanding and then minimizing the effects of scanner variability and identifying reliable and accurate diffusion metrics. This study describes the effect of site, scanner vendor, field strength, and TE on two diffusion metrics: the first moment of the diffusion tensor field (mean diffusivity, MD), and the fractional anisotropy (FA) using two common analyses (region-of-interest and mean-bin value of whole brain histograms). The goal of the study was to identify sources of variability in diffusion-sensitized imaging and their influence on commonly reported metrics. The results demonstrate that the site, vendor, field strength, and echo time all contribute to variability in FA and MD, though to different extent. We conclude that characterization of the variability of DTI metrics due to site, vendor, field strength, and echo time is a worthwhile step in the construction of multi-center trials.

1. INTRODUCTION

As multi-site imaging studies become more common, it becomes imperative that methods are developed to both determine the sources of variability in MRI measurements as well as to quantitatively compare imaging metrics across site. This is especially important for diffusion MRI measurements in which changes in quantitative diffusion metric values are used to detect pathology. It is also of great interest to understand how the variability in the metric values depends upon the amount of data acquired. This paper explores a commonly-used method (comparison of mean region-of-interest metric values for selected regions¹) as well as a newer method² that uses histograms of metric from ROIs and from the whole brain, extended to the multi-site scenario.

Multi-site investigations of diffusion metric reproducibility have previously been reported. Cercignani et al.³ studied the inter-scanner and inter-sequence effects on FA and MD whole-brain histograms at 1.5T. They used histogram peak height, peak position, and mean value of both FA and MD as their histogram metrics. Data on another set of subjects were acquired twice on the same scanner to look at inter-subject reliability. Pfefferbaum et al.⁴, scanned subjects a total of three times on two different scanners made by the same vendor and determined the inter-scanner and within-subject variability using a voxel-by-voxel analysis of supratentorial brain, a slice-by-slice analysis of supratentorial white-matter slice profile and a ROI analysis of the corpus callosum. Vollmar et al.⁵ studied inter- and intra-site variability of FA on two scanners in both ROIs, as well as along tracts defined using probabilistic tractography at 3.0T. Bonekamp et al.⁶ evaluated intra-rater, inter-rater, and inter-scan reproducibility of the ADC and FA in healthy children at 1.5 T, using a ROI analysis. Pagani et al.⁷ studied the effects of site and scanner on FA, axial (D_ax), radial (D_rad), and MD using both ROIs and histograms. Protocols were harmonized as closely as possible to a standard protocol at eight different sites. The sites differed in scanner model, manufacturer (Siemens and Philips), and magnetic field strength (1.5T and 3.0T). . Takao, et al.⁸ showed the significant effect of scanner on axial (AD), radial diffusivity (RD), FA in longitudinal DTI studies using DTI data of 224 normal subjects acquired in two 3T scanners of the exact same model. Using an analysis-of-variance analysis, their work indicated that inter-scanner variability and scanner upgrade can significantly influence DTI metrics. Magnotta et al.⁹ scanned five healthy subjects in eight different scanners (5 Siemens and 3 Philips) comparing two separate protocols (using both vendor-supplied and independent gradient direction tables). And finally, Fox et al.¹⁰ scanned two healthy subjects on three Siemens and two GE scanners, with a matched 33-gradient direction pulse sequence. Sixteen white and gray matter ROIs were drawn on a single image set and mean FA, ADC, and longitudinal and transverse diffusivities were calculated for each ROI.

The effect of TE on DTI metrics has been investigated by Qin et al.¹¹ in a single-site study using rhesus monkeys. Both 1.5T and 3.0T scanners were used. The FA, MD, primary (λ₁), and transverse eigenvalues (λ₂₃) were measured in a ROI at the bilateral internal capsule and compared at each of the field strengths. For human brain, Chou et al.¹² investigated the effects of TE and b-value on the reproducibility and accuracy of DTI metrics at 1.5T. Five-repeated DTI data sets were acquired on a single subject in a single site using five different TEs and six different b-values. They noticed that the axial (AD), radial diffusivity (RD), MD, FA, and principal eigenvector (PEV) in both gray and white matter tissues were significantly affected by both TE and b-value.

In this study, we collected DWI data at five sites representing three vendors. We performed several analyses to characterize the variability in each and to thereby determine a reliable method for characterizing DWI metrics that arose from different sites, scanners and TE values. We also investigated the reliability of data when the number of diffusion-sensitizing gradient directions was varied. The goals of this study were:

• 1) to establish the variability of FA and MD values using ROI analysis of a specific set of brain structures that represent the full range of possible FA values (0 – 1.0) and to determine whether these result depends upon vendor, site, field strength or TE. The amount of data used in the metric calculation (number of data sets and gradient directions)

• 2) to determine the effects of vendor, site, and certain protocol parameters on the variability of brain FA and MD values over their entire ranges by constructing curves of histogram bin membership versus the amount of data used to calculate the diffusion metrics. Comparisons were then made between site, vendor, field strength, and TE value (within one site),

To address each of the above goals, we acquired 10 sets of DWI data with 30 gradient directions per subject. We then sub-sampled each set to a given number of gradient directions (6, 10, 15,) an created sets of increasing number of DWI volumes (set 1; sets 1,2; sets 1,2 and 3, … sets 1,2,3,…10) for each number of sub-sampled gradient direction. In this way, the effects of not only site, vendor, field strength, and echo time, but also in the number of gradient directions and amount of data can be calculated.

2. Methods

2.1 Imaging

All scanners had field strengths of 3.0T, except for a single Philips 1.5T scanner. Three scanner vendors were represented: Siemens (2 sites – Massachusetts General Hospital, UC-Irvine), GE (1 site - Duke), and Philips (2 sites – Johns Hopkins School of Medicine, UT Southwestern Medical Center, Dallas, 1.5T).

Ten DTI scans were performed on each subject during the scan session. Each scan consisted of 30 isotropic diffusion-weighted directions (DWD) using the Jones30 set of diffusion-weighted directions and 5 b=0 scans. Each 30 b>0 / 5 b=0 set was defined to be one “scan-time unit” (STU) (Landman et al.¹³ call this grouping a “scan time equivalent (STE)”); we choose a different nomenclature to emphasize the use of 1 STU as the unit of data used to calculate the tensor metrics). The pulse sequence used was a spin-echo Stejskal-Tanner sequence with echo-planar readout. Therefore no compensation for the eddy currents generated by the diffusion gradients was provided by the sequence. The sequences chosen were the standard vendor supplied sequences. Other protocol parameters include: b-value of 1000 s/mm2, 2.5 mm3 isotropic voxels, acquisition matrix size: 96 × 96, full k-space coverage, FOV: 240 × 240 mm, slice thickness: 2.5 mm, number of slices: 25, parallel imaging: SENSE (p = 2) for Philips, GRAPPA for Siemens and ASSET for GE, 1 signal average for each volume. TR/TE (ms) values were: Siemens = 4000/98 (MGH), 3800/98 (UCI); GE = 5200/69.8 and 4000/99.5 (Duke); Philips = 4000/101.2 (Dallas), 4000/100.0 (JHU).The achievable TR/TE is dictated by the achievable duty cycle of the scanner and the maximum gradient strength; the slight variations seen here were not expected to affect the results. Each scan was roughly 2:30 (except for the short TE sequence on the GE scanner) so the entire protocol could be completed in less than a half an hour.

2.2 Tensor Calculation

As noted above, data sets with different numbers of STU were constructed by concatenating a sequentially increasing number of data sets together before calculation of the tensors and associated metrics, i.e., data set 1 (STU=1), data set 1 and 2 (STU=2), et cetera. Each frame within the concatenated data set was registered to the first b=0 frame using a 12 degree-of-freedom registration code (FLIRT, FSL, University of Oxford). Tensors and the tensor metrics FA and MD were calculated using in-house code written in C. Noise and skull voxels were removed using a combination of Brain Extraction Tool (FSL, University of Oxford) and in-house code written in IDL (ITT-VIS, Boulder, CO, USA) to produce brain-only maps.

Sub-sampling of the gradient directions was performed by in-house code written in Matlab (Mathworks, Natick, MA, USA) using the Jones30 data as the set from which to select the smaller number of samples. Samples were made of 15, 10, and 6 directions by choosing the directions in the Jones30 set that most closely corresponded with separations that would be obtained using an electrostatic model. This same Matlab code calculated the bin mean values and created the whole brain histograms (described below).

3. Data Analysis

3.1 Contrasts

Three different vendors are represented (Siemens, GE, and Philips), two field strengths (1.5T and 3.0T), and two different echo times (TE = 69.8 ms and 99.5 ms, for the GE site at a single field strength, 3.0T). From these data, comparisons could be made across vendors (at the same field strength and TE, different sites), across field strengths (same vendor and TE, different sites), and across TE value (same vendor, site, and field strength). The full set of 11 contrasts are listed in Table 1.

Table 1.

Table of contrasts designed into this study. The contrasts are site, vendor, field strength and echo time (TE). “GEL” and GES” stand for the long and short TE values, respectively, acquired from the GE scanner. Sites are labeled by number or field strength if applicable, e.g., “SM1” refers to the first Siemens site and “PH3.0” refers to the Philips 3.0T scanner.

Site(s)	Vendor(s)	Field Strength (T)	TE (ms)	Comparison
SM1/ SM2	Siemens	3.0	98	site
PH3.0 / PH1.5	Philips	3.0 / 1.5	100.0 / 101.2	site, field strength
GES / GEL	GE	3.0	69.8 / 99.5	TE
SM1 / GEL SM2 / GEL	Siemens / GE	3.0	98 /99.5	site, vendor
PH3.0 / GEL	Philips / GE	3.0	99.5	site, vendor
SM1 / PH3.0 SM2 / PH3.0	Siemens / Philips	3.0	98 / 100.0	site, vendor
GES/ PH3.0	Philips / GE	3.0	69.8 / 101.2	site, vendor, TE
GES/ SM1 GES/ PH3.0	Siemens / GE	3.0	69.8 / 98 69.8 / 100.0	site, vendor, TE
SM1 / PH1.5 SM2 / PH1.5	Siemens / Philips	3.0 / 1.5	98 / 101.2 98 / 101.2	site, vendor, field strength
GES/ PH1.5	Philips / GE	3.0 / 1.5	69.8 / 101.2 ms	site, vendor, field strength
GEL/ PH1.5	Philips / GE	3.0 / 1.5	99.5 /101.2	site, vendor, field strength

3.2 Region-of-Interest Analysis

Regions-of-interest used in the present study were taken from Farrell et al.², which were chosen to cover the full range of possible FA values. ROI were manually defined in the putamen, globus pallidus, centrum semiovale, internal capsule, and splenium of the corpus callosum. ROI were manually defined on slices of the STU=10 FA maps for each subject, using the entire FA volume as a reference where necessary. ROI’s were then applied to each FA map calculated from data with increasing STU values (STU = 1-10). Statistical measures (mean and standard deviation) were calculated for each ROI in each FA map using in-house code written in IDL (ITT-VIS, Boulder, CO, USA). The same ROI was then applied to the corresponding MD map and the mean and standard deviation of the MD values in the ROI were also calculated. Therefore, for each comparison in table, a mean and standard deviation were calculated for each of 6 ROIs and 10 STU values resulting in a total of 60 values. These data were plotted as mean metric (FA or MD) versus STU number for each site, TE, or field strength as well as number of gradient directions. F-tests were then performed for each comparison in Table 1 between the ROI metric value distributions for each. An example of the results for the F-test are shown in Table 2. This analysis was performed only with metric maps calculated from the full 30 gradient direction data sets.

Table 2.

An example of p-value tables used to determine the significance of a comparison for different STU for FA data in six different ROI. The ROI are internal capsule (IC), frontal white matter (FW), centrum semiovale (CS), globus pallidus (GP), putamen (Put), and the splenium of the corpus callosum (SCC). This comparison is between scans on the same GE 3.0T scanner at two different TE values. Significant differences (p <0.05) are shaded in grey. The number of STU is on the horizontal axis and the ROI identity is represented on the vertical axis.

	STU	1	2	3	4	5	6	7	8	9	10
ROI	IC	2.2 × 10−4	6.1 × 10−5	3.7 × 10−5	5.9 × 10−5	9.7 × 10−5	7.6 × 10−5	9.0 × 10−5	6.4 × 10−5	4.5 × 10−5	5.6 × 10−5
	FW	0.51	0.56	0.62	0.59	0.59	0.51	0.50	0.57	0.59	0.57
	CS	0.12	0.087	0.13	0.14	0.14	0.18	0.19	0.22	0.22	0.23
	GP	9.1 × 10−3	3.5 × 10−3	0.14	0.79	0.94	0.79	0.61	0.40	0.35	0.32
	Put	0.028	0.086	0.19	0.37	0.39	0.41	0.46	0.44	0.37	0.31
	SCC	3.9 × 10−4	1.0 × 10−3	1.8 × 10−3	1.5 × 10−3	1.1 × 10−3	9.1 × 10−4	8.1 × 10−4	7.3 × 10−4	8.1 × 10−4	1.0 × 10−3

In addition, to compare the variation between ROI results for FA and MD, we calculated the inter-site correlation coefficient (ICC) defined by

$$ICC=\frac{{\sigma }_{BS}^2}{{\sigma }_{BS}^2+{\sigma }_{WS}^2},$$ (1)

where σ² is the standard deviation of either the between site (BS) or within site (WS) metric values.

3.3 Histogram Bin Analysis

Bin analysis was used to investigate how the mean and standard deviation of the bin FA and MD values changed for the various comparisons as the amount of data used to calculate the diffusion metrics gradient was varied. Whole-brain FA histograms were calculated from the Jones30 data sets and binned into 10, 0.1-wide bins over the range of FA values (0.0⁺ to 1.0); the mean FA value was calculated for each bin range at each STU. Histograms of MD were sorted into 21 bins: 1) values less than 0.0002 mm2/s, 2) between the values of 0.0002 mm2/s and 0.0040 mm2/s in 0.0002 mm2/s increments, and 3) values greater than 0.0040 mm2/s. The mean and standard deviation of the FA and MD values were calculated for each bin at each STU level. The STU=10 FA data set, calculated using all 10 co-registered runs, was used as a “gold standard” to identify the bin-range membership of each brain voxel. The corresponding bin means were then calculated at each of the other STU values using the same voxel sets for each STU. The bin memberships, defined using FA, were then applied to the MD data, i.e., the pixels that were assigned to a certain bin by their FA value at STU = 10 were also grouped together for the MD analysis. Therefore, even if a voxel’s value changes when the number of STU or gradient values are varied (see below), its value was used in the calculation of its original bin. This analysis gives estimates for the effect on the FA and the corresponding MD histograms of decreasing the amount of data used in the tensor calculation.

The same bin-mean vs. STU analysis was repeated on the sub-sampled data to determine the effect of reducing the number of gradient directions on the reproducibility of the FA and MD values as the number of STU was changed. Thus five samples, one for each subject, were generated for each site (two 5-subject samples for the GE site that used two different TE values). Each set of bin-mean samples at each STU value were compared using the F-test for the equivalence of mean values to those for the other comparisons (vendor, site, field strength, TE), generating an F-statistic and p-value for each comparison. There were, therefore, 100 total F-statistic and p-values for each FA comparison (10 bins × 10 STU). The bins with the lowest MD values and the top two bins exhibited large changes in mean due to the low frequency in those bins and so their data were not included in the final analysis. Therefore, there were 180 total (18 bins × 10 STU) F-statistic and p-value comparisons for each MD comparison. The number of SSD were tabulated for each subject and comparison, and the mean ± standard deviation were calculated for each comparison.

4. Results

4.1 Region-of-Interest Analysis

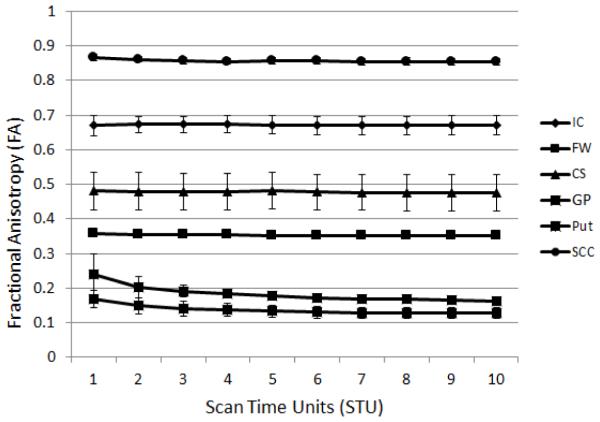
Mean FA and MD values were calculated at each STU value for the 5 subjects scanned at each site. An example of the resulting data is shown in Fig. 1 where it can be seen that a) the ROI FA values cover well the full range of possible FA values and b) the resulting means for low FA structures show a dependence upon the STU value. The corresponding data for MD is shown in Fig. 2. MD values for all sites fell within reported ranges¹⁴.

Figure 1.

An example plot of the mean FA values vs. STU for the six different ROI for a single site, in this case GE scanner, TE=99.5ms. Each data point represents the mean of the ROI data from 5 subjects at that site. The ROIs are internal capsule (IC), frontal white matter (FW), centrum semiovale (CS), globus pallidus (GP), putamen (Put), and the splenium of the corpus callosum (SCC).Contrasts between the distribution of ROI FA and MD values for each condition were calculated for all of the contrasts in Table 1. An example of the resulting p-values for a single contrast is show in Table 2.

Figure 2.

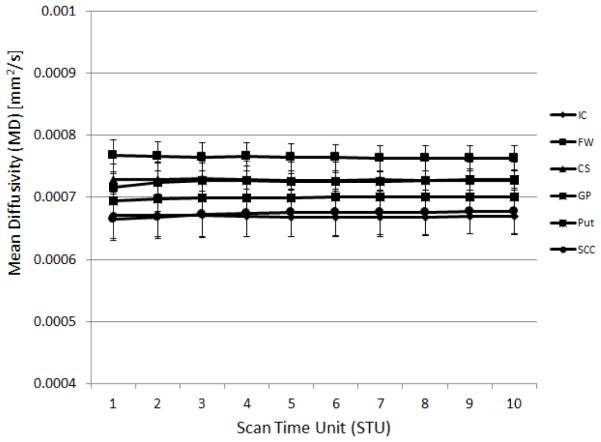
An example plot of the mean MD values vs. STU for the six different ROI for a single site, in this case GE scanner, TE=99.5ms. Each data point represents the mean of the ROI data from 5 subjects at that site. The ROIs are internal capsule (IC), frontal white matter (FW), centrum semiovale (CS), globus pallidus (GP), putamen (Put), and the splenium of the corpus callosum (SCC).

For each of the 60 ROI-STU combinations within each comparison, the F-statistic and corresponding p-value were calculated to determine statistically-significant differences (SSD). An example of the results of one such comparison is shown in Table 2, for the comparison of the GE scanner with data taken at two different TE values. Cells containing p-values, p < 0.05 are shaded grey.

We repeated these calculations for each contrast listed in Table 1. The number of SSD for each ROI were tabulated and the mean (± standard deviation), calculated both across all ROIs and across all contrasts.

The FA results show consistent differences in SSDs for specific ROIs, though there is also evidence of weak, but consistent, differences due to the set of contrasts explored here.The ranking of ROI from greatest to least number of SSD is: IC, SCC, GP, Put, FW, CS. Across the comparisons we find the ranking of SSD to be (from least effect to greatest): 1) the vendor is the same, but the site is different, 2) field strengths are different (vendor can be same or different), 3) site and vendor are different, but field strength is the same, 4) different vendor, TE, and field strength, and 5) TE and vendor is different.

In the MD results, there is evidence that specific ROI and specific contrasts again show consistent differences. The ranking of ROI from greatest to least number of SSD is: FW, CS, IC, SCC, Put, and GP. Across the comparisons we find the ranking of SSD to be (from least effect to greatest): 1) the vendor is the same, but the site is different, 2) site and vendor are different, but field strength is the same, 3) field strengths are different (vendor can be same or different), 4) different vendor, TE, and field strength, and 5) TE and vendor is different.

In addition we characterized the variability of ROI FA and MD using the inter-site correlation coefficient (ICC), defined in Eq. 1 that here measures the relative magnitude of the between- and within-site variability. In general, the variability in ICC coefficients is greater in MD than with FA. For FA, four of the six ROIs have ICCs that are around 0.5 over the full range of STU values (SCC, GP, FW, and CS). The Put ICC data are widely variable, and the IC ICC was constant around a value of 0.7. The site-effect for the SCC ICC was the smallest out of all the ROI.

4.2 Histogram Bin Analysis

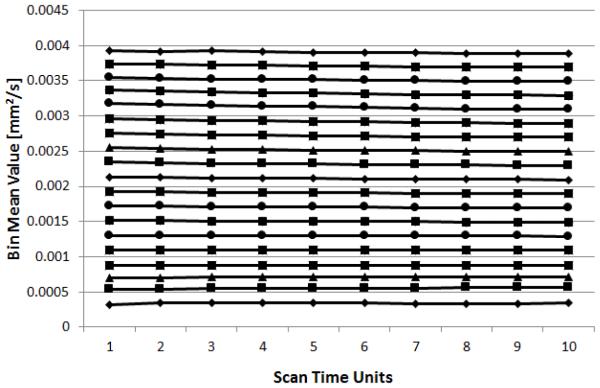
For the histogram bin analysis, the whole brain histograms were binned as detailed above and the percentage of histogram bin mean SSD for all the contrasts and each of the different gradient subsamplings, were calculated. The results were then evaluated for both the mean percentage of SSD and the effect of decreasing the number of gradient directions. An example of the analysis for GE site at TE = 99.5ms is shown in Fig. 3.

Figure 3.

An example plot of the mean MD values vs. STU for the whole-brain histogram analysis for a single site, in this case GE scanner, TE=99.5ms. Each data point represents the mean of the MD values for voxels who were members of the bin for the STU=10 data.

Several trends were observed in the FA data. They are:

• 1) For the same vendor, but different site, the percentages of SSD are negligible for all gradient subsamplings, showing that the effect of site in this case is small.

• 2) For different vendors and sites, but the same field strength and TE, there is generally a constant percentage of SSD for a given comparison across gradient subsamplings. The percentage of SSD, however are different between different vendors. The largest percentage of SSD is between Siemens and Philips. The percentages of SSD between Siemens and GE sites are comparable to those observed between the two Siemens sites, i.e., in this case the vendor and site effect is comparable to the site effect.

• 3) Decreasing the number of gradient directions used in the calculation of the tensors increased the percentage of SSD in the case where the two sites had different field strengths, but the same TE. The percentage of SSD ranged from 33 ± 9 to 47 ± 12.

• 4) For the case in which the TE was different between the two sites, a roughly constant percentage of SSD were observed for all gradient subsamplings. The percentage of SSD was large however, 42 ± 4, when the site was the same and ranged from 27 ± 2 to 63 ± 3 when the sites were different.

• 5) The largest percentage of SSD observed was in the case in which the site, vendor, TE, and field strength was different (70 ± 5).

Similar trends were observed in the MD data as well:

• 1) The MD data exhibited a smaller range of observed SSD for the different comparisons (from 7 ± 2 to 41 ± 8; total possible SSD = 190) than did the FA data (from 2 ±1 to 70 ± 5; total possible SSD = 100).

• 2) For the same vendor, but different site, the percent of SSD are negligible for all gradient subsamplings, showing that the effect of site in this case is small.

• 3) For different vendors and sites, but the same field strength and TE, there is a generally constant percent of SSD for a given comparison across gradient subsamplings. The percentage of SSD, however are different between different vendors. The largest percentage of SSD is between Siemens and Philips. The percentages of SSD between Siemens and GE sites and between GE and Philips are the same and roughly constant across subsampling.

• 4) Decreasing the number of gradient directions used in the calculation of the tensors increased the percentage of SSD in the case where the two sites had different field strengths, but the same TE. The percentage of SSD ranged from 10 ± 4 to 41 ± 8.

• 5) For the case in which the TE was different between the two sites, a roughly constant percentage of SSD were observed for all gradient subsamplings. The percentage of MD SSD was smaller than in the FA case however, 16.1 ± 0.8, when the site was the same and ranged from 27 ± 2 to 63 ± 3 when the sites were different.

5. Conclusions

The overall goal of this work was to investigate and characterize two methods for measuring variability in imaging experiments. Here we have presented methods of measuring FA and MD variability in DW imaging experiments based on regions-of-interest and whole brain histograms, discussing the merits and drawbacks of each. In general, the FA is more useful as a metric since the range of variation over different brain tissue types and structures is greater than that for MD. However, we have observed variation in MD values in all of the contrasts explored here.

Generally, the ROI method suffers from the difficulty of identifying specific regions-of-interest of small, internal structures in the face of variation in brain orientation and slice placement. The problem of inter-rate variability with this method has been documented elsewhere. It is useful, however, in that the variability of specific structures of interest in a given disease can be investigated.

The bin-mean analysis method has the advantage that structures do not need to be visually identified and manually outline. If their FA is known from previous work, this method can provide guidance on the amount of data needed for an accurate measurement of the derived parameters. This method observed a known bias for small FA values at low STU. In addition, it provides a method for comparing, at a known STU, the variability for a given FA across the full range of possible FA values.

In order of effect size, echo time (TE), field strength, and vendor, had the greatest variability effect. Data collected at the two sites with the same magnet and software version (SM1/SM2) were virtually identical in all comparisons characterized here showed that site alone has little effect on diffusion metrics.