Abstract
Criticality reportedly describes brain dynamics. The main critical feature is the presence of scale-free neural avalanches, whose auto-organization is determined by a critical branching ratio of neural-excitation spreading. Other features, directly associated to second-order phase transitions, are: (i) scale-free-network topology of functional connectivity, stemming from suprathreshold pairwise correlations, superimposable, in waking brain activity, with that of ferromagnets at Curie temperature; (ii) temporal long-range memory associated to renewal intermittency driven by abrupt fluctuations in the order parameters, detectable in human brain via spatially distributed phase or amplitude changes in EEG activity. Herein we study intermittent events, extracted from 29 night EEG recordings, including presleep wakefulness and all phases of sleep, where different levels of mentation and consciousness are present. We show that while critical avalanching is unchanged, at least qualitatively, intermittency and functional connectivity, present during conscious phases (wakefulness and REM sleep), break down during both shallow and deep non-REM sleep. We provide a theory for fragmentation-induced intermittency breakdown and suggest that the main difference between conscious and unconscious states resides in the backwards causation, namely on the constraints that the emerging properties at large scale induce to the lower scales. In particular, while in conscious states this backwards causation induces a critical slowing down, preserving spatiotemporal correlations, in dreamless sleep we see a self-organized maintenance of moduli working in parallel. Critical avalanches are still present, and establish transient auto-organization, whose enhanced fluctuations are able to trigger sleep-protecting mechanisms that reinstate parallel activity. The plausible role of critical avalanches in dreamless sleep is to provide a rapid recovery of consciousness, if stimuli are highly arousing.
I. Introduction
Consciousness is a product of brain activity, but, paradoxically, it is maintained stable when the activity itself is not stationary [1]. Conversely, physiological breakdown of consciousness is associated with sleep phases whose recorded brain activity (e.g., via EEG) is stationary or quasistationary. Can this neurophysiological paradox be settled using the notion of second-order phase transitions [2]? Systems undergoing these transitions do indeed possess a stable feature, i.e., a correlated giant cluster among the system’s many components, when the system is affected by fluctuations at all scales (critical point). Brain criticality during awake resting state has been envisaged by both the neuroscience and the complexity-science communities [3,4], and this hypothesis has been corroborated by the finding of critical avalanches [5], i.e., domino-like cascades of neural firings, with scale-free properties in terms of the number of neurons involved. Neural avalanches, namely excitations spreading among neurons, resemble the sand-pile model of self-organized criticality (SOC) [6]; however, current models predict avalanches as a phase transition between excitation quenching and excitation explosion, at a critical “branching ratio” ρ = 1 (see, e.g., the work of Vespignani and Zapperi [7]), where ρ is the control parameter associated to the sum over the nearest neighbors in a network of the probabilities that an excitation spreads there. Another remarkable finding is the scale-free structure of brain functional connectivity [8], with a remarkable coincidence with criticality models: functional magnetic resonance imaging (fMRI) of brain activity and a Montecarlo of the Ising model for ferromagnetism at the Curie temperature share the same network topology for suprathreshold voxel-voxel (or spin-spin) pairwise correlation network.
At a critical point we have the presence of circular causation among different structure and time scales, leading to rescaling relations, that reduce the many degrees of freedom into well orchestrated dynamics of the order parameter. The causation is circular because while auto-organization moves from the lower to the higher scales (onward causation), the emerging modes impose constraints on the lower ones (backwards causation). This hierarchical interplay intuitively explains the fractal properties of the renormalization group relations. This fractal, integrated, unitary dynamics, fits the fringe-focus, low-information, serial properties of consciousness [9]. Furthermore, criticality means infinite susceptibility, i.e., a large response to stimuli, hence responsiveness. This is ultimately caused by the exploitation of long-range correlations already present in absence of external fields [2]. This, in turn, reflects extended dynamical coherence of the local order parameter, that, at any time, spans a large portion of the system. This ever-changing emergent mode is the aforementioned giant cluster [10].
Can this latter property be associated to the global workspace [11], the commonly adopted heuristics for consciousness? The global workspace is commonly described as a serial function selecting information out of massively parallel activity. A positive answer to the posed question is suggested by some fairly recent papers [12] that proved that order-parameter fluctuation dynamics affecting the critical giant cluster obey Type-I intermittency [12], i.e., a serial process with power-law-tailed waiting-time distributions between crucial events [13]. A fractal renewal process, namely the stochastic counterpart of Type-I intermittency, was recently reported by our group for human EEG resting-state wakefulness activity [14].
Many authors have identified in sleep the principal function to study, to understand consciousness. Indeed, dreamless sleep is the only physiological state characterized by unconsciousness, and therefore neural correlates of consciousness (NCC) must be absent there. The aim of this paper, focusing on some differences in critical features between conscious and unconscious states, is to provide a heuristics that connects criticality and consciousness. In other words, studying whether and how critical features can be considered NCCs, and how they break during dreamless sleep will also clarify some aspect on brain criticality during wakefulness. Thus, we will focus on the differences between conscious states, namely wakefulness and REM sleep (by consensus a phase where most conscious dreaming occurs) on the one side, and unconscious non-REM (NREM) sleep, both the shallow-sleep N2 phase and the deep-sleep N3, on the other side.
Seriality, hence criticality, seems to break during NREM sleep. Recent studies have shown parallel modularity in NREM sleep with respect to wakefulness or REM sleep [15,16]. Nevertheless, the situation is not so clear: studies on fMRI and EEG data have recently shown that long-range moduli or pathways are maintained from wakefulness to NREM sleep. These structures include traveling neural activity in response to sensory stimuli [17], local and global scale-free avalanches [16,18], and fMRI default modes [19]. Therefore, the brain, admittedly a critical system in awake resting state, cannot be simply represented, during sleep, via increase or decrease of some control parameter, i.e., by a drift from the critical to a subcritical or to a supercritical regime. This explanation would not be compatible, in the supercritical hypothesis, with the presence of NREM parallel activity, or, in the subcritical case, with long-range connections or critical avalanches.
In addition, the precise fine tuning required by a second-order phase transition has been questioned, and proposed solutions either rest on an order-parameter feedback onto control parameter (a common explanation of SOC) or on a critical-point stretching, due to brain-architecture-based quenched disorder [20]. Finally, a recent paper connects the two aforementioned approaches of SOC and envisages some feedback by which wakefulness brain activity avoids branching-process criticality, posing itself on a slightly subcritical regime very close to the critical one [21]. It is, however, known that critical features (anomalous diffusion, critical slowing down, double-scale relaxation, weak ergodicity breakdown, non-Gaussian behavior) are typical of pericritical states (either slightly sub- or supercritical), also in more complex thermodynamical conditions like glass transitions and turbulence.
A recent alternative approach consists in focusing on dynamical criticality instead of statistical criticality. The authors of Ref. [22] have shown that the dynamical model resulting from a linear regression of multichannel data in monkeys display vicinity of bifurcation points only during wakefulness, with identical enhancement of dynamical stability in two kinds of anesthetics that otherwise produce opposite spectral modifications. Although the presence of marginal stability is connected with statistical criticality [12], this connection is still unclear [23].
Here we do not attempt a theory for brain criticality, and we do not even clarify in which sense brain is critical, supercritical, or subcritical during conscious or unconscious states. We try, however, to focus on the differences between onward and backwards causation, the former being a mechanism for auto-organization and complexity emergence, the other for critical slowing down and for maintenance of global (meta)stability. Both these properties are possibly present in both conscious and unconscious states, with, we conjecture, differences mainly in the backwards causation process.
We adopt the following perspective to describe sleep unconsciousness [16]: The different milieu of neurotransmitters in NREM sleep may not change the local complex, supposedly critical, thermodynamical behavior, by a change in the control parameter, but with some mechanism that protects parallel activity in segregated moduli. One of these mechanisms is the well-known phenomenon of evoked neural bistability (very large deflections in the EEG signal called evoked K-complexes): The same spreading (avalanching) excitations, that in wakefulness would result in consciousness, trigger, during sleep, a massive neural reset, i.e., a fall of many neurons in an hyperpolarized state (electrical silence), abolishing any synaptic and network activity [17,24]. The K-complex phenomenon, caused by the opening of some K+ channels, is more general and can take place spontaneously, i.e., without a precise stimulus triggering. Such neural hyperpolarization, lasting a few hundreds of milliseconds, is at the basis of all NREM low-frequency (<1 Hz) activity, termed sleep slow oscillation. Remarkably, the occurrence of such oscillation is regularly preceded by integrative cortical excitations [24]. As a result, auto-organization caused by synaptic communication can take place at a local level, and even spread to larger territories, but cannot be globally maintained. The presence of possibly conflicting independent mentations, may not be compatible with a unitary scene or gestalt.
In this paper we prove that hypothesizing some mechanism that keeps brain activity fragmented when the fluctuations are high (a signal of a serial giant cluster emerging) explains the differences that we find in critical features when passing from wakefulness or dreaming (REM sleep) to NREM sleep. The outline of the paper is as follows. In Sec. II we review how intermittency can be tested, in particular how the corresponding metastability suggests the identification of temporal point processes (events) and how these events can be used to unravel temporal long-range correlations. We will confirm that intermittency is lost in NREM sleep, and complete the analysis of our research group, providing results for shallow sleep. We will then show how fragmentation, correlated to neural bistability, is able to explain the reported results. In Sec. III we will shift focus from temporal to functional complexity. We will review already-reported results on fractal clusters and avalanches that, although a critical feature, fail in being a consciousness correlate. We will then define, starting from events, a functional connectivity based on extended-time-window cross-correlations and describe it as a NCC. Section IV is devoted to a final discussion.
II. Temporal Complexity as a Correlate of Consciousness
A. Temporal point processes
Complex systems are characterized by metastable states, i.e., dynamical states that are not real thermodynamical equilibria, but are quasistable for a duration much longer than the transition periods from one metastable state to another. These transition periods can be considered, at a first approximation, as a succession of temporal point processes, or, in other words, of events. As said, metastability is associated with intermittency in the case of critical systems. As a confirmation of this fact, recent fMRI studies on brain activity have highlighted that a smart identification of events is able to account for almost all information that a complex signal can carry [25]. Limitations of this strategy obviously lay in the proper identification of events. On the other hand, here we provide (in the Appendix) some rigorous results that can turn into strengths the weaknesses of this approach. We prove that the detected indices are robust with respect to spurious events (noncrucial events that are randomly wrongly identified as events) and to a random selection of them (events randomly not identified). Finally, we refer to literature on “pseudoevents,” namely observable events that are not crucial but are caused by undetectable (or simply undetected) genuine crucial events. From a modeling point of view, in the cases when undetectable genuine events trigger regular or quasideterministic processes [26,27] or slowly modulate the parameters of some stochastic activity [28,29], the anomaly of complexity indices extracted by the procedures described herein (long-range correlations) have been analytically and numerically proven to be robust, even though event identification provides a more reliable measure of the underlying complexity indices when dealing with limited statistics [30].
Intermittency can be tested via different techniques. Our approach is to extract events called rapid transition processes (RTPs) [31] from the EEG signal, and to use them to construct pseudorandom walks. The anomalous statistics of the walk is a measure of long-range autocorrelation of the original signal. RTPs, i.e., temporal instants where one or more EEG channels have an abrupt change in frequency, amplitude, or phase, can be extracted via Hilbert transform and are, in principle, the best possible choice to look for intermittency, as they mark a birth-death process of moduli of brain activity, so they should correlate with changes in information content, hence with crucial events [32]. Finally, a scaling analysis on constructed walks is able to assess intermittency even in the presence of superimposed Poisson events (noise or identification of spurious events) [33].
B. DFA analysis of avalanche events
Original signals are the same as Ref. [16], i.e., 29 whole-night, 128-channel EEG recordings, manually annotated for cycles and phases (sampling rate 250 Hz, referenced to apex, rereferenced to mastoids to extract pseudomonopolar signals, RTPs extracted as in Ref. [16]). All subjects signed informed consent according to local ethical committees. Figure 1 shows a grand-average detrended fluctuation analysis (DFA) [34] for the diffusion stemming from a process of counting how many multichannel RTPs occur in temporal windows of varying duration t. For details on data and on how average DFA is implemented we refer to Ref. [16]. The presence of long-range correlations [Fd(t) ∝ tα with α > 0.5] is apparent (and superimposable) for wakefulness and REM sleep. NREM sleep displays an asymptotic α = 0.5, with a difference between shallower sleep (phase named N2, with background EEG activity in the θ band, with K-complexes and spindles) and deeper phase N3, also called slow wave sleep (SWS, with background slow activity in the delta band): The asymptotic regime is attained earlier for SWS in comparison to N2, correlating with a higher rate of SSO events (in average 1 every 3 s in SWS and every 20 s in N2).
Fig. 1.
(Color online) DFA analysis. Asymptotic time range in the DFA computed for multichannel RTP counting process applied to different sleep phases (cycle I). Presleep wakefulness, shallow sleep, slow-wave sleep, and REM sleep are, respectively, indicated with open red squares, filled green circles, blue filled up triangles, and purple open down triangles. Red continuous and green dashed lines are eye guides for slopes α = 0.75 and α = 0.5, respectively.
We recall (see, e.g., Ref. [14]) that a simple formula connects α to a renewal process with a waiting-time distribution Ψ(t) asymptotically decaying as t−µ, namely
| (1) |
Equation (1) states that µ = 3 signals the passage to anomalous to standard diffusion for the counting process, and therefore, according to literature on complexity (see, e.g., Ref. [14]) signals the breakdown of long-range correlations (infinite correlation time). Figure 1 tells that this transition from infinite to finite memory is mirrored by the physiological transitions from conscious to unconscious states (and vice versa).
The reported results are partly expected, as some literature has pointed out similar results, including our group of research [16]. The reason why we reported them is to keep the paper self contained, and, more important, to show lack of complexity even in shallow sleep (phase N2), which is often overlooked in literature on NCCs, and not present in Ref. [16]. Adopting the hypothesis that consciousness is a function that is either present or absent, Fig. 1 shows that N2, the filled circle curve, displays H = 0.5 only in the asymptotic regime. Notice that infinite correlation time is indeed an asymptotic property and is necessary for a deviation from H = 0.5 in the asymptotic regime. In summary, the presence of genuine (untruncated) long-range autocorrelations is a robust neural correlate of consciousness.
C. Brain-dynamics fragmentation abolishes complex intermittency
The described transition can be theoretically modeled by means of a functional fragmentation in brain dynamics, in line with NREM-sleep fragmentation reported in recent literature [15].
1. The theoretical framework
We adopt the hypothesis that, during NREM sleep, disconnected complex subsystems coexist, each with fluctuations driven by a renewal process. The different subsystems are taken mutually independent. From time to time an event from a particular region is able to induce communication between subsystems and trigger a global event. This is exactly the way in which the global workspace is numerically implemented in artificial intelligence [35]. However, during NREM sleep we hypothesize that this global event, instead of eliciting consciousness, triggers a massive reset of many subsystems. Here for simplicity we model a global reset for all subsystems.
We now use renewal theory [36] to show that this breakdown of the system unitarity quenches long-range autocorrelations in the global fluctuations so that α = 0.5. Let us assume a number Nd of domains each driven by a renewal process described by a survival probability Ψ(τ) that for τ → ∞ decays as , where Ti is a timescale marking the onset of the inverse-power-law asymptotic. The simplest possible form,
| (2) |
makes the treatment analytical for all times in the case where all Ti = T and μi = μ, corresponding to the Cox event rate [36] ri(τ) = ai/(1 + biτ),with μi = 1 + ai/bi and Ti = 1/bi. The global process is described by the superposition of Nd independent processes. Let us first derive a global index making the crude assumption that the first event in any domain resets the whole system. This hypothesis, sufficient for having renewal global events, can be relaxed for a more realistic model, as later shown. Imagining that all processes are equal (ai = a, bi = b) and prepared at time t = 0 the Cox rate at time t reads
| (3) |
corresponding to a global Ψ(τ) of the form of Eq. (2) with the same T and with a global index µG given by
| (4) |
Notice that in general, according, e.g., to Ref. [37], the local values of μ are larger than 2. Therefore, a minimal fragmentation yielding just two separate regions (Nd = 2) is already sufficient to give µG > 3, hence α = 0.5. In general, the domains may have different complexity indices; nevertheless, it is possible to perform an exact treatment in the asymptotic limit. In the limit t ≫ T = maxi(Ti), it is possible to drop the 1 in the denominator of Eq. (2), yielding ri(t) ≃ ai/bit, and thus, defining , we have
| (5) |
| (6) |
where . We have therefore demonstrated that the renewal process stemming from a global resetting due to the first event of N parallel renewal processes with complexities μi yields a global complexity,
| (7) |
larger than 3, hence yielding α = 0.5, for Nd ⩾ 2 if all μi ⩾ 2, or for larger Nd in case 1 < μi ⩽ 2.
2. A generalization toward a modeling of the global workspace
The result can be generalized to be adherent to the theoretical description of the global workspace. It is assumed [35] that due to the serial activation of the global workspace, not every peripheral fluctuation gets the attention of the global workspace, but there must be a filter, so that only large fluctuations are taken care of, one at a time. Since, according to our heuristics, we are dealing with independent critical phenomena, we know [12] that macroscopic fluctuations are described by an intermittent process, and we have already assumed that waiting times between large fluctuations are statistically independent. We assume that, among these fluctuations, only the largest ones can spread, so they get to consciousness in wakefulness, while in sleep, using the same cluster connectivity [16], are able to produce a spreading SSO. This means that only a selection of events are globally resetting. We now show that Eq. (7) holds true also for the resulting waiting time distribution of the large fluctuations . Let us assume a random selection of events, with probability pi. For the sake of simplicity let us omit the subscript i in the following treatment, without loss of generality. The effective survival probability,
| (8) |
can be written as
| (9) |
where here the subscript n in ψ(n), written between parentheses, does not refer to the nth region. ψ(n) is defined as the waiting time distribution density of the nth event. Equation (A1) should be read as follows. Ψ(L)(t) is, according to Eq. (8), the probability that at time t the globally resetting event has not happened yet. It may happen that an arbitrary number of subthreshold events have occurred, hence the sum over this infinite number of possibilities. These must be weighted with the probability of the last event being the nth, given by the Laplace convolution of ψ(n) (in turn an n-times convolution of ψ with itself) with Ψ, and the fact that occurred events were under threshold, namely with the term (1 − p)n.
For t → ∞, a first approximation reads (see Appendix for a derivation)
| (10) |
As T denotes the time scale after which the function becomes indistinguishable from an inverse power law, Eq. (18) means that a random selection induces a rescaling of the transient time scales of the form . In fact, for dimensional reasons,
III. Structural Complexity: Avalanches and Functional Connectivity
A. Avalanches
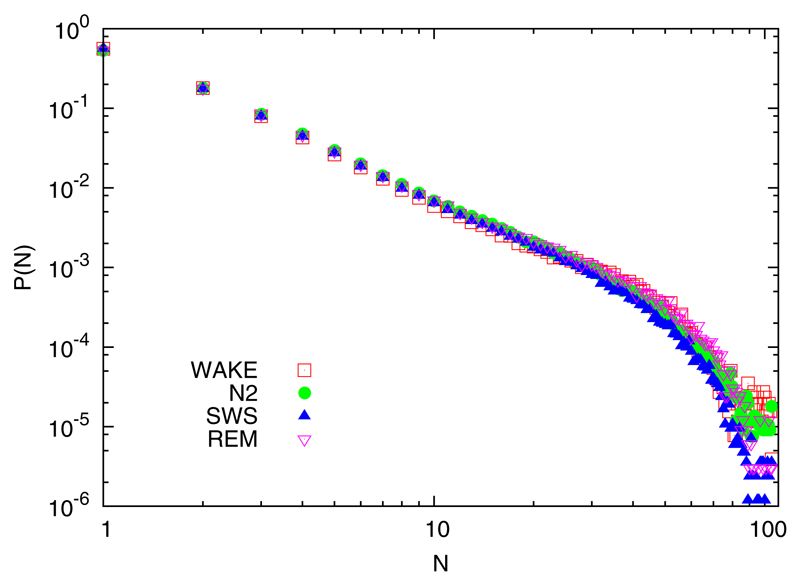
Figure 2 shows, for the different sleep phases, the probability density P(N) of avalanche sizes N, namely the probability to have N simultaneous (within a time tolerance of ∆t = 4.0 ms) events in N different electrodes.
Fig. 2.
(Color online) Probability density function P(N) of the number of concurrent events for different stages, limited to the first sleep cycle. Concurrency is defined within a tolerance time ∆t, i.e., adopting the prescriptions of previous works [5,14,37]. Point legend as in Fig. 1: pre-sleep wakefulness, shallow sleep, slow-wave sleep, and REM sleep are, respectively, indicated with open red squares, filled green circles, blue filled up triangles, and purple open down triangles.
These results have already been presented in a previous work [16], where it was stated that there was no difference in the distributions. This may be at odds with a similar result that recently appeared in a recent work [38]. Therein, authors find some significance in the small deviations among phases. According to the nonparametric Kolmogorov-Smirnov test, differences of the cumulative distributions should be described by the D statistics if they belong to the same stochastic model. A difference, for the degrees of freedom used herein, has to be larger than approximately 0.02 to be significant. We do in fact find significant differences, in line with the mentioned work [38]. Visually, however, the density functions are remarkably similar, with differences that seem to correlate with a numerosity difference (trivially the time spent in N2 is much larger than the time spent in REM sleep in the first cycle). Remarkably, the avalanching of the different phases here reported are numerically similar to those reported in Ref. [38]. Notice, however, that herein we adopt a different choice of event. This either means that a large deflection in intracranial activity correlate with an EEG RTP, or, alternatively, that some fractal temporal dynamics lead to deflections in both signals, and that the kind of analyses that we adopt are robust with respect to the arbitrarity of event definition.
In synthesis, although with some small difference, there is no qualitative change in avalanches in the different phases of sleep. This means that the emerging property of scale-free avalanches are not sensitive to the neurobiological differences between conscious and unconscious states. This leads to conjecture that RTP coincidences exploit the anatomic pathways that, elicited during NREM sleep, can sustain the temporary formation of large clusters, before some protection mechanism occurs to prevent further integration. This is in line with a recent work [17], showing that early sensory processing is not changed during NREM sleep, probably due to the fact that they are projected to cortical sensory areas by the thalamus.
B. Degree distribution
In this subsection we try to keep together some apparently contradictory pieces of evidences collected thus far. How is it possible, for instance, that sensory process integration is maintained during NREM sleep, spreading to large cortical territories [17] and, in the same, modular parallel activity is preserved [15,47]? We conjecture that the integration caused by sensory processing elicits the onward causation responsible for scale-free avalanches. However, since this process favors the emergence of a global mode, we may have two alternative outcomes. In the one case, sleep is protected by some mechanism and a new kind of backwards causation is able to reinstate parallel modular activity; in the other case, we have an awakening and the emerging of conscious behavior.
Let us focus on the first outcome alternative, i.e., the subject keeps sleeping. What should we expect that our structures of events show? If modularity is protected, the backwards causation of NREM-sleep does not slow down the dynamics of the giant cluster, but resets the system, renewing all subsystems. Therefore, we can expect that avalanches do not have memory of the preceding ones. At variance, in slowed-down systems, like the Ising model at Curie temperature, for an extended time, structurally correlated spins are also temporally correlated. This has been made popular by recent works [8], which showed a scale-free topology of spin-spin autocorrelation network, and showed a remarkable similarity with fMRI voxel-voxel network for brain activity during wakefulness.
In Fig. 3 we test this topological feature of criticality. Starting from the extracted point processes (RPTs), we define a pairwise correlation, for each EEG channel pair, as follows:
| (11) |
where # stands for the cardinality and AND means the presence of simultaneous events (i.e., belonging to the same avalanche). Equation (11) approximates the correlation function when the ξ’s are signals of zero value, assuming the value 1 at the time of the RTP event. Pairwise correlation matrices are transformed in dichotomous adjacency matrices Aij through thresholding. We choose a threshold = 0.5, but results are robust with respect of other threshold choices. We then compute the degree distribution P(k) (probability for an electrode to correlate with k others) for the different nights and sleep stages.
Fig. 3.
(Color online) Average degree distribution Pav(k) for different sleep phases (cycle I). Point legend as in Fig. 1: Presleep wakefulness, shallow sleep, slow-wave sleep, and REM sleep are, respectively, indicated with open red squares, filled green circles, blue filled up triangles, and purple open down triangles. Green dashed and red continuous lines are eye guides for exponential exp(−k/3) and inverse-power law ∝ 1/k1.1, respectively.
Segments pertaining to the same phase and night were glued together to compute the relative symmetric adjacency matrix Aij = θ(Cij − 0.5) (θ is the Heaviside step function) stemming from Eq. (11) with threshold 0.5. The unnormalized degree distribution was calculated as F(k), i.e., the number of lines with k ones. F(k) is averaged over the 29 nights and normalized, i.e.,
| (12) |
The degree distributions averaged over all nights, Pav(k) of Fig. 3, show a long-range network topology during wakefulness or REM sleep that breaks down into a short-range topology in unconscious sleep (the maximum degree is around 20, both for N2 and SWS). Although data are not clear enough to support a transition from scale-free to random networks, guides to the eye of Fig. 3 seem to support this intriguing hypothesis. The difference in the degree distribution between the conscious and the unconscious states is nevertheless clear, with a larger number of highly connected nodes during conscious states. A Kolmogorov-Smirnov test supports the classification between conscious and unconscious states.
We stress that the very fact that we find a difference rules out the null hypothesis that event coincidences are simply caused by volume conduction, in case this effect is purely linear, i.e., independent of the frequency. Some caution must be exerted for low frequencies (<12 Hz), where volume attenuation seems to be lower, particularly around 9 Hz [39]. This may account for more extended coherence in relaxed presleep wakefulness. Notice, however, that (i) the curves of N2 and SWS are both short range, but have very different spectral component, especially in the mentioned band. Moreover, assuming that coherence is due to volume conduction for unconscious states, should have been reflected in the cluster analysis of Fig. 2, which, as mentioned, is remarkably similar to the same analysis on deep intracranial recordings [38].
IV. Concluding Remarks
In this paper we have studied brain-activity critical features through event identification. The identification of events has the advantage of efficiently compressing a continuous signal by connecting time-series analysis with information theory. Indeed, information increases when the determinism is broken, i.e., when signals display unpredictable changes. Coincidences of such changes in many EEG electrodes mark an increase in network information. Moreover, coincidences are not likely to occur by chance.
We have discussed the strengths and limitations of this approach. We have shown that consciousness and sleep unconsciousness have similar critical features in terms of cluster-avalanches connectivity (see Fig. 2), in turn remarkably similar to that reported in other studies where events were differently extracted, namely identifying large excursions of local field potentials measured via intracranial depth recording in epileptic patients [38]. This, in our opinion, means that, while event selection is somewhat arbitrary, different choices provide similar results. Alternatively, one can think of a common origin of both kinds of events, as well as of others.
Another feature of brain criticality is the presence of long-range correlations. We decided to adopt a popular technique to unravel infinite-memory effects, namely the detrended fluctuation analysis. We recovered the established fact that infinite memory is only present in conscious states, and not in NREM sleep [40]. Our analysis is performed on the events coincidences only, instead of the multidimensional continuous signal. Remarkably, we showed infinite-memory breakdown also for shallow sleep, which shares the temporal-complexity scale-free properties typical of consciousness for long transient times before the asymptotic truncation.
The core of the paper is the heuristics exposed in Sec. IIB. We showed that one way of explaining the breakdown of infinite memory is a fragmentation of brain activity, without making any assumption on a substantial deviation from criticality, at least from a thermodynamic point of view. Notice that imposing a deviation from criticality (either subcritical or supercritical, far from criticality) would have the straightforward consequence of providing system fragmentation (entropy becomes extensive). This, however, may be at odds with the presence of preserved scale-free integrative excitations. We proved that a reparallelizing reset of the system into independent components, triggered by large (integrative) fluctuations, can explain both the maintaining of scale-free avalanches and the breakdown of infinite memory. The reason for the emergence of such a mechanism, present during NREM sleep only, is beyond the scope of the paper.
We then tested our heuristics by studying extended-time cross-correlations. For genuine critical systems, i.e., with circular causation and critical slowing down, the scale-free network generated by these cross-correlations is expected to be long lasting, like the fMRI critical network of the works of Fraiman and Chialvo’s group [8]. On the other hand, assuming the presence of a neural reset should result on more random adjacency matrices. This has been in fact verified with the new experimental analysis described in Sec. III B.
In synthesis, a new kind of self-organized criticality emerges in sleep unconsciousness. We no longer have a thermodynamical feedback of the order parameter on the control parameter, like that envisaged, e.g., in Ref. [38]. The feedback corresponding to sleep unconsciousness is rather dynamical: Auto-organization that, e.g., caused by sensory processing, emerges in the cortex, is naturally accompanied with large fluctuations that, in turn, trigger a massive neural reset. One mechanism able to do this is the sleep slow oscillation [24], but it may not be the only one. Other mechanisms are probably hidden in some not yet well understood functional role of θ and σ activity [41], or in other thalamocortical oscillation [42]. It is, however, certain that consciousness-related downwards causation is destroyed by SSOs, which reset the system after a process of organization.
Subcortical patternization is probably the general mechanism by which the cortex is prevented from global intercommunication during unconscious sleep. Spindles (and activity in the 𝜎 band in general), typical of shallow sleep (N2), are direct markers of thalamocortical entrainment. This entrainment may give the false impression that the system is globally integrated in a supercritical state. In fact, corticocortical activity is diminished with respect to wakefulness, at least in terms of firing rate [41,43], so one may, on the contrary, be tempted to cast the cortex into a subcritical state. Anyway, we conjecture that sensory stimuli, involving the thalamus, weaken thalamic patternization and allow critical organization in the transient regime, before parallelism is again reestablished.
In SWS the cellular mechanism is somewhat different. The δ rhythm is preserved and actually increased when thalamic driving is absent [44]. However, it is tempting to conjecture that, even without subcortical driving, the quasiperiodic activity of alternation of bursting and silence [45,46] may be a limit cycle of the self-organized complex dynamics herein exposed.
Future work will be devoted to studying why K-complexes are not always evoked, or, in other words, why neural reset is not always required to protect sleep. It is possible that very slow fluctuations may induce an alternation of large and small network global excitability [42]. In the presence of low levels of excitability, a spreading excitation may not be capable of establishing a level of integration so large as to trigger neural bistability.
This paper does not attempt to describe the role of anatomy in the described mechanisms. We however mentioned that transient auto-organization can be the consequence of natural stimuli. On the other hand, Ref. [47] describes how a transcranial magnetic impulse, sent to premotor cortical areas, triggers excitation spreading (quenching) in conscious (unconscious) states. In other words, excitation is not sufficient, per se, to trigger critical avalanches in NREM. It is however plausible that avalanches are favored if they take place exploiting the presence and directionality of the circuits that usually process information during wakefulness.
Acknowledgments
The work is partially supported by MIUR (Italian Ministry for Instruction, University and Research) through project SUONO (Code No. SCN_00306, funded under Smart Cities and Communities) and by the European Research Council, through Project ECSPLAIN (Ref. No. 338866, funded under FP7-IDEAS-ERC).
Appendix: Robustness of μ for Random Selection and Deletion
We recall from the main text that the effective survival probability can be written as
| (A1) |
where here the subscript n in is the waiting time distribution density of the nth event. Equation (A1) should be read as follows. Using as our notation for the Laplace transform, we can rewrite Eq. (A1) as
| (A2) |
where we used the property
| (A3) |
with the condition ψ0(t) = δ(t), a Dirac δ, so that, by induction, We make use of the properties of Laplace transform of integral functions, namely
| (A4) |
and use the formula of geometric series to get
| (A5) |
For t → ∞, i.e., s → 0, as a first approximation we get
| (A6) |
as, for dimensional reasons, , where T denotes the time scale after which the function become indistinguishable from an inverse power law, Eq. (A6) means that a random selection induces a rescaling of the transient time scales of the form
| (A7) |
This result can be made more rigorous with the use of a Tauberian theorem. This reads
| (A8) |
where the steplike Heaviside function θ means that the last term has to be considered only if μ ≥ 2, where . Plugging Eq. (A8) into Eq. (A5) yields for 1 < μ < 2
| (A9) |
whose inverse Laplace transform reads
| (A10) |
where Eα(z) is the Mittag-Leffler function, which obeys the asymptotic property
| (A11) |
yielding again Eq. (A6). The rigorous Eq. (A10) tells us that for μ < 2 the Mittag-Leffler function is expected to show independently of the detailed form of ψ(t).
The case 2 < μ < 3 is a little more complicated, in the sense that an exact analytical treatment requires a choice for ψ(t). However, we prove that a Mittag-Leffler solution is stable with respect to random selection or deletion. If Ψ(t) is a Mittag-Leffler function,
| (A12) |
then
| (A13) |
and plugging Eq. (A13) into Eq. (A5) yields
| (A14) |
whose inverse Laplace transform is
| (A15) |
References
- [1].Kaplan AY, et al. Signal Process. 2005;85:2190. [Google Scholar]
- [2].Stanley HE. Introduction to Phase Transitions and Critical Phenomena. Oxford University Press; Oxford: 1971. [Google Scholar]
- [3].Tononi G. Biol Bull. 2008;215:216. doi: 10.2307/25470707. [DOI] [PubMed] [Google Scholar]
- [4].Grigolini P, Chialvo DR. Chaos, Solitons Fractals. 2013;55:1. [Google Scholar]
- [5].Beggs JM, Plenz D. J Neurosci. 2003;23:11167. doi: 10.1523/JNEUROSCI.23-35-11167.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Tang C, Bak P. Phys Rev Lett. 1988;60:2347. doi: 10.1103/PhysRevLett.60.2347. [DOI] [PubMed] [Google Scholar]; Bak P, Tang C, Wiesenfeld K. ibid. 1987;59:381. doi: 10.1103/PhysRevLett.59.381. [DOI] [PubMed] [Google Scholar]
- [7].Vespignani A, Zapperi S. Phys Rev E. 1998;57:6345. [Google Scholar]
- [8].Fraiman D, Balenzuela P, Foss J, Chialvo DR. Phys Rev E. 2009;79:061922. doi: 10.1103/PhysRevE.79.061922. [DOI] [PMC free article] [PubMed] [Google Scholar]; Chialvo DR. Nat Phys. 2010;6:744. [Google Scholar]
- [9].Baars BJ. A Cognitive Theory of Consciousness. Cambridge University Press; Cambridge, UK: 1998. [Google Scholar]
- [10].Stauffer D, Aharony A. Introduction to Percolation Theory. Taylor and Francis; London: 1992. [Google Scholar]
- [11].Edelman GM, Gally JA, Baars BJ. Front Psychol. 2011;2:4. doi: 10.3389/fpsyg.2011.00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Contoyiannis YF, Diakonos FK, Malakis A. Phys Rev Lett. 2002;89:035701. doi: 10.1103/PhysRevLett.89.035701. [DOI] [PubMed] [Google Scholar]
- [13].Grigolini P, Palatella L, Raffaelli G. Fractals. 2001;9:439. [Google Scholar]
- [14].Allegrini P, Menicucci D, Bedini R, Fronzoni L, Gemignani A, Grigolini P, West BJ, Paradisi P. Phys Rev E. 2009;80:061914. doi: 10.1103/PhysRevE.80.061914. [DOI] [PubMed] [Google Scholar]
- [15].Boly M, et al. Proc Natl Acad Sci USA. 2012;109:5856. doi: 10.1073/pnas.1111133109. [DOI] [PMC free article] [PubMed] [Google Scholar]; Lewis LD, et al. ibid. 2012;109:E3377. [Google Scholar]
- [16].Allegrini P, et al. Chaos, Solitons Fractals. 2013;55:32. [Google Scholar]
- [17].Laurino M, et al. Neuroimage. 2014;86:433. doi: 10.1016/j.neuroimage.2013.10.030. [DOI] [PubMed] [Google Scholar]
- [18].Ribeiro TL, et al. PLoS ONE. 2010;5:e14129. doi: 10.1371/journal.pone.0014129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Horovitz SG, et al. Hum Brain Mapp. 2008;29:671. doi: 10.1002/hbm.20428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Moretti P, Muñoz MA. Nat Commun. 2013;4:2521. doi: 10.1038/ncomms3521. [DOI] [PubMed] [Google Scholar]
- [21].Priesemann V, et al. Front Syst Neurosci. 2014;8:108. doi: 10.3389/fnsys.2014.00108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Solovey G, et al. J Neurosci. 2015;35:10866. doi: 10.1523/JNEUROSCI.4895-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Mora T, Bialek W. J Stat Phys. 2011;144:268. [Google Scholar]
- [24].Menicucci D, et al. Int J Psychophysiol. 2013;89:151. doi: 10.1016/j.ijpsycho.2013.01.014. [DOI] [PubMed] [Google Scholar]; PLoS ONE. 2009;4:e7601. doi: 10.1371/journal.pone.0007601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Tagliazucchi E, et al. Front Physiol. 2012;3:15. doi: 10.3389/fphys.2012.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Allegrini P, Grigolini P, Hamilton P, Palatella L, Raffaelli G. Phys Rev E. 2002;65:041926. doi: 10.1103/PhysRevE.65.041926. [DOI] [PubMed] [Google Scholar]
- [27].Mega MS, Allegrini P, Grigolini P, Latora V, Palatella L, Rapisarda A, Vinciguerra S. Phys Rev Lett. 2003;90:188501. doi: 10.1103/PhysRevLett.90.188501. [DOI] [PubMed] [Google Scholar]
- [28].Allegrini P, Grigolini P, West BJ. Phys Lett A. 1996;211:217. [Google Scholar]
- [29].Allegrini P, Barbi F, Grigolini P, Paradisi P. Phys Rev E. 2006;73:046136. doi: 10.1103/PhysRevE.73.046136. [DOI] [PubMed] [Google Scholar]
- [30].Altmann EG, Cristadoro G, Degli Esposti M. Proc Natl Acad Sci USA. 2012;109:11582. doi: 10.1073/pnas.1117723109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Fingelkurts AA, Fingelkurts AA. Open Neuroimag J. 2008;2:73. doi: 10.2174/1874440000802010073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Fingelkurts AA, Fingelkurts AA. Brain and Mind. 2001;2:261. [Google Scholar]
- [33].Allegrini P, Menicucci D, Bedini R, Gemignani A, Paradisi P. Phys Rev E. 2010;82:015103(R). doi: 10.1103/PhysRevE.82.015103. [DOI] [PubMed] [Google Scholar]
- [34].Peng CK, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL. Phys Rev E. 1994;49:1685. doi: 10.1103/physreve.49.1685. [DOI] [PubMed] [Google Scholar]
- [35].Franklin S, Graesser A. Conscious Cogn. 1999;8:285. doi: 10.1006/ccog.1999.0391. [DOI] [PubMed] [Google Scholar]
- [36].Cox DR. Renewal Theory. Methuen; London: 1962. [Google Scholar]
- [37].Allegrini P, Paradisi P, Menicucci D, Gemignani A. Front Physiol. 2010;1:128. doi: 10.3389/fphys.2010.00128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Priesemann V, Valderrama M, Wibral M, Le Van Quyen M. PLoS Comp Biol. 2013;9:e1002985. doi: 10.1371/journal.pcbi.1002985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Winter WR, Nunez PL, Ding J, Srinivasan R. Statistic Med. 2007;26:3946. doi: 10.1002/sim.2978. [DOI] [PubMed] [Google Scholar]
- [40].Lee J-M, Kim D-J, Kim I-Y, Park KS, Kim SI. Med Eng Phys. 2004;26:773. doi: 10.1016/j.medengphy.2004.07.002. [DOI] [PubMed] [Google Scholar]; Zempel JM, et al. Front Neurol. 2012;3:76. doi: 10.3389/fneur.2012.00076. [DOI] [PMC free article] [PubMed] [Google Scholar]; Zorick T, Mandelkern MA. PLoS ONE. 2013;8:e68360. doi: 10.1371/journal.pone.0068360. [DOI] [PMC free article] [PubMed] [Google Scholar]; Farag AF, El-Metwally SM, Morsy AA. In: Automated Sleep Staging Using Detrended Fluctuation Analysis of Sleep EEG, in Soft Computing Application, Advances in Intelligent Systems and Computing. Balas VM, et al., editors. Vol. 195. Springer; Berlin: 2013. pp. 501–510. [Google Scholar]; Goshvarpour A, Abbasi A, Goshvarpour A. I J Intell Syst Appl. 2013;5:68. [Google Scholar]
- [41].Sejnowski TJ, Destexhe A. Brain Res. 2000;886:208. doi: 10.1016/s0006-8993(00)03007-9. [DOI] [PubMed] [Google Scholar]
- [42].Vanhatalo S, Palva JM, Holme MD, Miller JW, Voipio J, Kaila K. Proc Natl Acad Sci USA. 2004;101:5053. doi: 10.1073/pnas.0305375101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Evarts EV. J Neurophysiol. 1964;27:152. doi: 10.1152/jn.1964.27.2.152. [DOI] [PubMed] [Google Scholar]; Steriade M. Behav Brain Sci. 1978;3:465. [Google Scholar]
- [44].Ball GJ, Gloor P, Schaul N. Electroencephalogr Clin Neurophysiol. 1977;43:346. doi: 10.1016/0013-4694(77)90258-9. [DOI] [PubMed] [Google Scholar]
- [45].Steriade M, McCormick DA, McCormick DA. Science. 1993;262:679. doi: 10.1126/science.8235588. [DOI] [PubMed] [Google Scholar]
- [46].McCormick DA, Bal T. Annu Rev Neurosci. 1997;20:185. doi: 10.1146/annurev.neuro.20.1.185. [DOI] [PubMed] [Google Scholar]
- [47].Massimini M, et al. Science. 2005;309:2228. doi: 10.1126/science.1117256. [DOI] [PubMed] [Google Scholar]