Recent reports have called for integrating quantitative reasoning into biology courses to prepare students for careers in research and medicine. This article describes the development, implementation, and assessment of modules designed to incorporate quantitative reasoning and skill development into introductory biology courses.
Abstract
Redesigning undergraduate biology courses to integrate quantitative reasoning and skill development is critical to prepare students for careers in modern medicine and scientific research. In this paper, we report on the development, implementation, and assessment of stand-alone modules that integrate quantitative reasoning into introductory biology courses. Modules are designed to improve skills in quantitative numeracy, interpreting data sets using visual tools, and making inferences about biological phenomena using mathematical/statistical models. We also examine demographic/background data that predict student improvement in these skills through exposure to these modules. We carried out pre/postassessment tests across four semesters and used student interviews in one semester to examine how students at different levels approached quantitative problems. We found that students improved in all skills in most semesters, although there was variation in the degree of improvement among skills from semester to semester. One demographic variable, transfer status, stood out as a major predictor of the degree to which students improved (transfer students achieved much lower gains every semester, despite the fact that pretest scores in each focus area were similar between transfer and nontransfer students). We propose that increased exposure to quantitative skill development in biology courses is effective at building competency in quantitative reasoning.
INTRODUCTION
The field of biology has become increasingly reliant on interdisciplinary approaches to address complex biological problems, and these approaches typically require significant use of quantitative analysis. However, preparation of students for this new era of quantitative biology has been lacking, in part because undergraduate biology courses have been slow to incorporate quantitative reasoning into the classroom setting (Bialek and Botstein, 2004; Feser et al., 2013). Greater emphasis on quantitative skill development has been noted as increasingly important for preparing biology students for medical (see Association of American Medical Colleges/Howard Hughes Medical Institute report [AAMC/HHMI, 2009]) and graduate school (Barraquand et al., 2014). In addition, lack of training in quantitative sciences has been noted as an impediment to advances in research by practicing biologists (Chitnis and Smith, 2012; Fawcett and Higginson, 2012; Fernandes, 2012). Many recent papers and reports have called for a “revolution” in undergraduate biology education in which analysis, graphical thinking, and quantitative skills receive greater emphasis (e.g., National Research Council [NRC], 2003, 2009; Bialek and Botstein, 2004; Feser et al., 2013; Aikens and Dolan, 2014). A vision of how new curricula might look is laid out in a widely cited American Association for the Advancement of Science (AAAS) report Vision and Change in Undergraduate Biology Education (AAAS, 2010). Of note, the second core competency listed as necessary for all biology students in Vision and Change is the ability to use quantitative reasoning. The call for students to be better trained in quantitative reasoning has also been echoed by the AAMC/HHMI report (2009), which emphasizes the need to train life sciences students in how to integrate knowledge across scientific disciplines (e.g., mathematics, chemistry, physics). The MCAT has also been redesigned to reflect this view (Kirch et al., 2013).
At most universities, biology majors obtain quantitative skills through courses offered by other departments, such as mathematics, physics, and computer science. Until recently, little effort has been made to integrate quantitative reasoning into biology courses themselves (Brent, 2004; Gross, 2004; Hoy, 2004). This compartmentalization may give students the false impression that biological knowledge can be acquired with minimal understanding of the more quantitative fields (e.g., mathematics and statistics) and leads to all-too-familiar situations in which students are unable to apply, or transfer, concepts learned in one domain to another, such as applying the math they know in a biological context (NRC, 2000; Haskell, 2001; Mastascusa et al., 2011). Further, the level of quantitative rigor in mathematics and physics courses taught for biology students is often lower than that taught to mathematics, chemistry, physics, and engineering undergraduates (Bialek and Botstein, 2004), which leaves many biology students unable to “think in math,” even if they understand its importance for their field (NRC, 2003). While students often receive some practice in quantitative thinking and analysis in upper-level courses, this may be too late in the curriculum to have much effect. The NRC’s BIO2010 paper specifically encourages integrating mathematics into biology courses early in the curriculum, particularly in courses taken by first-year students (NRC, 2003).
In this paper, we report on the development and assessment of four stand-alone modules that require students to integrate quantitative thinking into an introductory undergraduate biology course focused on ecology and evolution. These modules are designed for use in weekly group-based active-learning class sessions. Each module is designed as a dry laboratory exercise (pencil and paper/computer based) that applies quantitative thinking to biological problems that are ideally covered concurrently in the lecture component of the course. Applying mathematical and statistical concepts in a biological context would, we hoped, teach students that quantitative thinking was a useful, practical, and indeed indispensable way to approach biological problems. We assessed the influence of these modules on development of student competencies in three focal areas, as outlined in the AAMC/HHMI Report (2009): 1) their ability to demonstrate quantitative numeracy and facility with the language of mathematics (skill E1.1 in AAMC/HHMI, 2009, hereafter referred to as “quantitative numeracy”), 2) their ability to interpret data sets and communicate those interpretations using visual and other appropriate tools (skill E1.2, hereafter referred to as “data interpretation”), and 3) their ability to make inferences about natural phenomena using mathematical models (skill E1.5, hereafter referred to as “mathematical modeling”). We assessed these skills with a pre- and postassessment test over each of four semesters in large introductory biology courses (class sizes ranged from ∼65 students in the Summer to >250 in the Fall and Spring semesters). We analyzed student gains in reference to demographic and other background student information (e.g., transfer vs. nontransfer student) after the posttest was administered.
We also conducted a small, qualitative, interview-based study of students’ reasoning on quantitative problems. While this study was quite limited in its scope and aims, it provides some insights into the various forms of reasoning students bring to bear on problems that call for quantitative reasoning and highlights certain concepts and terminology of quantitative biology with which students struggle.
METHODS
Module Development
The first-year biology sequence at University of Maryland–Baltimore County (UMBC) comprises two courses: 1) molecular/cellular biology and 2) ecology and evolution. This paper focuses only on modules used in the eco/evo course. However, we have developed an additional 10 quantitative modules that have yet to be implemented, including four additional modules for use in ecology and evolution and six in cellular and molecular biology. These, and the four modules reported on in this study, are available by request at http://nexus.umbc.edu.
To develop each module, we first chose a topic in the course that we felt naturally lent itself to quantitative treatment and for which we thought quantitative treatment could enhance student understanding of the biological concept. We then designed the modules with several components to make it easy for faculty to adopt them in their courses: 1) a tutor guide that includes an introduction to the biological content; 2) a summary of the contents, including a table aligning each activity with learning objectives and quantitative competencies related to quantitative reasoning (as outlined by the AAMC/HHMI report, 2009); 3) a list of the mathematical and statistical concepts covered and quantitative skills required and estimated time to complete the in-class component of the module; 4) an in-class worksheet component of the module that the students receive, which provides an introduction to the biological problem and the activities to be completed; 5) preclass exercises designed to review the mathematical and statistical concepts needed to successfully complete the module; 6) a student survey form to be completed online after completion of the module, to obtain feedback on how helpful the module was to their learning; 7) a suggested list of formative assessment questions along with their alignment to AAMC/HHMI core competencies and learning objectives; and 8) a teacher’s guide for implementation. An example of the instructional guide typical of all modules, including a table of learning goals cross-referenced to specific activities in the module, is provided in Appendix 1 in the Supplemental Material.
Module Implementation
The in-class worksheet is designed for groups of three or four students to complete in a 50- to 60-min discussion section. At UMBC, these modules were implemented in a smart classroom with a capacity of 90 students in 75-min discussion sections (allowing time to discuss the modules before and after completion). One to two graduate teaching assistants and two undergraduate teaching assistants were assigned to each section. Course instructors met weekly with the teaching assistants to go over the module activities for the upcoming week and to discuss ways to facilitate student learning in the discussion sessions. These meetings were also used to discuss how well the students did on different aspects of the modules after they had been implemented the prior week and to field suggestions on improving module activities/clarifying questions for the future.
Each group of students in the class had access to computer terminals, although not all modules require their use. Students were asked to complete the premodule exercises before attending the discussion section, and also to carefully read the module, which was enforced with three-question reading quizzes administered either online before class or at the start of each session. Each student submitted a completed worksheet at the end of the discussion session. The modules constituted 20% of the overall course grade.
Contents of the Four Modules
A summary of the contents of each module is provided below in the order in which the modules were delivered each semester.
Mendelian Genetics.
This module allows students to calculate and predict the genotype and phenotype frequencies of a Mendelian trait resulting from monohybrid and dihybrid crosses. Students also learn how to calculate and interpret the results of a chi-squared statistical analysis to test hypotheses about the independent assortment of traits. This module addresses the following general learning goals from the AAMC/HHMI report: students will demonstrate quantitative numeracy (skill E1.1) and make statistical inferences from data sets. The module includes application of basic mathematics to Mendelian patterns of inheritance, including simple calculations of proportions (frequencies), calculations of chi-squared statistics, and a single question on probability. Students also use their data to calculate and interpret the results of a chi-squared statistical analysis to test hypotheses about independent assortment of traits.
Introduction to Mathematical Modeling.
This module is designed to introduce students to a simple linear mathematical model in the context of negative frequency-dependent selection. This module addresses the following general learning goals from the AAMC/HHMI report: students will demonstrate quantitative numeracy (skill E1.1), interpret data sets, and communicate those interpretations using visual tools (skill E1.2); make statistical inferences from data sets (evaluating best-fit linear relationships based on calculating error sums of squares); and make inferences about natural phenomena using mathematical models (skill E1.5). The module includes data on the frequency of red-finned cichlid fish within a population and the number of offspring produced by red-finned adults as a function of their frequency in the population. The students are asked to graph the data by hand and in Excel, draw a line of best fit through the points on the handwritten graph (by eye), and provide an algebraic formula for this best-fit line. They are then walked through the basics of regression to demonstrate how the best-fit line is determined statistically, by finding the line through the data that minimizes the sum of the squared errors between the actual data points and the line (this is done using calculations in Excel). Students are then asked to interpret the relationship between variables. They are also asked how their interpretation might differ if certain characteristics such as slope and intercept of the line changed. The prelaboratory exercises require students to create a mathematical model in a nonscientific application. For example, one problem states, “On her way to her volleyball game, Joanne stops by the grocery store for a healthy snack that will give her energy for the game. She decides to get a jar of peanut butter and some bananas. She notices that the peanut butter costs $3.99 for a jar and that the bananas cost $0.49 per pound of bananas. 1. How much will one pound of bananas and a jar of peanut butter cost? 2. Joanne decides to bring a snack for each of the 6 girls on the volleyball team. How much will it cost for six pounds of bananas and a jar of peanut butter? 3. On the grid provided below, draw a Cartesian coordinate system with number of pounds of bananas on the x-axis and the total cost of the peanut butter and bananas on the y-axis. Plot the two points that you found for the previous two questions. Plot the line on the grid above through the two points that you found. Now compute the slope of the line that goes through these two points (remember, “rise over run”: (y2 − y1) = m(x2 − x1), where m is the slope of the line). Now write the equation of the line in slope-intercept form, y = mx + b, where b is the y-intercept (the place where the line crosses the y-axis). Congratulations! You have just made a mathematical model of the cost you will pay to provide peanut butter and bananas to your teammates!” The idea is to allow students to practice the type of mathematical thinking they will be using in the module, but to use examples more relevant to their daily lives. After this, the students are given a more biologically oriented example in the prelab using data on conifer density that students are asked to graph and draw a best-fit line through. Similar questions regarding characteristics of the line are asked as in the worksheet itself.
Population Genetics I—Breeding Bunnies and Natural Selection.
This module explores the effect of natural selection on allele frequencies, and it also allows students to use calculations of expected and observed allele frequencies to determine whether populations are in Hardy-Weinberg equilibrium. This module addresses the following general learning goals from the AAMC/HHMI report: students will demonstrate quantitative numeracy (skill E1.1), interpret data sets, and communicate those interpretations using visual tools (skill E1.2); make statistical inferences from data sets; and explain how evolutionary mechanisms contribute to change in gene frequencies in populations. This module uses as an example a hypothetical recessive trait (furlessness) in a small population of wild rabbits. A collection of red and white kidney beans are used to simulate the genotypes in the population of rabbits, with the red beans representing the alleles conferring the dominant trait (fur), and the white beans representing the recessive alleles (homozygotes are furless). The rabbits are bred by randomly picking two alleles (or beans). The number of rabbits with the recessive allele is recorded (to estimate allele frequency), and the rabbits with two recessive alleles (two white beans) are discarded (reflecting strong truncating selection against these rabbits). The students are asked to repeat the above steps, imposing selection across several generations, and record and plot their data (allele and genotype frequencies). The students then draw conclusions regarding the Hardy-Weinberg principle based on allele and genotype frequencies in the data they collected. Finally, the students perform a chi-squared test on the data to test the null hypothesis that the population experiencing selection is in Hardy-Weinberg equilibrium. The prelab exercises present a similar experiment with gumballs, and the students are asked basic probability questions.
Population Genetics II—Gene Flow and Genetic Drift.
This module is designed to immediately follow the previous module on natural selection of furless rabbits. The learning goals of this module are the same as the other population genetic module discussed above. In this module, again using the furless rabbits example, students explore how gene flow and genetic drift can act to influence the response to natural selection. Two groups of three students each work together, forming a population of rabbits on an island, separated by a river. One side of the river has a mild climate favorable to furless rabbits, and the other side of the island has a harsher climate less favorable to furless rabbits. The students go through the natural selection process described in the previous module for several generations, then the groups exchange three individuals from each population, representing gene flow between the populations on both sides of the river. The students then go through the natural selection process and record the allele frequency in each population. Once the data have been collected, students are asked to draw conclusions about the effect of gene flow and genetic drift on natural selection.
Assessment Tool
We developed a pre/posttest for summative assessment of competency in the focal quantitative skills and reasoning. Beginning in the Fall of 2011 and continuing every semester thereafter until Spring 2013, we calculated the discrimination and difficulty of pre–post questions and modified questions to develop a valid pre/postassessment exam. For discrimination, we wanted to determine whether questions were discriminating between high-performing students and low-performing students. Items that had a point-biserial correlation coefficient (Kornbrot, 2014) <0.20 were classified as “low discrimination” and were revised for subsequent semesters. A point-biserial correlation coefficient measures the correlation between a continuous variable (in our case, the student score on the posttest) and an ordinal or nominal variable (in our case, whether the student answered an individual question correctly or not). Higher coefficients indicate both a strong correlation between score on the assessment and answering an item correctly and a high level of discrimination.
For difficulty, items that were answered correctly by ≥ 90% of the students who took the exam were deemed too easy, and items answered correctly by <20% of students were deemed too difficult. These items were also revised before the first formal use of this instrument to obtain data for this study (Spring 2013). The validated pre/posttest was given across four semesters, Spring 2013, Summer 2013, Fall 2013, and Spring 2014 (Appendix 2 in the Supplemental Material). We continued the discrimination and difficulty analyses of the questions on the pre/postexam each semester and made minor changes in two questions (changed distractors) after the Summer of 2013. In addition, two questions did not appear on all exams every semester (see Appendix 2 in the Supplemental Material for details).
The actual content of the test consisted of questions to assess the level at which students have achieved the desired competencies, one attitude assessment question, and other questions about concepts in the course that were not quantitative in nature.
The postassessment exam was given on the final day of discussion. Student motivation was stimulated in two ways. First, we told students that some of the questions or alternative versions of them would appear on the final exam and so this exam was good practice. Second, students were awarded one participation point for a valid attempt at the exam (the exams were curated after they were given, and there was no evidence of any inauthentic attempts [e.g., filling in the same letter for every answer or leaving half the questions blank]).
To see whether individual characteristics of students were associated with changes in student performance, we also asked a series of questions designed to gather demographic and educational history data for each student (Appendix 1 in the Supplemental Material). These demographic surveys were administered immediately after students took the posttest exam in Spring 2013, Summer 2013, and Spring 2014 to minimize the influence of stereotype threat on exam performance (Steele and Aronson, 1995; Spencer et al., 1999). Further, a qualitative study involving individual interviews with seven students in the freshman-level ecology and evolution class was undertaken in Spring 2015 to investigate how the interviewees understood the pre/posttest questions and what forms of reasoning they used in answering them. We received institutional review board approval for the entire study (UMBC IRB Y13WL04051).
Statistical Analyses
We used a nested logistic regression analysis (using SAS, version 9.3) to test for changes in performance in the skills of quantitative numeracy (skill E1.1), data interpretation (skill E1.2), and mathematical modeling (skill E1.5) based on pre–post questions associated with each skill. We used the statistical model y = trt + question(trt) + e, where y = 0 if the question was answered incorrectly, or 1 if correct; trt = pre- or posttest; question is the multiple-choice question nested within either the pre- or posttest; and e is the error term. Instead of analyzing the total test score, we partitioned the quantitative questions into three subgroups, with one set of questions for each quantitative skill (to see how questions were partitioned among skills, see Appendix 2 in the Supplemental Material). We then analyzed the data separately for each of the three subgroups, with one analysis for each skill each semester.
We used Cohen’s d to estimate the magnitude of change in the proportion that answered correctly in each skill from the pre-exam to the postexam (Cohen, 1992). Because multiple questions in the pre/postexam addressed each skill, we used the proportion correct for each question associated with a particular skill to calculate Cohen’s d. We used the formula (M1 − M2)/SDpooled, where M1 was the mean proportion of correct answers on questions addressing a particular skill in the posttest, and M2 was the mean proportion of correct answers on questions addressing that skill in the pretest. SDpooled was calculated as √(SD12 + SD22)/2, where SD1 and SD2 are the standard deviations in the proportion correct among questions in the pre- and posttest, respectively. Data were analyzed separately for each semester. All analyses used only the data from students who completed both the pre- and posttest.
Multiple regression (Theobald and Freeman, 2014) was used to determine the relationships between the background characteristics and performance on the three skills. Three models were run, one for each skill (quantitative numeracy, data interpretation, and mathematical modeling). Each model included the following independent variables:
Score on the preassessment
Transfer status (transfer student or nontransfer student)
Took algebra 1 in high school
Took algebra 2 in high school
Took precalculus in high school
Took calculus in high school
Earned advanced placement (AP) credit for calculus or currently taking calculus 1 at UMBC
Earned AP credit or currently taking calculus 2 at UMBC
Took Stat 350 (introductory statistics for biology majors) at UMBC
Student Interviews
Individual interviews were conducted with seven undergraduate students enrolled in the ecology and evolution course to inquire into their reasoning processes in answering four questions (questions 2–5) excerpted from the pre/posttest (see Appendix 2 in the Supplemental Material). The interviews were conducted during the 11th and 12th weeks of the semester, after students had already participated in a subset of the quantitative modules (Appendix 4 in the Supplemental Material). The purpose of the interviews was to provide data about the nature and quality of students’ reasoning on questions related to the quantitative thinking portions of the modules. Our research questions for this portion of the study were
What types of reasoning did students use to answer these questions?
For questions that students answered incorrectly, which forms of reasoning were they using and which aspects of the concepts did they struggle with?
Was there a discernible pattern in reasoning processes among students who answered the same questions incorrectly?
Was there a discernible pattern in reasoning processes among students who performed similarly in terms of their final course grades?
Students were selected for interviews by their instructor based on their average grades on the first two exams. (The interviewers did not know the performance level of any of the students at the time of the interview.) Initially, nine students were chosen to participate in the interview process (three who had “A’s” at the time of the interviews, three who had “B’s,” and three who had “C’s,” all of whom were chosen randomly from within each letter grade). Of the nine who originally agreed to the interview, only seven actually participated (three with “A’s,” two with “B’s,” and two with “C’s” at the time of the interview). Each interview lasted ∼20 min and involved an interviewer engaging each student in a semistructured review of their answers to all four test questions after they had read and answered them. The interview questions were designed to elicit and probe the students’ thought processes by having them explain how they came to their answers. (See the Interview Protocol in Appendix 3 in the Supplemental Material.) All of the interviews were audio recorded, and an observer listened and took notes. The interviews were transcribed from the observer’s notes and the audio recordings.
A grounded theory approach (Corbin and Strauss, 2014) was used to code the interview transcripts for the types of reasoning students used in their explanation of their answers for the test questions. This approach allowed us to derive the categories of reasoning the students were using directly from their utterances, rather than to predict and apply a priori certain forms of reasoning to our analysis of the interview data. Such a methodological stance is common in qualitative research, in which the experiences of the participants in the research are considered to be fundamental to the development of theory.
RESULTS
Assessment of Student Learning Outcomes from Pre/Postexam
The first question on the pre/postexamination asked students how useful they thought quantitative approaches (e.g., mathematical modeling, statistical analyses) are to the study of biology. In all four semesters, students came in with a fairly strong opinion that quantitative approaches were important for studies in biology (Table 1). In every semester, greater than 90% of the students thought that quantitative approaches were, at a minimum, “very important” for studying modern biological problems (summing the top three rows of Table 1). This attitude was little changed (a 1% or less increase) at semester’s end.
Table 1.
Results of student attitude assessment from pre- and postexam. The question was “How useful do you think that quantitative approaches (e.g., mathematical modeling, statistical analyses) are to the study of biology?”
| Spring 2013 | Summer 2013 | Fall 2013 | Spring 2014 | |||||
|---|---|---|---|---|---|---|---|---|
| Opinion | % Pre | % Post | % Pre | % Post | % Pre | % Post | % Pre | % Post |
| It’s impossible to study modern biological problems without such approaches. | 41 | 32 | 43 | 32 | 36 | 37 | 25 | 28 |
| Such approaches are extremely important for studying modern biological problems. | 40 | 48 | 41 | 48 | 45 | 36 | 47 | 51 |
| Such approaches are very important for studying modern biological problems. | 15 | 19 | 14 | 19 | 17 | 23 | 23 | 18 |
| Such approaches are somewhat important for studying modern biological problems. | 3 | 1 | 3 | 1 | 3 | 4 | 3 | 2 |
| Such approaches are not important for studying modern biological problems. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The remaining portion of the pre/postexamination was designed to assess students in the three focus skills described above: quantitative numeracy, data interpretation, and mathematical modeling, aligning with AAMC/HHMI (2009) skills E1.1, E1.2, and E1.5, respectively. While these skills are not mutually exclusive, an effort was made to test each skill separately in the pre/postexam (see Appendix 2 in the Supplemental Material for categorization of questions). All modules required students to use quantitative numeracy and data interpretation skills; however, only one explicitly required students to develop, use, and interpret mathematical models. Although there was slight variation from semester to semester (two of the validated questions did not appear each semester), the pre/postexam used approximately five questions to assess quantitative numeracy, six questions to assess data interpretation, and three questions to assess mathematical modeling.
Proficiency of Students in Quantitative Numeracy
Students improved their quantitative numeracy from the pre- to posttest, although the magnitude of the effect varied widely among semesters, and the gain was not significant in the Fall 2013 session (Table 2 and Figure 1A). There was considerable variation in the pretest scores from semester to semester, ranging from a low of 41% (Spring 2014) to a high of 68% (Fall 2013). While the difference among semesters in the range of scores on the pretest was 27%, on the posttest the range was much smaller (from a low of 61% to a high of 68%). Note that the effect size was strongest in those semesters in which students came in with lower pretest scores (Spring 2013 and Spring 2014; Table 2). This suggests that, regardless of initial student ability, students obtained comparable levels of proficiency in this skill by the end of the semester. However, this also indicates that students with a high level of proficiency at the start of the course did not improve much during the semester.
Table 2.
Results from the nested logistic regression analysis of student performance in pre/postexam scores (p values are those associated with the overall treatment effect in the model) in quantitative numeracy, data interpretation, and mathematical modelinga
| Spring 2013 | Summer 2013 | Fall 2013 | Spring 2014 | |||||
|---|---|---|---|---|---|---|---|---|
| Skill | p | d | p | d | p | d | p | d |
| Quantitative numeracy | <0.0001 | 0.4 | 0.03 | 0.2 | NS | – | 0.001 | 1.5 |
| Data interpretation | 0.001 | 0.4 | 0.01 | 0.1 | <0.0001 | 0.2 | 0.001 | 0.5 |
| Mathematical modeling | 0.001 | 0.9 | NS | – | 0.02 | 1.1 | 0.001 | 0.2 |
ap Values reported are for Wald’s chi-squared values. d Values are Cohen’s d effect sizes. All significant changes from the pre- to posttest scores represent positive gains in student skills.
Figure 1.
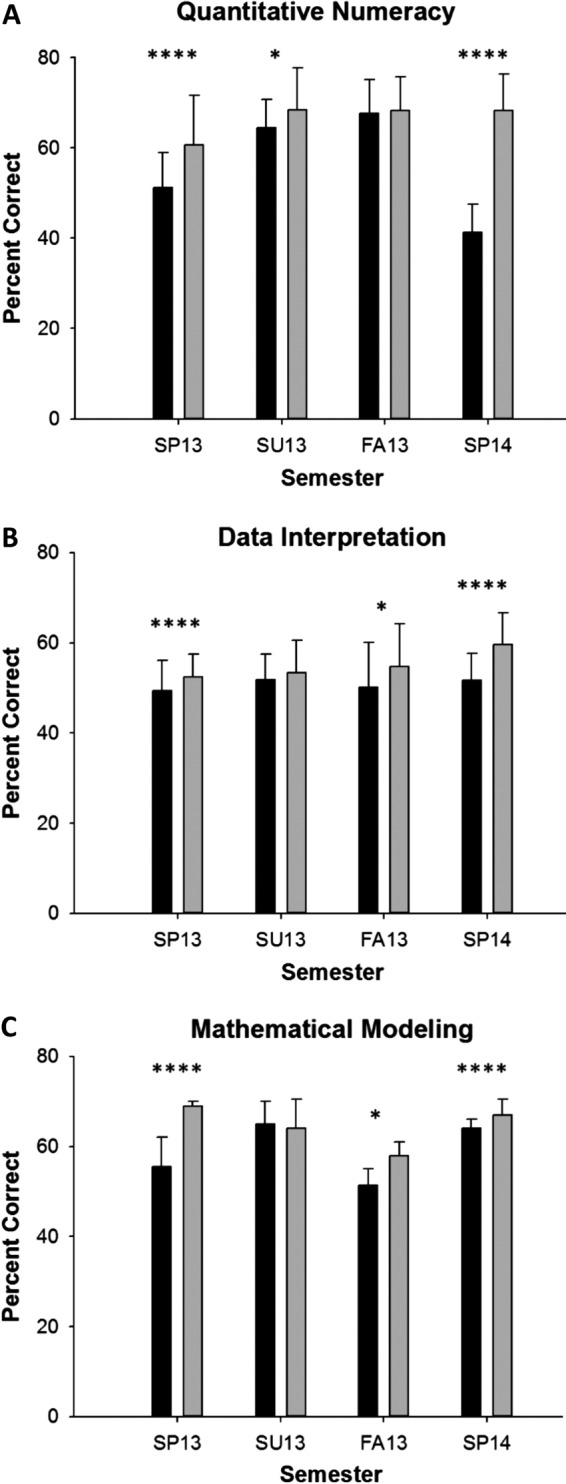
Results of pre/posttest for (A) quantitative numeracy, (B) data interpretation, and (C) mathematical modeling. Data reflect the average percent of students (±1 SE) who provided the correct answer on the pre- and posttest on questions that addressed each skill. Significant differences from the nested logistic regression between the pre- and posttest scores are indicated above the bars for each semester: ****, p < 0.0001; *, p < 0.05.
Proficiency of Students in Interpreting Data
Students showed significant improvement every semester in their ability to interpret data sets and communicate those interpretations using visual tools, although the magnitude of improvement varied among semesters (Table 2 and Figure 1B). The effect sizes of the gains were generally more modest compared with those associated with quantitative numeracy (average d: quantitative numeracy = 0.54, data interpretation = 0.29). The range of scores on the pretest across semesters was much smaller than that for quantitative numeracy above (low of 49% in Spring 2013 to a high of 52% in Spring 2014). The skill level both initially and on the posttest was generally lower than that for quantitative numeracy (posttest scores ranged from 52 to 59%).
The Ability of Students to Make Inferences from Mathematical Models in Biology
Gains in the ability of students to make inferences about natural phenomena using mathematical models were highly variable across semesters, but on average were slightly lower than in the other two skills (Table 2 and Figure 1C). As was the case for quantitative numeracy, there was a broad range in pretest scores from semester to semester (range: 51% in Fall 2013 to 65% in Summer 2013), but unlike the results for quantitative numeracy, there was also a broad range of scores across semesters in posttest results (from 58% in Fall 2013 to 69% in Spring 2013).
Student Demographics and Background Characteristics on Gains
We gathered demographic and background data on students to examine their potential influence on the posttest scores in the different quantitative skills. In the three semesters for which we had demographic data, just more than half the students were female. Greater than 70% were either white or Asian. In Spring 2013 and Spring 2014, most students had a grade point average (GPA) of 3.1–4.0 (65 and 59%, respectively). Fewer students had a GPA of 3.1–4.0 in Summer 2013 (48%). Students in Summer 2013 were less likely to have completed math and physics courses in high school than students in either Spring 2013 or Spring 2014. They were also less likely to have taken calculus 1 or 2 at UMBC. Summer 2013 had the most transfer students (33% compared with 16% in Spring 2013 and 27% in Spring 2014).
We used multiple regression analysis to determine whether any of these demographic or student background variables were significant predictors of student scores in the posttest exam. We included the pretest score of each student in this model as well (as suggested by Theobald and Freeman, 2014). Results are shown in Appendix 5 (Tables A–C) in the Supplemental Material. For quantitative numeracy (Appendix 5A), in Spring 2013, three characteristics were significant predictors of postassessment performance: the pretest score, student transfer status, and whether the students had taken precalculus in high school. On the basis of the regression coefficients of each significant effect for each additional point a student scores on the preassessment, we expect a student’s score on the postassessment to increase by 0.273 points (β = 0.273, p < 0.0001). Transfer students were expected to score 8.072 points lower on the postassessment than nontransfer students (p < 0.05). Students who took precalculus in high school were expected to score 9.853 points lower on the postassessment than students who did not take precalculus in high school (p < 0.05). In the Summer of 2013, only the preassessment score was related to postassessment performance in quantitative numeracy; a student’s score on the postassessment is expected to increase by 0.444 points for each additional point scored on the preassessment (p < 0.01). In Spring 2014, four variables predicted student scores on the posttest: student pretest scores, transfer status, whether students had taken high school algebra, and whether students had AP credit for calculus or were taking calculus one at the same time as they were enrolled in the course. A student’s score on the postassessment was expected to increase by 0.384 points for each additional point the student scored on the preassessment (p < 0.0001). Transfer students were expected to score 11.493 points lower on the postassessment than nontransfer students (p < 0.0001). Students who took algebra 1 in high school were expected to score 5.708 points lower on the postassessment than students who did not take algebra 1 in high school (p < 0.05). Students who received AP credit for calculus 1 or who already took or were currently taking calculus 1 at UMBC were expected to score 8.736 points higher on the postassessment than their counterparts (p < 0.01).
Results for data interpretation are shown in Appendix 5B in the Supplemental Material. In Spring 2013 and Summer 2013, the only variable related to postassessment performance was the score on the preassessment. In Spring 2013, for each additional point scored on the preassessment, a student’s score on the postassessment was expected to increase by 0.390 points (p < 0.0001). In Summer 2013, for each additional point scored on the preassessment, a student’ score on the postassessment was expected to increase by 0.754 points (p < 0.0001). In Spring 2014, two variables were significant, the score on the pretest and whether the student had AP credit for calculus or was taking calculus at UMBC at the time. In this case, for each additional point scored on the preassessment, a student’s score on the postassessment was expected to increase by 0.356 points (p < 0.0001). In addition, students who received AP credit for calculus 1 or who already were currently taking calculus 1 at UMBC were expected to score 14.520 points higher on the postassessment than their counterparts (p < 0.0001).
Results for mathematical modeling are shown in Appendix 5C in the Supplemental Material. In Spring 2013, two variables were significant, the pretest score and whether students received AP credit for calculus 1 or already were currently taking calculus 1 at UMBC. For each additional point scored on the preassessment, a student’s score on the postassessment was expected to increase by 0.257 points (p < 0.0001). Students who received AP credit for calculus 1 or who already took or were currently taking calculus 1 at UMBC were expected to score 16.447 points higher on the postassessment than their counterparts (p < 0.001). In Summer 2013, no variables were related to performance on the postassessment for this skill. In Spring 2014, three variables were significant: the score on the preassessment, transfer status, and whether students received AP credit for calculus 1 or had already taken or were currently taking calculus 1 at UMBC. For each additional point scored on the preassessment, a student’s score on the postassessment was expected to increase by 0.240 points (p < 0.0001). Transfer students were expected to score 12.648 points lower on the postassessment than nontransfer students (p < 0.05). Students who received AP credit for calculus 1 or who had already taken or were currently taking calculus 1 at UMBC were expected to score 12.081 points higher on the postassessment than their counterparts (p < 0.05).
Investigation of Students’ Reasoning on Selected Pre/Posttest Questions
Three main categories of reasoning were discerned in these interviews: quantitative, disciplinary (biology), and general logic. To distinguish these categories of reasoning, we read and reread the transcripts several times, looking for instances in which students explicated their reasoning processes and analyzing them for similarities and connections. Initially, we detected six types of reasoning that students applied in their explanations: 1) reasoning in which students referred to the graph provided in the test questions or other graphic knowledge (quantitative reasoning: graphic); 2) quantitative forms of reasoning that did not specifically mention the graph (quantitative reasoning: general); 3) reasoning through use of biology concepts (biology knowledge: conceptual); 4) reasoning through appeal to how research in biology is conducted (biology knowledge: process); 5) rationales based on how tests are constructed and/or how they should be taken (test-taking knowledge); and 6) general, nonquantitative, non–disciplinary-specific knowledge or logic (general knowledge).
While each of these six types of reasoning seemed to be distinct, and each occurred in more than one interview, distinguishing between, for example, quantitative reasoning that specifically referred to the graph and that which made no reference to the graph or graphic knowledge was not relevant to our purposes. Thus, we combined these two categories into one category of quantitative reasoning. Likewise, it was not necessary to distinguish reasoning that appealed to knowledge of biological concepts from that which appealed to knowledge of how biological research was conducted, so those two categories were combined into one type of reasoning we refer to as disciplinary knowledge. And, finally, distinctions between reasoning that appealed to knowledge of best practices in test writing or test taking and other more general forms of logic were not relevant to our purposes, so we combined those two categories into one general logic category.
Of the three main categories of reasoning, by far the one used most prevalently was quantitative reasoning. The fact that quantitative reasoning was used so widely is not surprising, given that the questions each referenced a graph that preceded the question and each of the questions and their answer options referred to quantitative reasoning concepts. For example, one high-performing student reasoned his way to the correct answer on question 5 (see Appendix 2 in the Supplemental Material), saying, “I decided that [the most reasonable hypothesis is] c. [Student reads the answer from the test sheet aloud:] When density is between 20–30 plants, we would expect no more than 20 seeds per plant. [Interviewer: You mean 200?] 200, yeah. Because between 20 and 30 for the plant density, we definitely see that there’s no data points above that, so we shouldn’t expect, if it were to follow this trend, to be like that. And I just decided that the other answers were either too specific or incorrect.” We coded this part of his explanation as quantitative reasoning, because the student refers to information that is provided only in the graph, and he correctly interprets the graph to say that there are no data points above 200 seeds per plant in the plant density range of 20–30 plants.
It is notable, however, that the interviewed students did not always apply quantitative reasoning concepts accurately, and at times, they used other forms of reasoning as well as quantitative reasoning, including approaches commonly taught as test-taking strategies (coded as general logic) and knowledge of how field biologists conduct research (coded as disciplinary knowledge). A lower-performing student answered question 5 correctly also, but his thinking was based less on reasoning around his reading of the graph and more on the wording of the answers and which one sounded, in his words, “most reasonable.” He did use some quantitative reasoning in eliminating answer “a,” noting: “There’s a wide range of seeds but they all look higher than as soon as you have more density, so I guess that’s an effect.” Likewise, to eliminate answer “b,” he looked at the graph, “If you look at the chart, after 30 it’s not the highest. Ten to 20 is a much higher rate of chance than 30–40.” But in choosing answer “c,” his rationale was based more on the way it sounded: “The way that one is worded it just seems to me like it could actually be something that you could use as a hypothesis to apply to something else … It’s using this information to explain to you that if you have this range of plants based on this information we shouldn’t see any more than this number of seeds. Because it’s between this range, correlated with this information from this other place.” He drew on all three types of reasoning—quantitative, logical, and disciplinary—to eliminate answer “e.” Reading from the answer, he said: “When plants get to a density of 50, we expect none of them to produce seeds. This chart doesn’t say that at all, and it doesn’t really make any sense. If there’s any plants at all you would expect some of them to have seeds. I didn’t think that was right.”
The question that posed the most difficulty for the students interviewed was question 2. Three of the seven interviewees answered this question incorrectly, and each of their incorrect responses was different. One of these students relied on quantitative reasoning to choose answer “e” (40 plants). Although he was able to use the key to focus correctly on the red marks on the graph for Assateague Island, he seemed to have confused the notions of plant density and plant sampling.
Another student who answered this question incorrectly, chose “d” (20 plants), noting in his explanation that he first read the background information, then looked at the chart, and then looked at the question. He said, “None of [these sources of information] told me a specific number where it said how many populations were selected. So I counted the individual observations and that was my answer … I assume that these [pointing to dots on the graph] are each individual plants.” This student seems to have drawn on general test-taking strategies (an approach that we coded as logic based) at first to see whether the answer was explicitly stated in either the background information or on the graph. When it was not, he then made an assumption (correctly) that each of the points on the graph represents a sample. His error was in not realizing, or perhaps not reading carefully enough to notice, that the question specifically asked for the number of samples of plants on Assateague, not both islands.
The third student who answered question 2 incorrectly selected “a” (100 plants) as her answer. She indicated that she had multiplied each plot point on the graph by the corresponding plant density on the x-axis and then added them together to arrive at an estimate that roughly corresponded to 100. She said: “I kind of tried to add them up, but I didn’t really add them all up. I just gave a rough estimate. I mean, adding up plant density for Assateague Island because it says that plant density is based on counts of the number of individual plants. So I just added up x values of the square ones, and 1000 is too large of a number. But it was much more greater than 40, so it must be around 100.” So, although she was using quantitative reasoning, like the other two students who answered this question incorrectly, she seems to have confused plant density with the sampling of plants, not realizing that each plot point represents a sample.
In general, the students who ended the course with higher grades were more likely to use quantitative reasoning as their major or sole source of reasoning in answering the questions. Lower-performing students also used quantitative reasoning, but often poorly or incorrectly, and often supplemented with general logic or disciplinary knowledge when their quantitative reasoning skills were not sufficient to the task of answering the question. For example, lower-performing students chose answers that reversed the causal relationships from what was displayed in the figure, were unable to recognize whether a figure displayed a positive or negative correlation between variables, did not understand what a change in slope of a regression line would represent for the relationship between two variables, and had difficulty understanding the concept of individual points on a figure representing data samples taken at different time points. However, these students sometimes reached the correct answer to a question using appropriate biological logic, for example, “Well, if there are more plants in this area, they must be more crowded, so it doesn’t make sense that each one would make more seeds.”
For some questions, nearly all students struggled to apply quantitative reasoning appropriately, due to lack of familiarity with the quantitative concept or term. For example, their explanations suggested that few of the students interviewed understood what it meant for one variable to be “sensitive” to changes in another (question 4, answers “b” and “c”).
DISCUSSION
We saw significant improvement in all skill areas tested in most semesters, though the effect sizes were often modest and varied from semester to semester. On the basis of the average gains in performance, students improved the most in skills reflecting quantitative numeracy. Their ability to make biological inferences from mathematical models and to interpret data in biological contexts (primarily interpreting graphical results) showed smaller gains. To the extent that the module activities contributed to this skill development, we hypothesize that the prelaboratory activities, which reviewed key skills needed before students came to class, and the repeated application of similar skills to different biological settings were important aspects of the modules that contributed to the learning gains of students. We feel that it is also important to allow students to practice using quantitative skills in the lecture portion of the course (in small groups or through clicker questions). This emphasizes to students the importance of quantitative skill development and integrates the lecture and module activity components of the course. Further research is necessary to tease out the contributions of each aspect of the design and implementation of the modules toward enhancing students’ performance.
The fact that students improved most in quantitative numeracy is not surprising, given that they used this skill in each module during the semester. The other skills were used less often (in particular mathematical modeling, which was only formally used in one module), and students may need additional practice to achieve greater gains in these competencies. Of course, the smaller gains could also be attributable to other factors, such as the fact that interpreting data and using mathematical modeling are difficult skills to master, the modules were perhaps not very effective in improving these skills, there may have been poor alignment between modules and assessment, or our assessments may not have been sensitive enough to measure improvements that were made.
The variability in gain also seems to be based on how much scope for improvement students had coming into the course; gains were typically higher in semesters when the pretest scores were lowest. Despite the fact that the course was taught by four different instructors in different semesters, the degree of competency attained in each skill (at least as reflected by the posttest scores) was similar in each semester, regardless of the level of proficiency that students had coming into the course.
The degree of improvement was greater for some populations of students than others. Aside from the predicted case, in which students who did well on the pretest did well on the posttest, the most general finding was that transfer students showed lower gains during the semester in skills associated with quantitative numeracy and mathematical modeling compared with their classmates who were nontransfer students. Many other studies have also noted poorer performance of transfer students (e.g., Graunke and Woosley, 2005; Duggan and Pickering, 2008), especially those majoring in mathematics and the sciences (Cejda et al., 1998; D’Amico et al., 2014). There could be many reasons for this, including poorer academic preparation, differences in demands on their time (e.g., jobs, family obligations), and differences between transfer and nontransfer students in their sense of community on campus (Townley et al., 2013). Understanding the reasons for the disparity of gains between transfer and nontransfer students will require further study. The only other fairly consistent demographic that predicted enhanced student performance was having received AP credit for calculus or taking calculus concurrently with the introductory biology course in ecology and evolution. None of the modules required calculus, however, and the only pre/corequisite for our course is precalculus. As such, we suspect that the explanation has less to do with preparation in calculus than it does with general student academic preparation. There is also the possibility that prior experience with calculus develops higher-order problem-solving skills. Again, more research is needed in this area to see whether this is a general pattern for other courses (particularly in science, technology, engineering, and mathematics [STEM] areas) and to understand the reasons for this, if so.
There was one curious finding from our demographic analysis related to posttest performance on questions related to quantitative numeracy: students who took algebra 1 in high school scored significantly lower on the postassessment than students who did not take algebra 1 in high school. Although this relationship was only formally significant in one of the semesters (Spring 2014), the sign and magnitude of the regression coefficient was negative and similar in magnitude every semester, suggesting that this is a consistent relationship. While we do not know the exact cause of this relationship, we note that the sign of the regression coefficients associated with students who had taken algebra 2 in high school was fairly large and positive in two of the three semesters measured (indicating a positive influence of completing algebra 2 on quantitative numeracy, although this effect was not significant in our analysis). This would indicate that, if algebra 1 is the highest level of mathematics completed in high school, this has a negative effect on student performance in tasks related to quantitative numeracy as freshman college students.
A number of efforts to infuse more quantitative reasoning into biology courses have been described in the literature, and many of these have seen positive effects on both student attitudes (Matthews et al., 2010; Thompson et al., 2010; Goldstein and Flynn, 2011; Barsoum et al., 2013) and skill development (e.g., Thompson et al., 2010; Colon-Berlingeri and Burrowes, 2011; Goldstein and Flynn, 2011; Madlung et al., 2011; Hester et al., 2014). For example, Hester et al. (2014) designed a new course in molecular and cell biology that required greater reliance on mathematical skills and reasoning to understand biological concepts. They found that students initially had poor ability to apply their quantitative skills to biological contexts but improved when quantitative reasoning was integrated throughout the course, including in in-class exercises and on exams. Another course redesign was implemented with development of a new textbook that integrated more quantitative reasoning into introductory biology courses (Barsoum et al., 2013). The new course and accompanying text focused more on the process of science and less on biological content knowledge. Data interpretation by students taking the new course was significantly better than those taking the traditional course. In addition, despite the decrease in content focus, students taking the new course did just as well on tests of biology content knowledge as did those in the traditional course. Thus, the improved quantitative skills did not come at the expense of biological knowledge, a finding consistent with at least one other study (Madlung et al., 2011). Interestingly, the difference in quantitative skills between students in the new and traditional course disappeared when students were tested on similar skills one semester removed from the experience. Speth et al. (2010) found that infusing quantitative concepts using modules throughout an undergraduate biology course, including on the assessments, led to a significant improvement in their students’ ability to interpret graphically represented data and to create graphical representations of numerical data. They did find, however, that students still had difficulty in constructing scientific arguments based on data, and they note that this is a difficult skill to master in only one semester.
In our case, the gains in student skills were fairly modest, which could be explained by two major factors. First, students are often attracted to biology because they perceive it as the least quantitative of STEM disciplines. As a result, they may be less academically (and even emotionally) prepared to integrate quantitative reasoning in biological settings. Second, the changes we imposed occurred in a single course, with only four modules implemented across the semester. Many authors, as noted above, have emphasized that short-term exposure is unlikely to make a lasting difference in students’ skills and attitudes (e.g., Barsoum et al., 2013; van Vliet et al., 2015). The findings of our small qualitative study of students’ reasoning seem to offer further support for this notion. Although all the students we interviewed demonstrated their ability to apply quantitative reasoning to problems that clearly called for it, their application of such reasoning was uneven and at times incorrect, which may suggest that it takes further exposure and practice for these skills to be well integrated into students’ thought processes. Thus, we believe that it is likely that greater and longer-lasting improvements in quantitative competencies will only be possible through broader curricular reform, including consistent integration of mathematics and statistics (ramping up the sophistication of each across the levels) throughout the biology curriculum. Even within a course, stand-alone modules may not be the best way to promote our goals; Hester et al. (2014, p. 55) report, “We found that stand-alone modules, done on the students’ own time, perpetuated the perception that math was an ‘add-on’ that was not representative of the core content in biology.” Some have even argued that biology, mathematics, physics, and chemistry should be taught in a fully integrated manner (Bialek and Botstein, 2004), and there appears to be some movement in this direction (e.g., Depelteau et al., 2010). Because the barriers to this integration are so high and so many, we continue to see value in our approach. Alternatively, our approach may be seen as the first step toward a truly interdisciplinary curriculum for life sciences students.
The question to which we must always return in pedagogy is: What is the very best use of the very limited time we have in the classroom with our students? Fortunately, this is an empirical question. Though still promulgated, the view that employing deeper learning techniques such as our modules requires reduction in the number of topics discussed or results in students attaining lower degrees of content knowledge has been empirically overturned (e.g., Fatmi et al., 2013; Freeman et al., 2013; Nanes, 2014). Courses and curricula organized as if our role is to pour our knowledge into students’ brains, a school of thought that is still prevalent, harm those students by focusing on lower-level cognitive skills to the exclusion of analysis and critical thinking (Momsen et al., 2010). Our goal should be to equip students with the cognitive tools they need to investigate questions of interest to them (Gross, 2004), and the evidence is clear that students can only acquire such tools via active application of course concepts to realistic and significant problems. To be effective, these pedagogical reforms must escape single courses of individual motivated faculty and become part of the fabric of undergraduate science education.
Supplementary Material
Acknowledgments
We thank the many people who helped us with this project. Sarah Hansen helped with data analysis. Archer Larned, Chia hua Lue, Sarah Luttrell, Karan Odom, and Tory Williams implemented the modules and assessments and gave us a great deal of constructive feedback. Brian Dalton, Chia hua Lue, Michael Martin, and Tracy Smith were graduate students who developed much of the content of the modules. We are also grateful to our colleagues Tory Smith, Tamara Mendelson, and Kevin Omland, who supported the use of these modules in their courses. William LaCourse and Kathy Sutphin provided organizational support. We also thank our colleagues from the NEXUS project for advice, especially Kaci Thompson, Edward (Joe) Redish, Michael Gaines, Jane Indorf, Daniel DiResta, and Liliana Draghici. Special thanks to David Hanauer for his patient and incisive guidance on the assessment component of this project. This project was funded in part by a National Institutes of Health National Institute of General Medical Sciences grant (1T36GM078008) to Lasse Lindahl (UMBC), and an award from the HHMI to the UMBC under the Precollege and Undergraduate Science Training Program. Thanks to Tim Ford for help with the figures. We also thank two anonymous reviewers and Janet Batzli for helpful comments on the manuscript. All modules and course materials are freely available at http://nexus.umbc.edu or can be obtained by contacting the corresponding author.
REFERENCES
- Aikens ML, Dolan EL. Teaching quantitative biology: goals, assessments, and resources. Mol Biol Cell. 2014;25:3478–3481. doi: 10.1091/mbc.E14-06-1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- American Association for the Advancement of Science. Vision and Change in Undergraduate Biology Education: A Call to Action. Washington, DC: 2010. (accessed 28 April 2016) [Google Scholar]
- Association of American Medical Colleges and Howard Hughes Medical Institute. Scientific Foundations for Future Physicians. Washington, DC: 2009. (accessed 28 April 2016) [Google Scholar]
- Barraquand F, Ezard THG, Jorgensen PS, Zimmerman N, Chamberlain S, Salguero-Gomez R, Curran TJ, Poisot T. Lack of quantitative training among early-career ecologists: a survey of the problem and potential solutions. PeerJ. 2014;2:e285. doi: 10.7717/peerj.285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barsoum MJ, Sellers PJ, Campbell AM, Heyer LJ, Paradise CJ. Implementing recommendations for introductory biology by writing a new textbook. CBE Life Sci Educ. 2013;12:106–116. doi: 10.1187/cbe.12-06-0086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bialek W, Botstein D. Introductory science and mathematics education for 21st-century biologists. Science. 2004;303:788–789. doi: 10.1126/science.1095480. [DOI] [PubMed] [Google Scholar]
- Brent R. Intuition and numeracy. Cell Biol Educ. 2004;3:88–90. doi: 10.1187/cbe.04-03-0041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cejda B, Kaylor AJ, Rewey KL. Transfer shock in an academic discipline: the relationship between students’ majors and their academic performance. Community Coll Rev. 1998;26:1–13. [Google Scholar]
- Chitnis N, Smith TA. Mathematical illiteracy impedes progress in biology. Proc Natl Acad Sci USA. 2012;109:E3055. doi: 10.1073/pnas.1213115109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J. A power primer. Psychol Bull. 1992;112:155–159. doi: 10.1037//0033-2909.112.1.155. [DOI] [PubMed] [Google Scholar]
- Colon-Berlingeri M, Burrowes PA. Teaching biology through statistics: application of statistical methods in genetics and zoology courses. CBE Life Sci Educ. 2011;10:259–267. doi: 10.1187/cbe.10-11-0137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbin JM, Strauss AL. Basics of Qualitative Research: Techniques and Procedures for Developing Grounded Theory. 4th ed. Thousand Oaks, CA: Sage; 2014. [Google Scholar]
- D’Amico MM, Dika SL, Elling TW, Algozzine B, Ginn DJ. Early integration and other outcomes for community college transfer students. Res High Educ. 2014;55:370–399. [Google Scholar]
- Depelteau AM, Joplin KH, Govett A, Miller HA, Seier E. SYMBIOSIS: development, implementation, and assessment of a model curriculum across biology and mathematics at the introductory level. CBE Life Sci Educ. 2010;9:342–347. doi: 10.1187/cbe.10-05-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duggan MH, Pickering JW. Barriers to transfer student academic success and retention. J Coll Stud Ret. 2008;9:437–459. [Google Scholar]
- Fatmi M, Hartling L, Hillier T, Campbell S, Oswald A. The effectiveness of team-based learning on learning outcomes in health professions education. Med Teacher. 2013;35:e1608–1624. doi: 10.3109/0142159X.2013.849802. [DOI] [PubMed] [Google Scholar]
- Fawcett TW, Higginson AD. Heavy use of equations impedes communication among biologists. Proc Natl Acad Sci USA. 2012;109:11735–11739. doi: 10.1073/pnas.1205259109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandes AD. No evidence that equations cause impeded communication among biologists. Proc Natl Acad Sci USA. 2012;109:E305. doi: 10.1073/pnas.1211892109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feser J, Vasaly H, Herrera J. On the edge of mathematics and biology integration: improving quantitative skills in undergraduate biology education. CBE Life Sci Educ. 2013;12:124–128. doi: 10.1187/cbe.13-03-0057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman S, Eddy S, McDonough M, Smith M, Okoroafor N, Jordt H, Wenderoth M. Active learning increases student performance in science, engineering, and mathematics. Proc Natl Acad Sci USA. 2013;111:8410–8415. doi: 10.1073/pnas.1319030111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein J, Flynn DFB. Integrating active learning and quantitative skills into undergraduate biology curricula. Am Biol Teach. 2011;73:454–461. [Google Scholar]
- Graunke SS, Woosley SA. An exploration of the factors that affect the academic success of college sophomores. Coll Stud J. 2005;39:367–376. [Google Scholar]
- Gross LJ. Interdisciplinarity and the undergraduate biology curriculum: finding a balance. Cell Biol Educ. 2004;3:85–87. doi: 10.1187/cbe.04-03-0040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haskell R. Transfer of Learning: Cognition, Instruction, and Reasoning. San Diego, CA: Academic; 2001. [Google Scholar]
- Hester S, Buxner S, Elfring L, Nagy L. Integrating quantitative thinking into an introductory biology course improves students’ mathematical reasoning in biological contexts. CBE Life Sci Educ. 2014;13:54–64. doi: 10.1187/cbe.13-07-0129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoy R. New math for biology is the old new math. Cell Biol Educ. 2004;3:90–92. doi: 10.1187/cbe.04-03-0042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirch DG, Mitchell K, Ast C. The new 2015 MCAT: testing competencies. J Am Med Assoc. 2013;310:2243–2244. doi: 10.1001/jama.2013.282093. [DOI] [PubMed] [Google Scholar]
- Kornbrot D. Point Biserial Correlation. 2014. Wiley StatsRef: Statistics Reference Online. [Google Scholar]
- Madlung A, Bremer M, Himelblau E, Tullis A. A study assessing the potential of negative effects in interdisciplinary math-biology instruction. CBE Life Sci Educ. 2011;10:43–54. doi: 10.1187/cbe.10-08-0102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mastascusa EJ, Snyder WJ, Hoyt B. Effective Instruction for STEM Disciplines: From Learning Theory to College Teaching. San Francisco, CA: Wiley; 2011. [Google Scholar]
- Matthews KE, Adams P, Goos M. Using the principles of BIO2010 to develop an introductory, interdisciplinary course for biology students. CBE Life Sci Educ. 2010;9:290–297. doi: 10.1187/cbe.10-03-0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Momsen JL, Long TM, Wyse SA, Ebert-May D. Just the facts? Introductory undergraduate biology courses focus on low-level cognitive skills. CBE Life Sci Educ. 2010;9:435–440. doi: 10.1187/cbe.10-01-0001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nanes K. A modified approach to team-based learning in linear algebra courses. Int J Math Educ. 2014;45:1208–1219. [Google Scholar]
- National Research Council (NRC) How People Learn: Brain, Mind, Experience, and School. Washington, DC: National Academies Press; 2000. [Google Scholar]
- NRC. BIO2010: Transforming Undergraduate Education for Future Research Biologists. Washington, DC: National Academies Press; 2003. pp. 51–78. [PubMed] [Google Scholar]
- NRC. A New Biology for the 21st Century: Ensuring the United States Leads the Coming Biology Revolution. Washington, DC: National Academies Press; 2009. [PubMed] [Google Scholar]
- Spencer SJ, Steele CM, Quinn DM. Stereotype threat and women’s math performance. J Exp Soc Psychol. 1999;35:4–28. [Google Scholar]
- Speth EB, Momsen JL, Moyerbrailean GA, Ebert-May D, Long TM, Wyse S, Linton D. 1,2,3,4: infusing quantitative literacy into introductory biology. CBE Life Sci Educ. 2010;9:323–332. doi: 10.1187/cbe.10-03-0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele CM, Aronson J. Stereotype threat and the intellectual test performance of African Americans. J Pers Soc Psychol. 1995;69:797–811. doi: 10.1037//0022-3514.69.5.797. [DOI] [PubMed] [Google Scholar]
- Theobald R, Freeman S. Is it the intervention or the students? Using linear regression to control for student characteristics in undergraduate STEM education research. CBE Life Sci Educ. 2014;13:41–48. doi: 10.1187/cbe-13-07-0136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson KV, Nelson KC, Marbach-Ad G, Keller M, Fagan WF. Online interactive teaching modules enhance quantitative proficiency of introductory biology students. CBE Life Sci Educ. 2010;9:277–283. doi: 10.1187/cbe.10-03-0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Townley G, Katz J, Wandersman A, Skiles B, Schillaci MJ, Timmerman BE, Mousseau TA. Exploring the role of sense of community in the undergraduate transfer student experience. J Community Psychol. 2013;41:277–290. [Google Scholar]
- Van Vliet E, Winnips J, Brouwer N. Flipped-class pedagogy enhances student metacognition and collaborative-learning strategies in higher education but effect does not persist. CBE Life Sci Educ. 2015;14:ar26. doi: 10.1187/cbe.14-09-0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


