Data interpretation is an important skill that should be developed within undergraduate biology courses. The authors present instruction in which students collaborate to understand authentic data using biological models. Research in this classroom utilized real-time student dialogues to reveal students’ data-interpretation strategies.
Abstract
We present our design for a cell biology course to integrate content with scientific practices, specifically data interpretation and model-based reasoning. A 2-yr research project within this course allowed us to understand how students interpret authentic biological data in this setting. Through analysis of written work, we measured the extent to which students’ data interpretations were valid and/or generative. By analyzing small-group audio recordings during in-class activities, we demonstrated how students used instructor-provided models to build and refine data interpretations. Often, students used models to broaden the scope of data interpretations, tying conclusions to a biological significance. Coding analysis revealed several strategies and challenges that were common among students in this collaborative setting. Spontaneous argumentation was present in 82% of transcripts, suggesting that data interpretation using models may be a way to elicit this important disciplinary practice. Argumentation dialogue included frequent co-construction of claims backed by evidence from data. Other common strategies included collaborative decoding of data representations and noticing data patterns before making interpretive claims. Focusing on irrelevant data patterns was the most common challenge. Our findings provide evidence to support the feasibility of supporting students’ data-interpretation skills within a large lecture course.
INTRODUCTION
Current undergraduate science, technology, engineering, and mathematics education reform efforts include a significant focus on teaching students to engage in scientific thinking and not merely learn the facts that result from science. Reform documents at the undergraduate level, such as Vision and Change in Undergraduate Biology Education (American Association for the Advancement of Science, 2011), call for students to be able to “apply the process of science” and “use modeling and simulation.” Likewise, the medical community is promoting similar ideas with the recent release of a reformatted MCAT exam that will test students on “reasoning about scientific principles, theories and models,” “interpreting patterns in data presented in tables, figures, and graphs,” and “reasoning about data and drawing conclusions from them” (MCAT, 2015, online materials). A similar trend is also occurring in precollege science classrooms. Backed by a number of empirical accounts of classroom designs that engage students in more authentic science (summarized in Duschl et al., 2007), the K–12 community has now rallied around the Next Generation Science Standards (NGSS), which lay out a plan for integration of specific scientific practices with key ideas in science. Though most agree that such shifts in the teaching and learning of science are necessary, many questions remain about the most practical and effective ways to implement such change and about how the resultant process of learning may be affected by redesign of classrooms, particularly at the undergraduate level.
As a response to calls for change, an increasing number of biology instructors have designed courses and teaching approaches that aim to bring undergraduate students in closer contact with authentic science, often through examination of primary literature. For example, the CREATE method, which includes a step-by-step cycle in which students examine portions of a set of related papers, has been shown to positively impact students’ critical-thinking skills and their confidence in their own data-interpretation skills (Hoskins et al., 2007, 2011; Stevens and Hoskins, 2014). Other instructional interventions have suggested approaches such as focusing on data figures (Round and Campbell, 2013), teaching students to identify rhetorical moves within articles (Van Lacum et al., 2014), and pairing of a literature-based seminar with laboratory research (Kozeracki et al., 2006). In addition to examination of primary literature, a small number of undergraduate instructional interventions have directly targeted inclusion of “disciplinary practices,” such as argumentation and use of models (Brewe, 2008; Svoboda and Passmore, 2010; Walker et al., 2012).
In almost all cases, the courses described enrolled a relatively small number of students and were focused primarily on teaching students scientific skills. Another approach is to integrate learning of data-interpretation skills within content courses throughout the biology major. At most institutions, this would necessitate the addition of disciplinary practices to existing large-enrollment courses, which poses potential practical challenges. However, the potential benefits of integrating scientific skills and content in a larger number of courses include fostering deeper understanding of biology concepts and exposing a greater number of students to the nature of how scientific knowledge is created. This paper describes research within a large-enrollment cell and developmental biology course that uses a novel instructional approach to integrate core biological ideas with interpretation of authentic biological data through the use of biological models. Thus, the course is designed to help students develop skills for two scientific practices: use of models and data analysis.
Background
Interpreting Data with Models.
Models are an important way scientists mentally process and make sense of their work (Dunbar, 1999; Nersessian, 2008). For biologists, the term “model” can refer to physical models (e.g., a mouse model of cancer), computational models (e.g., a mathematical model of a gene regulatory network), or mental models (e.g., the working set of causal interactions for any system that is the focus of a scientist’s research). Mental models are often made explicit in external representations such as pictures, diagrams, videos, and equations. These external representations of mental models are the focus of our current work, specifically how students use instructor-provided biological models from textbooks and primary literature to interpret data. Passmore and colleagues have proposed the “practice framework,” which describes how scientists explain natural phenomena through data collection and/or experimentation to identify data patterns used to construct models (Passmore et al., 2009). Scientific understanding of natural phenomena is hence embedded within and inseparable from models. In addition to providing insight into the scientific process, the practice framework has been applied to methods of learning in science classrooms (Campbell et al., 2012; Neilson et al., 2010; Passmore and Svoboda, 2012). Several studies have suggested that employing modeling practices in science classrooms engages students in the scientific thinking regularly practiced by scientists and offers students the opportunity to understand the nature of knowledge (Stewart et al., 2005; Lehrer and Schauble, 2006; Windschitl et al., 2008).
Models are useful for scientists and students, because they represent real-world phenomena in easily manipulative, comprehensible ways. They allow for mental simulations of the causes and effects in a system, much like running a “movie in the head” with the privilege of “pausing” or “rewinding” (Nersessian, 2008). Model practices include constructing, evaluating, revising, and using models to ultimately make sense of natural phenomena and to make predictions about those phenomena. To use modeling practices, one must form or recognize ways in which the model relates to the natural phenomena. This link between model and phenomena often contains multiple levels of abstraction in the form of successive representations. For example, Bruno Latour described how a botanist constructed an explanation of the vegetation dynamics in the Amazon rain forest (Latour, 1999). When collecting soil samples, the botanist recorded each sample’s location and matched its color using a standardized color scale. In this process, the “lump of earth” became represented as x, y coordinates and a discrete color code. This information then became represented as a specific data point in a diagram with other data points, where patterns could more easily emerge. The diagram then became represented as a figure in a scientific paper. For the botanist to construct an explanation of the Amazon’s soil, the actual soil had to transcend a series of representations, each displaced further away from the original/natural source.
Scientific explanations are not constructed directly from the real-world event but instead are instantiated through meaningful symbols, codes, and other representational forms. Importantly, for any representation to have meaning, one must interpret its meaning (Greeno and Hall, 1997); some meanings, though, in the perspective of a community, are conventional and shared. The data interpretations scientists make feed directly into their model of the natural phenomenon. The integrity of the model is upheld because the model must be consistent with the data collected about the phenomenon. However, an important feature of models is that they do not perfectly match real-world phenomena. In many ways, this absence of realism can serve as an advantage for fostering reasoning within a simplified system and for highlighting potential gaps that are a driving force in scientific inquiry (Wilensky and Stroup, 2002; Svoboda and Passmore, 2013).
Models are useful in science as a generative tool, meaning they provide a space from which one may generate ideas (Odenbaugh, 2005; Nersessian, 2008; Schwarz et al., 2009). For instance, hypotheses and predictions can be generated from the mechanistic gaps that models can specifically reveal; additionally, hypothetical scenarios can be explored through models. Generative reasoning, which is particularly important for solving problems in complex disciplines, can be defined as exploring plausible and appropriate explanations to describe a phenomenon (Duncan, 2007). That is, the generative explanations, albeit novel, must be somewhat rooted in the realm of what is scientifically normative and not violate the assumptions therein. Importantly, generative reasoning is not about accuracy, in the sense of a learner being able to recall the exact mechanism for a phenomenon (Duncan, 2007). Instead, generative reasoning allows a learner to be creative and willing to enter the border of what is known and unknown to generate novel explanations for a phenomenon. This type of reasoning, entering a zone of “what if,” is regularly used by scientists as they produce new knowledge to ultimately propel scientific discoveries. Thus, generative reasoning should be an aim in science instruction (Duncan, 2007) and has been demonstrated in a number of studies that engaged precollege students in work with models (Windschitl et al., 2008; Schwarz et al., 2009).
Argumentation in Classrooms Using Models.
Another important scientific practice that has been described in classrooms is argumentation, which is defined as the social process of developing an argument. There are many components to an argument that vary in levels of sophistication, but minimally an argument must contain a claim, evidence, and some reasoning that connects the evidence to the claim (Driver et al., 2000; McNeill and Krajcik, 2007). There are two types of arguments: didactic and dialogic. A didactic argument is made to convince an audience that an idea is reasonable, such as a professor lecturing to students on scientific claims or a prosecutor convincing the jury of a case (Boulter and Gilbert, 1995). In contrast, a dialogical argument involves discussion from multiple perspectives on the idea until an agreement is reached (Driver et al., 2000). Practicing the latter form of argumentation in a classroom empowers students to think critically about scientific claims instead of viewing them as “irrevocable truths” and encourages students to articulate their own understanding to others in a coherent and convincing way (Driver et al., 2000). In classrooms, argumentation dialogue is typically promoted by the instructor, often by framing classroom tasks using an oppositional structure (e.g., debating socioscientific issues or posing two sides in discussion groups). Argumentation in the classroom has been shown to increase student understanding of scientific concepts (Zohar and Nemet, 2002; Von Aufschnaiter et al., 2008).
A few studies have suggested that argumentation may naturally emerge in the classroom when experimentation is coupled with model practice (Passmore and Svoboda, 2012; Mendonça and Justi, 2013). Passmore and Svoboda (2012) provided examples of students engaged in argumentation in a classroom that used the practice framework. For example, students constructed arguments to justify why a model they had developed was consistent with experimental data. Mendonça and Justi (2013) described how secondary students were asked to make a concrete three-dimensional model of the intermolecular interactions between iodine and between graphite after performing an experiment comparing the behaviors of the two molecules before and after being heated. The students made sense of their empirical observations by making claims they incorporated into their three-dimensional models. The concrete model was an important resource in the argument process for both visualizing and constructing explanations. Thus, this classroom context of coupling models with experimentation/data interpretation evoked argumentation and led students to build meaningful, evidence-based explanations about scientific phenomena.
In the scientific world, the reliability, validity, and integrity of proposed models are upheld by the argumentative process. Driver and colleagues called argument “the mechanism of quality control in the scientific community” (Driver et al., 2000, p. 301). Therefore, when scientists construct and evaluate their models, they must make arguments for whether the most current data fit their model or judge between competing models to pick which explains their data best. Importantly, scientists are not constructing these arguments solely to persuade the scientific community of their findings but to construct arguments for themselves to help make sense of the phenomenon being studied (Berland and Reiser, 2009). Berland and Reiser (2009) have proposed three goals for using argumentation in science classrooms: to make sense of an idea, to articulate an idea, and to persuade others of an idea. These three goals of argumentation build on, support, and influence one another to ultimately support the practice of argumentation in classrooms.
Instructional Context
We designed Cell and Developmental Biology (CDB) to bring authentic research to a required content course within our molecular and cellular biology (MCB) major. The aim of the curricular design for this course was to encourage an appreciation for research, but more importantly to begin the development of skills needed for students to critically analyze and draw conclusions from experimental data. Though many of our students have the opportunity to conduct research in authentic laboratories, we wanted the research approach to additionally influence the ways in which the students understood science content presented in their required courses. Given the large enrollment of our course, typically ∼170 students at the junior or senior level, we aimed to create a new approach that would make integration of content and practice possible without one-on-one or small-group mentoring by a professor. Thus, the course was built primarily with “active learning” in mind—including extensive small-group work, trained graduate and undergraduate preceptors to increase individual mentoring during class, and formative assessment feedback through use of clicker questions, quizzes, and in-class work.
Using the practice framework (Passmore et al., 2009) as a guide for instructional design, we explicitly focused the course design around biological models that we provided to students in class. These models will be referred to as “target models,” as the instructional purpose was to guide students in using and evaluating established biological models rather than developing their own models. Target models were the topic of whole-group instruction, followed by small-group activities in which the students had the opportunity to interact with those models. Student groups worked together during class on problem sets that included a brief description of one of the target models from lecture, followed by data figures from published scientific articles that supported (or sometimes contradicted) the target model. For each data figure, groups were asked to describe the data, interpret the data, and relate the data to the given target model. Thus, in keeping with the practice framework, we aimed to situate students’ developing understanding of biological phenomena at the interface between models and data, providing students with tasks in which they could see how data patterns were used to develop models and models could be used to explain data patterns.
Problem sets were designed to simplify the data-interpretation process by taking data figures from primary research articles, removing some of the potentially distracting and confusing details, and embedding the task within the context of a biological model. Thus, we refer to our approach for simplifying and scaffolding students’ examination of authentic data as “TRIM” (teaching real data interpretation with models). Our decision to TRIM papers was based on our experience that students within our population had difficulty navigating primary literature. Our observations are supported by previous research, which suggests a myriad of difficulties that can be encountered by students when asked to read novel representations, including an overload of working memory when asked to simultaneously view pictorial representations and lengthy text (Mayer and Moreno, 1998; Brna et al., 2001). By using this TRIM method, we anticipated that students would more readily draw conclusions from the data, and their attention would be focused on the biological relevance of that data through the target model. At the same time, problem sets preserved several aspects of the complexity of interpreting authentic data. The provided data were always taken directly from primary literature (rather than imagined by the instructor). The target models presented within the problem set were sometimes incomplete in comparison with current models (with current models from textbooks presented later), because we felt it was important for students to begin to understand the complexity of science.
Finally, though several papers have reported instructional designs targeted at helping undergraduate students understand published biological data (Kozeracki et al., 2006; Hoskins et al., 2007; Round and Campbell, 2013; Van Lacum et al., 2014), very few have closely examined how students learn to interpret data. Bowen et al. (1999) examined how undergraduate biology students and expert ecologists interpreted a particular data figure. They found that the biologists brought a wealth of knowledge and reasoning resources that the students lacked, which significantly impaired the students’ ability to make sense of the data figure, even though the students had seen a similar figure in class. These authors went on to suggest that “more time is needed [in the biology curriculum] to allow students to develop their own interpretations in a social learning space which permits multiple interpretations of inscriptions.” In keeping with this recommendation, our design for TRIM problem sets required students to create their own interpretations of data rather than simply understand the interpretations proposed by the authors of the paper. Our hypothesis was that, in a collaborative, supported learning environment, it would be possible for students to develop interpretation skills. The focus of our research was to investigate the extent to which students were able to make quality data interpretations in this setting and to understand the mechanisms by which they did so through small-group collaboration.
Research Questions
Our research approach did not aim to quantitatively compare students in TRIM classrooms with students in traditional classrooms. Instead, we performed systematic, qualitative analysis on recorded in-class discussions from consenting individuals in CDB and analysis of these students’ written work. This approach gave us the flexibility to delve more deeply into how students were using scientific practices such as model use and data interpretation throughout our course and to describe the reasoning patterns that could underlie their learning process. Three questions guided our analysis of students’ ability to critically examine authentic data in the CDB course:
To what extent do students build quality interpretations of authentic biological data in this instructional setting?
How do students use the target models to complete the data-interpretation tasks?
What are the most common strategies students use to interpret data in this setting? What are common challenges?
Overall, our goal is to present information about a new instructional approach aimed at integrating model use and data interpretation with biological content in a large-enrollment course. Prior approaches on fostering student work with biological data have been reported in small-course settings and have not focused on explicit model use to support student learning. Second, our research approach, which focused on investigating student understanding through recorded conversations between students during class and artifacts of their in-class work, has the potential to illuminate undergraduate reasoning in this domain. Dialogue between students is a key aspect of science classrooms (Lemke, 1990). Analysis of classroom dialogue can provide unique insights on learning and has been extensively used in research on K–12 education (Talbot-Smith et al., 2013). However, this approach has remained mostly unexplored in undergraduate science education, with some notable exceptions in biology (Knight et al., 2013) and the physical sciences (Brewe, 2008; James and Willoughby, 2011; Walker et al., 2011; Walker and Sampson, 2013).
METHODS
Instructional Design
CDB is co-taught by two instructors, typically enrolls 150–170 students, and employs three graduate teaching assistants (TAs) and three to six undergraduate preceptors. Students are juniors and seniors, most majoring in MCB, with many pursuing careers in medicine. CDB is a four-unit class that meets for two 75- and one 50-min sessions per week. Students are required to form self-selected groups of three to five. Groups are stabilized during the second week of class, with each group creating an individual team name. Groups are stable throughout the semester, unless a student does not work well with his/her group and seeks instructor permission to change. Feedback and points for in-class work are awarded at the group level (for all members in attendance), and instructors randomly call on groups to provide answers to questions during class. Lectures are interactive, with frequent clicker questions and opportunities for small-group discussion. One or two times per week, students work in small groups for 30–50 min on problem sets that are submitted to the instructor. During this time, instructors, TAs, and preceptors assist students.
Problem sets are given as a worksheet handout per group and consist of a short description of a biological model that is the target of instruction, and two to four data figures that students are asked to describe, interpret, and relate to the model. Examples of the problem sets that were the focus of analysis in this study are provided in Supplemental Material 1. Iterative refinement of problem sets took place over 3 years, taking into account feedback from students and preceptors about details such as clarification of figure legends and labels, removal of redundant or confusing figure panels, or sequencing of figures to ensure flow of argument. Also, length and number of problem sets were adjusted to ensure achievement of learning goals within the developing curriculum.
Several features of models and authentic data interpretation guided our design of problem sets. First, arguments and/or topics from primary literature papers were selected to enrich students’ understanding of the basic cell biology concepts that are covered in the course. Second, experimental data were selected from these papers for students to analyze only when directly related to a specific aspect of cartoon models that were chosen to illustrate a given concept. Sometimes models and data came from the same published paper, but sometimes they did not. Third, when choosing data figures to include, we considered whether the experimental technique used would be familiar to the students (a small set of techniques were covered during class and in assigned readings). Experimental techniques that were conceptually simple to follow in basic terms through brief coverage in lecture or short explanation within the problem set were also included. Data figures often came from a single article but sometimes from a pair of related articles. Fourth, students needed to be able to interpret a data figure with relatively little guiding text and make basic conclusions about how that figure would relate to the overall argument or was consistent with some aspect of the model being tested. In a few cases, the data added new information or disconfirmed some aspect of the model, but these higher-order modeling practices were scaffolded by targeted questions in the problem set and instructor discussion. Finally, we made an effort to include some problem sets that exposed students to both the historical work behind important canonical models and cutting-edge research behind current problems. The former was often useful, because the logic and techniques behind experiments was easy to follow and problem sets could be folded into complete stories of how models evolve over time. The latter was a useful way to talk about the uncertainty of science and how scientists are always pushing the boundary of what is known.
An important aspect of the course that evolved over time was the development and implementation of explicit learning objectives aligned with formative and summative assessments. Similar to the NGSS, we took the approach that learning objectives would integrate practice and content when applicable, for example, “Relate experimental data to the signal hypothesis model.” Objectives were shared with students, used to guide exam writing, and emphasized to students as a study tool. Examples of learning objectives and assessments from the course are provided in Supplemental Material 2.
Study Design
Participants.
The CDB course from which we recruited students to participate in this study in the Fall of 2012 and 2013 is taught at the University of Arizona. The University of Arizona is a large, southwestern, public university with a typical enrollment size of 41,000 students. Minority enrollment (excluding international students) at the University of Arizona was 34.9% in 2012 and 36.3% in 2013. Almost all students in the course were MCB majors or double majors pursuing careers in science and/or medicine; about half were juniors and half seniors. Students in the CDB course were recruited for participation, which could involve allowing us to have access to their exams, make copies of their group written work, and audio-record their group during problem set activities. Participants received a small financial incentive for participation. All research activities were approved by our university internal review board.
Ideally, we would have collected data on all students in the course; however, we were limited to the subset of students who consented to participation through audio recording and/or allowing us to analyze their written work for our research. Because our research aim was to analyze student understanding, we wanted to know whether this subset of student participants was representative of the course population as a whole. To determine this, we performed Student’s t tests on exam scores and final course grades. No statistical difference between the participating subset and the class as a whole is ideal, because it would indicate a representative sample. In year 1, from a class of 154 students, 58 participated; all were audio-recorded (14 groups); no written work was collected that year. In year 2, from a class of 138 students, 88 participated; all provided access to written work (21 groups), and 45 also agreed to be audio-recorded (11 groups). Table 1 shows a comparison between the mean exam scores of students who did and did not consent to study participation in each year; Table 2 shows similar data for final course grades.
Table 1.
Comparison of all students to consenting students on mean exam scoresa
| Year | All students | Students consenting for written work | p | Students consenting for audio recording | p |
|---|---|---|---|---|---|
| 1 | 76 (1.3) | NA | NA | 78 (1.6) | 0.227 |
| 2 | 76 (0.9) | 78 (0.9) | 0.130 | 80 (1.1) | 0.030 |
aNumbers in parentheses represent SE. Student’s t tests were used to generate p values.
Table 2.
Comparison of all students to consenting students on final course gradesa
| Year | All students | Students consenting for written work | p | Students consenting for audio recording | p |
|---|---|---|---|---|---|
| 1 | 82 (1.1) | NA | NA | 85 (1.0) | 0.100 |
| 2 | 86 (0.7) | 87 (0.7) | 0.211 | 89 (1.0) | 0.044 |
aNumbers in parenthesis represent SE. Student’s t tests were used to generate p values.
In year 1, there were no significant differences between all students and those who consented to study participation, by either measure. In year 2, there were no significant differences between all students and those who provided access to written work, but there were significant differences between all students and those who agreed to be audio-recorded, on both measures. Thus, for the majority of data collected for the current study, we can assume results are representative of the class as a whole, but for the audio data collected in the second year, we cannot rule out the possibility that students were performing at a somewhat higher level than their peers.
Data Collection.
Data consisted of audio recordings of groups discussing problem sets on worksheets during class, scanned copies of written responses on these worksheets, and copies of course exams and exam scores. Audio recordings provided an accurate picture of the process students used to solve problems during class. An additional benefit was that these recordings revealed many student thoughts, as individual students tended to think out loud or elaborate their thoughts when communicating with their group members. From the data set, we sampled four problem sets spanning the semester to transcribe and analyze. These problem sets were selected because they covered diverse topics in cell biology and represented a range of difficulty for students. This diversity of problem sets helps to ensure that findings could be generalized beyond the specific context of one worksheet and increases the overall number of instances examined. The selected problem set topics include ion channels and membrane potentials in cystic fibrosis, cell cycle control, receptor-tyrosine cell signaling in cancer cells, and development of therapeutic drugs to target BRCA2-deficient tumors. All problem sets are presented in the Supplemental Material; subsequent references to these problem sets will include the titles: Cystic Fibrosis, Cell Cycle, RTK Signaling, and BRCA Tumors, respectively. Any audio files that were too poor quality to transcribe or transcripts that appeared incomplete were omitted from the data set. Thus, only transcripts containing a full discussion of at least one data figure were included in data analysis (n = 55 transcripts from four problem sets over 2 yr).
Analysis of Student Dialogue.
Owing to the exploratory nature of our study, we wanted to approach the audio transcripts with a relatively open mind. Thus, rather than selecting an existing theoretical framework or determining coding categories a priori, we decided to use a constant comparison method in which themes and eventually coding categories emerged from (and were grounded in) our data (Saldaña, 2008). Analysis began with open reading of transcripts from different groups on different problem sets to identify themes across the data set. All authors read and discussed what they noticed, with particular attention paid to ways that groups used the target model and any common strategies used or challenges faced as groups interpreted data figures. These observations were organized into three themes from which three coding schemes were developed: “productive model use” and “common strategies for interpreting data,” which respond to our primary research questions and the “presence of argumentation” coding scheme, which emerged from the data. When we discovered “argumentation” as an emergent theme in our data, we used several previous studies to frame further analysis and refine our coding scheme (Boulter and Gilbert, 1995; Driver et al., 2000; Berland and Reiser, 2009). All coding schemes for this study can be found in Supplemental Material 3. Briefly, the productive model use coding scheme was developed to describe the different ways groups used the target model; a preliminary scheme was refined through application to 20% (n = 11) of transcripts. For the remaining transcripts (n = 44), two coders independently coded every data figure discussion (n = 104) for the incidence of at least one instance of “productive model use.” If no “productive model use” occurred, then the data figure discussion was coded as “vague, unproductive model use,” “missing a model link,” or “too difficult to tell.” The percent agreement between two coders was 75%. The “presence of argumentation” coding scheme determined whether transcripts (n = 55) included at least one instance of argumentation. Argumentation was defined as dialogue between at least two students engaged in building claims through evidence. Percent agreement was high (92%), for a random sample of 20% of the data (n = 13 transcripts). Therefore, the remainder of the data were coded by one researcher. The third coding scheme focused on common strategies groups used to interpret authentic data in this classroom setting and some common challenges. Two coders determined whether transcripts (n = 55) included at least one instance of each code. Percent agreement was 86%. All results (with the exception of presence of argumentation) are reported as the consensus between coders.
Finally, to demonstrate the extensive nature of student–student conversations recorded (relatively uninterrupted by whole-class instruction), we counted the number of speaker turns for a random selection of 14 transcripts. There were an average of 35 speaker turns per data figure and an average of three data figures per in-class activity (therefore, ∼105 speaker turns per recorded conversation).
Analysis of Written Work.
Analysis for the scanned copies of groups’ written responses to in-class problem sets was performed to measure quality of final written data interpretations. We developed a coding scheme (provided in Supplemental Material 3) dividing the quality of data interpretations into two components: validity (V) and generativeness (G). For validity (appropriate data claims supported by evidence in the data figure), we developed a list of two to three key points per data figure. Written responses were coded on a three-point scale for no key points present (level 1), at least one present (level 2), or all present (level 3). Generativeness (the degree to which the interpretation moved beyond a literal description of the figure) was coded on a four-point scale. Written responses were coded as level 1 if they were only descriptions of data that did not include an inference, level 2 if they included an inference tied to the immediate context of the figure, level 3 if they moved beyond the literal details depicted in the figure to include connections to biology and/or the target model, and level 4 if they were far-ranging enough to necessitate additional experimentation. Only problem set prompts that asked students explicitly to interpret the data and relate to the target model were coded. These question prompts were Cystic Fibrosis (questions 4–6), Cell Cycle (questions 1 and 3), RTK Signaling (questions 3 and 4), and BRCA Tumors (questions 3, 5, and 6). Agreement between two coders was 73% across the sample (133 responses from 21 different groups on four different problem sets). All results are reported as the consensus between coders.
RESULTS
Measuring Data-Interpretation Quality
We measured the quality of students’ written data interpretations in terms of validity and generativeness. Validity referred to whether or not students included ideas that could be reasonably concluded from the data provided. Generativeness referred to how well the interpretation expanded beyond what was immediately present in the data figure. We included generativeness because the ability to interpret data requires a level of inference beyond what can be literally seen and because scientists must use generative thinking when examining data to build new hypotheses and novel ideas. The two components, validity and generativeness, were treated independently, since one can be generative about invalid ideas or one can make valid points but make interpretations within a limited scope.
We scored 133 written responses, sampled from 21 different groups across four different in-class activities. Validity and generativeness were each scored on a three-point scale (as described in the Methods section). Scores are shown in Table 3.
Table 3.
Percent and range of scores for written data responsesa
| Level 1 | Level 2 | Level 3 | Level 4 | |
|---|---|---|---|---|
| Generative | 13% (0–29) | 20% (0–40) | 64% (43–84) | 2% (0–15) |
| Valid | 13% (0–36) | 49% (29–69) | 38% (14–50) | NA |
an = 133 group responses across four in-class activities. Range is in parentheses.
The majority of the responses contained one or more valid conclusions (score of 2 or above). Of the responses containing all key points (score of 3), only 5% revealed nominal mistakes, such as an improper word use. Because we asked students to describe and interpret each data figure and relate it to the target model, we anticipated that it was possible for each group to receive at least a level 3 score for generativeness on any data figure. Indeed, scoring demonstrated that more than half of the student responses did include inferences about data that expanded beyond literal descriptions of figures to include ties to a biological context, typically that of the target model (level 3). In addition to the three primary levels, a very small number of responses included interpretations that expanded beyond the target model to include a hypothesis that would require additional experiments to test. Because we wanted to capture the full range of generative thinking that was possible in this task, we placed these responses in a separate, higher category, level 4.
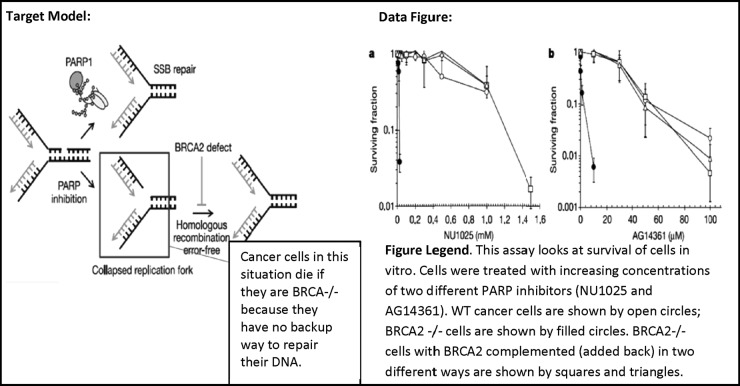
To illustrate how we defined the levels of generativeness, we provide examples from students’ written responses below. These examples are taken from our BRCA Tumors problem set, whose topic is cancer cell–specific therapy (see target model and data panel in Figure 1).
Figure 1.
Example of a target model and data figure taken from the BRCA Tumors in-class problem set. Images were taken from a published research article (Bryant et al., 2005; Helleday et al., 2005); the explanatory box pointing to collapsed replication fork was added. Figure legends were written by the course instructor and were provided to students. The target model shows PARP protein repairing single-stranded breaks (SSB) in DNA, but if inhibited, the SSB can cause a collapsed replication fork, which includes a double-stranded break in DNA that BRCA2 protein repairs through homologous recombination. Therefore cancer cells that are BRCA2-deficient are sensitive to PARP inhibition. The data figure consists of two line graphs that show how cancer cells missing BRCA2 are more sensitive to PARP inhibitor drugs than wild-type cancer cells containing BRCA2; and this phenotype can be rescued to behave similar to wild type by complementing BRCA2.
Level 1 interpretation:
A & B shows defect in the BRCA2 would have less chances to survive. A & B w/ BRCA2 added back show the same pattern as wild-type BRCA2. (Group 27)
Level 2 interpretation:
The data shows that cells with deficient BRCA2 treated with PARP inhibitors have a significantly lower surviving fraction than cells with wild-type BRCA2 added back. Also, cancer cells behave similarly to cells with complemented BRCA2, with the surviving fraction decreasing as the PARP inhibitor concentration rises. From this, we can infer that BRCA2 addition to BRCA2-deficient cells is sufficient to rescue the cell by increasing the surviving fraction in higher concentrations of PARP inhibitors. (Group 29)
Level 3 interpretation:
Survival of BRCA2 mutants is exceptionally lower than wild-type cancer cells in the presence of small amounts of the PARP inhibitors. The cells cannot utilize the SSB [single-stranded breaks] repair pathway, and ultimately apoptose when homologous repair fails. How it relates to the model: When PARP proteins are inhibited, the only available repair pathway is Homologous Recombination, which is absent in the BRCA2 mutants. When BRCA2 is added back, cells survive like wild-type cancer cells. (Group 16)
Group 27’s response essentially describes the behavior of the lines in the graph. The students noticed that BRCA2-deficient cells “have less chances to survive” and that BRCA2 complemented and wild-type cell lines have the “same pattern.” Therefore, this group demonstrates its ability to read the graph but does not expand its observations into an inference. In contrast, Group 29 made the same observations that BRCA2-deficient cells “have a significantly lower surviving fraction” and that BRCA2 complemented and wild-type cell lines “behave similarly.” However, they expanded these observations into an inference that BRCA2 is “sufficient to rescue” the cells, indicating that BRCA2 is important for cell survival when PARP is inhibited. Finally, Group 16 observed the same pattern that BRCA2-deficient cells (which they call “BRCA mutants”) have “exceptionally lower” survival and that BRCA2-complemented cells “survive like wild type.” However, this group’s inference is tied into the biology from the target model. Group 16 conceptualizes that PARP inhibitors are causing single-stranded breaks (SSBs) in the cells and mentions the biological consequence that when BRCA2 is absent, homologous repair of the DNA fails. This group uses words directly from the target model (“SSB repair,” “homologous repair”) that are not immediately present in the data figure to expand the scope of their data interpretation; thereby providing a biological mechanism that is not present in the data figure.
How Student Groups Used the Target Model
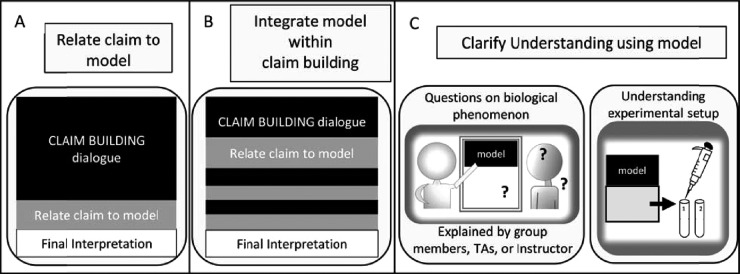
Our second research question focused on understanding whether and how the target models we provided may have served as an instructional tool for students. We first examined transcripts from different groups working on diverse in-class activities using the open question: How are students using the target model? Through this analysis, we identified three primary ways in which the students used the target model (Figure 2).
Figure 2.
Different forms of model use observed during small-group discussions. Students used models productively in three primary ways, shown in A–C, while interpreting data during in-class problem-solving sessions.
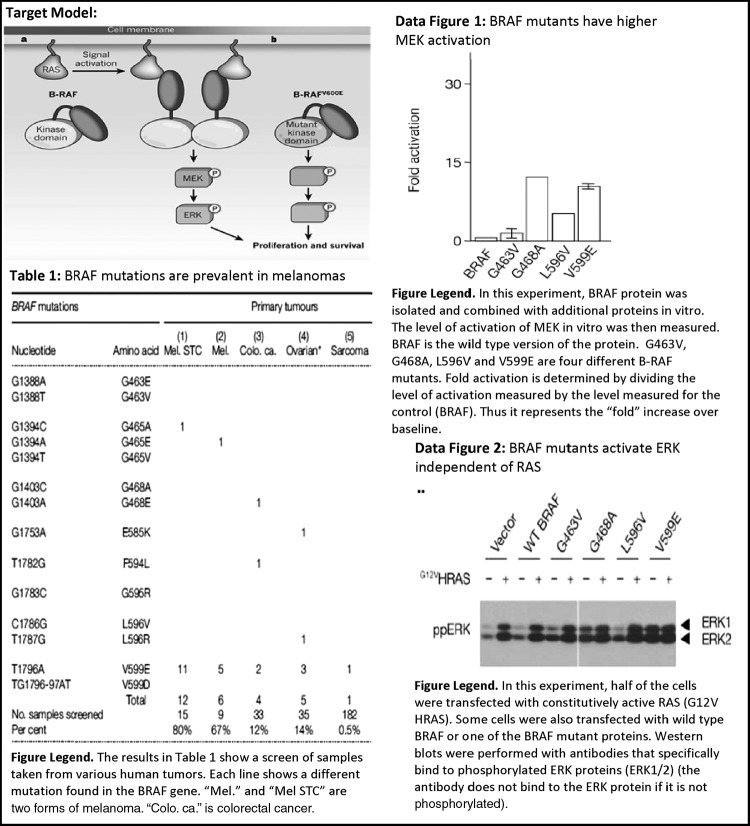
In the first form (Figure 2A), students focused on data to make and refine claims until a consensus was reached, and then they related that claim to the target model, sometimes explicitly reacting to the activity prompt “relate to the model.” Relating to the claim meant expanding the data inference with biology directly from the target model; this included adding greater mechanistic detail or defining a biological role, such as “this is why cancer cells survive” or “this is why cancer cells die with this drug treatment.” To illustrate, the group quoted below was working on the RTK Signaling problem set, exploring BRAF as an oncogene (Figure 3). The group discussed the bar graph shown and the target model (Figure 3). The excerpt begins at a point where a claim has been made about the graph showing how various BRAF mutants have higher levels of MEK activation compared with wild-type BRAF. Before this excerpt, the group discussed the experiment:
S1: In here, it says MEK activation is what it is, so I would say that, um, basically it’s showing that the mutant versions of BRAF have higher, are, um, able to increase MEK activation, or have, like, a higher MEK activation than, um, just wild-type BRAF.
S2: What is the MEK activation leading to? Oh, it increases proliferation.
S1: What?
S2: So then the MEK increases proliferation and can cause it to be cancerous. Right here, that’s where I’m getting it from, the MEK proliferation and survival
(Group 1, RTK Signaling)
Figure 3.
Examples taken from the RTK Signaling in-class problem set. Target model image was taken from a review article (Lavoie and Therrien, 2011); data images were taken from a published research article (Davies et al., 2002). Figure legends were written by the course instructor and were provided to students. The target model on the problem set shows the normal signaling cascade of RAS→BRAF→MEK→ERK compared with a BRAF mutant that activates its downstream effectors independent of its upstream activator, RAS, thereby promoting cell proliferation and survival. Data Table 1 demonstrates the high incidence of certain mutations in BRAF in melanoma tissue samples. The bar graph in Data Figure 1 shows higher bars (indicating activation of MEK) for certain BRAF mutants listed on the x-axis. The Western blot in “Data Figure 2” is measuring the change in ERK phosphorylation with and without the presence of a constitutively active RAS and with the addition of various mutant forms of BRAF. The data figure demonstrates how the RTK signaling cascade can be short-circuited with a mutant BRAF activating its downstream effectors (MEK and ERK) in the absence of upstream RAS signaling.
S1 correctly infers from the bar graph that BRAF mutants tend to induce higher levels of MEK activation. Without additional information or knowledge about the biological mechanism, this is as far as the interpretation may go. Instead, S2 refers to the target model to broaden the claim to include the biological role or significance of increased MEK activation, that is, the role of mutant BRAF in promoting cell proliferation and survival, which are associated with cancer. In this case, S2’s question, “What is the MEK activation leading to?,” prompted the group to use the target model to relate the group’s claim to a biological context. In other cases, students read aloud the activity prompt “How do these data support the model?,” which seemed to guide them to expand their claim.
In the second form of model use, students used ideas from the target model while making sense of data figures (Figure 2B). In these cases, biological ideas, often from the target model, were woven through the dialogue in which students formed interpretations of data figures. Because using models and interpreting data are highly integrated cognitive processes for scientists, student groups using this form appeared to be working at a higher level. We illustrate with an example from a group on the BRCA Tumor problem set discussing the line graph, shown in Figure 1. For ease, ideas that are exclusive to the line graph are highlighted in bold, while ideas exclusive to the target model are underlined:
S3: What I can see is that if you increase the concentration, survival goes down more and more.
S1: Well BRCA2, when you have a deficient BRCA2 it stops the, no. When you don’t have BRCA2, you don’t have proper homologous recombination. So if BRCA2 is there then it doesn’t inhibit that? So wild-type BRCA in this case will facilitate homologous repair
S4: Not facilitate it, it just doesn’t inhibit.
S1: No, well BRCA2 is an important part of the homologous recombination. Without it, it doesn’t go. So basically wild type will fix double-stranded breaks. So that’s the function of BRCA2.
[…]
S1: So the black ones are the ones without BRCA2, and then the open circles are wild-type, so you see it has survivability, same here. Increasing PARP inhibitor, meaning the more single-stranded breaks we create, the more it dies, right?
S4: I’m sorry?
S1: The more you increase the PARP inhibitors, the more single-stranded breaks, the more you die. Survival goes down.
(Group 21, BRCA Tumors)
The students in this group are noticing data patterns, such as how higher concentrations of the PARP inhibitor drug correspond to lower levels of cell survival. These data patterns are given biological significance using ideas from the target model. For example, since the PARP protein repairs single-stranded breaks, S1 reasons that, in the line graph, increasing a PARP inhibitor drug means “the more single-stranded breaks we create.” Additionally, in the line graph, the wild-type cells containing BRCA2 display “survivability,” and S1 pairs this with the idea that BRCA2 “will fix double-stranded breaks.” Therefore, student groups conceptualize what BRCA2 and PARP proteins are doing in the cells by working at the interface between model and data.
In addition, integrated model use was sometimes used by one group member to add support to a potential data interpretation being considered by the group. To illustrate, we provide a second example from Group 21 as group members continue to work on the BRCA Tumors problem set. The quoted text begins during the students’ discussion of Figure 2, which shows cell survival rates with various combinations of short interfering RNA (siRNA)-induced knockdowns of the BRCA2, PARP1, or PARP2 genes. Ideas from the data figure are highlighted in bold and ideas exclusive to the target model are underlined:
S2: So that just shows that this alone can significantly increase the survival rate of the cell.
S1: Which one?
S2: Just this one, see, compared to this one, which has both of them.
S1: Well this one doesn’t have that and it’s high.
S2: Yeah, so then, wait no, wait. You’re right. I don’t know then, [crap]. I’m confused
S1: It’s because PARP1 is pretty [dang] important. But then you don’t have any PARP1 and you’re fine because you have BRCA2.
S2: But you have this one, are you talking about this one?
S1: Well I mean, it shows that like there’s two different pathways to fix these breaks and keep the cell alive and it’s BRCA2 and PARP1. PARP1 is the one that fixes single-stranded breaks and BRCA2 is the one that fixes this step right here.
S2: Alright, but if you, so if you see these three, each of them is very high, so…
S1: That’s because only one is missing, so they can each save each other. So we’re missing this, but PARP1 can do that job. We’re missing this but BRCA2 can do that job. But this one we’re missing, I don’t get why that one’s perfect though. I guess PARP1 is sufficient enough to do it all by itself.
(Group 21, BRCA Tumors)
In the first line, S2 poses a potential interpretation of the data figure. S1 immediately challenges this idea, eventually leaving S2 unable to respond and confused. S1 then attempts to pose a new potential data interpretation, suggesting that BRCA2 is a backup DNA repair mechanism when PARP1 is missing. S2 attempts to challenge or clarify S1’s suggestion by pointing to the data figure. S1 immediately refers to the target model as support for his interpretation. Finally, the discussion turns back to the data figure with insinuations from the target model integrated within, such as how BRCA2 and PARP1 “can save each other.” Thus, integrated model use was not only used by students to make sense of data figures during interpretation but in a few cases as a means to convince group members of the validity of potential interpretations.
The last form of model use involved using the target model as an explanation tool (Figure 2C). In some cases, students used the target model to better understand the experimental setup for a particular data figure. For example, the student below begins to read the figure legend for the MEK activation bar graph figure on the RTK Signaling problem set (Figure 3) and refers to ideas in the target model to help conceptualize the experiment before attacking the data figures:
S1: Isolated and combined with additional proteins in vitro. MEK was then measured [reading from figure legend], which is the protein, the phosphorylated protein one step down in the pathway [from model]. Okay. RAF … So.
(Group 13, RTK Signaling)
S1 applies information from the target model to mentally orient the MEK protein’s place in the pathway, whose activity is being measured and represented in the y-axis. Thus, the target model was used by this student to make sense of what the data figures might show before developing any data claims. We also found the target model was used by TAs, instructors, and group members as an explanatory teaching resource when students had questions about the biological phenomenon being studied. In all, the target model was used by the groups in various ways to help develop and biologically situate data interpretations. However, we did identify a few cases in which students had model-based reasoning errors with the target model and in some instances misinterpretation of the model hampered understanding of problem sets.
To provide more information about how often the model was used in these productive ways, we performed coding analysis in which we examined discussions of individual data figures. This analysis included 55 transcripts from 23 groups over four different in-class problem sets. We found that 59% of total figures discussed to completion (n = 104) contained at least one productive use of the target model (Table 4). Discussions marked with this code fell into one of the three productive forms of model use shown in Figure 2. In discussions that were not coded as “productive model use,” students either failed to mention the target model or were unable to form a coherent link between the data and the target model. In a small number of cases, it was too difficult for coders to determine from the available dialogue whether the target model was being used productively. Overall, coding analysis revealed that, although prompting students to relate interpretations to the target model at the end of each data figure generally encouraged groups to successfully enhance their interpretations, it was not sufficient to cause students to form explicit biological connections in every case.
Table 4.
Frequency of qualitative coding categories within transcriptsa
| Category | Frequency (%) |
|---|---|
| Productiveb model use | 59 |
| Argumentation | 82 |
| Decoding | 89 |
| Noticing patterns | 98 |
| Rabbit hole | 20 |
| Rabbit hole aversion | 5 |
an = 55 transcripts coded at whole transcript level with the exception of “productive model use,” which was coded for the discussion of each individual data figure.
bn = 44 transcripts; 104 data figures.
Common Strategies and Challenges for Data Interpretation in Group Settings
Argumentation: Students Spontaneously Used Argumentation as a Sense-Making Tool to Interpret Data Collaboratively.
An interpretation of data can be thought of as one’s argument for what the data mean or signify. Hence, tasking students to arrive at a data interpretation in a group setting creates an opportunity for students to build arguments for what data may mean. Indeed, one of the strategies to emerge from analysis of the in-class dialogue was argumentation. We defined argumentation as at least two students engaged in building claims or inferences about data figures and providing direct evidence from the data figures to support those claims. Argumentation was common despite the lack of explicit prompting from the instructor, occurring at least once in 82% of coded transcripts (n = 55; Table 4).
Argumentation dialogue in this setting was surprisingly collaborative. Students often engaged in sense-making dialogue, co-constructing claims and arguments collectively. For example, if a student posed a claim, another student might spontaneously offer evidence as backing so that at the group level, the argument had support. To illustrate, Group 16 below is discussing a data table that lists various clinical tumors found to contain mutations in the BRAF gene, with a majority occurring in melanoma tumors (see Figure 3):
S2: Mutations in BRAF are associated with the incidence of skin cancer, or melanoma. [INITIAL CLAIM]
S1: You can also get colorectal or ovarian, but you are right, skin cancer dominates.
S3: Yeah, you have 80 and 67 then you have 12 and 14 [percent]. [EVIDENCE]
S2: Melanoma dominates as the primary tumor for these BRAF mutations, however. [CLAIM]
[…]
S1: These are both melanoma, the first 2. So you see really large percentages there. [EVIDENCE]
S2: So in other words, mutations in BRAF pretty much are gonna [inaudible] melanoma cancers.
S4: Melanoma?
S2: Yeah.
S3: You have higher incidence of mutated BRAF than, in skin cancer, than in other cancers. [FINAL CLAIM]
(Group 16, RTK Signaling)
The group co-constructs the argument that BRAF mutations are primarily found in melanoma tumors (claim) because a larger percent of melanoma tumors compared with other tumors contain a BRAF mutation (evidence). S2 and S1 propose the claim; S3 offers the specific evidence to back it up. The claim evolves, subtly, through the dialogue. Where the initial claim only captures the simple relationship that BRAF is associated with melanoma, the final claim considers other variables in a comparative relationship in which BRAF is more common in melanoma than the other cancers.
We also found that sometimes when students spontaneously offered evidence to the previously mentioned claim, they found the evidence was not supportive and instead contradicted the claim. The newly revealed evidence either led to a claim refinement or the original claim had to be justified in some way. To illustrate, Group 6 below makes a claim refinement in light of new evidence offered by S2. Group 6 is discussing the data from a Western blot experiment from the RTK Signaling problem set (see Figure 3):
S1: Oh. Okay, so that makes sense then, because only if it’s phosphorylated do you get the antibody that shows up. So it means that when you have the mutant form of RAS, you are getting a band in the positive lanes because it is always being phosphorylated. Do we agree with that? [INITIAL CLAIM, WITH EVIDENCE]
S2: But in some of the mutants, you are getting bands in the negative lanes too. [EVIDENCE]
S3: So, like, here and here, those two mutants have bands in the minus parts showing that the mutant form of RAF is constitutively active. [REFINED CLAIM, WITH EVIDENCE]
S2: Independent of RAS.
S3: Independent of RAS, so it doesn’t need a signal from RAS to be active. [REFINED CLAIM]
S1: Oh, I see what you’re saying. Wait, can you say that again, [name omitted]?
S2: It means it’s [mutant BRAF] active without the RAS doing anything to it. [FINAL CLAIM]
(Group 6, RTK Signaling)
In this case, S1 makes an initial claim with evidence, S2 checks that claim against the evidence, and S3 refines that claim in light of the new evidence. Together S2 and S3 add to the argument to enhance its quality, thereby arriving at a final valid data interpretation.
In the aforementioned examples, instead of forming individual back-and-forth arguments, the groups worked collaboratively to co-construct arguments that ultimately became the final data interpretation, which we view as sense-making argumentation. Occasionally, argumentation took a persuasive form in which a student provided a claim with evidence that was countered by another student with a different claim with evidence (∼5–7 times less often than the sense-making form). For example, Group 17 is discussing data from the BRCA Tumors problem set (Figure 1), debating which PARP inhibitor drug is more effective at killing cancer cells:
S1: This one’s more effective, I mean NU’s more effective. [INITIAL CLAIM]
S3: I think AG is more effective, because if you look at that really steep curve, if you have this one … [counterARGUMENT because CLAIM with EVIDENCE]
S1: This one?
S3: Yeah, if you look at that line.
S1: But I feel like this one’s more steep, right? I feel like this is more gradual than this one. [counterARGUMENT because CLAIM with EVIDENCE]
S3: I think you also have to look at the concentrations, ‘cause this one’s in micro and this one’s in millimoles. [EVIDENCE supporting own argument earlier]
S1: Oh.
[…]
S3: Yes, so this in micromoles, a little bit would be enough to kill all of them. And this one in millimoles … [CLAIM]
[…]
S1: And it should be somewhere around here, right? So this curve, so this is more effective then. [FINAL CLAIM]
S3: Yeah, I would think so.
(Group 17, BRCA Tumors)
In contrast to the previous examples, the argumentation in this example takes a persuasive form, which is highlighted by three main differences. First, the arguments in this example are not co-constructed, because each speaker offers a complete argument (claim and evidence). Second, two competing arguments are in discussion, so that any further evidence offered by group members is aimed to support one argument over the other. By contrast, in the sense-making form, one argument is discussed so that any further evidence offered either supports or contradicts it. Third, in persuasive argumentation, the final claim arises from the argument that “out-competes” the other argument. In the sense-making strategy, the final claim arises through group refinement of the initial claim.
Thus argumentation in this authentic biological data–interpretation classroom setting was primarily sense-making rather than persuasive (Berland and Reiser, 2009), because group members rarely used evidence in an attempt to convince the group of their individual claims but rather offered evidence to support or contradict the groups’ working claim. However, in both of these forms, the argumentation is dialogical, because multiple claims or evidences or arguments are considered until an agreement is reached as a group. By contrast, we did find didactic situations of argumentation in group contexts in which a leader voice would guide the rest of the students in a teaching manner, but this was quite uncommon (roughly 10% of discussions).
Decoding Data Representations: “Dude I can’t even read these graphs, I don’t know what the triangles mean.”—Students Worked Together to Make Meaning of Symbols and Graphs.
Data representations are embedded with meaningful symbols, numbers, lines, and so on. As the student quote above suggests, to interpret a data figure, one must decode the meaning of these representational features. Indeed, most transcripts contained at least one instance of students stating or questioning aloud what markers, numbers, symbols, or codes meant in the data figure (Table 4). To illustrate, Group 6 below discusses a data figure on the RTK Signaling problem set shown in Figure 3 (the Western blot):
S1: Like, what are these …
S2: These are different types of mutants of the RAF. So they either added wild-type RAF or various mutant forms of RAF.
S1: Oh, okay.
S2: And I guess this plus means that it is [a] constitutively active thing and the minus means it doesn’t?
S3: It does mean that or minus doesn’t mean mutation, does it?
S2: Cause it’s like each RAS here …
S3: Okay, so plus means it does have it.
S2: Yeah.
S3: Okay.
(Group 6, RTK Signaling)
S1 questions what the different codes arranged at the top of the Western blot display mean, and S2 immediately responds that they represent the different BRAF mutants. Likewise, S2 and S3 work together to establish that the pluses and minuses signify addition or absence of constitutively active RAS to the cells. We found students routinely relied on their group as a resource to decode the data figures as opposed to individual processing, despite the presence of that information in the simplified legend on the problem set (see Supplemental Material 1 for the complete problem set). It was also typical for students to ask and answer their own decoding questions out loud in their group. There was not any case in which the data-interpretation process became stalled at the decoding stage; however, groups did vary in the amount of time spent decoding figures, and they encountered varying degrees of hindrance, including in some cases incorrect decoding. If students did reach a point where they could not decode the figure, they sought out and received instructor/TA help. Finally, decoding did not necessarily have to occur before the claim-building dialogue. We often found decoding dialogue happened concurrently with claim building, showing that the data-interpretation process did not follow a rigid, linear progression.
Finding Patterns: Students Used Patterns in Data to Build Interpretations.
One of the most difficult aspects of data interpretation is assigning meaning to the patterns in the data, as exemplified in the following student quote:
All I said is that one decreases, that one stays, and then this one, like, it’s the same thing as these two overlapped. That one stays and that one decreases, but I don’t know why.
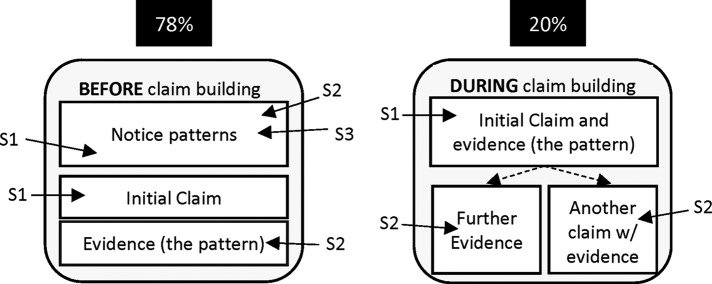
Student groups very aptly noticed and explicitly pointed out patterns in the data figures, almost all containing at least one instance of pattern noticing (Table 4). These instances included remarking on differences between variables in the data figure, such as if something is darker, lighter, shorter, longer, wider, higher, lower, increasing, decreasing, and so on. However, as exemplified in the student quote above, making claims or arguments for “why” the data behave the way they do can be more difficult. Just as group members collaboratively constructed claims and arguments about data figures, we also found the majority of pattern noticing occurred at the group level. Of the 98% of transcripts containing an instance of pattern noticing, 78% contained instances of students explicitly pointing out patterns within the group until a claim or argument was subsequently developed (Figure 4).
Figure 4.
Student dialogue during pattern noticing took two primary forms. Most commonly, students within the group described data patterns before making claims about the meaning of the data figure. Less commonly, data patterns were described during claim building. In both forms, patterns within data figures would then be used as evidence to support the claim.
In the remaining 20% of transcripts, students referred to patterns only within the claim-building dialogue. In other words, groups in this minority either noticed patterns individually before posing interpretive claims or simultaneously made claims while noticing patterns. We infer from these findings that, in most cases, group members were helping each other determine which patterns to focus on before using those patterns to form conclusions about the data.
Falling Down the Rabbit Hole: When Pattern Hunting Goes Wrong.
Authentic data representations are littered with extraneous variables or patterns, and we found that student groups typically were able to sift through these features. However, in some cases, students drew inappropriate comparisons or focused on irrelevant patterns. Unless rectified, students may build invalid claims based on the distracting pattern, become lost and frustrated, and ultimately spend limited classroom time on an unfruitful path. When students in a group focused their attention too long on a distracting pattern or aspect of the data representation, we called this a “rabbit hole.” We defined a rabbit hole as 10 or more speaker turns on the distraction. To put this number in context, there are an average of 35 speaker turns per data figure. Thus, for a discussion to be coded as a rabbit hole, a group had to spend close to a third of its figure discussion time on a distracting pattern. Falling down rabbit holes was uncommon relative to other behaviors we coded (Table 4).
To illustrate a rabbit hole, we provide an example from a group discussing the ERK phosphorylation Western blot that is shown in Figure 3. To arrive at the relevant conclusion (mutations within the BRAF gene lead to a constitutively active form of the BRAF protein that induces signaling independent from upstream factor RAS), one must focus on the fact that some of the BRAF mutants (G468A and V599E) have phosphorylated ERK (ERK1/2) in both the plus and minus RAS lanes compared with wild-type BRAF, which has phosphorylated ERK only in the plus RAS lane. A potentially distracting variable in this figure is the subtle differences between ERK1 and ERK 2 (two very similar protein kinases). Here, one group focuses on these differences:
S2: How is ERK1 and ERK2 different though? Like in this pathway, like?
S3: What are the differences?
S2: Are they both like the orange things? [reference to target model]
S3: Isn’t ERK1, like, in one pathway and ERK2 goes in another pathway?
S2: That’s what I was thinking, but it really doesn’t seem like ERK on the left is phosphorylated and it says both are …
S3: Yeah, I don’t know where we see ERK1 and ERK2, where they are at, like, separately.
S2: Yeah, I don’t know, that’s what I am saying.
S1: Yeah, I don’t get it. I don’t know the difference between ERK1 and ERK2.
S2: I don’t know how that makes a difference here.
(Group 16, RTK Signaling)
It is not necessarily detrimental to focus on irrelevant patterns during data interpretation, but eventually one needs to notice the appropriate pattern to make a relevant, valid data interpretation. The time spent on distracting patterns was more costly for some groups than others. For example, we found some groups eventually focused on the relevant pattern and made valid interpretations. However, other groups became lost and frustrated, which led to either seeking instructor help or running out of classroom time.
Fortunately, we found the group setting sometimes did offer the opportunity for members to redirect attention away from a rabbit hole. For example, the following discussion is focused on the same distracting variable in Figure 3 as was discussed above:
S1: Um … So I don’t get, though, like, what is the difference between ERK1 and ERK2?
S2: I think it’s just different forms of this kinase, like, they’re different kinds of this kinase.
S1: Right. But I mean, like … is ERK2 in this pathway or, I mean, what is the …
S2: I think there’s just multiple ERKs, like, just, don’t worry about it. Like MEK phosphorylates ERK when there’s more than one, like … types 1 and 2 … I think.
(Group 5, RTK Signaling)
S1 from Group 5 begins to focus on ERK2 and even attempts to uncover significance for it in “this pathway,” but S2 redirects the attention away from the ERK1/2 distraction. The rationale that S2 gives briefly involves recentering on the purpose of the model, or the signaling cascade where “MEK phosphorylates ERK.” Hence, for S2, the different types of ERKs did not matter for the purpose of this data figure. We coded this type of explicit redirection of a student who was focused on a distracting variable as a “rabbit hole aversion” (RHA). These explicit instances were rare (Table 4). In other instances that were not included in this coding category, RHA occurred more subtly from students listing different patterns (relevant and irrelevant) and eventually settling on a relevant pattern for data interpretation.
In summary, we found that, in order for students to interpret data in our classroom setting, they decode the data representation, notice patterns in the data, and assign meaning to the patterns through cycles of argumentation. Argumentation was prevalent and primarily took the form of sense-making. All of the strategies for data interpretation that we identified relied to a large extent on collaboration between group members, suggesting that learning authentic data interpretation is a complex cognitive task that benefits from group interactions.
DISCUSSION
Data interpretation is a complex skill that should not be ignored in undergraduate biology course work. We propose that engaging with scientific data should be integrated in some way within all undergraduate biology courses, not only specialized electives. We propose an instructional design for integrating interpretation of authentic data with key ideas in cell biology through the use of models (TRIM). The intent of the design is to allow students not only to practice scientific skills but also to provide the potential for students to gain a deeper understanding of concepts by tying those concepts to experiments. Our design is relatively simple and can be used to make changes within courses focused on other content topics. We have demonstrated that students working in groups within a large-enrollment course can make valid and generative data interpretations that directly tie to conceptual ideas within the course. By carefully analyzing students’ data interpretations as well as how they made these interpretations through group dialogue, we have uncovered several important features of the process of student reasoning in this domain. First, we demonstrated that models can be used by students to help students connect the patterns they observe in data figures to a broader biological context, much in the same way that scientists use models as a framework for experimentation and other forms of data analysis. Second, we showed several ways that peers serve as a rich resource for data interpretation in a group setting, in particular through the scientific process of argumentation. Third, we revealed some of the different ways that students approach the symbols, patterns, and trends within data figures and how group interactions impact this process.
Challenges of Working with Authentic Data in the Classroom
In examining how students interpreted authentic data, we uncovered several challenges they faced in this task. The first challenge was decoding symbolic features within data representations. Scientists not only use complex reasoning, but also have complex practices of communication (Greeno and Hall, 1997). Such practices of communication include conventional representations for reporting on domain-specific experimental results. Knowing these conventions enables scientists to more easily decode and interpret data representations that are not their own. Given the complexity of scientific representations, we were not surprised that reading figures posed a challenge for undergraduate students, but we were surprised at the extent to which students relied on group conversation (as opposed to individual processing) to decipher the symbols and numbers within each figure. We did not find students, within the group setting, unable to move beyond initial decoding of figures, indicating that this task is difficult but not insurmountable. Part of learning to interpret data representations includes practice with the standard forms of representations (Greeno and Hall, 1997). Our data suggest that instructors should consider explicit discussions of the affordances of particular representational forms, especially those that are conventional in the field being explored in a course. Further, our data strongly suggest the potential for students to support each other in learning to decode figures through collaboration, underscoring the importance of giving students time to work through authentic data in small groups.
Another challenge that students faced when interpreting authentic data was determining which patterns were important. In some cases, students tried to give meaning to noticeable, distracting features that would probably be ignored by an expert (e.g., incomplete siRNA knockdown or band smudging on Western blots). As experts, scientists approach problems or data with a different lens than beginners (Chi et al., 1981). Undergraduates are still novice experimenters, especially with regard to domain-specific experiments, and some do not have access to authentic undergraduate laboratory research experiences. If students focus on distracting variables, limited classroom time may be wasted; fortunately, we found that this challenge occurred in less than one quarter of the transcripts we analyzed. At the group level, students seemed to work together to identify which features or patterns to pay attention to, sometimes explicitly discouraging fellow group members from focusing on potentially distracting variables. The approach most groups took to data interpretation was collaborative noticing of patterns, followed by building of claims with relatively little time spent on discussing experimental technique in most cases. This approach may have been influenced by our instructional design. Compared with other designs (Hoskins et al., 2011), our approach placed less emphasis on the details of experimental techniques and asked students to draw their own conclusions from data fairly rapidly. Some basic experimental techniques were discussed in class and in assigned readings, but the emphasis during in-class activities was on drawing biological relevant conclusions from data rather than on preparing students to understand how to conduct experiments in a lab. Despite this lack of emphasis on experimental technique, we observed that students were often able to construct valid, generative data interpretations in this setting. This observation is not necessarily consistent with the existing literature on how experts approach interpretation of novel data figures (Bowen et al., 1999). We suggest that more research is needed to follow up on this preliminary observation in more detail.
There is much complexity in working with authentic data and the multivariable causal models that are predominant in MCB. It must be acknowledged that a student’s ability to understand target models (which includes their representational competence; diSessa, 2004) is essential to his or her ability to fully succeed on TRIM data sets. An important aspect of instruction was instructor discussion of target models and student interaction with target models before and after students engaged in data-interpretation activities. Instructors cannot assume that providing students with our problem sets or similar will result in productive data interpretation or learning without appropriate context. While most of the written interpretations produced by student groups in our study were at least partially valid, fewer than half contained all of the relevant points that might be reasonably concluded from a figure, despite our attempts to provide appropriate instructional context. Further, while most of these written interpretations were connected to a broader biological context, ∼30% were not. Corroborating this, our analysis of student dialogue revealed that, while students productively used models to aid data interpretation in the majority of cases, sometimes they were unable to understand how a particular figure related to a given model. Though causal complexity is difficult to capture in our coding scheme, we did qualitatively observe that it was sometimes a challenge for students. This could be in the form of an experiment with multiple variables or a model with a complex series of causal links. These findings are reminiscent of studies demonstrating K–12 students’ difficulty in learning control-of-variables strategies (Chen and Klahr, 1999) and in navigating multivariable contexts (Kuhn et al., 2009). Our data suggest that, at the upper-division undergraduate level, almost all students understand the idea of controlling variables, but complex, multivariable data and models can still pose a challenge. Most students in this setting rose to the challenge of interpreting data patterns in complex, multivariable contexts. However, instructors should be aware of the cognitive demands of such tasks and be sure to provide students with adequate instructional time to process such data and routinely assess comprehension, providing support or adjusting tasks when needed.
Students Collaboratively Building Data Interpretations through Argumentation
Argumentation is an important disciplinary practice that has been the emphasis of much instructional reform (Duschl and Osborne, 2002; Berland and Reiser, 2011; Sampson and Blanchard, 2012). Here, we demonstrate that argumentation spontaneously occurred within small groups in our instructional setting. This is a surprising outcome, because our instructional design did not provide any explicit scaffold to elicit argumentation, and supporting argumentation was not deliberately planned by the instructional team. Within K–12 educational research, where argumentation has been most thoroughly studied, it is generally accepted that supporting argumentation in classrooms requires instructional support in the form of intentional norms of conversation or written tasks that explicitly scaffold argument (Duschl and Osborne, 2002; Osborne et al., 2004). By investigating undergraduate dialogue, our study provides a window into the forms of scientific dialogue that students use to interpret data. Our findings relate to work by Knight and colleagues, who explored undergraduate student dialogue in small-group settings (Knight et al., 2013). Their study also showed students exchanging evidence-based reasoning during group discussion of clicker questions.
A key difference between the student dialogue in our study and others investigating argumentation among undergraduate biology students was that the dialogical argumentation in our context was predominantly sense-making over persuasive. In contrast, the clicker discussions previously described included many disagreements between student ideas, with each giving conflicting reasoning to support his or her claims (Knight et al., 2013). It is the nature of clicker questions that there is often one right answer from a given set of multiple choices, which may have encouraged persuasive arguments to form more readily. Furthermore, the clicker discussions took place after students had initially voted individually, which allowed students to form ideas before engaging in peer discussion. A feature of our instructional design was for students to encounter the data figures for the first time together, which may have promoted more sense-making over persuasive argumentation. Another feature of our instructional design that we believe fostered argumentation was that students were required to reach consensus in order to submit a single problem set per group. While one could postulate that this would encourage frequent persuasive argumentation, our analysis suggests that this was not the case. Instead, we found that the backing of claims with evidence often took place at the group level. For example, if a student posed a claim, another student would spontaneously offer evidence to confirm or alter that claim.
Berland and Reiser (2009) described three goals of argumentation—sense-making, articulation, and persuasion—with the idea that they build on and support one another. We suggest that the extent to which different features of argumentation will be present is heavily influenced by the nature of the task, though individual group dynamics will certainly play a role regardless of task design. In this study, we show that students engaged in argumentation, primarily in the form of sense-making, without the oppositional prompts or teacher direction that have been often used in K–12 classrooms (Osborne et al., 2004). Instead, we demonstrate that, within an undergraduate curriculum designed to engage students in model-based data interpretation, argumentation emerged naturally. Others have suggested the interdependence of scientific practices; for example, Passmore and Svoboda (2012) used the practice framework to illustrate various ways that using models and data to explain natural phenomena in a classroom could elicit argumentation. Our findings provide an example of an instructional setting in which model use, argumentation, and data interpretation all occurred. Within our analysis, we found a few examples that suggest potential interaction between these practices. Most often students used target models to confirm or expand evidence-backed claims that were constructed through argumentation around data figures. In these cases, models provided a biological context in which students could make sense of data patterns either after or during examination of data figures. Less commonly, students seemed to use the target model itself as further evidence to support their claims about the validity of a potential data interpretation. While our data suggest the possibility of coordinated model use, argumentation, and data interpretation, a complete analysis along these lines is beyond the scope of the current paper. We suggest that further study is needed in this area.
Connecting Data Interpretations to Biology through Models
Though modeling has long been proposed as an important practice in science classrooms (Penner et al., 1997; Lehrer and Schauble, 2000), there has been a recent surge of interest in this instructional approach. Several groups have significantly advanced our understanding of how models may be used in the classroom (Lehrer and Schauble, 2006; Windschitl et al., 2008; Passmore et al., 2009; Schwarz et al., 2009), and modeling has been included as a disciplinary practice in the NGSS. Within the undergraduate biology community, significant discussions about the use of models have also begun, for example, Dauer and coworkers have proposed using box-and-arrow models as a way for students to represent their developing understanding of evolution and variation in a classroom setting (Dauer et al., 2013), and Svoboda and Passmore (2010) have evaluated a program that engaged a small group of undergraduates in researching mathematical models of biological data. It should be noted that the term “model” here can be used to mean quite different things: in the case of Dauer and coworkers, conceptual models that students use to represent their own developing understanding; in the case of Svoboda and Passmore, mathematical models of data sets developed by students to explain biological phenomena. The target models used in our study were in some ways similar to those from the Svoboda and Passmore study in that they were designed to explain biological phenomena and map to experimental data. However, target models in our study differed in that they were not mathematical or student generated.
Much interest in modeling begs the question: Why have so many decided that models hold such potential for science education? Modeling is an integral component of how scientists conduct research. Models act as mental organizers for the accumulating data-based conclusions researchers have made and help scientists make sense of new data. Thus, models are the frame of reference for conducting scientific research, making the use of models a key practice for students to understand or engage in. Additionally, mental models, and external representations of these models, provide the space for generative reasoning, a place to mentally animate the spatial, temporal, and causal features that are the basis for understanding the mechanisms investigated in our field (Dunbar, 1999; Nersessian, 2008). In our case, the goal of instruction was to integrate biological content with the scientific practice of data interpretation. We found that the two actually support each other: models provided a useful thinking tool for the complex task of data interpretation while simultaneously providing a pictorial representation of the set of biological ideas we wished to convey. Similarly, we aimed to help students understand that textbook diagrams represent hypotheses that have been derived through interpretation of experimental evidence.
Our investigation revealed that productive use of models by students took three main forms. First, students used the target model to expand the interpretive claims they had already formed about what might be inferred from a particular data figure. Often, this behavior seemed to be guided by the task prompt to “relate to the model.” Second, some groups of students used ideas from the target model throughout the data-interpretation process, seemingly using the biological content of the model to make sense of the data figure in a relatively integrated manner. Finally, the target model provided a readily available resource for reviewing or discussing potentially confusing biological ideas or features of the experimental design.
We did find cases in which students in our study spontaneously generated hypotheses related to target models, although these occurrences were relatively rare. We found more of these “highly generative” written interpretations in the context of one of the four problem sets we investigated. We speculate that this generative reasoning may have been prompted by the fact that some of the data presented an idea that could not be fully explained by what was represented in the target model. The in-class tasks that were the focus of this study asked students to interpret data figures and explain how those interpretations related to a provided model. Some other activities in the course, not examined in the research study, asked students to expand models to accommodate new data, compare competing models, or determine that a data figure did not support a model. We suspect that, through these types of activities, models might provide an even greater support for students’ generative reasoning.
Finally, we conclude with the suggestion that viewing “data interpretation” as a stand-alone set of skills is no more productive than teaching biology as a series of “isolated facts to be memorized.” When students are asked to examine how real data are used to explain, refine, or build models of key biological concepts, the facts and the skills take on meaning as a cohesive unit. Thus, we hope that more instructors, including those of large-enrollment courses, can begin to view the inclusion of data interpretation within their curricula as a feature that will strengthen students’ understanding of key biological ideas rather than an additional set of skills for students to learn that will take time away from the content instructors wish to cover.
Supplementary Material
REFERENCES
- American Association for the Advancement of Science. Vision and Change in Undergraduate Biology Education: A Call to Action. Washington, DC: 2011. [Google Scholar]
- Berland LK, Reiser BJ. Making sense of argumentation and explanation. Sci Educ. 2009;93:26–55. [Google Scholar]
- Berland LK, Reiser BJ. Classroom communities’ adaptations of the practice of scientific argumentation. Sci Educ. 2011;95:191–216. [Google Scholar]
- Boulter CJ, Gilbert JK. Argument and science education. In: Costello PSM, Mitchell S, editors. Competing and Consensual Voices: The Theory and Practice of Argumentation. Clevedon, UK: Multilingual Matters; 1995. [Google Scholar]
- Bowen GM, Roth W, McGinn MK. Interpretations of graphs by university biology students and practicing scientists: toward a social practice view of scientific representation practices. J Res Sci Teach. 1999;36:1020–1043. [Google Scholar]
- Brewe E. Modeling theory applied: modeling instruction in introductory physics. Am J Phys. 2008;76:1155. [Google Scholar]
- Brna P, Cox R, Good J. Learning to think and communicate with diagrams: 14 questions to consider. Artif Intell Rev. 2001;15:115–134. [Google Scholar]
- Bryant HE, Schultz N, Thomas HD, Parker KM, Flower D, Lopez E, Helleday T. Specific killing of BRCA2-deficient tumours with inhibitors of poly (ADP-ribose) polymerase. Nature. 2005;434:913–917. doi: 10.1038/nature03443. [DOI] [PubMed] [Google Scholar]
- Campbell T, Oh PS, Neilson D. Discursive modes and their pedagogical functions in model-based inquiry (MBI) classrooms. Int J Sci Educ. 2012;34:2393–2419. [Google Scholar]
- Chen Z, Klahr D. All other things being equal: acquisition and transfer of the control of variables strategy. Child Dev. 1999;70:1098–1120. doi: 10.1111/1467-8624.00081. [DOI] [PubMed] [Google Scholar]
- Chi MT, Feltovich PJ, Glaser R. Categorization and representation of physics problems by experts and novices. Cogn Sci. 1981;5:121–152. [Google Scholar]
- Dauer JT, Momsen JL, Speth EB, Makohon-Moore SC, Long TM. Analyzing change in students’ gene-to-evolution models in college-level introductory biology. J Res Sci Teach. 2013;50:639–659. [Google Scholar]
- Davies H, Bignell GR, Cox C, Stephens P, Edkins S, Clegg S, Bottomley W. Mutations of the BRAF gene in human cancer. Nature. 2002;417:949–954. doi: 10.1038/nature00766. [DOI] [PubMed] [Google Scholar]
- diSessa AA. Metarepresentation: native competence and targets for instruction. Cogn Instr. 2004;22:293–331. [Google Scholar]
- Driver R, Newton P, Osborne J. Establishing the norms of scientific argumentation in classrooms. Sci Educ. 2000;84:287–312. [Google Scholar]
- Dunbar K. How scientists build models: in vivo science as a window on the scientific mind. In: Magnani L, Nersessian N, Thagard P, editors. Model-Based Reasoning in Scientific Discovery. New York: Plenum; 1999. pp. 85–99. [Google Scholar]
- Duncan RG. The role of domain-specific knowledge in generative reasoning about complicated multileveled phenomena. Cogn Instr. 2007;25:271–336. [Google Scholar]
- Duschl RA, Schweingruber HA, Shouse AW. Washington, DC: National Academies Press; 2007. Taking Science to School: Learning and Teaching Science in Grades K–8. [Google Scholar]
- Duschl RA, Osborne J. Supporting and promoting argumentation discourse in science education. Stud Sci Educ. 2002;38:39–72. [Google Scholar]
- Greeno JG, Hall RP. Practicing representation. Phi Delta Kappan. 1997;78:361. [Google Scholar]
- Helleday T, Bryant HE, Schultz N. Poly (ADP-ribose) polymerase (PARP-1) in homologous recombination and as a target for cancer therapy. Cell Cycle. 2005;4:1176–1178. doi: 10.4161/cc.4.9.2031. [DOI] [PubMed] [Google Scholar]
- Hoskins SG, Lopatto D, Stevens LM. The C.R.E.A.T.E. approach to primary literature shifts undergraduates’ self-assessed ability to read and analyze journal articles, attitudes about science, and epistemological beliefs. CBE Life Sci Educ. 2011;10:368–378. doi: 10.1187/cbe.11-03-0027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoskins SG, Stevens LM, Nehm RH. Selective use of the primary literature transforms the classroom into a virtual laboratory. Genetics. 2007;176:1381–1389. doi: 10.1534/genetics.107.071183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James MC, Willoughby S. Listening to student conversations during clicker questions: what you have not heard might surprise you. Am J Phys. 2011;79:123–132. [Google Scholar]
- Knight JK, Wise SB, Southard KM. Understanding clicker discussions: student reasoning and the impact of instructional cues. CBE Life Sci Educ. 2013;12:645–654. doi: 10.1187/cbe.13-05-0090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozeracki CA, Carey MF, Colicelli J, Levis-Fitzgerald M, Grossel M. An intensive primary-literature-based teaching program directly benefits undergraduate science majors and facilitates their transition to doctoral programs. Cell Biol Educ. 2006;5:340–347. doi: 10.1187/cbe.06-02-0144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn D, Pease M, Wirkala C. Coordinating the effects of multiple variables: a skill fundamental to scientific thinking. J Exp Child Psychol. 2009;103:268–284. doi: 10.1016/j.jecp.2009.01.009. [DOI] [PubMed] [Google Scholar]
- Latour B. Pandora’s Hope: Essays on the Reality of Science Studies. Cambridge, MA: Harvard University Press; 1999. Circulating reference: sampling the soil in the Amazon forest; pp. 24–79. [Google Scholar]
- Lavoie H, Therrien M. Cancer: a drug-resistant duo. Nature. 2011;480:329–330. doi: 10.1038/480329a. [DOI] [PubMed] [Google Scholar]
- Lehrer R, Schauble L. Developing model-based reasoning in mathematics and science. J Appl Dev Psychol. 2000;21:39–48. [Google Scholar]
- Lehrer R, Schauble L. Cultivating model-based reasoning in science education. In: Keith SR, editor. The Cambridge Handbook of the Learning Sciences. New York: Cambridge University Press; 2006. pp. 371–387. [Google Scholar]
- Lemke JL. Talking Science: Language, Learning and Values. Norwood, NJ: Ablex; 1990. [Google Scholar]
- Mayer RE, Moreno R. A split-attention effect in multimedia learning: evidence for dual processing systems in working memory. J Educ Psychol. 1998;90:312. [Google Scholar]
- MCAT Preview Guide for the MCAT 2015. File downloaded from https://aamc-orange.global.ssl.fastly.net/production/media/filer_public/f7/e5/f7e57fb2-44fa-4c00-83dd-c17cee034c47/mcat2015-content.pdf.
- McNeill KL, Krajcik J. Middle school students’ use of appropriate and inappropriate evidence in writing scientific explanations. In: Lovett M, Shah P, editors. Thinking with Data: The Proceedings of the 33rd Carnegie Symposium on Cognition. Mahwah, NJ: Erlbaum; 2007. [Google Scholar]
- Mendonça PCC, Justi R. The relationships between modelling and argumentation from the perspective of the model of modelling diagram. Int J Sci Educ. 2013;35:2407–2434. [Google Scholar]
- Neilson D, Campbell T, Allred B. Model-based inquiry in physics: a buoyant force module. Sci Teach. 2010;77:38. [Google Scholar]
- Nersessian NJ. Creating Scientific Concepts. Cambridge, MA: MIT Press; 2008. [Google Scholar]
- Odenbaugh J. Idealized, inaccurate but successful: a pragmatic approach to evaluating models in theoretical ecology. Biol Philos. 2005;20:231–255. [Google Scholar]
- Osborne J, Erduran S, Simon S. Enhancing the quality of argumentation in school science. J Res Sci Teach. 2004;41:994–1020. [Google Scholar]
- Passmore C, Stewart J, Cartier J. Model-based inquiry and school science: creating connections. School Sci Math. 2009;109:394–402. [Google Scholar]
- Passmore CM, Svoboda J. Exploring opportunities for argumentation in modelling classrooms. Int J Sci Educ. 2012;34:1535–1554. [Google Scholar]
- Penner DE, Giles ND, Lehrer R, Schauble L. Building functional models: designing an elbow. J Res Sci Teach. 1997;34:125–143. [Google Scholar]
- Round JE, Campbell AM. Figure facts: encouraging undergraduates to take a data-centered approach to reading primary literature. CBE Life Sci Educ. 2013;12:39–46. doi: 10.1187/cbe.11-07-0057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saldaña J. The Coding Manual for Qualitative Researchers. London: Sage; 2008. [Google Scholar]
- Sampson V, Blanchard MR. Science teachers and scientific argumentation: trends in views and practice. J Res Sci Teach. 2012;49:1122–1148. [Google Scholar]
- Schwarz CV, Reiser BJ, Davis EA, Kenyon L, Achér A, Fortus D, Shwartz Y, Hug B, Krajcik J. Developing a learning progression for scientific modeling: making scientific modeling accessible and meaningful for learners. J Res Sci Teach. 2009;46:632–654. [Google Scholar]
- Stevens LM, Hoskins SG. The CREATE strategy for intensive analysis of primary literature can be used effectively by newly trained faculty to produce multiple gains in diverse students. CBE Life Sci Educ. 2014;13:224–242. doi: 10.1187/cbe.13-12-0239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart J, Cartier JL, Passmore CM. Developing understanding through model-based inquiry. In: National Research Council, editor. How Students Learn: History, Mathematics, and Science in the Classroom. Washington, DC: National Academies Press; 2005. pp. 515–565. [Google Scholar]
- Svoboda J, Passmore C. Evaluating a modeling curriculum by using heuristics for productive disciplinary engagement. CBE Life Sci Educ. 2010;9:266–276. doi: 10.1187/cbe.10-03-0037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svoboda J, Passmore C. The strategies of modeling in biology education. Sci Educ. 2013;22:119–142. [Google Scholar]
- Talbot-Smith M, Abell SK, Appleton K, Hanuscin DL. Handbook of Research on Science Education. New York: Routledge; 2013. [Google Scholar]
- Van Lacum EB, Ossevoort MA, Goedhart MJ. A teaching strategy with a focus on argumentation to improve undergraduate students’ ability to read research articles. CBE Life Sci Educ. 2014;13:253–264. doi: 10.1187/cbe.13-06-0110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Aufschnaiter C, Erduran S, Osborne J, Simon S. Arguing to learn and learning to argue: case studies of how students’ argumentation relates to their scientific knowledge. J Res Sci Teach. 2008;45:101–131. [Google Scholar]
- Walker JP, Sampson V. Learning to argue and arguing to learn: argument-driven inquiry as a way to help undergraduate chemistry students learn how to construct arguments and engage in argumentation during a laboratory course. J Res Sci Teach. 2013;50:561–596. [Google Scholar]
- Walker JP, Sampson V, Grooms J, Anderson B, Zimmerman CO. Argument-driven inquiry in undergraduate chemistry labs: the impact on students’ conceptual understanding, argument skills, and attitudes toward science. J Coll Sci Teach. 2012;41(4):74–81. [Google Scholar]
- Walker JP, Sampson V, Zimmerman CO. Argument-driven inquiry: an introduction to a new instructional model for use in undergraduate chemistry labs. J Chem Educ. 2011;88:1048–1056. [Google Scholar]
- Wilensky U, Stroup W. Participatory simulations: envisioning the networked classroom as a way to support systems learning for all. 2002. Annual Meeting of the American Research Education Association, April 1–5, 2002, New Orleans, LA.
- Windschitl M, Thompson J, Braaten M. Beyond the scientific method: model-based inquiry as a new paradigm of preference for school science investigations. Sci Educ. 2008;92:941–967. [Google Scholar]
- Zohar A, Nemet F. Fostering students’ knowledge and argumentation skills through dilemmas in human genetics. J Res Sci Teach. 2002;39:35–62. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.