Abstract
It is shown that surface conduction can stabilize electrodeposition in random, charged porous media at high rates, above the diffusion-limited current. After linear sweep voltammetry and impedance spectroscopy, copper electrodeposits are visualized by scanning electron microscopy and energy dispersive spectroscopy in two different porous separators (cellulose nitrate, polyethylene), whose surfaces are modified by layer-by-layer deposition of positive or negative charged polyelectrolytes. Above the limiting current, surface conduction inhibits growth in the positive separators and produces irregular dendrites, while it enhances growth and suppresses dendrites behind a deionization shock in the negative separators, also leading to improved cycle life. The discovery of stable uniform growth in the random media differs from the non-uniform growth observed in parallel nanopores and cannot be explained by classic quasi-steady “leaky membrane” models, which always predict instability and dendritic growth. Instead, the experimental results suggest that transient electro-diffusion in random porous media imparts the stability of a deionization shock to the growing metal interface behind it. Shock electrodeposition could be exploited to enhance the cycle life and recharging rate of metal batteries or to accelerate the fabrication of metal matrix composite coatings.
Pattern formation by electrodeposition has fascinated scientists in recent decades since Brady and Ball1 first attributed the mechanism of copper dendritic growth to diffusion-limited aggregation2. It was later discovered that morphology selection is also influenced by electromigration and convection in free solutions3,4,5,6,7,8,9,10. Here, we report some surprising effects of electromigration on electrodeposition in weakly charged porous media, including the possibility of stabilizing the growth and eliminating dendrites at high rates.
Suppressing dendrites in porous separators is a critical challenge for high-energy-density batteries with Li11,12, Zn13, Na, Cd or other metal anodes. Dendrites accelerate capacity fade and cause dangerous short circuits11,12. Dendrites can be blocked by stiff, dense separators14,15, but usually only at the cost of large internal resistance. Another strategy is to manipulate ionic fluxes near the anode via competing side reactions that interfere with electrodeposition at protrusions16,17,18,19 or enhance surface diffusion20. More stable metal cycling has also been demonstrated by altering the separator chemistry, e.g. with lithium-halide salts20, nanoparticles with tethered ionic-liquid anions21, hydrophilic separators22, electrolytes with large anions23, and certain solid polymer electrolytes24.
Motivated by reducing space charge25,26, several studies have shown that supplying extra anions by charged nanoparticle dispersion27 or solvent-in-salt electrolyte28 can improve battery cycling, although dendrites were not visualized. However, according to theory29 and experiments on dendritic growth8 and electrodialysis30,31,32, it is unlikely that extended space charge ever forms in free solutions. In the case of copper electrodeposition, morphological instability occurs immediately upon salt depletion at the cathode, which enhances ionic flux to the tips, avoid space charge, and preserves thin double layers7,16,33. At the same time, the Rubinstein-Zaltzman hydrodynamic instability can lead to vortices that sustain over-limiting current (OLC), faster than electro-diffusion30,31,32,34,35. This phenomenon is well established in electrodialysis30,31,32,35,36,37,38 and nanofluidics39 and may also explain electroconvection observed around dendrite tips3,8.
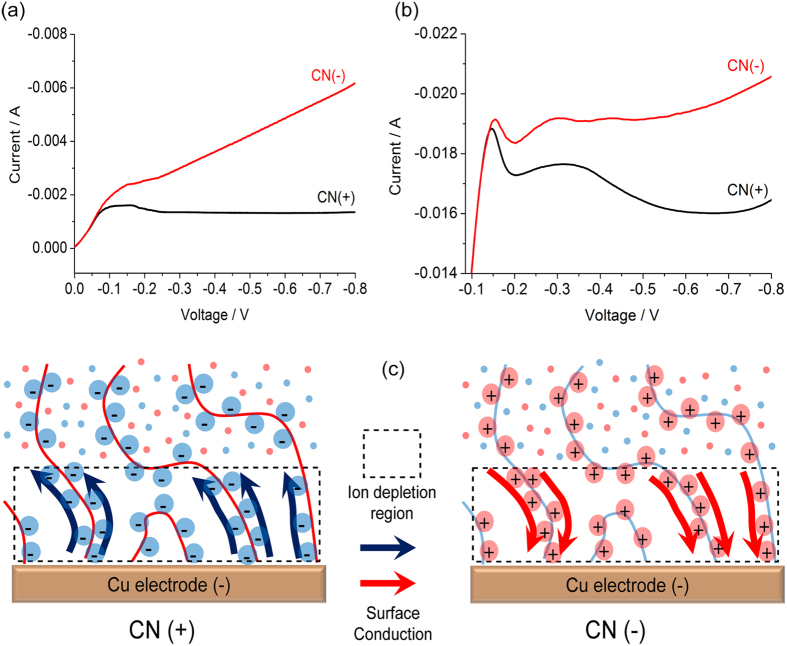
Here, we establish new principles of morphology control for electrodeposition in porous media. By exploiting the physics of deionization shock waves40, we show that porous separators with thin electric double layers (“leaky membranes”41) can either stabilize or destabilize metal electrodeposition at high rates, depending on the sign of their surface charge. Our initial model system is a symmetric copper cell consisting of a porous cellulose nitrate (CN) or polyethylene (PE) separator with positive or negative polyelectrolyte coatings, which is compressed between two flat copper electrodes in copper sulfate solutions. The current-voltage relations in both cases (Fig. 1a,b) show common plateaus around the diffusion-limited current because surface conduction is negligible compared to bulk electro-diffusion. At higher voltages, however, strong salt depletion occurs at the cathode, and dramatic effects of the surface charge are observed (Fig. 1c). The positive separator exhibits reduced cation flux, opposed by surface conduction42, while the negative separator exhibits OLC sustained by surface conduction7,41,42, which also leads to a transient deionization shock30,40,43,44 ahead of the growth.
Figure 1.
Voltammetry of positively and negatively modified cellulose nitrate (CN) membranes of exposed area 1.327 cm2 between Cu electrodes in (a) 10 mM CuSO4 at 1 mV/s and (b) 100 mM CuSO4 at 10 mV/s. (c) Physical pictures of the effect of surface conduction on electrodeposition in a charged random porous media, driven by large electric fields in the ion depletion region.
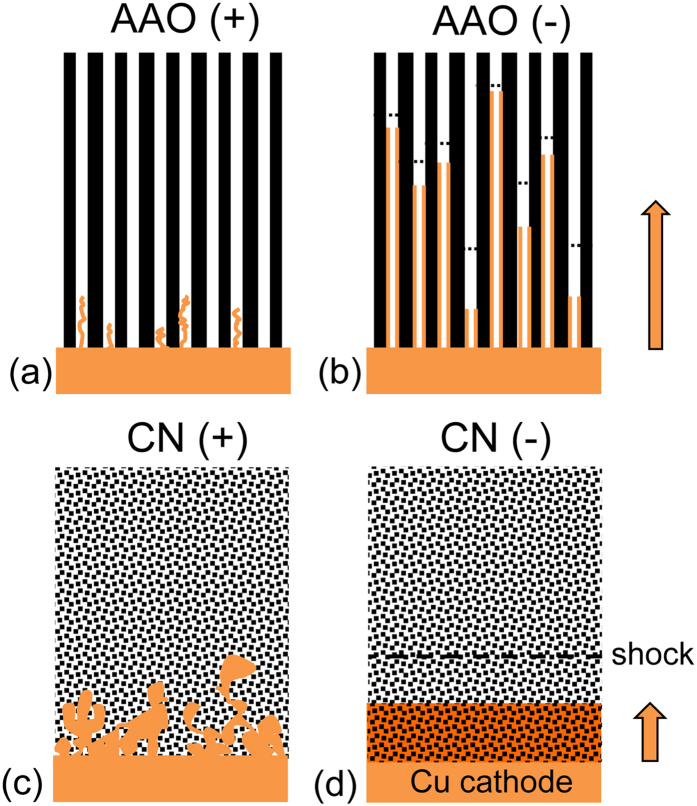
We have discovered that the interaction between these nonlinear transport phenomena and the growing deposit is strongly dependent on the porous microstructure, as shown in Fig. 2. In a recent publication42, we showed that surface conduction can profoundly influence the pore-scale morphology of copper growth in ordered anodic aluminum oxide (AAO) membranes. In such materials with non-intersecting parallel nanopores, diffusion-limited metal growth is inherently non-uniform and leads to a “race of nanowires”45. Above the limiting current, there is a transition to new non-uniform growth modes, either nanotubes following separate deionization shock waves in each pore of the negatively-charged membrane (Fig. 2b) or slowly penetrating, pore-center dendrites in the positively-charged membrane (Fig. 2a). Here, we demonstrate nearly opposite effects of surface conduction on the electrode-scale morphology in random CN membranes with well-connected pore networks. Above the limiting current, some low-density dendritic structures penetrate into the positive membrane (Fig. 2c), but, remarkably, the growth is uniform, dense, and reversible in the negative membrane, which we attribute to the propagation of a single flat, stable deionization shock ahead of the deposit (Fig. 2d).
Figure 2. Morphology selection principles for fast electrodeposition (exceeding diffusion limitation) in charged, porous media with ordered pores (e.g. anodic aluminum oxide, AAO, from our previous work42) versus random pores (e.g. cellulose nitrate, CN, from this work).
In parallel nanopores, (a) positive surface charge suppresses metal penetration or allows thin dendrites avoiding the pore walls, while (b) negative charge promotes non-uniform surface coverage leading to metal nanotubes of different lengths growing behind deionization shock waves (dashed lines). In well-connected, random nanopores, (c) positive surface charge blocks penetration or allows low-density porous dendrites, while (d) negative charge leads to a flat metal-matrix composite film, stabilized by a macroscopic shock wave propagating ahead of the growth.
Theory
In porous media, the physical mechanisms for OLC are very different from those in free solutions and just beginning to be explored. According to theory7, supported by recent microfluidic experiments44, if the counterions (opposite to the pore surface charge) are the ones being removed, then extended space charge is suppressed, and electro-osmotic instability is replaced by two new mechanisms for OLC: (1) surface conduction by electromigration, which dominates in submicron pores41,42, and (2) surface convection by electro-osmotic flow, which dominates in micron-scale pores29,38,41,46. Regardless of whether OLC is sustained by constant current40,43 or constant voltage47, the ion concentration profile develops an approximate discontinuity that propagates into the porous medium, leaving highly deionized fluid in its wake, until it relaxes to a steady linear profile in a finite porous slab41,48. This “deionization shock wave”40 is analogous to concentration shocks in chromatography, pressure shock waves in gases, stop-and-go traffic, glaciers, and other nonlinear kinematic waves49.
The influence of surface conduction on electrodeposition was recently discovered in our investigations of copper electrodeposition in AAO membranes with modified surface charge42. Below the limiting current, surface conduction is negligible if the double layers are thin (small Dukhin number), but surface conduction profoundly affects the growth at high currents. With positive surface charge, growth is blocked at the limiting current by oppositely-directed surface conduction (electro-migration) and surface convection (electro-osmotic flow); above a critical voltage, some dendrites are observed avoiding the pore walls, likely fed by vortices of reverse electro-osmotic flow returning along the pore centers. With negative surface charge, the growth is enhanced by surface conduction until the same critical voltage, when surface dendrites and ultimately smooth surface films grow rapidly along the walls. These phenomena are consistent with the theory of OLC in a single microchannel7,44, but we expect different behavior in random media with interconnected pores.
The motivation for our experiments is the theoretical prediction that a flat deionization shockwave is nonlinearly stable to shape perturbations40, since we hypothesize that this stability could be imparted to an electrodeposit growing behind a propagating shock. In free solution, dendritic growth occurs soon after salt depletion, owing to the simple fact that a surface protrusion receives more flux, thereby causing it to protrude further1 (Fig. 3a). This is the fundamental instability mechanism of Laplacian growth, which leads to fractal patterns by continuous and deterministic viscous fingering50 or discrete and stochastic diffusion-limited aggregation (DLA)2. In contrast, the propagation of deionization shockwaves is controlled “from behind” by the high resistance of the ion depletion zone. As shown in Fig. 3b, a lagging region of the shock will have more flux leaving by surface conduction, causing it to advance back to the stable flat shape. The dynamics of a thin shock is thus equivalent to Laplacian dissolution40, the stable time reversal of Laplacian growth51, and this suggests that transport-limited electrochemical processes occurring behind the shock might proceed more uniformly as well.
Figure 3. Basic physics of shock electrodeposition.
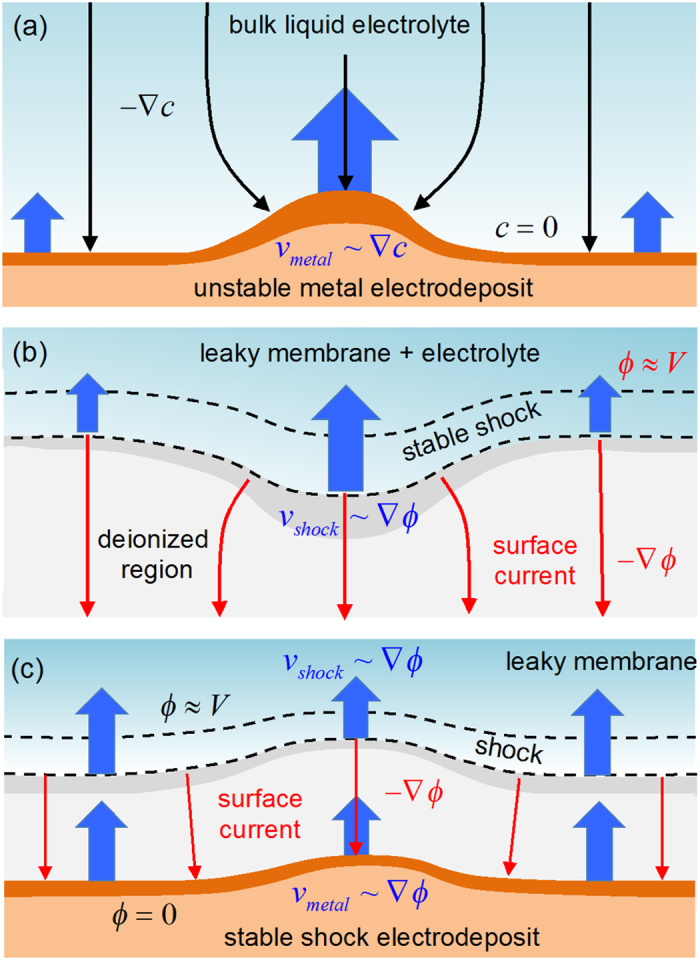
(a) Dendritic instability of electrodeposition in free solution upon diffusion limitation in the electrolyte, where the scarce supply of cations focuses onto a protrusion and results in a self-amplifying process. (b) Stability of deionization shock propagation in response to over-limiting current in a leaky membrane, where a lagging part of the shock wave is removed by large Ohmic currents through the depleted region and results a flat, stable shock wave. (c) Stabilization of electrodeposition behind a deionization shock, if the second effect overcomes the first during fast growth at over-limiting current.
What would happen if a stable deionization shock precedes an unstable growing electrodeposit in a charged porous medium? According to the simplest theoretical description, the classical52 “leaky membrane” model40,41,48 (LMM), the answer depends on the importance of transient diffusion ahead of the shock. The ion concentrations 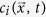 and electrostatic potential
and electrostatic potential 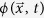 satisfy the Nernst-Planck equations,
satisfy the Nernst-Planck equations,
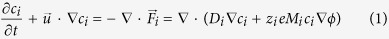 |
and macroscopic electroneutrality,
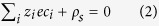 |
including the surface charge density per volume, ρs. The mean flow is incompressible, driven by gradients in dynamical pressure, electrostatic potential, and chemical potential, respectively,
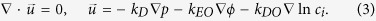 |
The macroscopic ionic diffusivities, Di, and mobilities, Mi, Darcy permeability, kD, electro-osmotic mobility, kEO, and diffusio-osmotic mobility, kDO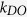 , depend on ci and ϕ, but not on their gradients or (explicitly) on position. This approximation is reasonable for surface conduction in nanopores, but neglects hydrodynamic dispersion due to electro-osmotic flow in micron-sized pores53 or pore network loops38, for which no simple model is available29,46. Assuming a transport limited growth process, the moving electrode surface has Dirchlet (ci = ϕ = 0) and Neumann (
, depend on ci and ϕ, but not on their gradients or (explicitly) on position. This approximation is reasonable for surface conduction in nanopores, but neglects hydrodynamic dispersion due to electro-osmotic flow in micron-sized pores53 or pore network loops38, for which no simple model is available29,46. Assuming a transport limited growth process, the moving electrode surface has Dirchlet (ci = ϕ = 0) and Neumann (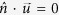 ) boundary conditions.
) boundary conditions.
With these general assumptions, we observe that the steady-state LMM, Eqs (1, 2, 3), falls into Bazant’s class of conformally invariant nonlinear partial differential equations54. The profound implication is that quasi-steady transport-limited growth in a leaky membrane (with growth velocity opposite to the active-ion flux, 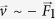 ) is in the same universality class55 as Laplacian growth56,57 and thus always unstable. This explains the recent theoretical prediction that negative charge in a leaky membrane cannot stabilize quasi-steady electrodeposition, although it can reduce the growth rate of the instability58, consistent with the improved cycle life of lithium batteries with tethered anions in the separator21,27.
) is in the same universality class55 as Laplacian growth56,57 and thus always unstable. This explains the recent theoretical prediction that negative charge in a leaky membrane cannot stabilize quasi-steady electrodeposition, although it can reduce the growth rate of the instability58, consistent with the improved cycle life of lithium batteries with tethered anions in the separator21,27.
In contrast, copper electrodeposition experiments in free solution have shown that the salt concentration profile is unsteady prior to interfacial instability33 and forms a “diffusive wave” ahead of growing dendrites4,5,6,7 with the same asymptotic profile as a deionization shock40. In a negatively charged medium, before the salt concentration vanishes at Sand’s time, the diffusion layer sharpens and propagates away from the electrode as deionization shock41,48, which could perhaps lead to stable, uniform “shock electrodeposition” in its wake, as outlined in Fig. 3c. Since the LMM neglects many important processes, however, such as surface diffusion59, surface convection29,53,59, pore-scale heterogeneity60, and electro-hydrodynamic dispersion38,46,53, we turn to experiments to answer this question.
Experimental Results
In order to isolate the effects of charged porous media, we use the same copper system (Cu|CuSO4|Cu) studied over the past three decades by physicists, as a canonical example of diffusion-limited pattern formation1,3. Compared to lithium electrodeposition and electrodissolution, which involves complex side reactions related to the formation and evolution of the solid-electrolyte interphase (SEI), this system is simple enough to allow quantitative interpretation of voltammetry in nanopores42 and microchannels3,7,33. A unique feature of our experiments is that we control the surface conductivity by modifying the separator surface charge by layer-by-layer (LBL) deposition of charged polymers. We also demonstrate the role of pore connectivity for the first time by choosing random porous media, such as cellulose nitrate (CN), with similar pore size (200 ~ 300 nm) as the parallel nanopores of AAO from our recent study that introduced this method42. We denote the charge-modified positive and negative membranes as CN(+) and CN(−), where excess sulfate ions (SO42−) and cupric ions (Cu2+), respectively, are the dominant counter-ions involved in surface conduction (Fig. 1c).
As noted above, voltammetry clearly shows the nonlinear effect of surface conduction. Figure 1a shows current-voltage curves of CN(+) and CN(−) in 10 mM CuSO4 at a scan rate of 1 mV/s, close to steady state. In the low-voltage regime of slow reactions42 (below −0.07 V), the two curves overlap since the double layers are thin, and surface conduction can be neglected compared to bulk diffusion (small Dukhin number)38,41. At the diffusion-limited current, huge differences in CN(+) and CN(−) are suddenly observed. While the current in the CN(+) reaches −1.5 mA around −0.1 V and maintains a limiting current of −1.3 mA, the CN(−) shows a strong linear increase in current, i.e. constant over-limiting conductance. The data are consistent with the surface conduction (SC) mechanism (Fig. 1c), which is sensitive to the sign of surface charge42,53. With negative charge, Cu2+ counter-ions provide surface conduction to “short circuit” the depletion region to maintain electrodeposition. With positive charge, the SO42− counter-ions migrate away from the cathode, further blocking Cu2+ ions outside the depletion region in order to maintain neutrality. At higher salt concentration, 100 mM CuSO4, sweeping at 10 mV/s, the results are similar (Fig. 1b) with no effect of SC below −0.15 V, limiting current of −19 mA for CN(+), and overlimiting conductance for CN(−), although the effect of SC is weaker (smaller Dukhin number), and transient current overshoot and oscillations are observed42,61.
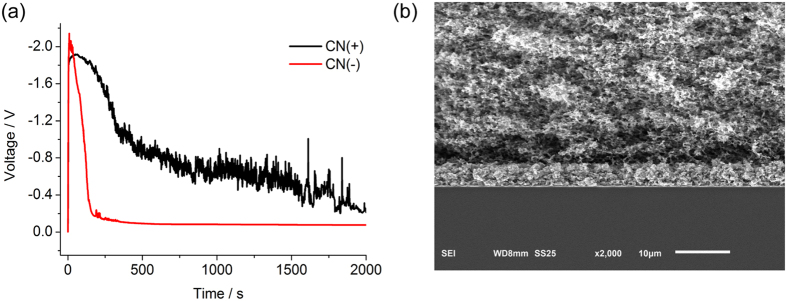
Striking effects of surface charge are also revealed by chronopotentiometry (Fig. 4). When constant OLC (−5 mA) is applied in 10 mM CuSO4 solution, CN(+) exhibits large, random voltage fluctuations, which we attribute to the blocking of cation transport by the reverse SC of SO42− counter-ions near the cathode. Large electric fields drive unstable electro-osmotic flows, some dendritic growth, and water electrolysis, consistent with observed gas bubbles. Metal growth is mostly prevented from entering the CN(+) membrane, so it is easily separated from the cathode after the experiment. In stark contrast, CN(−) maintains low voltage around −100 mV, as expected since the SC of Cu2+ counter-ions sustains electrodeposition under OLC regime. More importantly, the electrodeposited Cu film in CN(−) is perfectly uniform, as shown in the SEM image of Fig. 4(b), consistent with the theoretical motivation above, based on the stability of deionization shock propagation ahead of the growth.
Figure 4.
(a) Chronopotentiometry data for CN(+) and CN(−) membranes at −5 mA for 2000 s in 10 mM CuSO4. (b) SEM image of a uniform Cu film in CN(−) grown by shock electrodeposition during OLC.
Figure 5 clearly shows the suppression of dendritic instability. When OLC (−20 mA) is applied in 100 mM CuSO4 for 2000 s, irregular electrodeposits are generated in CN(+) (Fig. 5a). This imposed current exceeds the limiting current (−17 mA) measured by voltammetry (Fig. 1b), so the observed low-density stochastic growth, which is opposed by surface conduction, may result from vortices of surface electroconvection, driven in the reverse direction by huge electric field in the depletion region. Once again, under the same experimental conditions, we obtain a highly uniform Cu film in CN(−) (Fig. 5b) by shock electrodeposition.
Figure 5.
Morphologies of Cu film depending on surface charge of CN membrane: CN(+) (a,c) and CN(−) (b,d). Cu electrodeposition is carried out in 100 mM CuSO4 by applying −20 mA for 2000 s. SEM images (a,b) and EDS mapping analysis of Cu (c,d).
The difference in morphology of Cu electrodeposits between CN(+) and CN(−) can also be precisely confirmed by EDS mapping analysis of Cu element (Fig. 5c,d). The Cu film in CN(−) shows more compact and flat morphology, consistent with simple estimates of the metal density. Based on the applied current (−20 mA), nominal electrode area (1.0 cm × 1.5 cm) and time (2000 s), pure copper would reach a thickness of 19.6 μm, which would be increased by porosity, but also lowered by fringe currents, side reactions, and metal growth underneath the membrane. The penetration of copper dendrites in CN(+) to a mean distance of 45 μm, supports the direct observation of low density ramified deposits, while the smaller penetration, 12.8 μm, into CN(−) suggests that shock electrodeposits densely fill the pores.
The variation of morphology with applied current is demonstrated in Fig. 6. For under- limiting current (−15 mA), both cases exhibit a uniform Cu film (Fig. 6a,b), independent of surface charge, as expected when surface conduction is weak compared to bulk electro-diffusion within the pores (small Dukhin number). As the applied current is increased, highly irregular, dendritic electrodeposits are generated in CN(+). When extreme OLC (−25 mA) is applied, CN(+) shows much less dense dendritic growth, and weak adhesion of the membrane to the cathode leading to its peeling off (Fig. 6e). On the other hand, shock electrodeposition in CN(−) suppresses dendritic growth and produces uniform, dense Cu films, which show signs of instability only at very high currents (Fig. 6f).
Figure 6. EDS mapping analysis of Cu element.
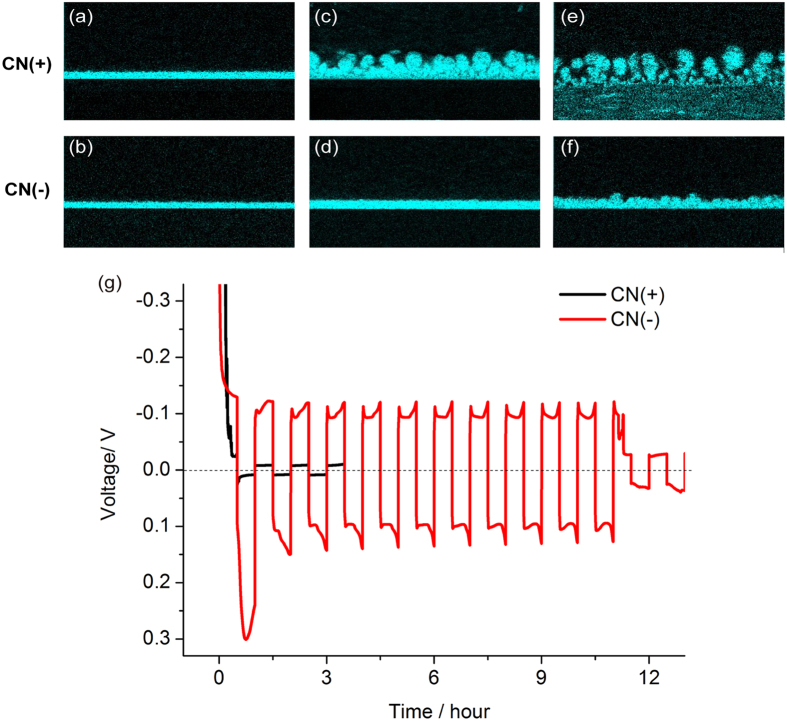
Cu is electrodeposited in CN(+) (a,c,e) and CN(−) (b,d,f) membranes at constant current densities in 100 mM CuSO4 for 2000s (a,b) −15 mA, (c,d) −20 mA, and (e,f) −25 mA. (g) Galvanostatic cycling profiles of CN(+) and CN(−) using a symmetric copper cell: Cu is electrodeposited and electrodissolved under extreme OLC (25 mA) for 1800 s in 100 mM CuSO4.
The observed morphologies shed light on the different cycling behavior for positive and negative membranes under extreme currents (±25 mA), as shown in Fig. 6g. The unstable dendritic growth of CN(+) results in short-circuit paths that cause the voltage to drop quickly to 5 mV in the first cycle. Although further cycles are possible, the voltage never recovers. In contrast, the more uniform growth observed in CN(−) is associated with stable cycling around ±100 mV, in spite of the large nominal current density (±18.8 mA/cm2), well above the limiting current during 10 hours. After eleven cycles, short circuit occurred. Improved cycling life has also recently been reported for lithium metal anodes with separators having tethered anions20, albeit at much lower currents (0.5 mA/cm2) without observing the deposits. Our observation of stable shock electrodeposition may thus have broad applicability, including rechargeable metal batteries.
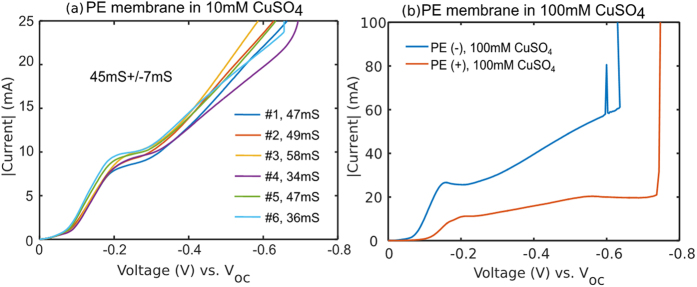
In order to investigate the generality of this phenomenon and its potential application to batteries, we repeated the same experimental procedures for several commercially available, porous polymeric battery separators. Here, we report results for a 20 μm thick Celgard K2045 polyethylene (PE) membrane with a pore size of 50 nm, porosity of 47%, and a tortuosity of 1.5, which was modified using the same layer-by-layer (LBL) assembly sequence for either positively or negatively charged membrane. As is evident in the voltammetry of PE(+) and PE(−) membranes (Fig. 7a), similar OLC behavior, consistent with the nonlinear effect of surface conduction, is observed as the copper electrode is polarized at a scan rate of 2 mV/s in 10 mM CuSO4 solution. Once diffusion limitation begins to dominate at approximately −0.2 V, consistent discrepancies in the current-voltage curve can again be attributed to surface conduction, which enhances Cu2+ transport in the PE(−) membrane, as anions (SO42−) in the double layer of the PE(+) membrane further block the transport of Cu2+ inside the depleted region near the cathode. Although the current-voltage response for both PE membranes is similar to that of the CN membranes, minor discrepancies may be observed at a voltage below −0.2 V, where differences in the current output are significant. This is possibly a result of differences in solvent uptake, affected by the extent of membrane wetting by the aqueous solvent, despite the fact that the membranes were soaked in electrolyte overnight before cells were assembled for analysis.
Figure 7.
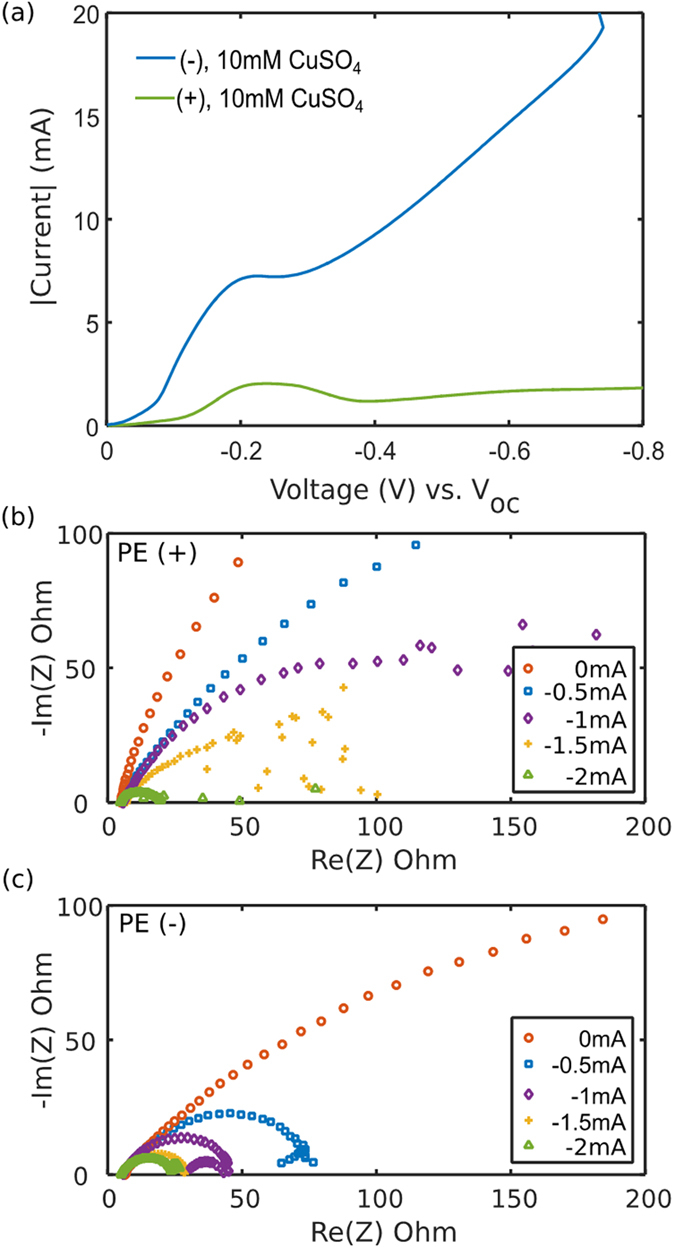
Linear sweep voltammetry (LSV) of (a) PE(+) and PE(−) membranes of exposed area 1.327 cm2 between two Cu electrodes in 10 mM CuSO4 at 2 mV/s. Nyquist plot of the Galvanostatic electrochemical impedance spectroscopy of (b) PE(+) and (c) PE(−) membranes in 10 mM CuSO4 with the same cell configuration as that of (a).
As in other systems with deionization shock waves, it can be more stable to control the current rather than the voltage42,62, so we perform galvano-electrochemical impedance spectroscopies (GEIS) for PE(+) and PE(−) membranes, in Fig. 7b,c, at different direct current biases with alternating currents of 10 μA from 100 kHz to 100 mHz. When applying no dc-bias, the impedance for both cases exhibits a similar response, devoid of any diffusional resistance. When applying a dc-bias, the Warburg-like arc for PE(−) shrinks as the current increases, and is surprisingly followed by a “reversed” semicircle at intermediate current densities (−0.5 mA and −1.0 mA in Fig. 7c), which might be attributed to the growths of copper layer on the cathode, as well as the pitting on the surface of the anode during the measurements. In contrast, as a result of ion blocking by surface conduction in PE(+), the low frequency response becomes noisy. This may also indicate effects of electro-osmotic surface convection29,44,53, mostly likely around connected loops in the porous network38, which could serve to bypass the blocked surface conduction pathways in PE(+) and lead to the observed dendrite penetration. In any case, it is clear that the positive and negative membranes exhibit distinct low frequency responses with increasing dc-bias, which indicates a significant difference in the mass-transfer mechanism for Cu2+ associated with the surface charge of the porous medium.
Seven copper cells with PE(−) membranes were individually assembled and examined to testify the repeatability of our methodology. As is evident in Fig. 8(a), repeatability can be achieved with stringent LBL-coating procedure as well as cell-assembly process to further validate our proposition of surface conduction phenomenon. We observe similar current-voltage response of surface-modified PE membranes in 100 mM CuSO4 solution as those of PE membranes in 10 mM CuSO4 solution. The nonlinear effect of surface conduction dominants the charge transport as the cathode is polarized beyond −0.15 V. As evident in Fig. 8(b), a sharp difference between the current-voltage behavior of PE(+) and PE(−) membranes further supports the proposition of surface charge sensitivity. The sudden increase in current beyond a voltage of −0.6 V for both cases corresponds to short-circuit conditions, where some copper dendrites have spanned from cathode to anode, thereby allowing electrons to pass freely.
Figure 8.
(a) LSV of PE(−) membrane between two Cu electrodes in 10 mM CuSO4 solution. (b) LSV of PE(+) and PE(−) membrane between two Cu electrodes in 100 mM CuSO4 solution.
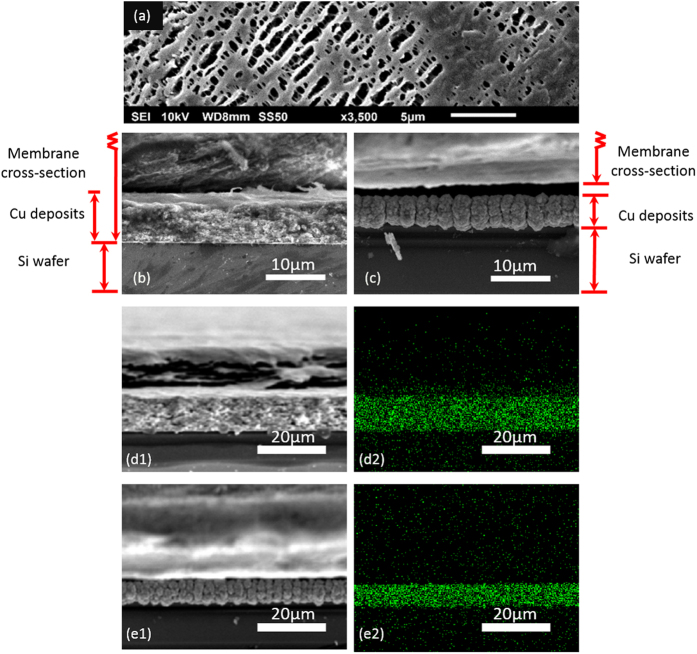
To further support the electrochemical evidence for SC-controlled growth, we performed SEM and EDS mapping analyses to examine the morphological differences between copper electrodeposits using both positive and negative PE membranes. The surface of a random porous membrane before electrodeposition is shown in Fig. 9(a). After galvanostatic deposition of copper onto a silicon wafer (with a thin layer of copper) in 100 mM CuSO4 for 2000 s, two distinct cross-sectional morphologies are observed, depending only on the surface charge of the membrane. In the case of PE(−), in Fig. 9(b,d1), a dense copper film (approx. 8 μm thick) is observed. Due to the existence of denser copper inside the lower portion of the membrane, the upper portion of the membrane above the Cu deposits is tapered, deformed, and torn away when the cell is disassembled for imaging. In contrast, a layer of porous copper grown directly on the wafer is observed for PE(+), in Fig. 9(c,e1). The whole membrane above the Cu deposits is clearly separated from the wafer/copper complex with little adhesion. It is worth mentioning that whether the metal deposits can grow into the porous membranes depends on many factors, e.g. elasticity, strength and wettability of the membrane, salt concentration of the solution, and the applied currents. The common features that emerge from the comparison of Figs 5 and 9 are: (i) negatively charged membranes always produce a uniform layer of metal deposits (Fig. 5b CN(−) and Fig. 9b PE(−)), and (ii) positively charged membranes always yield random/porous structures (Fig. 5a CN(+) and Fig. 9c PE(+)). This direct observation of the dependence of the growth morphology on membrane charge appears to be the first, and rather compelling, validation of the hypothesis depicted in Fig. 3.
Figure 9.
SEM images of (a) the top surface of PE membrane (Celgard K2045), the cross sections of (b) PE(−) and (c) PE(+) membranes after galvanostatic deposition of Cu in 100 mM of CuSO4 at −20 mA for 2000 s. Low magnification SEM images and the associated EDS mapping of the corresponding (b) PE(−) and (c) PE(+) membranes.
Conclusions
This work provides fundamental insights into the physics of transport-limited pattern formation in charged porous media. We show that the surface charge and microstructure of porous separators can strongly influence the morphology of copper electrodeposition, which is considered to be the prototypical case of unstable diffusion-limited growth in free solutions. For the first time, we directly observe the suppression of dendritic instability at high rates, exceeding diffusion limitation. With negative surface charge, uniform metal growth is stabilized behind a propagating deionization shock, and reversible cycling is possible. Under the same conditions with positive surface charge, dendrites are blocked from penetrating the medium, and at high rates the growth becomes unstable and cannot be cycled.
Besides its fundamental interest, shock electrodeposition may find applications in energy storage and manufacturing. High-rate rechargeable metal batteries could be enabled by charged porous separators or charged composite metal electrodes11,12,13,63. The rapid growth of dense, uniform metal electrodeposits in charged porous media could also be applied to the fabrication of copper64 or nickel10 metal matrix composites for abrasives or wear-resistant coatings.
Methods
Chemicals
Polydiallyldimethylammonium chloride (pDADMAC, 100,000 ~ 200,000 Mw, 20 wt% in water), (poly(styrenesulfonate) (pSS, 70000 Mw), copper sulfate (CuSO4, ≥98%), sodium chloride (NaCl, ≥98%), and sodium hydroxide (NaOH, ≥98%) are purchased from Aldrich and used without further purification. Ultrapure deionized water is obtained from Thermo Scientific (Model No. 50129872 (3 UV)) or from a Milli-Q Advantage A10 water purification system. Cellulose nitrate (CN) membranes (pore diameter 200 ~ 300 nm, porosity 0.66–0.88, thickness 130 μm, diameter 47 mm) are purchased from Whatman. Polyethylene (PE) membranes (K2405) with a pore size of 50 nm, a porosity of 47% and a thickness of 20 μm, are obtained from Celgard. Copper plates (1/8” thickness) were purchased from McMaster Carr and machined down to appropriate dimensions using a water jet cutter.
Sample Preparation
The surface charge of CN and PE membranes is modified by layer-by-layer (LBL) method of charged polyelectrolytes. Polydiallyldimethylammonium chloride (pDADMAC) is directly deposited on the membrane to make a positive surface charge, CN(+). For this, the bare CN is immersed in polycation solution (1 mg/mL pDADMAC in 20 mM NaCl at pH 6) for 30 min. Then, the membrane is triple rinsed (10 min each) with purified water purification system) to remove unattached polyelectrolyte. Negatively charged CN(−) is obtained by coating negative polyelectrolytes (poly(styrenesulfonate), pSS) on the pDADMAC-coated CN by immersion in a polyanion solution (1 mg/mL pSS in 20 mM NaCl at pH 6) for 30 min and followed by the same washing procedure. The polyelectrolytes coated CN membranes are stored in a CuSO4 solution.
The surface charge of PE membranes are modified using a similar LBL procedures described above. Bare PE membranes are air-plasma treated for 10 min before being immersed in pDADMAC solution for 12 h to make the positively charged membrane (PE(+)). The membrane is triple rinsed (30 min each) with purified water is needed to remove any unattached polyelectrolyte. For the negatively charged PE membrane, thoroughly rinsed PE(+) membranes are immersed in pSS for 12 h, followed by the same washing procedure as that of the PE(+) membrane. The surface-modified PE membranes are stored in purified water and soaked in a CuSO4 solution 12 h before cell-assembly.
Experiments Apparatus
The experimental set-up is from previous our work (see ref. 42). The modified membrane is clamped between two Cu disk electrodes (13 mm diameter) under constant pressure, where Cu is stripped from the anode and deposited on the cathode. Electrode polishing consists of grinding by fine sand paper (1200, Norton) followed by 3.0 μm alumina slurry (No. 50361-05, Type DX, Electron Microscopy Sciences) and thorough rinsing with purified water. For SEM images, a Cu-sputtered Si wafer (1.0 cm × 1.5 cm) is used as a cathode, in place of a copper disk electrode. To prevent the evaporation of the binary electrolyte solution inside the CN or PE membrane, the electrochemical cell is immersed in a beaker containing the same electrolyte. All electrochemical measurements are performed with a potentiostat (Reference 3000, Gamry Instruments). The morphology and composition of electrodeposited Cu films are confirmed by scanning electron microscopy (SEM) with energy-dispersive spectroscopy (EDS) X-ray detector (6010LA, JEOL) at 15 kV accelerating voltage.
Additional Information
How to cite this article: Han, J.-H. et al. Dendrite Suppression by Shock Electrodeposition in Charged Porous Media. Sci. Rep. 6, 28054; doi: 10.1038/srep28054 (2016).
Acknowledgments
This work was supported by Saint Gobain Ceramics and Plastics, Northboro Research and Development Center and by Robert Bosch LLC through the MIT Energy Initiative. J.-H. H. also acknowledges initial support from the Basic Science Research Program of the National Research Foundation of Korea funded by the Ministry of Education (2012R1A6A3A03039224).
Footnotes
Author Contributions J.-H.H. and M.Z.B. conceived the idea and designed the experiments. J.-H.H. and M.W. prepared the samples. J.-H.H., M.W. and P.B. performed electrochemical and SEM analysis. F.R.B. and M.Z.B. supervised the study. J.-H.H. and M.Z.B. wrote the manuscript. All the authors discussed the results and commented on the manuscript.
References
- Brady R. M. & Ball R. C. Fractal growth of copper electrodeposits. Nature 309, 225–229 (1984). [Google Scholar]
- Witten T. A. & Sander L. M. Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 47, 1400–1403 (1981). [Google Scholar]
- Rosso M. Electrodeposition from a binary electrolyte: new developments and applications. Electrochim. Acta 53, 250−256 (2007). [Google Scholar]
- Fleury V., Rosso M., Chazalviel J. N. & Sapoval B. Experimental aspects of dense morphology in copper electrodeposition. Phys. Rev. A 44, 6693–6705 (1991). [DOI] [PubMed] [Google Scholar]
- Barkey D. & Laporte P. The dynamic diffusion layer in branched growth of a conductive‐polymer aggregate in a 2‐D electrolysis cell. J. Electrochem. Soc. 137, 1655–1656 (1990). [Google Scholar]
- Bazant M. Z. Regulation of ramified electrochemical growth by a diffusive wave. Phys. Rev. E 52, 1903–1914 (1995). [DOI] [PubMed] [Google Scholar]
- Léger C., Elezgaray J. & Argoul F. Dynamical characterization of one-dimensional stationary growth regimes in diffusion-limited electrodeposition processes. J. Phys. Rev. E 58, 7700–7709 (1998). [Google Scholar]
- Huth J. M., Swinney H. L., McCormick W. D., Kuhn A. & Argoul F. Role of convection in thin-layer electrodeposition. Phys. Rev. E 51, 3444–3458 (1995). [DOI] [PubMed] [Google Scholar]
- Erlebacher J., Searson P. C. & Sieradzki K. Computer simulations of dense-branching patterns. Phys. Rev. Lett. 71, 3311–3314 (1993). [DOI] [PubMed] [Google Scholar]
- Grier D., Ben-Jacob E., Clarke R. & Sander L. M. Morphology and microstructure in electrochemical deposition of zinc. Phys. Rev. Lett. 56, 1264 (1986). [DOI] [PubMed] [Google Scholar]
- Xu W. et al. Lithium metal anodes for rechargeable batteries. Energ. Environ. Sci. 7, 513–537 (2014). [Google Scholar]
- Aurbach D., Zinigrad E., Cohen Y. & Teller H. A short review of failure mechanisms of lithium metal and lithiated graphite anodes in liquid electrolyte solutions. Solid State Ionics 148, 405–416 (2002). [Google Scholar]
- Lee J.-S. et al. Metal–air batteries with high energy density: Li–air versus Zn–air. Adv. Energy Mater. 1, 34–50 (2011). [Google Scholar]
- Monroe C. & Newman J. The impact of elastic deformation on deposition kinetics at lithium/polymer interfaces. J. Electrochem. Soc. 152, A396–A404 (2005). [Google Scholar]
- Hallinan D. T., Mullin S. A., Stone G. M. & Balsara N. P. Lithium metal stability in batteries with block copolymer electrolytes. J. Electrochem. Soc. 160, A464–A470 (2013). [Google Scholar]
- Akolkar R. Mathematical model of the dendritic growth during lithium electrodeposition. J. Power Sources 232, 23–28 (2013). [Google Scholar]
- Nishikawa K., Fukunaka Y., Sakka T., Ogata Y. H. & Selman J. R. Measurement of concentration profiles during electrodeposition of Li metal from LiPF6-PC electrolyte solution: The role of SEI dynamics. J. Electrochem. Soc. 154, A943–A948 (2007). [Google Scholar]
- Nishikawa K., Mori T., Nishida T., Fukunaka Y. & Rosso M. Li dendrite growth and Li+ ionic mass transfer phenomenon. J. Electroanal. Chem. 661, 84–89 (2011). [Google Scholar]
- Ding F. et al. Dendrite-free lithium deposition via self-healing electrostatic shield mechanism. J. Am. Chem. Soc. 135, 4450–4456 (2013). [DOI] [PubMed] [Google Scholar]
- Lu Y., Tu Z. & Archer L. A. Stable lithium electrodeposition in liquid and nanoporous solid electrolytes. Nat. Mater. 13, 961–969 (2014). [DOI] [PubMed] [Google Scholar]
- Schaefer J. L., Yanga D. A. & Archer L. A. High lithium transference number electrolytes via creation of 3-dimensional, charged, nanoporous networks from dense functionalized nanoparticle composites. Chem. Mater. 25, 834–839 (2013). [Google Scholar]
- Ryou M.-H. et al. Excellent cycle life of lithium-metal anodes in lithium-ion batteries with mussel-inspired polydopamine-coated separators. Adv. Energy Mater. 2, 645–650 (2012). [Google Scholar]
- Park M. S. et al. A highly reversible lithium metal anode. Sci. Rep. 4, 3815 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khurana R., Schaefer J. L., Archer L. A. & Coates G. W. Suppression of lithium dendrite growth using cross-linked polyethylene/poly(ethylene oxide) electrolytes: A new approach for practical lithium-metal polymer batteries, J. Am. Chem. Soc. 136, 7395–7402 (2014). [DOI] [PubMed] [Google Scholar]
- Brissot C., Rosso M., Chazalviel J. N. & Lascaud S. Dendritic growth mechanisms in lithium/polymer cells. J. Power Sources 81–82, 925–929 (1999). [Google Scholar]
- Chazalviel J. N. Electrochemical aspects of the generation of ramified metallic electrodeposits. Phys. Rev. A 42, 7355–7367 (1990). [DOI] [PubMed] [Google Scholar]
- Lu Y., Das S. K., Moganty S. S. & Archer L. A. Ionic liquid-nanoparticle hybrid electrolytes and their application in secondary lithium-metal batteries. Adv. Mater. 24, 4430–4435 (2012). [DOI] [PubMed] [Google Scholar]
- Suo L., Hu Y.-S., Li H., Armand M. & Chen L. A new class of solvent-in-salt electrolyte for high-energy rechargeable metallic lithium batteries. Nat. Commun. 4, 1481 (2013). [DOI] [PubMed] [Google Scholar]
- Rubinstein I. & Zaltzman B. Convective diffusive mixing in concentration polarization: from Taylor dispersion to surface convection. J. Fluid Mech. 728, 239–278 (2013). [Google Scholar]
- Yossifon G. & Chang H.-C. Selection of nonequilibrium overlimiting currents: universal depletion layer formation dynamics and vortex instability. Phys. Rev. Lett. 101, 254501 (2008). [DOI] [PubMed] [Google Scholar]
- Rubinstein S. M. et al. Direct observation of a nonequilibrium electro-osmotic instability. Phys. Rev. Lett. 101, 236101 (2008). [DOI] [PubMed] [Google Scholar]
- Nikonenko V. et al. Intensive current transfer in membrane systems: Modelling, mechanisms and application in electrodialysis. Adv. Colloid Interface Sci. 160, 101–123 (2010). [DOI] [PubMed] [Google Scholar]
- Elezgaray J., Léger C. & Argoul F. Linear stability analysis of unsteady galvanostatic electrodeposition in the two‐dimensional diffusion‐limited regime. J. Electrochem. Soc. 145, 2016–2024 (1998). [Google Scholar]
- Zaltzman B. & Rubinstein I. Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 579, 173–226 (2007). [Google Scholar]
- Nikonenko V. V. et al. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 342, 85–106 (2014). [Google Scholar]
- Krol J. J., Wessling M. & Strathmann H. Chronopotentiometry and overlimiting ion transport through monopolar ion exchange membranes. J. Membrane Sci. 162, 155–164 (1999). [Google Scholar]
- Balster J. et al. Morphology and microtopology of cation-exchange polymers and the origin of the overlimiting current. J. Phys. Chem. B 111, 2152–2165 (2007). [DOI] [PubMed] [Google Scholar]
- Deng D. et al. Overlimiting current and shock electrodialysis in porous media. Langmuir 29, 16167−16177 (2013). [DOI] [PubMed] [Google Scholar]
- Liu Y., Huber D. E. & Dutton R. W. Limiting and overlimiting conductance in field-effect gated nanopores. Appl. Phys. Lett. 96, 253108 (2010). [Google Scholar]
- Mani A. & Bazant M. Z. Deionization shocks in microstructures. Phys. Rev. E 84, 061504 (2011). [DOI] [PubMed] [Google Scholar]
- Dydek E. V. & Bazant M. Z. Nonlinear dynamics of ion concentration polarization in porous media: The leaky membrane model. AIChE Journal 59, 3539–3555 (2013). [Google Scholar]
- Han J.-H., Khoo E., Bai P. & Bazant M. Z. Over-limiting current and control of dendritic growth by surface conduction in nanopores. Sci. Rep. 4, 7056 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mani A., Zangle T. & Santiago J. On the propagation of concentration polarization from microchannel−nanochannel interfaces Part I: analytical model and characteristic analysis. Langmuir 25, 3898–3908 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nam S. et al. Experimental verification of overlimiting current by surface conduction and electro-osmotic flow in microchannels. Phys. Rev. Lett. 114, 114501 (2015). [DOI] [PubMed] [Google Scholar]
- Shin S., Al-Housseiny T. T., Kim B. S., Cho H. H. & Stone H. A. The race of nanowires: Morphological instabilities and a control strategy, Nano Lett. 14, 4395–4399 (2014). [DOI] [PubMed] [Google Scholar]
- Yaroshchuk A., Zholkovskiy E., Pogodin S. & Baulin V. Coupled concentration polarization and electroosmotic circulation near micro/nanointerfaces: Taylor–Aris model of hydrodynamic dispersion and limits of its applicability. Langmuir 27, 11710–11721 (2011). [DOI] [PubMed] [Google Scholar]
- Zangle T., Mani A. & Santiago J. On the propagation of concentration polarization from microchannel−nanochannel interfaces Part II: numerical and experimental study. Langmuir 25, 3909–3916 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaroshchuk A. Over-limiting currents and deionization “shocks” in current-induced polarization: Local-equilibrium analysis. Adv. Colloid Interface Sci. 183–184, 68–81 (2012). [DOI] [PubMed] [Google Scholar]
- Whitham G. B. Linear and Nonlinear Waves. 1 edition edn, (Wiley-Interscience, 1999). [Google Scholar]
- Bensimon D., Kadanoff L. P., Liang S., Shraiman B. I. & Tang C. Viscous flows in two dimensions. Rev. Mod. Phys. 58, 977–999 (1986). [Google Scholar]
- Bazant M. Z. Interfacial dynamics in transport-limited dissolution. Phys. Rev. E 73, 060601 (2006). [DOI] [PubMed] [Google Scholar]
- Spiegler K. S. Polarization at ion exchange membrane-solution interfaces. Desalination 9, 367–385 (1971). [Google Scholar]
- Dydek E. V. et al. Overlimiting current in a microchannel. Phys Rev Lett. 107, 118301 (2011). [DOI] [PubMed] [Google Scholar]
- Bazant M. Z. Conformal mapping of some non-harmonic functions in transport theory. Proc. Roy. Soc. Math. Phys. Eng. Sci. 460, 1433–1452 (2004). [Google Scholar]
- Bazant M. Z., Choi J. & Davidovitch B. Dynamics of conformal maps for a class of non-Laplacian growth phenomena. Phys. Rev. Lett. 91, 045503 (2003). [DOI] [PubMed] [Google Scholar]
- Hastings M. B. & Levitov L. S. Laplacian growth as one-dimensional turbulence. Phys. D 116, 244–252 (1998). [Google Scholar]
- Barra F., Davidovitch B. & Procaccia I. Iterated conformal dynamics and Laplacian growth. Phys. Rev. E 65, 046144 (2002). [DOI] [PubMed] [Google Scholar]
- Tikekar M. D., Archer L. A. & Kocha D. L. Stability analysis of electrodeposition across a structured electrolyte with immobilized anions. J. Electrochem. Soc. 161, A847–A855 (2014). [Google Scholar]
- Nielsen C. P. & Bruus H. Concentration polarization, surface currents, and bulk advection in a microchannel. Phys. Rev. E 90, 043020 (2014). [DOI] [PubMed] [Google Scholar]
- Mirzadeh M., Gibou F. & Squires T. M. Enhanced charging kinetics of porous electrodes: Surface conduction as a short-circuit mechanism. Phys. Rev. Lett. 113, 097701 (2014). [DOI] [PubMed] [Google Scholar]
- Moya A. A., Belashova E. & Sistat P. Numerical simulation of linear sweep and large amplitude ac voltammetries of ion-exchange membrane systems. J. Membrane Sci. 474, 215–223 (2015). [Google Scholar]
- Schlumberger S., Lu N. B., Suss M. E. & Bazant M. Z. Scalable and continuous water deionization by shock electrodialysis. Environ. Sci. Technol. Lett. 2, 367–372 (2015). [Google Scholar]
- Ellis B. L. & Nazar L. F. Sodium and sodium-ion energy storage batteries. Curr. Opin. Solid State Mater. Sci. 16, 168–177 (2012). [Google Scholar]
- Zhu J., Liu L., Zhao H. B. S & Hu W. Microstructure and performance of electroformed Cu/nano-SiC composite. Mater. Des. 28, 1958–1962 (2007). [Google Scholar]