Inference and Decoding of Motor Cortex Low-Dimensional Dynamics via Latent State-Space Models

Abstract

Motor cortex neuronal ensemble spiking activity exhibits strong low-dimensional collective dynamics (i.e., coordinated modes of activity) during behavior. Here, we demonstrate that these low-dimensional dynamics, revealed by unsupervised latent state-space models, can provide as accurate or better reconstruction of movement kinematics as direct decoding from the entire recorded ensemble. Ensembles of single neurons were recorded with triple microelectrode arrays (MEAs) implanted in ventral and dorsal premotor (PMv, PMd) and primary motor (M1) cortices while nonhuman primates performed 3-D reach-to-grasp actions. Low-dimensional dynamics were estimated via various types of latent state-space models including, for example, Poisson linear dynamic system (PLDS) models. Decoding from low-dimensional dynamics was implemented via point process and Kalman filters coupled in series. We also examined decoding based on a predictive subsampling of the recorded population. In this case, a supervised greedy procedure selected neuronal subsets that optimized decoding performance. When comparing decoding based on predictive subsampling and latent state-space models, the size of the neuronal subset was set to the same number of latent state dimensions. Overall, our findings suggest that information about naturalistic reach kinematics present in the recorded population is preserved in the inferred low-dimensional motor cortex dynamics. Furthermore, decoding based on unsupervised PLDS models may also outperform previous approaches based on direct decoding from the recorded population or on predictive subsampling.

I. Introduction

Spiking activity in recorded ensembles of motor cortex neurons is known to exhibit strong low-dimensional collective dynamics [1]–[3]. These low-dimensional dynamics are likely to reflect the constraints imposed by highly recurrent neuronal networks on the spontaneous and evoked single-neuron and population activities. In the particular case of motor cortex, these low-dimensional dynamics also likely reflect the fact that the motor system controls a considerably lower dimensional system, the sensorimotor muscle-skeletal plant. In many motor tasks, neural state trajectories inferred via latent state-space models can be relatively well characterized in much lower dimensions than the number (~100) of neurons randomly sampled by current microelectrode arrays (MEAs). It is not known, however, how well information about movement parameters is preserved in these inferred low-dimensional neural state trajectories. Here, we addressed this question by studying ensembles of neurons simultaneously recorded via triple microelectrode array recordings in two monkeys performing a naturalistic 3-D reach-to-grasp task.

We explored several approaches to infer latent low-dimensional dynamics in recorded neuronal ensembles. Previous work based on dimensionality reduction [4], [5] focused on classification of discrete parameters (e.g., identification of reach target), or on state-space models to account for hidden factors in otherwise supervised learning of kinematic decoding models [6]. Here, instead, we considered unsupervised approaches that included a dimensionality reduction algorithm (jPCA), which targets rhythmic/rotational dynamics in primary motor cortex [7], [8], and explicit latent state-space models (SSMs). Latent SSMs included linear dynamic system (LDS) models, i.e., state-space models with Gaussian linear dynamics and observations [9], [10], and Poisson-LDS (PLDS) models, where the point or count process nature of neuronal spiking observations is preserved. In the PLDS model, spike counts in small time bins (e.g., 1–25 ms) were modeled as conditional Poisson observations given evolving latent neural states [6], [11], [19], [13]–[15].

We assessed how well information about reach kinematics was preserved in each low-dimensional representation approach relative to the entire recorded population by comparing neural decoding performances. Once low-dimensional neural state trajectories were estimated via different approaches and models, we used Kalman filters to decode 3-D kinematics under a leave-one-trial-out cross-validation scheme. Positions of the hand (at the wrist), measured via a motion capture system [16], [17], were decoded separately for each (x, y, z) coordinate. The number of dimensions of the latent state space was varied to assess its effects on decoding performance.

We also considered the possibility that specific neuronal subsets (of the same size as the dimension of estimated latent neural states) could potentially yield a better decoding performance than decoding from the latent states. It has been shown before that decoding on neuronal subsets can outperform decoding based on the entire population (e.g., [16] and [17]). For this reason, we compared decoding based on latent low-dimensional states with decoding based on a predictive subsampling of the recorded neuronal population. An exhaustive search for optimal subsets that optimizes decoding would be computationally impractical even for small sets of tens of neurons. Instead, a greedy selection procedure was used to select subsets of neurons (of various sizes) that optimized performance within the Kalman filter decoding approach [17]. We emphasize that, in contrast to the unsupervised estimation of low-dimensional neural state trajectories, predictive subsampling was based on supervised learning.

Decoding based on PLDS models consistently outperformed decoding directly from the entire population or from the greedy predictive subsampling approaches. For example, a 3-D PLDS led to comparable or even higher decoding performance than the population decoding when decoding z-position trajectories. These contrasting results, based on separate decoding analyses for each motor cortical area, were enhanced when examining larger populations including neurons from all three recorded areas. Overall, our findings demonstrate that decoding based on low-dimensional dynamics (coordinated collective modes of activity), revealed by unsupervised latent state-space models, can allow better 3-D kinematics reconstruction than previous approaches based on direct decoding from the entire recorded population.

II. Methods

A. Behavioral Task: Naturalistic 3-D Reach to Grasp Movements

Two monkeys (S and R) were trained to sit on a chair and reach to grasp objects presented in front of them. Upon go cue, the subject moved its hand, initially rested on a handle, to grasp the object. The object hanging from a string was presented by the experimenter. The swinging motion of the object allowed for a wider range of hand kinematics to be recorded as the subject reached for the object. Upon grasping correctly the object for about 1 second, a juice reward was given.

Three different objects were used to allow three main types of grips: key, precision and power grips. Each object allowed two of these three grip types. A grip cue specified the type of grip. In a key grip, the object was held between the tip of thumb and index fingers, while in a precision grip, the object was held by the tip of all fingers. By contrast, in a power grip the object was held by wrapping all fingers around it. In a typical recording session ~30 successful trials were obtained for each object type. A total of two sessions for each subject were examined in this study. Sessions from subject S included 88 and 79 trials, and sessions from subject R included 79 and 104 trials.

Kinematics were recorded using a Vicon motion capture system (~240 frames per second). The system tracks reflective markers positioned on the arm and hand. The wrist position was estimated by averaging the 3-D location of four markers placed on the monkey’s wrist. This allowed us to obtain robust measurements of wrist position under situations where some reflective markers could be optically cluttered. Fig. 1 shows the 3-D wrist positions for Subjects S and R in x (horizontal: right-left), y (horizontal: forward-backward), and z (vertical: upward-downward) coordinates. Since it took a variable amount of time for the subjects to start a movement after the go cue, we estimated the movement onset as the time the wrist elevated more than 10 mm in the z coordinate. The beginning of the trial was set as 300 ms before the detected movement onset. On average it took more time for subject S to complete the trials and receive a reward (mean: 1.44, SD: 1.07 s) compared to subject R (mean: 0.83, SD: 0.74 s). The distribution of wrist positions in x, y and z coordinates differed between the two subjects, indicating that the subjects might have adopted slightly different strategies to perform the task.

Fig. 1.

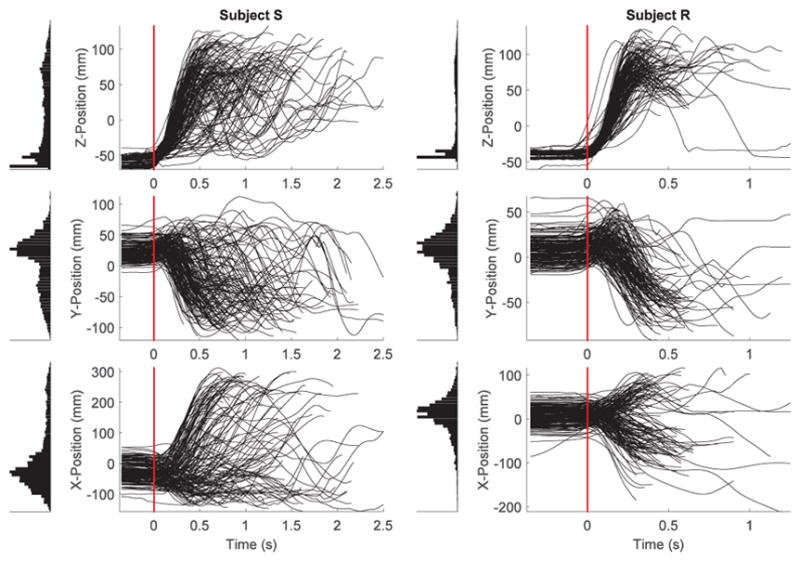
3-D reach-to-grasp task: position trajectories. 3-D wrist position in the x, y and z coordinates. Trials for both subjects were collected from two recording sessions. Movement onset corresponds to time zero (horizontal red line). Data used in the decoding analyses begin 300 ms before the movement onset. Distribution of wrist positions in each coordinate is shown by the histogram on the left of each subplot. Vertical axis in the plots spans different ranges to facilitate visualization of trajectories in different position coordinates and across the two subjects.

B. Data Recording and Preprocessing

Neural recordings were obtained from chronically implanted MEAs in the M1, PMd, and PMv areas. Three microelectrode arrays were implanted. One 96-channel MEA was implanted in PMv; two other 48-channel MEAs were implanted in M1 and PMd areas, respectively. Details on the surgery and location of electrodes are described elsewhere [16], [17]. (The datasets presented here relate to two new subjects recorded after these two studies.) Electric field potentials sampled at 30 kHz and analog band-pass filtered between 0.3 Hz–7.5 kHz were processed offline to extract extracellular action potentials (spikes). IIR notch-filters at 60, 120 and 180 Hz, and a 5th-order Butterworth high-pass filter with a cutoff frequency at 250 Hz were applied to obtain high-pass filtered signals for spike detection. Spikes were extracted as events that crossed the detection threshold. Detected spike waveforms were then aligned with respect to their minimum peak. The detection threshold was chosen as three times the standard deviation of the channel’s noise plus the smoothed high-pass signal, which was estimated by a local-averaging of the high-pass signal with an overlapping 150 ms rectangular window. Detected spikes were manually sorted for each channel. Thresholded spike waveforms were represented on a PCA feature space, where clusters were identified. Only clusters with an average signal-to-noise ratio SNR ≥ 6 dB were included in the sorting. The SNR was defined as

$$\text{SNR}=10{log}_{10}\frac{{\sigma }_{\mathrm{s}}^2}{{\sigma }_{\mathrm{n}}^2}$$ (1)

where σ_s and σ_n correspond to the standard deviations of the signal (spike waveform) and the noise, respectively. Single units consisted of sorted spikes whose cluster in the PCA feature space did not overlap with other clusters containing noise samples or other units. Sorted multiunit consisted of those cases where there was a clear cluster but with some overlap with the noise cluster. As stated above, these multiunit clusters also satisfied an average SNR ≥ 6 dB. Only sorted units that spiked at least once per trial over 80% of all trials were included in the analyses. The number of sorted units per cortical area and experimental session corresponded to: (a) Subject S, M1 (52, 40), PMd (57, 55), PMv (86, 71); (b) Subject R, M1 (37, 41), PMd (33, 49), PMv (34, 46).

Neuronal spiking activity was represented in the form of spike counts in 25-ms nonoverlapping time bins. These spike counts were used as inputs to estimate the low-dimensional dynamics and for decoding neuronal population activity.

C. Inferring Low-Dimensional Neural Dynamics: Rotational Dynamics (jPCA)

We considered several different approaches to infer low-dimensional dynamics in motor cortex neuronal ensemble spike data. These approaches included a dimensionality reduction approach that targets rhythmic/rotational dynamics in primary motor cortex (jPCA [7], [8]). When inferring low-dimensional dynamics via jPCA, we adopted the approach described in [8]. In this case, jPCA estimation consisted primarily of computing the principal components of the neural data matrix and computing the polar decompositions of the lag-1 covariance matrix of the data projections on the first n chosen principal components, where n corresponds here to the number of dimensions in the low-dimensional representation. This approach was much faster and provided the same qualitative results as the approach described in [7].

D. Inferring Low-Dimensional Neural Dynamics: Linear Dynamic System (LDS)

In addition to jPCA, we considered a low-dimensional representation based on explicit latent state-space models—the focus of this study. In the simplest case, we modeled the neuronal ensemble activity as Gaussian linear observations of an evolving Gaussian linear system, often referred to as Linear Dynamic System (LDS) models [10], expressed as

$$\begin{array}{ll}\hfill {\mathrm{x}}_{\mathrm{t}+1}& ={\mu }_{\mathrm{x}}+{\text{Ax}}_{\mathrm{t}}+{\epsilon }_{\mathrm{t}}\hfill \\ \hfill {\mathrm{y}}_{\mathrm{t}}& ={\mu }_{\mathrm{y}}+{\text{Bx}}_{\mathrm{t}}+{\eta }_{\mathrm{t}}\hfill \end{array}$$ (2)

where x_t ∈ ℝ^p denotes the latent p-dimensional evolving state at time t = 1, …, T; μ_x is a mean offset, A ∈ ℝ^p×p corresponds to the state transition matrix, the {ε_t} are independently and identically distributed (i.i.d.) Gaussian with zero mean and covariance Σ_x ∈ ℝ^p×p, ε_t ~ 𝒩(0, Σ_x); y_t ∈ ℕ^q is the observed activity (square-root transformed spike counts) in the recorded q neurons, μ_y is a mean offset, B ∈ ℝ^q×p is the observation matrix, and the {η_t} are i.i.d. zero mean Gaussian with covariance Σ_y ∈ ℝ^q×q, η_t ~ 𝒩(0, Σ_y). We applied a square-root transformation to the spike counts in order to better approximate the assumption of Gaussian observations in the LDS model.

Here, we used a standard approach to estimate the above LDS state-space model based on the Expectation-Maximization (EM) algorithm [9], except that we initialized the EM iterations with a solution obtained via factor analysis. A different initialization based on subspace system identification methods [18], [19] provided the same qualitative results. EM learning is typically computationally intensive and requires a large number of iterations to converge. By initializing the LDS parameters with nonrandom solutions, we could significantly reduce the number of required iterations. Once the LDS model parameters were estimated, we used the Kalman filter forward recursions to compute the mean and variance of the posterior density p(x_t|y_1:t), where y_1:t corresponds to the square-root of the observed spike counts in the recorded neuronal population from the beginning of the trial up to time t. Each single trial in the task should be considered a realization of the above process. The mean of the posterior density was used as the estimated low-dimensional latent state, which is henceforth denoted as x̂_t [10].

E. Inferring Low-Dimensional Neural Dynamics: Poisson Linear Dynamic System (PLDS)

In order to preserve the count process nature of spike counts, we also examined a state-space model [6], [11]–[15], [19], [20] where the observations are Poisson conditioned on the latent state, specifically

$$\begin{array}{ll}\hfill {\mathrm{x}}_{\mathrm{t}+1}& ={\mu }_{\mathrm{x}}+{\text{Ax}}_{\mathrm{t}}+{\epsilon }_{\mathrm{t}}\hfill \\ \hfill {\mathrm{y}}_{\mathrm{i},\mathrm{t}}& ~\text{Poisson}({\lambda }_{\mathrm{i}}({\mathrm{x}}_{\mathrm{t}}))\hfill \end{array}$$ (3)

where the latent state has the same dynamics as defined in (2), and λ_i(x_t) corresponds to the intensity of the conditional Poisson observation process for neuron i, modeled as

$$log{\lambda }_{\mathrm{i}}({\mathrm{x}}_{\mathrm{t}})={\mu }_{\mathrm{i},\mathrm{y}}+{\theta }_{\mathrm{i}}·{\mathrm{x}}_{\mathrm{t}}$$ (4)

where μ_i,y relates to a background level of activity and θ_i is a vector of coefficients. This observation model corresponds to a generalized linear model [15]. To estimate the Poisson LDS (PLDS) state-space model, we used the general approach presented in [6], except that the EM algorithm was initialized with solutions obtained from an exponential family PCA (e.g., [21]) and that the solutions for the density posterior p(x_t|y_1:T) during EM learning were obtained via a Laplace approximation [14], [15], [19]. A Gaussian variational Bayes approximation [22] was also explored (Fig. 2). We used algorithms provided by Lars Buesing (personal communication) to compute the exponential family PCA initialization and the Gaussian variational approximation for computation of the posterior densities. Otherwise stated, for assessment of decoding performance we use the mean of the state posterior density, under a Laplace approximation [14], [15], [20], as the estimate for the latent state.

Fig. 2.

Comparing Laplace approximation and variational Bayes methods for EM learning of PLDS model parameters. (a) Decoding performance (Pearson correlation coefficient) based on the PLDS model using either the Laplace or the variational Bayes approximation during EM learning. Each dot corresponds to one area, session, subject, and for a latent state dimension ranging from 10 (light green) to 20 (dark blue). (b) Computational time required for EM learning using either the Laplace or the variational Bayes approximation. (EM algorithm was run until convergence or until a maximum of 500 iterations was reached.) (c) Decoding performance based on the PLDS model (Laplace approximation) using either a maximum of 100 or 500 iterations.

F. Decoding of 3-D Reach Kinematics From Recorded Neural Population and Latent Low-Dimensional Neural Dynamics

To decode kinematics directly from the entire population activity, we used another state-space model such that the observed neuronal population activity y_t and the kinematic states z_t are related accordingly to

$$\begin{array}{ll}\hfill {\mathrm{z}}_{\mathrm{t}+1}& ={\mu }_{\mathrm{z}}+{\text{Dz}}_{\mathrm{t}}+{\nu }_{\mathrm{t}}\hfill \\ \hfill {\mathrm{y}}_{\mathrm{t}}& ={\mu }_{\mathrm{y}}+{\text{Ez}}_{\mathrm{t}}+{\zeta }_{\mathrm{t}}\hfill \end{array}$$ (5)

where μ_z is the mean of the kinematics, the {ν_t} are i.i.d. Gaussian, ν_t ~ 𝒩(0, Σ_z), and the {ζ_t} are i.i.d. Gaussian, ζ_t ~ 𝒩(0, Σ_z). Each kinematics variable was decoded separately, thus D is a scalar and E an observation vector. Given the measured kinematics and the recorded neuronal population activity in a training dataset, the parameters of this state-space model are estimated by a conditional maximum likelihood estimator [23].

To decode kinematics from latent states estimated via jPCA, LDS, and PLDS, the following state space representation was used:

$$\begin{array}{ll}\hfill {\mathrm{z}}_{\mathrm{t}+1}& ={\mu }_{\mathrm{z}}+{\text{Dz}}_{\mathrm{t}}+{\nu }_{\mathrm{t}}\hfill \\ \hfill {\widehat{\mathrm{x}}}_{\mathrm{t}}& ={\mu }_{\widehat{\mathrm{x}}}+{\text{Fz}}_{\mathrm{t}}+{\xi }_{\mathrm{t}}\hfill \end{array}$$ (6)

where, as in (5), the kinematics is one-dimensional, x̂_t corresponds to the latent state estimated via one of the three examined approaches (jPCA, LDS, PLDS), μ_x̂ is the mean of estimated latent state, F is the observation vector and the {ξ_t} are i.i.d. with ξ_t ~ 𝒩(0, Σ_x̂). As in the previous case, the state-space model parameters are estimated from training data via a conditional maximum likelihood estimator.

The Kalman filter was used to compute the posterior density of the kinematic (position) variable being decoded from the entire recorded population, p(z_t|y_1:t), or to compute the posterior based on the inferred low-dimensional latent states, p(z_t|x̂_1:t). The mean of the posterior was then used as the estimated position. Fig. 3 in Section III shows the schematics for the decoding approach based on PLDS. In that case, a point process filter using the Laplace approximation [15] is coupled in series with a Kalman filter. We note that, given LDS and PLDS parameters estimated on training data, this neural decoding approach can be easily implemented in real time. In other words, both the posteriors p(z_t|x̂_1:t) and p(x_t|y_1:t) can be computed in real time. Decoding performance was assessed under a leave-one-trial-out cross-validation scheme.

Fig. 3.

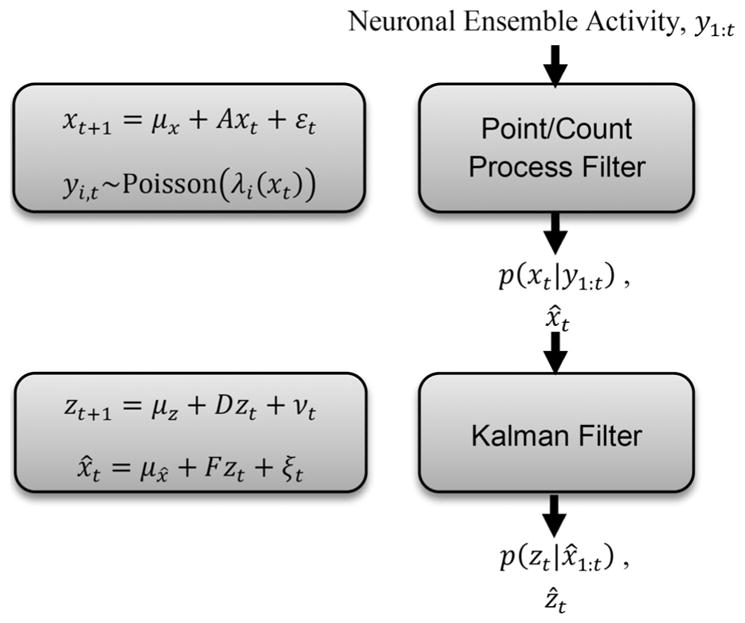
Schematics for the neural decoding approach based on latent state-space models. Schematic illustrates the specific case of PLDS latent state-space models applied to decoding kinematics on test trials. Blocks on the left indicate the corresponding state-space model representation [(3), (4) and (6); Methods]. Parameters for the state-space models are estimated on training data. The flow-chart on the right indicates the main estimation steps for decoding on test data at each time t. Term y_1:t denotes the spike train or counts over the recorded ensemble up to time t. Terms x̂_t and ẑ_t correspond to the means for the posterior densities of the latent state and kinematics, respectively.

To evaluate the chance level (statistical significance) of the decoding performance based on the entire recorded population, we used a random permutation approach. Spike counts in different trials were randomly permutated in time and independently across neurons. A decoding performance was then obtained under this random permutation. This procedure was repeated 1000 times. We report the 95 percentile of the decoding performances obtained under this random permutation approach as the 95 percentile of the chance level decoding.

G. Decoding of 3-D Reach Kinematics Based on Random and Predictive Subsampling of Recorded Neuronal Populations

It is possible that a subset of neurons, much smaller in size than the recorded population, could allow for better decoding than the entire population (e.g., [16] and [17]), or even than the low-dimensional dynamics based on state-space models examined here. Therefore, we also considered an approach, henceforth referred to as predictive subsampling, where we search for neuronal subsets of different sizes that optimize decoding. An exhaustive search of all possible subsets is obviously not practical for even small recorded populations (>10 neurons). We adopted instead a greedy search algorithm [17].

Specifically, we start by initializing the subset for size n = 1 with the neuron that, among all recorded neurons, provides the best decoding performance. In the next iteration, we add to the subset the next best neuron, such that n = 2. This procedure continues iteratively until all neurons in the population are selected and added to the subset. To minimize overfitting to the training data, the decoding in all iterations of this greedy selection were performed under a leave-one-trial-out cross-validation scheme. We also emphasize that, as the term predictive subsampling implies, this is a supervised approach, in contrast with the unsupervised latent state-space models used here.

In addition, we also examined the decoding performance based on subsets of neurons of various sizes that were randomly chosen, i.e., irrespective of their decoding performance, from the entire recorded population.

III. Results

A. Low-Dimensional Motor Cortex Dynamics During Naturalistic 3-D Reach-to-Grasp Actions

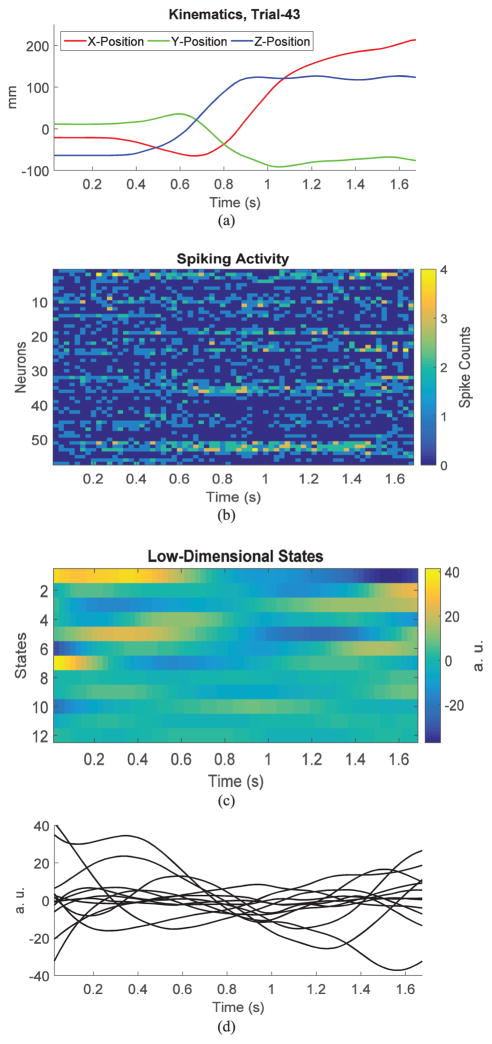
The spiking activity for Subjects S and R was recorded from the M1, PMd and PMv cortical areas in two recording sessions. Monkey S performed 88 and 79 successful trials in the two sessions of the reach-to-grasp task, respectively, while monkey R performed 79 and 104 successful trials. Fig. 1 shows the distribution of 3-D wrist position for the two subjects and all trials in the two sessions. The reach-to-grasp task was designed to minimize correlations among different coordinates or degrees of freedom in hand/arm movements [16] and to optimize the use of the subject’s workspace. Fig. 4(a) and (b) illustrates the kinematics and corresponding neural data of a sample reach trial for subject S. The neural ensemble spike-count raster corresponding (25 ms time bins) to 57 neurons simultaneously recorded during a single trial in one experimental session, area PMd, is shown in Fig. 4(b).

Fig. 4.

Example of low-dimensional neural dynamics inferred via a PLDS state-space model. (a) 3-D wrist position in x, y and z coordinates for a reach trial from subject S. (b) Spike counts (25 ms time bins) during the trial recorded from a population of 57 neurons from the PMd area. (c), (d) Low-dimensional neural dynamics inferred via a PLDS state-space model (12-dimensional state).

Latent state-space models were first estimated for each motor cortical area separately and for the combined three areas in later analyses. The LDS models were fitted to the square-root transformed spike counts. This transformation was applied to better match the Gaussian assumption for the state-space observations. The Poisson LDS (PLDS) was fitted directly to the spike count data. Fig. 4(c) and (d) shows the latent PLDS states corresponding to one example trial. In this case, a 12-dimensional state was estimated.

As stated above, parameters for the state-space models were estimated in an unsupervised fashion, i.e., without knowledge of the motor behavior. Different dimensions of the inferred low-dimensional states can reflect different aspects of neural dynamics, some potentially related to the motor behavior (e.g., kinematics) during the reach-to-grasp task, and some potentially related to other processes such as ongoing cortical activity, for example.

We assessed how well information about kinematics was preserved in the inferred low-dimensional neural dynamics estimated from separate motor cortical areas by comparing how well 3-D reach kinematics could be decoded from the inferred latent states and directly from the full recorded neuronal population. We used the Pearson correlation coefficient (CC) between the decoded and true kinematics, computed separately for x, y, and z position coordinates, to assess decoding performance. Comparable decoding performances would indicate the preservation of information about 3-D reach actions in the estimated low-dimensional dynamics. A Kalman filter was used to decode trajectories separately for the x, y, and z coordinates and from each motor cortical area individually. The observations in the state-space model underlying the Kalman Filter decoding varied depending on the approach being assessed (Section II). The more complex case based on the PLDS model consisted of a point/count process filter and a Kalman filter coupled in series, as illustrated by the schematics in Fig. 3. Maximum likelihood estimates for the Kalman filter were obtained from training data under a leave-one-trial-out cross-validation scheme (Section II). For decoding purposes, all kinematics were down-sampled to the sampling rate of the spike counts at 40 Hz (i.e., 25 ms time bins).

In the case of the PLDS state-space model, an approximation to the latent state posterior density and its mean and variance is required both during model estimation and decoding because there is no closed-form solution for the posterior [24]. Thus, before proceeding with the assessment of decoding performance based on the different approaches, we examined two alternative implementations of the expectation step in the EM algorithm for the learning of the PLDS state-space model parameters: the Laplace approximation or the variational Bayes for the inference of the mean and variance of the state posterior densities. The EM algorithm was run until convergence or until a maximum of 500 iterations was reached. As stated in Section II, exponential-family PCA was used for the initialization of the latent states in both cases. The Laplace approximation was not only much faster in our specific application, but also resulted in slightly better decoding performance [Fig. 2(a) and (b)]. Based on the above-mentioned results, we adopted the Laplace approximation in the PLDS model estimation and decoding analyses. We also note that fewer EM iterations can be used while preserving decoding performance and speeding up considerably the PLDS estimation. Specifically, in our datasets, an EM estimation with at most 100 iterations under the Laplace approximation resulted in about the same decoding performance as that based on an EM estimation with at most 500 iterations. The computational time in the at most 100 iterations case assessed on a Dell Precision Workstation (2 Intel Xeon processors @ 3.1 GHz) running Matlab, resulted in 40.77±9.78 (mean ±2SD) minutes for 15 dimensions (monkey S), and 23.05±8.8 minutes for nine dimensions (monkey R). (The choice of these two different dimensions is clarified in Fig. 6.) These results were obtained on the same datasets corresponding to three different cortical areas and two experimental sessions used in the analyses that follow. For actual applications in brain-machine interfaces, this computational time can be substantially reduced with the use of standalone executables and/or with the use of embedded digital signal processing hardware. Furthermore, the computational time during real-time decoding, i.e., once the PLDS model has been already estimated based on some training data, is not a concern here, since in this case one simply needs to iterate a small set of forward filtering equations for both the point process and Kalman filters coupled in series.

Fig. 6.

Dependence of decoding performance on the dimension of inferred latent neural states. Decoding performance is assessed via the Pearson correlation coefficient (CC), averaged over sessions, for each subject and area PMd. In addition to low-dimensional dynamics inferred via LDS, PLDS and jPCA, the figure compares the performances achieved by decoding from the full population, and neuronal subsets of varying sizes obtained via random or predictive subsampling. Similar results were obtained for areas M1 and PMv.

Decoded position trajectories from low-dimensional states estimated via PLDS tended to be smoother than trajectories decoded directly from the full population, LDS, random subsampling, and greedy predictive subsampling (Section II). Fig. 5 shows a single trial example [same as in Fig. 4(a)] illustrating the decoding of x, y, and z position coordinates from the recorded entire population spiking activity in M1, PMd and PMv areas, and from lower dimensional inputs consisting of 12-dimensional latent state trajectories estimated via jPCA, LDS and PLDS, and from neuronal subsets obtained via random or predictive subsampling of the same size as the latent state dimension.

Fig. 5.

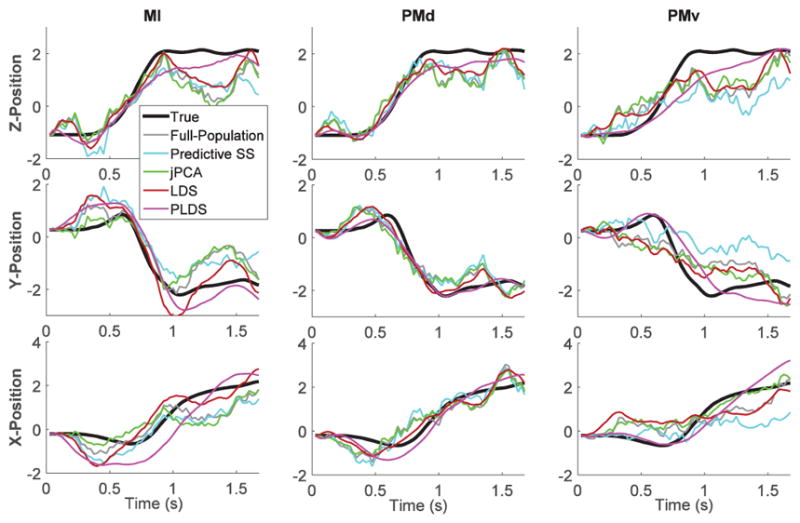
Example of 3-D position decoding. Decoding of the reach trial shown in Fig. 4(a) based on recorded spike trains (full-population, random subsampling, predictive subsampling) and inferred low-dimensional dynamics (LDS, PLDS, jPCA) from areas M1, PMd and PMv. Decoded position trajectories based on different approaches are compared to true trajectories (black curves). Position trajectories have been normalized (z-score).

B. Decoding 3-D Reach Kinematics From Single-Area Motor Cortex Low-Dimensional Dynamics: Dependence on Latent State Dimension

We examined how the number of state dimensions in the latent state-space models, jPCA and subsampling affected decoding performance. Fig. 6 shows the CC performance based on different decoding approaches averaged over sessions for subjects S and R as the number of latent state dimensions increased, from 2 to 30 dimensions. Decoding performance grew roughly monotonically and reached a plateau after a given number of dimensions.

The number of dimensions at which a plateau was reached varied according to subject and according to position coordinate, being smaller for decoding of z-position. For example, as few as 2–3 dimensions were sufficient for PLDS to show better z-position decoding performance than the full population in subject R, while a larger number of dimensions was required for x- and y-position coordinates. Similar trends were observed for decoding from M1, PMv and PMd areas.

C. Decoding 3-D Reach Kinematics From Single-Area Motor Cortex Low-Dimensional Dynamics: Summary Across Cortical Areas and Position Coordinates

To simplify the comparisons and based on the results shown in Fig. 6, we fixed the state dimensions to 15 for monkey S and 9 for monkey R, regardless of the recording area, since dependency on dimension did not seem to vary substantially with motor cortical area. The same dimensions were applied to the size of neuronal subsets obtained via random and predictive subsampling.

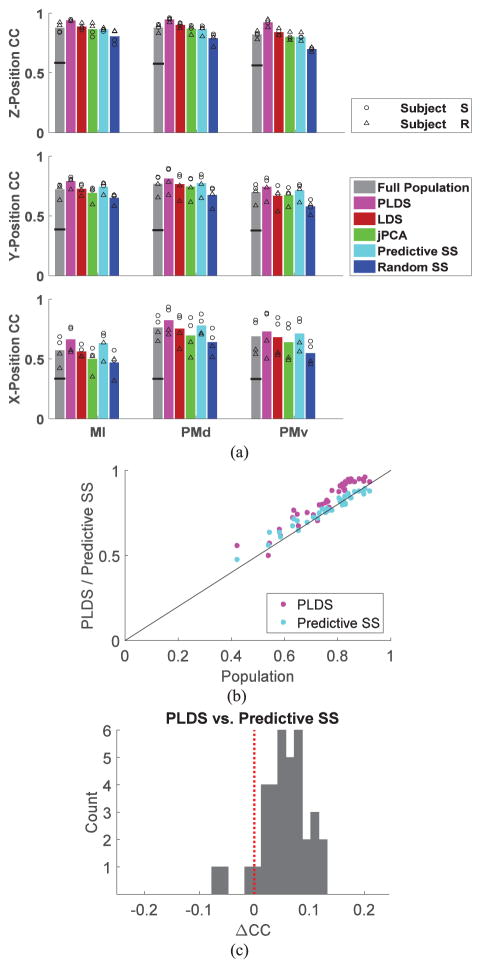
Overall, decoding based on low-dimensional state trajectories inferred via the PLDS approach achieved consistently higher performance relative to direct decoding from the entire population, LDS, jPCA, random and predictive subsampling (Fig. 7). We used a nonparametric approach, the Kruskal-Wallis test, to determine statistical significance. The correlation coefficient of the decoded kinematics (x, y and z coordinates) for different sessions/areas using the PLDS model was significantly higher than the decoding from the full population, p-value <0.05, and significantly higher than the decoding based on predictive subsampling (with the same set sizes as the state dimensions used in the PLDS approach), p-value <0.05. The differences between the decoding performances based on the full population and on the predictive subsampling were not statistically significant according to the Kruskal-Wallis test. The comparative performance between PLDS and predictive subsampling was consistent across cortical areas, position coordinates, experimental sessions and subjects (Fig. 7(b) and (c)), with PLDS outperforming predictive subsampling in 92% of the cases. Comparison of the different decoding approaches in terms of normalized root mean square errors, averaged over the three position coordinates, is shown in Table I.

Fig. 7.

Summary of decoding performance based on different decoding approaches: separate motor cortical areas. (a) Decoding performance (Pearson correlation coefficient, CC) based on different approaches is shown separately for x-, y-, z-position coordinates, motor cortical areas (M1, PMd, PMv), sessions and subjects. Each bar shows the average CC over subject/sessions based on a given decoding approach. Dimension of the latent state in LDS, PLDS and jPCA was fixed to 15 (subject S) and 9 (subject R). (See also Fig. 6 for the dependence of decoding performance on state dimension.) Same number of dimensions was used for the number of neurons in the neuronal subsets obtained via random subsampling and predictive subsampling. Horizontal black line in each bar indicates the average chance level CC for decoding based on the full population. (b) Comparison between decoding based on PLDS or predictive subsampling and the decoding based on the full population. Each dot corresponds to one position coordinate, motor cortical area, session and subject. (c) Distribution of the differences between the CCs (ΔCC) based on the PLDS and predictive subsampling decoding approaches.

TABLE I.

Decoding Performance: Root Mean Square Error Averaged Across Three Position Coordinates

	Population	PLDS	LDS	jPCA	Predictive Subsampling
MI	0.52 ± 0.06	0.44 ± 0.09	0.59 ± 0.04	0.61 ± 0.06	0.47 ± 0.04
PMd	0.38 ± 0.06	0.28 ± 0.04	0.42 ± 0.09	0.44 ± 0.08	0.37 ± 0.06
PMv	0.49 ± 0.07	0.43 ± 0.11	0.56 ± 0.09	0.56 ± 0.07	0.48 ± 0.06

We note that in the previous analysis we used a simple cross-validation scheme (leave-one-trial-out) instead of partitioning the data into training, validation and testing sets. For the main result of our decoding performance assessment, we think the latter scheme is not necessary because the decoding performance of the PLDS model was typically above the decoding performance based on the full population or on the predictive subsampling approach, after a given low dimension was reached (Fig. 6). Thus. the use of separate validation and testing sets does not seem critical for the examination of the dimension of the latent state space (or subset size) and its effects on the comparison between the PLDS and other approaches.

D. Decoding 3-D Reach Kinematics From Motor Cortex Low-Dimensional Dynamics: Combined Motor Cortical Areas

We extended the analyses to the case of combining neurons from the three different cortical areas (M1, PMv, PMd) and estimating a single state-space model for the combined population, as opposed to separate areas as done previously. The dependence on the number of state dimensions was qualitatively similar to the dependence observed when treating each cortical area separately, even though the total number of neurons had increased substantially. As for the separate area case, decoding performance based on PLDS latent state-space model increased roughly monotonically with number of dimensions, outperforming direct decoding from the full population with as few as 3–5 dimensions (z-position) and ~10 dimension for x- and y-position, and reaching a plateau after that. This dependence on the number of state dimensions was also similar for LDS, jPCA, and predictive subsampling. Fig. 8 shows the results for the PLDS and predictive subsampling approaches.

Fig. 8.

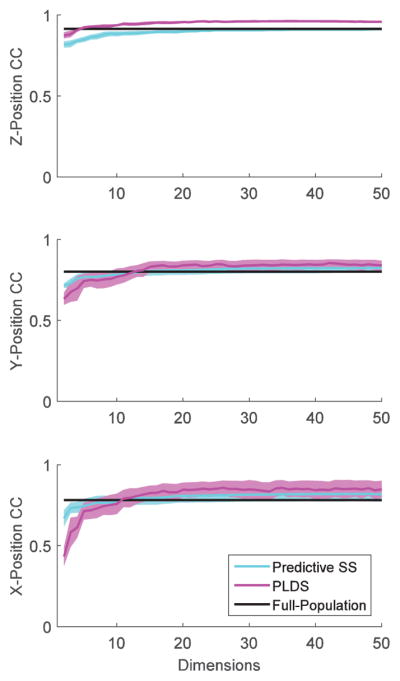
Dependence of decoding performance on the dimension of inferred latent neural states: combined motor cortical areas (M1, PMd, PMv). Low-dimensional dynamics were inferred from neuronal activity recorded from the combined three cortical areas (M1, PMv and PMd) using PLDS models. For comparison, the decoding performance based on the full combined population and on predictive subsampling is also shown. Decoding performance was assessed via the Pearson correlation coefficient (CC). Each curve corresponds to the decoding performance CC averaged across subjects and sessions. Shaded areas correspond to the 95% confidence intervals (mean ±2 SE).

For a more detailed comparison of decoding performance based on combined motor cortical areas, we fixed the latent state dimensions (or subset size in the case of predictive subsampling) to 25 for both subjects. The total number of simultaneously recorded neurons in the combined populations across the three motor cortical areas in each of the two sessions corresponded to 195 and 166 (subject S), and 104 and 136 (subject R). Decoding performance based on PLDS low-dimensional state trajectories for the combined motor cortical areas improved relative to the case of separate motor areas [Fig. 9(a)] and, as before, outperformed decoding directly from the entire recorded population [Fig. 9(b)]. Decoding performance based on predictive subsampling was similar to the performance based on the entire population and typically lower than the performance based on the PLDS approach [Fig. 9(c)].

Fig. 9.

Summary of decoding performance based on PLDS, predictive subsampling and full population: separate versus combined motor cortical areas. (a) Decoding performance (Pearson correlation coefficient, CC) based on PLDS models applied to each of the three motor cortical areas separately or to the combined three areas. There are 36 dots corresponding to three position coordinates, three areas, two sessions, and two subjects. (b) Comparison of decoding performance based on PLDS models, predictive subsampling and full combined population. Each dot corresponds to a position coordinate, session and subject. (c) Distribution of the differences between the CCs (ΔCC) based on the PLDS and predictive subsampling decoding approaches applied to the combined areas.

IV. Discussion

Recent studies have emphasized the low-dimensional nature of collective dynamics at the level of ensembles of single-neuron spiking activity in motor cortex [1]–[3], [10], [11]. Here, we addressed the question of how well information about reach kinematics during a naturalistic 3-D reach-to-grasp task is preserved in low-dimensional dynamics estimated via latent state-space models. Our analyses demonstrate that decoding based on low-dimensional state trajectories tended to outperform decoding directly from the entire population and decoding based on predictive (supervised) neuronal subsampling. This result suggests that information about movement parameters is largely preserved in the estimated low-dimensional collective dynamics. This is not an obvious finding since these low-dimensional dynamics, inferred via unsupervised methods, could potentially relate to many other ongoing cortical processes, not directly associated with arm/hand kinematics. This finding was consistent across different subjects and across different cortical areas including primary motor, ventral and dorsal premotor areas. Furthermore, we compared different latent state-space models and showed that a state-space approach (PLDS) that preserves the point/count process nature of neural spiking observations outperformed approaches that did not (LDS, jPCA).

Given the characteristics and length (1.5 mm) of the microelectrode arrays used in study, it is likely that our recordings originated primarily from large pyramidal neurons in deep layers responsible for motor output. Because motor cortex output is involved in the control of a much lower dimensional system (the muscle-skeletal plant), the corresponding neural dynamics likely live in a lower dimensional manifold and are primarily related to parameters of intended movement. Our findings that unsupervised inference of latent low-dimensional state trajectories preserved information about reach kinematics during this 3-D reach-to-grasp task seem to reflect the features of motor cortex dynamics.

Low-dimensional representations of neural dynamics, as used here, are thought to “denoise” neural spike train observations [2]. As a result of the modeled temporal dynamics in the latent state evolution, inferred latent state trajectories are typically much smoother than the observed neuronal spiking activity. In this way, these low-dimensional dynamics seem also to capture neural variability more directly related to slower time scale behavioral parameters rather than faster and private variability in single-neuron spiking [7], [25]. We also note that we did not enforce stability of the latent state dynamics in the estimation of LDS and PLDS models. As suggested in [19], stability constraints can lead to even smoother dynamics. This could potentially lead to higher performance gains in decoding from latent low-dimensional state-space models. In addition, this “denoising” operation could reduce the overfitting capacity of the decoder and improve generalization to test data.

Our study focused on decoding of 3-D reach kinematics at the wrist. It remains an open question how these findings generalize to higher dimensional degrees of freedom and much more complex sensorimotor tasks. The inferred low-dimensional dynamics resulting from the highly recurrent connectivity in motor cortex may also impose important constraints to adaptation and skill learning [26], particularly relevant for BMIs. Another important open issue is the contrast between the dimensionality of collective neural dynamics in early (especially visual) sensory and motor cortices. Because of the seemingly much higher bandwidth in the early visual cortex output, we would expect collective neural dynamics to live in much higher dimensional spaces in this case. We also note that our analyses were based on neuronal recordings consisting of high signal-to-noise ratio single and multiunit activity. Different findings could potentially result from applying the same analyses to thresholded but unsorted spikes.

Predictive subsampling provided the closest performance to the PLDS approach when decoding 3-D reach kinematics from motor cortex. However, we emphasize that so far there is no computationally efficient way to select an optimal subset of neurons, especially in the context of decoding based on probabilistic Bayesian state-space model approaches, e.g., Kalman and point process filters. Exhaustive search of optimal subsets is computationally impractical even for tens of neurons. The greedy approach adopted here is limited in this sense because its forward search restricts the assessment to a very small fraction of all of the possible neuronal subsets of a given size. In addition, the approach becomes very slow once neuronal subsets consisting of a range of different sizes need to be searched and assessed in terms of decoding performance, especially when applied to larger neuronal ensembles resulting from multiple recorded cortical areas. Approaches based on input–output system identification (e.g., [27]), rather than the probabilistic state-space models adopted here, may provide an alternative for future investigation. For these reasons, low-dimensional latent state-space models remain an attractive approach in the context of neural decoding based on probabilistic Bayesian state-space models. It remains, however, an important research problem: the development of discriminative or predictive latent state-space models, i.e., algorithms that find latent state-space representations that maximize decoding performance in a supervised manner.

The latent PLDS state-space models used here can be easily implemented in real-time closed-loop decoding applications for BMIs. Estimation of the PLDS parameters from training data can be accelerated substantially by starting the EM iterations with adequate initial conditions. Fast convergence requiring only tens of iterations has been demonstrated before [19] by initializing EM with solutions obtained via Factor analysis, exponential-family PCA and subspace identification methods. Once the PLDS model parameters have been estimated, the mean and variance of the latent state posterior density (approximated via Laplace or Gaussian variational methods) can be recursively tracked in real-time similarly to what is commonly done in Kalman and point process filters for neural decoding [15], [23], [24], [28]. We hope to investigate the performance of BMIs based on latent low-dimensional dynamics in the future.

Biographies

Mehdi Aghagolzadeh (M’14) received the B.Sc. degree (with honors) from University of Tabriz, and the M.Sc. degree from University of Tehran, Iran, and the Ph.D. degree from Michigan State University, USA, all in electrical and computer engineering.

Since 2013, he has been a Postdoctoral Research Associate at the Department of Neuroscience, Brown University, Providence, RI, USA. His research focuses on machine learning and statistical signal processing tools for brain-machine interfaces that aim at restoring function in people with neurological disorders.

Wilson Truccolo received the Ph.D. degree in complex systems from Florida Atlantic University, Boca Raton, FL, USA, and postdoctoral training in the Department of Neuroscience, Brown University, Providence, RI, USA.

He is currently an Assistant Professor of Computational Neuroscience, Brown University and Investigator at the Center for Neurorestoration and Neurotechnology, U.S. Department of Veterans Affairs, Providence. His research focuses on neural dynamics, statistical neuroscience, and neuromedical systems for prediction and control of neurological disorders.