Empirical Corrections to the Amber RNA Force Field with Target Metadynamics

Abstract

The computational study of conformational transitions in nucleic acids still faces many challenges. For example, in the case of single stranded RNA tetranucleotides, agreement between simulations and experiments is not satisfactory due to inaccuracies in the force fields commonly used in molecular dynamics simulations. We here use experimental data collected from high-resolution X-ray structures to attempt an improvement of the latest version of the AMBER force field. A modified metadynamics algorithm is used to calculate correcting potentials designed to enforce experimental distributions of backbone torsion angles. Replica-exchange simulations of tetranucleotides including these correcting potentials show significantly better agreement with independent solution experiments for the oligonucleotides containing pyrimidine bases. Although the proposed corrections do not seem to be portable to generic RNA systems, the simulations revealed the importance of the α and ζ backbone angles for the modulation of the RNA conformational ensemble. The correction protocol presented here suggests a systematic procedure for force-field refinement.

Introduction

Molecular dynamics is a powerful tool that can be used as a virtual microscope to investigate the structure and dynamics of biomolecular systems.¹ However, the predictive power of molecular dynamics is typically limited by the accuracy of the employed energy functions, known as force fields. Whereas important advances have been made for proteins,^2,3 their accuracy for nucleic acids is still lagging behind.^4,5 Force fields for RNA have been used for several years in many applications to successfully model the dynamics around the experimental structures.⁶ Traditionally, the functional form and parameters of these energy functions have been assessed by checking the stability of the native structure. This has lead, for instance, to the discovery of important flaws in the parametrization of the backbone⁷ and of the glycosidic torsion.⁸ However, to properly validate a force field, it is necessary to ensure that the entire ensemble is consistent with the available experimental data. This can be done only using enhanced sampling techniques or dedicated hardware. Recent tests^5,9 have shown that state-of-the-art force fields for RNA are still not accurate enough to produce ensembles compatible with NMR data in solution in the case of single stranded oligonucleotides. Similar issues have been reported for DNA and RNA dinucleosides.^10,11

Previous studies have shown that the distribution of structures sampled from the protein data bank (PDB) may approximate the Boltzmann distribution to a reasonable extent^2,12−14 and could even highlight features in the conformational landscape that are not reproduced by state-of-the-art force fields.^15,16 This has been exploited in the parametrization of protein force fields. For example, a significant improvement of the force fields of the CHARMM family has been obtained by including empirical corrections commonly known as CMAPs, based on distributions from the PDB.^17,18

In this work, we apply these ideas to the RNA field and show how it is possible to derive force-field corrections using an ensemble of X-ray structures. At variance with the CMAP approach, we here correct the force field using a self-consistent procedure where metadynamics is used to enforce a given target distribution.^19,20 Correcting potentials are obtained for multiple dihedral angles using the metadynamics algorithm in a concurrent fashion. Since the target distributions are multimodal, we also use a recently developed enhanced sampling technique, replica exchange with collective-variable tempering (RECT),²¹ to accelerate the convergence of the algorithm. The correcting potentials are obtained by matching the torsion distributions for a set of dinucleoside monophosphates. The resulting corrections are then tested on tetranucleotides where standard force field parameters are known to fail in reproducing NMR data.

Methods

In this Section we briefly describe the target metadynamics approach and discuss the details of the performed simulations.

Targeting Distributions with Metadynamics

Metadynamics (MetaD) has been traditionally used to enforce an uniform distribution for a properly chosen set of collective variables (CV) that are expected to describe the slow dynamics of a system.²² However, it has been recently shown that the algorithm can be modified so as to target a preassigned distribution which is not uniform.^19,20 In this way a distribution taken from experiments, such as pulsed electron paramagnetic resonance, or from an X-ray ensemble, can be enforced to improve the agreement of simulations with empirical data. We refer to the method as target metadynamics (T-MetaD), following the name introduced in ref.¹⁹ For completeness, we here briefly derive the equations. It is also important to notice that the same goal could be achieved using a recently proposed variational approach.^23,24

In our implementation of T-MetaD a history dependent potential V(s,t) acting on the collective variable s at time t is introduced and evolved according to the following equation of motion

1

Here β = 1/k_BT, where k_B is the Boltzmann constant; T is the temperature; ω is the initial deposition rate of the kernel function, which is here defined as a Gaussian with width σ; F̃(s) is the free-energy landscape associated with the target distribution; F̃_max indicates the maximum value of the function F̃; and D is a constant damping factor. The target distribution is thus proportional to e^–βF̃(s). We define 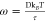, where τ is the characteristic time of bias deposition. The term e^{β(F̃(s)–F̃_max)} adjusts the height of the bias potential, making Gaussians higher at the target free-energy maximum and lower at its minimum. This forces the system to spend more time on regions where the targeted free-energy is lower. We notice that a similar argument has been used in the past to derive the stationary distribution both of well-tempered metadynamics, where Gaussian height depends on already deposited potential,²⁵ and of adaptive-Gaussian metadynamics, where Gaussian shape and volume are changed during the simulation.²⁶ The subtraction of F̃_max sets an intrinsic upper limit for the height of each Gaussian, thus avoiding the addition of large forces on the system. We notice that other authors used terms such as the minimum of F or the partition function to set an intrinsic lower limit for the prefactor e^{β(F̃(s)–F̃_max)}.^19,20 At the same time, the term acts as a global tempering factor²⁷ and makes the Gaussian height decrease with the simulation time, so as to make the bias potential converge instead of fluctuate. As observed in ref (19), the tempering approach used in well-tempered MetaD in this case would lead to a final distribution that is a mixture of the target distribution with the distribution from the original force field. For this reason, we prefer to use here a global tempering approach.²⁷

In the long time limit (quasi-stationary condition), the bias potential will, on average, grow as^25,27

2

where P(s) is the probability distribution of the biased ensemble. Defining the function we can see this equation is a convolution of a Gaussian and a positive definite function.

3

As shown in refs (25 and 27), this average should be independent of s under stationary conditions, so that the function g(s′) P(s′) should be also independent of s′, though still dependent on time

4

By recognizing that F̃_max and V_max do not depend on s, one can transform the last equation to

5

which implies that

6

Thus, the system will sample a stationary distribution of s that is identical to the enforced one.

Whereas the equations are here only described for a single CV, this method can be straightforwardly applied to multiple CVs in a concurrent manner. In this case, the total bias potential is the sum of the one-dimensional bias potentials applied to each degree of freedom. Indeed, similarly to the concurrent metadynamics used in RECT,²¹ all the distributions are self-consistently enforced.²⁰ This is particularly important when biasing backbone torsion angles in nucleic acids, since they are highly correlated.^28,29 In this situation, it is also convenient to use a biasing method that converges to a stationary potential through a tempering approach, to include in the self-consistent procedure of MetaD an additional effective potential associated with the correlation between the dihedral angles that is as close as possible to convergence.

Simulation Protocols

RNA Dinucleoside Monophosphates

Fragments of dinucleoside monophosphate with the sequences CC, AA, CA, and AC were extracted from the PDB database of RNA X-ray structures at medium and high resolution (resolution <3 Å). The selected structures were protonated using the pdb2gmx tool from GROMACS 4.6.7.³⁰ Free-energy profiles along the backbone dihedral angles were calculated with the driver utility of PLUMED 2.1.³¹

Molecular dynamics simulations of the chosen RNA dinucleoside monophosphate sequences were performed using the Amberff99bsc0_χOL3 force field (named here Amber14).^7,8,32 The systems were solvated in an octahedron box of TIP3P water molecules³³ with a distance between the solute and the box wall of 1 nm. The system charge was neutralized by adding one Na⁺ counterion. The LINCS³⁴ algorithm was used to constrain all bonds containing hydrogens, and equations of motion were integrated with a time step of 2 fs. All the systems were coupled to a thermostat through the stochastic velocity rescaling algorithm.³⁵ For all nonbonded interactions, the direct space cutoff was set to 0.8 nm and the electrostatic long-range interactions were treated using the default particle-mesh Ewald³⁶ settings. An initial equilibration in the NPT ensemble was done for 2 ns, using the Parrinello–Rahman barostat.³⁷ Production simulations were run in the NVT ensemble. All the simulations were run using GROMACS 4.6.7³⁰ patched with a modified version of the PLUMED 2.1 plugin.³¹

T-MetaD simulations were run to enforce the probability distributions of the angles ϵ₁, ζ₁, α₂, and β₂ (see Figure 1), which were calculated from the X-ray fragments. The target free-energy profiles were calculated with PLUMED 2.1. Distributions were estimated as a combination of Gaussian kernels, with a bandwidth of 0.15 rad, and written on a grid with 200 bins spanning the (−π,π) range. The bias potential used for the T-MetaD was grown using a characteristic time τ = 200 ps and a damping factor D = 100. Gaussians with a width of 0.15 rad were deposited every N_G = 500 steps.

Figure 1.

Representation of a Cytosine–Cytosine dinucleoside monophosphate. The backbone dihedrals selected for the force-field correction are shown in black, and the CVs accelerated in the RECT simulations are shown in black or blue.

We underline that simulations performed using T-MetaD could be nonergodic for two reasons. First, there could be significant barriers acting on CVs that are not targeted and thus not biased at this stage (e.g., χ dihedral angles). Second, if the enforced distribution of a CV is bimodal, it will be necessary to help the system in exploring both modes with the correct relative probability. It is thus necessary to combine the T-MetaD approach with an independent enhanced-sampling scheme. Here we used RECT, a replica-exchange method where a group of CVs is biased concurrently using a different bias factor for each replica and one reference replica is used to accumulate statistics.²¹ When T-MetaD and RECT are combined, in each replica a T-MetaD is run with the same settings, including the reference replica. The T-MetaD/RECT simulation was run with 4 replicas for 1 μs each. For each residue, the dihedrals of the nucleic acid backbone (α, β, γ, ϵ, ζ), together with one of the Cartesian coordinates of the ring puckering³⁸ (Zx) and the glycosidic torsion angle (χ), were chosen as accelerated CVs (see Figure 1). To help the free rotation of the nucleotide heterocyclic base around the glycosidic bond, the distance between the center of mass of nucleobases was also biased. For the dihedral angles, the Gaussian width was set to 0.25 rad, and for the distance it was set to 0.05 nm. The Gaussians were deposited every N_G = 500 steps. The initial Gaussian height was adjusted to the bias factor γ of each replica, according to the relation 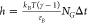, in order to maintain the same τ_B = 12 ps across the entire replica ladder. The bias factor γ ladder was chosen in the range from 1 to 2, following a geometric distribution. In replicas with γ ≠ 1, the target free-energy was scaled by the factor 1/γ. Exchanges were attempted every 200 steps. Statistic was collected from the unbiased replica. A sample input file is provided as Supporting Information (see Figure S1).

Finally, a new RECT simulation was run for each dinucleoside with the bias potentials obtained from the T-MetaD applied statically on each replica. These calculations represent the results obtained with a force field that includes the corrections from the PDB distributions, and they are thus labeled as Amber_pdb. Statistics from these simulations were collected to evaluate the effects of the corrections. The simulation time was 1 μs per replica.

RNA Tetranucleotides

To test the force-field corrections derived from dinucleoside monophosphates, temperature replica-exchange molecular dynamics (T-REMD) simulations³⁹ were performed on different tetranucleotide systems with the sequences CCCC, GACC, and AAAA. The correcting potentials calculated for the AA and CC dinucleosides were applied to all the backbone angles of AAAA and CCCC tetranucleotides, respectively. For the GACC tetranucleotide, we combined the correcting potentials from the T-MetaD simulations of AA, AC, and CC, assuming a similarity between purines A and G.

The T-REMD data related to the Amber14 force field and the protocol for the new simulations performed using the Amber_pdb force field were taken from ref (16). The systems were solvated with TIP3P waters and neutral ionic conditions. We used 24 replicas with a geometric distribution of temperatures from 300 to 400 K. Exchanges were attempted every 200 steps. The simulation length was 2.2 μs per replica.

Analysis

The result of the molecular dynamics simulations was compared to NMR experimental data of dinucleosides^10,40−42 and tetranucleotides.^9,43,443J vicinal coupling constants were calculated using Karplus expressions.^45,46 We took into account the analysis made in refs (10, 47, and 48) to select the most precise sets of parameters. Calculations were performed using the software tool baRNAba.⁴⁹ Details are given in the Supporting Information, subsection 1.1.

Results

As a first step, we used our approach to enforce the dihedral distribution from the X-ray fragments on monophosphate dinucleosides AA, AC, CA, and CC. Then, we show that the corrections are partly transferable and could improve agreement with solution experiments for tetranucleotides.

Calculation of Correcting Potentials for Dinucleoside Monophosphates

The Amber14 force field is considered to be one of the most accurate ones for RNA, though it fails to reproduce solution experiments for short flexible oligomers. Recent benchmarks of different Amber force field modifications based on reparametrization of the torsion angles and nonbonded terms have shown that these changes did not lead to a satisfactory agreement with solution experiments for tetranucleotides.^5,9 On the other hand, ensembles of tetranucleotides taken from the PDB have a very good agreement with NMR data.¹⁶ We thus decided to add correcting potentials to the dihedral angle terms of Amber14, based on information recovered from high-resolution X-ray structures of RNA deposited in the PDB. We analyzed enhanced sampling simulations of dinucleosides (described in this paper) and tetranucleotides (described in a previous publication¹⁶), to select a minimal amount of degrees of freedom to modify. This analysis indicated the backbone angles ϵ, ζ, α, and β could benefit from a correction (a full description is presented in Supporting Information, section 2). We used T-MetaD to enforce on those dihedrals the probability distributions obtained from fragments of X-ray structures. RNA dinucleoside monophosphates were chosen as model systems to obtain the correcting potentials. As the corrections are sequence dependent, for each nucleobase combination, we generated an ensemble of experimental conformations from the PDB database that had the same sequence as the dinucleoside monophosphates.

In Figure 2 we show the free-energy profiles of AA and CC dinucleosides projected on the ϵ, ζ, α, and β angles. Amber14, Amber_pdb, as well as the target PDB ensembles are represented. The profiles of AC and CA are shown in Figure S.7. The similarity between the PDB and Amber_pdb profiles makes it clear that the corrections efficiently enforce the distributions taken from the X-ray ensemble. Although some differences are visible around the free-energy barriers, they are expected not to be relevant for room temperature properties at equilibrium. Nevertheless, the transition times and the behavior of the Amber_pdb potential at high temperatures could be affected by these barriers. In general, barriers in the experimental ensemble are several k_bT lower than those from the Amber14 force field. In the corrected ensemble, the multimodal character of the force-field probability distributions for the angles ϵ, ζ, and α is reduced, to favor the conformations corresponding to the canonical A-form. The observed agreement between the PDB and Amber_pdb one-dimensional probability distributions for the selected angles is not necessarily translated into equivalence of the respective ensembles. This is seen, for example, in the two-dimensional distributions shown in Figures S.8–S.11.

Figure 2.

Free-energy profiles of backbone dihedral angles for the AA and CC dinucleoside monophosphates from the X-ray ensemble (PDB) and the RECT simulations with the standard force-field (Amber14) and the correcting potential (Amber_pdb).

Correcting potentials might, in principle, also affect the distribution of nonbiased degrees of freedom if the latter ones are correlated with the former ones. The distribution of nonbiased degrees of freedom, such as the angles γ and χ and the puckering coordinate Z_x, is shown in Figure S.12. Overall, no difference is observed between the Amber14 and Amber_pdb free-energy profiles, with the exception of the ratio between the C3′-endo and C2′-endo conformations in CC. This is a consequence of the significant correlation between the backbone angle ϵ and the puckering.

To asses the validity of the corrections, we compared all the ensembles against NMR experimental data¹⁰ (Figure 3). Individual ³J vicinal coupling values from the experiments and the simulations are reported in Table S.2. In the case of AA, AC, and CA dinucleosides, the agreement of Amber_pdb with the experimental data is better than that of Amber14 and of the X-ray ensemble. This can be explained by noticing that Amber_pdb combines the good agreement obtained with NMR experiments of Amber14 for angles in the nucleoside (dihedrals γ, ν₃, and χ) with that of the PDB distribution for angles in the backbone (dihedrals ϵ and β), as shown in Figure S.13. A notable exception is the CC dinucleoside, where the correlation of backbone angles with puckering mentioned above leads to a slightly larger deviation in Amber_pdb with respect to Amber14. It should be noticed that the NMR observables analyzed here cannot be used to directly determine the conformation around the phosphodiester backbone (α/ζ), so the comparison with the NMR ³J vicinal coupling data set does not take into account the distribution of these angles.

Figure 3.

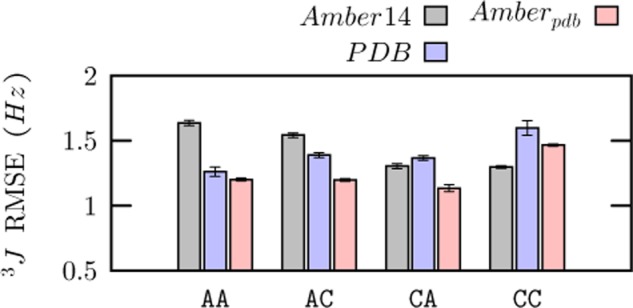
Agreement with the NMR ³J vicinal coupling data set of dinucleosides, measured using the root-mean-square error (RMSE), for the ensembles of X-ray structures (PDB), the Amber force field (Amber14), and the corrected Amber force field (Amber_pdb). Statistical errors were calculated using block averaging.

We noticed that, whereas the NMR data was measured at 293 K (AA, CA, and AC) and 320 K (CC), simulations were performed at 300 K. However, the agreement between the data for CC obtained at 320 K and similar NMR data obtained for a smaller number of couplings at 280 K⁴² shows that deviations induced by temperature changes are expected to be much smaller than the typical deviations between molecular dynamics and experiment observed here. It is also important to mention that these RMSE values do not take into account systematic errors in the Karplus formulas employed in this study.

It is also interesting to measure the effect of the proposed backbone corrections on the stacking interactions. Stacking free energies computed according to the definition used in a recent paper⁹ show that the correcting potentials have barely any effect on stacking (Figure S.14). These numbers can also be compared with experimental values,^41,42,50 and they indicate that the Amber force field is likely overestimating stacking interactions, as suggested by several authors.^51,52 This comparison is, however, affected by the definition of a stacked conformation, which introduces a large arbitrariness in the estimation of stacking free energies from MD.

Validation of Amber_pdb Potential on RNA Tetranucleotides

The correcting potentials discussed above are designed so as to enforce the PDB distribution on dinucleosides monophosphates. We here used these corrections to perform simulations on larger oligonucleotides. In particular, we performed extensive simulations of tetranucleotides, which are considered as good benchmarks for force-field testing, as their small size makes the generation of converged ensembles accessible to modern enhanced sampling techniques. We performed three T-REMD simulations with the Amber_pdb potential for the tetranucleotide sequences AAAA, GACC, and CCCC. These systems have been used before in very long (hundred of μs) simulations,^5,53−56 and NMR experimental data is available.^9,43,44 The Amber14 T-REMD data were taken from ref (16).

The ³J coupling RMSE, the NOE-distance RMSE, and the number of distance false positives, i.e. the MD predicted NOEs not observed in the experiment, are presented in Figure 4. For these systems the number of false positives is one of the most important parameters to assess the quality of the MD ensembles.⁹ In the case of tetranucleotides containing pyrimidines (GACC and CCCC), the correcting potential improves significantly the agreement with the experimental data, mostly for the NOEs (see Figure S1.5). This is confirmed by the root-mean-square deviation (RMSD) distribution shown in Figure S.16, where it can be appreciated that for these two sequences the corrections lead to an overall improvement of the ensemble by disfavoring the intercalated and inverted structures with a large RMSD from native. A completely different scenario is found for the Amber_pdb ensemble of AAAA, where the corrections surprisingly diminish the agreement with experiments. This can also be appreciated in a shift of the Amber_pdb RMSD distribution peaks to higher RMSD values due to an increase in the population of compact structures (Figure S.16). It should be noticed that the effect of the correcting potentials in purines and pyrimidines depends strongly on the sequence length. Whereas the AAAA tetranucleotide is negatively affected by the corrections, the AA dinucleoside is the one that benefits the most from them.

Figure 4.

Agreement with the experimental ³J vicinal couplings and NOE distances of tetranucleotides. For the calculation of the ³J RMSE, the RNA torsion angles were divided into two groups: (a) the dihedral angles in the ribose-ring region (χ, ν, and γ) and (b) the phosphate-backbone angles (ϵ, ζ, α, and β). In (c) the RMSE between calculated and predicted average NOE distances is presented, and in (d) is shown the number of false positives, i.e. the predicted distances below 5 Å not observed in the experimental data.

As discussed in section 2 of the SI, the conformation along the phosphodiester backbone is very different between compact and extended tetranucleotide structures. The probability distribution maps of the α₂/ζ₁ backbone dihedral angles from the tetranucleotides T-REMD simulations and the dinucleosides X-ray ensembles used to generate the corrections are depicted in Figure 5. Only phosphodiester backbone torsion angles are shown, because they are the ones mostly affected by the correction. The other backbone angles maps are shown in the SI (Figures S.17–S.25). In the PDB ensembles, the distributions are always unimodal, independently of the sequence, with a peak at the α(g−)/ζ(g−) conformation, whereas, in the Amber14 ensemble, the α(g+)/ζ(g+) and α(g−)/ζ(g–) conformations are both significantly populated. The effects of the corrections, as seen before, are highly sequence dependent. In the case of GACC and CCCC, the α(g−)/ζ(g−) rotamer is stabilized in the Amber_pdb distributions, with the population of α(g+)/ζ(g+) significantly decreased with respect to Amber14. On the contrary, for AAAA the α(g+)/ζ(g+) conformation is not unfavored by the correcting potentials, despite not being significantly present in the PDB ensemble. This could be due to the fact that the one-dimensional target free-energy profile for dihedrals α and ζ for the AA (Figure 2) exhibits barriers which are approximately 4k_bT smaller with respect to the ones from the Amber14 force field. The effect of the decreased barrier height can be appreciated in the α₂/ζ₁ probability distribution of AAAA, where the amount of torsional space explored is increased by the corrections.

Figure 5.

Probability distributions of the backbone dihedral angles of AAAA and CCCC tetranucleotides, in the region between residues 1 and 2. Results from the RECT simulations with the standard force-field (Amber14), the correcting potential (Amber_pdb), and the dinucleoside X-ray ensembles (PDB) used to generate the correcting potentials.

Consequences on Future Force Field Refinements

The good agreement of the Amber_pdb ensembles with the NMR observables, in the case of CCCC and GACC tetranucleotides, suggests that the RNA conformational space sampled by a state-of-the-art force field could be modified to better match experimental solution data by penalizing rotamers of the α and ζ angles. As a further test, we reweighted the T-REMD Amber14 ensembles with an additional two-dimensional penalizing Gaussian potential centered on the α(g+)/ζ(g+) conformation. Results are shown in Figure 6 for different Gaussian heights. Overall, the agreement with the NMR experimental data improves considerably with respect to the original force field as the Gaussian height increases. The relative population of the α/ζ conformations has an important impact on the number of false positive NOE contacts, which indicates the presence of intercalated structures. This improvement is achieved without changing the nonbonded interactions, as has also been proposed.⁵¹ It is, however, important to observe that these results are obtained by performing a reweighting, and that corrections should be validated by performing separate simulations with this bias potential.

Figure 6.

Agreement with the experimental data for the Amber14 reweighted ensemble as a function of the Gaussian potential height. The bias potential was centered on α(g+)/ζ(g+) conformation () with a sigma per angle of 0.7 rad. “A-form” represents a canonical A-form structure, and “X-ray” represents an ensemble of tetranucleotide fragments, with the same sequence, from the PDB (all taken from ref (16)).

Discussion

In this paper we apply targeted metadynamics to sample preassigned distributions taken from experimental data.^19,20 At variance with the original applications, we here combine T-MetaD with enhanced sampling, showing that these protocols can also be used when the investigated ensembles have nontrivial energy landscapes separated by significant barriers.

We apply the method to RNA oligonucleotides, for which the Amber14 force field was proven to be in significant disagreement with solution NMR data.^{5,9,43,44,53,54,56,57} Since tetranucleotide fragments extracted from high-resolution structures in the PDB were shown to match NMR experiments better than the Amber14 force field,¹⁶ we here used X-ray structures to build reference distributions of backbone dihedral angles that are then used to devise correcting potentials. More precisely, we use T-MetaD to enforce the empirical distribution of the dihedral angles in the phosphate backbone (ϵ, α, ζ, and β) on four dinucleoside monophosphates.

We calculated the correcting potentials concurrently for all the four angles in order to change the distribution of these consecutive dihedrals along the backbone chain, taking into account their correlation. The method successfully enforced the distributions taken from the PDB on all the angles. The new ensemble generated by the corrected force field (Amber_pdb) was independently validated against solution NMR data that was not used in the fitting of the corrections. For three of the four dinucleosides studied, Amber_pdb showed a better agreement with the NMR data compared with Amber14 and with the X-ray ensemble.

We then tested the portability of the correcting potentials by simulating three tetranucleotides, GACC, CCCC, and AAAA. In the case of GACC and CCCC, the agreement with NMR data is significantly improved by the corrections. Surprisingly, for AAAA, the corrections have the opposite effect and increase the probability of visiting compact structures, making the simulated ensemble less compatible with solution experiments. It should be noticed here that this is a nonobvious result, since the PDB database is expected to have an intrinsic bias toward A-form structures and should thus, in principle, increase the agreement with solution experiments in this specific case. This indicates that porting the corrections from dinucleosides to tetranucleotides is not straightforward because the coupling between the multiple corrected dihedrals could affect the resulting ensemble in a nontrivial way. Additionally, corrections applied to dihedral angles alone might be not sufficient to compensate errors arising from inexact parametrization of van der Waals or electrostatic interactions.⁵¹ Overall, the tests we performed indicate that the corrections derived here should not be considered as portable corrections for the simulation of generic RNA sequences.

Nevertheless, by comparing the backbone angle distributions on the different RNA simulations and the X-ray ensembles, we were able to find possible hints pointing at where refinement of dihedral potentials could lead to an advancement in RNA force fields. In this respect, the results for GACC and CCCC show that the significant improvement observed in the Amber_pdb simulations for those systems could be reproduced by simply penalizing the α(g+)/ζ(g+) conformation, which is overpopulated in Amber14. By a straightforward reweighting procedure, we showed that simple Gaussian potentials that disfavor this conformation significantly improved the experimental agreement with solution experiments for all three tetranucleotides. Recent modifications of the Lennard-Jones parameters for phosphate oxygens⁵⁸ and different water models⁵⁶ were shown to affect the conformational ensemble of RNA tetranucleotides.^5,56 It might be interesting to combine these modified parameters for nonbonded interactions with the here introduced procedure for dihedral angle refinement.

The nature of the correction methodology discussed in this paper is very different from the classical approach to force field parametrization, as it aims to correct the free-energy of the system, instead of fitting the potential energy landscape of the dihedral angles while constraining the other degrees of freedom. It is important to notice that the dihedral angle distributions taken from the fragments of the PDB structures do not necessarily represent the conformational ensembles of dinucleosides or tetranucleotides in solution. Indeed, some of the interaction patterns that are present in large structures crystallized in the PDB do not exist in short oligonucleotides. For this reason, in this work the distributions were validated against independent solution NMR experiments. This allowed the dihedral angles from the PDB distributions that performed better than the force field to be identified. We also recall that in our procedure the force-field torsion energy function is not refitted, but a bias potential is added to the total energy of the system in order to match the free-energy profile of the torsion angles with target ones. Thus, a major advantage of this approach is that it takes explicitly into account the entropic contributions, the cross correlations between torsional angles, and inaccuracies in the nonbonded interactions, among other effects.

Conclusion

In conclusion, in this work we applied the target metadynamics protocol to modify dihedral distributions in dinucleosides. The procedure successfully enforces reference distributions taken from the PDB without affecting the distribution of the dihedral angles that were not biased. However, the attempt to port these corrections to tetranucleotides lead to ambiguous results when applied to different sequences. This could be partly due to the fact that distributions from the PDB are not necessarily a good reference for refinement.

Nevertheless, the simulations revealed the importance of the α/ζ angle rotamers for the modulation of the conformational ensemble, and that, by only penalizing the α(g+)/ζ(g+) rotamer, the quality of the ensemble is significantly improved to levels not reported before.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00299.

• Two sections discussing (1) the Simulation Protocols and (2) the Selection of the target collective variables. An example input file for the T-MetaD+RECT simulation (S.1); representative clusters of the Amber14 ensemble of AAAA (S.2); Jensen–Shannon divergence and Mutual Information among the dihedral distributions of the A-form and Non-A-form subensembles (S.3); probability distributions of A-form and Non-A-form subensembles of AAAA (S.4), CCCC (S.5), and GACC (S.6); free-energy profiles of backbone dihedral angles for all the dinucleosides (S.7); bidimensional probability distributions of the backbone angles of AA (S.8), CC (S.9), AC (S.10), and CA (S.11); free-energy profiles of noncorrected degrees of freedom (S.12); RMSE between experimental and calculated J scalar couplings (S.13); free-energy of stacking (S.14); predicted versus experimental NOE distance (S.15); empirical RMSD probability distribution (S.16); probability distributions of backbone dihedral angles of AAAA and AA (S.17, S.18, and S.19), CCCC and CC (S.20, S.21, and S.22), GACC, AA, AC, and CC (S.23, S.24, S.25); RMSD distribution as a function of the bias potential strength (S.26). (PDF)

The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement n. 306662, S-RNA-S.

The authors declare no competing financial interest.