Cross-sections for (p,x) reactions on natural chromium for the production of ^52,52m,54Mn radioisotopes

Abstract

The production of positron-emitting isotopes of manganese is potentially important for developing contrast agents for dual-modality positron emission tomography and magnetic resonance (PET/MR) imaging, as well as for in vivo imaging of the biodistribution and toxicity of manganese. The decay properties of ⁵²Mn make it an excellent candidate for these applications, and it can easily be produced by bombardment of a chromium target with protons or deuterons from a low-energy biomedical cyclotron. Several parameters that are essential to this mode of production—target thickness, beam energy, beam current, and bombardment time—depend heavily on the availability of reliable, reproducible cross-section data. This work contributes to the routine production of ^52gMn for biomedical research by contributing experimental cross-sections for natural chromium (^natCr) targets for the ^natCr(p,x)^52gMn reaction, as well as for the production of the radiocontaminants ^52m,54Mn.

GRAPHICAL ABSTRACT

The production of positron-emitting isotopes of manganese is potentially important for developing contrast agents for dual-modality positron emission tomography and magnetic resonance (PET/MR) imaging, as well as for in vivo imaging of the biodistribution and toxicity of manganese. The decay properties of ⁵²Mn make it an excellent candidate for these applications, and it can easily be produced by bombardment of a chromium target with protons or deuterons from a low-energy biomedical cyclotron. Several parameters that are essential to this mode of production—target thickness, beam energy, beam current, and bombardment time—depend heavily on the availability of reliable, reproducible cross-section data. This work contributes to the routine production of ^52gMn for biomedical research by contributing experimental cross-sections for natural chromium (^natCr) targets for the ^natCr(p,x)^52gMn reaction, as well as for the production of the radiocontaminants ^52m,54Mn.

1. Introduction

Both historically and in recent years, there has been significant interest in the biomedical roles and applications of manganese. A search of the PubMed database in 2013 showed that the number of publications with manganese in the title had an average annual increase of 7% or more over the previous five, ten, twenty, and fifty years, with an average approaching 800 publications per year over the five previous years (PubMed, 2013). This growing interest likely comes from several characteristics of manganese that have important consequences for biology and medicine, including: its roles as an essential nutrient in mammals; its toxicity in large amounts; its role in plant photosynthesis; and its paramagnetism in the Mn²⁺ oxidation state. Thus, there are many potential interesting applications for a manganese radiotracer, particularly for an isotope that is imageable by positron emission tomography (PET), which has very high sensitivity and better spatial resolution than other nuclear imaging modalities. Imageable isotope(s) of manganese could facilitate in vivo studies that utilize manganese as a radiotracer for antibodies, nanoparticles, etc. or as a means to image the biodistribution of manganese cations.

Based on nuclear decay properties, ⁵²Mn is a good candidate for these applications. This isotope has a half-life (t_1/2 = 5.6 d) that would make it convenient for processing, labeling, and shipping, as well as for imaging studies that require time points that are several days post-injection. ⁵²Mn emits positrons with a branching ratio (I_{β +} = 29.6%) (Huo et al., 2007) that is comparable to other PET radiometals (e.g., ⁶⁴Cu and ⁸⁹Zr) and with a very low average positron energy (E_{β +} = 242 keV) (Huo et al., 2007) that is even lower than ¹⁸F and therefore gives even better spatial resolution in PET (Prince and Links, 2005). However, ⁵²Mn also emits significant gamma radiation (Smith and Stabin, 2012), which can increase dose to research personnel and laboratory animals, as well as cause artifacts in PET. ^52mMn has also been investigated in PET studies as it has a high branching ratio for positron emission (I_{β +} = 95.0%), but its utility is limited by a short half-life (t_1/2 = 21.1 min), very high average positron energy (E_{β +, avg} = 1170 keV), and significant gamma radiation emission (Huo et al., 2007). Despite the interest in imaging ⁵²Mn and ^52mMn, routine production of useful quantities of these isotopes with high purity is still being developed (Buchholz et al., 2013; Topping et al., 2013).

Essential to any routine isotope production protocol is the ability to select target thickness, beam energy, beam current, and bombardment time based on predicted yield, which in turn is based on nuclear cross-section data. Target thickness and beam energy are typically selected so that the entry and exit energies of the beam will span a region of the excitation function with high cross-sections for the product and little or no cross-sections for other, competing reaction channels that may produce contaminant isotopes. Designing production runs to optimize this energy “window” can improve yield and radionuclidic purity of the final product. Thus, it is important to have accurate cross-section data for not only the reactions that produce the desired product, but also for the reactions that would produce contaminant isotopes. In this investigation, we bombarded natural chromium targets (^natCr= ⁵⁰Cr (4.3%), ⁵²Cr (83.8%), ⁵³Cr (9.5%), ⁵⁴Cr (2.4%)), which could potentially produce several product isotopes. This work focused primarily on measurements for the production of ⁵²Mn, but also for ^52mMn and ⁵⁴Mn as radiocontaminants. Only a few data sets are currently available with points at proton beam energy (E_p) ≤ 14 MeV for the ^natCr(p,x) reactions that produce ^52,52mMn (Barrandon et al., 1975; Buchholz et al., 2013; West Jr et al., 1987), and there are only data sets from enriched targets available for ⁵⁴Mn at these low energies (Gusev et al., 1990; Johnson et al., 1960; Kailas et al., 1975; Levkovskij, 1991; Skakun et al., 1986; Zyskind et al., 1978). In this work, we contribute new experimental cross-section data for each of these (p,x) reactions that produce ^52,52m,54Mn from bombardment of natural chromium with protons at low-energies.

2. Methods

2.1. Target preparation

2.1.1. Materials

Nitric acid (70%) was purchased from Sigma-Aldrich (St. Louis, MO, USA). Copper sheet (0.762 mm thick, 99.9% purity) was purchased from ESPI Metals (Ashland, OR, USA), and copper foil (0.025 mm, 99.999% purity) was purchased from Alfa Aesar (Ward Hill, MA, USA). Natural abundance chromium was electroplated by Four Star Finishing (St. Louis, MO, USA).

2.1.2. Production of thin ^natCr foils

Copper monitor foils were produced by punching ~9.5 mm disks from 0.762 mm (nominal) copper foil. However, Cr metal is very brittle, so cutting or punching disks from thin Cr foil was not feasible. Furthermore, thin Cr foil was not commercially avail able without a permanently attached Mylar (polyethylene terephthalate) backing.

Therefore, we developed a method for fabricating batches of thin Cr foils that would fit into target holders for one of the solid target stations connected to our cyclotron—without cutting Cr metal. Thin, circular foil disks were produced through a process of electrodeposition of non-enriched Cr onto small plugs of Cu backing material, followed by removal of the Cu backing, similar to a method previously used by Tanaka and Furukawa (1959). Holes (~10 mm diameter) were cut or punched from Cu sheet, and these holes were then filled using ~9.8 mm Cu disks that were punched from elsewhere on the Cu sheet. On the “back” side of the plate, these disks were fixed in place by soldering the back of each disk to one of several long strips of thick (~1–2 mm diameter) bus bar wire that was also soldered to the large copper plate. Fig. S1 shows a sample that contained a 13 × 13 grid of copper plugs soldered in place on the back.

The back of the sample was masked with a vinyl lacquer, and the entire sample was submerged (while connected to the cathode) into an industrial-scale chrome plating bath, and the unmasked side of the sample was electroplated with Cr. This bath electroplated with “hard chrome,” meaning thick (tens to hundreds of μm), ultra hard deposits of pure Cr metal. (The more popular type of chrome plating, “decorative chrome”, is roughly 1000 × thinner and usually plated over nickel or copper). The bath was an aqueous solution of 100:1 chromic acid (H₂CrO₄) and sulfuric acid (H₂SO₄). (Safety note: The chromic acid was made from chromium(VI) oxide (CrO₃ powder), which is acutely toxic (oral, inhaled, or dermal), damaging to eyes and skin, and carcinogenic, in addition to possible reproductive toxicity and germ cell mutagenicity (Sigma-Aldrich Co., 2014). The sulfuric acid was a commonly used additive that contributed sulfate groups to the solution, which catalyzed the electroplating reaction (Mandich and Snyder, 2010). To produce individual Cr disks, the bus bar wire was clipped on either side of each copper plug in the assembly, producing individual copper plugs plated on one side with chromium. These plugs were placed in ~3–8 M nitric acid in a large glass container. The nitric acid digested the copper while leaving the chromium intact, and the acid solution was changed several times during this process. The final result was numerous circular disks of thin (and very brittle) Cr metal foils with a diameter of 9.8 mm.

Before each stack of foils was assembled, the thickness of each Cr and Cu foil was calculated based on its diameter and mass, assuming cylindrical geometry. Based on instrumental uncertainty from the measurements of diameter and mass, the uncertainty in the calculated thickness of each Cu or Cr foil was <1.1%. Across all the Cr foil disks bombarded in targets in Configurations D–G (Table S1), the diameter was 9.8 mm for all disks, with an average thickness of 82 μm (±10.5%), and the Cu foil disks had a diameter of 9.5 mm and an average thickness of 18.6 μm (±2.6%).

A few Cr foils that were never bombarded were tested for elemental purity by a sixty-element screening performed by Galbraith Laboratories (Knoxville, TN, USA). The foil was dissolved in acid and analyzed by ICP-MS. The only contaminants >100 ppm (within error) were Sn (1195 ppm) and Se (134 ppm). (This was a semi-quantitative screening with relative error of up to 50% for all measurements.)

2.1.3. Target design

A custom target holder was designed and machined out of 6061-T6 aluminum alloy (95.8–98.6% aluminum) to hold the stacks of foils during cyclotron bombardment. Our design consisted of a base containing a dish with smooth vertical walls to hold the stack of foils yet allow for quick, easy removal of the foils from the dish after bombardment. The base had a blind hole on the non-vacuum side for improved contact with the circulating cooling water. The target holder also included a screw-on cap to hold the stack of foils in the holder when the foils were held vertically in the target station—perpendicular to the incident beam. This cap was threaded to match corresponding threads on the base, and the cap had a circular “window” (through hole) to expose the foils directly to the beam.

Four different stacked foil configurations consisting of Cu and Cr foils were used in this work to measure cross-sections in the Cr foils. The Cu foils were included for determination of beam current and entry beam energy from monitor reactions (Sections 2.4.2 and 2.4.3). The number of foils in a configuration was 4–5 Cr foils interspersed with 2–4 Cu foils, as summarized in Table S1. Each configuration was bombarded in three separate targets, for a total of 12 bombarded targets in this work. The energy of the proton beam at the middle of every chromium foil was predicted using The Stopping Range of Ions in Matter (SRIM) software (Ziegler et al., 2010), which implements the perturbative Bethe formula (with Bloch correction) for the stopping power (i.e., energy loss) of charged particles due to interactions with orbital electrons in a material.

2.2. Cyclotron bombardment

Each target assembly was bombarded with low-energy (E_p <15 MeV) protons from the CS-15 cyclotron (The Cyclotron Corporation, Berkeley, CA, USA) at the Mallinckrodt Institute of Radiology (MIR) at Washington University School of Medicine (WUSM). During bombardment, the back of the target holder was cooled by circulating chilled water (T≈2–5 °C), and the front of the target was cooled by a He gas jet. Bombardments used in this work were typically 1–3 μA for a duration of bombardment (t_b) that varied between 105 and 135 s, (120±15 s). This uncertainty was accounted for (Section 2.4.6) in our determination of beam energy, beam current, cross-sections, and saturation yields.

2.3. Gamma-ray spectroscopy

Proton bombardment of the stacked foil targets produced radioisotopes in each Cu and Cr foil, and these product isotopes were identified and quantified by gamma-ray spectroscopy from a high-purity germanium (HPGe) detector (model: GC2018; relative efficiency: 24.5%) that was connected to a digital spectrum analyzer (DSA; model: DSA-1000) and operated by the Gamma Acquisition & Analysis module of the Genie 2000 spectroscopy software package (v3.3). (All three components were from Canberra, Meriden, CT, USA.) The principal isotopes measured were ^63,65Zn in the Cu foils and ^52,52m,54Mn in the Cr foils, and their production and decay characteristics are summarized in Table 1.

Table 1.

Summary of the radioisotope products that were observed in irradiated Cu and Cr foils.

Primary targeta (Natural abundance)	Product (Half-life)	Gamma-raysb (Branching ratio)	Daughter (Half-life)
Cu foil:
63Cu (69.2%)	63Zn (38.5 min.)	670 keV (8.2%) 962 keV (6.5%)	63Cu (stable)
65Cu (30.9%)	65Zn (244 d)	1116 keV (50.0%)	65Cu (stable)
Cr foil:
52Cr (83.8%)	52Mn (5.6 d)	1434 keV (100%) 936 keV (94.5%) 744 keV (90.0%) 1334 keV (5.1%) 1246 keV (4.2%) 848 keV (3.3%)	52Cr (stable)
52Cr (83.8%)	52mMn (21.1 m)	1434 keV (98.3%) 378 keV (1.7%)	52Cr (stable) 52Mn (5.6 d)
54Cr (2.4%)	54Mn (312 d)	835 keV (99.98%)	54Cr (stable)

References; Evaluated Nuclear Structure Data File database, N.N.D.C., Brookhaven National Laboratory (ENSDF/NNDC/BNL).

^aAll of the product isotopes in this table are produced primarily by (p,n) reactions from proton bombardment of E_p <15 MeV.

^bIn our analysis, we only considered gamma-rays that were emitted by only one isotope/isomer, so the 1434 keV gamma-ray emitted by ^52,52mMn was excluded. (Nuclear data accessed via: (BNL/NNDC/ENSDF))

A few hours after each bombardment, the stacked foil target was carefully disassembled. For each gamma-ray counting experiment, one foil was placed in a small weigh boat that was then placed on a 3 mm thick plastic shelf positioned at one of several distances directly above the open end of the HPGe crystal. Various positions were utilized so that samples could be counted at various distances from the detector to ensure a detector dead time (t_d) or ≤ 5% of detector real time (t_r). Each Cu and Cr foil was counted for at least 10 min of detector live time (t_l). Additionally, all of the Cu foils were counted again several months later for 10 h each to measure a greater number of counts from the long-lived product ⁶⁵Zn (t_1/2 = 244 d) for better statistics.

The HPGe detector was calibrated for photopeak energy and detector efficiency. The energy calibration was performed using a mixed-gamma source in a sealed microcentrifuge tube (Eckert & Ziegler Analytics, Atlanta, GA, USA). We also performed our own detector efficiency calibrations using a mixed-gamma “point source” (Eckert & Ziegler Analytics). The detector efficiency (ε_c) was calculated for each gamma-ray energy (E_γ), and ln ε_c was plotted versus ln E_γ. This plot was linear between 166 and 1836 keV, so the data in this range were fit to the equation:

$$ln{\epsilon }_c=mln{E}_{\gamma }+b,$$ (1)

where m and b are the slope and intercept of the linear fit. All gamma-rays being measured in this investigation were within this range and are listed in Table 1. Eq. (1) was solved for ε_c and fitted by floating for m and b using the gnuplot software (v. 4.6.6) (Williams, 1986), which implemented a non-linear least squares algorithm (Levenberg–Marquardt algorithm) (Crawford, 2014). The resulting fits served as calibration curves for calculating detector efficiencies for gamma-rays emitted by radionuclide products in the irradiated Cu or Cr foils. This calibration was performed for each geometry counting of irradiated Cu or Cr foils.

The fitting method weighted the fit parameters based on the y-direction uncertainty in the data points. This uncertainty represented the uncertainty of the gamma emission rates for each gamma-ray from the calibration source (taken from the reference sheet), as well as the uncertainty in the counting of these emissions (Section 2.4.6). To improve the goodness-of-fit value, we would sometimes increase the level of statistical error to 1.5 or 2 standard deviations. This improved the fitting, and the additional uncertainty was accounted for in the uncertainty of the fitted parameters and propagated accordingly.

Additionally, to test for self-shielding in our Cr foils, we performed a calibration with the point source positioned directly above the same type of Cr foil used in our stacked foil experiments. The resulting efficiency calibration curve had a slope and the y-intercept that were both within 0.5% of the values in the efficiency curve that we used for foils that were counted from the same geometry.

2.4. Analysis

We concur with Gagnon et al. (2011a) that transparent, detailed explanation of analysis in cross-section experiments can reduce confusion in comparing and categorizing these studies. Here, we explain in detail the analysis that was used to transform counts from gamma spectroscopy into activity, then beam energy, then beam current, and finally into cross-section results for ^52,52m,54Mn. We also describe our uncertainty analysis. Unless otherwise stated, all analysis work was performed in Excel for Mac 2011 (v. 14.4.4) or Excel 2002 (v. 10) (Microsoft, Redmond, WA, USA).

2.4.1. Calculating activities of radioisotope products

The principal raw data for this investigation came from gamma spectroscopy, specifically the net peak area or number of counts (N_c) in each full-absorption photopeak of interest. For each such peak, the activity of the corresponding radioisotope at the beginning of counting (A_c) was proportional to the number of counts according to the following equation (Canberra, 2009):

$$A_c=\frac{N_c}{{\epsilon }_c{I}_{\gamma }{C}_d{t}_l},$$ (2)

where I_γ is the branching ratio for the gamma-ray, and C_d is the following correction factor for decay during counting of the first member of a decay chain (The Institute of Electrical and Electronics Engineers IEEE, 1999; Canberra, 2009; Moore, 1973):

$$C_d=\frac{1-e^{-\lambda t_r}}{\lambda t_r},$$ (3)

where λ is the decay constant for the isotope (λ= ln(2)/t_1/2). For isotopes with multiple characteristic gamma-rays, the activities (and uncertainties) calculated for the gamma peaks were combined to a single value by an inverse-variance weighted average. Then, each activity was decay-corrected to the activity at EOB (A_EOB).

2.4.2. Beam energy

The entry beam energy was calculated based on monitor reactions (Avila-Rodriguez et al., 2008; Blessing et al., 1995; Gagnon et al., 2011a; Kim et al., 2006; Kopecký, 1985; Kopecky et al., 1993; Piel et al., 1992; Scholten et al., 1994; Takacs et al., 1997; Tarkanyi et al., 1991). In this work, we used the ^natCu(p,x)^63,65Zn monitor reactions with recommended cross-section data provided by the Nuclear Data Section of the International Atomic Energy Agency (IAEA)/Nuclear Data Section (NDS) (2014). The activities were measured (Section 2.4.1) for ⁶³Zn and ⁶⁵Zn produced in a Cu monitor foil on top of the stack in n= 5 different targets. and the ratio of the activities, A_Zn-63/A_Zn-65, was used to find the corresponding proton beam entry energy. This was determined by linear interpolation between two adjacent points of the activity ratio calculated using the IAEA-recommended cross-section data (increment= 0.1 MeV) in the following equation (Avila-Rodriguez et al., 2009; Gagnon et al., 2011a,b):

$$\frac{A_{\text{Zn}-{63}_{\mathit{EOB}}}}{A_{\text{Zn}-{65}_{\mathit{EOB}}}}=\frac{{\sigma }_{\text{Zn}-63}(1-e^{-{\lambda }_{\text{Zn}-63}{t}_b})}{{\sigma }_{\text{Zn}-65}(1-e^{-{\lambda }_{\text{Zn}-65}{t}_b})},$$ (4)

where σ is the cross-section and t_b = 120 ±15 s. Uncertainty was propagated through Eq. (4) and through the linear interpolation equation.

After determining the proton beam energy in those foils, the inverse-variance mean of those energies was determined to be the beam energy at the midpoint of the Cu foil on top of the stack (E_p = 13.10±0.04 MeV) (Fig. S2). We used the TRIM module within the SRIM software package to perform Monte Carlo simulations of transmitted ions to determine to determine that the entry energy was 13.285±0.065 MeV, so we used this as the entry energy for simulating the energy of the proton beam at the midpoint of all foils in all targets. Because of the spread in the thickness of our Cr foils, the beam energies for all foils in all configurations (excluding top Cu foils) were simulated using individual thicknesses that had been determined by mass (Section 2.1.2). We excluded from the data set any Cr foils where the beam energy was degraded >1.5 MeV from the midpoint of the previous foil to the midpoint of that Cr foil. The longitudinal straggling of the protons was estimated as the population standard deviation of the energies of N≈1000 transmitted protons. We estimated that the uncertainty in the entry energy (±0.04 MeV) was not correlated to the uncertainty in entry energy, so we added this value (in quadrature) to the uncertainty due to longitudinal straggling in each TRIM simulation. We increased this uncertainty for the simulated beam energy at the midpoint of each foil by 1.1% to estimate the effect of the uncertainty in the measured thickness of each Cu and Cr foil (Section 2.1.2).

2.4.3. Beam current

Similar to published methods (Greene and Lebowitz, 1972; Kopecký, 1985; Lapi et al., 2007), the beam current was measured for each target based on a monitor reaction, in our case the production of ⁶³Zn in the Cu monitor foils. To calculate the beam current, we used the standard activation equation:

$$A_{\mathit{EOB}}=n\varphi \sigma (1-e^{-\lambda t_b}),$$ (5)

where A_EOB is the activity of a product at EOB; n is the number of target nuclei per area; and ϕ is the flux of beam particles passing through the target. The activity of ⁶³Zn produced from the ^natCu(p,x)⁶³Zn reaction was calculated as described in Section 2.4.1. The number of target nuclei per area was calculated by the following equation:

$$n=N_A\left(\frac{\rho }{A_r}\right)h,$$ (6)

where N_A was Avogadro’s constant; ρ was the density of Cu metal; A_r was the relative atomic mass of the non-enriched Cu metal; and h was the individual thickness of the Cu foil (determined by mass). To determine the cross-section for calculating beam current, we interpolated between adjacent cross-section points (interval: 0.1 MeV) from the IAEA-recommended excitation curve for the ^natCu(p,x)⁶³Zn reaction (Section 2.4.2). Uncertainty in the beam energy was propagated through the interpolation. Eq. (5) was solved for ϕ, and then ϕ was calculated based on the production of ⁶³Zn in the topmost Cu foil in each stacked foil target. The uncertainties in the values entered in these calculations were propagated (Section 2.4.6) to give the uncertainty in the beam current for that bombardment and eventually contributed to the uncertainty of the final results.

2.4.4. Cross-sections

Cross-sections were measured for isotopes that were detected in the Cr foils by solving Eq. (5) for σ for each Cr foil in all targets. To complete this calculation, the following values were used: A_EOB calculated for ^52,52m,54Mn in each Cr foil as in Section 2.4.1; n calculated using the mean thickness of our Cr foils as in Section 2.4.3; ϕ calculated for each bombardment as in Section 2.4.3; and t_b = 120 ±15 s. We bombarded three targets for each configuration, and although the thickness of every foil was measured individually, we assumed the same beam energy for every foil in the same position within a configuration (Section 2.4.2), as calculated using the TRIM module. We then grouped our cross-section results from foils across different configurations into “bins” based on beam energy. For each bin, the energy and cross-section result (and uncertainties) were determined by inverse-variance weighted averages in the x- and y-directions and reported as our final results (Figs. 1–3, Tables 2–4). As not all irradiated chromium foils were counted soon enough to detect ^52mMn, our calculation neglects its contribution to production of ⁵²Mn. Although the effect of isomeric transition to ⁵²Mn is rather small (branching ratio <2%), our cross-section results for ⁵²Mn should officially be classified as cumulative cross-section data. The cross-section data for the production of ^52m,54Mn do not need to be specified as cumulative, since both of them are likely produced directly.

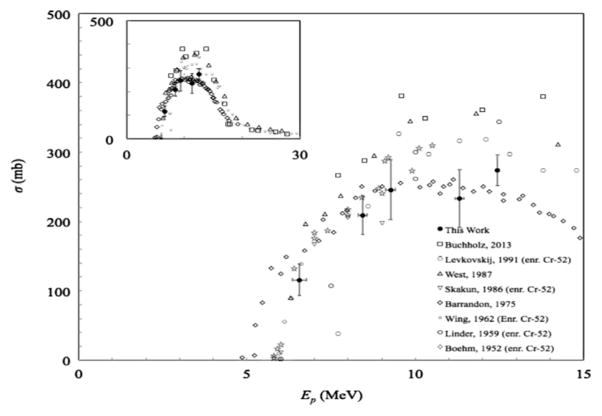
Fig. 1.

Plot showing cummulative cross-section results for the ^natCr(p,x)⁵²Mn reaction, as well as results from other published data sets, including rescaled results from enriched ⁵²Cr targets.

Fig. 3.

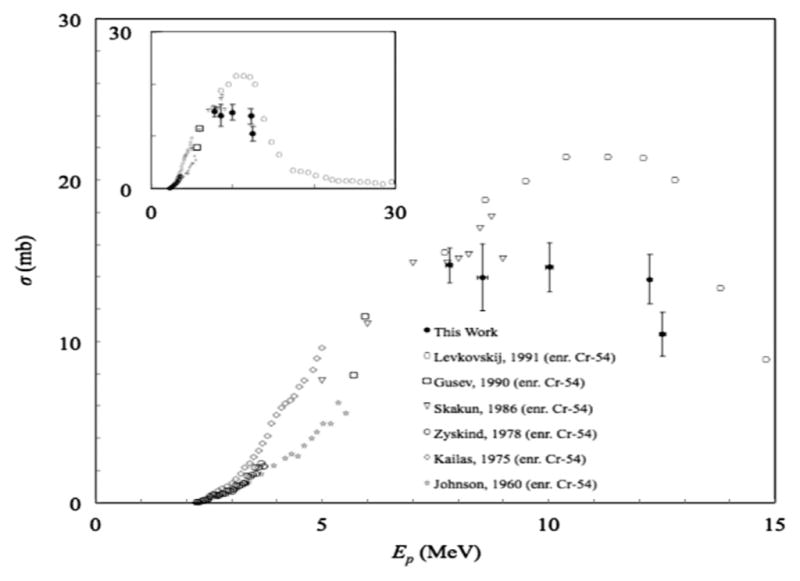
Plot showing cross-section results for the ^natCr(p,x)⁵⁴Mn reaction, as well as results from other published data sets, including rescaled results from enriched ⁵⁴Cr targets.

Table 2.

Cross-section results for the ^natCr(p,x)⁵²Mn reaction.

Energy		Cross-section
Ep (MeV)	Uncertainty	σ (mb)	Uncertainty
12.68	0.04	102	9
12.37	0.04	99	7
12.0	0.1	104	11
11.2	0.1	86	11
10.3	0.1	85	11
9.3	0.1	60	11
8.9	0.1	59	7
8.3	0.1	47	5
8.0	0.1	50	5
6.6	0.2	32	4

Table 4.

Cross-section results for the ^natCr(p,x)⁵⁴Mn reaction.

Energy		Cross-section
Ep (MeV)	Uncertainty	σ (mb)	Uncertainty
12.5	0.1	10.5	1.4
12.24	0.05	13.8	1.5
10.0	0.1	14.6	1.5
8.5	0.1	14	2
7.8	0.1	14.7	1.1

2.4.5. Predicted saturation yields

We used our cross-section results to calculate the activity yield of Cr targets that were bombarded with protons at our beam entry energy for long enough to reach saturation of each isotope product. The activation equation (Eq. (5)) was used to calculate yields at saturation from our cross-section data, setting proton flux to be 6.24 ×10¹² s⁻¹ to correspond with a proton beam current I= 1 μA. For each step in energy in our data, we determined the associated thickness of Cr using the “Ion Stopping and Range Tables” module in the SRIM software, and we interpolated (unweighted) the midpoint of the two cross-sections on either side of the step and used that value to determine the yield from each step of a target. Table 5 shows the predicted saturation yields that we calculated for each isotope product using our measured cross-section data.

Table 5.

Predicted yields for ^natCr(p,x) reactions at saturation.

Energy		Cross-section
Product	Energy range (MeV)	Predicted yield mCi μA−1 (GBq μA−1)	Uncertainty
52Mn	12.7→ 6.6	27.1 (1.00)	1.0 (0.04)
52mMn	12.4→ 6.6	82.2 (3.0)	5.1 (0.2)
54Mn	12.5→ 7.8	4.5 (0.165)	0.2 (0.008)

Saturation defined as bombardment time= 10 · t_1/2.

2.4.6. Error analysis

Error was propagated from their origin to our final results as absolute uncertainty, not as percentages. However, any uncertainty that was <0.05% was neglected. Instrumental uncertainty was considered for every measurement, and random uncertainty was calculated for every repeated measurement and for counting of a random process (i.e., gamma spectroscopy). Our statistics are presented in a descriptive (not inferential) manner and thus we present the mean, standard deviation, and sample size for all of our final cross-section results (Tables 2–4).

Instrumental uncertainty was typically either provided by the instrument, or otherwise estimated to be ±0.5 times the most precise digit of the measurement from that instrument. All random uncertainties were calculated as ± one standard deviation for a sample, population, or Poisson distribution, and this standard deviation was propagated onward. For the foil counting, we estimated that the uncertainty in the net peak area to be one standard deviation of the Poisson distribution (i.e., the square root of the number of counts in each peak). Whenever an average was calculated, the error was expressed as either a sample standard deviation (for sample size, N<20) or a population standard deviation was calculated (e.g., for Monte Carlo results for ~1000 transmitted ions from simulations in TRIM). Whenever a weighted average was appropriate, the inverse-variance weighted mean, x̄_w, was calculated by the equation:

$${\overline{x}}_w=\frac{{\sum }_i{x}_i/s_i^2}{{\sum }_{i}1/s_i^2},$$ (7)

where x_i is a measurement and s_i is the uncertainty in that value. This type of weighting minimizes the uncertainty in the mean, which was:

$$s^2({\overline{x}}_w)=\frac{1}{{\sum }_{i}1/s_i^2}.$$ (8)

Uncertainties were propagated through our calculations. This was performed by applying the following equation (Arras, 1998; NIST/SEMATECH) for the propagation of relatively small uncertainties through any calculation that used input values that had uncertainty:

$$s^2(f)=\sum _i{\left(\frac{\partial f}{\partial X_i}\right)}^2{s}_i^2+\sum \sum _{i\ne j}\left(\frac{\partial f}{\partial X_i}\right)\left(\frac{\partial f}{\partial X_j}\right)s_{ij},$$ (9)

where s(f) is the error in the calculated value f; X_i is each variable used to calculate f; s_i is the standard deviation in X_i; and s_ij is the covariance for variables i and j (for i≠j). Our only correlated sources of error were the fitted parameters for our efficiency calibrations, so the second term of Eq. (9) was zero for all other propagations of error. The partial derivative(s) in Eq. (9) account for the relative influences of the uncertainty of each quantity on the uncertainty of the calculated quantity. All uncorrelated uncertainties for the same value, such as rounding error, instrumental error, and statistical error, were added in quadrature to give the total uncertainty for that quantity.

3. Results and discussion

The stacked-foil experiments performed in this work produced cross-section data for the ^natCr(p,x)^52,52m,54Mn reactions for proton energies <14 MeV. Based on threshold energies (discussed below), we believe that both ⁵²Mn and ^52mMn were exclusively produced from the ⁵²Cr(p,n) reaction and that ⁵⁴Mn was produced from the ⁵⁴Cr(p,n) reaction. We did not observe any other isotopes in the Cr foils from any other reactions or from the two other stable isotopes of Cr: ⁵⁰Cr (4.3% natural abundance) or ⁵³Cr (9.5% natural abundance). Our final cross-section results are plotted in Figs. 1–3.

3.1. ^natCr(p,x)⁵²Mn

The primary isotope that we were examining in this work was ⁵²Mn. At low proton energies, ⁵²Mn was likely only produced by the ⁵²Cr(p,n)⁵²Mn reaction (threshold: 5.600 MeV; ⁵²Cr: 83.8% natural abundance) as the ⁵³Cr(p,2n)⁵²Mn reaction (threshold: 13.688 MeV; ⁵³Cr: 9.5% natural abundance) (BNL/NNDC/QCalc, 2014) has an energy threshold above the upper limit for our calculated entry beam energy. Therefore, at our proton energies, our results can be compared to published cross-sections for not only the ^natCr(p,x)⁵²Mn reaction, but also the ⁵²Cr(p,n)⁵²Mn reaction, after scaling down the published results from enriched targets based on natural abundance of ⁵²Cr. Our results for the ^natCr(p,x)⁵²Mn reaction are shown in Fig. 1. This plot shows that our cross-section results are very close to published results for natural chromium targets (Barrandon et al., 1975; Buchholz et al., 2013; West Jr et al., 1987)., as well as re-scaled results from enriched targets (Boehm et al., 1952; Levkovskij, 1991; Linder and James, 1959; Skakun et al., 1986; Wing and Huizenga, 1962).

3.2. ^natCr(p,x)^52mMn

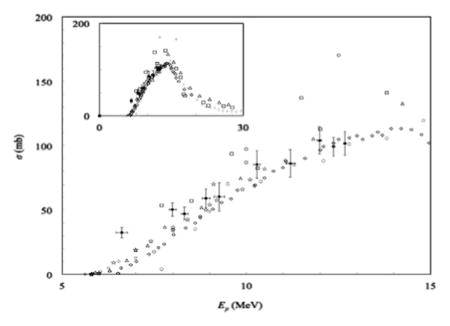
^52mMn has cross-sections roughly three times larger than ⁵²Mn in our energy range, and ^52mMn can be produced by the ⁵²Cr(p,n)^52mMn reaction (same threshold as the ground-state reaction) (BNL/NNDC/QCalc, 2014). Just as with the ^natCr(p,x)⁵²Mn results, there are no competing reactions that produce ^52mMn from natural Cr in our proton energy regime. Therefore, our cross-section results can be compared to published results for both the ^natCr(p,n)^52mMn reaction, as well as for the ⁵²Cr(p,n)^52mMn reaction, after scaling down the published results from enriched targets based on natural abundance of ⁵²Cr. Our results for the ^natCr(p,x)^52mMn reaction are shown in Fig. 2. For this reaction product, we only have 4 cross-section results as because many Cr foils were not counted quickly enough to detect ^52mMn before it decayed. The results from Barrandon, et al. (1975) are noticeably less than all other published results at E_p >10 MeV. However, our results appear to agree well with ^52mMn cross-section data from other natural chromium target publications that were cited for ⁵²Mn in Section 3.1 (Barrandon et al., 1975; Buchholz et al., 2013; West Jr et al., 1987), as well as re-scaled results from enriched targets (Boehm et al., 1952; Levkovskij, 1991; Linder and James, 1959; Skakun et al., 1986; Wing and Huizenga, 1962). It appears that the excitation peak from Barrandon et al. (1975) is not as high as all of these other published cross-sections, and our results are closer to the other studies.

Fig. 2.

Plot showing cross-section results for the ^natCr(p,x)^52mMn reaction, as well as results from other published data sets, including rescaled results from enriched ⁵²Cr targets.

3.3. ^natCr(p,x)⁵⁴Mn

⁵⁴Mn was detected in some of our foils, even though the produced radioactivity was quite low compared to ^52,52mMn. The only logical reaction channel that would have produced this isotope in natural Cr was the ⁵⁴Cr(p,n)⁵⁴Mn reaction (threshold: 2.200 MeV; ⁵⁴Cr: 2.4% natural abundance) (BNL/NNDC/QCalc, 2014). Again, because we do not believe that any competing reactions were present that produced ⁵⁴Mn, we compared our results to cross-section results from enriched targets that were scaled down based on the natural abundance of ⁵⁴Cr. Our results for the ^natCr(p,x)⁵⁴Mn reaction are shown in Fig. 3. We only found one published data set for the production of ⁵⁴Mn from natural chromium with E_p ≤ 30 MeV, and this data set only included cross-sections for E_p ~17–38 MeV. Our results may be the first published for the ^natCr(p,x)⁵⁴Mn reaction at E_p <14 MeV, which might be useful for predicting yield of the ⁵⁴Mn radiocontaminant during production of ⁵²Mn. Therefore, we compared our results with published cross-sections from enriched ⁵⁴Mn targets (Gusev et al., 1990; Johnson et al., 1960; Kailas et al., 1975; Levkovskij, 1991; Skakun et al., 1986; Zyskind et al., 1978) by rescaling the published cross-sections according to the natural abundance of ⁵⁴Cr.

4. Conclusion

⁵²Mn is a potentially useful PET isotope that could be used for in vivo imaging related to the biochemistry and toxicity of manganese, as well as being used as a radiotracer for the biodistribution of macromolecules and nanoparticles. Reliable cross-section data that includes results from multiple groups is beneficial for confirming cross-section results, which in turn affect several parameters for accelerator-based isotope production that are essential to product yield and radionuclidic purity. However, few published studies currently exist for the reaction channels that produce ^52gMn and other isotopes from bombardment of natural Cr with protons at energies <14 MeV, which is an important energy range for many biomedical cyclotrons worldwide. In this work, we have measured cross-sections for the ^natCr(p,x)^52,52m,54Mn reactions, including possibly the first published cross-sections for the ^natCr(p,x)⁵⁴Mn reaction at E_p<14 MeV. Our results were generally very similar to published results from natural Cr targets and re-scaled results from isotopically enriched Cr targets. Although our results are similar to the few data sets that are currently published, we believe that our additional data increases confidence in the available cross-section data for natural Cr targets by demonstrating reproducibility. Ultimately, we hope that our cross-section results will contribute to more accurate yield predictions and enhanced radio-nuclidic purity in the production of the isotopes studied here, particularly ⁵²Mn.

Table 3.

Cross-section results for the ^natCr(p,x)^52mMn reaction.

Energy		Cross-section
Ep (MeV)	Uncertainty	σ (mb)	Uncertainty
12.45	0.04	274	22
11.3	0.1	233	42
9.3	0.1	246	43
8.4	0.1	209	28
6.6	0.2	116	23

HIGHLIGHTS.

• Produced large batch of natural Cr foils for cyclotron bombardment.

• Bombarded stacked foil targets with protons <14 MeV to measure cross-sections.

• Report new cross-section results for the ^natCr(p,x)⁵²Mn, ^natCr(p,x)^52mMn, and ^natCr(p,x)⁵⁴Mn reactions.

Appendix A. Supplementary material

Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.apradiso.2014.12.001