Molecular dynamics simulations on the effect of size and shape on the interactions between negative Au₁₈(SR)₁₄, Au₁₀₂(SR)₄₄ and Au₁₄₄(SR)₆₀ nanoparticles in physiological saline

Abstract

Molecular dynamics simulations employing all-atom force fields have become a reliable way to study binding interactions quantitatively for a wide range of systems. In this work, we employ two recently developed methods for the calculation of dissociation constants K_D between gold nanoparticles (AuNPs) of different sizes in a near-physiological environment through the potential of mean force (PMF) formalism: the method of geometrical restraints developed by Woo et al. and formalized by Gumbart et al. and the method of hybrid Steered Molecular Dynamics (hSMD). Obtaining identical results (within the margin of error) from both approaches on the negatively charged Au₁₈(SR)₁₄ NP, functionalized by the negatively charged 4-mercapto-benzoate (pMBA) ligand, we draw parallels between their energetic and entropic interactions. By applying the hSMD method on Au₁₀₂(SR)₄₄ and Au₁₄₄(SR)₆₀, both of them near-spherical in shape and functionalized by pMBA, we study the effects of size and shape on the binding interactions. Au₁₈ binds weakly with K_D = 13mM as a result of two opposing effects: its large surface curvature hindering the formation of salt bridges, and its large ligand density on preferential orientations favoring their formation. On the other hand, Au₁₀₂ binds more strongly with K_D = 30μM and Au₁₄₄ binds the strongest with K_D = 3.2nM.

1. Introduction

The interactions in aqueous solutions of NPs with sizes less than 3 nm have recently become quantifiable through molecular dynamics (MD) simulations. [1, 2, 3, 4] Experimental studies performed on large NPs (100 nm) have shown that aspherical shapes require a smaller salt concentration to aggregate, due to the larger contact areas between them;[5, 6] while smaller sizes require larger salt concentrations to aggregate, due to the weaker van der Waals forces of attraction.[7, 8] Such small-sized NPs have presented novel challenges to traditional colloid science theories such as Derjaguin-Landau-Verwey-Overbeak (DLVO). In particular, since the radius of sodium r_Na = 1.36 Å is more than 10% of the NP’s radius, the Poisson-Boltzmann theory for electrostatic interactions is not reasonable because it considers the ions as point charges.[9] Additionally, the DLVO assumption that the surfaces of interaction are flat cannot be applied to NPs of such large curvatures as these.[10, 11] The presence of charged surface coatings also introduces steric and bridging effects (mediated by sodium) and it thus becomes necessary to replace simple analytic expressions by a PMF obtained from atomistic numerical computations.

In recent years, the computational methods for obtaining binding affinities through molecular dynamics simulations employing all-atom force fields have matured to a point that experimental measurements can be reproduced. In this paper, we illustrate the use of two such methods, both based on the potentials of mean force (PMF) formalism.[12, 13, 14] The first of these methods, which was developed in 2005 by Woo and Roux,[15] and whose procedures were formalized by Gumbart, Roux, and Chipot in 2012, “invokes a series of geometrical restraints acting on collective variables designed to alleviate sampling limitations inherent to classical molecular dynamics simulations.”[16] The other method, which is called hybrid Steered Molecular Dynamics (hSMD)[17, 18], is a brute force approach developed in 2015 and involves mainly “simultaneously steering n centers of mass of n selected segments of the ligand using n springs of infinite stiffness”.

In this work, we employ both methods on the Au₁₈(SR)₁₄ NP[19, 20, 21, 22] in a near-physiological environment (see Fig. 1(a)). Gold NPs have shown such a promising potential in medical procedures that the result has been called “a golden age” of biomedical nanotechnology.[23, 24] For example, they have been found suitable as drug delivery vehicles for selective targeting of cells,[25] as passive contrast agents for labelling, visualizing and tracking specific receptors,[26] as active sensors whose optical properties change in the presence of analyte molecules,[27] or as heat sources for the treatment of cancer through absorption of light.[28] With regard to biomedical applications, a desirable property of gold nanoparticles is their ability to aggregate reversibly into nanoclusters of controlled size when placed in a special solution, and to dissociate back into individual nanoparticles when introduced into the body.[29, 30, 31, 32] Finally, we compare the binding affinity of Au₁₈ with those of Au₁₀₂[33] and Au₁₄₄[34, 35, 36, 37, 38, 39, 40, 32], functionalized by the same ligand under the same near-physiological conditions.

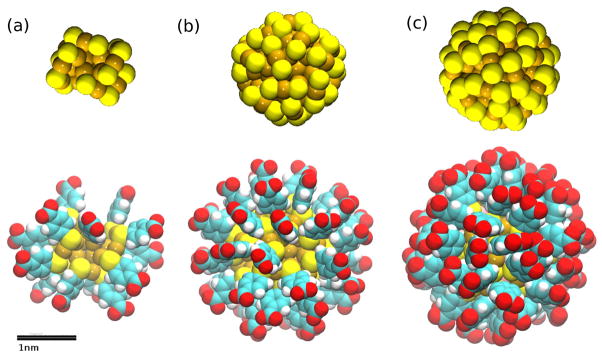
Figure 1.

Systems under study: (a) the Au₁₈(SR)₁₄ (diameter ~ 1nm), (b) Au₁₀₂(SR)₄₄ (diameter ~ 1.5nm) and (c) Au₁₄₄(SR)₆₀ (diameter ~ 2nm) NPs represented as spheres (with van der Waals radius). The coloring scheme throughout this paper is the following: sulfur, yellow; oxygen, red; carbon, cyan; hydrogen, white; gold, golden; nitrogen, blue. All graphics were rendered with VMD.[41]

2. Methods

Simulation Parameters

All interactions were represented with the CHARMM36 force field.[42] Water was represented with the TIP3P[43] model. The cut-off distance applied to the vdW interactions was 1.2 nm, with a switching distance of 1.0 nm and a pair list distance of 1.35 nm. Langevin dynamics were implemented with a time-step of 1.0 fs for short range interactions and 2.0 fs for long range interactions, and with a Langevin damping of 1.0 ps⁻¹. The temperature was kept at 298 K and the pressure at 1.0 bar using the Nose-Hoover Langevin piston control.[44, 45] Periodic boundary conditions were applied in all dimensions. Full electrostatic interactions were computed through the Particle-Mesh Ewald (PME) method. All simulations were performed with NAMD.[46]

Building procedure for the AuNP

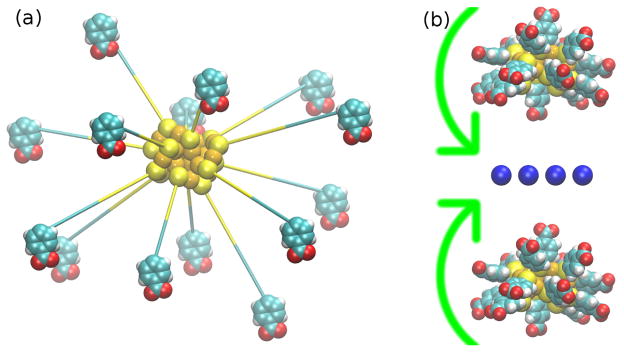
The coordinates of the Au₁₈S₁₄ and Au₁₀₂S₄₄ cores were obtained in Refs. [19] and [33] respectively. We chose the negatively charged 4-mercapto-benzoate ligand because of its experimental relevance. [47, 48] We bound a copy of this ligand to each sulfur and minimized the resulting structure in vacuum while fixing the core atoms (see Video 1 in the Supplementary data). The distances between each gold atom were restrained to their initial values in order to make the core rigid, while still allowing it to move freely. A copy of the NP was then placed 4 nm apart. Since Au₁₈S₁₄ is non-spherical, we determined the orientation of strongest attraction by placing 16 sodium ions in the plane at the middle and allowing the NPs to rotate freely in vacuum (see Fig. 2(b)). After removing the ions at the middle, the NPs were placed in a 70x70x140 ų water box with a 150 mM concentration of NaCl. The system comprised a total of 64 964 atoms.

Figure 2.

Building procedure: (a) The Au₁₈ NP structure undergoing energy minimization after attaching 14 ligands to its surface. (b) The Au₁₈ NP pair undergoing free rotation in the presence of a layer of Na⁺ located at the middle, in order to find the orientation of minimum energy.

Computing binding affinities from potentials of mean force

Following the standard literature,[15] the dissociation constant K_D for the process of binding between two rigid NPs can be computed through the potential of mean force 𝒲(r) formalism as:

$$\frac{c_0}{K_D}=c_0{e}^{-\beta \mathrm{\Delta }{G}_{\text{bind}}}=\frac{c_0{\int }_{\text{site}}d\mathbf{r}{e}^{-\beta \mathcal{W}(\mathbf{r})}}{{\int }_{\text{bulk}}d\mathbf{r}\delta (\mathbf{r}-{\mathbf{r}}_{\infty })e^{-\beta \mathcal{W}(\mathbf{r})}}$$ (1)

where the sampling in the numerator of Eq. (1) is performed on the ensemble of microstates belonging to the bound state, while the sampling in the denominator is performed on the ensemble of microstates from the unbound state. r_∞ is defined to be any microstate belonging to the unbound state, β= 1/k_BT, c₀ is the concentration at standard conditions, equal to 1M on the left-hand side of the equation, and $\frac{6.02\times {10}^{23}\text{nanoparticles}}{{10}^{27}{Å}^3}$ on the right-hand side. Further details are presented in the supplementary information (SI), section 1.

The hSMD method

If we define r₀ to be one of the states from the ensemble of bound states, r_∞ to be one of the states from the ensemble of unbound states, and the free-energy difference between these two states to be Δ𝒲_0,∞ ≡ 𝒲(r₀) − 𝒲(r_∞), then, as in Ref. [17], we have

$$\mathrm{\Delta }{G}_{\text{bind}}=\mathrm{\Delta }{\mathcal{W}}_{0,\infty }-k_{B}Tln\left(\frac{c_0{Z}_0}{Z_{\infty }}\right)$$ (2)

where Z₀ ≡ ∫_site dre^{−β[𝒲(r)−𝒲(r₀)]} and Z_∞ ≡ ∫_bulk dre^{−β[𝒲(r)−𝒲(r_∞)]} correspond to sampling over the ensembles of bound states and unbound states, respectively, and constitute the entropic contribution to the binding affinity. The scheme of simulations employed to drag the system along the dissociation path from r₀ to r_∞ is presented in the SI, Fig. S1.

The hSMD method applied to the Au₁₈ NP

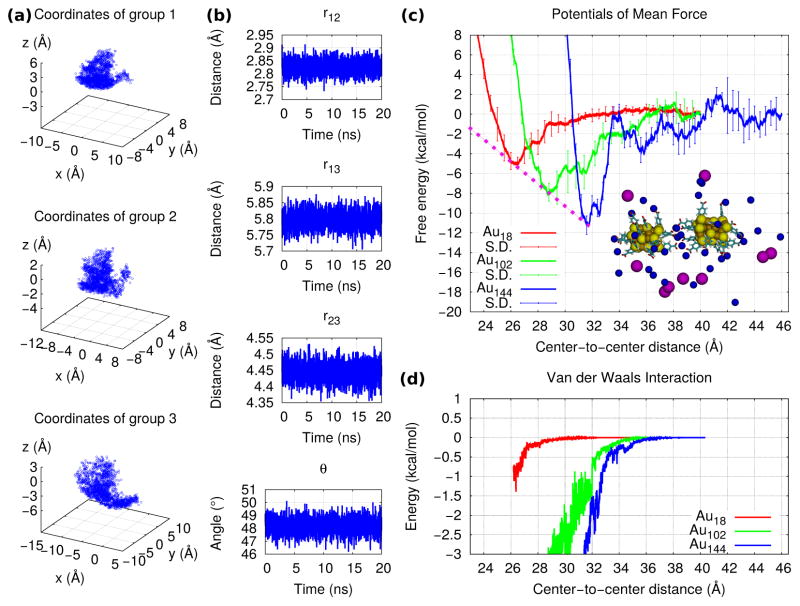
The energetic interactions were studied by selecting arbitrarily three atoms (r₁, r₂, r₃) at the center of the NP whose core was not fixed and pulling them individually along straight lines relative to the NP whose core was fixed until the NPs became aggregated. In this way, the one-dimensional PMF as function of center-to-center distance was obtained, and the NPs were not allowed to rotate at this stage. In order to study the entropic interactions, we performed two runs of 20 ns each under equilibrium conditions: one in which the NPs were bound, and another in which they were unbound. During the bound-state simulation, the core of one NP was fixed while the other NP moved freely (see Video 2 in the Supplementary data) and Z₀ was approximated as a Gaussian integration:

$$Z_0=\sqrt{{(2\pi )}^9\mid \mathrm{\sum }\mid }{e}^{\frac{1}{2}({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)•{\mathrm{\sum }}^{-1}•{({\mathbf{r}}_1,{\mathbf{r}}_2,{\mathbf{r}}_3)}^T}$$ (3)

where Σ is the matrix containing the variances of the coordinates in time:

$$\mathrm{\sum }=\left[\begin{array}{ccccccc}\langle \delta x_1^2\rangle & \langle \delta x_1\delta y_1\rangle & \langle \delta x_1\delta z_1\rangle & \dots & \langle \delta x_1\delta x_3\rangle & \langle \delta x_1\delta y_3\rangle & \langle \delta x_1\delta z_3\rangle \\ \langle \delta y_1\delta x_1\rangle & \langle \delta y_1^2\rangle & \langle \delta y_1\delta z_1\rangle & \dots & \langle \delta y_1\delta x_3\rangle & \langle \delta y_1\delta y_3\rangle & \langle \delta y_1\delta z_3\rangle \\ \langle \delta z_1\delta x_1\rangle & \langle \delta z_1\delta y_1\rangle & \langle \delta z_1^2\rangle & \dots & \langle \delta z_1\delta x_3\rangle & \langle \delta z_1\delta y_3\rangle & \langle \delta z_1\delta z_3\rangle \\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ \langle \delta x_3\delta x_1\rangle & \langle \delta x_3\delta y_1\rangle & \langle \delta x_3\delta z_1\rangle & \dots & \langle \delta x_3^2\rangle & \langle \delta x_3\delta y_3\rangle & \langle \delta x_3\delta z_3\rangle \\ \langle \delta y_3\delta x_1\rangle & \langle \delta y_3\delta y_1\rangle & \langle \delta y_3\delta z_1\rangle & \dots & \langle \delta y_3\delta x_3\rangle & \langle \delta y_3^2\rangle & \langle \delta y_3\delta z_3\rangle \\ \langle \delta z_3\delta x_1\rangle & \langle \delta z_3\delta y_1\rangle & \langle \delta z_3\delta z_1\rangle & \dots & \langle \delta z_3\delta x_3\rangle & \langle \delta z_3\delta y_3\rangle & \langle \delta z_3^2\rangle \end{array}\right]$$ (4)

This approximation is valid when the binding is tight. Since the Au₁₈ NPs are non-spherical, their binding is tight only when their orientations correspond to the maximum contact area between them, that is, to a maximum formation of salt bridges. Because of this, we would not expect the NPs to roll on top of each other, but rather to remain in the initial binding orientation (the Euler angles of the free NP are plotted in Fig. 6(b)).

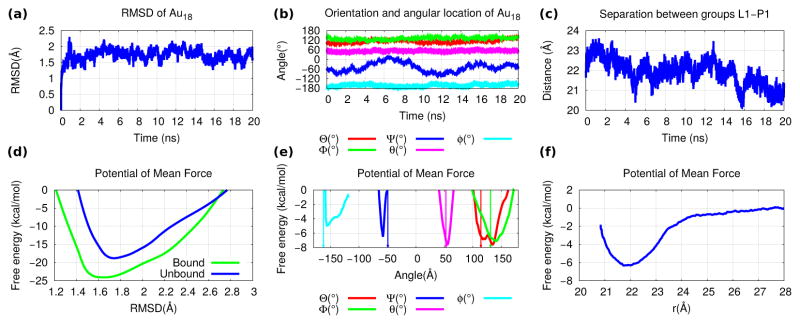
Figure 6.

Geometrical restraint results for Au₁₈: The (a) conformational (i.e. RMSD), (b) angular (i.e. Euler angles for orientation and spherical angles for location) and (c) radial collective variables as functions of time for the 20 ns of simulation under equilibrium conditions. The PMF profiles as functions of the (d) conformational, (e) angular and (f) radial collective variables. The values employed as minima for each of the constraint potentials are indicated by arrows.

During the unbound-state simulation, only one NP was employed. Z_∞ was obtained by sampling over the coordinates of groups 2 and 3 while keeping group 1 fixed:

$$\begin{array}{l}{Z}_{\infty }={\int }_{\mathit{bulk}}d{\mathbf{r}}_{2}d{\mathbf{r}}_3{e}^{-\beta [\mathcal{W}({\mathbf{r}}_{1\infty },{\mathbf{r}}_2,{\mathbf{r}}_3)-\mathcal{W}({\mathbf{r}}_{1\infty },{\mathbf{r}}_{2\infty },{\mathbf{r}}_{3\infty })]}\\ ={\int }_{\text{bulk}}d{\mathbf{r}}_3{e}^{-\beta [\mathcal{W}({\mathbf{r}}_{1\infty },{\mathbf{r}}_{2\infty },{\mathbf{r}}_3)-\mathcal{W}({\mathbf{r}}_{1\infty },{\mathbf{r}}_{2\infty },{\mathbf{r}}_{3\infty })]}\times {\int }_{\text{bulk}}d{\mathbf{r}}_2{e}^{-\beta [\mathcal{W}({\mathbf{r}}_{1\infty },{\mathbf{r}}_2)-\mathcal{W}({\mathbf{r}}_{1\infty },{\mathbf{r}}_{2\infty })]}\end{array}$$ (5)

The first term of equation 5 is obtained by sampling over the distance r₂₃ between groups 2 and 3, as well as over the angle θ formed by the three groups. This corresponds to placing group 2 at the origin and group 1 at the z axis. r₂₃, θ, ϕ are then the spherical coordinates of group 3, where ϕ is integrated out. In the second term of equation 5 we can then integrate out θ and ϕ, and sample over the distance r₁₂ between groups 1 and 2. These integrations are also made through the Gaussian approximation:

$$Z_{\infty }\approx \left[2\pi r_{23\infty }^{2}sin{\theta }_{\infty }\sqrt{{(2\pi )}^2\mid r_{23},\theta \mid }{e}^{\frac{1}{2}(r_{23},\theta )•{\mathrm{\sum }}_{(r_{23},\theta )}^{-1}•{(r_{23},\theta )}^T}\right]\times \left[4\pi r_{12\infty }^2\sqrt{2\pi \mid {\mathrm{\sum }}_{r_{12}}\mid }{e}^{\frac{1}{2}{r}_{12}•{\mathrm{\sum }}_{r_{12}}^{-1}•r_{12}}\right]$$ (6)

where r_12∞, r_23∞ and θ_∞ are the average values of the simulation, ${\mathrm{\sum }}_{(r_{23},\theta )}=\left[\begin{array}{cc}\langle \delta r_{23}^2\rangle & \langle \delta r_{23}\delta \theta \rangle \\ \langle \delta r_{23}\delta \theta \rangle & \langle \delta {\theta }^2\rangle \end{array}\right]$ and ${\mathrm{\sum }}_{r_{12}}=\langle \delta r_{12}^2\rangle$ (more details are presented in the SI, section 2).

The hSMD method applied to the Au₁₀₂ and Au₁₄₄ NPs

Since these NPs are near-spherical, the PMF is independent of the Euler angles defining their orientation, as well as of the angular spherical coordinates defining their angular position. The PMF is a one-dimensional function of the radial separation between the NPs: [49]

$$\frac{c_0}{K_D}=c_0{\int }_{\mathit{site}}d\mathbf{r}{e}^{-\beta \mathcal{W}(\mathbf{r})}=4\pi c_0{\int }_0^{r^{\ast }}{r}^{2}dr{e}^{-\beta \mathcal{W}(r)}$$ (7)

where r^* is a reference position far away in the bulk (i.e. at the dissociated state, where 𝒲(r) → 0 by definition). In the case of the Au₁₀₂ NP, we pulled the center of mass of the 7 gold atoms located at the center, considered as a single atomic group. In this way, we allowed the particle to rotate freely during the dissociation. As for the Au₁₄₄ NP, we chose the 12 gold atoms at the center which form an icosahedron, and the same procedure was followed (see the SI, section 3 for additional details).

The method of geometrical restraints

Following Ref. [16], three atomic groups are defined on each of the binding partners. Six collective variables are then defined in terms of these groups: three Euler angles (Θ, Φ, Ψ) specifying the orientation of the body, and three spherical coordinates specifying its position (θ, ϕ, r), where r is the separation between the partners. A seventh collective variable is the body’s conformation, expressed by its root-mean-square deviation (RMSD) with respect to its time-averaged structure at the bound state. These variables each represent a component of the dissociation path. The free energy of binding is given by:

$$\mathrm{\Delta }{G}_{\text{bind}}=-G_c^{\text{site}}-G_0^{\text{site}}-G_a^{\text{site}}-k_{B}Tln(c_0{S}^{\ast }{I}^{\ast })+G_c^{\text{bulk}}+G_0^{\text{bulk}}$$ (8)

where I^* ≡ ∫_site dre^{−β[𝒲(r)−𝒲(r_∞)]} and $S^{\ast }\equiv {({\mathbf{r}}_{\infty })}^2{\int }_0^{\pi }d\theta sin\theta {\int }_0^{2\pi }d\varphi e^{-\beta u_a}$ correspond to the positional contributions to the free energy as the object is dragged away from the binding site; $G_c^{\text{site}}$ and $G_c^{\text{bulk}}$ correspond to the contributions of the RMSD degree of freedom at the site and the bulk regions, respectively; $G_0^{\text{site}}$ and $G_0^{\text{bulk}}$ correspond to the orientational degrees of freedom, and $G_a^{\text{site}}$ corresponds to the two spherical angles at the bound state (the term $G_a^{\text{bulk}}$ is implicit in the S^*I^* product). Further specifics of this methodology are presented in the SI, section 5.

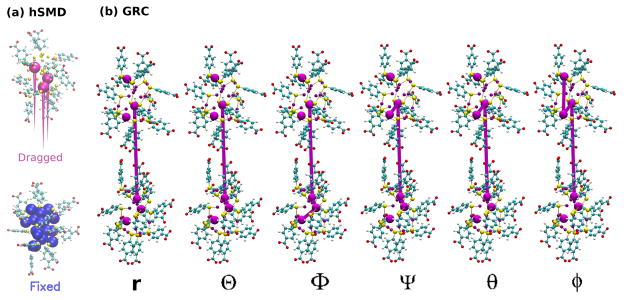
The method of geometrical restraints applied to the Au₁₈ NP

Since the shape of the Au₁₈ NP is non-spherical, sampling over its orientational degrees of freedom becomes necessary. We defined three groups of atoms on the NP whose core was fixed, and three on the other NP. In Fig. 3(a), as well as in Video 3 in the Supplementary data, we present the collective variables defining both the orientation and the location of the free Au₁₈(SR)₁₄ NP relative to the fixed one.

Figure 3.

Methodology for the PMF calculations of Au₁₈ (a) The hSMD method: The displacements of the 3 pulling gold atoms are shown as magenta cones. (b) The method of geometrical restraints: The six groups employed to define the six collective variables are represented as purple spheres. The groups involved in the definition of each collective variable are connected by purple lines.

3. Results

From the hSMD method

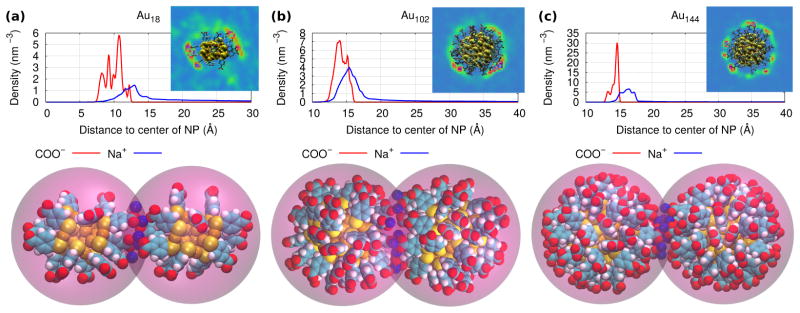
In Fig. 4(a) we plot the location over time of the three pulling atoms during a bound-state equilibration. Fig. 4(b) shows the separations among the atoms and the angle made by them during an unbound-state equilibration. From this sampling we obtained the entropic contributions to the K_D of Au₁₈, shown in Table 1. In Fig. 4(c) we show the PMF for the dissociation and compare it to those of Au₁₀₂ and Au₁₄₄(the results for Au₁₄₄ were taken from Ref. [40]). Through these PMFs we obtained the energetic contributions to K_D. These simulations are presented in Videos 4, 5 and 6 in the Supplementary data. The PMFs were obtained from the work profiles shown in the SI, Fig. S4. As shown in Fig.4(d), the smaller the NP was, the weaker the van der Waals attraction became. The non-spherical shape of Au₁₈ originated the non-isotropic distribution of ligands and ions shown in Fig. 5(a). During the bound-state simulation, five sodium were observed to lie on average at the region in-between the two Au₁₈ and forming salt-bridges between them. As for Au₁₀₂ and Au₁₄₄, we found on average eight and eleven salt-bridges in their bound states, respectively (see Figs. 5(b),(c)). The average number of salt bridges was estimated by counting the amount of ions lying within 0.35nm of both nanoparticles simultaneously (this value was taken from ref. [35] as the cutoff distance of contact between an ion and a terminal group).

Figure 4.

hSMD results : (a) Histogram of the coordinates of the three Au₁₈ pulling atoms during the bound-state equilibration employed to compute Z₀. (b) The distances among the three Au₁₈ pulling atoms and the angle formed by them vs. time during the unbound-state equilibration employed to compute Z_∞. (c) The PMFs of Au₁₈, Au₁₀₂ and Au₁₄₄ as functions of distance between the cores’ centers of mass. The minima are connected by a dashed pink line. The snapshot shows the bound state of Au₁₈ and all ions within 20 Å of the NPs colored by name: sodium, blue; chloride, magenta. (d) The energetic contributions to the PMF from the van der Waals interactions.

Table 1.

The free energy calculations for the Au18, Au102 and Au144 NPs.

hSMD
	Au18	Au102	Au144[40]
Z0	1.5 × 106
$\mathrm{\Delta }{\mathcal{W}}_{0,\infty }\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−5.0	−8.2	−11
Z∞	5.6 × 104
$\mathrm{\Delta }{G}_{\text{bind}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−2.6	−6.2	−12
KD	13 mM	30 μM	3.2 nM
Geometrical Restraints (Au18)
$\mathrm{\Delta }{G}_c^{\text{site}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−13	$\mathrm{\Delta }{G}_{\varphi }^{\text{site}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−2.3
$\mathrm{\Delta }{G}_{\mathrm{\Theta }}^{\text{site}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−1.4	$-k_{B}Tln\left(c_0{S}^{\ast }{I}^{\ast }\right)\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−3.0
$\mathrm{\Delta }{G}_{\mathrm{\Phi }}^{\text{site}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−1.0	$\mathrm{\Delta }{G}_o^{\text{bulk}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	6.7
$\mathrm{\Delta }{G}_{\mathrm{\Psi }}^{\text{site}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−3.5	$\mathrm{\Delta }{G}_c^{\text{bulk}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	15.0
$\mathrm{\Delta }{G}_{\theta }^{\text{site}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−0.33	$\mathrm{\Delta }{G}_{\text{bind}}\left(\frac{\mathit{kcal}}{\mathit{mol}}\right)$	−2.8
KD	9.0 mM

Figure 5.

The radial density distributions of the carboxyl groups and the sodium counterions around (a) Au₁₈(SR)₆₀, (b) Au₁₀₂(SR)₄₄ and (c) Au₁₄₄(SR)₆₀. The snapshots on the top show the density maps of sodium around the NP (the coloring scheme in order of increasing density is: blue, green, red). The snapshots at the bottom show the sodium lying within 3.5 Å of both NPs simultaneously at the bound state.

From the method of geometrical restraints

In Figs. 6(a),(b),(c) we plot the collective variables as functions of time during a run under equilibrium conditions as it was bound to another Au₁₈ whose core’s location was fixed. Figs. 6(d),(e),(f) show the PMFs as functions of the collective variables. In Table 1 we present the contributions to the free energy from each collective variable, which resulted in a dissociation constant of ≈ 9.0 mM.

Spontaneity of the aggregation

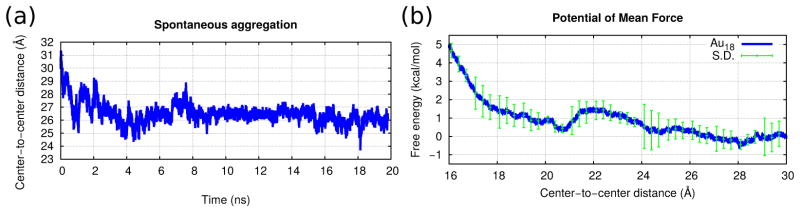
We performed a simulation under equilibrium conditions of a pair of free Au₁₈ NPs in order to verify the spontaneity of their aggregation, in the absence of external forces or constraints. The initial center-to-center distance was set at 3 nm, since at this point the PMF of Fig. 4(c) starts becoming attractive. The center-to-center distance is plotted vs. time in Fig. 7(a) and the simulation is shown in Video 7 of the supplementary data. Notice how the separation between the NPs decreases to the value corresponding to the minimum in the PMF within the first 5 ns, and it remains stable for the next 15 ns.

Figure 7.

(a) The center-to-center separation between two free Au₁₈ NPs vs. time. Starting with an initial value of 3 nm, their aggregation is spontaneous. (b) The PMF of Au₁₈ as a function of the center-to-center separation, employing the opposite orientation as in Fig. 4. The net interaction becomes repulsive.

Specificity of the binding site

In the case of the Au₁₄₄ and Au₁₀₂ NPs, due to their spherical shape the binding site could lie anywhere at the surface. Thanks to this their dissociation constant can be obtained from eq. 7 without the need to sample over their bound and unbound states. A one-dimensional PMF as function of separation between the NPs connecting one of the bound states to one of the dissociated states contains implicitly the sampling over the full surface area of the sphere.[49] However, in the case of the Au₁₈, their non-spherical shape causes the binding site to become specific to those orientations which allow for the formation of a maximum amount of salt bridges. In order to verify this, we measured an additional PMF using the opposite orientation from that employed in Fig. 4. The PMF profile of Fig. 7(b) became repulsive and thus no binding was observed.

4. Discussion

The aggregation process of Au₁₈ NPs

In the SI, Fig. S2(a), we see that as the NPs approach, the direct electrostatic repulsion between them appears much sooner than the van der Waals attraction, which is weak when compared with the PMF. As the NPs approach, the electrostatic energy between them and the sodium ions decreases (see the SI, Fig. S2(b)), since the sodium is able to form salt bridges between the two NPs. However, as the sodium ions transition from being bound with one ligand to being bound with two ligands, they have to be partially dehydrated. This repulsive interaction opposes the decrease in the ion-NP electrostatic energy. Such hydration repulsion is a general property of hydrophilic surfaces.[50, 51, 52] An additional repulsive interaction of the binding process is the decrease in entropy of both the sodium ions and the ligands as their motion becomes more restricted during the formation of the salt bridges. We may observe from the method of geometrical restraints that the entropic contributions to the free energy were: $\mathrm{\Delta }{G}_c^{\text{bulk}}+\mathrm{\Delta }{G}_c^{\text{site}}=2\text{kcal}/\text{mol}$ for the conformational component, $\mathrm{\Delta }{G}_o^{\text{bulk}}+\mathrm{\Delta }{G}_{\mathrm{\Theta }}^{\text{site}}+\mathrm{\Delta }{G}_{\mathrm{\Phi }}^{\text{site}}+\mathrm{\Delta }{G}_{\mathrm{\Psi }}^{\text{site}}=0.8\text{kcal}/\text{mol}$ for the rotational component and $\mathrm{\Delta }{G}_{\theta }^{\text{site}}+\mathrm{\Delta }{G}_{\varphi }^{\text{site}}-k_{B}Tln(c_0{S}^{\ast }{I}^{\ast })=5.6\text{kcal}/\text{mol}$ for the translational component. Both the conformational and rotational components favor the unbound states, where the entropic freedom is larger. However, the translational component (which favors the bound state) is larger than the other two combined.

Size and Shape effects of AuNPs

Because of the small size of the Au₁₈ NP (≈ 1 nm for the core diameter) the resulting large curvature decreases the contact area between two such NPs, thus hindering the formation of salt bridges between them. The small size also decreases the strength of the van der Waals attraction. On the other hand, the non-spherical shape of this NP increases the contact area on those sides whose curvatures are smaller, thus facilitating the formation of salt bridges at preferential orientations. Yet by limiting the orientations which are available for binding, an entropic repulsion is also originated, since there is a decrease in the amount of bound states. In Fig. 7 we saw that for some orientations the interaction actually becomes repulsive. Because of these reasons, as shown in Fig. 4(h), when we compare the PMF of Au₁₈ with those of Au₁₀₂ and Au₁₄₄ (functionalized by the same ligand and in the same near-physiological conditions), the attraction between the Au₁₈ NPs was observed to be the weakest, while that of Au₁₄₄ was the strongest. This result agrees with recent experimental data from ultrasmall glutathione-coated gold nanoparticles.[53] The minima in the PMF profiles of the three NPs studied in this work was found to decrease linearly with the size:

$${\mathcal{W}}_{\mathit{min}}~1-6\times D$$ (9)

where D is the diameter of the NP in units of nm.

Application of the methods on the Ligand-Protein problem

In the supplementary data we show the results from both methods on a protein-ligand binding process with known experimental value of dissociation constant: the acetazolamide (AZM) drug bound to the aquaporin 4 (AQP4) water-channel protein (see Video 8 of the Supplementary data). AZM has been found to inhibit water permeation through AQP4 with an IC₅₀ of ≈ 3 mM.[54] Identical results (within the margin of error) were obtained from both approaches, in agreement with experimental measurements.

5. Conclusion

In this work, we compared the interactions of Au₁₈, Au₁₀₂ and Au₁₄₄, all three functionalized by the same SPh(COO⁻) ligand under the same near-physiological saline conditions. On the one hand, the smaller size of the Au₁₈ hinders the formation of salt bridges between two NPs because of its larger curvature and thus smaller contact area. At the same time, its smaller size decreases the strength of the van der Waals attraction. On the other hand, the non-isotropic shape of Au₁₈ facilitates the formation of salt bridges by increasing the contact area on preferential orientations; yet it also increases the entropy of the bound state by limiting the orientations available for binding. This resulted in dissociation constants of 13mM, 30μM and 3.2nM for Au₁₈, Au₁₀₂ and Au₁₄₄ respectively. The results for Au₁₈ from two different methods agreed with each other. We therefore expect our results to be confirmed in future experiments.

We employed two computational methods for the calculation of absolute binding free energies from the PMF. The method of geometrical restraints is able to separate the contributions to the free energy into nine different geometrical components, in this way providing a great amount of detail regarding the origins of the result. The hSMD method is able to compute the free energy in a brute-force way without losing accuracy, in this way saving much effort during its implementation. Depending on the system under consideration, one may be interested in maximizing the output of information through the use of a series of biasing and constraining potentials, or in computing the result in a straightforward way through the use of steering/pulling simulations. Both methods provide a complete atomic-level picture of the interactions which lie at the origin of the result.