An Empirical Comparison of Joint and Stratified Frameworks for Studying GxE Interactions: Systolic Blood Pressure and Smoking in the CHARGE Gene-Lifestyle Interactions Working Group

Abstract

Studying gene-environment (GxE) interactions is important, as they extend our knowledge of the genetic architecture of complex traits and may help to identify novel variants not detected via analysis of main-effects alone. The main statistical framework for studying GxE interactions uses a single regression model that includes both the genetic main and GxE interaction effects (the ‘joint’ framework). The alternative ‘stratified’ framework combines results from genetic main-effect analyses carried out separately within the exposed and unexposed groups. Although there have been several investigations using theory and simulation, an empirical comparison of the two frameworks is lacking. Here, we compare the two frameworks using results from GWAS of systolic blood pressure for 3.2 million low frequency and 6.5 million common variants across 20 cohorts of European ancestry, comprising 79,731 individuals. Our cohorts have sample sizes ranging from 456 to 22,983 and include both family-based and population-based samples. In cohort-specific analyses, the two frameworks provided similar inference for population-based cohorts. The agreement was reduced for family-based cohorts. In meta-analyses, agreement between the two frameworks was less than that observed in cohort-specific analyses, despite the increased sample size. In meta-analyses, agreement depended on 1) the minor allele frequency, 2) inclusion of family-based cohorts in meta-analysis, and 3) filtering scheme. The stratified framework appears to approximate the joint framework well only for common variants in population-based cohorts. We conclude that the joint framework is the preferred approach and should be used to control false positives when dealing with low frequency variants and/or family-based cohorts.

Introduction

Genome-wide association studies (GWAS) and subsequent meta-analyses have successfully identified hundreds of genetic variants associated with many disease traits (http://www.genome.gov), accelerating the progress in the genetic dissection of complex human traits. Meta-analysis has become a key component of GWAS to increase sample sizes and therefore power [de Bakker, et al. 2008; Evangelou and Ioannidis 2013], and most new discoveries are now driven by large-scale consortia such as the CHARGE (Cohorts for Heart and Aging Research in Genetic Epidemiology) [Psaty, et al. 2009], GIANT (Genetic Investigation of Anthropometric Traits) [Shungin, et al. 2015; Willer, et al. 2009], ICBP (International Consortium of Blood Pressure) [International Consortium for Blood Pressure Genome-Wide Association, et al. 2011], and MAGIC (the Meta-Analyses of Glucose and Insulin-related traits Consortium) [Prokopenko, et al. 2009]. The identified genetic variants, however, typically have small effects, explaining only a small part of the heritability of most complex traits [Manolio, et al. 2009].

Studying gene-environment (GxE) interactions is becoming popular as it can potentially identify novel genetic variants not detected via main-effects analysis alone [Manning, et al. 2012], extend our knowledge of the genetic architecture of complex traits [Hunter 2005], and enable “profiling” of individuals at high risk for disease [Le Marchand and Wilkens 2008; Thomas 2010]. Meta-analysis is more critical for analysis of GxE interactions, as identifying GxE interactions requires even larger sample sizes than those needed to identify genetic main effects [Thomas 2010]. The main statistical framework for the analysis of GxE interactions is using a single regression model that includes both genetic main and GxE interaction effects; we call this the ‘joint’ framework. Under this framework, one can use the traditional 1 degree of freedom (DF) test of the interaction effect or a 2 DF test that jointly tests for both the genetic main and interaction effects [Kraft, et al. 2007]. The 2 DF test has been shown to be particularly useful to identify variants with low main effect and moderate interaction effects, as such variants would be difficult to detect when using either a marginal genetic main effect or the aforementioned 1DF interaction test [Kraft, et al. 2007]. Meta-analysis approaches for the 2 DF test have been developed by Manning et al [Manning, et al. 2011], and by combining data from 52 studies and accounting for body mass index as a possible interaction variable, MAGIC identified multiple novel loci associated with fasting insulin levels [Manning, et al. 2012].

For dichotomous exposure variables, such as yes/no status of smoking or drinking, another framework has emerged, which we call the ‘stratified’ framework. Under this framework, samples are stratified into two groups: the exposed and unexposed groups. Genetic main-effect analysis is performed separately in each stratum. These stratum-specific genetic effects are subsequently combined to perform a 1DF test [Randall, et al. 2013] or a 2DF test [Aschard, et al. 2010]. Although the stratified framework approximates the joint framework, because main-effect models are readily available in many software packages, it is easier to implement in a large-scale consortium setting. Indeed, the stratified framework has been used in several projects of the GIANT consortium including a recent publication [Shungin, et al. 2015].

As of today, there is no clear consensus on which framework (joint versus stratified) should be preferred. Several papers compared specific aspects of each approach. This includes simulation-based studies demonstrating power comparisons [Magi, et al. 2010; Manning, et al. 2011], theoretical work demonstrating close equivalence (in large samples) between statistical tests from the two frameworks [Aschard, et al. 2010; Magi, et al. 2010], and power computations [Behrens, et al. 2011]. However, no empirical comparison using real data has been performed so far. As part of the CHARGE Gene-Lifestyle Interactions Working Group, we performed GWAS of systolic blood pressure for 3.2 million low frequency variants (with 1% ≤ MAF < 5%) and 6.5 million common variants (with MAF ≥ 5%), imputed using reference haplotypes from the 1000 Genomes Project [1000 Genomes Project Consortium, et al. 2012], across 20 cohorts of European ancestry. Using this unique resource we provide a comparison of the two frameworks in several ways. First, to explore the role of the total sample size on the extent of agreement between the two frameworks; second, to understand the impact of unequal sample size between the two (exposed and unexposed) strata, using ‘current-smoking’ status, which leads to highly unequal sample sizes in the two strata, and ‘ever-smoking’ status, which leads to similar sample sizes in the two strata; third, to understand the impact of meta-analysis, by comparing cohort-specific GWAS results and results from meta-analysis; and fourth, to understand the impact of family-based cohorts on meta-analysis by comparing meta-analysis results from1) population-based cohorts only, 2) family-based cohorts only, and 3) all cohorts.

Methods

Study Samples, Genotype and Phenotype Data

We used data from 20 studies with participants of European ancestry. Table 1 summarizes these studies; a detailed description is provided in the Supplemental Materials. Each study obtained informed consent from participants and approval from the appropriate institutional review boards. Genotyping was performed using Illumina (San Diego, CA, USA) or Affymetrix (Santa Clara, CA, USA) genotyping arrays. To infer genotypes for single nucleotide polymorphisms (SNPs), short insertions and deletions (indels), and larger deletions that were not genotyped directly on the genotyping arrays but are available from the 1000 Genomes Project [1000 Genomes Project Consortium, et al. 2012], each study performed imputation using MACH [Li, et al. 2010], Minimac [Howie, et al. 2012], IMPUTE2 [Howie, et al. 2009], or BEAGLE [Browning and Browning 2009] software. For imputation, all studies used the 1000 Genomes Project Phase I Integrated Release Version 3 Haplotypes (2010–11 data freeze, 2012-03-14 haplotypes), which contain haplotypes of 1,092 individuals of all ethnic backgrounds. Information on genotype and imputation for each study is presented in Table S1.

Table 1.

The 20 Participating Cohorts of European Ancestry and their Sample Sizes. Cohorts are divided into two groups (population-based and family-based) and ordered with respect to sample size within each group.

	Cohort	Sample Size	CurSmk			EverSmk
			Yes	No	% Yes	Yes	No	% Yes
Population	CROATIA-Korcula	456	112	344	24.6%	237	219	52.0%
	CROATIA-Vis	483	141	342	29.2%	277	206	57.3%
	BioMe	1,480	134	1,346	9.1%	441	1,039	29.8%
	CARDIA	1,649	406	1,243	24.6%	693	956	42.0%
	HealthABC	1,662	106	1,556	6.4%	951	711	57.2%
	RS2	1,998	408	1,590	20.4%	1,410	588	70.6%
	AGES	2,410	345	2,065	14.3%	1,440	970	59.8%
	MESA	2,591	298	2,293	11.5%	1,447	1,144	55.8%
	RS3	2,966	673	2,293	22.7%	2,031	935	68.5%
	CHS	2,975	357	2,618	12.0%	1,595	1,380	53.6%
	RS1	4,991	1,162	3,829	23.3%	3,317	1,674	66.5%
	GS:SFHS*	6,439	994	5,445	15.4%	3,133	3,306	48.7%
	ARIC	9,465	2,339	7,126	24.7%	5,685	3,780	60.1%
	WGHS	22,983	2,680	20,303	11.7%	11,284	11,699	49.1%
Family	HERITAGE	499	75	424	15.0%	191	308	38.3%
	GENOA	1,064	169	895	15.9%	535	529	50.3%
	HyperGEN	1,251	114	1,137	9.1%	424	827	33.9%
	ERF	2,491	984	1,507	39.5%	1,721	770	69.1%
	FamHS	3,683	523	3,160	14.2%	1,668	2,015	45.3%
	FHS	8,195	2,520	5,675	30.8%	4,281	3,914	52.2%
	Total	79,731	14,540	65,182	18.2%	42,761	36,970	53.6%

Abbreviations: BioMe, Biobank of Institute for Personalized Medicine at Mount Sinai; CARDIA, Coronary Artery Risk Development in Young Adults; HealthABC, Health, Aging, and Body Composition study; RS2, Rotterdam Study cohort 2; AGES, Age Gene Environment Susceptibility Study; MESA, Multi-Ethnic Study of Atherosclerosis; RS3, Rotterdam Study cohort 3; CHS, Cardiovascular Health Study; RS1, Rotterdam Study cohort 1; GS:SFHS, Generation Scotland Scottish Family Health Study; ARIC, Atherosclerosis Risk in Communities; WGHS, Women’s Genome Health Study; HERITAGE, Health, Risk Factors, Exercise Training and Genetics; GENOA, Genetic Epidemiology Network of Arteriopathy; HyperGEN, Hypertension Genetic Epidemiology Network; ERF, Erasmus Rucphen Family study; FamHS, Family Heart Study; FHS, Framingham Heart Study

^*For this manuscript, GS:SFHS, although a family-based study, removed related individuals using IBS values calculated from genetic data.

In total, 79,731 subjects between 18 and 80 years of age with genotype, phenotype and covariate information were available in this analysis. Resting SBP was measured on an mmHg scale. For subjects taking antihypertensive or BP lowering medications, the SBP value was adjusted by adding 15 mmHg [Newton-Cheh, et al. 2009; Tobin, et al. 2005]. This medication-adjusted SBP variable is approximately normally distributed. In addition, to reduce the effect of possible outliers, winsorising has been applied for this SBP value that is more than 6 standard deviations away from the mean. Two smoking exposure variables were considered: ‘current smoking’ status (CurSmk), defined as being a smoker at the time of the blood pressure measurements, and ‘ever smoking’ status (EverSmk), defined as being a smoker at the time of the measurement or else being a former smoker. If subjects had partially missing data for SBP, smoking variable, and any covariates, they were excluded from analysis.

Cohort-specific GWAS Analysis

For the ‘joint’ framework, a regression model including both genetic main and GxE interaction effects

$$Y={\beta }_0+{\beta }_{E}E+{\beta }_{G}G+{\beta }_{GE}E\ast G+{\mathit{\beta }}_{\mathit{C}}\mathit{C}+e,e~N(0,{\sigma }^2)$$ (Equation 1)

was applied to the entire sample. Y is the medication-adjusted SBP value, E is the smoking variable (with 0/1 coding for the absence/presence of the smoking exposure), G is the dosage of the imputed genetic variant coded additively (from 0 to 2), and C is the vector of all other covariates, which include age, sex, field center (for multi-center studies), principal components (to account for population stratification and admixture) and additional cohort-specific covariates (if any). Each study conducted GWAS analysis and provided the genetic main effect β_G and the interaction effect β_GE and their 2×2 robust covariance matrix. For the 1 DF test, we used a Wald test statistic that approximately follows a chi-squared distribution with 1 DF under H₀: β_GE = 0. Similarly for the 2 DF test, we used a Wald test statistic, which approximately follows a chi-squared distribution with 2 DF under H₀: β_G = β_GE = 0.

For the ‘stratified’ framework, analyses of the genetic main-effect regression models

$$\begin{array}{l}Y={\gamma }_0^{(0)}+{\gamma }_G^{(0)}G+{\mathit{\gamma }}_{\mathit{C}}^{(\mathbf{0})}\mathit{C}+e,e~N(0,{\sigma }^{2(0)})\\ Y={\gamma }_0^{(1)}+{\gamma }_G^{(1)}G+{\mathit{\gamma }}_{\mathit{C}}^{(\mathbf{1})}\mathit{C}+e,e~N(0,{\sigma }^{2(1)})\end{array}$$ (Equation 2)

were applied separately to the E = 0 unexposed group and to the E = 1 exposed group. Note that C is the same vector of the covariates as used in Equation (1). Each study conducted GWAS analysis and provided the stratum-specific effects ${\gamma }_G^{(0)},{\gamma }_G^{(1)}$ and their robust standard errors (SE). Robust covariance matrices and robust SEs were sought as a safeguard against mis-specification of the mean model [Tchetgen Tchetgen and Kraft 2011; Voorman, et al. 2011]. To obtain robust covariance matrices and robust SEs, studies of unrelated subjects used either the R package sandwich [Zeileis 2006] or ProbABEL [Aulchenko, et al. 2010]. To account for relatedness in families, four family studies used the generalized estimating equations (GEE) approach, treating each family as a cluster, with the R packages geepack [Halekoh, et al. 2006]. The remaining two studies used the linear mixed effect model approach with a random polygenic component (for which the covariance matrix depends on the kinship matrix) with GenABEL [Aulchenko, et al. 2007] or R (Table S1).

For the 1 DF test in the stratified framework, we used the approach of Randall et al [Randall, et al. 2013], who define

$$Z_{\mathit{diff}}=\frac{{\gamma }_G^{(1)}-{\gamma }_G^{(0)}}{\sqrt{SE{\left({\gamma }_G^{(1)}\right)}^2+SE{\left({\gamma }_G^{(0)}\right)}^2-2rSE\left({\gamma }_G^{(1)}\right)SE\left({\gamma }_G^{(0)}\right)}}$$ (Equation 3)

where ${\gamma }_G^{(1)}$ and ${\gamma }_G^{(0)}$ are stratum-specific genetic effects; $SE\left({\gamma }_G^{(1)}\right)$ and $SE\left({\lambda }_G^{(0)}\right)$ are their respective robust standard errors; and r is the Spearman rank correlation coefficient between ${\gamma }_G^{(1)}$ and ${\gamma }_G^{(0)}$, calculated from the genome-wide results. The statistic Z_diff approximately follows a standard normal distribution under H₀: β_GE = 0. For the 2DF test in the stratified framework, we used the test proposed by Aschard et al [Aschard, et al. 2010]:

$$X_{\mathit{joint}}={\left[\frac{{\gamma }_G^{(1)}}{SE\left({\gamma }_G^{(1)}\right)}\right]}^2+{\left[\frac{{\gamma }_G^{(0)}}{SE\left({\gamma }_G^{(0)}\right)}\right]}^2$$ (Equation 4)

which approximately follows a 2 DF chi-squared distribution under H₀: β_G = β_GE = 0 when the two strata are independent. Note that the 1DF test includes the correlation term “r” to correct for any relatedness between E = 1 and E = 0 strata, whereas such correction is not available for the 2 DF test. Both tests in the stratified framework were computed using the R package EasyStrata [Winkler, et al. 2015].

Meta-analysis of GWAS Results

Variants with minor allele frequency (MAF) below 1% were excluded from each cohort-specific analysis. Extensive quality control (QC) using the R package EasyQC [Winkler, et al. 2014] was performed for all cohort-specific GWAS results. In meta-analysis, to exclude unstable cohort-specific results that reflect small sample size and low MAF, variants were excluded based on the minor allele count (MAC). In the joint framework, variants were included in the meta-analysis if MAC0 (= 2 * MAF_E0 * N_E0) ≥ 10, (with MAF_E0 and sample size N_E0 for E=0 stratum) and MAC1 (= 2 * MAF_E1 * N_E1) ≥ 10. In the stratified framework, we considered two filtering schemes (schemes A and B). Scheme A applied the MAC filter in each stratum separately: variants with MAC0 ≥ 10 (regardless of MAC1 values) were included in the meta-analysis for E = 0 and variants with MAC1 ≥ 10 were included in the meta-analysis for E = 1. Scheme B applied the same filter as the joint framework in both strata (E = 0 and E = 1). Variants were further excluded if imputation quality measure < 0.5. This value of 0.5 was used regardless of the software used for imputations, because imputation quality measures are shown to be similar across imputation software (Supplementary Information S3 through S5 from Marchini and Howie [Marchini and Howie 2010]).

To compare the two frameworks when using meta-analysis, we first performed meta-analysis using the 1 DF and 2 DF tests in each framework. For the 1 DF test in the joint framework, inverse-variance weighted meta-analysis was performed on the cohort-specific interaction effects β_GE, using METAL [Willer, et al. 2010]. For the 2 DF test, the joint meta-analysis of Manning et al [Manning, et al. 2011] was performed using the cohort-specific β_G, β_GE, and their corresponding robust covariance matrix. In the stratified framework, meta-analysis was performed separately within each stratum using METAL. These stratum-specific meta-analysis results for ${\gamma }_G^{(1)}$ and ${\gamma }_G^{(0)}$ were subsequently combined to perform the 1DF test (Equation 3) and the 2DF test (Equation 4) using EasyStrata [Winkler, et al. 2015]. During meta-analysis, genomic control correction [Devlin and Roeder 1999] was applied to cohort-specific GWAS results if their genomic control lambda value was greater than 1. After meta-analysis was performed, a variant was excluded if the overall sample size, i.e. the sample size combined across multiple cohorts, for the variant was below 2,000.

Cohort-specific Results

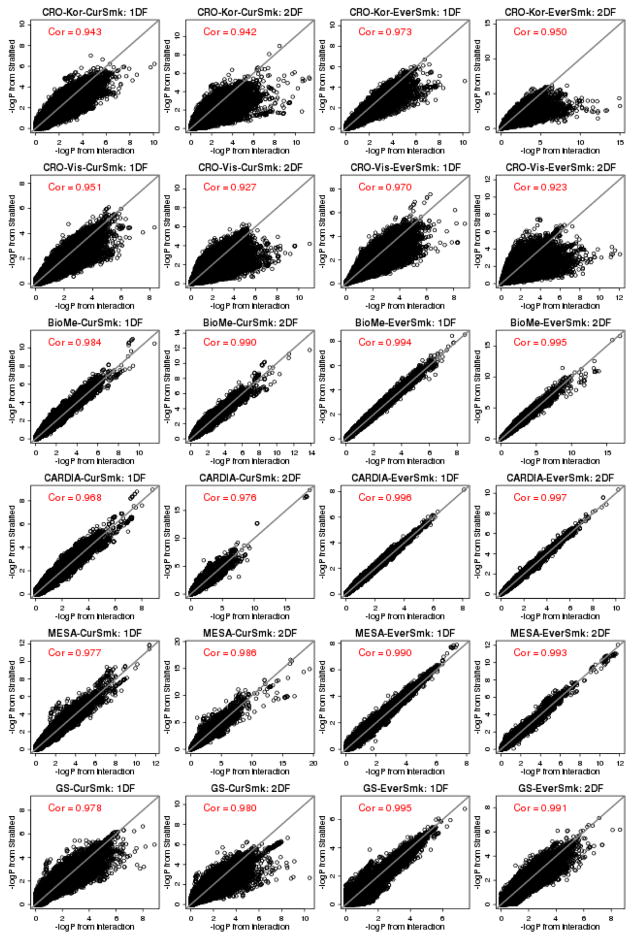
To compare the performance of the two frameworks for all cohort-specific GWAS results, we made scatterplots of −log₁₀P values obtained from the joint framework (x-axis) and the stratified framework (y-axis) using both the 1 DF interaction and 2 DF joint tests (Figures 1, 2, and Figure S1); correlation is shown in Table 2. Cohort-level comparison was restricted to variants with MAC0 ≥ 10 and MAC1 ≥ 10. The genomic control lambda values of cohort-specific GWAS results ranged from 0.98 to 1.15 (Table S2).

Figure 1.

Scatterplots of cohort-level −log₁₀(p) values for the 6 select population-based cohorts showing the weakest correlations. Each point shows −log₁₀(p) value from the joint framework (x-axis) and the stratified framework (y-axis) at a variant. Cohorts are ordered with respect to sample sizes (shown in Table 1). The remaining 8 population-based cohorts that had correlation over 0.99, which are shown in Figure S1.

Figure 2.

Scatterplots of cohort-level −log₁₀(p) values for the 6 family-based cohorts. Each point shows −log₁₀(p) value from the joint framework (x-axis) and the stratified framework (y-axis) at a variant. Cohorts are ordered with respect to sample size (shown in Table 1).

Table 2.

Correlation between the two frameworks for cohort-specific GWAS results. Scatterplots are shown in Figures 1, 2, and S1.

	Cohort	CurSmk		EverSmk
		1DF	2DF	1DF	2DF
Population	CROATIA-Korcula	0.943	0.942	0.973	0.950
	CRO-Vis	0.951	0.927	0.970	0.923
	BioMe	0.984	0.990	0.994	0.995
	CARDIA	0.968	0.976	0.996	0.997
	HealthABC	0.993	0.994	0.998	0.998
	RS2	0.992	0.994	0.999	0.999
	AGES	0.997	0.998	0.999	0.999
	MESA	0.977	0.986	0.990	0.993
	RS3	0.998	0.999	1.000	1.000
	CHS	0.991	0.994	0.999	0.999
	RS1	0.996	0.998	0.996	0.997
	GS:SFHS	0.978	0.980	0.995	0.991
	ARIC	0.992	0.994	0.992	0.993
	WGHS	0.999	1.000	1.000	1.000
Family	HERITAGE	0.762	0.819	0.886	0.902
	GENOA	0.998	0.998	0.992	0.992
	HyperGEN	0.885	0.921	0.935	0.942
	ERF	0.973	0.979	0.974	0.979
	FamHS	0.926	0.950	0.960	0.968
	FHS	0.935	0.951	0.939	0.951

Impact of imbalance in exposure groups

Within each cohort, the number of current smokers is smaller than the number of non-smokers, with percentages of current smokers ranging from 6% to 39% of the cohort sample. When considering ever-smoking instead, the two strata are much more balanced, with percentages of ever smokers ranging from 29% to 70% within each cohort. When all cohorts are combined, current smokers are 18.2% of the entire sample, whereas ever smokers are 53.6% (Table 1).

For both tests and for almost all studies, we observed a higher correlation of the −log₁₀P values between the two frameworks for EverSmk compared to CurSmk. The impact of unequal sample sizes in the two strata can be seen from cohorts with small sample sizes. For example, for CROATIA-Korcula study (N = 456; 25% CurSmk; 52% EverSmk), the smallest population-based cohort, the correlation between the two frameworks for the 1 DF test was 0.94 and 0.97 for CurSmk and EverSmk, respectively (the first row in Figure 1). The scatterplot exhibited many variants that are away from the diagonal line, showing weak agreement. The joint framework had higher genomic control values for this cohort (and the CROATIA-Korcula cohort) (Table S2). However, this pattern was not consistent across cohorts, as the stratified framework had higher genomic control values than the joint framework for several other cohorts.

Sample size for asymptotic equivalence

For population-based cohorts, correlation of −log₁₀P values between the two frameworks generally increased with sample sizes. Out of 14 population-based cohorts, 8 cohorts had excellent agreement between the two frameworks showing correlations over 0.99 for both tests and for both smoking measures (Figure S1): the sample size of these population-based cohorts ranges from 1,663 to 22,983. For the Women’s Genome Health Study (WGHS, N=22,983, 11.7% CurSmk; 49.1% EverSmk), the largest cohort, both frameworks provided almost identical −log₁₀P values, demonstrating the asymptotic equivalence (the last row in Figure S1).

Family-based cohorts

For family-based cohorts, we found less agreement between the two frameworks. For Health, Risk Factors, Exercise Training and Genetics (HERITAGE; N=499; 15% CurSmk; 38% EverSmk), the smallest family-based cohort, the correlation between the two frameworks for the 1 DF test was 0.78 and 0.88 for CurSmk and EverSmk, respectively (the first row in Figure 2). In contrast to population-based cohorts, agreement between the two frameworks did not increase with their sample sizes for family-based cohorts. Out of 6 family-based cohorts, only one cohort GENOA (N = 1,064; 16% CurSmk; 50% EverSmk) showed correlations over 0.99 for both tests and for both smoking measures (Figure 2). The Framingham Heart Study (FHS; N=8,195; 31% CurSmk; 52% EverSmk) is the largest family-based cohort, but the correlation between the two frameworks for the 1 DF test was only 0.94 for both smoking measures (the last row in Figure 2). These correlations were less than those found for the smallest population-based cohort CROATIA-Korcula (N=456).

The complexity of pedigree structure may have a greater impact on the agreement between the two frameworks than sample sizes alone. The GENOA cohort consists of mostly sibling pairs without parents and therefore has the simplest pedigree structure. FamHS, HERITAGE and HyperGEN cohorts have mostly nuclear families. Two remaining cohorts ERF and FHS consist of multi-generation families and therefore have more complex pedigree structures. In family-based cohorts, in particular with large extended pedigrees, most families often are split into the two strata under the stratified framework (making the strata non-independent). Note that the 1 DF test in the stratified framework includes the Spearman rank correlation coefficient between stratum-specific genetic effects to correct for any relatedness between E = 1 and E = 0 strata in Equation (3). Indeed, we observed higher Spearman rank correlation between stratum-specific effects with family-based cohorts (Table 3), ranging from 0.000 to 0.016 with population-based cohorts, and from 0.017 to 0.105 with family-based cohorts. Although the 2 DF test in the stratified framework does not take account for such potential relatedness across strata, correlation between two frameworks for the 2 DF test was generally higher than correlation for the 1 DF test.

Table 3.

Spearman rank correlation coefficients between the two stratum-specific genetic effects calculated from the genome-wide results used for the 1 DF test in the stratified framework

	Cohort	CurSmk	EverSmk
Cohort-level for population-based cohorts	CROATIA-Korcula	0.000	−0.003
	CROATIA-Vis	0.014	0.005
	BioMe	0.001	0.002
	CARDIA	0.000	−0.002
	HealthABC	0.007	0.010
	RS2	0.003	−0.001
	AGES	0.016	0.014
	MESA	0.012	0.044
	RS3	0.006	0.006
	CHS	0.001	0.004
	RS1	0.013	0.005
	GS:SFHS	0.003	0.006
	ARIC	0.012	0.012
	WGHS	0.014	0.027
Cohort-level for family-based cohorts	HERITAGE	0.105	0.076
	GENOA	0.017	0.030
	HyperGEN	0.052	0.093
	ERF	0.053	0.066
	FamHS	0.071	0.078
	FHS	0.091	0.112
Meta-level	Population-based cohorts	0.034	0.045
	Family-based cohorts	0.090	0.095
	All cohorts	0.055	0.065

Meta-analysis Results

Meta-analysis was performed under three scenarios: 1) using 14 population-based cohorts, 2) using 6 family-based cohorts and 3) using all 20 cohorts. For each scenario, meta-analysis was performed once for the joint framework and twice (using two filtering schemes) for the stratified framework. Figure 4 shows the agreement between the two frameworks when the stratified framework used a filtering scheme A. Figure 5 shows the agreement when the stratified framework used scheme B. Correlation is shown in Table 4. We observed that scheme B improved the agreement between the two frameworks.

Figure 4.

Scatterplots of meta-level −log₁₀(p) values using a scheme A in the stratified framework. The joint framework used a filtering scheme B. Row 1 shows results for meta-analysis including the 14 population-based cohorts, row 2 for meta-analysis including the 6 family-based cohorts, and row 3 for meta-analysis including all 20 cohorts.

Figure 5.

Scatterplots of meta-level −log₁₀(p) values using a scheme B in the stratified framework. The joint framework used a filtering scheme B. Row 1 shows results for meta-analysis including the 14 population-based cohorts, row 2 for meta-analysis including the 6 family-based cohorts, and row 3 for meta-analysis including all 20 cohorts.

Table 4.

Correlation between the two frameworks for meta-analysis results. Scatterplots are shown in Figures 4 and 5.

Stratified Framework with	Meta-analysis with	CurSmk		EverSmk
		1DF	2DF	1DF	2DF
Scheme A	Population cohorts	0.942	0.970	0.950	0.982
	Family cohorts	0.860	0.893	0.889	0.924
	All cohorts	0.904	0.947	0.927	0.965
Scheme B	Population cohorts	0.957	0.990	0.965	0.995
	Family cohorts	0.882	0.946	0.905	0.950
	All cohorts	0.923	0.98	0.948	0.985

Filtering schemes

Each cohort contributed more variants to meta-analysis with filtering scheme A (applying the MAC filter separately to each stratum) (Table S3). This is more noticeable in cohorts with small sample sizes with CurSmk variable because of the unbalanced sample sizes between the two strata. For example, the CROATIA-Korcula cohort contributed 8.46 million variants to E=0 stratum meta-analysis but 6.641 million variants to E=1 meta-analysis under scheme A. The difference (roughly 1.82 million) corresponding to the number of variants with MAC0 ≥ 10 and MAC1 < 10 arose from highly unbalanced sample sizes in the two strata. Under scheme B (applying the same filter to both strata in the stratified framework and in the joint framework), a smaller number of variants (6.640 million for CROATIA-Korcula) were contributed to the meta-analysis as variants needed to have MAC0 ≥ 10 and MAC1 ≥ 10.

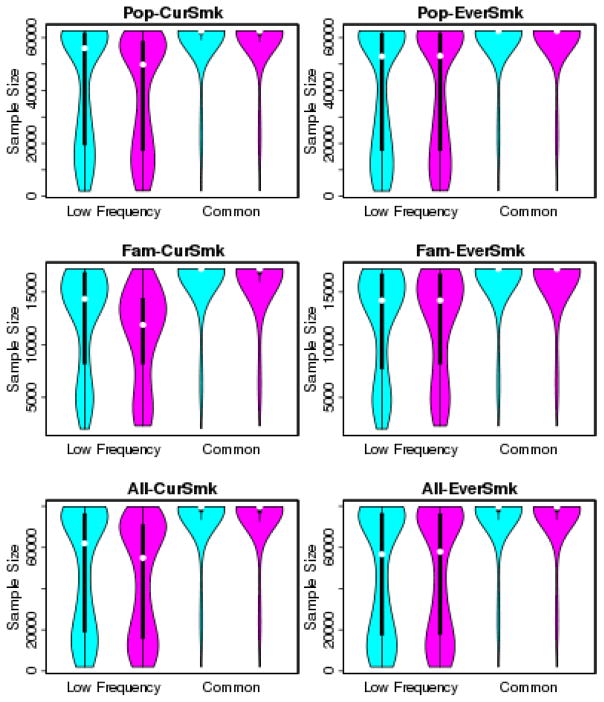
The final number of variants resulting from meta-analysis was slightly larger under scheme A (9.76 million variants under scheme A vs. 9.68 million variants under scheme B in meta-analysis combining all cohorts for CurSmk, Table S4). The difference was mostly from low frequency variants (with 1% ≤ MAF < 5%) (3.2 million variants under scheme A vs. 3.1 million under scheme B); there were 6.5 million common variants (with MAF ≥ 5%) under both schemes. Because each cohort contributed more variants under scheme A, there were more cohorts contributing to each variant, resulting in larger sample sizes under scheme A. The difference in the overall sample size, the sample size combined across multiple cohorts, was more notable for low frequency variants and for CurSmk (Figure 3).

Figure 3.

Violin plots of sample sizes arising from meta-analysis under two filtering schemes. Cyan color under scheme A (a stratum-specific filter) and magenta color under scheme B. Row 1 shows results for meta-analysis including the 14 population-based cohorts (with total sample size 62,548), row 2 for meta-analysis including the 6 family-based cohorts (with sample size 17,183), and row 3 for meta-analysis including all 20 cohorts (with total sample size 79,731).

In meta-analysis, the stratified framework had higher genomic control lambda values for the 1 DF test, regardless of filtering schemes. The Spearman rank correlation between stratum-specific effects for the 1 DF test was also slightly increased (0.034) after meta-analysis of population-based cohorts (Table 3). The lambda values for the 2 DF test were generally similar between the two frameworks (Table S5).

Population-based vs. family-based results

Regardless of the schemes (A and B), we found a surprising reduction of agreement between the two frameworks in meta-analysis compared to cohort-specific analyses. For meta-analysis combining 14 population-based cohorts (with a total sample size of 62,548), the correlation between the two frameworks for the 1 DF test was 0.94 and 0.96 with the use of schemes A and B in the stratified framework, respectively, for CurSmk (the top left in Figures 4 and 5). Note that we had found higher correlations on the cohort-level: for population-based cohorts, about 80% of sample (49,450 subjects) was from the 8 cohorts that had correlation over 0.999 between the two frameworks for the 1 DF test and for CurSmk. Compared to the 1 DF test, using the 2 DF test generally increased the significance of p-values, possibly reflecting true main effect associations that are missed by the 1 DF tests. The 2 DF test also had higher correlation between the two frameworks compared to the 1 DF test.

When meta-analysis included family-based cohorts, the level of agreement became even less. For meta-analysis combining the 6 family-based cohorts (with sample size 17,183), the correlation between the two frameworks for the 1 DF test was 0.86 and 0.88 with the use of schemes A and B in the stratified framework, respectively, for CurSmk (the middle left in Figures 4 and 5). Again, these correlation values on the meta-level were lower than those observed on the cohort-level. Furthermore, there were a noticeable number of variants that had highly discrepant p-values between two frameworks using the 2 DF test with the use of the scheme A in the stratified framework (the middle second and fourth columns in Figure 4).

When all 20 cohorts were combined (with total sample size 79,731), the correlation was approximately the average of the two values for the two meta-analysis results (population-based and family-based). With the use of scheme A in the stratified framework, the scatterplot for the 2 DF test still included those variants with highly discrepant p-values between two frameworks (the last row of Figure 4).

Low-frequency vs common variants

To examine how the concordance between the two frameworks depends on the MAF, we generated two scatterplots for each scatterplot in Figures 4 and 5, one including about 3 million low frequency variants (with MAF < 5%) and another including 6.5 million common variants (with MAF ≥ 5%). The filtering scheme in the stratified framework had a larger impact on the concordance of low frequency variants (Supplemental Figures 2 and 4). For common variants, the two schemes for the stratified framework provided almost identical performance, providing similar agreement between the two frameworks (Supplemental Figures 3 and 5). Moreover, when meta-analysis included family-based cohorts (rows 2 and 3 of Figure 4), those variants that showed highly discrepant p-values between the two frameworks were all low frequency variants (Figure S2).

To further understand this discrepancy for low frequency variants, we examined the variants from the meta-analysis of the 6 family-based cohorts for the CurSmk measure (the middle second in Figure 4). The three selected variants are presented in Table 5. For all variants, meta-analysis for the E=1 stratum is identical regardless of filtering schemes. The difference came from meta-analysis of the E = 0 stratum. For example, with the first variant (2:48619812, MAF = 1.2%), the meta-analysis for E = 0 stratum used 3 cohorts under scheme A but one cohort (FamHS) under scheme B. When two remaining cohorts were included, the final 2 DF p-values were changed dramatically. The second variant shared this feature although all 6 cohorts contributed to the scheme A meta-analysis for E=0 stratum. However, the 2 DF p-values for both schemes were similar for the third variant. It appears that the use of the generalized estimating equations (GEE) approach for the analysis of the family-based cohorts may lead to spurious results for low frequency variants. This finding is consistent with the recent publication [Sitlani, et al. 2015]. The variants that showed highly discrepant p-values from meta-analysis combining all cohorts (the third row in Figure 4) also shared this feature.

Table 5.

Comparison of schemes A and B for family-based meta-analysis for CurSmk at select variants

Marker	Level	Type	N	MAC	MAC	Effect	StdErr	P	Stratified	Interaction
			E=0	E=0	E=1	E=0	E=0	E=0	2DF P	2DF P
2:48619812 (MAF=1.2%)	Meta	Scheme A	4,479			12.8	1.0	7.8E-41	8.5E-40
	Meta	Scheme B	3,160			0.6	2.7	0.83	0.63	0.89
	Cohort	FamHS	3,160	77.7	13.7	0.6	2.6	0.83	0.60	0.89
	Cohort	GENOA	895	29.9	<10	3.2	3.1	0.30
	Cohort	HERITAGE	424	10.3	<10	15.8	1.0	1.2E-54
6:142093034 (MAF=1.7%)	Meta	Scheme A	12,798			4.7	0.5	3.8E-23	2.2E-22
	Meta	Scheme B	10,342			−0.1	1.0	0.89	0.47	0.61
	Cohort	ERF	1,507	66.9	52.7	1.2	2.1	0.58	0.68	0.78
	Cohort	FamHS	3,160	140.3	25.2	0.2	1.6	0.88	0.98	0.89
	Cohort	FHS	5,675	141.8	63.0	−0.5	1.5	0.74	0.47	0.5
	Cohort	GENOA	895	43.8	<10	−4.0	2.6	0.12	0.15	0.12
	Cohort	HERITAGE	424	19.1	<10	−6.3	0.5	1.9E-33
	Cohort	HyperGEN	1137	30.5	<10	0.3	4.4	0.95
12:5679139 (MAF=1.3%)	Meta	Scheme A	4,479			1.9	2.1	0.37	1.8E-09
	Meta	Scheme B	3,160			4.1	2.8	0.15	5.0E-09	1.9E-11
	Cohort	FamHS	3,160	84.1	12.5	−4.1	2.8	0.14	6.3E-10	3.8E-12
	Cohort	GENOA	895	33.5	<10	3.1	3.7	0.41	0.2	0.21
	Cohort	HERITAGE	424	10.5	<10	−3.6	4.8	0.46	0.59	2.4E-08

Discussion

Gene-environment interactions play important roles in the pathobiology of disease traits, improving our understanding about which combinations of genes and environments may be predisposed to unfavorable health outcomes. Modeling gene-lifestyle interactions may discover more trait loci through context dependent (or “refined”) main effects as well as true interactions. To actively investigate the role of such interactions on cardiovascular traits, we have established a Gene-Lifestyle Interactions Working Group within the CHARGE Consortium. The working group includes over 50 cohorts from around the world, spanning four race/ethnic groups (European, African, Hispanic, and Asian ancestry). This offers us an opportunity to compare and contrast two analysis frameworks for studying gene-environment interactions.

Using actual results from 20 cohorts of European ancestry, we empirically compared the two frameworks. In cohort-specific analyses, we observed that agreement between the two frameworks were generally good and depended on 1) balance between sample sizes of the two strata, 2) total sample size, and 3) whether the cohort is population-based or family-based. In meta-analyses, agreement between the two frameworks was less than that observed in cohort-specific analyses, despite the increased sample size. In meta-analyses, agreement depended on 1) the minor allele frequency, 2) inclusion of family-based cohorts in meta-analysis, and 3) filtering scheme. The discrepancy was more notable for low frequency variants.

The joint framework that considers the genetic main and interaction effects jointly in a single linear model has been the main statistical approach for studying interactions. It utilizes the entire sample and works well whether environmental exposures are categorical or continuous. The stratified framework has emerged because main-effect models are readily available in many software packages and easier to implement in a large-scale consortium setting. However, the stratified framework, appropriate for population-based cohorts, was developed to approximate the joint framework. Our findings from cohort-specific results support the equivalence between the two frameworks for population-based cohorts. For family-based cohorts, however, we found less agreement between the two frameworks. Most family-based cohorts, in particular large extended pedigrees, include both exposed and unexposed members within each family. The stratified framework is unable to fully account for family structures across strata. The Spearman rank correlation coefficient in the 1 DF test may partly correct for any correlation between the strata (that may arise from family data). In contrast, the 2 DF test does not take into account any relatedness across the strata: the null distribution of the 2 DF test holds when the exposed and unexposed groups are independent. We observed that the stratified framework was less suitable for approximating the joint framework for family studies with complex pedigree structures (such as the Framingham heart study).

To increase the sample sizes, most large scale consortia include both population-based and family-based studies. It is also becoming standard to perform analysis of low frequency variants imputed using the 1000 Genomes project. In our meta-analysis, we had about 3 million low frequency variants. However, with inclusion of family-based studies in meta-analysis, disagreement between the two frameworks was more pronounced for low frequency variants. With the use of stratum-specific filters, we observed less agreement and a notable number of variants that had highly discrepant p-values between the two frameworks, where 20% of subjects were from family-based cohorts. If the stratified framework is already in use, then using a consistent filter for both strata may improve the agreement, thereby providing a similar inference as the joint framework.

To our knowledge, this is the first report comparing the joint and stratified frameworks using real data. The stratified framework appears to approximate the joint framework well only for common variants in population-based cohorts. We conclude that the joint framework is the preferred approach and should be used to control false positives when dealing with low frequency variants and/or family-based cohorts. As our findings were based on an empirical evaluation using one phenotype, they may not be generalized to all situations. Even though we focused on a continuous outcome, the methods are generally applicable to dichotomous outcomes under the logistic regression framework [Aschard, et al. 2010; Magi, et al. 2010]. With dichotomous outcomes, we expect similar conclusion but may require more stringent MAC thresholds to produce valid logistic regression results [Ma, et al. 2013]. A more comprehensive investigation covering the various scenarios with both continuous and dichotomous outcomes, among others, would strengthen our findings.