Metabolite concentrations, fluxes, and free energies imply efficient enzyme usage

Abstract

In metabolism, available free energy is limited and must be divided across pathway steps to maintain ΔG negative throughout. For each reaction, ΔG is log-proportional both to a concentration ratio (reaction quotient-to-equilibrium constant) and to a flux ratio (backward-to-forward flux). Here we use isotope labeling to measure absolute metabolite concentrations and fluxes in Escherichia coli, yeast, and a mammalian cell line. We then integrate this information to obtain a unified set of concentrations and ΔG for each organism. In glycolysis, we find that free energy is partitioned so as to mitigate unproductive backward fluxes associated with ΔG near zero. Across metabolism, we observe that absolute metabolite concentrations and ΔG are substantially conserved, and that most substrate (but not inhibitor) concentrations exceed the associated enzyme binding site affinity. The observed conservation of metabolite concentrations is consistent with an evolutionary drive to utilize enzymes efficiently given thermodynamic and osmotic constraints.

Introduction

Absolute metabolite concentrations determine enzyme binding site occupancies¹ and the thermodynamics of metabolic reactions². Accordingly, knowledge of absolute metabolite concentrations is valuable for dynamic modeling of metabolism^3,4. Such knowledge is also useful for conducting in vitro enzyme assays under physiologically relevant conditions^5,6, for predicting whether antimetabolites will outcompete with endogenous metabolites for relevant enzyme binding sites⁷, and for engineering enzymes that selectively bind desired substrates in the complex cellular environment⁸.

A variety of methods exist for measuring cellular metabolite concentrations, with liquid chromatography-mass spectrometry (LC-MS) enabling measurements of many metabolites with sensitivity and specificity^9,10. A deficiency of LC-MS is that absolute signal intensity depends on ionization efficiency and therefore does not reliably reflect absolute concentrations. This limitation can be overcome by comparing the signal of endogenous metabolites to isotopically labeled standards, whose addition prior to extraction also accounts for losses in sample handling¹¹. Because, isotopically labeled standards of many metabolites are not commercially available, it is often more convenient to feed isotopically labeled substrates to cells and compare labeled intracellular metabolites to unlabeled standards¹². Through this approach, we have previously measured the absolute concentrations of 103 metabolites in E. coli¹. The concentrations of these metabolites are typically higher than the associated Michaelis constants (K_m) of the enzymes consuming them, suggesting that most active sites in E. coli are occupied.

Using these absolute concentrations, the thermodynamics (Gibbs energy, ΔG) of metabolic reactions have also been assessed based on the fundamental equation, where ΔG°′ is ΔG at standard biochemical conditions, Q is the reaction quotient (the ratio of the product to reactant activities), R is the gas constant, T is the temperature in kelvins, and K_eq is the equilibrium constant (the ratio of product to reactant activities at equilibrium) at standard biochemical conditions:

$$\mathrm{\Delta }\mathrm{G}=\mathrm{\Delta }{{\mathrm{G}}^{\circ }}^{\prime }+\text{RT}ln\mathrm{Q}=\text{RT}ln(\mathrm{Q}/{\mathrm{K}}_{\text{eq}})$$ (1)

For simplicity, Q is typically calculated based on concentrations, not activities, using ΔG°′ determined at cellular ionic strength and divalent cation concentrations.

Gibbs free energy of reaction (ΔG) has been applied in metabolic analysis to eliminate flux loops that violate the second law of thermodynamics^13,14 and to constrain the directions of cellular metabolic reactions¹⁵. In addition, it determines the fraction of flux through metabolic reactions that is in the forward direction and thus productive, and thereby relates to the efficiency of enzyme utilization¹⁶. Thermodynamic analysis also can provide regulatory insights, with enzymes operating far from equilibrium being more effective targets for regulating pathway flux¹⁷.

Here we explore the potential to infer cellular reaction free energies based on relative forward to backward flux. Specifically, where J⁺ and J⁻ are forward and backward fluxes^18–20:

$$\mathrm{\Delta }\mathrm{G}=-\text{RT}ln({\mathrm{J}}^{+}/{\mathrm{J}}^{-})$$ (2)

We validated that the relative forward and backward flux ratios through reversible reactions like triose phosphate isomerase can be measured using isotope tracers. Moreover, we recognized that the resulting ΔG measurements can be used to evaluate the metabolite concentrations. For example, given direct measurements of the reversibility and all but one of the substrates or products of a reaction, the missing concentration can be determined by combining equations (1) and (2). More generally, concentrations, fluxes, and thermodynamics are all interrelated, and we aimed to obtain coherent values of each.

Here we report the application of such integrative analysis to E. coli, yeast, and a cultured mammalian cell line. The mammalian cell line was derived by immortalization of baby mouse kidney cells (iBMK cells)²¹. Each cell type was grown in nutrient-rich conditions including high glucose. Under such media conditions, we observed that absolute metabolite concentrations are significantly conserved across these highly divergent cell types, arguing for a common set of constraints on their metabolomes. We propose that the three most important constraints are thermodynamics, osmotics, and efficient enzyme utilization.

Results

Isotope tracers reveal reaction reversibility and thus ΔG

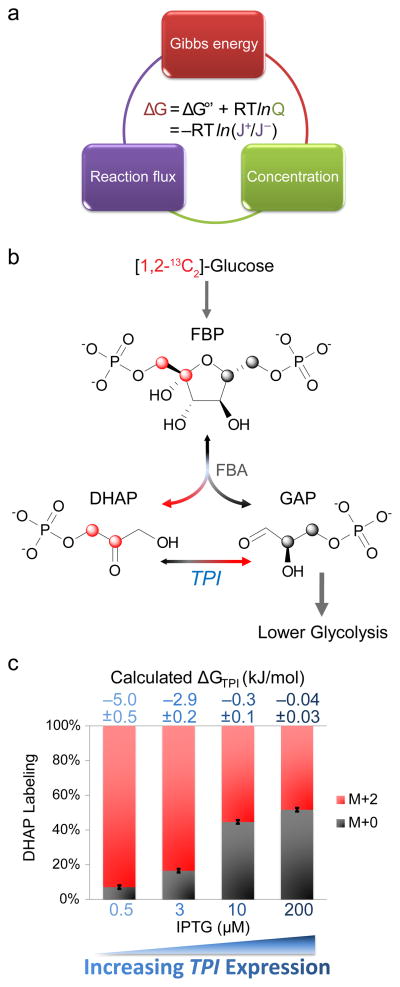
To lay the groundwork for integrative analysis of metabolite concentrations, fluxes, and free energies (Fig. 1a), we initially set out to validate the ability to measure the reversibility of a single glycolytic reaction catalyzed by triose phosphate isomerase (TPI) using isotope tracers. TPI converts dihydroxyacetone phosphate (DHAP) into glyceraldehyde-3-phosphate (GAP). To determine TPI reversibility, we needed a tracer that differentially labels DHAP and GAP. We selected [1,2-¹³C₂]-glucose, which yields [1,2-¹³C₂]-fructose-1,6-bisphosphate, the parent molecule of DHAP and GAP. DHAP is formed from carbons 1–3 and GAP from carbons 4–6 (Fig. 1b). Thus, in the absence of backwards flux through TPI, all DHAP molecules would be labeled (M+2), with reverse flux through TPI resulting in the appearance of unlabeled DHAP.

Figure 1. Tracing forward-to-backward flux through triose phosphate isomerase (TPI).

(a) The free energy of cellular reactions (ΔG) is independently determined by i) the reaction standard free energy adjusted for substrate and product concentrations and ii) the ratio of forward-to-backward fluxes. The integration of experimental measurements of forward-to-backward reaction fluxes and of metabolite concentrations results in more coherent and precise determination of both concentrations and ΔG. (b) [1,2-¹³C]-glucose (red atom: ¹³C) yields [1,2-¹³C]-fructose-1,6-bisphosphate (FBP), the parent molecule of dihydroxyacetone phosphate (DHAP) and glyceraldehyde-3-phosphate (GAP). FBP carbons 1–3 form DHAP. Thus, in the absence of backwards flux through triose phosphate isomerase (TPI), all DHAP molecules would be labeled (M+2). Reverse flux through TPI results in the appearance of unlabeled DHAP. (c) To verify that we can measure different extents of reversibility, we knocked out in E. coli the chromosomal TPI and introduced a plasmid containing TPI under the control of inducer IPTG. The fraction of unlabeled DHAP progressively increased with IPTG addition. The extent of DHAP labeling at pseudo-steady state was used to determine the ratio of forward-to-backward TPI flux by isotopomer balancing. The flux ratio then yields ΔG as per (a). Labeling fraction error bars represent standard deviations (n=3) and calculated ΔG errors represent 95% confidence intervals.

To verify that we can measure different extents of reversibility, we knocked out the chromosomal TPI in E. coli and introduced an inducible TPI plasmid. At low inducer levels, DHAP was almost completely labeled, indicating nearly unidirectional forward flux (Fig. 1c). Increasing the inducer level resulted in unlabeled DHAP, up to a maximum value of 50% unlabeled as expected for complete reversibility (Fig. 1c). The extent of DHAP labeling at pseudo-steady state can be converted into a ratio of forward to backward TPI flux based on isotopomer balancing (see Methods). Using equation (2), the forward-to-backward flux ratios yield ΔG_TPI. Since DHAP absolute concentration can be directly measured, we can determine the absolute concentration of GAP (which is less abundant and can be obscured by analytical interferences²²) using equation (1).

Large-scale determination of net and exchange fluxes

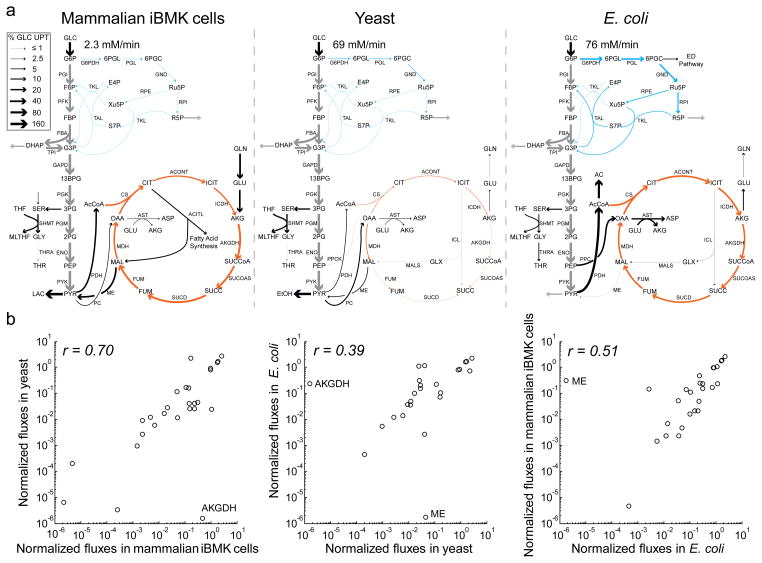
The same conceptual approach that was applied to TPI can be expanded to cover a wide spectrum of central metabolic reactions. Analyzing the broader network advantageously accounts for all major sources and sinks of each metabolite, but requires a diversity of tracers to quantitate fluxes throughout central metabolism. Independent experiments feeding multiple different ¹³C-glucose tracers and measuring pseudo-steady-state metabolite labeling patterns by LC-MS were conducted in E. coli, yeast, and the mammalian cell line iBMK. In addition, for the mammalian cells, tracer analysis was also conducted with [U-¹³C₅]-glutamine, another important carbon source for these cells. Labeling data are shown in Supplementary Results, Supplementary Data Set 1. Together with nutrient uptake and waste excretion data, the labeling data were sufficient to determine pseudo-steady-state net fluxes throughout central metabolism by isotopomer and flux balancing. Results of all of the tracer experiments were integrated into a single unified flux set for each organism (Fig. 2a, Supplementary Table 1).

Figure 2. Metabolic flux distributions in mammalian iBMK cells, yeast, and E. coli.

Fluxes were determined by integrating direct nutrient uptake and waste secretion rate measurements and data from multiple isotope tracers by metabolic flux analysis. (a) Net fluxes. Arrow widths indicate absolute magnitudes of fluxes, normalized to glucose uptake, as per the legend. Absolute magnitude of glucose uptake is shown for each organism. Grey, glycolysis; blue, pentose phosphate pathway; orange, TCA cycle; black, other. (b) Comparison of normalized net fluxes across organisms. Fluxes were normalized to the organism’s glucose uptake rate. Plotted data are restricted to linearly independent fluxes (e.g., lower glycolysis is shown once per graph, not repeatedly for each pathway enzyme).

Substantial differences in net fluxes were observed across the three organisms. The absolute glucose uptake rate, normalized to cell volume, was about 30-fold lower in the mammalian iBMK cells than in E. coli or yeast. While the largest intracellular flux in each organism was glycolysis, utilization of the pentose phosphate pathway and the TCA cycle differed. Net flux through the oxidative pentose phosphate pathway was 20% of glucose uptake in E. coli, but only 3% and 2% in yeast and mammalian iBMK cells respectively. Flux of glucose-derived two-carbon units into the TCA cycle consumed 24% of pyruvate made in E. coli, but only 13% in the mammalian iBMK cells and 2% in yeast, which had minimal α-ketoglutarate dehydrogenase flux with malate dehydrogenase operating net in reverse. Malic enzyme flux was substantial in yeast and mammalian cells, but not E. coli. Overall, fluxes were more similar in the two eukaryotic cell types than across the two microbes (Fig. 2b).

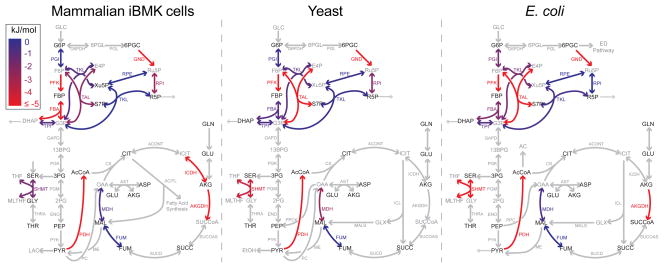
In addition to determining net fluxes, an in-house algorithm was developed to quantitate forward-to-backward flux ratios and their confidence intervals and associated ΔG (See Methods). The ability to obtain informative flux ratios depends on the backwards reaction producing a distinctive labeling pattern. The tested tracers enabled such direct measurement of forward-to-backward flux ratios for selected reactions in the pentose phosphate pathway, glycolysis, the tricarboxylic acid (TCA) cycle, and folate-mediated serine-glycine interconversion (Supplementary Table 2, Fig. 3).

Figure 3. Reaction free energy determined with isotope tracers in mammalian iBMK cells, yeast, and E. coli.

Flux reversibility and ΔG were determined from forward and backward fluxes. Blue, equilibrium (ΔG ≈ 0 kJ/mol); red, substantially forward driven (ΔG ≤ −5 kJ/mol); grey, not measured based solely on isotope tracer data (for reversibility of glycolytic reactions inferred from combined flux and concentration data, see Fig. 4b).

Integrating metabolite concentrations and free energies

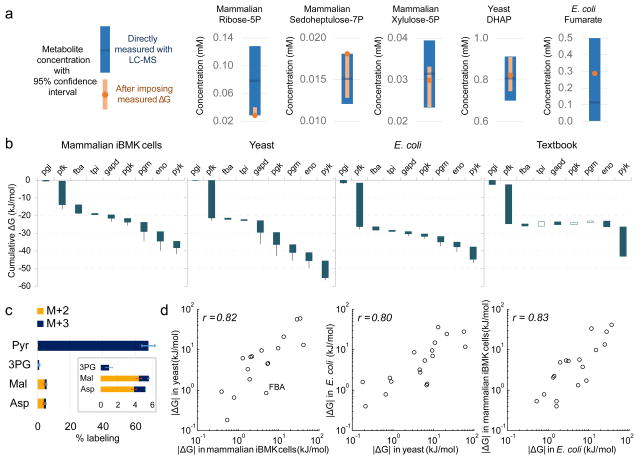
With an eye towards a better understanding of the overall thermodynamics of central carbon metabolism, we aimed to combine the flux-based free energy measurements from Figure 3 with direct measurements of metabolite concentrations by LC-MS into a coherent unified picture of central carbon metabolite concentrations and free energies. To this end, we obtained ΔG°′ by a group contribution method (component contribution)²³ and searched for sets of central carbon metabolite concentrations that best matched both i) the directly observed concentrations for measured metabolites and ii) the observed cellular ΔG for measured reactions (see Methods). For reactions where free energy was not measured, ΔG was constrained to be negative in the direction of net flux. Metabolite sets were penalized when either concentrations or free energies fell outside of the 95% confidence intervals of the measurements. We subsequently obtained upper and lower boundaries for metabolite concentrations and reaction free energies by linear programming. This approach identified previously unmeasured absolute metabolite concentrations and more tightly constrained those of metabolites that were involved in multiple reactions with measured cellular ΔG values (e.g. DHAP and pentose phosphates) (Fig. 4a and Supplementary Table 3). Particularly valuable was obtaining reliable measurements for species that were difficult to measure due to analytical interferences or instability, including ribulose-5-phosphate, erythrose-4-phosphate, 1,3-bisphosphoglycerate, 2-phosphoglycerate, and oxaloacetate.

Figure 4. Integration of flux and concentration measurements via ΔG.

(a) The absolute concentrations of those metabolites involved in reactions with ΔG determined from reaction reversibility (Fig. 3b) were refined by combining confidence intervals from direct LC-MS measurement of their concentrations (blue) with thermodynamic constraints to obtained more precise values (orange). For example, the concentration of fumarate is informed also by that of malate, in combination with the reversibility of fumarase. (b) ΔG for glycolysis based on integration of metabolite concentrations and reaction reversibilities. Blue and white bars depict negative and positive ΔG, respectively. Whiskers show 95% confidence limits (see Methods). (c) An unexpected finding from the thermodynamic analysis in (b) is partial reversibility of pyruvate kinase. To demonstrate directly this reversibility, [U-¹³C]-pyruvate (0.45 mM) was added to the media of growing iBMK cells for 20 min and upstream and downstream metabolites were analyzed for labeling. Error bars represent standard errors of the means (n=3). (d) Comparison of ΔG across organisms. Plotted data are for all measured reactions with ΔG < −0.1 kJ/mol.

Combining these concentrations together with ΔG°′ values, we determined ΔG for most central carbon metabolic reactions (Supplementary Table 4). Focusing on glycolysis, the cumulative free energy change from phosphoglucose isomerase (PGI) to pyruvate kinase (PYK) was on average −46 kJ/mol (Fig. 4b). In each case, phosphofructokinase was the most strongly forward driven glycolytic step, consuming nearly half of the available free energy. Downstream of phosphofructokinase, the available free energy was relatively evenly distributed across pathway steps, except for triose phosphate isomerase which was always the reaction closest to equilibrium. Such even flux partitioning, with a bias towards fast reactions such as triose phosphate isomerase being close to equilibrium, has been predicted to maximize the efficiency of enzyme utilization¹⁶.

Along with phosphofructokinase, pyruvate kinase is generally considered a committed step in glycolysis. Current textbooks indicate that almost all of the energy drop in glycolysis occurs at the phosphofructokinase and pyruvate kinase steps (Fig. 4b). Accordingly, we were surprised when our global analysis resulted in only a modest driving force for pyruvate kinase in the mammalian cell line iBMK (ΔG = −3.8 kJ/mol implying a forward-to-backward flux ratio of 4.3). To evaluate further the free energy of the pyruvate kinase reaction, we added labeled pyruvate to growing cells and monitored the formation of lower glycolytic intermediates. Although the concentration of phosphoenolpyruvate was too low to measure its labeling directly, we observed labeling of 3-phosphoglycerate, confirming some back flux through the phosphoglycerate mutase-enolase-pyruvate kinase reaction sequence (Fig. 4c). The observed labeling was not due to canonical gluconeogenic flux, as this would have resulted in 3-phosphoglycerate being both M+2 and M+3 labeled²⁴, whereas only M+3 was observed. Thus, the pyruvate kinase reaction can be partially reversible.

Overall, reaction free energies were highly conserved across the three organisms (Fig. 4d). The details of free energy utilization, however, differed. Compared to mammalian iBMK cells, yeast had higher glucose-6-phosphate, ADP/ATP, and NAD⁺/NADH, with the net effect being nearly a doubling of the free energy drop in glycolysis. This larger free energy drop likely facilitates rapid fermentation. Intriguingly, despite most glycolytic reactions being more forward driven in yeast, aldolase was closer to equilibrium. This could potentially further favor yeast fermentation by enhancing the free energy available for downstream glycolytic steps. Thus, the details of free energy partitioning may be optimized to organism-specific metabolic objectives.

Conservation of absolute metabolite concentrations

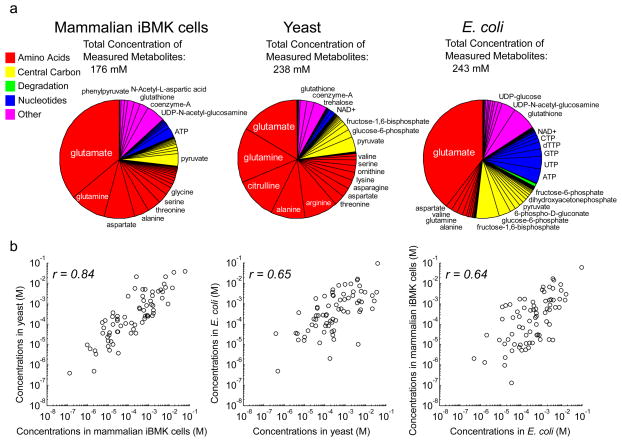
Given the fundamental connection between ΔG and metabolite concentrations, the similarity of reaction free energies across species suggested similarity in the metabolomes. A compilation of metabolite concentrations, from a combination of direct concentration measurements and the above approach integrating free energy measurements, is provided in Supplementary Table 5. Across the organisms, amino acids composed the largest fraction of metabolome (Fig. 5a) and were similar in intracellular abundances despite the presence of amino acids in the mammalian but not the microbial culture media. Central carbon metabolites were the next most abundant class followed by nucleotides (including nucleotide-derived cofactors such as NAD⁺). The most abundant individual metabolite in each organism was glutamate, the amino group donor in many transamination reactions, whose high concentration may be required to drive transamination forward. Other abundant intracellular metabolites included reduced glutathione and pyruvate (Fig. 5a). Globally, the metabolite concentrations of E. coli, yeast, and mammalian iBMK cells were all correlated with each other (Fig. 5b and Supplementary Fig. 1), with the fraction of variance in absolute metabolite concentrations explained by the inter-organism correlation (r²) ranging from 40% to 70%. The remaining 30% to 60% of variance reflects some combination of measurement error and true inter-organism differences. In the previous work comparing the E. coli metabolome across three different carbon sources¹, we found that ~75% of variance was explained by correlation across conditions, suggesting a nutrient contribution of no more than 25%. Thus, the impact of organism on absolute metabolite concentrations is stronger than that of carbon source. Nevertheless, in spite of different lifestyles, physiology, culture conditions across organisms, and the potential for metabolite concentrations to change without overt effects on cell physiology²⁵, absolute metabolite concentrations are substantially conserved across kingdoms of life.

Figure 5. Conservation of absolute metabolite concentrations.

(a) Pie chart showing fractional contribution of each measured metabolite in each organism. Concentrations were obtained by the integrative analysis as per Fig. 4a. Names are shown for metabolites whose fractional concentration exceeds 1%. (b) Comparison of absolute metabolite concentrations across organisms. Plotted data are for all measured metabolites.

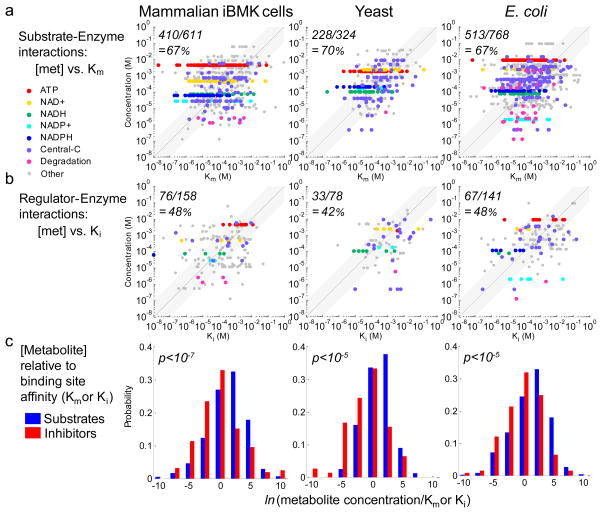
Substrate and inhibitor enzyme binding site occupancy

To infer enzyme binding site occupancies, we compared the absolute concentrations of metabolites to the affinities of the enzyme sites to which they bind. Binding affinities (the inverse of the dissociation constants K_m and K_i) were taken from the BRENDA database²⁶ (see Supplementary Data Sets 2 and 3). Similar prior analysis in E. coli had focused exclusively on substrate binding and found a propensity for most active sites to be occupied¹. Here we validated this basic observation also for yeast and mammalian iBMK cells, with metabolite concentration exceeding K_m for roughly two-thirds of sites in each case (Fig. 6a). As described previously for E. coli, the ubiquitous cofactors ATP, NAD+, and NADPH were almost always saturating. In contrast, NADP⁺ was not reliably saturating, perhaps reflecting prioritization of a high NADPH/NADP⁺ ratio over complete enzyme site occupancy (Supplementary Fig. 2). Central carbon metabolite concentrations were often near K_m, perhaps to facilitate efficient regulation or switching to gluconeogenesis¹, whereas the concentrations of the substrates of degradative enzymes (e.g. of nucleotide catabolism) were typically below K_m. Such pathways are presumably useful only when substrate concentrations rise. In contrast to the general propensity for substrates to be saturating, inhibitor concentrations tended to be near or below K_i (Fig. 6b). This was despite a propensity for ATP, NAD⁺, and NADPH to be saturating also at inhibitory sites, although to a lesser degree than at substrate ones (Supplementary Fig. 2). The greater propensity for substrates than inhibitors to be saturating was statistically significant in each organism (Fig. 6c). Thus, metabolite concentrations seem to be tuned to saturate enzyme active sites but not effector binding sites in freely growing cells. This favors efficient enzyme utilization, with inhibitor concentrations near K_i positioning the system for regulation to kick in if significant deviations from homeostasis occur.

Figure 6. Comparison of absolute concentrations to enzyme binding site affinities for substrates and for inhibitors.

(a, b) Comparison of absolute metabolite concentrations (Y-axis) to enzyme binding site affinities (X-axis). The fraction of concentrations exceeding K_m or K_i (i.e., data points above the line of unity) is shown in the top left of each graph. (c) Enzyme active sites are in general more saturated than inhibitor sites (p-values are from the Kolmogorov-Smirnov test).

Discussion

Metabolism is the process of converting nutrient inputs into usable energy and biomass building blocks. Like all chemical networks, metabolism must obey the second law of thermodynamics: each pathway step must cost free energy. A fundamental challenge is partitioning the available free energy across pathway steps. Too large a drop in free energy at any one step wastes the energy available in scarce nutrients. Too small a drop results in the associated enzyme catalyzing unproductive backwards flux.

To understand how cells manage this challenge, biochemists have long relied on the ability to infer the free energies of cellular reactions (ΔG) based on metabolite concentrations combined with standard free energies^27,28 as per equation (1). Recently, such analyses have been conducted for increasingly large metabolic networks^29,30. Here, using isotope tracers and mass spectrometry, we augmented the tool set for probing cellular thermodynamics by determining relative forward-to-backward reaction fluxes and thus ΔG directly as per equation (2). Measurement of reaction reversibility is based on the backward reaction producing a distinctive isotope labeling pattern in the substrate. This was exemplified by the formation of unlabeled DHAP via backwards triose phosphate isomerase flux after feeding [1,2-¹³C₂]-glucose (Fig. 2). To obtain forward and backward fluxes for a substantial fraction of central metabolism, we integrated data from multiple different ¹³C-tracers (see Supplementary Table 2). More precise and comprehensive determination of flux reversibility should be possible in the future through dynamic ¹³C-labeling experiments³¹ and/or application also of ²H- and ¹⁵N-tracers.

Compartmentation introduces an unaccounted-for complexity into these flux and thermodynamic determinations. The analysis reported here is for metabolites collected from whole cells and does not distinguish forward-and-backward flux occurring through a single enzyme in one compartment from a pair of enzymes (such as distinct isozymes) in different compartments. Mitigating compartmentation concerns, however, similar results were obtained from E. coli and the eukaryotic cells, despite much more extensive compartmentation in the eukaryotes. Development of methods that enable compartmental analysis of metabolite concentrations, fluxes, and free energies is an important future objective.

In addition to the methodology for measuring ΔG, a key contribution of this work is a coherent systems-level set of fluxes, free energies, and metabolite concentrations for E. coli, yeast, and a mammalian cell line (iBMK) (Figs. 2, 3, 4, and 5, and Supplementary Tables 1, 4, and 5). Prior work has integrated metabolite concentrations and fluxes in dynamic labeling experiments³¹ based on the relationship between metabolite pool sizes, turnover times, and fluxes: metabolites turn over (and thus tend to label) rapidly when flux is large or pool size is small^31,32. This relationship, which is not applicable to the steady-state labeling experiments reported here, could be used to further constrain concentration and flux estimates in future work. More directly relevant to our current approach, prior studies have integrated metabolite concentration and free energies to achieve systems-level estimates of both^1,2,17. By augmenting such thermodynamic analysis with the direct flux-based ΔG measurements for a subset of reactions, the present work markedly refines the overall thermodynamic estimates, providing useful quantitative values of cellular ΔG for many reactions.

In addition to providing a valuable reference, these data shed light on metabolic design principles. Consider glycolysis, which is the highest flux pathway in each of the studied organisms and localizes to the cytosol, obviating compartmentation concerns. The textbook view involves three strongly thermodynamically forward-driven reactions, which cannot reverse flux direction during gluconeogenesis and thus must be bypassed, linked by near equilibrium ones that, during gluconeogenesis, flip their direction of net flux (Fig. 4b). The three committed reactions are glucose phosphorylation (hexokinase in yeast in mammals, phosphotransferase system in E. coli), phosphofructokinase, and pyruvate kinase. Glucose phosphorylation was omitted from our analysis, due to our inability to quantitate the intracellular glucose concentration (given the abundance of media glucose). For phosphofructokinase and pyruvate kinase, we found that the former is substantially more forward driven: ΔG for phosphofructokinase ranges from −13 to −25 kJ/mol, which results in minimal back flux (< 0.7% of forward flux), whereas for pyruvate kinase, it ranges from approximately −4 to −10 kJ/mol, which results in 2% to 20% backward-to-forward flux. Thus, while both reactions are far enough from equilibrium for changes in the associated enzyme activities to exert flux control, phosphofructokinase functions as a classic irreversible step, whereas some backward flux at pyruvate kinase is tolerated to achieve energy efficiency.

The lower free energy drop at pyruvate kinase results in a greater amount of free energy available to drive the reversible reactions of lower glycolysis. According to a standard textbook³³, the net free energy drop from fructose-1,6-bisphosphate to phosphoenolpyruvate is only 1.7 kJ/mol. Spread evenly across six reactions, this would result in a drop per reaction of only 0.3 kJ/mol, which is associated with a forward-to-backward flux ratio of roughly 10 to 9, or one unit of productive flux for 18 units of exchange flux, resulting in only ~5% of enzyme contributing productive net flux. Given the high cellular levels of glyceraldehyde-3-phosphate dehydrogenase, phosphoglycerate kinase, and enolase^34–37, the expense of protein synthesis³⁸, and cellular space limitations³⁹, there should be strong evolutionary pressure to use these enzymes at greater than 5% efficiency. Indeed, the actual situation in cells is different from the current textbook description. The free energy drop over this six reaction sequence is not 1.7 kJ/mol but instead at least 6-fold higher (11.4 – 24.2 kJ/mol) (Fig. 4b), with only the triose phosphate isomerase step having a drop less than 2 kJ/mol in all organisms. Thus, in glucose-fed cells, the “difficult” steps of lower glycolysis that require high enzyme levels are sufficiently forward driven to avoid excessive wasteful backwards flux.

The more even free energy distribution in lower glycolysis may impact both pathway regulation and dynamics. Unlike reactions very close to equilibrium, where changes in enzyme activities do not impact overall pathway flux, several reversible glycolytic reactions including aldolase, glyceraldehyde-3-phosphate dehydrogenase, and phosphoglycerate mutase are sufficiently forward driven, in at least some organisms, for these enzymes to exert physiologically significant flux control. Indeed, glyceraldehyde-3-phosphate dehydrogenase is inactivated in response to oxidative stress, and this has been shown to inhibit glycolysis and thereby promote pentose phosphate pathway flux and NADPH production⁴⁰. More generally, these observations are consistent with findings from metabolic control analysis that flux control, while unevenly distributed across glycolytic enzymes, is not concentrated in one or two key steps^41–43. Indeed, any reaction of lower glycolysis that is significantly forward driven could be used to control pathway flux or the levels of upstream and downstream intermediates, which are themselves important precursors for biosynthetic pathways such as serine synthesis. A disadvantage of such more even free energy distribution is slower return of the pathway intermediates to steady-state levels following perturbations and less ability to control pathway flux via any single effector-enzyme interaction⁴⁴. Apparently, at least for cells fed copious glucose, these disadvantages are outweighed by greater efficiency of enzyme utilization, which requires substantial driving force for all but the most rapid reactions, so as to mitigate backwards flux and thus the required amount of enzyme.

Maintaining sufficient driving force is expected to favor efficient enzyme utilization not only in glycolysis, but throughout metabolism. Selective pressure is presumably greatest for high flux pathways where adequate total free energy is available. In this respect, glycolysis in glucose-fed cells may reflect an extreme case. Indeed, we have previously reported that lower glycolytic reactions are closer to equilibrium in cells fed glycerol (where flux remains in the glycolytic direction) or acetate (where net flow is in the opposite direction). In general, one would also expect evolutionary pressure to maintain adequate ΔG to be greatest for steps where the total enzyme level is substantial, either due to high flux or low k_cat.

Throughout metabolism, substrate-to-product ratios are tied together by thermodynamics. Because each metabolite is simultaneously the substrate and product of one or more reactions, the above considerations globally constrain the concentration ratios of all metabolites. Because ΔG depends on the ratio of substrate and product concentrations, but not their absolute magnitude, other factors determine the absolute concentration of the collective metabolome. A cap on metabolite concentrations is likely enforced by osmotics. In each of the studied organisms, the sum of all measured metabolite concentrations is around 200 mM, similar to the salt concentration in human plasma. Within this upper osmotic bound, an important determinant of absolute metabolite abundances is saturation of enzyme binding sites. Enzyme evolution is subject to dual pressures to enhance both substrate binding affinity and turnover rate. These competing pressures are captured by the classical metric of enzyme performance k_cat/K_m. Higher metabolite concentrations render low K_m values unnecessary, thereby facilitating higher k_cat and thereby enabling more net flux per enzyme. Thus, there is selective pressure to maintain metabolite pools as large as feasible given thermodynamic and osmotic bounds. As for maintaining substantial thermodynamic driving force, this pressure is greatest for “hard” reactions in high flux pathways. Reactions may be “hard” due to universal chemical reactivity constraints, or due to specific environmental challenges such as nutrient scarcity. Natural variation across organisms in pathway utilization and nutrient availability should therefore result in organism-specific tailoring of absolute metabolite concentrations. The observed impressive, but incomplete, conservation of absolute metabolite concentrations reflects the balance of this tailoring against universal reactivity and thermodynamic constraints on the metabolome.

Online Methods

Strains and culture conditions

E. coli K-12 strain NCM3722 was grown at 37°C in Gutnick minimal media⁴⁵ containing 10 mM NH₄Cl and 0.4% (w/v) D-glucose. To create the inducible triose phosphate isomerase strain, the chromosomal tpiA was knocked out by P1 phage transduction of a deletion allele with a kanamycin resistance cassette from the Keio collection, and a pAC24N::tpiA ASKA plasmid under the control of isopropyl β-D-thiogalactopyranoside (IPTG) was introduced by electroporation. S. cerevisiae derived from prototrophic strains S288C and W303 were grown at 30°C in 2% (w/v) D-glucose media containing 6.7 g/L Difco Yeast Nitrogen Base (YNB) without amino acids. BAX^−/−/BAK^−/−-immortalized baby mouse kidney epithelial cells (iBMK)²¹ were grown at 37°C, 5% CO₂ in Dulbecco’s modified Eagle medium without pyruvate (DMEM) supplemented with 10% dialyzed fetal bovine serum. For steady state flux analysis, E. coli were cultured in media containing [1,2-¹³C₂], [3-¹³C₁], or 50% [U-¹³C₆] glucose; yeast in [1,2-¹³C₂] or 50% [U-¹³C₆] glucose; and iBMK in [1,2-¹³C₂] glucose, [U-¹³C₆] glucose, or [U-¹³C₅] glutamine (99%; Cambridge Isotope Laboratories) until isotopic steady states were reached; microbes were labeled starting from overnight cultures and mammalian cells were labeled for at least 24 hours. To verify the reversibility of mammalian pyruvate kinase, [U-¹³C₃] pyruvate (as the sodium salt) was spiked into culture medium (which had been changed 3 hours beforehand) to a final concentration of 0.005% (0.45 mM) and metabolism was quenched after 20 minutes.

Metabolite measurements and absolute quantitation

Metabolism of exponentially growing cells was quickly quenched and metabolites were extracted in pre-cooled extraction solvents. Briefly, small portions of E. coli or yeast culture (3 mL at OD₆₀₀ ≈ 0.3 for E. coli and 0.6 for yeast) were vacuum-filtered onto nylon membrane filters (0.45 μm; Millipore) resting on a vacuum filter support. Once cells were loaded, the membranes were immediately submerged in pre-cooled −20°C 40:40:20 acetonitrile:methanol:water in petri dishes. For iBMK cells at ~80% confluency, cells were supplied with fresh media, and two to three hours thereafter the media was aspirated and metabolism immediately quenched by adding −80°C 80% methanol to the culture dishes. Extraction continued for 20 minutes at −20°C, and metabolite extracts were collected into Eppendorf tubes after thoroughly washing the filters (E. coli and yeast) and detaching the cells from the culture plates using cell lifters (iBMK cells). The extracts were centrifuged at 4°C. The supernatants were dried under nitrogen gas and reconstituted in HPLC-grade water for LC-MS analysis. OD₆₀₀ (E. coli and S. cerevisiae) and packed cell volume (iBMK cells) at the time of quenching were measured and later used in calculating cellular metabolite concentrations.

For absolute metabolite quantitation, cells were grown in [U-¹³C₆] glucose (and also [U-¹³C₅] glutamine for the mammalian cells) but otherwise the same media as above and extracted with solvents containing known concentrations of authenticated standards¹². E. coli was cultured atop filters from OD₆₀₀ 0.03 to 0.3 with the labeled media diffusing through agarose and filters until extraction¹². The metabolomes of E. coli filter culture and liquid culture are similar (Supplementary Fig. 3). To measure cellular concentrations of amino acids that are present in DMEM, we cultured iBMK cells in standard unlabeled DMEM and used [U-¹³C, ¹⁵N] amino acids as internal standards. In this case, cells were washed with warm PBS twice to remove exogenous amino acids prior to adding the extraction solvent. Nucleotides, nucleosides, and bases in E. coli as well as NADH and NADPH in E. coli, yeast, and mammalian cells were measured using acidic extraction solvents (0.1 M formic acid⁴⁶). The extracts were neutralized with 15% NH₄HCO₃ prior to centrifugation.

Samples were analyzed by reversed-phase ion-pairing liquid chromatography coupled to a high-resolution orbitrap mass spectrometer by electrospray ionization operating in negative ion mode (Exactive, Thermo)^9,22. Cysteine was measured after derivatization with S-methyl methanethiosulfonate (MMTS) on an LC-MS/MS instrument performing hydrophilic interaction liquid chromatography (HILIC) coupled to tandem MS in positive ion mode (Quantum Ultra; Thermo)⁴⁷. Resulting mass spectra and chromatograms were processed using the Metabolomic Analysis and Visualization Engine (MAVEN)⁴⁸ and corrected for natural ¹³C abundance as well as incomplete labeling due to ¹²C impurities (and also CO₂ incorporation for absolute metabolite quantitation). Many LC-MS ion-specific chromatograms were complicated by multiple peaks (e.g. for glucose-6-phosphate, due to its isomers; for fumarate due to an ion of identical molecular formula being produced by in-source degradation of malate). Care was taken to pick the peak at the correct retention time as validated by standard injection, not simply the largest peak of the correct exact mass. To provide additional constraints for flux analysis, some metabolite functional group labeling fractions were computed via the inverse Cauchy product of other measured metabolites (e.g. the acetyl group labeling in acetyl-CoA can be computed given the labeling of both acetyl-CoA and CoA).

Uptake and secretion rate measurements

Nutrient uptake and product secretion rates were determined by the rates of disappearance and appearance of metabolites in the media after accounting for the amount of cells and their growth rate. E. coli and yeast media samples were analyzed by proton nuclear magnetic resonance (¹H-NMR) spectroscopy. To convert media concentration changes to cellular fluxes, we used the following conversion factors: for E. coli, 1.0 OD₆₀₀ = 0.47 gCDW/L, 3×10⁻¹³ gCDW/cell, and 7×10⁻¹⁶ L aqueous volume/cell; and for yeast, 1.0 OD₆₀₀ = 0.62 gCDW/L, 1.9×10⁻¹¹ gCDW/cell and 5.6×10⁻¹⁴ L aqueous volume/cell⁴⁹. For iBMK cells, the rates of glucose, glutamine, and serine uptake as well as pyruvate, lactate, alanine, and ammonia excretion and fatty acid biosynthesis were previously reported⁵⁰, and we assumed that 70% of packed cell volume was aqueous volume. Organism-specific biomass precursor effluxes were calculated using the measured growth rates and biomass composition incorporated in respective genome-scale models⁵¹.

Organism-specific metabolic models

Organism-specific metabolic networks and carbon mappings were manually curated based on genome-scale metabolic reconstructions⁵¹, the BioCyc database collection (e.g. HumanCyc, EcoCyc, YeastCyc), and standard textbooks. The full set of reactions included in the flux modeling is shown in Supplementary Table 6. Care was taken to avoid reaction inclusion bias by considering all known routes to and from experimentally measureable metabolites and their neighboring compounds in the networks. Reactions and metabolites included in the networks were mapped to their corresponding identification numbers in the Kyoto Encyclopedia of Genes and Genomes (KEGG)⁵², BRaunschweig ENzyme DAtabase (BRENDA)²⁶, and a Biochemical Genetic and Genomic Knowledgebase (BiGG)⁵¹ to facilitate integration among these existing databases.

Metabolic flux analysis including determination of flux ratios with confidence intervals

Using the carbon mapping networks and 13CFLUX2 (www.13cflux.net) package⁵³, we obtained cumulated isotopomer models⁵⁴ for further analysis in Matlab (MathWorks). Under net flux balance constraint, optimal balanced flux distributions (a vector with two entries per reaction, one for the net flux and another for exchange flux; the exchange flux was constrained to be negligible for known strongly thermodynamically forward-driven reactions) were obtained by minimizing the variance-weighted sum of squared residuals between the simulated and experimental i) isotope distributions and ii) uptake and excretion rates using the interior-point algorithm:

$$\underset{v}{min}\sum {\left(\frac{{\mathit{iso}}_{\mathit{exp}}-\mathit{iso}(v)}{s_{\mathit{iso}}}\right)}^2+\sum {\left(\frac{v_{\mathit{exp}}-v}{s_v}\right)}^2$$

ν is flux, iso(ν) is simulated labeling, and s is the measurement standard deviation. Each flux distribution simulated all isotope tracer studies simultaneously for individual organisms. To account for other potential local minima, the non-convex optimization problem was solved starting from over a thousand initial flux sets until similar flux sets that best simulated the experimental data were obtained repeatedly.

To determine confidence intervals, i) the net and the exchange flux for each reaction were each, one-by-one, successively increased or decreased, ii) the other fluxes were again optimized with that one flux fixed, iii) any balanced flux sets where the variance weighted sum of squared residuals did not increase by more than a fixed value (χ²) were accepted⁵⁵, and iv) for those accepted flux sets, forward fluxes, backward fluxes, and their ratios for all reactions were calculated from the resulting net and exchange fluxes. To obtain 95% confidence intervals, the χ² cutoff (1 degree of freedom) was 3.84. Maximum and minimum values (among the accepted flux distributions) of each individual flux and of the forward-to-backward flux ratios are reported as the 95% confidence intervals. The algorithm was scripted in Matlab to run in parallel on Linux clusters and is available as open-source code at https://github.com/PrincetonUniversity/flux-ratio-based-gibbs-energy.

Standard Gibbs free energy

Component contribution²³ was performed in Matlab to calculate standard Gibbs free energy of formation (Δ_fG°′) and reaction (ΔG°′) at physiological ionic strength, pH, and electric potential. Based on extended Debye-Hückel theory, determination of ΔG°′ at physiological ionic strength serves to incorporate the activity coefficients of reactants and products into ΔG°′, thereby allowing calculation of Q based on concentrations not activities. For example, component contribution takes into account the effect of [Mg²⁺] on the ΔG°′ of ATP hydrolysis by using the data from the NIST Thermodynamics of Enzyme-Catalyzed Reactions database regarding the ATP hydrolysis equilibrium constant at typical cellular [Mg²⁺]. Compartment-specific values for ionic strength, pH, and electric potential were employed, where ‘c’ stands for cytosol, ‘e’ for extra-organism, ‘p’ for periplasm, ‘m’ for mitochondria: for E. coli¹⁵, compartment=[‘c’; ‘e’; ‘p’], pH=[7.7; 7.2; 7.2], ionic strength (M)=[0.25; 0.25; 0.25], electric potential relative to cytosol (mV)=[0; 90; 90]⁵⁶; for yeast, compartment=[‘c’; ‘e’; ‘m’], pH=[7.2; 5.4; 7.5], ionic strength (M)=[0.14;0.14;0.14], electric potential relative to cytosol (mV)=[0; 128; −155]⁵; and for iBMK cells, compartment=[‘c’; ‘e’; ‘m’], pH=[7.2; 7.4; 8.0], ionic strength (M)=[0.15;0.15;0.15], electric potential relative to cytosol (mV)=[0; 30; −155]⁵⁷. The sensitivity of ΔG°′ on pH and ionic strength, and the standard error of ΔG°′ are shown in Supplementary Tables 7 and 8. The uncertainties were generally greater than the perturbations of ΔG°′ resulting from changes up to ±0.4 pH and ±0.1 M ionic strength, and therefore, the impact of pH and ionic strength variation within these ranges should minimally affect the subsequent integrative analysis.

Integration of metabolite concentrations and Gibbs free energies

The set of metabolite concentrations ([met]) and reaction free energies (ΔG) associated with central carbon metabolism (CCM; see Supplementary Fig. 4) that best matched i) the directly observed concentrations for measured metabolites ([met]_exp) and ii) the observed cellular ΔG for measured reactions (ΔG_exp) were computed. An important consideration in this calculation is that literature values for ΔG°′ may themselves contain error. In addition, these ΔG°′ values are interrelated, such that ΔG°′ for any sequence of metabolic reactions must be given by the sum of the formation energies of the products minus the formation energies of the reactants. Accordingly, we set out to optimize both metabolite concentrations and formation energies so as to maximize consistency with prior estimates of Δ_fG°′ based on the component contribution method (which itself incorporates prior literature data on ΔG°′) and our experimental observations of metabolite concentrations and cellular reaction free energies. To this end, a quadratic programming problem was formulated with independent variables ln[met] and Δ_fG°′, with the optimization objective of minimizing the departure from the expected Δ_fG°′ and measured ln[met] and ΔG:

$$\underset{ln[\mathit{met}],{\mathrm{\Delta }}_f{G^{\circ }}^{\prime }\in \mathit{CCM}}{min}\frac{1}{N_{\mathit{exp}}^{\mathit{met}}}\sum {\left(\frac{ln{[\mathit{met}]}_{\mathit{exp}}-ln[\mathit{met}]}{s_{\mathit{met}}}\right)}^2+\frac{1}{N_{\mathit{exp}}^{\mathit{for}}}\sum {\left(\frac{{\mathrm{\Delta }}_f{G}_{\mathit{exp}}^{{\circ }^{\prime }}-{\mathrm{\Delta }}_f{G^{\circ }}^{\prime }}{s_{{\mathrm{\Delta }}_{f}G}}\right)}^2+\frac{1}{N_{\mathit{exp}}^{\mathit{rxn}}}\sum {\left(\frac{\mathrm{\Delta }{G}_{\mathit{exp}}-\mathrm{\Delta }G}{s_{\mathrm{\Delta }G}}\right)}^2,$$

• where ΔG = S^T(Δ_fG°′ + RT ln[met]),

• subject to ln[met] ∈ [ln[met]_exp − 2 s_met, ln[met]_exp + 2 s_met],

• ${\mathrm{\Delta }}_f{G^{\circ }}^{\prime }\in \left[{\mathrm{\Delta }}_f{G}_{\mathit{exp}}^{{\circ }^{\prime }}-2s_{{\mathrm{\Delta }}_f{G}^{{\circ }^{\prime }}},{\mathrm{\Delta }}_f{G}_{\mathit{exp}}^{{\circ }^{\prime }}+2s_{{\mathrm{\Delta }}_f{G^{\circ }}^{\prime }}\right]$,

• and ΔG ∈ [ΔG_exp − 2 s_ΔG, ΔG_exp + 2 s_ΔG]

S is the stoichiometric matrix with rows and columns representing individual metabolites and reactions, respectively. ΔG, Δ_fG°′, and ln[met] are vectors of free energy of reaction, standard free energy of formation, and log-concentrations. s refer to the standard errors of the measurements or component contribution estimates. $N_{\mathit{exp}}^{\mathit{for}},N_{\mathit{exp}}^{\mathit{met}}$, and $N_{\mathit{exp}}^{\mathit{rxn}}$ are the number of input metabolite formation energies, experimentally measured metabolite concentrations and ΔG.

For reactions whose ΔG were not precisely determined, ΔG was constrained to be negative in the direction of net flux. For the eukaryotic cells, Δ_fG°′ of TCA metabolites depended on whether they are in cytosol or mitochondria due to pH difference across compartments, and the values of Δ_fG°′ calculated for mitochondria were used. Inorganic phosphate concentrations were input as follows: 20 mM in E. coli⁵⁸; 50 mM in yeast⁵; and 5 mM in mammalian iBMK cells⁵⁹. Mitochondrial coenzyme A concentration was input as 5 mM⁶⁰. The inorganic phosphate and coenzyme A concentrations were allowed to vary within 20% of these values.

Confidence intervals of metabolite concentrations and reaction free energies

The lower and upper bounds for individual metabolite concentrations were determined by searching within the experimentally measured metabolite concentration 95% confidence interval for the minimum and maximum concentrations that also resulted in ΔG falling within its measured 95% confidence interval. Since ΔG is linear with respect to ln[met], concentration lower bounds were obtained by solving the following linear programming problem¹⁷:

$$\underset{ln[\mathit{met}]\in \mathit{CCM}}{min}ln[\mathit{met}],$$

• subject to ln[met] ∈ [ln[met]_exp − 2 s_met, ln[met]_exp + 2 s_met],

• and ΔG ∈ [ΔG_exp − 2 s_ΔG, ΔG_exp + 2 s_ΔG],

• where ΔG = S^T(Δ_fG°′ + RT ln[met])

For upper bound calculation, $\underset{ln[\mathit{met}]\in \mathit{CCM}}{max}ln[\mathit{met}]$ was solved with the same set of constraints.

Similarly, reaction free energy lower bounds were obtained by solving:

$$\underset{ln[\mathit{met}]\in \mathit{CCM}}{min}\mathrm{\Delta }G,$$

• where ΔG = S^T(Δ_fG°′ + RT ln[met]),

• subject to ln[met] ∈ [ln[met]_exp − 2 s_met, ln[met]_exp + 2 s_met],

• and ΔG ∈ [ΔG_exp − 2 s_ΔG, ΔG_exp + 2 s_ΔG]

For upper bound calculation, $\underset{ln[\mathit{met}]\in \mathit{CCM}}{max}\mathrm{\Delta }G$ was solved with the same set of constraints. The linear programming problem was solved using Matlab linprog function (interior point algorithm).

Michaelis and inhibitor dissociation constants, K_m and K_i

The Python implementation of the Simple Object Access Protocol (SOAPpy) was employed to extract the K_m and K_i values in E. coli, S. cerevisiae, Mus musculus, and Homo sapiens from BRENDA²⁶. The exported data were further processed to filter out entries for mutant enzymes. The parameters for mammalian cells are from enzymes in Mus musculus whenever possible, but otherwise in Homo sapiens. When multiple entries for the same enzyme-metabolite pair were available, its K_m or K_i was represented by their geometric mean.

Code availability

The code used for flux and flux ratio calculation, metabolite concentration and Gibbs energy integration, and confidence interval determination as well as the SOAPpy script, the carbon mapping, and cumulated isotopomer models are available on the GitHub public repository: https://github.com/PrincetonUniversity/flux-ratio-based-gibbs-energy