Identifying Activation Centers with Spatial Cox Point Processes Using FMRI Data

Abstract

We developed a Bayesian clustering method to identify significant regions of brain activation. Coordinate-based meta data originating from functional magnetic resonance imaging (fMRI) were of primary interest. Individual fMRI has the ability to measure the intensity of blood flow and oxygen to a location within the brain that was activated by a given thought or emotion. The proposed method performed clustering on two levels, latent foci center and study activation center, with a spatial Cox point process utilizing the Dirichlet process to describe the distribution of foci. Intensity was modeled as a function of distance between the focus and the center of the cluster of foci using a Gaussian kernel. Simulation studies were conducted to evaluate the sensitivity and robustness of the method with respect to cluster identification and underlying data distributions. We applied the method to a meta data set to identify emotion foci centers.

1 Introduction

Functional neuroimaging is a new branch within the neurosciences that is being credited with advancing our understanding of the human brain and its processes in neuroscientific research related to public health. Accurately identifying activated foci or regions in the brain in association with an outcome of interest is crucial in terms of disease prediction and prevention. Functional magnetic resonance imaging (fMRI) is the most widely used method for this type of study. FMRI is able to measure changes in tissue perfusion, blood oxygenation, and blood volume [1]. The amount and location of these changes are measured when subjects are under some situational environment or experiment that provokes a thought, emotion, or action. Brain activation recorded in fMRI happens before, during, and after the expected stimulation and thus gives rise to background noise or simulation occurring that is not due to the stimulant and therefore must decipher which areas of activation are statistically greater than the general mass activity or noise [2]. Furthermore, because of the high cost, fMRI studies tend to have very small number of participants (less than 20) which causes inflated type II error (low power) and lack of reproducibility [3]. To increase sample size and testing power, meta analyses are being implemented to summarize these smaller individual studies ([4], [5], [6], [7], [8]). Two types of meta analyses are commonly used, intensity based meta analysis (IBMA) and coordinate based meta analysis (CBMA) [7], corresponding to the two types of individual fMRI data with one represented a statistical image/map (intensity based) and the other as a coordinate system (coordinate based), respectively. Our primary focus is on the more commonly used coordinate based meta analysis data [1].

Meta data of CBMA only supplies the (x, y, z) coordinates or foci (focus-single) of peak activations. The activation magnitude may or may not be given [7]. The overall aim of CBMA is to identify areas within the brain that are statistically activated during a given stimulant. A variety of statistical methods for analyzing CBMA have been proposed: activation likelihood estimation (ALE) ([6], [9], [10], [11], [12]), kernel density analysis (KDA) ([5], [13], [14]), and a hierarchical spatial point process model proposed in [8].

Activation likelihood estimation (ALE), based on the assumption that all foci are independent, divides the brain into a smaller cubes called voxels. The probability of a foci being within a particular voxel is modeled using a 3-D Gaussian function. All probabilities are summed for each voxel resulting in an activation likelihood estimate, which is interpreted that at least one of the activated foci is within that voxel ([6], [9], [10]). Advancements have been made to improve this original work such as methods to determine the probability distribution size, estimating clusters between studies instead of within, and controlling for false discovery ([10], [11], [12]). The need for these advancements indicates the results can vary due to voxel size, Gaussian kernel standard deviation, and controlling for multiple testing.

Kernel density analysis (KDA), similar to ALE in that it treats each foci independent and divides the brain into voxels, implements a smoothing kernel which is a spherical indicator function with a given radius for each foci. After the smoothing, a smoothed histogram reflects the estimated density of each activation location in each voxel ([13], [15]). Advancements have been made to treat studies as a unit of analysis rather than foci (multilevel KDA). In this case, the proportion of studies becomes the focus rather than the number of foci that are activated in a specific region of the brain [14]. Activation peaks are nested within studies when the test statistics are calculated which allows each study to contribute proportionally ([5], [14]). Although this multilevel KDA made significant improvements, the analysis is still driven by voxel size, radius size for the smoothing spherical kernel, and an underlying distribution assumption [7].

The hierarchical spatial point process model proposed by Kang et al. [8] is formulated from a marked Cox process and identifies population centers that represent the most likely activation location of a foci across studies. The model is comprised of three levels. The first layer models the individual foci, assumed independent, by clustering with an independent cluster process controlled by a random intensity function. At this level, two types of foci are considered: singly and multiply reported, which were assigned a ’mark’ as to identify the specific types. The second level models the latent study activation center, again assumed independent and clustered by an independent cluster process and driven by a random intensity function. These two layers are both assumed conditional on the realization of latent study activation centers or latent population centers, respectively, and normally distributed. Also, both layers allow for individual foci and study centers to be singleton clusters and model this by an independent homogeneous Cox process. The third and final level models the latent population centers with a homogeneous Cox process controlled by a homogeneous random intensity. This method has the power to identify clusters at different levels with final focus on the population level. However, assuming the realization of both the foci and studies to be normally distributed limits the model to only identify clusters of a certain distribution or shape and therefore can miss or mis-cluster foci.

In this article, we take a different route and propose a Bayesian hierarchical spatial Cox point process model [16] to identify individual foci clusters while adjusting study effects using meta data. The method incorporates two nesting Dirichlet processes (DPs) [17]. To adjust for study effect, we implemented a Dirichlet process because of its ability to describe abnormal studies effects. The Gaussian kernel is utilized to measure the contribution of a focus with respect to a cluster center to the intensity of the Cox point process. The foci clusters are identified after adjusting for study effect and through a Dirichlet process as well. Via these two DPs, we gain the potential to describe possibly more complicated patterns of spatial effects on the intensity. This approach is different from the method by [8] in that the focus there was at the population level, while the proposed method is on clustering individual foci while adjusting study effect. Both ALE and KDA methods, on the other hand, are voxel based approaches with no focus on clustering and are conditional on those specific brain locations. Our method is a method for clustering. Compared to the existing clustering methods (such as the K-means approach), the proposed approach is able to incorporate prior knowledge of study effect into the clustering process, has the potential to incorporate other factors, and can identify foci centers with irregular shapes.

Model details including prior, joint posterior, and conditional posterior distributions and the algorithm applied to exercise the Dirichlet process, are discussed in section 2. Section 3 presents 7 simulation studies and section 4 describes an application of the method to a meta data set, which was discussed in [8] and [5]. Finally, section 5 presents a discussion of the findings, thoughts on our model, and future research.

2 Model

2.1 Notation

The general spatial Poisson point process is defined on a space M, such that M ⊆ ℜ³ and driven by a locally integrable intensity function, ν: M → [0, ∞) and ∫_R ν(ξ)dξ < ∞ for all bounded R ⊆ M [16]. Define an intensity measure μ(R) = ∫_R ν(ξ)dξ, which is also locally finite for bounded R ⊆ M and diffuse, μ(ξ) = 0 for ξ ∈ M [16]. By letting this intensity function be a realization of a nonnegative random field, Z = {Z(ξ) : ξ ∈ M}, this extends to a Cox process. Straightforwardly, by restricting this Cox process to |R| < ∞ the following density function can be attained [16]:

$$f(x)=\mathit{exp}\left\{\mid R\mid -{\int }_{R}Z(\xi )d\xi \right\}\prod _{\xi \in x}Z(\xi ).$$

Due to the process’ ability to model and cluster within spatial randomness, we can directly apply this model to any spatial data but in particular, CBMA data. Let the intensity measure be driven by multiplicative of a Gaussian kernel which is bounded by the brain space B, such that B ⊆ ℜ³ and |B| < ∞. Furthermore, let s_ij = (x, y, z) denote a single focus which represents a talairach or Montreal Neurological Institute (MNI) coordinate in the brain, for sub-study j in study i, i = 1, …, I, j = 1, …, J_i. We have ${\sum }_{i=1}^I{J}_i=n$, where n is the total number of observed foci. Denoted by s = s_1,1…s_I,JI represents all foci in the CBMA study such that s ⊂ B. The density function above can now be redefined as:

$$\begin{array}{l}f(\mathit{s})=E\left[\mathit{exp}\left\{\mid B\mid -{\int }_B\mathit{exp}(a_{ij}K(s_{ij}))d{s}_{ij}\right\}\prod _{s_{ij}\in \mathit{s}}K(s_{ij})\right]\\ \propto \mathit{exp}\left\{\mid B\mid -{\int }_B\mathit{exp}(a_{ij}K(s_{ij}))d{s}_{ij}\right\}\prod _{s_{ij}\in \mathit{s}}K(s_{ij}),\end{array}$$

where a_ij allows multiplicative focus impact on the intensity. We let the contribution of each focus be comprised of two components: expected 3-D individual focus effect (θ_ij) and expected 3-D study effect (p_i). Consequently, the Gaussian kernel is defined as K(s_ij) = exp (−||s_ij − p_i − θ_ij ||²/ρ), where ρ is a scale parameter. To avoid the unidentifiability problem due to the inclusion of a_ij, we set ρ = 1. This then yields the probability density function:

$$\begin{array}{l}f(\mathit{s})=\mathit{exp}\left[-{\int }_B\mathit{exp}\left(a_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right)d{s}_{ij}\right]\times \prod _{s_{ij}\in \mathit{s}}\mathit{exp}\left[a_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right]\\ \approx \mathit{exp}\left[-\frac{{\sum }_B\mathit{exp}\left(a_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right)}{n}+\sum _{s_{ij}\in \mathit{s}}{a}_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right].\end{array}$$

To identify foci clusters and centers, we assume each realization s_ij is from the following mixture

$$f(\mathit{s})\propto \sum _{c=1}^C\mathit{exp}\left(-{\int }_B\mathit{exp}\left[a_c\mathit{exp}\left\{a_c\mathit{exp}\left(-\frac{{\Vert s_{ij}-p_i-{\theta }_c\Vert }^2}{\rho }\right)\right\}\right]d{s}_{ij}\right),$$

after adjusting for study effect. To infer the clusters and their centers, we implement a fully Bayesian approach. This approach will also allow us to incorporate prior knowledge on the strength of study effect, which enables a proper adjustment for study effect and avoids biased inferences on the locations of cluster centers.

2.2 Prior and hyperprior distributions

Following the standard Bayesian framework, all estimable parameters are assigned a prior distribution. We assume study effect, p_i, follows distribution G₁, which is generated from a Dirichlet process (DP), p_i ~ G₁ and G₁ ~ DP(α₁, G₀₁) where α₁ is a precision parameter and G₀₁ is a base distribution. The precision parameter controls the aggregation of G₁ around G₀ [17]. This setting results in a conditional prior for p_i, $p_i\mid p^{(i)}~\frac{{\alpha }_1}{({\alpha }_1+I-1)}{G}_{01}(p_i)+\frac{1}{({\alpha }_1+I-1)}{\sum }_{q=1,q\ne i}^I{\delta }_{p_q}(p_i)$, where p⁽ⁱ⁾ represents all study effects except for study i and δ_pq (p_i) denotes a unit point mass at p_i = p_q [17]. The base distribution, G₀₁, is chosen as a 3-dimensional truncated multivariate normal distribution, TMV N₃(μ, Σ₁, a, b), where the hyper-prior distribution for μ is assumed to be multivariate normal, $\mathit{\mu }~{\mathit{MVN}}_3({\mathit{m}}_{\mathbf{0}},{\sigma }_{\mu }^2{I}_3)$ with m₀ = 0 and I₃ being a 3-dimensional identity matrix. Parameter ${\sigma }_{\mu }^2$ can take small values, e.g., ${\sigma }_{\mu }^2=0.1$, assuming a apriori minimal study effect. Note that m₀ can choose a different value based on prior knowledge on study effect. Parameters ${\mathrm{\sum }}_1={\sigma }_1^2{I}_3$ and ${\sigma }_1^2$ follows an inverse gamma distribution with shape and scale parameters e and f, i.e., ${\sigma }_1^2~IG(e,f)$, a = r_a(|R_x|, |R_y|, |R_z|)′ representing the lower limit and b = −r_b(|R_x|, |R_y|, |R_z|)′ representing the upper limit, where r_a and r_b control the amount of truncation, set at 15%, and |R_d| represents the absolute value of the range of data for coordinate d. The truncation was selected based on the assumption of small study effects and can be adjusted based on prior beliefs. The shape and scale parameters (e and f) in the inverse gamma distributions are set at both of being 0.5, IG(0.5, 0.5), following the suggestion by Kass and Wasserman [18]. This prior, approximately centered at 1 and termed as “unit-information prior”, allows the conditional posterior distribution of ${\sigma }_1^2$ to be more influenced by data. On the other hand, when prior knowledge for study effect is clearer, an informative prior may be preferred. For θ_ij, we follow similar choices for p_i and assume θ_ij ~ G₂ and G₂ ~ DP(α₂, G₀₂), with a base distribution of G₀₂ = TMV N₃(c₀, Σ₂, c, d) where c₀ takes the median of the observed data in each dimension, ${\mathrm{\sum }}_2={\sigma }_2^2{I}_3,{\sigma }_2^2~IG(g,h)$ with g = 0.5 and h = 0.5, c = (min(x), min(y), min(z))′ and d = (max(x), max(y), max(z))′ where min(d) represents the minimum value for coordinate d and max(d) represents the maximum value to coordinate d. In both Dirichlet processes, we assume the precision parameters are known. We discuss their selection in Section 2.5. Lastly, the prior for multiplicative effect a_ij is conditional on identified clusters and $a_{ij}\mid {\theta }_c~N(0,{\sigma }_a^2)$ with ${\sigma }_a^2$ known and large.

2.3 Conditional posterior distributions and posterior computing

Posterior inference of p_i, θ_ij, and a_ij is obtained by successfully sampling values from their full conditional posterior distributions through the Markov Chain Monte Carlo (MCMC) simulations, specifically, the Gibbs sampling scheme. With s representing observed CBMA data, the joint posterior distribution of all the parameters is, up to a normalizing constant:

$$\begin{array}{l}P(p_i,{\theta }_{ij},a_{ij},\mathit{\mu },{\mathrm{\sum }}_1,{\alpha }_1,{\mathrm{\sum }}_2,{\alpha }_2\mid \mathit{s})\propto P(\mathit{s}\mid p_i,{\theta }_{ij},a_{ij},\mathit{\mu },{\mathrm{\sum }}_1,{\alpha }_1,\\ \times {\mathrm{\sum }}_2,{\alpha }_2)\prod _i^{I}P(p_i\mid G_1)P(G_1\mid {\alpha }_1,G_{01})\\ \times P(p_i\mid G_{01};\mathit{\mu },{\mathrm{\sum }}_1)P(\mathit{\mu })P({\mathrm{\sum }}_1)\\ \times \prod _{c\in C}\prod _{i,j\in c}P(a_{ij}\mid {\theta }_{ij})\prod _{j\in J_i}P({\theta }_{ij}\mid G_2)\\ \times P(G_2\mid {\alpha }_2,G_{02})P({\theta }_{ij}\mid G_{02};{\mathit{c}}_{\mathbf{0}},{\mathrm{\sum }}_2)P({\mathrm{\sum }}_2),\end{array}$$

from which full conditional posteriors for p_i, θ_ij, a_ij, along with their hyper-priors are obtained and listed below. In the following expressions, “·” represents all other parameters,

$$\begin{array}{l}P(p_i\mid s_{ij},{\theta }_{ij},·)\propto P(s_{ij}\mid p_i,{\theta }_{ij},·)P({\theta }_{ij}\mid ·)P(p_i\mid G_1)P(G_1\mid {\alpha }_1,G_{01})\\ =\mathit{exp}\left[-\frac{{\sum }_B\mathit{exp}\left(a_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right)}{n}+\sum _{j=1}^{J_i}{a}_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right]\\ \times \left\{\frac{{\alpha }_1{\mathit{TMVN}}_3(\mathit{\mu },{\mathrm{\sum }}_1)}{({\alpha }_1+I-1,\mathit{a},\mathit{b})}+\frac{{\sum }_{q=1,q\ne i}^I{\delta }_{p_q}(p_i)}{({\alpha }_1+I-1)}\right\},\\ P(\mathit{\mu }\mid {\mathrm{\sum }}_1,p_i,·)\propto \prod _i^{I}P(p_i\mid G_{01};\mathit{\mu },{\mathrm{\sum }}_1)P({\mathrm{\sum }}_1)P(\mathit{\mu })\\ =\mathit{exp}\left[-\frac{1}{2}\left\{\prod _i^I{(p_i-\mathit{\mu })}^{\prime }{\mathrm{\sum }}_1^{-1}(p_i-\mathit{\mu })+{(\mathit{\mu }-{\mathit{m}}_{\mathbf{0}})}^{\prime }{({\sigma }_{\mu }^2{I}_3)}^{-1}(\mathit{\mu }-{\mathit{m}}_{\mathbf{0}})\right\}\right]\\ \mathit{\mu }\mid ·~{\mathit{TMVN}}_3({({\sigma }_{\mu }^{-2}+I{\sigma }_1^{-2})}^{-1}(I{\sigma }_1^{-2}\overline{p}+{\mathit{m}}_{\mathbf{0}}{\sigma }_{\mu }^{-2}),{({\sigma }_{\mu }^{-2}+I{\sigma }_1^{-2})}^{-1}{I}_3,\mathit{a},\mathit{b}),\\ P({\sigma }_1^2\mid \mathit{\mu },p_i,·)\propto \prod _i^{I}P(p_i\mid G_{01};\mathit{\mu },{\mathrm{\sum }}_1)P(\mathit{\mu })P({\mathrm{\sum }}_1)\\ =\mathit{exp}\left[-\frac{1}{2}\left\{\sum _i^I{(p_i-\mathit{\mu })}^{\prime }{({\sigma }_1^2{I}_3)}^{-1}(p_i-\mathit{\mu })\right\}+-\frac{f}{{\sigma }_1^2}\right],\\ {\sigma }_1^2\mid ·~IG\left(\frac{I}{2}+e,\frac{{\sum }_i^I\left\{{\Vert p_i-\mathit{\mu }\Vert }^2\right\}}{2}+f\right),\\ P({\theta }_{ij}\mid s_{ij},p_i,·)\propto P(s_{ij}\mid {\theta }_{ij},p_i,·)P(p_i\mid ·)P({\theta }_{ij}\mid G_2)P(G_2\mid {\alpha }_2,G_{02})\\ =\mathit{exp}\left[-\frac{{\sum }_B\mathit{exp}\left(a_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right)}{n}+a_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}\right]\\ \times \left\{\frac{{\alpha }_2{\mathit{TMVN}}_3({\mathit{c}}_{\mathbf{0}},{\mathrm{\sum }}_2,\mathit{c},\mathit{d})}{({\alpha }_2+n-1)}+\frac{{\sum }_{q=1,q\ne ij}^n{\delta }_{{\theta }_q}({\theta }_{ij})}{({\alpha }_2+I-1)}\right\},\\ P({\sigma }_2^2\mid {\mathit{c}}_{\mathbf{0}},{\theta }_{ij},·)\propto \prod _i^I\prod _j^{J_i}P({\theta }_{ij}\mid G_{02};{\mathit{c}}_{\mathbf{0}},{\sigma }_2^2)P({\sigma }_2^2)\\ =\mathit{exp}\left[-\frac{1}{2}\left\{\sum _i^I\sum _j^{J_i}{({\theta }_{ij}-{\mathit{c}}_{\mathbf{0}})}^{\prime }{({\sigma }_2^2{I}_3)}^{-1}({\theta }_{ij}-{\mathit{c}}_{\mathbf{0}})\right\}+-\frac{h}{{\sigma }_2^2}\right],\\ {\sigma }_2^2\mid ·~IG\left(\frac{n}{2}+g,\frac{{\sum }_{i,j}^n{\Vert {\theta }_{ij}-{\mathit{c}}_{\mathbf{0}}\Vert }^2}{2}+h\right),\\ P(a_{ij}\mid s_{ij},p_i,{\theta }_{ij},c,·)\propto \prod _{i,j\in c}P(s_{ij}\mid {\theta }_{ij},p_i,·)P({\theta }_{ij}\mid c,·)\times P(p_i\mid ·)P(a_{ij})\\ =\mathit{exp}[-\frac{{\sum }_B\mathit{exp}(a_{ij}}{n}\times \frac{\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\})}{n}+\sum _{i,j\in c}{a}_{ij}\mathit{exp}\left\{-\frac{{\Vert s_{ij}-p_i-{\theta }_{ij}\Vert }^2}{\rho }\right\}-\frac{{(a_{ij})}^2}{2{\sigma }_a^2}].\end{array}$$

Non-standard conditional posteriors, a_ij, are updated using the Metropolis-Hastings steps in the Gibbs sampler. The parameters p_i and θ_ij are sampled via using an algorithm introduced in [19] that is discussed below.

The algorithm, specifically algorithm 8, noted in [19], is appropriate for models with non-conjugate priors. It introduces m auxiliary parameters to represent potential values for parameters of interest, i.e., p_i or θ_ij, that are not associated with any other observations [19]. The original algorithm for updating cluster assignments, c, is as follows:

• Let the state of the Markov chain consist of c = {c₁, …, c_n} and Φ = (ϕ_c; c ∈ c₁, …, c_n) with ϕ_c denoting cluster parameters, e.g. θ_c in our application. Repeatedly sample as follows:

• For i = 1, …, n: Let k⁻ be the number of distinct c_l for l ≠ i, and h = k⁻ +m. Label these c_l with values in {1, …, k⁻}. If c_i = c_l for some l ≠ i, draw values independently from base distribution G₀ for those ϕ_c for which k⁻ < c ≤ h. If c_i ≠ c_l for all l ≠ i, let c_i have the label k⁻+1, and draw values independently from G₀ for those ϕ_c for which k⁻+1 < c ≤ h. Draw a new value for c_i from {1, …, h} using the following probabilities:

  $$P(c_i=c\mid c_{-i},y_i,{\varphi }_1,\dots ,{\varphi }_h)=\{\begin{array}{ll}\frac{n_{-i,c}}{n-1+\alpha }F(y_i,{\varphi }_c)\hfill & \text{for}1\le c\le k^{-}\hfill \\ \frac{(\alpha /m)}{n-1+\alpha }F(y_i,{\varphi }_c)\hfill & \text{for}{k}^{-}<c\le h\hfill \end{array},$$

  where F(y_i, θ_c) is the likelihood with θ_c and observation i, y_i, involved. In our case, it is s_ij.

• Where n_−i,c is the number of c_l for l ≠ i that are equal to c, and b is the appropriate normalizing constant. Change the state to contain only those ϕ_c that are now associated with one or more observation.

• For all c ∈ {c₁, …, c_n}: Draw a new values from ϕ_c|y_i such that c_i = c, or perform some other update to ϕ_c that leaves this distribution invariant. [19]

To illustrate, F(y_i, ϕ_c) and P(ϕ_c|y_i) in our application are F(s_ij, θ_c) for θ_ij and P(θ_c|s_ij, c, ·), respectively, with:

$$F(s_{ij},{\theta }_c)=\mathit{exp}\left\{-{\int }_B\left(\mathit{exp}\left\{a_{ij}\mathit{exp}\left[-\frac{{\Vert s_{ij}-p_i-{\theta }_c\Vert }^2}{\rho }\right]\right\}\right)d{s}_{ij}+a_{ij}\mathit{exp}\left[-\frac{{\Vert s_{ij}-p_i-{\theta }_c\Vert }^2}{\rho }\right]\right\},$$ (1)

and

$$\begin{array}{l}P({\theta }_c\mid s_{ij},c,·)\propto \mathit{exp}\{-\frac{1}{n}\sum _B\left(\mathit{exp}\{a_{ij}\times \mathit{exp}\left[-\frac{{\Vert s_{ij}-p_i-{\theta }_c\Vert }^2}{\rho }\right]\}\right)\\ +\sum _{s_{ij}\in c}{a}_{ij}\mathit{exp}\left[-\frac{{\Vert s_{ij}-p_i-{\theta }_c\Vert }^2}{\rho }\right]\}\\ \times \mathit{exp}\left(-\frac{1}{2}{({\theta }_c-{\mathit{c}}_{\mathbf{0}})}^{\prime }{\mathrm{\sum }}_2^{-1}({\theta }_c-{\mathit{c}}_{\mathbf{0}})\right),\end{array}$$ (2)

where θ_c is the center for individual foci cluster c.

Similar expressions as in (1) and (2) are applied to p_i. To accommodate the 3-D nature of our data and to improve sampling efficiency, we modified algorithm 8 by introducing auxiliary parameters into one, two, or three dimensions of the centers at the current MCMC iteration. Specifically, we allowed m=7 auxiliary parameters. For example, let ${\theta }_{c_i}=\{{\varphi }_{c_i}^{(x)},{\varphi }_{c_i}^{(y)},{\varphi }_{c_i}^{(z)}\}$ be the current center for focus i assigned to cluster c. The 7 auxiliary parameters are every combination of the current cluster center and a newly generated center ${\varphi }_0=\{{\varphi }_0^{(x)},{\varphi }_0^{(y)},{\varphi }_0^{(z)}\}$ from G₀₂:

• ( ${\varphi }_{c_i}^{(x)},{\varphi }_{c_i}^{(y)},{\varphi }_0^{(z)}$) updating z-dimension only

• ( ${\varphi }_{c_i}^{(x)},{\varphi }_0^{(y)},{\varphi }_{c_i}^{(z)}$) updating y-dimension only

• ( ${\varphi }_0^{(x)},{\varphi }_{c_i}^{(y)},{\varphi }_{c_i}^{(z)}$) updating x-dimension only

• ( ${\varphi }_{c_i}^{(x)},{\varphi }_0^{(y)},{\varphi }_0^{(z)}$) updating y and z-dimensions only

• ( ${\varphi }_0^{(x)},{\varphi }_{c_i}^{(y)},{\varphi }_0^{(z)}$) updating x and y-dimensions only

• ( ${\varphi }_0^{(x)},{\varphi }_0^{(y)},{\varphi }_{c_i}^{(z)}$) updating x and y-dimensions only

• ( ${\varphi }_0^{(x)},{\varphi }_0^{(y)},{\varphi }_0^{(z)}$) updating all dimensions only.

By designing the auxiliary parameters as above, i.e., based on the current sampled values, the probability of making a movement is improved compared to randomly generating the auxiliary parameters from the base distribution. To further speed up the convergence, we limit the choice of auxiliary parameters within the defined brain space. All these efforts are aimed to improve MCMC sampling efficiency and achieve quick convergence.

2.4 Determining the clusters

To estimate cluster centers and infer cluster assignment, we implement the least-squared Euclidean distance method introduced in [20], and outline below.

1. After the MCMC burn-in, continue the MCMC simulations for an additional W iterations. Let A denote an n × n matrix. The (i, j)^th entry of A is the proportion of iterations such that foci i and j (i, j = 1, …, n) are in the same cluster. The matrix A is referred to as an averaged clustering matrix.

2. Continue to run an additional F iterations of the MCMC simulations. For each iteration,

   1. form an n×n matrix composed of indicators of clustering for that particular iteration. For instance, if foci i and j are in one cluster, then the (i, j)^th entry is 1; otherwise, it is zero.

   2. calculate the Euclidean distance between the matrix formed above and the averaged clustering matrix A.

3. Sort the Euclidean distances obtained from the F iterations, and the final selection on the number of clusters is in favor of simpler clusters and relatively small Euclidean distances. The parameters will then be inferred accordingly based on the identified clusters.

Determining the clusters in this way enable us to incorporate information collected in all the iterations after burn-in [20]. The cluster patterns to be inferred and summarized will focus on individual foci clusters as they are our primary interest.

2.5 Selection of α

The specification of α can have a potentially significant effect on the number of clusters identified due to its direct impact on the aggregation of G about G₀. A smaller choice of α places less weight upon the base distribution, resulting in a smaller number of clusters. The extent of this sensitivity and various ways to estimate α have been discussed rigorously in the literature [21], [22], [23], but so far an objective and efficient method for determining α is not available. Instead, given the importance of α, we decide to select α based on information in the data, i.e., posterior joint likelihood of the parameters. Specifically, the choice of α₁ for p_i and α₂ for θ_ij were selected iteratively based on a grid search on a set of possible values for α₁ and α₂ that minimize and stabilize the deviance information criterion (DIC) [24].

3 Inference

3.1 Simulation designs

Simulations were performed to demonstrate and assess the proposed method. In total, we considered 50 studies each with 10 foci or sub-studies. Three individual foci clusters are simulated centered at (1,1,1), (2,2,2), and (4,4,4) covering 150, 150, and 200 foci, respectively. Two study centers are assumed with centers held at (0.1, 0.1, 0.1) and (0.4, 0.4, 0.4) with each including 25 studies. We considered the following four scenarios:

1. The first scenario is used to demonstrate the proposed method. We simulate data via multivariate normal with mean at the individual foci centers and variance small Σ = 0.002I₃ (i.e., the standard deviation is 0.045). In the fourth scenario below, we assess the robustness of the method with respect to variations in data.

2. The second scenario is to demonstrate its ability to cluster outliers. We follow the same setting as in scenario 1) but added an additional focus in the third individual foci cluster located in the right 5% tail of a multivariate normal with mean (4, 4, 4) and variance as in scenario 1.

3. It is important to examine the robustness of the method with respect to abnormal patterns. We follow the same scenarios as in 1) to simulate clusters 1 and 2. Cluster 3 is simulated using truncated normal distribution with mean c(4, 4, 4) and variance 0.002I₃. The lower bound is set at c(1, 1, 1) and upper bound at ∞.

4. It is often that the boundaries between clusters are not clear due to large variance. The last scenario is aimed to assess the sensitivity of the method when the variance increases. Besides Σ = 0.002I₃, we considered additional four levels of Σ: Σ = 0.01I₃, 0.05I₃, 0.1I₃, and 0.2I₃. Other settings are as in scenario 1).

In total, 100 Monte Carlo (MC) replicates are generated under each scenario. For each setting, the values of α₁ and α₂ are determined using the method discussed in Section 2.5 based on one randomly selected MC replicate. In total, 3,500 converged MCMC iterations are used for this purpose. After α₁ and α₂ are determined, for each data set, we used 1,500 as burn in iterations, 2,500 iterations to determine the average clustering matrix, and 1,000 additional iterations to infer the clusters and individual foci cluster centers.

Three statistics are used to assess the method: sensitivity, specificity, and percentage of correct clustering. Sensitivity is defined per cluster as the proportion of foci that are correctly assigned to that given cluster, Se=TP/(TP+FN) and specificity is defined per cluster as the proportion of foci that are correctly not assigned to a cluster, Sp=TN/(TN+FP). In these definitions, true positive (TP) denotes that a focus in a respective cluster is also assigned to that cluster, false negative (FN) denotes that a focus is in a respective cluster but not assigned to that cluster, true negative (TN) is a focus that is not in the respective cluster and not assigned to that cluster, and false positive (FP) denotes a focus that is not in the respective cluster but assigned to that cluster. Percentage of correct clustering is an overall measure defined as the proportion of foci that are correctly clustered. Note that the definition of correctness takes into account both TP and TN. The program to implement the method was written in R and the authors will gladly provide the programs to researchers upon request.

3.2 Results

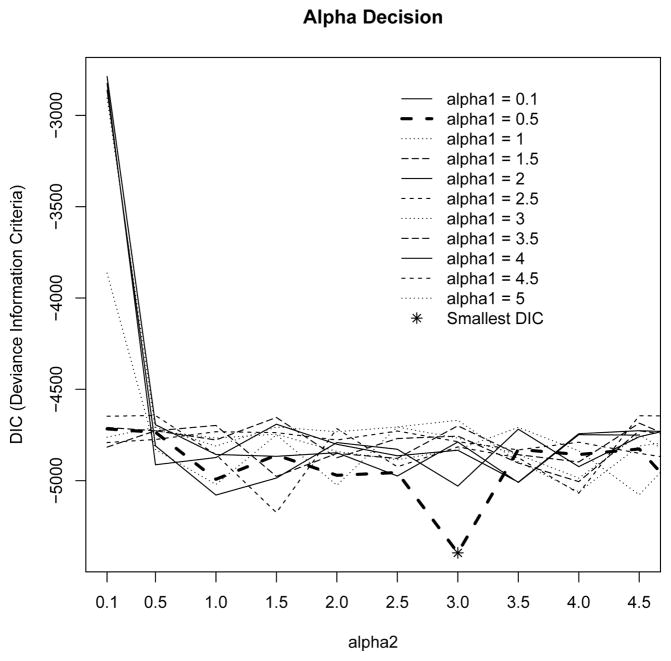
To illustrate the choice of α₁ and α₂ via grid search, we use data generated from scenario 1). As indicated in Figure 1, DIC is stabilized in all situations, and the optimal choice for α₁ and α₂ is α₁ = 0.1 and α₂ = 3. These two precision parameters are then utilized in all simulated data generated under scenario 1) to infer the individual foci clusters. Our further simulations indicate that neighboring values of the selected α₁ and α₂ in general give consistent findings.

Fig. 1.

Example of grid search for selection of α₁ and α₂ based on deviance information criterion.

Table 1 summaries the findings on individual foci cluster identification and the quality of the identified clusters. Overall, the method is robust with resect to outliers, skewness, and large variation in each foci clusters. Among the 100 MC replicates, the proposed method correctly identified clusters in at least 89% of the replicates across all scenarios except for the situation of the largest variance (0.2I₃), in which case the percentage of correct identification is still high enough, 80%. As variances increase, the sensitivity and correctness decrease. This is expected given the potential that two clusters may overlap as variances get large. Unlike variances, outliers and skew foci cluster patterns do not impact the quality of identified foci clusters; sensitivity, specificity, and percentage of correct foci cluster identification are all high (Table 1).

TABLE 1.

Summary Statistics of Clustering Results under Different Simulation Scenarios (Simulated Data).

Scenario:	Median Num. of Clusters (SD)*	Cluster index	Average Sensitivity (SD)*	Average Specificity (SD)*	Average % Correctness rate (SD)*
Normal	** IC: 4 (0.9)	1	0.99 (0.01)	1.00 (0.00)	99.00 (1.00)
		2	0.99 (0.01)	1.00 (0.00)
		3	1.00 (0.00)	1.00 (0.00)
	** SC: 2 (0.9)	1	0.98 (0.04)	1.00 (0.00)	98.00 (5.00)
		2	0.97 (0.09)	1.00 (0.01)
Outlier	IC: 4 (0.82)	1	0.99 (0.00)	1.00 (0.00)	100.00 (0.00)
		2	0.99 (0.01)	1.00 (0.00)
		3	1.00 (0.00)	1.00 (0.00)
	** SC: 2 (0.82)	1	0.95 (0.12)	1.00 (0.00)	95.00 (7.00)
		2	0.96 (0.10)	1.00 (0.01)
Skewed	IC: 3 (0.42)	1	1.00 (0.00)	1.00 (0.00)	100.00 (0.00)
		2	1.00 (0.00)	1.00 (0.00)
		3	1.00 (0.00)	1.00 (0.00)
	SC: 4.5 (0.42)	1	0.85 (0.18)	1.00 (0.00)	85.00 (12.00)
		2	0.85 (0.16)	1.00 (0.00)
Large1	IC: 3 (0.41)	1	0.92 (0.27)	0.96 (0.11)	90.00 (19.00)
		2	0.94 (0.24)	0.96 (0.10)
		3	0.85 (0.31)	0.93 (0.17)
	SC: 4 (0.41)	1	0.84 (0.18)	1.00 (0.02)	85.00 (12.00)
		2	0.85 (0.16)	1.00 (0.02)
Large2	IC: 3 (0.45)	1	0.99 (0.01)	1.00 (0.00)	100.00 (0.00)
		2	0.99 (0.01)	1.00 (0.00)
		3	1.00 (0.00)	1.00 (0.00)
	SC: 2 (0.45)	1	0.99 (0.02)	0.99 (0.02)	99.00 (2.00)
		2	0.99 (0.03)	1.00 (0.01)
Large3	IC: 3 (0.44)	1	0.97 (0.1)	0.93 (0.12)	89.00 (17.00)
		2	0.96 (0.14)	0.93 (0.11)
		3	0.78 (0.4)	0.98 (0.08)
	SC: 4 (0.44)	1	0.84 (0.17)	0.97 (0.05)	85.00 (11.00)
		2	0.87 (0.14)	0.96 (0.05)
Large4	IC: 9 (2.13)	1	0.72 (0.18)	0.97 (0.01)	80.00 (8.00)
		2	0.71 (0.19)	0.97 (0.01)
		3	0.93 (0.07)	0.98 (0.01)
	SC: 4 (2.13)	1	0.71 (0.21)	0.91 (0.09)	73.00 (15.00)
		2	0.75 (0.17)	0.88 (0.12)

^*SD: standard deviation across 100 MC replicates;

^**IC: individual foci cluster; SC: study effect clusters; Covariance matrices: Σ = 0.01I₃ (Large1), 0.05I₃ (Large2), 0.1I₃ (Large3), and 0.2I₃ (Large4).

The scenarios we chose represent important facets of variability that a spatial models need to be able to handle and overcome in order to accurately perform. Based on our simulations, it can be inferred that across all the scenarios, our proposed model in general performed well in correctly identifying individual foci clusters.

3.3 Further simulations for comparison

To further assess the proposed method, we designed additional simulation scenarios to examine how sensitive the method is with respect to the choice of prior distributions of variance parameters and the choice of abnormal distributions of foci, as well as to compare with existing methods for clustering such as the K-means approach.

Scenarios

For each of the following scenarios, we simulate 10 MC replicates and, as before, the statistics to evaluate the quality of identified clusters include means and standard deviations of sensitivity, specificity, and correctness rate.

1. Sensitivity to the choice of prior distribution of variance parameters in the base distributions. In the earlier setting, we took IG(0.5, 0.5) as the prior distribution following the suggestion by Kass and Wasserman [18]. We considered an additional prior distribution, IG(0.001, 0.001), a vague prior commonly chosen for variance parameters. Each MC replicates is generated based on the first simulation scenario discussed previously.

2. Sensitivity to skewness pattern of foci distribution. The truncated multivariate normal distribution utilized to simulate foci with skew pattern (the third simulation scenario) has a short tail and is still closely related to normal distribution. To generate data with much longer tail, we revised simulation scenario 3 by using a chi-square distribution with mean of 4 and a degrees of freedom being 0.5 for each dimension. Other settings were remained the same as in the original scenario 3.

3. Comparison with existing clustering methods. The proposed method has the potential to cluster foci abnormally distributed and has the ability to adjust other factor effects, e.g., study effect, when clustering individual foci. We expect it outperforms existing clustering methods; here, we use the commonly used K-means approach as a representative. To perform the comparison, each MC replicate is simulated based on the first simulation scenario with study effects centered at 1 and 2. In the clustering process, for the proposed method, prior knowledge of study effects is incorporated into the clustering process.

Results

Table 2 summarizes the results for these further simulation scenarios. The findings demonstrate that the method is reasonably insensitive to the choice of prior distributions for variance parameters in the Dirichlet process, as seen by the statistics of sensitivity, specificity, and accuracy, which are comparable to the results when using IG(0.5, 0.5) as the prior distribution. Nevertheless, it is worth noting that posterior inferences can be influenced by the choice of prior distributions, especially when the priors are informative [25]. When data generated from a chi-square distribution, although the data are severely right skewed, the proposed method is still able to correctly cluster individual foci 90% of the time. Lastly, when comparing our method with the K-means approach, our method showed much higher sensitivity, specificity, and accuracy, compared to the K-means approach, which is lack of the ability of incorporating prior knowledge into the clustering process.

TABLE 2.

Assessment of the Robustness of the Method and a Comparison with the K-means Approach (Simulated Data).

Scenario:	Median Num. of Clusters (SD)*	Cluster index	Average Sensitivity (SD)*	Average Specificity (SD)*	Average % Correctness rate (SD)*
Vague Prior	** IC: 3 (0.32)	1	1.00 (0.00)	1.00 (0.00)	100.00 (0.00)
		2	1.00 (0.00)	1.00 (0.00)
		3	1.00 (0.00)	1.00 (0.00)
	** SC: 2.5 (0.32)	1	0.99 (0.02)	1.00 (0.00)	97.00 (4.00)
		2	0.96 (0.07)	1.00 (0.00)
Skewed with Chi-Squared	IC: 5.5 (2.42)	1	1.00 (0.00)	0.96 (0.01)	90.00 (2.00)
		2	0.99 (0.01)	0.95 (0.01)
		3	0.76 (0.06)	1.00 (0.00)
	SC: 4 (2.41)	1	0.78 (0.17)	1.00 (0.00)	81.00 (11.00)
		2	0.84 (0.18)	1.00 (0.01)
K-means vs Our method	Our method IC: 3 (0.63)	1	1.00 (0.00)	1.00 (0.00)	100.00 (0.00)
		2	1.00 (0.00)	1.00 (0.00)
		3	1.00 (0.00)	1.00 (0.00)
	K-means IC: 3 (0.00)	1	0.55 (0.5)	0.89 (0.11)	69.00 (19.00)
		2	0.55 (0.28)	0.83 (0.2)
		3	0.90 (0.21)	0.98 (0.08)

^*SD: standard deviation across 10 MC replicates;

^**IC: individual foci cluster; SC: study effect clusters.

4 Data Application

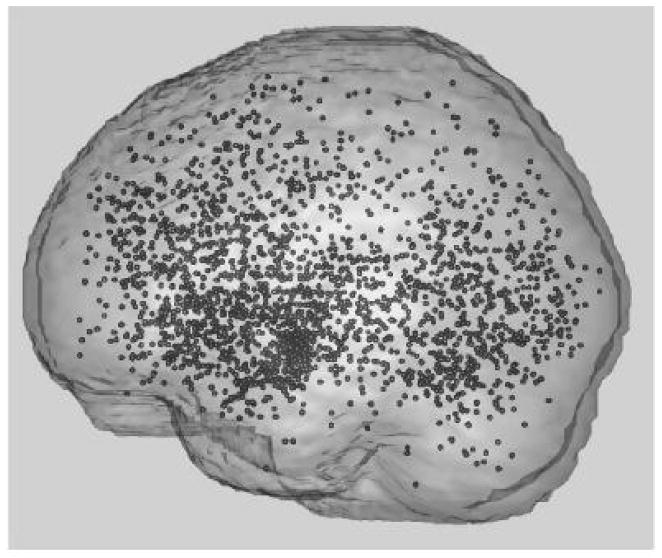
We applied the proposed model to the meta analysis data set implemented in [8] and [5] (Figure 2). This meta data were constructed from 164 different neuroimaging publications. Each publication had a number of statistical comparisons or contrasts within it, totaling 437 contrasts. We identify these contrasts as “studies”. In terms of individual foci, 2,478 were reported ([5], [8]). As seen in Table 3, on average there were 15.11 foci per publication and 5.67 foci per study. Additionally there was an average of 2.67 studies per publication. Affective (Table 4) was the most frequent emotion found in 175 studies and surprise the least frequent emotion found in only 2 studies.

Fig. 2.

The fMRI meta-data implemented in Kang et al. [8]

TABLE 3.

Descriptive Statistics of the Meta Data.

	Min.	1st Qu.	Median	Mean	3rd Qu.	Max.
Number of foci per pub.	1.00	5.75	10.00	15.11	17.25	110.00
Number of foci per study	1.00	2.00	4.00	5.67	7.00	47.00
Number of subjects per pub.	4.00	9.00	11.00	12.26	14.00	40.00
Number of studies per pub.	1.000	1.000	2.000	2.67	4.000	12.000

^*Min: minimum, 1st Qu: 25% percentile, 3rd Qu: 75% percentile, Max: maximum, pub: publication

TABLE 4.

Frequency of Emotions (Meta Data).

Emotions	Frequency of studies (% of total studies)	Frequency of foci (% of total foci)
aff*	175 (40.05%)	881 (35.55%)
anger	26 (5.95%)	166 (6.7%)
disgust	44 (10.07%)	337 (13.6%)
fear	68 (15.56%)	367 (14.81%)
happy	36 (8.24%)	178 (7.18%)
mixed	41 (9.38%)	195 (7.87%)
sad	45 (10.3%)	348 (14.04%)
surprise	2 (0.46%)	6 (0.24%)
Total	437	2478

^*aff:affective.

Clustering across anatomical structures or other specific regions of interest are important issues in the neuroscience field. Therefore, the Automated Anatomical Labeling [26] system was utilized and identified 116 brain regions of interest (ROI). Not all foci fell within these regions of interest, 498 did not fall within a ROI; however, they were included within the analysis due to their potential influence on cluster centers.

We were advised by researchers familiar with the data construction that the study effects were likely to be quite small. Introducing this prior knowledge into the application of the prior distributions for μ (the mean in the base distribution for study effect) and for ${\sigma }_1^2$, we set ${\sigma }_{\mu }^2=0.04$ (standard deviation is 0.063) and took ${\sigma }_1^2~IG(3,0.5)$. Accordingly, the amount of truncation for the base distribution in modeling study effects was set at 10% (r_a = r_b = 10%). Other prior assumptions were as those proposed in the simulations. To avoid computational overflow, the data was re-scaled down by 10.

4.1 Results

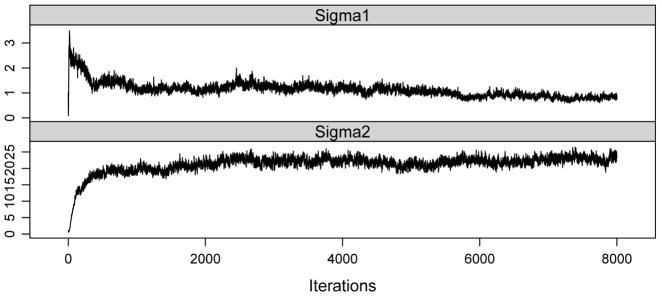
As in the simulations, α₁ and α₂ were determined by use of grid search, which resulted in α₁ = 0.1 and α₂ = 3. We then ran 8,000 iterations with 4,000 for burn-in. Trace plots were used to monitor the convergence of the MCMC chains. To illustrate, trace plots for posterior samples of ${\sigma }_1^2$ and ${\sigma }_2^2$ were included in Figure 3, showing reasonable convergence of the chains after 4,000 iterations.

Fig. 3.

Convergence plots for the conditional sampling of ${\sigma }_1^2$ and ${\sigma }_2^2$.

The proposed method identified 46 study clusters and 44 individual clusters, of which 34 individual clusters were located in a ROI (Table 5) and were included in our following discussions. The break down of each cluster by its foci frequency and emotion frequency can be seen in Table 6. The largest cluster is cluster 1 centered at (26.89, −0.2, −10.10). It was located in the right amygdala region of the brain and contained foci from all 8 emotions. The next two largest clusters identified were clusters 2 and 5. Cluster 2 had 122 foci; it was related to 7 emotions and located in the left frontal inferior triangularis. Cluster 5 (101 foci) was located in the left amygdala and also related to 7 emotions.

TABLE 5.

Meta Data Cluster Results Based on the Proposed Method.

Individual Foci Clusters
Cluster Centers	Brain Regions	Cluster Index	# of foci per cluster (% of total foci)	# of foci not in ROI (% of cluster foci)	# of studies per cluster (% of all studies)
(26.89,−0.2,−10.1)	Amygdala R	1	227 (9.16)	51 (22.47)	169 (38.67)
(−38.93,30.28,−0.54)	Frontal Inf Tri L	2	122 (4.92)	18 (14.75)	99 (22.65)
(−15.51,−0.42,−11.88)	Amygdala L	3	101 (4.08)	25 (24.75)	84 (19.22)
(48.47,12.21,−13.08)	Temporal Pole Sup R	4	91 (3.67)	21 (23.08)	81 (18.54)
(53.66,29.64,14.95)	Frontal Inf Tri R	5	91 (3.67)	14 (15.38)	76 (17.39)
(2.05,32.23,32.04)	Cingulum Ant L	6	90 (3.63)	21 (23.33)	75 (17.16)
(5.83,40.37,4.93)	Cingulum Ant R	7	81 (3.27)	15 (18.52)	67 (15.33)
(−32.4,−63.7,−13.15)	Fusiform L	8	79 (3.19)	25 (31.65)	66 (15.1)
(19.16,−14.05,3.23)	Thalamus R	9	78 (3.15)	36 (46.15)	66 (15.1)
(52.37,−61.45,5.89)	Temporal Mid R	10	72 (2.91)	10 (13.89)	65 (14.87)
(45.04,−46.63,−17.55)	Fusiform R	11	69 (2.78)	14 (20.29)	64 (14.65)
(−3.09,−87.92,0.41)	Calcarine L	12	69 (2.78)	10 (14.49)	64 (14.65)
(−26.05,13.34,−15)	Insula L	13	67 (2.7)	15 (22.39)	60 (13.73)
(−33.05,−1.88,0.76)	Insula L	14	63 (2.54)	15 (23.81)	56 (12.81)
(−36.93,2.86,8.66)	Insula L	15	59 (2.38)	15 (25.42)	53 (12.13)
(24.44,−49.21,−11.97)	Fusiform R	16	58 (2.34)	10 (17.24)	52 (11.9)
(4.56,53.78,37.04)	Frontal Sup Medial L	17	57 (2.3)	3 (5.26)	50 (11.44)
(57.35,−40.14,11.52)	Temporal Mid R	18	55 (2.22)	11 (20)	48 (10.98)
(−25.2,34.18,−6.25)	Frontal Inf Orb L	19	53 (2.14)	4 (7.55)	50 (11.44)
(3.6,−58.78,24.09)	Precuneus R	20	53 (2.14)	8 (15.09)	46 (10.53)
(−36.05,−49.14,−14.47)	Fusiform L	21	44 (1.78)	5 (11.36)	38 (8.7)
(35.74,33.65,−4.05)	Frontal Inf Orb R	22	44 (1.78)	8 (18.18)	43 (9.84)
(46.33,33.4,−6.22)	Frontal Inf Orb R	23	44 (1.78)	9 (20.45)	42 (9.61)
(47.43,19.45,5.17)	Frontal Inf Tri R	24	43 (1.74)	5 (11.63)	37 (8.47)
(44.35,2.6,12.7)	Insula R	25	41 (1.65)	9 (21.95)	39 (8.92)
(−35.76,9.07,36.63)	Frontal Mid L	26	41 (1.65)	6 (14.63)	39 (8.92)
(6.52,10.28,64.77)	Supp Motor Area R	27	34 (1.37)	4 (11.76)	30 (6.86)
(−39.51,−68.82,15.92)	Temporal Mid L	28	25 (1.01)	4 (16)	25 (5.72)
(30.72,9.29,7.29)	Putamen R	29	21 (0.85)	3 (14.29)	21 (4.81)
(45.86,−46.89,27.05)	Angular R	30	8 (0.32)	1 (12.5)	8 (1.83)
(−33.37,−1.77,47.85)	Precentral L	31	7 (0.28)	1 (14.29)	7 (1.6)
(1.15,−75.77,14.66)	Calcarine L	32	7 (0.28)	0 (0)	7 (1.6)
(46.48,19.42,0.33)	Insula R	33	5 (0.2)	0 (0)	5 (1.14)
(5.92,−3.57,43.04)	Cingulum Mid R	34	5 (0.2)	2 (40)	5 (1.14)

R: right hemisphere, L: left hemisphere.

TABLE 6.

Breakdown of Emotions and their Frequencies by Individual Foci Cluster^*.

Cluster Index: Total foci in that cluster Emotion Frequency of emotion (% of total cluster foci)
Cluster: 1	227	Cluster: 2	122	Cluster: 3	101	Cluster: 4	91	Cluster: 5	91
aff	86 (37.89)	aff	42 (34.43)	aff	27 (26.73)	aff	36 (39.56)	aff	30 (32.97)
fear	40 (17.62)	disgust	15 (12.3)	fear	23 (22.77)	anger	12 (13.19)	fear	18 (19.78)
disgust	32 (14.1)	sad	15 (12.3)	sad	18 (17.82)	sad	12 (13.19)	disgust	17 (18.68)
sad	25 (11.01)	fear	14 (11.48)	disgust	12 (11.88)	fear	10 (10.99)	sad	11 (12.09)
mixed	18 (7.93)	mixed	13 (10.66)	anger	7 (6.93)	disgust	8 (8.79)	mixed	9 (9.89)
happy	14 (6.17)	happy	12 (9.84)	happy	7 (6.93)	happy	7 (7.69)	happy	4 (4.4)
anger	11 (4.85)	anger	11 (9.02)	mixed	7 (6.93)	mixed	6 (6.59)	anger	2 (2.2)
surprise	1 (0.44)
Cluster: 6	90	Cluster: 7	81	Cluster: 8	79	Cluster: 9	78	Cluster: 10	72
aff	29 (32.22)	aff	32 (39.51)	aff	29 (36.71)	aff	25 (32.05)	aff	25 (34.72)
fear	18 (20)	disgust	11 (13.58)	fear	16 (20.25)	sad	15 (19.23)	fear	16 (22.22)
sad	12 (13.33)	fear	11 (13.58)	disgust	13 (16.46)	disgust	12 (15.38)	sad	14 (19.44)
disgust	11 (12.22)	anger	9 (11.11)	sad	13 (16.46)	fear	8 (10.26)	disgust	8 (11.11)
mixed	8 (8.89)	sad	8 (9.88)	anger	3 (3.8)	anger	7 (8.97)	mixed	4 (5.56)
happy	7 (7.78)	happy	5 (6.17)	happy	3 (3.8)	mixed	6 (7.69)	happy	3 (4.17)
anger	5 (5.56)	mixed	5 (6.17)	mixed	2 (2.53)	happy	4 (5.13)	anger	2 (2.78)
						surprise	1 (1.28)
Cluster: 11	69	Cluster: 12	69	Cluster: 13	67	Cluster: 14	63	Cluster: 15	59
aff	20 (28.99)	aff	27 (39.13)	aff	29 (43.28)	aff	19 (30.16)	aff	22 (37.29)
fear	11 (15.94)	disgust	13 (18.84)	fear	11 (16.42)	fear	11 (17.46)	disgust	11 (18.64)
mixed	10 (14.49)	happy	9 (13.04)	sad	11 (16.42)	disgust	10 (15.87)	sad	8 (13.56)
disgust	9 (13.04)	fear	6 (8.7)	disgust	6 (8.96)	happy	8 (12.7)	anger	5 (8.47)
sad	9 (13.04)	mixed	6 (8.7)	happy	5 (7.46)	sad	7 (11.11)	fear	5 (8.47)
anger	5 (7.25)	sad	5 (7.25)	anger	3 (4.48)	anger	5 (7.94)	happy	4 (6.78)
happy	5 (7.25)	anger	3 (4.35)	mixed	2 (2.99)	mixed	3 (4.76)	mixed	4 (6.78)
Cluster: 16	58	Cluster: 17	57	Cluster: 18	55	Cluster: 19	53	Cluster: 20	53
aff	23 (39.66)	aff	18 (31.58)	aff	17 (30.91)	aff	22 (41.51)	aff	20 (37.74)
fear	9 (15.52)	sad	12 (21.05)	disgust	9 (16.36)	fear	10 (18.87)	fear	7 (13.21)
disgust	8 (13.79)	fear	8 (14.04)	mixed	8 (14.55)	sad	8 (15.09)	mixed	7 (13.21)
sad	7 (12.07)	anger	6 (10.53)	fear	7 (12.73)	disgust	6 (11.32)	disgust	6 (11.32)
mixed	6 (10.34)	happy	6 (10.53)	anger	6 (10.91)	mixed	4 (7.55)	happy	5 (9.43)
anger	3 (5.17)	disgust	4 (7.02)	sad	4 (7.27)	happy	2 (3.77)	sad	5 (9.43)
happy	2 (3.45)	mixed	3 (5.26)	happy	3 (5.45)	anger	1 (1.89)	anger	3 (5.66)
				surprise	1 (1.82)
Cluster: 21	44	Cluster: 22	44	Cluster: 23	44	Cluster: 24	43	Cluster: 25	41
aff	19 (43.18)	aff	19 (43.18)	aff	17 (38.64)	aff	15 (34.88)	aff	21 (51.22)
sad	7 (15.91)	disgust	7 (15.91)	disgust	8 (18.18)	disgust	7 (16.28)	sad	8 (19.51)
fear	6 (13.64)	sad	7 (15.91)	mixed	8 (18.18)	fear	7 (16.28)	disgust	3 (7.32)
disgust	5 (11.36)	mixed	4 (9.09)	fear	5 (11.36)	sad	7 (16.28)	fear	3 (7.32)
anger	3 (6.82)	fear	3 (6.82)	happy	3 (6.82)	anger	4 (9.3)	anger	2 (4.88)
happy	3 (6.82)	happy	3 (6.82)	anger	2 (4.55)	happy	1 (2.33)	happy	2 (4.88)
mixed	1 (2.27)	anger	1 (2.27)	sad	1 (2.27)	mixed	1 (2.33)	mixed	2 (4.88)
						surprise	1 (2.33)
Cluster: 26	41	Cluster: 27	34	Cluster: 28	25	Cluster: 29	21	Cluster: 30	8
aff	14 (34.15)	aff	10 (29.41)	aff	10 (40)	aff	11 (52.38)	disgust	2 (25)
sad	8 (19.51)	mixed	8 (23.53)	disgust	4 (16)	fear	4 (19.05)	happy	2 (25)
fear	6 (14.63)	sad	5 (14.71)	fear	4 (16)	sad	4 (19.05)	sad	2 (25)
disgust	5 (12.2)	anger	4 (11.76)	anger	2 (8)	anger	1 (4.76)	anger	1 (12.5)
happy	4 (9.76)	disgust	2 (5.88)	happy	2 (8)	disgust	1 (4.76)	fear	1 (12.5)
anger	2 (4.88)	fear	2 (5.88)	mixed	2 (8)
mixed	2 (4.88)	happy	2 (5.88)	sad	1 (4)
		surprise	1 (2.94)
Cluster: 31	7	Cluster: 32	7	Cluster: 33	5	Cluster: 34	5
sad	3 (42.86)	disgust	3 (42.86)	aff	2 (40)	sad	2 (40)
anger	2 (28.57)	aff	1 (14.29)	happy	1 (20)	disgust	1 (20)
aff	1 (14.29)	anger	1 (14.29)	mixed	1 (20)	happy	1 (20)
fear	1 (14.29)	fear	1 (14.29)	sad	1 (20)	mixed	1 (20)
		happy	1 (14.29)

^*aff:affective.

We identified cluster centers located in 18 different regions of the brain, 25 if differentiating between left and right hemispheres. The functionality of the majority of these regions have been associated with emotions or emotional response, task performance, or consciousness/self-awareness. For example, two of the largest clusters are located in the amygdala, a region typically activated when subjects are emotional provoked [27]. These regions are also identified by studies elsewhere as areas of high activation [8]. Other regions that have been found associated with emotions due to brain activation are cingulum, insula, thalamus, and inferior frontal orbitofrontal [27] and these regions are also included in the clusters identified by the proposed method. Given the agreement of the findings with the literature, the clustering results have the potential to inform the centers of those activation regions.

We next compared the results with those from the K-means approach. By maximizing between cluster variations and minimizing the within cluster variation, the K-means approach identified 20 clusters, centered in 19 different brain regions, 20 if hemisphere is differentiated. With the exception of the cerebelum 6 (left and right), cerebelum 4 5, and the rolandic operculum region, all brain regions were consistent with those identified by the purposed method. The two largest clusters identified by the K-means approach are located in the amygdala and hippocampus, respectively. Given the small study effects, the proposed method and the K-means approach showed certain agreement in this application. However, as seen in Figure 2, the foci tends to be skew distributed. Many existing clustering methods including the K-means approach are sensitive to non-spherical patterns, which may explain the difficulty of the K-means approach in differentiating between different clusters, and consequently the result of smaller number of clusters.

5 Discussion

The proposed spatial Cox point process model with a Gaussian kernel driven intensity function was motivated by the need to spatially cluster coordinate-based meta analysis data to identify activated regions with the brain. The Gaussian kernel incorporated a study and sub-study effects that were estimated using a Dirichlet process (DP). The advantage of the proposed method exists in its ability to adjust for study effect (or other factor effects) and to fit irregular spatial patterns.

Findings from simulations indicated that the method is robust with respect to outliers and skewed distributions. For clusters with wide variations, the method still performed well enough as long as the overlaps between clusters are not substantial. The model was further applied to an emotion meta data set. In total, 34 clusters located in regions of interest were identified, and 14 of the 34 were in the regions known to be associated with emotion. Several regions of interest appear in multiple clusters suggest potential overlapping over clusters. It also stands to mention the natural limitation of this meta-data as it contains studies from both fMRI and positron emission tomography (PET) scans. FMRI and PET scans have different resolutions and time constraints. Thus, brain activations identified in one may not be consistent in the other.

Multiple future research directions exist. First, when the study effect is large and we do not have any prior knowledge regarding its strength, the estimates on the number of clusters will be unbiased but the estimates of the centers can be biased. This issue of identifiability can be solved by constructing parameter constraints in the clustering process, but given the dynamic feature of the clustering process, a great effort is needed to ensure that the same constraint is implemented from one MCMC iteration to the next. Additionally, due to the nature of the Dirichlet process for estimating distribution functions, using DP to perform cluster analysis can possibly produce redundant clusters, e.g., two clusters identified but their centers are so close that they should be viewed as one cluster. There is a need to design an approach which has the ability to merge clusters with centers close to each other. One possible direction is to consider mixtures of Dirichlet process to describe foci distribution patterns. In this case, two groups of foci with close centers will likely be included in one cluster. However, by use of mixtures of Dirichlet process, the modeling will be more complicated compared to the proposed method and techniques to simplify the sampling process are necessary.

TABLE 7.

Meta-data cluster results using K-means.

Individual Foci Clusters
Cluster Centers	Brain Regions	Cluster Index	# of foci per cluster (% of total foci)	# of studies per cluster (% of all studies)
(−27.28,−0.19,−19.05)	Amygdala L	1	192 (7.75)	93 (21.28)
(22.77,−5.71,−11.72)	Hippocampus R	2	187 (7.55)	81 (18.54)
(0.25,40.41,29.08)	Frontal Sup Medial L	3	169 (6.82)	82 (18.76)
(−1.63,−12.42,6.01)	Thalamus L	4	150 (6.05)	61 (13.96)
(−36.33,32.16,−3.46)	Frontal Inf Orb L	5	145 (5.85)	77 (17.62)
(5.35,35.91,−5.57)	Cingulum Ant R	6	134 (5.41)	60 (13.73)
(32.09,−56.43,−21.02)	Cerebelum 6 R	7	132 (5.33)	65 (14.87)
(42.2,13.91,−17.98)	Temporal Pole Sup R	8	131 (5.29)	65 (14.87)
(43.25,25.94,13.5)	Frontal Inf Tri R	9	131 (5.29)	61 (13.96)
(−2.38,−85.17,−3.49)	Calcarine L	10	123 (4.96)	54 (12.36)
(47.22,−61.42,7.4)	Temporal Mid R	11	121 (4.88)	56 (12.81)
(−36.22,−66,−19.17)	Cerebelum 6 L	12	108 (4.36)	52 (11.9)
(0.48,3.82,52.69)	Supp Motor Area L	13	105 (4.24)	57 (13.04)
(44.82,−11.83,22.29)	Rolandic Oper R	14	102 (4.12)	43 (9.84)
(4.57,−58.63,33.8)	Precuneus L	15	101 (4.08)	46 (10.53)
(−39.73,0.6,3.34)	Insula L	16	99 (4)	50 (11.44)
(−6.12,−40.69,−16.93)	Cerebelum 4 5 L	17	94 (3.79)	44 (10.07)
(−37.37,−67.84,22.79)	Temporal Mid L	18	86 (3.47)	45 (10.3)
(−49.48,−31.56,11.59)	Temporal Sup L	19	85 (3.43)	42 (9.61)
(−40.82,7.34,38.09)	Precentral L	20	83 (3.35)	45 (10.3)

R: right hemisphere, L: left hemisphere.

Biographies

Meredith Ray is serving as an assistant professor in biostatistics at the University of Memphis for the School of Public Health in the Division of Epidemiology, Biostatistics, and Environment health. Her research focuses on Bayesian methods, semi-parametric modeling, and fMRI brain imaging data analysis.

Jian Kang is an Assistant Professor of Biostatistics at the University of Michigan. He is also affiliated with Kidney Epidemiology and Cost Center, at the University of Michigan. His research focuses on statistical methods and theory for large-scale complex biomedical data. He is particularly interested in Bayesian methods, high dimensional variable selection with applications to imaging and genetic studies.

Hongmei Zhang is serving as an associate professor in biostatistics at the University of Memphis for the School of Public Health in the Division of Epidemiology, Biostatistics, and Environment health. Her research focuses on Bayesian methods, bioinformatics, variable selection, clustering methods, and measurement error modeling.