Enrichment of diluted cell populations from large sample volumes using 3D carbon-electrode dielectrophoresis

Abstract

Here, we report on an enrichment protocol using carbon electrode dielectrophoresis to isolate and purify a targeted cell population from sample volumes up to 4 ml. We aim at trapping, washing, and recovering an enriched cell fraction that will facilitate downstream analysis. We used an increasingly diluted sample of yeast, 10⁶–10² cells/ml, to demonstrate the isolation and enrichment of few cells at increasing flow rates. A maximum average enrichment of 154.2 ± 23.7 times was achieved when the sample flow rate was 10 μl/min and yeast cells were suspended in low electrically conductive media that maximizes dielectrophoresis trapping. A COMSOL Multiphysics model allowed for the comparison between experimental and simulation results. Discussion is conducted on the discrepancies between such results and how the model can be further improved.

I. INTRODUCTION

Cell enrichment and purification are necessary steps in a number of clinical diagnostic and environmental assays where the targeted species are highly diluted in the sample. The timely identification of the pathogen causing an infection is one application where the capability to isolate few targeted species, in the order of 1–100 per ml, from a large sample volume, >10 ml, can have tremendous impact. The administration of the correct antibiotic at this stage can eradicate low pathogen loads before they replicate further and originate life-threatening conditions such as sepsis. Sepsis is estimated to afflict 20–30 × 10⁶ patients worldwide every year and claim the lives of up to 30% of these.¹ The clinical gold standard to diagnose the cause of an infection is blood culture to encourage pathogen replication and enable their detection. Culturing the highest volume of blood possible, depending on age and health of the patient, is recommended to obtain conclusive results. 1–2 ml of blood are recommended for neonates while up to 10 ml from 2 to 3 different body sites is recommended for adults.^2,3 Automated machines (i.e., BACTEC from Becton Dickinson) are commonplace in the clinical laboratory to monitor microbial growth in the blood culture, by measuring production of carbon dioxide, and alert staff if growth is detected. When present, growth is usually detected between 24 and 48 h after starting incubation and depends on the organism. Fastidious bacteria might not be detected using this approach. In the case of a positive culture, nucleic acid amplification tests and mass spectroscopy are becoming common alternatives to the more traditional practice of overnight growth in agar plates to identify the pathogen.^4,5 Conclusive identification has been demonstrated in a couple of hours using mass spectroscopy, which still require a minimum number of bacteria in the order of 10⁴–10⁵ and benefit from the use of samples containing purified bacteria. A number of biosensors are also in development to identify specific pathogens,^6–8 but most of them still require an idealized sample volume with a critical population concentration above 10³ copies/ml or equivalent. Thus, there is a critical need for sample preparation technologies that are capable of processing large sample volumes to rapidly extract and concentrate the few particles that resemble the targeted pathogen. Once these particles are isolated in a specific media, this idealized sample could be fed to polymerase chain reaction (PCR)-based assays, mass spectroscopy, or biosensor arrays for pathogen identification, for example, increasing the concentration of the particles resembling a viable pathogen from 10⁰–10¹ cells/ml in the original sample to 10³–10⁴ cells/ml in an ideal sample.

Although common in the clinic, cell sorting technologies such as FACS and MACS^® (Fluorescence-Activated and Magnetic-Activated Cell sorting, respectively) are not well suited for sample preparation of diluted samples. In case of low-abundance cells, these techniques require at least 20 h to enrich the cell population^9,10 and a minimum of 10⁵ cells is often required as well.^11,12 Furthermore, the use of labels might not be economically viable when sample volumes of tens of milliliters are required as in the case of sepsis diagnosis. Label-free enrichment techniques can be a more viable solution and a number have been reported, but mostly at high cell concentrations (>10⁴ cells/ml).^13–15 The following works merit a more detailed review given their capability to extract low cell numbers from a sample, some of them when processing large sample volumes. Hwang et al. employed surface-modified micropillar arrays to extract Escherichia coli from up to 50% whole blood at concentrations above 10³ cells/ml.¹⁶ This approach required tailoring the pH of the sample to optimize trapping. They demonstrated high capture efficiency as long as the cell concentration was below 10⁷ cells/ml due to saturation of the array. Sample volume was only 400 μl and was processed at 200 μl/min. Free flow zone electrophoresis (FFE) was also used as an enrichment technique^17,18 by exploiting the charge distribution on the surface of the cells. For example, Podszun and colleagues processed a 100 μl-volume of a laboratory sample featuring E. faecalis at concentration as low as 266 ± 35 cells/ml to obtain a maximum enrichment factor of 11 when sample was processed at 3 μl/min. Mach et al. introduced the concept of “centrifuge-on-a-chip” for cell concentration, size-based sorting, and solution exchange using volumes in the ml range. By using microscale fluid vortices, they were able to separate and concentrate large cancer cells (20 μm) from 10 ml of 5% v/v blood in under 3 min with a capture efficiency of 20%.¹⁹ Jakobsson et al. have reported the use of acoustofluidics to enrich cells from up to 100 ml of sample at concentrations down to 10³ cells/ml. Their protocol allowed for a thousand-fold enrichment at throughput >500 μl/min when processing laboratory samples of either latex particles, red blood or cancer cells suspended in FACS buffer.²⁰ Recently, Hammarström and colleagues also used acoustic trapping aided by silica particles to prepare a 100 μl-volume of a highly concentrated (10⁷ cells/ml) positive blood culture for mass spectroscopy.²¹

Dielectrophoresis (DEP) is a powerful technique that has been used for the separation and concentration of different bioparticles including bacteria, DNA, and infected cells from blood.^9,22–28 A significant challenge when using DEP for particle trapping is the need for low electrically conductive media, since most, if not all, of the relevant biological samples such as blood and urine feature high electrical conductivity, re-suspension of the sample in optimized DEP buffers is necessary. Another challenge in DEP has been improving throughput. Hence, of particular interest here is the use of 3D electrodes, spanning the height of the microfluidic channel, to improve throughput when compared to more traditional planar devices. 3D electrodes have been implemented using different fabrication techniques²⁹ such as electroplating,^30,31 metallization of 3D structures,^32–34 and casting of conductive resins.³⁵ Here, we use 3D carbon electrodes to implement dielectrophoresis (carbonDEP) and enrich a yeast population originally diluted in a large sample volume. The fabrication details of such 3D carbon electrodes have been extensively covered by previous publications by our group and are briefly detailed below. In a nutshell, glass-like carbon electrodes are obtained by pyrolysis of SU-8 structures that are made using photolithography. CarbonDEP has also been previously demonstrated in a yeast viability assay³⁶ as well as trapping of E. coli,³⁷ drosophila,²² and λ-DNA.³⁸ The use of carbonDEP in sample preparation includes the removal of polymerase inhibitors to increase the sensitivity of a PCR assay³⁹ and a protocol to enrich a population of antibiotic-treated Mycobacterium smegmatis.⁴⁰ The advantages and disadvantages of using carbonDEP over other DEP techniques have been detailed several times before.^22,29,41,42 Briefly, the fabrication of 3D electrodes is relatively low cost and straightforward; carbon has a wider electrochemical stability window than noble metals which reduces the chance of sample electrolysis for a given applied voltage; and carbon offers excellent chemical inertness and biocompatibility. Although the electrical conductivity of glassy carbon is less than that of metals, it is in the same order of indium tin oxide,^43–45 and an effective DEP force can be generated by polarizing the carbon electrodes with tens of volts.

In this work, we focus on processing sample volumes up to 4 ml featuring concentrations as low as 10² cells/ml. We aim at trapping, washing, and recovering an enriched, purified cell fraction that will facilitate downstream analysis. We used an increasingly diluted sample of Saccharomyces cerevisiae (yeast) to demonstrate the isolation and enrichment of few cells at increasing flow rates to expedite the assay time. We show a method to increase the concentration of a sample from 10² to 10⁴ cells/ml. Although the experimental conditions used here are idealized and still far from practical application, we aim at using such experimental data to validate a methodology that will enable a priori design of future devices. For example, to optimize electrode geometry, gaps between electrodes, and positioning of the electrodes within the microfluidics channel.

II. THEORY

A dielectrophoresis (DEP) force can be defined as the force acting on a polarized particle immersed in a non-uniform electric field. In practice, a targeted particle can either be attracted to the electric field gradient, as in positiveDEP, or repelled from it as in negativeDEP. In the case of carbonDEP, the electric field gradient is around the electrodes so the particle can either be attracted to or repelled from the electrodes. In flow-through systems, the DEP trapping force must compete with the hydrodynamic drag force, which is mainly dependent on the particle velocity in the channel. When this velocity is high, as it is the case in high throughput systems desired in practical applications, the impact of sedimentation can be neglected.⁴⁶ Hence, the particle experiences a total force F_t that determines its direction and velocity in the device and is given by

$$F_t=m_p\frac{\mathit{d}\mathit{v}}{\mathit{d}\mathit{t}}=6\pi \eta r\left(u-v\right)+2\pi {\epsilon }_m{r}^{3}Re\left[f_{\mathit{C}\mathit{M}}\right]\nabla {E_{\mathit{r}\mathit{m}\mathit{s}}}^2,$$ (1)

where η is the dynamic viscosity of the media, r is the radius of the spherical cell, u is the flow velocity, and v is the particle velocity. The second term on the right-hand side represents the DEP force with ε_m the permittivity of the media, Re[f_CM] the real part of the Clausius Mossotti factor, and $\nabla E$ the electric field gradient in the device. Further details about DEP theory can be found elsewhere.⁴⁷ Solution of Equation (1)⁴⁸ for $\frac{\mathit{d}\mathit{v}}{\mathit{d}\mathit{t}}\hspace{0.17em}\hspace{0.17em}$ yields the vector form of the particle velocity shown in Equation (2); after assuming the particle velocity at t = 0 is that of the flow, and that the characteristic time scale given by $\frac{m_p}{6\pi \eta r}\hspace{0.17em}$ is much smaller than the time scale of variation of external forces given the size of the cell

$$\mathit{v}=\mathit{u}+\frac{{\mathit{F}}_{\mathit{DEP}}}{6\pi \eta r}.$$ (2)

The x, y, and z components of Equation (2) give the velocity components for the streamlines that represent potential particle trajectories. The vectors of F_DEP and u were obtained using COMSOL Multiphysics (see Sec. III D).

III. MATERIALS AND METHODS

A. Fabrication of device

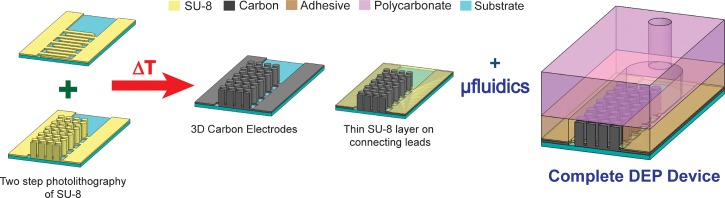
The microfluidic device used in this work features 3D glass-like carbon microelectrodes. The fabrication procedure has been detailed several times before.^37,38,41,49 Briefly, microstructures were fabricated by a two-step photolithography process of SU-8 (Gersteltec, Switzerland), a negative-tone photoresist, on a silicon wafer. These structures were then carbonized by heat treatment to 1000 °C in a nitrogen atmosphere. Each of the devices fabricated in this work featured 218 intercalated rows each of them featuring 14 or 15 electrodes for a total of 3161 electrodes; each of them 100-μm high and 50 μm-diameter. A thin layer of SU-8 was then fabricated to insulate the planar connecting leads and to planarize the channel bottom. A 1.8 mm-wide, 3.2 cm-long channel was cut from a 127 μm-thick double sided pressure sensitive adhesive, or PSA (Switchmark 212R, Flexcon, USA) and adhered to a previously drilled polycarbonate piece, in a process recently detailed by the authors.⁵⁰ This arrangement was then manually positioned around the carbon electrode array and sealed using a rolling press. The complete process is shown in Fig. 1, emphasizing the cross-section at the center of an experimental device.

FIG. 1.

Representative fabrication of 3D carbon electrode dielectrophoresis device. The process starts by fabricating SU-8 post geometries on interdigitated planar fingers using photolithography. The pyrolysis of the SU-8 structures was conducted in a nitrogen atmosphere at 1000 °C. A thin layer of SU-8 is then made to planarize the bottom of the device. The microfluidic channel is made in a parallel process and then manually positioned around the carbon electrodes to obtain the cross-section shown in the figure. See text for electrode and channel dimensions.

B. Sample preparation

All reagents were purchased from Sigma Aldrich unless noted otherwise. S. cerevisiae cells (Yeast) were grown to a concentration of 10⁷ cells/ml in a 0.01 M phosphate buffer saline (PBS). The experimental media for DEP, also identified as clean buffer from now on, was prepared by dissolving 0.1 wt. % bovine serum albumin (BSA), 8.6 wt. % sucrose, and 0.3 wt. % dextrose in distilled water. The conductivity of this clean buffer was 12.6 μS/cm. The experimental samples were prepared by pelleting the cell culture by centrifugation at 5000 rpm for 5 min followed by washing and re-suspending the cells in clean buffer. The cell concentration in this stock was determined by direct cell count using a hemocytometer with improved Neubauer ruling (Hausser Scientific, USA). Dilution of this stock with clean buffer was then implemented as needed to obtain specific cell concentrations between 10² and 10⁶ cells/ml.

C. Experimental protocol

The experimental protocol featured three main steps: DEP treatment, washing, and elution. The entire sample volume was flowed through an electrically polarized electrode array to trap targeted cells. Clean buffer was flowed afterwards to wash the trapped cells and remove any debris from the channel. After such wash, the electrode array was turned off to release the particle and elute them for retrieval at the end of the channel. Although fractions of 20 μl-volume were collected all throughout the experiment, only 9 of them were analyzed using direct counting to determine the enrichment capability of the carbonDEP device. These fractions were the control fraction to determine the initial concentration in the sample; the 4 wash fractions just before turning the electric field off; and 4 more fractions, the elutes, right after turning the field off. Of particular interest is the concentration difference between the last wash fraction and the first elute.

To implement the positive DEP trapping force, the carbon electrodes were stimulated with a sinusoidal AC signal with magnitude of 20 V_pp and 100 kHz frequency (Function Generator BK Precision 4052, USA). The behavior of yeast cells under a DEP force is well characterized,^51–53 and the 100 kHz frequency was chosen to enable the trapping of all yeast cells, as previously demonstrated by one of the authors.²² The use of higher frequencies is expected to enable separation of yeast cells based on viability.³⁶ A sample volume of 500 μl was processed when the cell concentration was above 10³ cells/ml. For samples featuring a concentration below 10³ cells/ml, the focus of this work, the sample volume was increased to 4 ml to guarantee enough cells are retrieved to permit the use of the hemocytometer for cell counting. The flow rate reported here for a given experiment was established using a syringe pump (FusionTouch 200, Chemyx, USA) and maintained constant throughout the experiment. Each of the experiments at a given initial cell concentration and flow rate was repeated at least 3 times.

D. Numerical simulation

COMSOL Multiphysics 4.4 was used to obtain the vector fields of F_DEP and flow velocity u. F_DEP was calculated here for the specific case of a yeast cell of 2.5 μm-radius immersed in water (ε_m = 80.2ε₀) with conductivity 12.6 μS/cm and under the influence of an electric field with frequency of 100 kHz. Hence, a Re[f_CM] of 0.5 was used. This value was obtained using a previously reported model²² to obtain the Re[f_CM] of yeast cells at different frequencies and media conductivities following the work by Huang et al.⁵² The electric field in the polarized carbon electrode array was obtained using Equation (3) for electric currents in stationary domain

$$\mathit{E}=-\nabla \mathit{V}\mathrm{,}$$ (3)

where E is the Electric Field computed in the domain and V is the voltage assigned to the electrode surface (14 or 0 V in our case).

The flow velocity u for the laminar flow field in the channel was calculated using Equations (4) and (5), where fluid density is denoted by ρ, u is the flow velocity, p denotes the pressure, I is the identity matrix, ${\mathit{F}}_t$ is the total force acting on the fluid (see Equation (1)), and T represents the transpose of the matrix

$$\hspace{0.17em}\rho (\mathit{u}\cdot \nabla )\mathit{u}=\nabla \cdot [-pI+\mu (\nabla \mathit{u}+{(\nabla \mathit{u})}^T]+{\mathit{F}}_t,$$ (4)

$$\hspace{0.17em}\rho \nabla \cdot \mathit{u}=0.$$ (5)

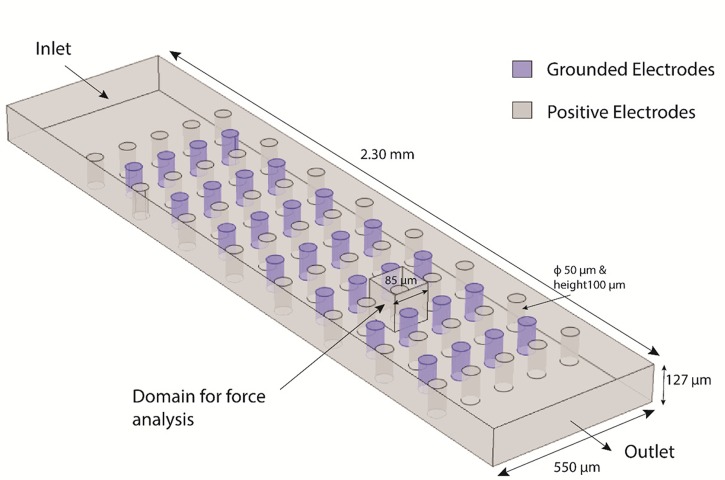
The geometrical model used is illustrated in Fig. 2 and is a simplified version of the experimental device. The channel was modeled as 550 μm wide (1/3 of the width of the experimental device), 2.30 mm-long and 127 μm-high. In order to reduce the computational power required, a representative array of cylindrical electrodes of only 15 rows was implemented. Rows with 4 or 5 electrodes each were placed alternately. The individual electrode dimension mimicked those of the experimental device: 50 μm-height, 100 μm-high and center-to-center distance between electrodes of 115 μm. The electrodes were assigned a value of 14 V (positive) or 0 V (grounded). This voltage value was assigned based on previous work and taking into consideration the resistive losses in the carbon electrodes, from the connection pad to an individual electrode.³⁸ All parameters used in the simulation are detailed in Table I in the supplementary material. A region defined by the cube shown in Fig. 2 was selected to enable a detailed study of the forces acting around a single electrode.

FIG. 2.

COMSOL Model for simulation of net forces in the electrode array resulting from the interaction of DEP and drag forces. This model is a simplified version of the experimental device. All details are explained in the text. Of particular importance is the “domain for force analysis” indicated in the figure as this is the domain used to present results in Figure 4. Positive electrodes were assigned a voltage of 14 V while Grounded electrodes were set at 0 V.

The Laminar flow and electric currents physics modules available in the software were used to compute the force fields acting in the simulation domain at steady state. All variables used in the simulation are defined in Table II in the supplementary material.⁵⁴ A mesh featuring around 4.0 × 10⁶ total elements was implemented and controlled by the fluid flow physics. The average element quality achieved was 0.66. An Intel^® Xeon^® CPU E5–1650 v2 at 3.50 GHz Processor with a RAM of 32 GB and a 64-bit Operating System was used for these simulations.

Ideal conditions were considered to model the flow of cells through the chip. A number of considerations were taken and described next. Cells were assumed to be non-porous and spherical. All the cells were released in the channel using static release, i.e., all the cells were released at one time with the velocities corresponding to a parabolic flow profile in the channel. The particles were released from randomly generated x, y, z coordinates at the channel inlet in an attempt to better reproduce experimental conditions. These coordinates were generated in Matlab and then exported to COMSOL Multiphysics. Particle rotation was assumed to not affect the translation of the particle and cell-cell interaction was assumed negligible. Furthermore, the electric field acting on the cell was assumed to not be affected by particles already trapped on the electrode surface and cell sedimentation due to gravity was considered negligible. All modeled materials were considered to be non-porous, while the properties of the media are uniform throughout the channel. Since flow occurred at Reynolds numbers lower than unity a creeping flow was assumed.

IV. RESULTS

A. Experimental

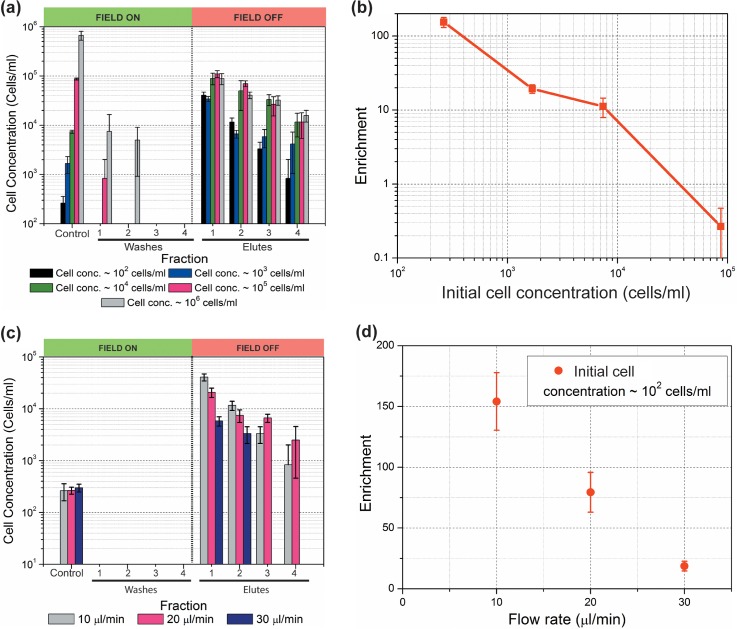
Trapping of yeast cells on the 3D carbon electrodes is shown in Fig. 3 and is compared to the control cases when the electrodes were not polarized. The results with different initial cell concentrations are shown in Fig. 4. The cell concentrations were plotted for a total of 9 fractions: the control fraction containing the initial sample cell concentration; 4 fractions just before the electrical signal was turned off (washes 1–4) and 4 fractions just after the electrical signal was turned off (elutes 1–4). The DEP force was turned on for particle trapping during the fractions labeled as washes 1–4. Hence, the cell concentration detected in these fractions was expected to be negligible. Elutes 1–4 were collected just after the field was turned off to release the cells. A concentration spike is thus expected for these fractions when compared to the last wash and the concentration of the control fraction. The tallest the spike, the best the performance of the device is. Close inspection of Fig. 4(a) allows for a number of observations. The fact that the maximum concentration obtained in elute 1 is around 10⁵ cells/ml regardless of the concentration of the initial sample suggests a saturation point of the device. The saturation limit of this specific device, under the experimental conditions specific to this work, is around 4000 yeast cells. This is calculated by adding the number of cells retrieved in each of the four 20 μl-volume elutes. The number of cells in further elutes is not expected to significantly add to this total.

FIG. 3.

(a) Yeast cells trapped on the 3D carbon electrodes (dark circles) using a sinusoidal signal with frequency 100 kHz and magnitude 20 V_pp. Note how the cells are trapped and accumulated at the back of the electrode. (b) Cells are not trapped when the carbon electrodes are not polarized. The electrical conductivity of the suspending media in both cases is 12.6 μS/cm and the flow rate in the channel was 10 μl/min.

FIG. 4.

(a) Experimental results showing enrichment of cell population at different initial cell concentrations. Sample was flowed at 10 μl/min and the electrode array polarized using a sinusoidal signal with amplitude 20 V_pp and 100 kHz frequency. Control fractions represent those retrieved from the device when the electrode array is not polarized. Of particular interest is the concentration obtained in the first elute, recovered immediately after turning the electric field off, and its comparison to the initial cell concentration to calculate enrichment. (b) Plot detailing cell enrichment as calculated using Equation (6) for different cell concentrations. Note the significant enrichment at low concentrations and how enrichment decreases as concentration increases, due to saturation of the electrode array; (c) Experimental results showing enrichment of a sample with concentration 10² cells/ml as the flow rate increases from 10 to 30 μl/min. The electrode array was polarized using a sinusoidal signal with amplitude 20 V_pp and 100 kHz frequency. (d) Cell enrichment, as calculated using Equation (6), for different flow rates but constant initial concentration of 10² cells/ml. Note how enrichment decreases as flow rate increases but still is significant at the fastest flow rate. Bars in all the figures indicate standard deviation for each set of measurements, n > 3.

The focus of this work is to validate the use of carbonDEP for cell enrichment. The enrichment obtained in each experiment is calculated according to Equation (6) and plotted in Fig. 4(b)

$$Cell\hspace{0.17em}Enrichment=\frac{Cell\hspace{0.17em}Conc.\hspace{0.17em}at\hspace{0.17em}Elute\hspace{0.17em}1\hspace{0.17em}fraction-Control\hspace{0.17em}cell\hspace{0.17em}conc.}{Control\hspace{0.17em}cell\hspace{0.17em}conc.}.$$ (6)

An enrichment of 154.2 ± 23.7 times is achieved when processing diluted samples with concentration down to 10² cells/ml. In this case, 1052 ± 380 cells were contained in the 4 ml of sample that were processed, and 816 ± 125 cells were recovered in the first 20 μl-fraction. The rest of the cells were recovered in the other three elutes. If one considers the 4 elute fractions, the enrichment is around 50 times: the 1052 ± 380 cells originally present in 4 ml were trapped, washed, and eluted in an 80 μl fraction. The concentration of the sample increased from the original 10² to 10⁴ cells/ml. The level of enrichment decreases as the concentration of the initial sample increases. Such behavior is due to the saturation point of the specific design and experimental conditions used here. Hence, negative enrichment in this case can be expected when the concentration of the initial sample is above 10⁵ cells/ml.

The next step was to quantify the impact on the enrichment as the flow rate in the channel was increased. A high level of enrichment was obtained at 10 μl/min, but the processing of 4 ml of sample took close to 7 h. One of the goals of this work is to minimize the assay time. Hence, we performed the experiments for the cell concentration of 10² cells/ml with the flow rates of 20 μl/min and 30 μl/min. The results are shown in Fig. 3(c). It can be observed that the cell concentration in the first elute decreased with an increase in the flow rate. However, an enrichment of around 25 times is still possible at flow rates as high as 30 μl/min as shown in Fig. 4(d). At such flow rate, the processing time of 4 ml of sample is reduced to 2 h and 30 min, or a 65% reduction in assay time, albeit enrichment is reduced by 84%.

B. Numerical simulation

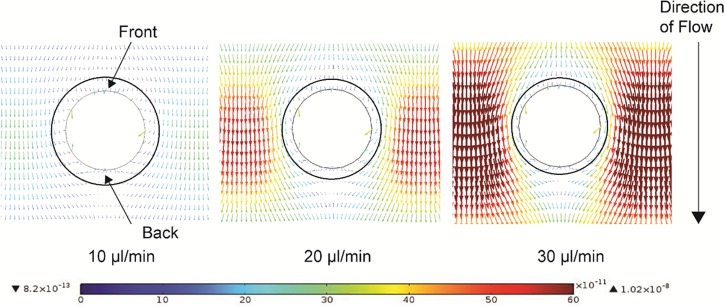
The top view of the net forces expected around an individual electrode at an x-y plane with height of 50 μm is shown in Fig. 5. At this mid-plane, the distribution of DEP and drag forces in the z axis is uniform since sedimentation is not considered and the field distortions of the electrode's bottom and top are not observed. The vectors shown in the figure depict the magnitude and direction of the net force resulting from the interaction between drag and DEP forces at that specific point. The color scale represents the force in N. As expected, the difference in magnitude between the vectors close and far away from the electrode surfaces increases proportional to the flow rate. The drag force is expected to dominate as the flow rate increases and thus the drastic difference between vector magnitudes in the case of 30 μl/min flow. Visual inspection of these results allow for the arbitrary drawing of a ring around the electrodes (denoted by the black circles and characteristic of each flow rate), in which the force vectors first follow the contour of the electrode, converge to a region after the electrode and then point to the back of the electrode. The width of this ring is inversely proportional to the flow rate as illustrated in the figure. Most of the cells flowing into this ring area are expected to contour the electrode and be accumulated in the trapping volume at its back; until there is no more trapping space available. At that point, the cells will be attracted to the electrode but no longer will they get trapped. Very few particles, on the order of a monolayer, are expected to trap on the front surface of the electrodes. Few cells are also expected to trap on the edge of the trapping volume due to particle-particle interactions and the distortion of the electric field due to the accumulated particles. These latter effects are not currently considered in the numerical model.

FIG. 5.

Top view of the net force vector field that results from the interaction of DEP and drag forces around a single electrode and at increasing flow rates. The plane analyzed is that at the height of 50 μm, or half the height of the electrode. The force vectors are calculated for a yeast cell under the influence of a carbon electrode array polarized at 14 V (to account for resistive losses from the connecting pad, polarized at 20 V in the experiments, to the carbon electrodes³⁸) at increasing flow rates of 10, 20, and 30 μl/min. The direction of the arrows corresponds to the direction of the net force while the length and color of the arrow indicates the magnitude of the force in N according the color scale showed in the figure. The rings around the electrodes were set arbitrarily after visual inspection to represent the region in which the force vectors orient the particles towards the electrode and can cause particle trapping. As expected, the width of such ring decreases with an increase in flow rate.

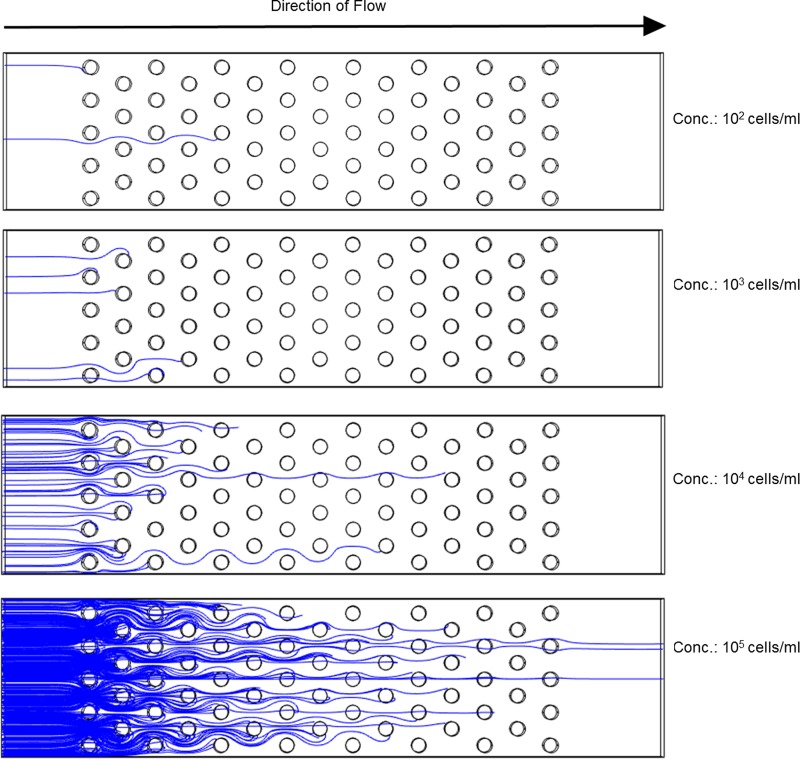
Although our initial thought was to use the volume of the mentioned rings around the electrodes to calculate the trapping capacity of the electrode array (dividing the ring volume by the volume of individual cells and considering a packing coefficient), we realized this approach was not entirely accurate in the case of diluted samples. The most important parameter when processing samples of low cell abundance is the probability that the targeted particle encounters a trapping region such as the rings around the electrodes in Fig. 5. One may implement many trapping sites but the cells may never come close to them. Thus, a number of 3D numerical simulations were performed to study the potential cell trajectories as the sample concentration changes. It was hypothesized that such results will facilitate future optimization of DEP devices to be used with diluted samples. Each of the experiments consisted on modeling a specific number of streamlines in the volume of the channel and studying the trapping behavior. As a reminder, streamlines were set to start at random locations throughout the cross-section of the channel inlet to better reflect experimental conditions. The number of streamlines at the entrance and exit of the electrode array were compared for each experiment to determine trapping efficiency. A trapping of 100% was obtained when all the streamlines terminated on an electrode and thus no streamlines were observed at the exit of the array. Representative results are presented in Fig. 6. For a 10² cells/ml concentration the number of modeled streamlines was 2; for 10³ was 5 while for 10⁴ and 10⁵ was 50 and 500, respectively. These numbers were fixed to reduce the computational power required and were based on the number of particles that can flow through the simulated channel in 1 min at the different concentrations at a flow rate of 10 μl/min. The reader is reminded that the computational model is a simplified representation of the experimental device and as such the width of the simulated channel is one third of the actual experimental channel and the number of electrode rows is only 15. 50 individual experiments were conducted in the case of 10² and 10³ cell/ml concentration; 5 experiments were conducted for the cases of 10⁴ and 10⁵, given the lengthy process of assigning random starting coordinates to each of the streamlines in these cases and that the focus of this paper is on low cell concentrations.

FIG. 6.

Representative examples of yeast cell trajectories through a polarized carbon electrode array as the concentration of yeast cells change from 10² to 10⁵ per ml. Trapping occurs as long as the streamline stops on the surface of an electrode due to the no-slip boundary condition established on all surfaces of the model. A 100% trapping in the array occurs when no streamlines are observed at the exit of the channel. Some streamlines do not finish on the electrode, instead they are adhered to the channel surfaces. Note the importance of electrode positioning to ensure an encounter between the particle and the electrode, and the fact that only a few electrodes may be necessary in the case of diluted samples.

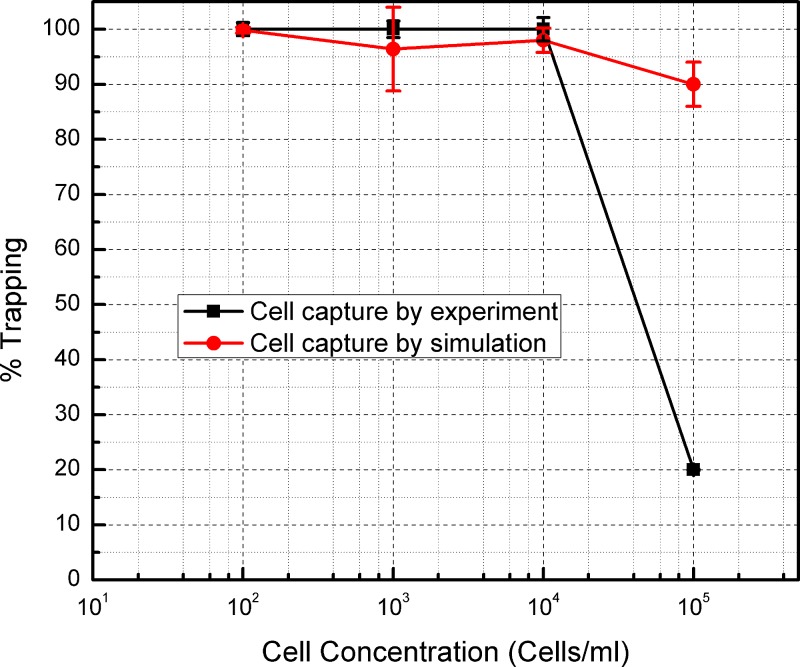
The results from this numerical simulation are shown in Fig. 7 when plotting percentage of trapping as the total number of streamlines ending on an electrode over the total number of streamlines at the entrance of the channel, against different cell concentrations. The percentage of trapping obtained in the experiments is calculated as the ratio of cells retrieved in all the elute fractions over the total number of cells introduced to the device, and is plotted in the same figure for comparison. The average probability of streamline capture for the flow rate of 10 μl/min at a concentration of 10² cells/ml is 99.8%. The probability for streamline capture for the cell concentration of 10³ and 10⁴ cells/ml is 96% and 98%, respectively. For the concentration of 10⁵ cells/ml, the probability of streamline trapping obtained from the simulation was 90%. Hence, the efficiency of trapping seems to be inversely proportional to the flow rate in the channel. This behavior is also replicated in the experiments. A trapping efficiency of 100% was obtained in the experiments as long as the sample concentration was below 10⁴. In these cases, all the cells flowed into the device could be recovered in the final elutes. As in the case of the simulation results, the percentage efficiency drops as the sample concentration increases. However, this drop is drastically higher in the case of experimental results.

FIG. 7.

Comparison between the percentages of trapping obtained experimentally and with simulation at different cell concentrations. Bars indicate standard deviation resulting from at least three measurements in each case. The bars for the experimental case are of the same size or slightly larger than the symbols. Bars in the simulation cases are due to the fact that particles are released from random coordinates throughout the channel inlet to better reflect experimental conditions. The results for simulation and experiment are in agreement for low cell concentrations but differ at high cell concentrations possibly due to cell crowding and the inability of the simulation to account for this phenomenon. See Sec. V for further details.

V. DISCUSSION

The results obtained in the experiments are comparable to the simulation results for the cell concentration of 10²–10⁴ cells/ml. In the case of simulation, the number of incoming streamlines in the channel is low when the sample is diluted. Given the high number of electrodes and its intercalated nature, the incoming streamlines have high possibility to enter the trapping region around any of the electrodes and get captured on the electrode. Similarly, the number of cells coming into the device at low sample concentration is significantly lower than the number of electrodes present, and the trapping volume available. Hence, all the incoming cells are highly likely to come across an electrode and be captured.

The drastic difference between simulation and experimental results at high concentrations can be explained as follows. During the experiment, it was observed that after the cells are attracted to the front electrode surface, most of them rolled down along the rounded surface of the electrode and finally captured at the back of the electrode. This behavior is predicted by the force vector field of Fig. 5 but cannot be replicated in the case of streamlines shown in Fig. 6 due to the fact that a no-slip boundary condition is implemented on all surfaces. The termination of streamlines on the front of the electrodes and on channel walls, as well as the lack of rolling, are simulation artifacts that artificially increase the percentage of trapping (the experimental sample features a surfactant, BSA, with the intention of minimizing cell adhesion to a surface). These artifacts could also impact the trapping efficiency at low cell concentrations, the focus of this paper, but the high number of experiments conducted in those cases likely diminished their impact. The simulation also does not take into account particle-particle interaction. During experiments, a cone-like shape at the back of the electrode could be seen as a result of cell accumulation. Depending on the sample cell concentration and time of experiment, such shape was observed to extend beyond the trapping zone. In this case, the cells beyond the trapping zone started escaping with the flow. This could not be modeled with the current simulation and lends itself to further study. Moreover, the current model only simulates streamlines and not particles. Simulation of particles was attempted but it quickly became impractical in terms of calculation time when attempting to model more than just a few particles. The streamlines modeled in the simulation are lines with no diameter, whereas a cell has a definite diameter. Even when the streamlines can be initially set apart a specific distance, there is no rule to prevent them from becoming unrealistically close during the simulation, i.e., flowing very close in between the electrodes. When the concentration is high (10⁵ cells/ml and higher) the simulation domain becomes crowded with streamlines and the simulation shows a high percentage of cell trapping. However, in reality cells cannot flow so closely.

The maximum number of cells that this particular experimental device, featuring 3161 posts, can trap when polarized with a 20 V_pp sinusoidal signal with frequency 100 kHz and under specific conditions has been determined as close to 4000 cells. Although this throughput may be considered low at first, the focus of this work is on enrichment of diluted cell populations in large sample volumes. The possibility of enriching 1–100 cells/ml from 30 to 40 ml of sample in the context of sepsis can have tremendous impact. This translates to 1.26 cells per electrode. However, the cell trapping observed in the experiments was not this low. Trapping was not consistent in all the electrodes present in the chip. Some of the electrodes actively trapped a large number of cells, whereas some electrodes did not trap any cells. Due to fabrication issues some of the electrodes may not be fully functional, whereas the simulation model considered all the electrodes to function perfectly. Fabrication issues include knocking off electrodes from the array during heat treatment or handling of the chip, as well as damage to the planar connecting leads which can disable the electric field of an entire row of electrodes; leading to no cells trapping on those electrodes. Although the model already takes into account the electric resistance of the path from the signal generator to the individual electrode³⁸ (calculated using a carbon resistivity of 1 × 10⁻⁴ Ω/m (Ref. 55)), this is considered uniform and constant. In the experiments, this is not always the case as the carbon pad may be scratched and the contact resistance of the platform may vary. These will lead to an applied voltage that is lower than expected and hence a weaker DEP force. A potential improvement to carbonDEP devices is increasing the thickness of the planar leads connecting the pad to the base of the electrodes to decrease the voltage losses. This can be considered for future devices.

Cell sedimentation has not been included in this model because initial calculations led to the conclusion that its impact would be minimal. The residence time of the yeast cells in the experimental channel described here goes from 44.16 s at 10 μl/min to 14.72 s at 30 μl/min. The expected time for the cell to sediment the entire height of this channel is 90.87 s. Those flowing closer to the channel bottom will reach the bottom in a shorter time. Hence, sedimentation was expected to affect the results to a minor degree. There are two scenarios of how sedimentation may impact future experiments. The first scenario is when the particle sediments before entering the electrode array. In this case, the volume available for trapping is reduced to that close to the channel bottom. The other scenario is when the cell is already trapped on the electrode before sedimentation. The cell will be trapped somewhere along the height of the electrode and eventually sediment along its wall. In this case, the cells will possibly keep accumulating vertically. Of these two scenarios, the latter is the more likely when processing diluted samples where the goal is to process the sample as fast of a flow rate as possible but requires processing a large sample volume, which will increase the total experiment time. Ongoing work is on implementing sedimentation in the simulation model to assess its impact in the processing of samples with low cell abundance.

We are targeting a device capable of concentrating the few viable cells originally present in large sample volumes in a small volume of specific media. This enrichment step will greatly increase the sensitivity of biosensors and reduce the possibility of obtaining a false negative, since DEP can discriminate cells based on viability. The enrichment capability of our device could be further increased by increasing the trapping volume of the electrode, which depends on the design of the device. Ongoing work is studying the impact of the electrode height, its cross section, and the electrode distribution in the channel. Besides increasing the trapping volume and decreasing the device footprint, the use of higher carbon electrodes enables the expansion of the cross section area of the channel. This would allow for higher flow rates (and shorter assay times) while maintaining the flow velocity and the drag force acting on the cells (flow rate = cross section area times flow velocity). The number and location of posts must also be optimized to equilibrate throughput and efficiency with the device cost for a given application. Thousands of posts may not be necessary when processing diluted samples; instead, few posts strategically positioned might suffice. An improved model that considers sedimentation and particle-particle interaction is being implemented to enable further optimization of carbonDEP devices.

A method to enrich targeted cells in a biological sample is desired to speed up the identification of the pathogen causing infection and enable timely administration of the correct antibiotic. In this work, we have demonstrated sample enrichment from 10² cells/ml up to 10⁴ cells/ml within few hours. However, enrichment was done using yeast cells, 2–3 times larger than the average bacterial pathogen, suspended in low conductive media to maximize DEP. Relevant biological samples, such as blood and urine, feature electrical conductivities much larger than that used here (up to 15 000 μS/cm) which will impede cell trapping using DEP. The first step to circumvent this is by optimizing a buffer that features low electrical conductivity but can sustain cell viability and function for a time window wide enough to enable experimentation. The use of an isotonic sugar solution with a tailored conductivity of ∼500 μS/cm has been shown to keep cells viable, ranging from microorganisms to stem cells.^47,56,57 Once a buffer is optimized for DEP experimentation, a cell re-suspension in, or dilution step with this buffer can be implemented. Dilution of the original sample with DEP buffer would be straightforward but will also increase the sample volume, and processing time, significantly. A several-fold improvement of the throughput of DEP devices will be crucial to pursue this direction, for example, by increasing the channel cross section as detailed above and/or stacking several DEP devices to work in parallel. Re-suspension in DEP buffer is also a possibility by implementing a centrifugation step that allows for the rapid sedimentation of all particles in the sample and facilitates media exchange. The loss of targeted cells can become an issue here, especially when processing samples with low cell abundance, and must be taken into account. Cell focusing using negativeDEP, controlling the distance the cells are repelled from the electrode surfaces, can also be used instead of trapping to implement cell sorting in the original sample.^58–61 However, this approach may not provide enough selectivity as all cells would likely be focused to the same stream in such high electrical conductivity media and re-suspension or dilution may still be necessary. In any case, a computational model to obtain the net force field and potential particle trajectories will be crucial to allow for the design of carbonDEP devices with an expected functionality. It is also important to note that is highly unlikely that a sole technology can solve the problem of sample enrichment, as no one of them features high throughput and high selectivity. The likely solution is an integration of different approaches that will exploit the advantages of each technology. For example, using centrifugation or acoustophoresis to enrich and re-suspend particles of a specific size range from tens of milliliters of sample, followed by DEP to perform separation based on viability and phenotype, and finally coupled to biosensors to accurately conclude on the identity of the cells. The envisioned goal is a step-by-step process to enrich and purify the targeted cells from several milliliters of sample into just few microliters in the most rapid way possible to enable timely diagnostics.

VI. CONCLUSION

In this work, we have demonstrated the capability of carbon-electrode DEP to trap yeast cells from a large sample volume and concentrate them in a small volume to achieve an enriched fraction. An enrichment of 154.2 ± 23.7 times was achieved when the sample flow rate was 10 μl/min and the cells were suspended in low electrically conductive media that maximizes DEP trapping. Simulation results show how the trapping region around the electrodes decreases and cell trajectories change with increasing flow rates. The experimental trapping efficiency was found to be close to 100% for the cell concentration 10²–10⁴ cells/ml, which was comparable with the trapping efficiency obtained from the simulation. For higher cell concentration, the experimental trapping efficiency deviated significantly from the simulation results. The current simulation model does not account for certain experimental conditions, such as particle-particle interaction and sedimentation, and further work is required to obtain a more comprehensive model that facilitates the virtual design of devices meant to meet performance specifications.