Segmentation of Perivascular Spaces in 7T MR Image using Auto- Context Model with Orientation-Normalized Features

Abstract

Quantitative study of perivascular spaces (PVSs) in brain magnetic resonance (MR) images is important for understanding the brain lymphatic system and its relationship with neurological diseases. One of major challenges is the accurate extraction of PVSs that have very thin tubular structures with various directions in three-dimensional (3D) MR images. In this paper, we propose a learning-based PVS segmentation method to address this challenge. Specifically, we first determine a region of interest (ROI) by using the anatomical brain structure and the vesselness information derived from eigenvalues of image derivatives. Then, in the ROI, we extract a number of randomized Haar features which are normalized with respect to the principal directions of the underlying image derivatives. The classifier is trained by the random forest model that can effectively learn both discriminative features and classifier parameters to maximize the information gain. Finally, a sequential learning strategy is used to further enforce various contextual patterns around the thin tubular structures into the classifier. For evaluation, we apply our proposed method to the 7T brain MR images scanned from 17 healthy subjects aged from 25 to 37. The performance is measured by voxel-wise segmentation accuracy, cluster- wise classification accuracy, and similarity of geometric properties, such as volume, length, and diameter distributions between the predicted and the true PVSs. Moreover, the accuracies are also evaluated on the simulation images with motion artifacts and lacunes to demonstrate the potential of our method in segmenting PVSs from elderly and patient populations. The experimental results show that our proposed method outperforms all existing PVS segmentation methods.

1. Introduction

Perivascular spaces (PVSs), also named Virchow-Robin spaces, are the CSF-filled spaces surrounding the penetrating arteries and veins in the brain. The PVSs usually have thin tubular structures less than 2 mm in diameter for healthy and young people. Recently, it has been revealed that the PVSs play an important role in the brain lymphatic system. (Iliff, Wang et al. 2013; Rangroo Thrane, Thrane et al. 2013; Yang, Kress et al. 2013; Kress, Iliff et al. 2014).

Many evidences have been also found that the enlargement or the increased number of PVSs is closely related to aging (Heier, Bauer et al. 1989; Zhu, Tzourio et al. 2010; Chen, Song et al. 2011), cognitive decline (Maclullich, Wardlaw et al. 2004), and small vessel diseases (Rouhl, van Oostenbrugge et al. 2008; Doubal, MacLullich et al. 2010; Zhu, Tzourio et al. 2010). Thus, the quantitative study of PVSs is important for analyzing the causes of these neurological diseases, as well as understanding the PVS functions. However, relevant studies have been relatively limited because the majority of non-dilated PVSs are too thin to be clearly visualized in the conventional 1.5T or 3T MR images. In addition, the manual delineation of thin tubular structures in a three-dimensional (3D) image is very time-consuming. Especially, since the appearances of lacunes and PVSs are very similar in a 2D slice view (Wuerfel, Haertle et al. 2008; Wardlaw, Smith et al. 2013), clinicians have to check multiple views for accurate PVS delineation. Due to these difficulties, PVS rating scales were often ambiguous in the literature, and the reported quantitative diameters and lengths were inconsistent (Hernandez Mdel, Piper et al. 2013). Recently, with the increased signal to noise ratio of 7T MR scanners (Bouvy, Biessels et al. 2014), PVSs can be shown even in the MR images scanned from healthy subjects. However, the manual delineation becomes more and more challenging, with the increased number of visible PVSs. For example, although Bouvy et al. (Bouvy, Biessels et al. 2014) demonstrated the increased sensitivity of 7T MR images to visualize PVS, their quantitative analysis was performed only on the 2D slice view due to the segmentation challenge. Thus, an accurate characterization of PVS morphology could not be achieved. Accordingly, development of an accurate and reliable automatic PVS segmentation method for 7T MR images is necessary to accelerate the relevant aging and disease studies.

However, so far, few automatic methods have been developed for PVS segmentation. Wuerfel et al. (Wuerfel, Haertle et al. 2008) segmented the PVSs by using a semi-automatic software, which can adjust intensity threshold (Makale, Solomon et al. 2002). Descombes et al. (Descombes, Kruggel et al. 2004) constructed a model defined by the pre-defined PVS filters and geometric properties, and then optimized it by the Markov chain Monte Carlo method. Uchiyama et al. (Uchiyama, Kunieda et al. 2008) enhanced the intensities of tubular structures using white top-hat transformation, and then extracted them by intensity thresholding. Subsequently, they identified the PVSs by using geometric properties such as the location, size, and degree of irregularity. Ramirez et al. (Ramirez, Gibson et al. 2011; Ramirez, Berezuk et al. 2015) proposed a semi-automatic segmentation method, namely Lesion Explorer, which exploited T1, T2, and PD images for the segmentation of subcortical hyperintensities. They first conducted tissue segmentation on T1 image, identified several anatomical landmarks required for regional parcellation, and, finally, extracted subcortical hyperintensities and PVSs by applying the adaptive local thresholds derived from the T2 and PD images. Recently, Wang et al. (Wang, Valdes Hernandez Mdel et al. 2016) proposed a thresholding-based semi-automatic approach to perform the PVS segmentation. They first adjusted image intensity based on the standard slices of basal ganglia and centrum semiovale, and then adaptively determined a threshold with respect to the characteristics of T2-weighted image. Although the target object was not exactly the PVSs, Wang et al. (Wang, Catindig et al. 2012) proposed a multi-stage segmentation method to delineate white matter hyperintensity, cortical infarct, and lacunar infarct. Note that the appearance of lacunar infarct is similar to the PVS except for its thickness (i.e., lacunar infarct is usually thicker than PVS) and the lack of well-defined orientation of the CSF-like region. In this method, the anatomical brain structure, appearance model, and morphological operations were used and performed for segmentation of the lacunar infarct. Yokoyama et al. (Yokoyama, Zhang et al. 2007) also proposed a method using intensity thresholding and morphological operations to segment the lacunar infarct. Although these existing methods generate reliable results under certain conditions, many parameters such as thresholds and/or geometric constraints have to be determined heuristically. Thus, these methods often require manual intermediate steps such as the measurement of image characteristics, landmark identification, and removal of partial brain structures. Moreover, the informative contextual patterns around the PVS were not considered in the simple thresholding-based methods.

To effectively use the contextual patterns of PVSs for guiding the segmentation, we propose a novel learning-based method. So far, many learning-based methods have been proposed to segment tubular structures in other applications. These methods usually consist of a feature extraction step and a classifier learning step. For example, Staal et al. (Staal, Abramoff et al. 2004) extracted various features from a convex region defined by ridges of image derivatives, and then learned the k-NN classifier. Soares et al. (Soares, Leandro et al. 2006) used Gabor wavelet transform responses at multiple scales as features, and then learned the Gaussian mixture model for building Bayesian classifier. Ricci et al. (Ricci and Perfetti 2007) detected a line through a target voxel, and then used line strengths as well as the intensity differences between the line and surrounding pixels as the features. You et al. (You, Peng et al. 2011) also found vessel centerlines, and then computed the vessel strengths by using the steerable complex wavelet. For the methods of Ricci et al. and You et al., support vector machine was used to learn the classifier. Lupascu et al. (Lupascu, Tegolo et al. 2010) extracted a feature vector utilizing intensity, vesselness, spatial properties, and Gabor-wavelet-transform responses at multiple scales. The classifier was then trained by the AdaBoost algorithm. Marin et al. (Marin, Aquino et al. 2011) extracted a feature vector that was composed of appearance patterns and moment- invariant-based features, and then trained the classifier by using the neural network method. Fraz et al. (Fraz, Remagnino et al. 2012) extracted the feature vector utilizing the orientation analysis of gradient vector field, and then trained the classifier using an ensemble learning method. Although these methods achieve good performances for their own applications, the properties of PVSs are different from their target objects in several aspects. First, PVSs are separated into the small and thin tubular structures with various directions and widely spread in the white matter region, including centrum semiovale and subcortical nuclei. Moreover, the overall PVS area is very small due to their thin shapes, compared to the whole MR image and there are many similar tubular structures outside the white matter region (Fig. 2(a)). Therefore, it is ineffective to learn a classifier for PVS segmentation in the whole MR image with the conventional features.

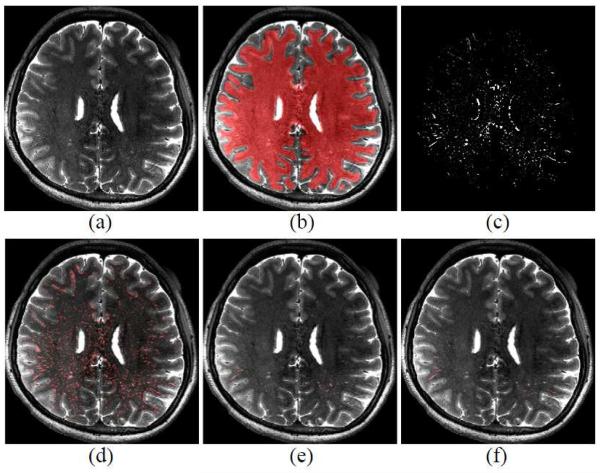
Figure 2.

(a) T2-weighted MR image, (b) dilated WM region, (c) vesselness map in the dilated WM region, (d) detected PVS ROI map by the vesselness thresholding, (e) PVS classification result, and (f) manual ground-truth.

To address these issues, we first define a region of interest (ROI) in the entire MR image as voxels with vesselness above a certain threshold within the white matter. Then, we learn a set of sequential classifiers by using the random forest model with the randomized 3D Haar features. To extract discriminative features for the tubular structures, we first normalize both the principal directions and the intensity distributions of local neighboring region, and then extract the randomized Haar features in that normalized region. In the testing stage, we predict the labels of all voxels in the ROI by using the trained sequential classifiers.

There are three major contributions in this paper. First, to the best of our knowledge, this is the first learning-based method for PVS segmentation. Unlike previous thresholding-based PVS segmentation methods, our method can learn the contextual patterns around the PVSs without any heuristic setting of threshold values. Second, our normalized features can capture consistent patterns of PVSs even in regions with intensity inhomogeneity. Moreover, since the random forest model used in our method can select informative features from a number of randomized Haar features, no specific handcrafted features are needed. Finally, our method can effectively distinguish between noisy PVS tubular structures and the ambiguous outliers by integrating the contextual features into the sequential classifiers. As a result, our method can achieve significantly higher segmentation accuracy.

2. Materials and Method

2.1. Experimental details

17 healthy volunteers aged from 25 to 37 participated in this study. Written consents were obtained from all volunteers following the guidelines provided by the institutional review board. The imaging was performed on a 7T Siemens Scanner using a 32-channel receive and a single- channel volume transmit coil (Nova Medical, Wilmington, MA). Both T1- and T2-weighted images were scanned for each subject. The T1-weighted images were acquired by the MPRAGE sequence (Mugler and Brookeman 1990) with 0.65 × 0.65 × 0.65mm³ voxel size, while the T2-weighted images were acquired by the 3D variable flip angle turbo-spin echo sequence (Busse, Hariharan et al. 2006) with 0.4 × 0.4 × 0.4 mm³ or 0.5 × 0.5 × 0.5mm ³ voxel sizes. The reconstructed images had the same voxel sizes as those acquired images, and no interpolation was applied during the image reconstruction. Details of the MR acquisition parameters are provided in Table 1.

Table 1.

The MR acquisition parameters of T1- and T2-weighted images.

	VFA-TSE (Resolution 1)	VFA-TSE (Resolution 2)	MP2RAGE
TE (ms)	457	319	1.89
TR (ms)	5000	5000	6000
Matrix size	448*362*288	512*404*208	308*304*256
Resolution (mm3)	0.48*0.48*0.50	0.41*0.41*0.40	0.65*0.65*0.65
FOV (cm3)	21.5*17.4*14.4	21.0*16.7*8.3	20.0*19.7*16.6
FA (degree)	Variable	Variable	4 (TI1), 4 (TI2)
Slice orientation	Axial	Axial	Sagittal
TI (ms)	N.A	N.A.	800/2700
GRAPPA factor	3 (PE1)	3 (PE1)	3 (PE1)
Bandwidth (Hz/Pixel)	700	349	290
Number of average	1	1	1
TA (min)	12:25	13:00	9:42

2.2. Generation of ground-truth PVS mask

To enable the training and evaluation of the proposed learning-based PVS extraction, we first generate ground-truth PVS masks by using a semi-automatic method based on the anatomical brain structure, vesselness thresholding, and geometric constraints (Wang, Catindig et al. 2012; Zong, Park et al. 2016), which is then followed by manual correction by two observers.

• ○ We first conduct intensity inhomogeneity correction and skull stripping by using the N3 correction method (Sled, Zijdenbos et al. 1998) and the Brain Extraction tool (Smith 2002), respectively on T1-weighted images. We then divide the brain into WM, GM, and CSF regions by using a method based on hidden Markov random field model (Zhang, Brady et al. 2001). Note that T1-weighted images are used for tissue segmentation since they have better gray-white matter contrast. Then the segmented tissue masks are rigidly aligned to the T2- weighted image by the Flirt registration method (Jenkinson, Bannister et al. 2002) for direct segmentation of the T2-weighted image. Afterwards, we dilate the segmented WM region for ensuring the inclusion of PVSs located at the boundaries of WM and GM. An example of such dilated WM region is shown in Fig. 2 (b).

• ○ Next, we calculate the vesselness (Frangi, Niessen et al. 1998; Shi, Shen et al. 2011; Cheng, Chen et al. 2012) for each voxel in the dilated WM region. Specifically, the T2-weighted image is used for vesselness measurement, since the contrast between PVSs and the surrounding tissues is much higher in the T2-weighted image. In particular, we pass the T2- weighted image through a Gaussian kernel with a scale s, and then compute the eigenvalues of the second derivative matrix (Hessian matrix) of kernel output. The three eigenvalues (λ₁ < λ₂ < λ₃) represent the magnitudes of derivative for their associated eigenvectors v₁, v₂, v₃, which represent three principal directions. By following the work of Frangi et al. (Frangi, Niessen et al. 1998), the vesselness V(x) of a voxel x is defined by the ratio of three eigenvalues as below:

  $$V\left(x\right)\{\begin{array}{cc}0,\hfill & if{\gamma }_2>0\text{or}{\gamma }_3>0\hfill \\ \left(1=\text{exp}\left(-\frac{{R_A}^2}{2{\alpha }^2}\right)\right)\text{exp}\left(-\frac{{R_B}^2}{2{\beta }^2}\right)\left(1-\text{exp}\left(-\frac{S^2}{2{\gamma }^2}\right)\right),\hfill & otherwise\hfill \end{array}\phantom{\}}$$ (1)

  where $R_A=\mid {\lambda }_2\mid ∕\mid {\lambda }_3\mid ,R_B=\mid {\lambda }_1\mid ∕\sqrt{\mid {\lambda }_2{\lambda }_3\mid }$, and $S=\sqrt{{{\lambda }_1}^2+{{\lambda }_2}^2+{{\lambda }_3}^2}$. The parameters a , f3 and y control the weights of R_A, R_B and S, respectively. Similar to the Frangi et al.’s work (Frangi, Niessen et al. 1998), α and β are set as 0.5, and γ is set as the half value of maximum Hessian norm in the image. If the smallest eigenvalue λ₁ is small while the other two eigenvalues λ₂ and γ₃ are relatively large, a high vesselness can be obtained with Eq. (1), and thus the respective voxel can be likely belonging to the tubular structure. More details of this vesselness measurement method can be found in (Frangi, Niessen et al. 1998). Since the thickness of PVS is often less than four voxels with our current imaging resolution, we compute the vesselness values with two small scales (s = 0.5 and s = 1) for extracting very thin or relatively thick tubular structures, and then use their maximum vesselness as the final vesselness for the respective voxel. We extract voxels with vesselness above a certain threshold value and divide the extracted voxels into connected clusters. Different vesselness thresholds are empirically chosen for different images.

• ○ Finally, the clusters with a certain range of length and thickness are set as the PVSs. Based on the prior geometric knowledge of PVS (Hernandez Mdel, Piper et al. 2013), the length range is set from 0.8 to 30 mm, while the thickness range is set from 0 to 2 mm. After generating PVS segmentations, two experienced imaging analysts manually modified the segmentations using the ITK-SNAP tool (Yushkevich, Piven et al. 2006) and the neurite tracer plugin in ImageJ (Longair, Baker et al. 2011). The manual correction is performed iteratively between the two imaging analysts until the final consensus is reached. The PVS masks are created for the entire brain in 6 subjects, while just for the right hemispheres for the remaining 11 subjects.

2.3. Learning-based PVS extraction

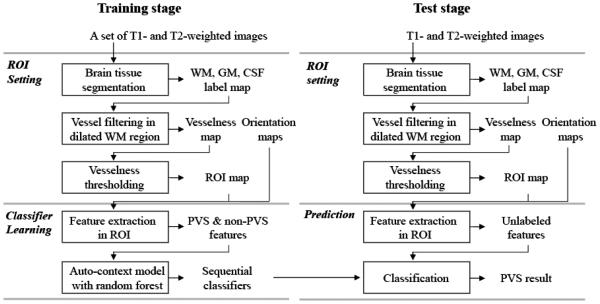
Our proposed method consists of 1) a training stage for classifier learning, and 2) a testing stage for PVS prediction, where both training and testing are applied only to voxels within an ROI. The overall procedure is shown in Fig. 1. The ROI is set as WM voxels with vesselness above a certain threshold. Unlike the thresholds used for delineating PVS for generating the ground-truth mask, the threshold for ROI definition is set to be a certain low value, such that 99% of the PVS voxels from the ground-truth masks are included in the resulting ROI. Examples of the vesselness map and its detected PVS ROI are shown in Figs 2 (c), and (d), respectively.

Figure 1.

Framework of the proposed PVS segmentation method.

2.3.1. Classifier learning

In the classifier learning step, we train a set of sequential classifiers by the random forest model with a number of randomized 3D Haar features.

• ○ First, we randomly sample the PVS and non-PVS voxels in the detected PVS ROI, with a ratio of their numbers as around 1:30. The feature vector f of each sample is directly related to the discriminative power of predictor. To capture the consistent patterns of PVSs with different orientations and intensity inhomogeneity, we first normalize both the principal directions and the intensity distribution of local region of each target sample voxel before extracting the feature vector. Specifically, when extracting the features at a target voxel x, we align its neighboring voxels ${\mathit{P}}_x=\{x_k\parallel x_k-x\mid <r\}=\{x_k\mid k=1,\dots K\}$, using the three eigenvectors v₁, v₂, v₃ as follows:

  $${{\mathit{p}}_x}^{\prime }={\left[v_1{v}_2{v}_3\right]}^T\ast {\mathit{p}}_x\prime$$ (2)

  where ${{\mathit{P}}_x}^{\prime }=\{{x_k}^{\prime }\mid k=1,\dots ,K\}$ is the set of aligned voxel positions relative to the voxel x, r is the range of local region, and K is the number of neighboring voxels. We extract a fixed- size 3D patch in the aligned local region, and then normalize the intensity distribution by the zero-mean unit-variance normalization. Here, r is determined to be the minimum radius that can make the fixed-size 3D patch completely included in the aligned local region. Four different patch sizes (5 × 5 × 5, 7 × 7 × 7, 9× 9 × 9, 11 × 11 × 11 voxels³) are tested in the training stage, and then the best one is used in the testing stage (Sec. 3.1). Fig. 3 shows typical examples of the original PVS patches, aligned PVS patches, and their (orientation and intensity) normalized PVS patches. Since we do not know which features are able to distinguish the PVS and non-PVS voxels, we extract a number of randomized Haar features in each normalized patch as follows:

  $$f\left(x\right)=\sum _{i=1}^{\theta }{\rho }_i\sum _{{{\parallel }_k}^{\prime }-x-{\mu }_i\parallel \le {\tau }_i}I\left({x_k}^{\prime }\right),$$ (3)

  where I(x_k′) denotes the intensity value of a voxel positioned at x_k′. The parameters θ, τ_i and τ_i represent the number of 3D cubic functions, polarity, center position, and size of i^th cubic function, respectively. Various Haar features can be generated by randomizing these values in Eq. (3). In this work, we randomly chose θ as 1 or 2, ρ_i as +1 or −1, ρ_i as 1 or 3, respectively. Since many informative features can be positioned near the tubular centerline, we extract more features near the tubular centerline by controlling the parameter μ_i. Specifically, μ_i is randomly selected with uniform distribution for the main direction of image derivative (i.e., the first principal direction of the aligned patch), while with the Gaussian distributions for other two directions (i.e., the second and third principal directions) within the range of patch size. In this way, more features are extracted along with the main direction.

• ○ Next, we learn the classifier using the random forest model (Criminisi, Shotton et al. 2011; Criminisi and Shotton 2013). The random forest model consists of an ensemble of decision trees randomly trained, with each decision tree t consisting of a collection of nodes and edges organized in a hierarchical structure. Each tree is a label/class predictor p_t(c|f), where c is a class index and f is a high-dimensional feature vector. The training is performed by splitting the training examples at each node in the tree. Specifically, a number of feature and threshold combinations are randomly selected to split the training examples into two groups, and then their informative gains are computed by using the entropy measure (Criminisi, Robertson et al. 2013). Among these random selections, the split is determined by the pair of feature and threshold that maximize the informative gain at the respective node. This node splitting is repeated until the tree has reached at the maximal depth. Note that the selected features and thresholds are used to build simple decision functions in the internal tree nodes, while their relevant predictors are finally established in the leaf nodes. By considering the computational time and memory, we set the tree size as 10, the maximum tree depth as 100, and the feature size as 2000, respectively.

• ○ Ending parts of thin PVSs often have weak intensity, while some non-PVSs have similar appearance patterns as the PVSs. Thus, using only the appearance model is often limited to generate robust results. To address this issue, we adopt the auto-context model to further integrate the contextual features of tubular structure into the classifier. In this model, the prediction map obtained by the previous classifier is used to extract the contextual features, with which the subsequent classifier is trained. Specifically, the first classifier is trained by the appearance features extracted from the T2-weighted image. This classifier is then applied to the training images for generating the prediction maps of training images. Next, the second classifier is trained by using the 3D Haar features extracted from both the T2-weighted image and the prediction map of the first classifier. The trained second classifier is similarly applied to the training images for generating the new prediction maps, which are used (together with the T2-weighted image) to train the third classifier. By repeating this procedure, the sequential classifiers are trained. Since the results usually converged after five iterations, we used five sequential classifiers.

Figure 3.

Demonstration of patch alignment and intensity normalization before feature extraction. (Top row): The original PVS patches extracted from the T2-weighted image; (Middle row): The orientation-aligned patches; (Bottom row): The (orientation and intensity) normalized patches.

2.3.2. PVS prediction

In the testing stage, we similarly extract the normalized Haar features at each target voxel in the detected ROI, and then pass them through the trained decision trees from the root node to a leaf node, with respect to the established decision functions of all selected nodes. Then, all the class labels in the selected leaf nodes of all decision trees are averaged, i.e., $p(c\mid f)=\frac{1}{n_t}{\sum }_t{p}_t(c\mid f)$ where n_t is the total number of trees. The class label of the underlying voxel is finally determined by the maximal prediction:

$$\widehat{c}={\text{argmax}}_{c}p(c\mid f).$$ (4)

Similar to the training stage, the label of each voxel in the detected PVS ROI is sequentially predicted by the learned sequential classifiers. An example of our PVS detection result for a testing subject is shown in Fig. 2 (e).

2.4 Comparison with other approaches

We compare our learning-based method using the normalized Haar features (LNHF) with 1) the method using simple intensity thresholding (IT), 2) the method using vesselness thresholding (VT), and 3) the learning-based method using the conventional Haar features (LHF). For fair comparison, only voxels within the segmented WM region is used in all comparison methods. In the IT method, we extract the voxels with their intensity higher than a certain value in the WM region, and then divide them into the connected clusters. Finally, we set the clusters with certain ranges of length and thickness as the final PVSs. In the VT method, we extract the voxels with their vesselness higher than a certain value in the WM region, and then set the connected clusters with certain ranges of length and thickness as the final PVSs. The threshold values for these two methods are found by cross-validations (Sec. 3.1), while the ranges of length and thickness are the same as the minimum and maximum lengths and thickness of manually-segmented PVSs in the training set. In the LHF method, the randomized Haar features are extracted in the patches that are not aligned with their respective principal directions as done in our proposed method. Except for using different features, both the LHF and LNHF methods start with the same ROI, and employ the same numbers of trees, maximum tree depth, feature size, and sequential classifiers. To find the optimal thresholds for IT and VT methods as well as the optimal parameters for LHF and LNHF methods, we divide the data into a training set and a testing set. Specifically, we use the 6 images with manual labeling of each entire image as the training set, and use the remaining 11 images with manual labeling of only the right hemisphere of each image as the testing set. Several model parameters are optimized for all comparison methods on the training set with a leave-one-out cross-validation approach, due to the limited number of training dataset. For the LHF and LNHF methods, the optimal parameters are then used for training the sequential classifiers with the entire training set. Finally, the trained sequential classifiers and the IT and VT methods with optimal thresholds are applied to the testing set.

The performance is evaluated in terms of Dice similarity coefficient (DSC), sensitivity (SN), and positive prediction value (PPV) as defined below:

$$\begin{array}{c}\hfill \text{DSC}=\frac{2\text{TP}}{2\text{TP}+\text{FP}+\text{FN}},\hfill \\ \hfill \text{SN}=\frac{\text{TP}}{\text{TP}+\text{FN}},\hfill \\ \hfill \text{PPV}=\frac{\text{TP}}{\text{TP}+\text{FP}},\hfill \end{array}$$ (5)

where TP, FP, FN denote the true positive, false positive, and false negative, respectively, as further illustrated in Table 2. DSC represents the ratio of total number of correctly classified voxels to the average number of all predicted PVS voxels and all true PVS voxels. Thus, it shows the overall classification performance, considering both the false positive and false negative cases. SN represents the ratio of total number of correctly classified PVS voxels to the total number of the true PVSs, and thus shows how many PVSs are not detected by an algorithm. On the other hand, PPV presents the ratio of total number of correctly classified PVS voxels to the total number of predicted PVS, and thus shows how many outliers are detected by an algorithm.

Table 2.

PVS classification

	PVS present	PVS absent
PVS detected	True Positive (TP)	False Positive (FP)
PVS not detected	False Negative (FN)	True Negative (TN)

Besides evaluating the segmentation performance with voxel-wise comparison, we also perform cluster-wise comparison, since the PVSs can be separated as small thin clusters and the number of clusters and their geometric properties (such as volume, length, and thickness) are closely related to the brain abnormalities (Maclullich, Wardlaw et al. 2004; Rouhl, van Oostenbrugge et al. 2008; Doubal, MacLullich et al. 2010). For this purpose, the cluster-wise detection ratios are defined as follows. Specifically, we divide both the automated segmentation result and its ground-truth into connected clusters, and then count the numbers of true positive, false positive, and false negative in terms of clusters. If a part of cluster in the automated segmentation result overlaps with a part of cluster in the manual ground-truth, we set this cluster as a true positive cluster. On the other hand, if a cluster is in the automated segmentation result, but not in the manual ground-truth, we set this cluster as a false positive cluster. Similarly, if a cluster is in the manual ground-truth, but not in the automated segmentation result, we set this cluster as a false negative cluster. Finally, the DSC, SN, PPV scores were calculated from the numbers of true positive, false positive, and false negative clusters.

To demonstrate that our proposed method can be used for quantitative study of PVSs, we also evaluate the cluster-wise segmentation performance in four sub-regions of the brain (i.e., the frontal lobe, parietal-occipital lobe, temporal lobe, and subcortical region), as well as the similarity of geometric properties between the predicted and true PVSs. The morphological PVS features extracted from different methods are computed by the volume (V), length (L), and diameter (D) of each cluster in the manual ground-truth and in the segmentation results by the VT and LNHF methods. Then, we compare these three distributions in each sub-region and the entire brain. To measure the length L, we first extract the centerline of tubular structure by using a thinning algorithm (Lee, Kashyap et al. 1994; Kerschnitzki, Kollmannsberger et al. 2013), and then compute the manifold distance of the longest path connecting any pair of voxels within the thinned cluster. The diameter D of each cluster is calculated as: $D=2\sqrt{V∕L\pi }$.

2.5 Simulation

To demonstrate the potential ability of our method against motion artifacts and other subcortical lesions, we generate two types of simulation images with motion artifacts and lacunes. The motion artifacts are simulated by adding random phase noise to the k-space images. Specifically, the magnitude images of the original TSE images are inversely transformed with Fourier transformation along all three spatial dimensions to obtain the k-space images. Then, a random phase shift is applied to each k-space data point. Since the phase noise caused by motion is proportional to the product of motion (i.e., head displacement) and the zero-order moments of the phase encoding gradients, the phase noise at each k-space position is simulated as: $2\pi [{\sigma }_y\cdot (\frac{n_y}{N_y}-0.5)+{\sigma }_z\cdot (\frac{n_z}{N_z}-0.5)]$, where N_y and N_z are the numbers of phase encoding steps along the y (left-right) and z (inferior-superior) directions, respectively, n_y (= 0, 1, … N_y − 1) and n^z(= 0, 1, … N_z − 1) are the phase encoding step indices, and a_y and a_z are two random numbers from a Gaussian distribution with zero mean and standard deviation of 0.4, where the standard deviation is proportional to the severity of motion. The value of 0.4 was chosen to achieve motion artifact levels comparable to those in typical clinical images. We assume no motion along the anterior-posterior direction because our subjects are lying on the back of their heads and thus motion along the anterior-posterior direction is less likely to happen. The lacunes are simulated by modifying image intensities of voxels near the PVSs. Specifically, we randomly select 20% of PVSs in each subject and dilate the masks of selected PVSs using a dilation filter with 5 × 5 × 5 voxels (2.0~2.5 mm³). For each dilated region, we compute the difference between the mean intensities of the PVS and the dilated region, and then increase the intensities of the dilated region with that difference. We apply the IT, VT, LHF, and LNHF methods to these two types of simulation images and then compare their voxel- and cluster-wise accuracies.

3. Results

3.1 Model Learning and Optimization

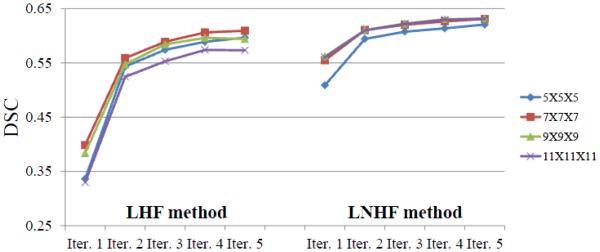
We tested six intensity threshold values (250, 300, 350, 400, 450, 500) for the IT method and six vesselness threshold values (0.002, 0.003, 0.004, 0.005, 0.006, 0.007) for the VT method. The average DSC of the IT method was from 0.12 to 0.34 for the six intensity thresholds, and the best DSC was obtained with the threshold value 300. On the other hand, the DSC of the VT method was from 0.37 to 0.52 for the six vesselness thresholds, and the best DSC was obtained with the threshold value 0.006. In both the LHF and LNHF methods, the segmentation accuracies were gradually improved and then converged as the numbers of trees and features increased. Fig. 4 shows the average DSC scores for five sequential predictions with the different patch sizes. Fig. 5 shows how the prediction maps and segmentation results change with respect to the sequential predictions. When using only the appearance features in the first iteration, the DSC was from 0.29 to 0.37 by the LHF method, while from 0.51 to 0.56 by the LNHF method. In the fifth iteration, the DSC was from 0.57 to 0.61 by the LHF method, while from 0.62 to 0.64 by the LNHF method. The best scores were obtained with the patch size 7 × 7 × 7 for both methods. Table 3 reports the respective average DSC, SN, and PPV scores. It can be observed that our proposed LNHF method outperformed all comparison methods in terms of all three scores.

Figure 4.

The average DSC scores for five sequential predictions, with respect to the use of 4 different patch sizes. For both LHF and our proposed LNHF methods, their scores were significantly improved by the second iteration, and then gradually converged.

Figure 5.

Segmentation refinement using the auto-context model. (a) and (e) show MR image and its manual ground-truth labels, respectively. (b), (c), and (d) show the prediction maps obtained by the first, second, and fifth classifiers, respectively; and (f), (g), and (h) show the segmentation results obtained by the prediction maps in (b), (c), and (d), respectively. By repeating the prediction steps, the tubular structures become clearer and clearer (as indicated by yellow arrows), while small outlier voxels become weaker and weaker (as indicated red arrows).

Table 3.

The average (standard deviation) of DSC, SN, and PPV scores for six fully-labeled images. (Iter. 1) denotes the prediction using the first classifier, while (Iter. 5) denotes the prediction using the fifth classifier. The best scores are highlighted as boldface.

	IT	VT	LHF		LNHF
			(Iter.1)	(Iter.5)	(Iter.1)	(Iter.5)
DSC	0.34 (0.09)	0.52 (0.05)	0.40 (0.07)	0.61 (0.04)	0.55 (0.05)	0.64 (0.04)
SN	0.32 (0.16)	0.54 (0.16)	0.28 (0.08)	0.57 (0.09)	0.47 (0.09)	0.59 (0.08)
PPV	0.46 (0.13)	0.56 (0.12)	0.72 (0.05)	0.71 (0.06)	0.74 (0.07)	0.73 (0.07)

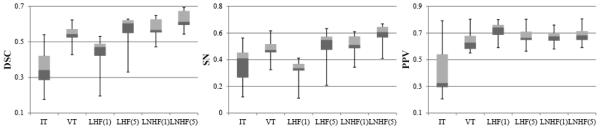
3.2. Model testing

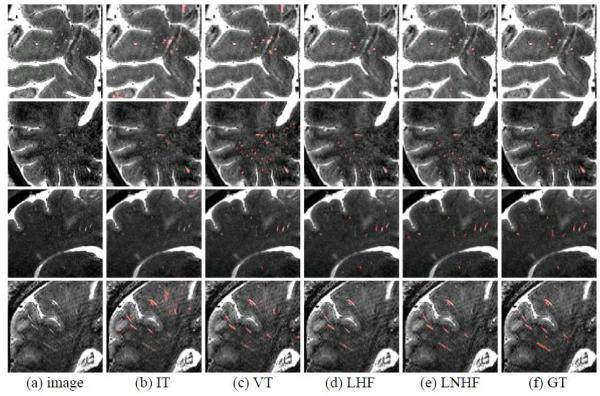
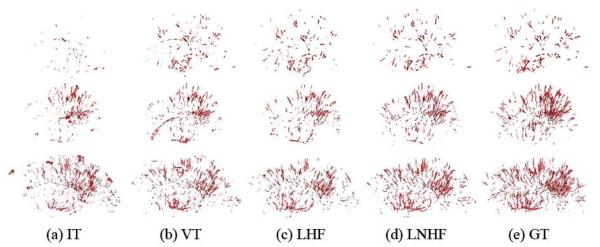
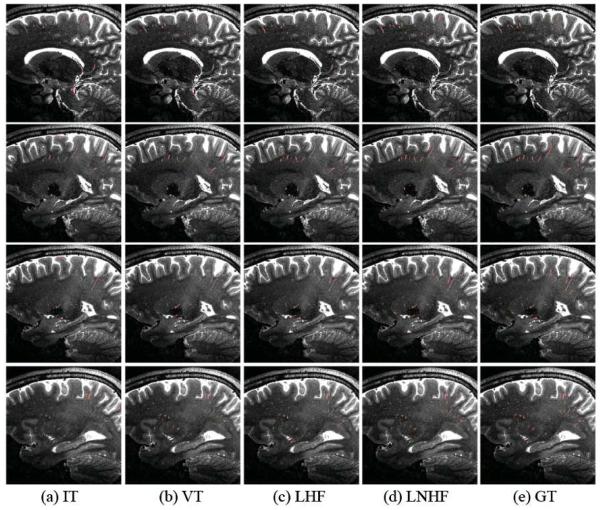
The methods, with the optimal parameters determined by the 6 training images, were then applied to the 11 testing images. Since the labels of testing images were created only in the right hemisphere, each brain image was first separated into the left and right hemispheres by an existing method (Li, Nie et al. 2013). Then, the prediction was conducted on the right hemisphere. Table 4 and Fig. 6 show the average (standard deviation) DSC, SN, PPV scores and their respective distributions for the voxel-wise segmentation accuracy. Table 5 shows the number of PVSs and the DSC, SN, PPV scores of the cluster-wise segmentation accuracy. Figs. 7 and 8 show typical examples of qualitative results in both 2D slice views and 3D rendering views. Fig. 9 further shows qualitative results on several sagittal slices extracted from the subject with large amount of PVSs as shown in the bottom row of Fig. 8.

Table 4.

The average (standard deviation) of DSC, SN, and PPV scores for 11 testing images. (Iter. 1) denotes the prediction result using the first classifier, while (Iter. 5) denotes the prediction result using the fifth classifier. The best scores are highlighted as boldface.

	IT	VT	LHF		LNHF
			(Iter.1)	(Iter.5)	(Iter.1)	(Iter.5)
DSC	0.35 (0.11)	0.54 (0.06)	0.44 (0.09)	0.56 (0.09)	0.58 (0.06)	0.63 (0.05)
SN	0.36 (0.15)	0.48 (0.08)	0.32(0.09)	0.51 (0.12)	0.52 (0.08)	0.59 (0.08)
PPV	0.43 (0.22)	0.64 (0.08)	0.72 (0.07)	0.67 (0.07)	0.67 (0.05)	0.68 (0.06)

Figure 6.

The distributions of DSC, SN, and PPV scores for 11 testing images. The top, center, and bottom lines of each box represent the upper quartile, median, and lower quartile scores, respectively; and also the upper and lower whiskers represent the maximum and minimum scores, respectively.

Table 5.

Evaluation of the cluster-wise segmentation performance with 11 testing images. The number of PVS is shown in the second column, while the DSC, SN, PPV scores are shown in the right columns. The best scores are highlighted as boldface.

ID	# of PVS	DSC				SN				PPV
		IT	VT	LHF	LNHF	IT	VT	LHF	LNHF	IT	VT	LHF	LNHF
1	274	0.50	0.7	0.71	0.72	0.36	0.65	0.6	0.64	0.83	0.77	0.86	0.84
2	299	0.47	0.57	0.63	0.74	0.55	0.57	0.56	0.69	0.41	0.57	0.71	0.79
3	124	0.44	0.66	0.75	0.78	0.57	0.75	0.82	0.8	0.36	0.59	0.69	0.76
4	448	0.60	0.71	0.72	0.76	0.46	0.7	0.71	0.73	0.75	0.72	0.73	0.78
5	187	0.34	0.56	0.64	0.72	0.21	0.52	0.58	0.66	0.66	0.6	0.71	0.79
6	125	0.30	0.61	0.68	0.67	0.19	0.77	0.77	0.71	0.62	0.51	0.62	0.64
7	579	0.52	0.68	0.72	0.78	0.36	0.58	0.65	0.72	0.79	0.82	0.8	0.86
8	319	0.46	0.65	0.69	0.80	0.39	0.78	0.66	0.78	0.56	0.56	0.73	0.81
9	480	0.52	0.64	0.69	0.76	0.66	0.67	0.67	0.76	0.43	0.61	0.71	0.77
10	240	0.41	0.57	0.65	0.72	0.72	0.59	0.59	0.66	0.29	0.55	0.73	0.80
11	207	0.27	0.57	0.42	0.61	0.57	0.71	0.28	0.46	0.17	0.48	0.85	0.93
Avg.	298	0.44	0.63	0.66	0.73	0.46	0.66	0.63	0.69	0.53	0.62	0.74	0.80
Std.	148	0.10	0.06	0.09	0.05	0.17	0.09	0.14	0.09	0.22	0.11	0.07	0.07

Figure 7.

Qualitative PVS segmentation results by IT, VT, LHF, and LNHF methods (from 2nd to 5th columns), with the manual ground-truth (GT) shown in the last column.

Figure 8.

The 3D rendering of PVS segmentation results on the sagittal view, for the subjects with small amount of PVS (first row), moderate amount of PVS (second row), and large amount of PVS (third row), respectively. The results of IT, VT, LHF, and LNHF methods are shown from 1st to 4th columns, with the manual ground truth (GT) shown in the last column.

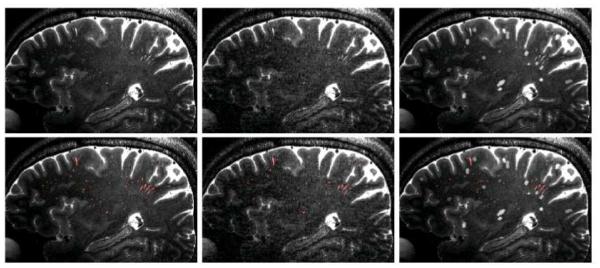
Figure 9.

PVS segmentation results in four different sagittal slices (along the inferior-superior direction) for the subject with large amount of PVS shown in the last row of Fig. 8. The results by the IT, VT, LHF, and LNHF methods are shown from 1st to 4th columns, with the manual ground-truth (GT) shown in the last column.

3.3. Morphological Properties

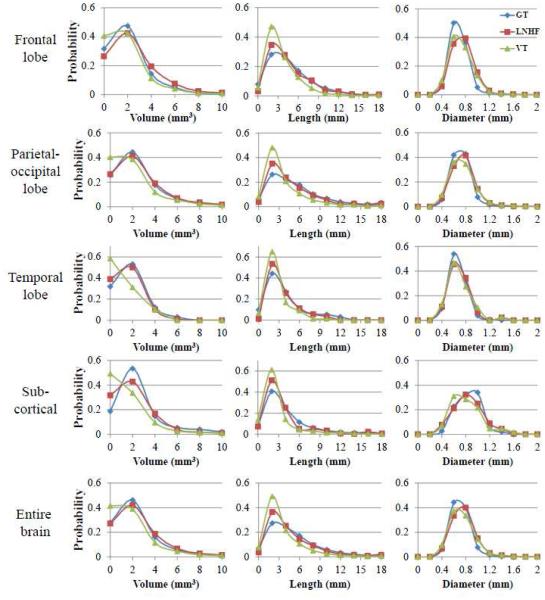
Table 6 shows the number of PVSs and the cluster-wise segmentation accuracy in the four sub- regions and the entire brain. In our testing dataset, 37.5%, 55.5%, 3.4%, and 3.6% of PVSs were positioned in the frontal lobe, parietal-occipital lobe, temporal lobe, and subcortical region, respectively. Our proposed LNHF method outperformed the other methods in almost all sub- regions and entire brain except for the SN score in the parietal-occipital lobe. Fig. 10 shows the volume (V), length (L), and diameter (D) distributions of the predicted and true PVSs in the four sub-regions and the entire brain. Compared to the other segmentation methods, the distributions for LNHF resemble more closely to the distributions of the ground-truth.

Table 6.

The cluster-wise segmentation performance in the frontal lobe, parietal-occipital lobe, temporal lobe, subcortical region, and entire brain region, respectively. The number of PVS in each region is shown in the second column, while the DSC, SN, PPV scores are shown in the right columns. The best scores are highlighted as boldface.

		DSC				SN				PPV
Region	# of PVS	IT	VT	LHF	LNHF	IT	VT	LHF	LNHF	IT	VT	LHF	LNHF
Frontal	1231	0.46	0.66	0.73	0.79	0.41	0.58	0.63	0.72	0.51	0.76	0.87	0.88
Parietal	1822	0.47	0.65	0.66	0.73	0.52	0.71	0.63	0.69	0.43	0.61	0.70	0.78
Temporal	110	0.44	0.51	0.62	0.67	0.43	0.45	0.53	0.62	0.45	0.58	0.73	0.75
Sub-cort.	119	0.30	0.42	0.54	0.65	0.42	0.67	0.75	0.78	0.24	0.30	0.43	0.55
Entire	3282	0.46	0.64	0.68	0.75	0.48	0.65	0.63	0.70	0.44	0.63	0.74	0.80

Figure 10.

The distributions of PVS volume (left), length (middle), and diameter (right) in the frontal lobe (1st row), parietal-occipital lobe (2nd row), temporal lobe (3rd row), subcortical region (4th row), and entire region (5th row) of brain. GT, LNHF, and VT denote the manual ground-truth (blue), our proposed LNHF (red), and the vesselness thresholding method (green), respectively.

3.4. Simulations

The two types of simulation images are shown in Fig. 11. Tables 7 and 8 provide the DSC, SN, and PPV for the voxel-wise and cluster-wise analyses, respectively. For the second simulation regarding the impact of lacunes, 11.8%, 22.4%, 2.0%, and 1.6% of lacunes were detected as PVSs (false positive) by the IT, VT, LHF, and LNHF methods, respectively. Since the simulation images included more ambiguous outliers, the overall performances decreased for all of the comparison methods. However, our LNHF method still outperformed other comparison methods for the most cases.

Figure 11.

Typical 2D slice views from the two types of simulation images (top) and their segmentation results (bottom). The slice views from an original image and its corresponding images with simulated motion artifact and simulated lacunes are shown in the left, middle, and right, respectively.

Table 7.

The voxel-wise segmentation accuracy for the simulation images with motion artifacts (simulation 1) and lacunes (simulation 2). The best scores are highlighted as boldface.

		IT	VT	LHF		LNHF
				(Iter.1)	(Iter.5)	(Iter.1)	(Iter.5)
Simulation 1	DSC	0.27 (0.12)	0.46 (0.06)	0.26 (0.08)	0.44 (0.09)	0.46 (0.07)	0.52 (0.06)
	SN	0.27 (0.09)	0.38 (0.06)	0.17 (0.06)	0.36 (0.11)	0.37 (0.07)	0.48 (0.08)
	PPV	0.36 (0.22)	0.58 (0.10)	0.58 (0.09)	0.57 (0.08)	0.58 (0.08)	0.57 (0.07)
Simulation 2	DSC	0.29 (0.10)	0.46 (0.05)	0.41 (0.10)	0.51 (0.09)	0.52 (0.06)	0.57 (0.05)
	SN	0.29 (0.08)	0.47 (0.06)	0.32 (0.10)	0.48 (0.13)	0.46 (0.09)	0.55 (0.10)
	PPV	0.31 (0.16)	0.47 (0.06)	0.56 (0.06)	0.56 (0.07)	0.56 (0.05)	0.58 (0.07)

Table 8.

The cluster-wise segmentation accuracy for the simulation images with motion artifacts (simulation 1) and lacunes (simulation 2). The best scores are highlighted as boldface.

		IT	VT	LHF		LNHF
				(Iter.1)	(Iter.5)	(Iter.1)	(Iter.5)
Simulation 1	DSC	0.31 (0.12)	0.53 (0.06)	0.52 (0.09)	0.54 (0.08)	0.62 (0.05)	0.63 (0.05)
	SN	0.38 (0.11)	0.55 (0.08)	0.42 (0.12)	0.46 (0.12)	0.57 (0.08)	0.58 (0.08)
	PPV	0.34 (0.22)	0.53 (0.12)	0.73 (0.12)	0.70 (0.09)	0.70 (0.10)	0.70 (0.08)
Simulation 2	DSC	0.31 (0.14)	0.51 (0.06)	0.58 (0.06)	0.59 (0.08)	0.64 (0.04)	0.67 (0.06)
	SN	0.42 (0.11)	0.61 (0.08)	0.57 (0.13)	0.57 (0.14)	0.65 (0.10)	0.64 (0.12)
	PPV	0.28 (0.17)	0.45 (0.09)	0.63 (0.09)	0.66 (0.09)	0.65 (0.10)	0.72 (0.08)

4. Discussion

We compared the segmentation accuracy between our LNHF method and other three methods (IT, VT, and LNH). Although the N3 correction method (Sled, Zijdenbos et al. 1998) was performed to address intensity inhomogeneity in the WM region, it was difficult to ensure a consistent intensity distribution for all PVSs. Due to inconsistent intensities of PVSs, the IT method could not find a single threshold that was suitable for all testing images. Thus, the IT method often either detected many outliers as the PVSs or missed many true PVSs. On the other hand, the VT method gave much better and robust results by considering the local structure. However, outliers with tubular structures near the boundaries between WM and GM were often extracted as PVSs (Figs. 7 and 8). Moreover, thin tubular structures (e.g., with the thickness less than 2 voxels) were often not extracted. Compared to these thresholding-based methods (IT and VT), the LHF method gave better segmentation accuracy by incorporating segmentation contextual patterns into the training of classifiers. Nonetheless, the discriminative power of classifier was still limited due to the use of inconsistent features. Especially, the accuracy of LHF method with the first classifier was often worse than that of VT method, since it was hard to capture the consistent appearance patterns of PVSs by using the conventional Haar features. On the other hand, our proposed LNHF method outperformed both thresholding-based methods, even using only the appearance features. Moreover, it is worth emphasizing that our proposed LNHF method is much more robust against the use of different patch size. As shown in the right panel of Fig. 4, the DSC scores of our proposed LNHF method were comparable with respect to the use of different patch size (i.e., 7 × 7 × 7, 9× 9 × 9, 11 × 11 × 11), since our method was able to consistently extract Haar features near the tubular centerline.

In both learning-based (LHF and LNHF) methods, many ambiguous PVS voxels were not classified as PVSs in the first iteration. Thus, although these two methods obtained the best PPV scores with the first classifiers in both training and testing stages (Tables 3 and 4), they also had high false negative errors. As a result, the DSC and SN scores in the first iteration were much lower than those in the final iteration. As the prediction was repeated iteratively, the accuracy of each of these two learning-based methods was progressively improved. Specifically, by integrating the contextual features into the training of sequential classifiers, the tubular structures were more clearly detected, while many small outlier voxels were removed, as shown in Fig. 5. Finally, the false negative errors were significantly reduced in the final iteration, while still keeping the comparable PPV score as in the beginning.

Our proposed LNHF method also outperformed all other methods in terms of both the subject- and region-wise segmentation accuracies as shown in Tables 5 and 6, respectively. Specifically, our method achieved the average DSC gains of 32%, 10%, and 7%, compared to the IT, VT, and LHF methods. Note that the VT method identified many ambiguous structures as the PVSs, and thus its SN score was slightly higher than our method in the parietal-occipital lobe. But its DSC and PPV scores were much lower than our method, due to its high false positive errors. Compared to the previous PVS rating scales that were often measured by the number of PVS on the partial 2D slices, we found much larger numbers of PVS (i.e., a few hundred vs. a few tens), even in the healthy young subjects. We believe that, with the optimized imaging sequence and PVS segmentation approaches we have developed, the PVS can be quantified in much greater details (such as obtaining the length, diameter, and volume distributions), compared to the previous PVS rating scales.

Regarding the geometric properties (Fig. 10), the VT method often over-segmented the PVSs and resulted in many small segments with volumes less than 1 mm³. Since these small segments partially overlapped with the true PVSs, the VT method often obtained good SN score in terms of the cluster-wise accuracy. However, in terms of voxel-wise accuracy, the VT method had high false positive error rates as well as low DSC score because only small parts of PVS overlapped with the ground truth. On the other hand, our proposed LNHF method could reliably segment the PVSs with various sizes. Compared to the manual ground-truth, our method segmented slightly more clusters with short lengths (around 2-3 mm). This was mainly because of the challenge of accurately segmenting the ending parts of PVSs due to their ambiguous appearance as shown in Figs. 5 (e)-(h). However, the overall shapes of volume and length distributions were more similar to those of manual ground-truth, compared to the VT method. The diameters of most predicted and true PVSs were less than 1 mm, and there was no significant difference between two methods.

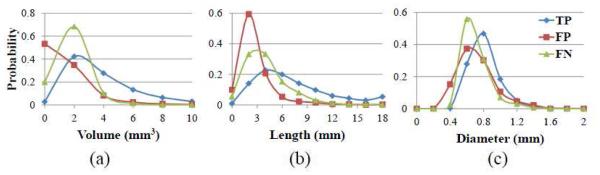
To analyze the tendency of segmentation errors, we further provide the distributions of volume, length, and diameter for the true positive, false positive and false negative clusters in Fig. 12. As can be seen, the volumes and lengths of most false positive clusters were relatively small and short, while the volumes and lengths of most false negative clusters were larger than those of false positive clusters, but less than those of true positive clusters. The diameters of most false positive and false negative clusters were also thinner than those of the true positive clusters. Fig. 12 indicates that most false positive and false negative errors of our method occur in very ambiguous cases, such as the PVSs with the short length (i.e., less than 2 mm, or 4-5 voxels) and with the thin diameter (i.e., less than 0.8 mm, or 1-2 voxels). Since these PVSs are similar to some outliers in the WM region, it is often ambiguous even for the observers to manually delineate them. On the other hand, most PVSs with long length and thick diameter are well classified by our proposed method. Since the PVSs are dilated in variable neurological diseases, our method may be especially useful for the study of PVS abnormality in such patients.

Figure 12.

The distributions of PVS volume (a), length (b), and diameter (c) for the true positive (TP), false positive (FP), and false negative (FN) clusters, respectively.

A potential limitation of our work is that the validations were conducted using the high- resolution images obtained from healthy young subjects. It is desirable to apply our method to clinical scenarios, where MR images are often acquired with shorter acquisition times and/or lower spatial resolution, along with motion artifacts and subcortical lesions (e.g., white matter hyperintensities/lacunes). Based on the simulation images, we have demonstrated that our method is more robust than other comparison methods for the cases with motion artifacts and lacunes (Section 3.4). In clinical populations, subcortical lesions such as WM hyperintensities can also coexist with PVSs. However, since such lesions are usually more distinct from PVSs than lacunes, our method may be more robust compared to the thresholding based methods. Another issue is that the increase of PVS density can make the gap between PVSs decrease. Although these effects may increase the ambiguity, we expect that our method will be able to learn the related patterns during the classifier learning phase, if enough training data with similar patterns are available. Specifically, a potential approach is to use cluster-wise information along the tubular centerline of the tentatively-segmented PVSs, such as intensity distribution or geodesic distance (Bai and Sapiro 2007), to distinguish the complex patterns. Regarding the motion artifacts, the current imaging sequence takes about 12 - 13 mins, which would be challenging for elderly subjects and patients, which are the target subjects in our future study. For these subjects, we are currently exploring different rapid acquisition approaches such as the variable flip angle GRASE sequences and compressed sensing image reconstruction. Finally, image resolution is another significant issue because it is difficult to acquire the 7T high- resolution images at lower fields. Since the contrast-to-noise ratio of image is generally higher at lower resolution and our method works well on thin PVS, we expect our approach to be applicable at millimeter resolution as well. However, due to the small size of PVS in normal subjects (0.13 – 0.96 mm; (Pesce and Carli 1988)), 1 mm resolution is unlikely to provide accurate characterization of the PVS morphology, especially in healthy young subjects. We expect that our method will be applicable to the lower-resolution images scanned from old subjects or patients due to their high density of PVSs. Accordingly, there are still some challenges on clinical imaging application of our method on the aging and patient populations such as with the focal atrophy, diffuse and punctate WM hyperintensities, loss in WM density, cerebral microbleeds and juxtacortical lesions. In the future, we will apply our method to quantitatively study the development of PVS abnormality in patients with neurological diseases, such as small vessel disease, multiple sclerosis, and Alzheimer’s disease (Doubal, MacLullich et al. 2010; Cai, Tain et al. 2015; Kilsdonk, Steenwijk et al. 2015).

5. Conclusion

We have proposed a learning-based method for PVS segmentation. Our method can effectively learn the intensity and contextual patterns of PVSs by using the (orientation and intensity) normalized Haar features, and train the sequential classifiers using the random forest model. Our method outperforms both the thresholding-based methods and a learning-based method using conventional Haar features. Our method can be used for future quantitative studies of PVS morphology which may help illuminate their relationship with neurological diseases.