A multivariate nonlinear mixed effects model for longitudinal image analysis: Application to amyloid imaging

Abstract

It is important to characterize the temporal trajectories of disease-related biomarkers in order to monitor progression and identify potential points of intervention. These are especially important for neurodegenerative diseases, as therapeutic intervention is most likely to be effective in the preclinical disease stages prior to significant neuronal damage. Neuroimaging allows for the measurement of structural, functional, and metabolic integrity of the brain at the level of voxels, whose volumes are on the order of mm³. These voxelwise measurements provide a rich collection of disease indicators. Longitudinal neuroimaging studies enable the analysis of changes in these voxelwise measures. However, commonly used longitudinal analysis approaches, such as linear mixed effects models, do not account for the fact that individuals enter a study at various disease stages and progress at different rates, and generally consider each voxelwise measure independently. We propose a multivariate nonlinear mixed effects model for estimating the trajectories of voxelwise neuroimaging biomarkers from longitudinal data that accounts for such differences across individuals. The method involves the prediction of a progression score for each visit based on a collective analysis of voxelwise biomarker data within an expectation-maximization framework that efficiently handles large amounts of measurements and variable number of visits per individual, and accounts for spatial correlations among voxels. This score allows individuals with similar progressions to be aligned and analyzed together, which enables the construction of a trajectory of brain changes as a function of an underlying progression or disease stage. We apply our method to studying cortical β-amyloid deposition, a hallmark of preclinical Alzheimer's disease, as measured using positron emission tomography. Results on 104 individuals with a total of 300 visits suggest that precuneus is the earliest cortical region to accumulate amyloid, closely followed by the cingulate and frontal cortices, then by the lateral parietal cortex. The extracted progression scores reveal a pattern similar to mean cortical distribution volume ratio (DVR), an index of global brain amyloid levels. The proposed method can be applied to other types of longitudinal imaging data, including metabolism, blood flow, tau, and structural imaging-derived measures, to extract individualized summary scores indicating disease progression and to provide voxelwise trajectories that can be compared between brain regions.

1. Introduction

It is important to characterize the temporal trajectories of disease-related biomarkers in order to monitor progression and to identify potential points of intervention. Such a characterization is especially important for neurodegenerative diseases, as therapeutic intervention is most likely to be effective in the preclinical disease stages prior to significant neuronal damage. For example, in Alzheimer's disease, brain changes evident in structural, functional, and metabolic imaging may occur more than a decade before the onset of cognitive symptoms (Bateman et al., 2012), with cortical amyloid-β (Aβ) accumulation being one of the earliest changes (Jack et al., 2013; Sperling et al., 2014a; Villemagne et al., 2013). Such brain changes can be measured using neuroimaging techniques and can be tracked over time at the individual level via longitudinal studies.

Given the focus on preventing and delaying the onset of incurable neurodegenerative diseases, the emphasis of clinical trials has shifted to studying clinically normal individuals with positive biomarkers, for example those exhibiting brain amyloid in the case of AD, in order to identify early intervention opportunities in the preclinical stages of disease (Sperling et al., 2014b). It is important to determine the temporal trajectories of hypothesized biomarkers in the early disease stages in order to better understand their associations with disease progression. Current neuroimaging methods allow for the characterization of the brain at the mm³ level, generating hundreds of thousands of measurements that can be used as potential biomarkers of neurodegenerative diseases. Understanding the temporal trajectories of these voxelwise measurements can provide clues into disease mechanisms by identifying the earliest and fastest changing brain regions.

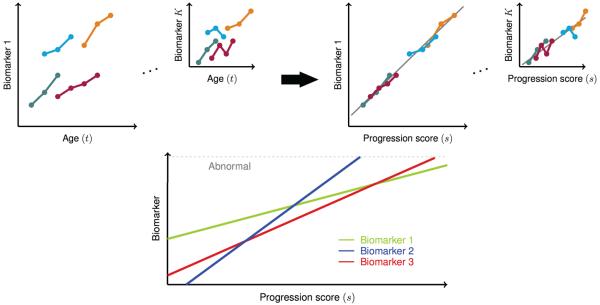
Changes in voxelwise neuroimaging measurements over time are commonly studied using linear mixed effects models (Bernal-Rusiel et al., 2012, 2013; Ziegler et al., 2015). Univariate linear mixed effects models use time or age to characterize changes in a single imaging measure. However, time or age may not be the appropriate metric for measuring disease progression due to variability across individuals. While covariates can be included in linear mixed effects models to account for this variability, choosing the correct set of covariates is difficult and covariates generally have a more complicated association with disease progression than the assumed linear relationship of linear mixed effects models. Instead, this variability can be accounted for by aligning individuals in time based on their longitudinal biomarker profiles within a multivariate framework. This is the premise of the Disease Progression Score method, which has been applied to studying changes in cognitive and biological markers related to Alzheimer's disease (Jedynak et al., 2012, 2014; Bilgel et al., 2014). It is assumed that there is an underlying progression score (PS) for each subject visit that is an affine transform of the subject's age, and given this PS, it is possible to place biomarker measurements across a group of subjects onto a common timeline. The affine transformation of age removes across-subject variability in baseline biomarker measures as well as in their rates of longitudinal progression. Each biomarker is associated with a parametric trajectory as a function of PS, whose parameters are estimated along with the PS for each subject. This allows one to “stitch” data across subjects to obtain temporal biomarker trajectories that fit an underlying model (Fig. 1).

Figure 1.

Illustration of the biomarker alignment concept in the progression score model. The biomarkers we consider in this work are PET measures of cerebral amyloid across a total of K ≈ 30, 000 voxels. Top: Progression score (PS) aligns longitudinal measures better than age, and allows for the estimation of a trajectory for each biomarker/voxel (in gray). Bottom: Estimated biomarker trajectories can be compared on the common PS scale. For references to color, the reader is referred to the web version of this article.

Previous approaches have used certain cognitive measures, such as ADAS-Cog (Caroli and Frisoni, 2010; Yang et al., 2011), MMSE (Doody et al., 2010) or CDR-SB (Delor et al., 2013) as a surrogate for disease progression to delineate the trajectories of other AD-related cognitive measurements. These methods operate with the assumption that disease progression is reflected by a single cognitive measurement rather than a profile of multiple measurements, and therefore are inherently limited in their characterization of disease evolution. Younes et al. (2014) fitted a piecewise linear model to longitudinal data assuming that each biomarker becomes abnormal a certain number of years before clinical diagnosis, and this duration was estimated for each biomarker to yield longitudinal trajectories as a function of time to diagnosis. A quantile regression approach was employed by Schmidt-Richberg et al. (2015) to align a sample of cognitively normals and mild cognitively impaired (MCI) with a sample of MCI and AD, and then to estimate biomarker trajectories. These approaches assume that all individuals are on a path to disease and require knowledge of clinical diagnosis. Therefore, they are not suitable for studying the earliest changes in individuals who have not converted to a clinical diagnosis. Donohue et al. (2014) applied a self-modeling regression model within a multivariate framework to characterize the longitudinal trajectories of a set of cognitive, CSF, and neuroimaging-based biomarkers. This approach allows for across-subject variability only in the age of onset, not in progression speed. Models incorporating fixed effects as well as individual-level random effects have been proposed to study ADAS-Cog (Ito et al., 2011; Schiratti et al., 2015b) and regional cortical atrophy (Schiratti et al., 2015b), and Schulam et al. (2015) used a spline model that incorporates longitudinal clustering and modeling of individual-level effects to study trajectories of scleroderma markers. These mixed effects models take into consideration each measure separately rather than using them within a unifying framework. Others have used event-based probabilistic frameworks to determine the ordering of changes in longitudinal biomarker measures as well as the appropriate thresholds for separating normal from abnormal measures (Fonteijn et al., 2012; Young et al., 2014). These methods characterize longitudinal biomarker trajectories in a discrete framework rather than a continuous one. Schiratti et al. (2015a) proposed an extension to their earlier approach to model multiple measures together. Biomarker trajectories are assumed to be identical except for a shift along the disease timeline, and this assumption prevents hypothesis testing regarding rate of change across biomarkers. Furthermore, biomarkers are assumed to be conditionally independent given the subject-level random effects, but this assumption is not realistic when biomarkers are voxel-based neuroimaging measurements.

Here, we adapt the disease progression score principle to studying longitudinal neuroimaging data by making substantial innovations to the progression score model and parameter estimation procedure. First, voxelwise imaging measures constitute the biomarkers in the model, and are analyzed together in a multivariate framework. Studying progression at the voxel level rather than using region of interest (ROI)-based measures allows for the discovery of patterns that may not be confined within any given ROI. Second, since voxelwise imaging measures have an underlying spatial correlation, we incorporate the modeling of the spatial correlations among the biomarker error terms. Modeling spatial correlations makes the inference of the subject-specific progression scores less susceptible to the inherent correlations among the voxels. Third, we incorporate a bivariate normal prior on the subject-specific variables that define the relationship between age and PS. The prior allows a better modeling of the variance within individuals and enables the incorporation of individuals with a single visit into the model fitting procedure. Fourth, instead of using an alternating least-squares approach for parameter estimation as presented by Jedynak et al. (2012), we formulate the model fitting as an expectation-maximization (EM) algorithm, which guarantees convergence to a local maximum and allows for an efficient model fitting framework for a large number of biomarkers. Finally, we present a statistical framework for comparing the onset and rate of progression across different regions. This paper extends our previous approach for analyzing longitudinal voxelwise imaging measures using the progression score framework by incorporating a prior on the subject-specific variables, presenting a hypothesis testing framework for determining biomarker ordering, and performing an extensive validation of the method (Bilgel et al., 2015c).

We first show using simulated data that the model parameters are estimated accurately and that modeling spatial correlations improves parameter estimation. We then apply the method to distribution volume ratio (DVR) images derived from Pittsburgh compound B (PiB) PET imaging, which show the distribution of cerebral fibrillar amyloid. Models fitted using data for 104 participants with a total of 300 PiB-PET visits reveal that the precuneus and frontal cortex show the greatest longitudinal increases in fibrillar amyloid, with smaller increases in lateral temporal and temporoparietal regions, and minimal increases in the occipital cortex and the sensorimotor strip. Our results suggest that the precuneus is the earliest cortical region to accumulate amyloid. The results are consistent across the two hemispheres, and the estimated PS agrees with a widely used PET-based global index of brain amyloid known as mean cortical DVR. The presented method can be applied to other types of longitudinal imaging data to understand voxelwise trajectories and to quantify each individual scan against the estimated progression pattern.

2. Method

2.1. Model

Our goal is to characterize the progression of disease or an underlying process as measured using a collection of relevant biomarkers. Disease or process stage, as indicated by a progression score (PS), s, is intrinsically related to time t, measured as the age of a subject. Since individuals differ in their onset and rate of progression, the relationship between s and t varies across individuals. We model the progression s as a linear function of time t for each individual and allow for the prediction of separate slopes and intercepts to account for this variability across individuals.

Generally, there is a particular presentation of symptoms and biomarker measurements at a given progression stage. Furthermore, as the disease or process progresses, there is a particular temporal progression of the biomarkers. In this work, we consider voxelwise PET measures as biomarkers and model the temporal trajectory of each biomarker, or voxel, as a linear function of the progression s. Considering voxelwise neuroimaging measures as biomarkers may appear unusual; however, these measures fit the NIH definition of a biomarker: “a characteristic that is objectively measured and evaluated as an indicator of normal biological processes, pathogenic processes, or pharmacologic responses to a therapeutic intervention” (Biomarkers Definitions Working Group, 2001). As illustrated in Figure 1, PS aligns longitudinal biomarker measures better than age since it accounts for differences across individuals in rates as well as baseline levels of progression. After this alignment in time, the estimated biomarker trajectories can be compared on the common PS scale.

In the following subsections, we describe the progression score model in detail.

2.1.1. Subject-specific model

The progression score s_ij for subject i at visit j is assumed to be an affine transformation of the subject's age t_ij:

$$\begin{array}{cc}\hfill s_{ij}& ={\alpha }_i{t}_{ij}+{\beta }_i\hfill \\ \hfill & ={\mathbf{q}}_{ij}^T{\mathbf{u}}_i,\hfill \end{array}$$ (1)

where ${\mathbf{q}}_{ij}=\left[\begin{array}{c}\hfill t_{ij}\hfill \\ \hfill 1\hfill \end{array}\right]$, and ${\mathbf{u}}_i=\left[\begin{array}{c}\hfill {\alpha }_i\hfill \\ \hfill {\beta }_i\hfill \end{array}\right]$. The subject-specific variables, α_i and β_i contained in the vector u_i, are assumed to follow a bivariate normal distribution, i.e., ${\mathbf{u}}_i~{\mathcal{N}}_2(\mathbf{m},V)$, which are independent and identically distributed across subjects. This model accounts for differences between subjects in the rate of progression via α, and in the baseline levels of disease progression via β.

2.1.2. Subject-specific prior covariance model

The prior covariance V is modeled as a 2×2 unstructured covariance matrix. Log-Cholesky parametrization of V, given by ν, ensures that V ≡ V (ν) is positive definite (Pinheiro and Bates, 1996). Let $U=\left[\begin{array}{cc}\hfill U_{11}\hfill & \hfill U_{12}\hfill \\ \hfill 0\hfill & \hfill U_{22}\hfill \end{array}\right]$ be an upper triangular matrix such that V = U^TU. If the diagonal elements of U are constrained to be positive, then this Cholesky decomposition is unique. To ensure that the diagonal elements of U are positive in an unconstrained optimization framework, we use the natural logarithm of the diagonal elements of U as parameters. We then vectorize the upper triangular elements (including the diagonal) of U to obtain the parameter vector ν = [log U₁₁ U₁₂ log U₂₂]^T, which uniquely parameterizes V and ensures its positive definiteness.

2.1.3. Biomarker trajectory model

The collection of K biomarker measurements form the K × 1 vector y_ij for subject i at visit j. Longitudinal trajectories associated with these biomarkers are assumed to be linear and parameterized by K × 1 vectors a and b:

$${\mathbf{y}}_{ij}=\mathbf{a}{s}_{ij}+\mathbf{b}+{ϵ}_{ij}.$$ (2)

Here, a = [a₁, a₂, …, a_K]^T, b = [b₁, b₂, …, b_K]^T, and ${ϵ}_{ij}~{\mathcal{N}}_K(0,R)$ is the observation noise. ϵ_ij are assumed to be independent and identically distributed across subjects and visits.

2.1.4. Noise covariance model

The matrix R is assumed to have the form R = ΛCΛ, where Λ is a diagonal matrix with positive diagonal elements λ and C is a correlation matrix parameterized by ρ. This parameterization guarantees that R is a positive definite matrix (Galecki and Burzykowski, 2013). For ease of notation, we let Λ ≡ Λ(λ), C ≡ C(ρ), and R ≡ R(λ, ρ).

When the biomarkers under consideration have a spatial organization, i.e., if they are voxelwise measurements from medical images, then the correlation matrix C can be described as a function of the spatial distance d ≡ d(k, k′) between pairs of voxels indexed by k and k′ as well as the spatial correlation parameter ρ. Possible univariate parameterizations (i.e., $\rho =\rho \in \mathbb{R}$) of C are presented in Table 1. All of these spatial correlation functions ensure that C is a valid correlation matrix (Galecki and Burzykowski, 2013).

Table 1.

Spatial correlation functions.

Exponential	Ckk′ = e−d/ρ
Gaussian	Ckk′ = e−(d/ρ)2
Rational quadratic	$C_{k{k}^{\prime }}=\frac{1}{1+{(d∕\rho )}^2}$
Spherical	$C_{k{k}^{\prime }}=\left(1-\frac{3}{2}\frac{d}{\rho }+\frac{1}{2}{\left(\frac{d}{\rho }\right)}^3\right)1(d<\rho )$

d ≡ d(k, k′) is the spatial distance between voxels indexed by k and k′.

2.1.5. Overall model

The overall model, diagrammatically summarized using plate notation in Fig. 2, is described by the following equations:

$$s_{ij}={\mathbf{q}}_{ij}^T{\mathbf{u}}_i$$ (3)

$${\mathbf{y}}_{ij}=\mathbf{a}{s}_{ij}+\mathbf{b}+{ϵ}_{ij}$$ (4)

$${\mathbf{u}}_i\sim {\mathcal{N}}_2(\mathbf{m},V(\nu \left)\right)$$ (5)

$${ϵ}_{ij}\sim {\mathcal{N}}_K(0,R(\lambda ,\rho \left)\right).$$ (6)

Figure 2.

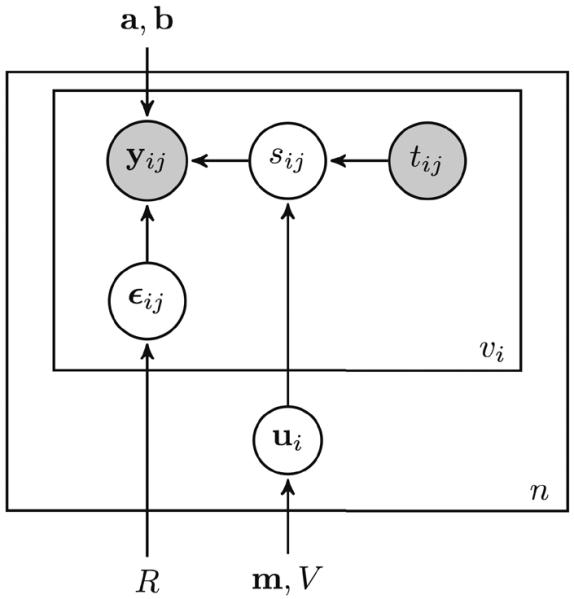
Probabilistic model of the progression score using plate notation. The progression score s_ij establishes the link between age t_ij and the voxelwise observations y_ij. Circles indicate variables, and known measures are shaded. Rectangles indicate that the same model applies across visits (inner rectangle) and individuals (outer rectangle). Arrows indicate dependencies between variables and parameters.

While this model is a mixed effects model since it incorporates the fixed effects a, b as well as the individual-level random effects u_i, and is nonlinear in the parameters, it departs from the form of the nonlinear mixed effects model described by Lindstrom and Bates (1990). Therefore, instead of pursuing a restricted maximum likelihood approach, we use an expectation-maximization (EM) approach, as described below.

Let θ be the collection of model parameters m, ν, a, b, λ, ρ. The complete log-likelihood for the model is

$$\ell (\mathbf{y},\mathbf{u};\theta )=\sum _i\ell ({\mathbf{y}}_i,{\mathbf{u}}_i;\theta )$$ (7)

$$=\sum _i\log f({\mathbf{y}}_i\mid {\mathbf{u}}_i;\theta )+\log f({\mathbf{u}}_i;\theta )$$ (8)

$$\begin{array}{cc}\hfill =& -\frac{1}{2}\sum _{i,j}\log \mid 2\pi R\mid -\frac{1}{2}\sum _{i,j}{({\mathbf{y}}_{ij}-Z_{ij}{\mathbf{u}}_i-\mathbf{b})}^T{R}^{-1}({\mathbf{y}}_{ij}-Z_{ij}{\mathbf{u}}_i-\mathbf{b})\hfill \\ \hfill & -\frac{1}{2}\sum _i\log \mid 2\pi V\mid -\frac{1}{2}\sum _i{({\mathbf{u}}_i-\mathbf{m})}^T{V}^{-1}({\mathbf{u}}_i-\mathbf{m}),\hfill \end{array}$$ (9)

where $Z_{ij}={\mathbf{aq}}_{ij}^T$. y_i is a vector of all biomarker measures stacked across all visits of individual i, and y_ij is a vector of all biomarker measures for individual i at visit j. Given n individuals, we use the summation notation Σ_i,j as a shorthand for ${\sum }_{i=1}^n{\sum }_{j=1}^{v_i}$, where v_i is the number of visits for individual i.

Since the marginal likelihood f(y; θ) involves an integral over all possible values of u_i, maximizing it directly is difficult. Therefore, we use the expectation-maximization (EM) approach, where we consider the subject-specific variables {u_i} as hidden. EM allows us to reformulate the maximization problem in terms of the complete log-likelihood ℓ(y, u; θ). The observations y include biomarker measurements {y_ij} at each visit. The unknown parameters are the subject-specific variable distribution parameters m and ν, the trajectory parameters a and b, and the noise covariance parameters λ and ρ.

2.2. E-step

(y, u) are the complete data. Let θ′ = {m′, ν′, a′, b′, λ′, ρ′} be the previous parameter estimates. By Proposition A.1, the E-step integral is proportional to ${\Sigma }_i\int \Phi ({\tilde{\mathbf{u}}}_i;{\widehat{\mathbf{u}}}_i^{\prime },{\Sigma }_i^{\prime })\ell ({\mathbf{y}}_i,{\tilde{\mathbf{u}}}_i;\theta )d{\tilde{\mathbf{u}}}_i$, where Φ is the multivariate normal probability density function with mean

$${\widehat{\mathbf{u}}}_i^{\prime }={\left(\sum _j{Z}_{ij}^{\prime T}{R}^{\prime -1}{Z}_{ij}^{\prime }+V^{\prime -1}\right)}^{-1}\left(\sum _j{Z}_{ij}^{\prime T}{R}^{\prime -1}({\mathbf{y}}_{ij}-{\mathbf{b}}^{\prime })+V^{\prime -1}{\mathbf{m}}^{\prime }\right),$$ (10)

and covariance ${\Sigma }_i^{\prime }={\left({\Sigma }_j{Z}_{ij}^{\prime T}{R}^{\prime -1}{Z}_{ij}^{\prime }+V^{\prime -1}\right)}^{-1}$. Note that for individuals with a single visit, ${\Sigma }_j{Z}_{ij}^{\prime T}{R}^{\prime -1}{Z}_{ij}^{\prime }$ is a singular matrix. Considering u_i as parameters, as in Jedynak et al. (2012) or Bilgel et al. (2015c), is equivalent to assuming that V has infinitely large diagonal elements (i.e., an uninformative uniform prior) such that its inverse disappears. Therefore, it is not possible to compute ${\widehat{\mathbf{u}}}_i^{\prime }$ for individuals having only one visit using this approach. On the other hand, incorporation of a bivariate normal prior on the subject-specific variables u_i allows Eq. 10 to be computed for individuals with a single visit.

Evaluation of the E-step integral involves second moments of a Gaussian random variable. We ignore the terms that do not depend on θ as they will not be relevant in the maximization step and obtain:

$$\begin{array}{cc}\hfill Q(\theta ,{\theta }^{\prime })=& -\frac{1}{2}\sum _{i,j}\log \mid R\mid \hfill \\ \hfill & -\frac{1}{2}\sum _{i,j}{({\mathbf{y}}_{ij}-Z_{ij}{\widehat{\mathbf{u}}}_i^{\prime }-\mathbf{b})}^T{R}^{-1}({\mathbf{y}}_{ij}-Z_{ij}{\widehat{\mathbf{u}}}_i^{\prime }-\mathbf{b})\hfill \\ \hfill & -\frac{1}{2}\sum _{i,j}\mathrm{Tr}\left(Z_{ij}^T{R}^{-1}{Z}_{ij}{\Sigma }_i^{\prime }\right)-\frac{1}{2}\sum _i\log \mid V\mid \hfill \\ \hfill & -\frac{1}{2}\sum _i{({\widehat{\mathbf{u}}}_i^{\prime }-\mathbf{m})}^T{V}^{-1}({\widehat{\mathbf{u}}}_i^{\prime }-\mathbf{m})-\frac{1}{2}\sum _i\mathrm{Tr}\left(V^{-1}{\Sigma }_i^{\prime }\right).\hfill \end{array}$$ (11)

2.3. M-step

Here, we provide the update equations for the EM algorithm obtained by maximizing Q(θ, θ′) with respect to each parameter, and provide derivations for these update equations in the Appendix. The update equations depend on previous parameter estimates θ′ = {m′, ν′, a′, b′, λ′, ρ′} as well as the progression score estimates $s_{ij}^{\prime }={\mathbf{q}}_{ij}^T{\widehat{\mathbf{u}}}_i^{\prime }$, where ${\widehat{\mathbf{u}}}_i^{\prime }$ is as given in Eq. 10:

$$\mathbf{a}=\frac{\left(\sum _i{v}_i\right)\left(\sum _{i,j}{\mathbf{y}}_{ij}{s}_{ij}^{\prime }\right)-\left(\sum _{i,j}{\mathbf{y}}_{ij}\right)\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}{\left(\sum _i{v}_i\right)\left(\sum _{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}\right)-{\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}^2},$$ (12)

$$\mathbf{b}=\frac{\left(\sum _{i,j}{\mathbf{y}}_{ij}\right)\left(\sum _{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}\right)-\left(\sum _{i,j}{\mathbf{y}}_{ij}{s}_{ij}^{\prime }\right)\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}{\left(\sum _i{v}_i\right)\left(\sum _{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}\right)-{\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}^2},$$ (13)

$$\mathbf{m}=\frac{1}{n}\sum _i{\widehat{\mathbf{u}}}_i^{\prime },$$ (14)

$$\nu =\underset{\nu }{\overset{\arg \max }{}}Q(\theta ,{\theta }^{\prime }),$$ (15)

$$\lambda ,\rho =\underset{\lambda ,\rho }{\overset{\arg \max }{}}Q(\theta ,{\theta }^{\prime }).$$ (16)

Note that if C is fixed to be the identity matrix, a closed form solution for λ exists, as given in Equation A.15. Once the optimal parameters are found, the subject-specific variables are predicted using Eq. (10).

2.4. Parameter standardization

As described in Proposition A.2, there are certain reparameterizations that yield identical models. For example, one can multiply the trajectory slope parameters by 2 and divide all progression scores by 2 (which is achieved by dividing all α and β values by 2) without altering the model. This is the scaling degree of freedom. There is also a translation degree of freedom. We account for these degrees of freedom and anchor the model by calibrating the progression score scale. We calibrate such that baseline PS has a mean of 0 and a standard deviation of 1. This involves replacing the model parameters {m, V (ν), a, b, R(λ, ρ)} with $\left\{w\mathbf{m}+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill z\hfill \end{array}\right],w^{2}V\left(\nu \right),\frac{1}{w}\mathbf{a},\mathbf{b}-\frac{z}{w}\mathbf{a},R(\lambda ,\rho )\right\}$, where $-\frac{z}{w}=\frac{1}{n}{\Sigma }_i{s}_{i1}$ is the mean progression score at baseline, and $\frac{1}{w}=\sqrt{\frac{1}{n}{\Sigma }_i{\left(s_{i1}-\frac{1}{n}{\Sigma }_i{s}_{i1}\right)}^2}$ is the standard deviation of baseline progression scores. We standardize the subject-specific estimates α_i, β_i, and s_ij accordingly: ${\alpha }_i^{\ast }=w{\alpha }_i$, ${\beta }_i^{\ast }=w{\beta }_i+z$, and $s_{ij}^{\ast }=w{s}_{ij}+z$. This reparametrization yields a PS scale where 0 corresponds to the sample average at baseline and the variance of PS at baseline is 1.

2.5. Implementation details

We first fit the model assuming that C = I_K×K and Λ is a diagonal matrix with positive elements λ. We denote the estimated Λ in this model as $\widehat{\Lambda }$. The estimates obtained from this model for the parameters a, b, m, V are used as initializations in the model where C = C(ρ). In this model where correlations are taken into account, we assume that $\Lambda =\lambda \widehat{\Lambda }$, where λ is an unknown parameter to be estimated. The spatial correlation function among those presented in Table 1 that results in the highest log-likelihood value is chosen for the final model.

The EM algorithm is implemented in MATLAB 8.1 and Statistics Toolbox 8.2 (The MathWorks Inc., Natick, MA). Our code is freely available online.¹

2.6. Confidence intervals

We use bootstrapping via Monte Carlo resampling to estimate confidence intervals for each model parameter. We sample with replacement from the original collection of subjects to generate a new dataset containing an equal number of subjects and fit the model on this generated sample. This sampling and fitting procedure is repeated to generate bootstrap estimates. We then compute 95% confidence intervals for each parameter across the bootstrap estimates. In the bootstrap experiments, we fix the value of ρ at its estimate on the whole sample to enable faster computation.

2.7. Comparison to linear mixed effects model

We compared our model to a linear mixed effects (LME) model that included random intercepts and slopes at each voxel. The LME model for subject i, visit j and voxel k is given by

$$y_{\mathit{ijk}}=({\eta }_k+{\eta }_{ik})t_{ij}+({\gamma }_k+{\gamma }_{ik})+{\epsilon }_{\mathit{ijk}},$$ (17)

where $\left(\begin{array}{c}\hfill {\eta }_k\hfill \\ \hfill {\gamma }_k\hfill \end{array}\right)$ are the fixed effects, $\left(\begin{array}{c}\hfill {\eta }_{ik}\hfill \\ \hfill {\gamma }_{ik}\hfill \end{array}\right)~\mathcal{N}(0,{\Xi }_k)$ are the random effects and ${\epsilon }_{\mathit{ijk}}~\mathcal{N}(0,{\sigma }_k^2)$ is the observation noise. We used the LME implementation in MATLAB Statistics Toolbox 8.2.

2.8. Simulated data set

We simulated visits such that the sample was similar to our PET data in terms of number of visits per subjects and age range. We generated a data set with 100 individuals, each with up to 7 visits with 5 × 5 × 5 images with 4 mm isotropic voxels. We fixed the ground truth values of the model parameters θ = {m, ν, a, b, λ, ρ} at values close to those we observed in exploratory models fitted to DVR data. We generated u_i from a bivariate normal distribution with mean m and variance V (ν). The progression score for each visit was then computed as $s_{ij}={\mathbf{q}}_{ij}^T\mathbf{u}$, and observations were generated using the PS model. We performed 1000 bootstrap iterations to obtain 95% confidence intervals for each parameter and subject-specific variable. We computed the cosine similarity for each variable for each bootstrap experiment using

$$\frac{{\varphi }^T\widehat{\varphi }}{{\Vert \varphi \Vert }_2{\Vert \widehat{\varphi }\Vert }_2},$$ (18)

where $\widehat{\varphi }$ is the estimate of the variable of interest (a, b, α, β, or s) and ϕ is the corresponding ground truth value. A value of 1 indicates a perfect estimate.

2.9. Amyloid imaging data set

We used longitudinal positron emission tomography (PET) data for participants from the Baltimore Longitudinal Study of Aging (Shock et al., 1984) neuroimaging substudy (Resnick et al., 2000). Participant demographics are presented in Table 2. Starting in 2005, amyloid-beta (Aβ) PET scans were acquired on a GE Advance scanner over 70 minutes following an intravenous bolus injection of Pittsburgh compound B (PiB), yielding dynamic PET scans with 33 time frames. PET images were reconstructed using filtered backprojection with a ramp filter, yielding a spatial resolution of approximately 4.5 mm full width at half max at the center of the field of view (image matrix = 128 × 128, 35 slices, pixel size = 2 × 2 mm, slice thickness = 4.25 mm).

Table 2.

Participant demographics.

Characteristic	N = 104
Baseline age in years, mean (SD)	77.0 (7.9)
Range	55.7–93.4
Female, n (%)	48 (46%)
PiB-PET scans, n	300
PiB-PET per subject, n	2.9 (1.8)
Range	1–7
Years between first and last scan, mean (SD)	3.3 (2.9)
Range	0.0–9.0
Mean cortical DVR at last visit (SD)	1.12 (0.19)
PiB+ at last visit, n (%)	42 (40%)
MCI diagnosis at last visit, n (%)	3 (3%)
Dementia diagnosis at last visit, n (%)	4 (4%)

MCI = mild cognitive impairment, SD = standard deviation.

The frames of each dynamic PiB-PET scan were aligned to the average of the first two minutes to remove motion (Jenkinson et al., 2002). For registration purposes, we obtained static images by averaging the first 20 minutes of the dynamic PiB-PET scan. Follow-up PiB-PET scans were rigidly registered onto the baseline PiB-PET within each participant using the 20-minute average images. Baseline magnetic resonance images (MRIs) were rigidly registered onto their corresponding 20-minute PiB-PET average, and their FreeSurfer segmentations (Dale et al., 1999; Desikan et al., 2006) were transformed accordingly. Distribution volume ratio (DVR) images were calculated in the native space of each PiB-PET image using the simplified reference tissue model with the cerebellar gray matter as reference tissue (Zhou et al., 2003). The MRIs coregistered with the PET were deformably registered (Avants et al., 2008) onto a study-specific template (Avants et al., 2010; Bilgel et al., 2015b) and transformed to 4 mm isotropic MNI space using a pre-calculated affine transformation. The resulting mappings were applied to the DVR images that have been registered to baseline to bring them into the MNI space. We used all voxels within the brain mask in the MNI space to fit the PS model.

Mean cortical DVR is a widely used measure obtained from PiB-PET images for quantifying the level of brain amyloid. We computed mean cortical DVR for each PiB-PET image by averaging the voxelwise DVR values across cingulate, frontal, parietal, lateral temporal, and lateral occipital cortices, excluding the sensorimotor strip. We used a mean cortical DVR threshold of 1.06, which was computed from a two-class Gaussian mixture model fitted on baseline measures, to separate individuals into PiB- and PiB+ groups, as described in Bilgel et al. (2015a).

2.10. Hypothesis testing

The confidence intervals obtained via bootstrapping allow for hypothesis testing. For the amyloid images, we focus on studying the precuneus, since previous cross-sectional amyloid imaging studies have suggested that precuneus has the highest deposition levels (Mintun et al., 2006) and provided preliminary evidence that it may be the most rapid accumulator (Rodrigue et al., 2012) among cortical regions. Our specific hypotheses are as follows:

1. The precuneus has the highest amyloid load along stages of amyloid accumulation.

2. The precuneus accumulates amyloid faster than other cortical regions.

We refer to the progression scores calculated using the DVR images as Aβ-PS. To test the first hypothesis, we compare the amyloid levels in the precuneus with other regions at various Aβ-PS values spanning the range observed in our data set. Our purpose in performing these comparisons is to shed light onto the temporal ordering of changes in di erent cortical regions. For each bootstrap experiment, we average the predicted DVR levels ${\widehat{y}}_k\left(s\right)=a_{k}s+b_k$ within each ROI to obtain

$${\widehat{y}}_r\left(s\right)=\frac{1}{\mid {\text{ROI}}_r\mid }\sum _{k\in {\text{ROI}}_r}{\widehat{y}}_k\left(s\right),$$ (19)

where k is the voxel index and r is the ROI index. We then compute the following statistic for each bootstrap:

$$T={\widehat{y}}_{\text{precuneus}}\left(s\right)-\underset{r\ne \text{precuneus}}{\max }{\widehat{y}}_r\left(s\right).$$ (20)

We reject the null hypothesis that the amyloid load in the precuneus at Aβ-PS = s is not different from other regions at significance level γ if the two-sided 100(1−γ) confidence interval of the test statistic T, computed using the bootstrap estimates of T, does not contain 0. The smallest value of γ such that the two-sided 100(1−γ) confidence interval of the test statistic T contains 0 is the p-value of the test.

To test the second hypothesis, we pursue a similar approach using the trajectory slope parameter a. For each bootstrap experiment, we obtain the average a_k per cortical ROI to obtain a_r, where r the ROI index. We then compute the following statistic for each bootstrap:

$$T=a_{\text{precuneus}}-\underset{r\ne \text{precuneus}}{\max }{a}_r.$$ (21)

The condition for the rejection of the null hypothesis that the rate of amyloid accumulation in the precuneus is not different from that of other regions is as described previously.

3. Results

3.1. Simulation

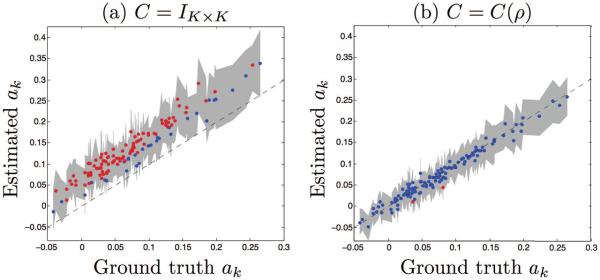
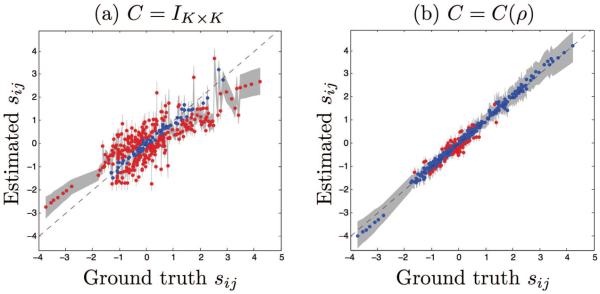
The Akaike information criterion (AIC) was 39.0 × 10³ for the LME model, 32.0 × 10³ for the PS model where C = I_K×K, and −1.6 × 10³ for the PS model where C = C(ρ), indicating that the PS model where spatial correlations are modeled fits the data the best. We computed the percentage of variables that are “correct” by counting the variables whose ground truth values fell within the 95% confidence interval computed via bootstrapping. For example, for a and b, a value of 10% indicates that 10% of the biomarkers had a correct estimate for a_k and b_k. For α and β, 10% indicates that 10% of the individuals had a correct estimate for α_i and β_i. For s, 10% indicates that 10% of the visits had a correct estimate for s_ij. Simulation results are presented in Table 3. When there are correlations in the data, not modeling them yields inaccurate estimates for the trajectory slope parameter a, the subject-specific variables α_i, β_i, and the progression scores s_ij. Using the correlation model improves these estimates significantly.

Table 3.

Simulation results. Mean cosine similarity values across 1000 bootstrap experiments (with standard deviation) and percentage of variable elements that are correct based on 95% confidence intervals are presented.

	C = IK×K		C = C(ρ)
Variable	Cosine similarity	% correct	Cosine similarity	% correct
a	0.9514 ± 0.0154	24	0.9821 ± 0.0073	98
b	0.9998 ± 0.0001	99	0.9998 ± 0.0001	98
α	0.1587 ± 0.0812	18	0.7922 ± 0.0332	40
β	0.1250 ± 0.0794	19	0.7835 ± 0.0339	38
s	0.8017 ± 0.0443	23	0.9881 ± 0.0053	85

3.2. Amyloid images

In our preliminary analysis of the noise spatial correlation structure using the semivariogram (Cressie and Hawkins, 1980; Bilgel et al., 2015c), we observed that the rational quadratic had the best fit to the empirical semivariogram (Inline Supplementary Fig. 1). Rational quadratic also yielded the fit with largest log-likelihood, and thus was selected as the correlation function for the model. AIC was −1.2 × 10⁷ for the LME model, −1.1 × 10⁷ for the model where C = I_K×K, and −2.0 × 10⁷ for the model where C = C(ρ), indicating that the PS model where spatial correlations are modeled fits the data the best. The spatial correlation parameter ρ for the rational quadratic correlation model was estimated to be 4.5 mm, and λ was estimated to be 0.929. A comparison of the PS values obtained from the di erent correlation models are presented in the Supplementary Material (Inline Supplementary Fig. 2). Model fitting using 104 subjects with a total of 300 visits each having about 30, 000 brain voxels took approximately 5 seconds on an Intel Xeon 8-core 3.1 GHz machine with 128 GB RAM for the case where voxels are assumed to be independent (i.e., C = I_K×K). The following model fitting with C = C(ρ) took approximately 30 minutes per EM iteration, with convergence achieved in 2 to 6 iterations depending on the correlation structure.

3.2.1. Comparison of Aβ-PS to mean cortical DVR

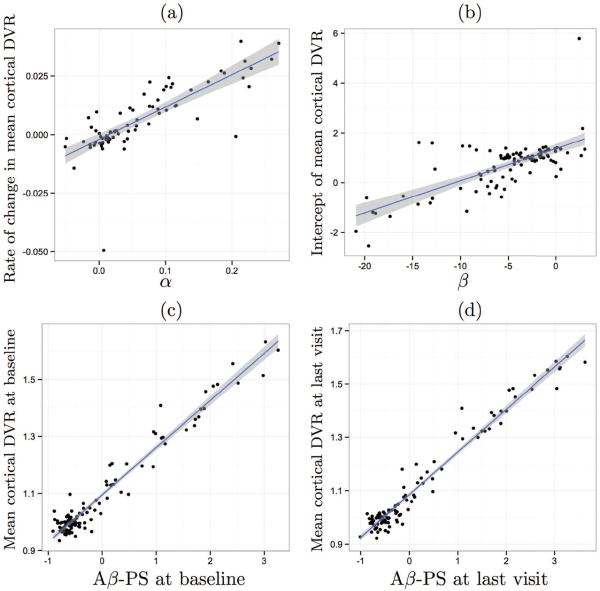
We compared the subject-specific variables obtained from model fitting to empirical values obtained from mean cortical DVR, which is the widely used measure for quantifying levels of brain amyloid (Fig. 5). For each individual with at least two visits, we fit a line to the mean cortical DVR data to estimate the slope of amyloid accumulation as well as the intercept. The subject-specific variable α_i, which represents the rate of amyloid progression, explained 62% of the variability in the empirical slope of amyloid accumulation computed from longitudinal mean cortical DVR. We observed a much higher correlation between mean cortical DVR and Aβ-PS (R² = 0.95 at baseline and 0.96 at last visit).

Figure 5.

Correlation of estimated subject-specific variables with mean cortical DVR measures. The line of best fit is shown in blue, and its 95% confidence band in gray. (a) Rate of annual change in mean cortical DVR vs. α, the predicted rate of change in amyloid progression score (R² = 0.62). (b) Intercept of mean cortical DVR vs. β, the progression score intercept (R² = 0.48). (c) Mean cortical DVR vs. Aβ-PS at baseline (R² = 0.95). (d) Mean cortical DVR vs. Aβ-PS at last visit (R² = 0.96).

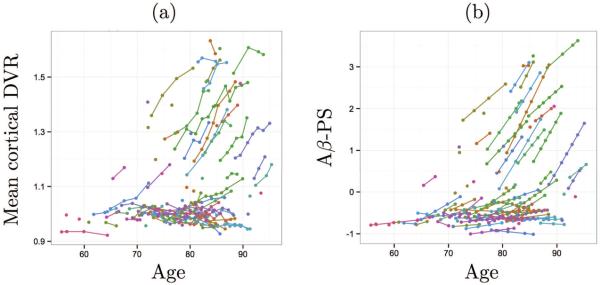
When plotted against age, mean cortical DVR and Aβ-PS revealed similar patterns (Fig. 6). The progression as measured using voxelwise DVR data is not linearly associated with age, and the Aβ-PS was able to capture this.

Figure 6.

(a) Mean cortical DVR and (b) Aβ-PS plotted against age. Longitudinal data points are connected by lines within each subject. Different colors indicate different subjects.

3.2.2. Amyloid trajectories

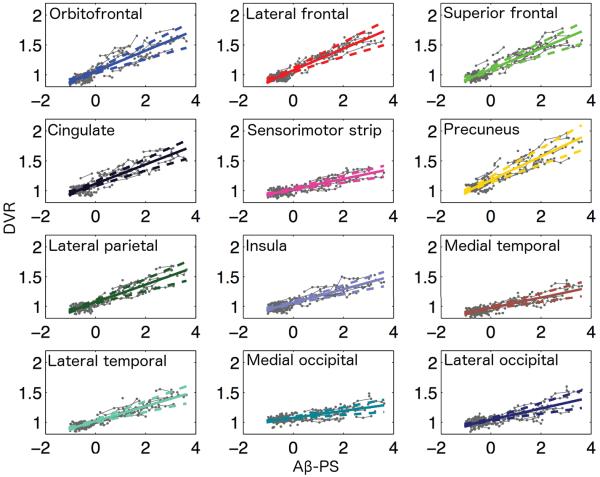
The trajectory slope parameters a_k obtained from the PS model (Fig. 7) revealed symmetric patterns across the cerebral hemispheres. The precuneus and frontal lobe showed the greatest increases in DVR with Aβ-PS, smaller increases in lateral temporal and temporoparietal regions, and minimal increases in the occipital lobe and the sensorimotor strip. Voxelwise trajectories are further illustrated in Fig. 8, which shows the predicted DVR values on the cortical surface at three Aβ-PS levels.

Figure 7.

Slope parameters a_k obtained from voxelwise PS model projected onto the cortical surface. For each unit increase in Aβ-PS, the DVR value at voxel k increases by a_k.

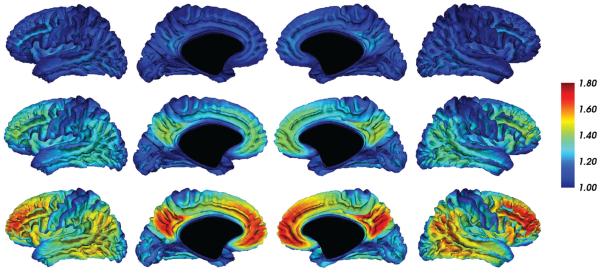
Figure 8.

Predicted DVR levels at Aβ-PS = −0.6 (top), 0.4 (middle row), and 1.5 (bottom).

In order to better investigate regional trends, we averaged the PS model results within each cortical ROI and plotted these ROI averages as a function of Aβ-PS (Fig. 9). We used bootstrap results to compute 95% confidence bands for these ROI averages. Based on the 95% confidence band of the precuneus illustrated in Fig. 9, precuneus appears to be the earliest accumulator and has the highest amyloid levels through late stages of amyloid accumulation (Aβ-PS≥ 2). We present confidence bands for other cortical regions in Fig. 10.

Figure 9.

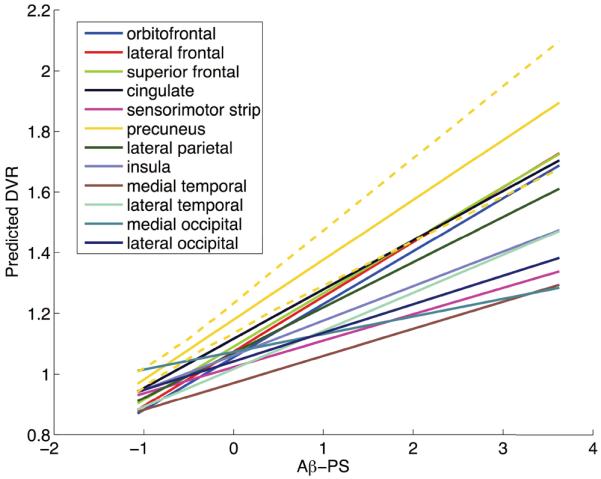
Regional trajectories as function of Aβ-PS. The PS model was used to make voxelwise predictions at a range of Aβ-PS values, and these predictions were averaged within each ROI to obtain regional trajectories. The dashed lines indicate the 95% confidence band obtained using bootstrap results for the precuneus.

Figure 10.

Regional trajectories as function of Aβ-PS. The PS model was used to make voxelwise predictions at a range of Aβ-PS values, and these predictions were averaged within each ROI to obtain regional trajectories. The dashed lines indicate the 95% confidence bands for the cortical regions. Estimated trajectories with their 95% confidence bands are superimposed on observed longitudinal data (in gray).

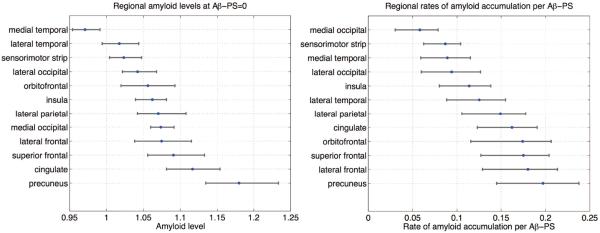
Based on our hypothesis testing procedure, we found that precuneus had the highest amyloid levels at Aβ-PS values of −0.5, 0, 1, 2, and 3 (all p < 0.01). On the other hand, while the estimated rate of amyloid accumulation was highest in the precuneus, this was not statistically significant (p = 0.33). A comparison of the levels of amyloid at Aβ-PS= 0 and rates of accumulation across ROIs is presented in Fig. 11.

Figure 11.

Comparison of levels of amyloid at Aβ-PS= 0 and rates of amyloid accumulation across cortical regions. The intercept parameter b obtained from the PS model was averaged within each ROI to obtain the regional amyloid levels at Aβ-PS= 0, and the trajectory slope parameter a was averaged within each ROI to obtain regional rates.

3.2.3. Comparison to LME results

The trajectories we obtained using the PS model were consistent with the results of the LME model (Inline Supplementary Figs. 3, 4). However, the fixed effects obtained from the LME model did not describe the observed data as well as the trajectory slopes obtained from the PS model (Inline Supplementary Fig. 5). Using the LME model estimates and a bootstrapping procedure similar to the one we applied for the PS model, we found that the precuneus had the highest regional amyloid levels compared to other cortical regions at ages 70, 80, and 90 (all p < 0.01), but not at age 65 (p = 0.12). Similar to our findings based on the PS model, the rate of amyloid accumulation was highest in the precuneus, but this was not statistically significant (p = 0.75). A comparison of the levels of amyloid at the mean baseline age of the sample and rates of accumulation across ROIs is presented in Inline Supplementary Fig. 6.

4. Discussion

We presented a statistical model for estimating longitudinal trajectories of voxelwise neuroimaging data. Our model is based on the concept that age is not a good metric for disease progression since each individual has his or her own onset and rate of progression of disease. We accounted for these inter-individual di erences to temporally align individuals based on their collection of voxelwise measurements. As a result of this temporal alignment, we obtained a metric of disease or underlying biological process stage as reflected in the neuroimaging data, and we call this metric “progression score”. By analyzing voxelwise neuroimaging data as a function of progression score rather than time, we constructed trajectories that better represent changes occurring with disease stage.

Simulation results showed that the progression score model fits the data better than the linear mixed effects model, as evidenced by AIC. Furthermore, the results showed that modeling spatial correlations is important for extracting accurate summary scores from data with underlying correlations. In the absence of correlation modeling when the underlying data are correlated, estimates of the trajectory slopes a as well as subject-specific variables α, β, and s were adversely affected. The difference in the subject-specific variables was mainly due to inaccurate estimates of the prior covariance V. Note that

$$\text{Cov}\left({\mathbf{y}}_{ij}\right)={\mathbf{aq}}_{ij}^{T}V{\mathbf{q}}_{ij}{\mathbf{a}}^T+R,$$ (22)

which explains why both a and V are affected when correlations are not modeled through the covariance matrix R. This highlights the importance of modeling spatial correlations in data where such effects are evident, especially in order to estimate correct trajectory slopes and individualized progression scores. To further understand this phenomenon, we conducted simulations (data not presented) where we duplicated biomarkers with lower signal-to-noise ratios and repeated model fitting including these duplicate biomarkers. We observed that the parameter estimates as well as the PS values were biased if we assumed independence across biomarkers. This might be because the model interprets each of the duplicated biomarkers as a separate piece of evidence towards the computation of individual progression scores. However, when we included a proper noise correlation model, we were able to recover our original results on the collection of unique biomarkers.

The proposed EM framework simplifies the estimation of spatial correlation parameters, and accurately estimates the trajectory parameters a and b as well as predicting the progression scores s. The performance of the fitting procedure in predicting α and β is worse than for s. This may be due to the modeling of α and β as random variables that do not directly contribute to the observations y. We observed a similar pattern in the amyloid data: the agreement between estimated Aβ-PS and mean cortical DVR was greater than the agreement between estimated α and the rate of change of mean cortical DVR per individual. This suggests that the progression scores are more reliable than the subject-specific variables. Aβ-PS was highly correlated with mean cortical DVR, a widely used measure for quantifying PiB-PET scans and assessing longitudinal change. This indicates that Aβ-PS is a meaningful score extracted from voxelwise imaging data. Unlike mean cortical DVR, there are no a priori assumptions regarding which regions or voxels should be included in the computation of Aβ-PS. This property of PS allows for the discovery of new patterns in longitudinal data.

Trajectories obtained from the PS model captured a wider dynamic range of DVR values and had a better fit to the observed data compared to the trajectories obtained using the LME model fixed effects. This difference between the PS and LME models underscores the fact that age is not an appropriate metric for staging amyloid accumulation. By aligning individuals based on their amyloid scans, the PS model enables a better temporal metric of amyloid staging.

Aβ-PS allows for the exploration of longitudinal voxelwise trajectories within a hypothesis testing framework due to its underlying statistical model. Our results suggest that the precuneus exhibits the earliest cortical amyloid changes, but that its rate of amyloid accumulation does not differ significantly from other cortical regions. Based on a qualitative evaluation of our estimated trajectories, we found that amyloid accumulation in the precuneus is followed by cingulate and frontal cortices, then by lateral parietal cortex, followed by insula and lateral temporal cortex. We observed minimal amyloid accumulation in visual cortex, hippocampal formation and the sensorimotor strip, which agrees with previous reports that these regions accumulate amyloid in later stages of AD (Braak and Braak, 1991). Previous reports have highlighted precuneus as an early amyloid accumulator (Mintun et al., 2006; Rodrigue et al., 2012) as well as frontal, cingulate, and parietal regions (Jack et al., 2008). Contrary to our finding highlighting precuneus as the earliest cortical accumulator, a study of cognitively normal adults found that the right medial frontal cortex accumulates amyloid the earliest, closely followed by bilateral precuneus based on cross-sectional voxelwise analyses (Villeneuve et al., 2015). We presented regional trajectories averaged bilaterally in this work; however, hemisphere-specific trajectories were consistent with our bilaterally-averaged trajectories and we did not observe that medial frontal cortex precedes precuneus. Further studies with larger samples will be instrumental in elucidating the regional progression of amyloid accumulation.

One of the strengths of our model for the progression scores s is that there are no a priori assumptions on the global form of s(t), which can be thought of as an underlying function that describes the evolution of progression score over time. Instead, the model makes linear local approximations to s(t) per individual. The linear form we use makes the EM approach analytically tractable and enables the discovery of the global form of s(t). On the other hand, the linear relationship we assume between s and t is also a limitation since it may be an oversimplification over long follow-up durations. In order to capture dynamics over longer periods more accurately, it is necessary to investigate the relationship between the progression scores s and time t, and select an appropriate function to link these variables.

Another limitation of our model is the assumption of linear biomarker trajectories. This assumption is not reflective of the fact that voxelwise DVR has a theoretical minimum of 1 (while in practice, there are DVR values lower than 1 due to noise). Furthermore, several studies of longitudinal amyloid deposition have found evidence for a ceiling effect in amyloid deposition in late AD, suggesting a sigmoid trajectory for amyloid levels (Villemagne et al., 2013; Villain et al., 2012). Our use of a linear rather than sigmoid trajectory inevitably results in inaccuracies in PS calculation for individuals whose voxelwise data lie along the plateaus of the sigmoid in reality. The linear trajectory assumption may also prevent us from characterizing subtler differences in the temporal ordering of the onset of amyloid accumulation across different regions. However, linear trajectories, unlike sigmoid trajectories, yield closed-form update equations for trajectory parameters, greatly facilitating the model fitting procedure.

The spatial covariance functions we used in our analyses are covariance functions of strictly stationary isotropic processes. The underlying spatial noise process is affected by the PET scanner, image reconstruction algorithm, radiotracer delivery and binding in different brain regions, kinetic parameter estimation algorithm, and registration methods used to bring all scans in alignment. To accurately model these influences on noise, complex noise spatial covariance models are needed. In this work, we made simplifying assumptions on the noise properties to facilitate the study of longitudinal trajectories of amyloid images. As a result of these simplifications, our model does not accurately capture noise properties; however, by eliminating the inaccurate assumption of independence across voxels, our approach improves the accuracy of the estimated trajectories and progression scores. Refined spatial noise models incorporating non-stationarity and anisotropy may further improve the estimation accuracy.

Our model can be applied to studying higher resolution images. To reduce computational memory burden, it may be necessary to impose sparsity on the spatial correlation matrix, which can be done by imposing a correlation value of 0 at large distances. The sparsity property of the correlation matrix can be taken advantage of to yield Cholesky decompositions using less memory and time.

In conclusion, the progression score model allows for extracting summary scores from longitudinal data for each scan. In this work, we have extended the progression score model proposed by Jedynak et al. (2012) to voxelwise imaging data by accounting for spatial correlations and enabling efficient handling of the large number of voxels through the EM framework. The incorporation of a prior on subject-specific variables allowed for the inclusion of individuals with a single visit in the model. Our method can be extended to the analysis of other types of imaging data, and in cases where a summary score such as mean cortical DVR is not available, the progression score estimates can be highly informative for progression staging.

Figure 3.

Estimated trajectory slope parameters α_k vs ground truth. Dashed line indicates x = y. Gray band corresponds to the 95% confidence intervals obtained from bootstrapping. Estimates are shown in blue if their 95% confidence interval intersects the x = y line, and in red otherwise. Results from the model where (a) C = I_K×K and (b) C = C(ρ).

Figure 4.

Predicted progression scores s_ij vs ground truth. Dashed line indicates x = y. Gray band corresponds to the 95% confidence intervals obtained from bootstrapping. Estimates are shown in blue if their 95% confidence interval intersects the x = y line, and in red otherwise. Results from the model where (a) C = I_K×K and (b) C = C(ρ).

HIGHLIGHTS.

• We present a method to estimate trajectories of voxelwise imaging biomarkers

• Method accounts for differences in rate of progression and onset across subjects

• Scores extracted from imaging data at each longitudinal visit represent disease stage

• Application on amyloid imaging reveals precuneus as the earliest cortical accumulator

Appendix A

Proposition A.1.

$$f({\tilde{\mathbf{u}}}_i\mid {\mathbf{y}}_i;{\theta }^{\prime })\propto \Phi ({\tilde{\mathbf{u}}}_i;{\widehat{\mathbf{u}}}_i^{\prime },{\Sigma }_i^{\prime }),$$ (A.1)

where Φ(·;μ, Σ) denotes the probability density function of a multivariate normal with mean μ and covariance matrix Σ,

$${\widehat{\mathbf{u}}}_i^{\prime }={\left(\sum _j{Z}_{ij}^{\prime T}{R}^{\prime -1}{Z}_{ij}^{\prime }+V^{\prime -1}\right)}^{-1}\left(\sum _j{Z}_{ij}^{\prime T}{R}^{\prime -1}({\mathbf{y}}_{ij}-{\mathbf{b}}^{\prime })+V^{\prime -1}{\mathbf{m}}^{\prime }\right),$$ (A.2)

and ${\Sigma }_i^{\prime }={\left({\Sigma }_j{Z}_{ij}^{\prime T}{R}^{\prime -1}{Z}_{ij}^{\prime }+V^{\prime -1}\right)}^{-1}$ is a covariance matrix.

Proof. Independence across visits allows us to write

$$\begin{array}{cc}\hfill f({\mathbf{y}}_i\mid {\tilde{\mathbf{u}}}_i;{\theta }^{\prime })& =\prod _{j}f({\mathbf{y}}_{ij}\mid {\tilde{\mathbf{u}}}_i;{\theta }^{\prime })\hfill \\ \hfill & =\prod _j\Phi ({\mathbf{y}}_{ij};Z_{ij}^{\prime }{\tilde{\mathbf{u}}}_i+{\mathbf{b}}^{\prime },R^{\prime })\hfill \\ \hfill & \propto \exp \left\{-\frac{1}{2}\left[{\tilde{\mathbf{u}}}_i^T\left(\sum _j{Z}_{ij}^{\prime T}{R}^{\prime -1}{Z}_{ij}^{\prime }\right){\tilde{\mathbf{u}}}_i-2\left(\sum _j{({\mathbf{y}}_{ij}-{\mathbf{b}}^{\prime })}^T{R}^{\prime -1}{Z}_{ij}^{\prime }\right){\tilde{\mathbf{u}}}_i\right]\right\},\hfill \end{array}$$ (A.3)

where we have ignored the terms that do not depend on ${\tilde{\mathbf{u}}}_i$.

By Bayes' rule,

$$f({\tilde{\mathbf{u}}}_i\mid {\mathbf{y}}_i;{\theta }^{\prime })\propto f({\mathbf{y}}_i\mid {\tilde{\mathbf{u}}}_i;{\theta }^{\prime })f({\tilde{\mathbf{u}}}_i;{\theta }^{\prime })$$ (A.4)

$$\propto \exp \left\{-\frac{1}{2}\left[{\tilde{\mathbf{u}}}_i^T\left(\sum _j{Z}_{ij}^{\prime T}{R}^{\prime -1}{Z}_{ij}^{\prime }+V^{\prime -1}\right){\tilde{\mathbf{u}}}_i-2\left(\sum _j{({\mathbf{y}}_{ij}-{\mathbf{b}}^{\prime })}^T{R}^{\prime -1}{Z}_{ij}^{\prime }+{\mathbf{m}}^{\prime T}{V}^{\prime -1}\right){\tilde{\mathbf{u}}}_i\right]\right\}$$ (A.5)

$$\propto \Phi ({\tilde{\mathbf{u}}}_i;{\widehat{\mathbf{u}}}_i,\sum _i^{\prime })$$ (A.6)

Below we derive the EM algorithm update equations given in Section 2.3:

Solving for the intercept parameter b

The value of b that solves $\frac{\partial Q}{\partial \mathbf{b}}=R^{-1}{\Sigma }_{i,j}({\mathbf{y}}_{ij}-Z_{ij}{\widehat{\mathbf{u}}}_i^{\prime }-\mathbf{b})=0$ is given by

$$\begin{array}{cc}\hfill \mathbf{b}& =\frac{1}{\sum _i{v}_i}\sum _{i,j}({\mathbf{y}}_{ij}-Z_{ij}{\widehat{\mathbf{u}}}_i^{\prime })\hfill \\ \hfill & =\frac{1}{\sum _i{v}_i}\sum _{i,j}({\mathbf{y}}_{ij}-\mathbf{a}{s}_{ij}^{\prime }).\hfill \end{array}$$ (A.7)

Plugging in the expression for a from Equation A.9 yields

$$\mathbf{b}=\frac{\left(\sum _{i,j}{\mathbf{y}}_{ij}\right)\left(\sum _{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}\right)-\left(\sum _{i,j}{\mathbf{y}}_{ij}{s}_{ij}^{\prime }\right)\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}{\left(\sum _i{v}_i\right)\left(\sum _{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}\right)-{\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}^2}.$$ (A.8)

Solving for the slope parameter a

The value of a that solves $\frac{\partial Q}{\partial \mathbf{a}}=R^{-1}\left[{\Sigma }_{i,j}({\mathbf{y}}_{ij}-\mathbf{b})s_{ij}^{\prime }-\mathbf{a}\left({\Sigma }_{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}\right)\right]=0$ is given by

$$\mathbf{a}=\frac{1}{\sum _{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}}\sum _{i,j}({\mathbf{y}}_{ij}-\mathbf{b})s_{ij}^{\prime }.$$ (A.9)

Plugging in the expression for b from Equation A.7 yields

$$\mathbf{a}=\frac{\left(\sum _i{v}_i\right)\left(\sum _{i,j}{\mathbf{y}}_{ij}{s}_{ij}^{\prime }\right)-\left(\sum _{i,j}{\mathbf{y}}_{ij}\right)\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}{\left(\sum _i{v}_i\right)\left(\sum _{i,j}{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}+s_{ij}^{\prime 2}\right)-{\left(\sum _{i,j}{s}_{ij}^{\prime }\right)}^2}.$$ (A.10)

Solving for the subject-specific variable variance parameter m

The value of m that solves $\frac{\partial Q}{\partial \mathbf{m}}=-{\Sigma }_i{V}^{-1}\mathbf{m}+{\Sigma }_i{V}^{-1}{\widehat{\mathbf{u}}}_i^{\prime }=0$ is given by

$$\mathbf{m}=\frac{1}{n}\sum _i{\widehat{\mathbf{u}}}_i^{\prime }.$$ (A.11)

Solving for the subject-specific variable variance parameter ν

We use numerical optimization to estimate ν:

$$\nu =\underset{\nu }{\arg \max }Q(\theta ,{\theta }^{\prime })$$ (A.12)

$$=\underset{\nu }{\arg \min }\sum _i(\log \mid V\mid +{({\widehat{\mathbf{u}}}_i^{\prime }-\mathbf{m})}^T{V}^{-1}({\widehat{\mathbf{u}}}_i^{\prime }-\mathbf{m})+\mathrm{Tr}(V^{-1}{\Sigma }_i^{\prime }\left)\right)$$ (A.13)

We can reconstruct V by undoing the log-Cholesky parametrization steps using the estimated parameter vector ν = [ν₁, ν₂, ν₃]^T as

$$V=\left[\begin{array}{cc}\hfill e^{{\nu }_1}\hfill & \hfill 0\hfill \\ \hfill {\nu }_2\hfill & \hfill e^{{\nu }_3}\hfill \end{array}\right]\left[\begin{array}{cc}\hfill e^{{\nu }_1}\hfill & \hfill {\nu }_2\hfill \\ \hfill 0\hfill & \hfill e^{{\nu }_3}\hfill \end{array}\right].$$ (A.14)

Solving for the noise covariance parameters λ and ρ

If C = I_K×K (i.e. ρ = 0 and fixed), then the diagonal elements λ_k of Λ can be estimated as:

$${\lambda }_k=\sqrt{\frac{1}{\sum _i{\upsilon }_i}\sum _{i,j}[{(y_{\mathit{ijk}}-a_k{s}_{ij}^{\prime }-b_k)}^2+a_k^2{\mathbf{q}}_{ij}^T{\Sigma }_i^{\prime }{\mathbf{q}}_{ij}]}.$$ (A.15)

If C is not fixed to be the identity matrix, then in general it is not possible to obtain closed-form solutions for λ and ρ and we must use numerical optimization over Q. When λ is a high-dimensional vector, this is not feasible. Therefore, we simplify the parametrization of the noise covariance matrix R as $R(\lambda ,\rho )={\lambda }^2\widehat{\Lambda }C\left(\rho \right)\widehat{\Lambda }$, where we now consider $\widehat{\Lambda }$ as a fixed diagonal matrix with positive diagonal entries. We fix $\widehat{\Lambda }$ at the estimate of Λ from the model with C = I_K×K. ρ is the correlation matrix parameter as defined previously, and λ > 0 is a scaling parameter. Now we need to perform numerical optimization over Q to estimate only two parameters:

$$\lambda ,\rho =\underset{\lambda ,\rho }{\arg \max }Q(\theta ,{\theta }^{\prime }).$$ (A.16)

Note that since the EM algorithm does not require the maximization of Q(θ, θ′) but simply requires an increase in this function with each iteration, performing numerical optimization until convergence is not necessary.

Proposition A.2. Consider the model given in Section 2.1.5 with θ = {m, V, a, b, R}. The reparametrization ${\theta }^{\ast }=\left\{w\mathbf{m}+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill z\hfill \end{array}\right],w^{2}V,\frac{1}{w}\mathbf{a},\mathbf{b}-\frac{z}{w}\mathbf{a},R\right\}$, where w, $z\in \mathbb{R}$, w ≠ 0 yields an equivalent model.

Proof. The incomplete log-likelihood is

$$\begin{array}{cc}\hfill \log f(\mathbf{y};\theta )=& \frac{1}{2}\sum _i(\log \mid 2\pi {\Sigma }_i\mid -\log \mid 2\pi V\mid -{\upsilon }_i\log \mid 2\pi R\mid )\hfill \\ \hfill & -\frac{1}{2}\sum _{i,j}{({\mathbf{y}}_{ij}-\mathbf{b})}^T{R}^{-1}({\mathbf{y}}_{ij}-\mathbf{b})\hfill \\ \hfill & -\frac{1}{2}\sum _i{\mathbf{m}}^T{V}^{-1}\mathbf{m}+\frac{1}{2}\sum _i{\widehat{\mathbf{u}}}_i^T{\Sigma }_i^{-1}{\widehat{\mathbf{u}}}_i.\hfill \end{array}$$ (A.17)

Here, we consider the case where z = 0 for algebraic simplicity. For the reparameterized model, we obtain ${\widehat{\mathbf{u}}}_i^{\ast }=w{\widehat{\mathbf{u}}}_i$ and ${\Sigma }_i^{\ast }=w^2{\Sigma }_i$. Therefore, each of the terms in log f(y; θ*) remain the same as those in log f(y; θ), yielding log f(y; θ*) = log f(y; θ).