Multivariate Statistical Analysis of Diffusion Imaging Parameters using Partial Least Squares: Application to White Matter Variations in Alzheimer’s Disease

Abstract

Diffusion magnetic resonance imaging (dMRI) is a unique technology that allows the noninvasive quantification of microstructural tissue properties of the human brain in healthy subjects as well as the probing of disease-induced variations. Population studies of dMRI data have been essential in identifying pathological structural changes in various conditions, such as Alzheimer’s and Huntington’s diseases^1,2. The most common form of dMRI involves fitting a tensor to the underlying imaging data (known as Diffusion Tensor Imaging, or DTI), then deriving parametric maps, each quantifying a different aspect of the underlying microstructure, e.g. fractional anisotropy and mean diffusivity. To date, the statistical methods utilized in most DTI population studies either analyzed only one such map or analyzed several of them, each in isolation. However, it is most likely that variations in the microstructure due to pathology or normal variability would affect several parameters simultaneously, with differing variations modulating the various parameters to differing degrees. Therefore, joint analysis of the available diffusion maps can be more powerful in characterizing histopathology and distinguishing between conditions than the widely used univariate analysis. In this article, we propose a multivariate approach for statistical analysis of diffusion parameters that uses partial least squares correlation (PLSC) analysis and permutation testing as building blocks in a voxel-wise fashion. Stemming from the common formulation, we present three different multivariate procedures for group analysis, regressing-out nuisance parameters and comparing effects of different conditions. We used the proposed procedures to study the effects of non-demented aging, Alzheimer’s disease and mild cognitive impairment on the white matter. Here, we present results demonstrating that the proposed PLSC-based approach can differentiate between effects of different conditions in the same region as well as uncover spatial variations of effects across the white matter. The proposed procedures were able to answer questions on structural variations such as: “are there regions in the white matter where Alzheimer’s disease has a different effect than aging or similar effect as aging?” and “are there regions in the white matter that are affected by both mild cognitive impairment and Alzheimer’s disease but with differing multivariate effects?”

1 Introduction

Diffusion-weighted magnetic resonance imaging (dMRI) has been used in a wide range of studies to understand basic tissue properties in healthy individuals as well as developmental and degenerative changes that occur across the lifespan (e.g.^3,4). Through modeling water diffusivity in tissue microstructure, several different voxel-wise parameter maps can be extracted from dMRI data, which have been shown to be sensitive measures for identifying structural variations across individuals and tissue changes resulting from disease^1,2,5,6. To date, the great majority of research studying dMRI-based maps have used the diffusion tensor imaging (DTI) model and either focused on a single parameter of interest (e.g. typically the fractional anisotropy (FA) or the mean diffusivity (MD)), or analyzed multiple parameters using univariate methods^1,5–14. Animal and postmortem studies have loosely linked these different diffusion markers to histological properties and/or specific pathologies, for example, ischemia, cell death and edema have been linked to mean diffusivity^15,16, myelinated fiber organization and dispersion to fractional anisotropy^17,18, and axonal injury¹⁹ and demyelination^20–22 to axial and radial diffusivity respectively. These studies were critical in providing fundamental evidence that the multiple contrasts obtained through diffusion modeling could be used in the differentiation of dynamic processes in brain tissue such as tissue degeneration across different conditions.

One detail that has been frequently neglected in previous research is that different diffusion parameters at the same location quantify different aspects of the same underlying tissue structure. Consequently, a complex phenomenon that alters tissue structure, such as aging or Alzheimer’s disease, often affects all the parameters. The proportions of the effects across parameters naturally might differ depending on the type of alteration and the relationships between the parameters extracted from dMRI data. Therefore, it is plausible that differing histopathology may result in different proportional changes to the various dMRI-derived parameters. Joint analysis of the diffusion parameters with a multivariate method may be able to detect such differences, and disentangle similar appearing effects to better characterize conditions, reveal complex spatial variations and yield higher power to differentiate between conditions.

Coutu et al. in ²³ recently focused on the utility of a multivariate approach across several diffusion parameters for examining tissue changes associated with aging. In their study, the authors focused on spatial variations in the effects of aging on the white matter. They used seven diffusion parameters available through a diffusion kurtosis-imaging model and identified three distinct classes of aging effects across the white matter. This initial result suggests that joint analysis of diffusion parameters with a multivariate approach may indeed provide important information about disease processes not available through examination of any parameter in isolation. The multivariate approach Coutu et al. took was to compute the Pearson’s correlation coefficient between each diffusion parameter and subjects’ age at each location in the white matter, and for each point separately define the set of coefficients as the “diffusion footprint”, a voxel-wise multivariate representation. In this work, motivated by the results in ²³, we focus on the joint analysis of diffusion parameters and extend Coutu et al.’s initial method.

We introduce a novel approach for multivariate statistical analysis of diffusion parameters. Our approach is a new interpretation of the diffusion footprint through Partial Least Squares Correlation (PLSC)²⁴ analysis. This interpretation combined with non-parametric permutation testing²⁵, yields a powerful methodological basis with which a new set of hypotheses regarding changes in tissue microstructure can be tested. We first present the PLSC-based group analysis of diffusion parameters and the associated statistical test. Then we define procedures for regressing out variables and comparing conditions in the multivariate setting. These procedures allow comparing conditions based on the type of effect they have on the diffusion parameters, i.e. relative proportions of effects on parameters, in addition to effect-size and location. The technical novelties introduced in this article are in the way PLSC is applied on the diffusion data and the two procedures that are defined using the PLSC interpretation of diffusion footprint.

We apply the proposed procedures to examine group differences in diffusion parameters in the white matter among non-demented elderly adults (CN), individuals with mild cognitive impairment (MCI) and individuals with Alzheimer’s disease (AD). We provide three different experiments to demonstrate the use of the proposed procedures. In the first set, we use our approach for detecting and visualizing spatial variations in the effects of aging, AD and MCI. These maps provide a more refined visualization of the spatial variation of condition effects compared to the work of Coutu et al. in ²³. In the second experiment, we apply the proposed procedures to identify areas where AD’s effects are structurally different than the cross-sectional effects of aging in a cognitively healthy population, as quantified through diffusion parameters. Lastly, we examine whether MCI and AD have different multivariate diffusion profiles suggesting possible differing histopathology (either in the pathological process or in the stage of pathology) between these conditions. In this work, we used the diffusion tensor-imaging model as a proof of concept to demonstrate the benefits of the proposed multivariate method given the availability of substantial data provided by the Alzheimer’s Disease Neuroimaging Initiative. However, the approach is not specific to diffusion tensor imaging and is applicable to any dMRI model and any set of parameters extracted from such models. More broadly the method can also be extended to any multi-parametric spatial dataset.

2 Methods

2.1 Multivariate modeling

2.1.1 Diffusion Footprint

Coutu et al. defined their voxel-wise multivariate representation, diffusion footprint, as the set of Pearson’s correlation coefficients between different diffusion parameters and the condition of interest. The underlying idea in using correlation coefficients was to “normalize” different parameters whose absolute values might not be comparable, e.g. mean diffusivity and fractional anisotropy. The set of correlation coefficients captures both the absolute effect size in each parameter, i.e. the value of each correlation coefficient, and how much the condition affects each diffusion parameter relative to each other, i.e. the proportions. Based on this representation one can construct multivariate voxel-wise maps and differentiate between condition effects at different voxels in the image, as the authors did for effect of aging²³.

In the next section we introduce the interpretation that the diffusion footprint is actually the result of a Partial Least Squares Correlation analysis performed on the set of diffusion parameters and the condition, which will lead to various extensions in the type of statistical analysis one can do in the multivariate setting. In this article we construct two such extensions: regressing out variables and comparing effects of different conditions.

2.1.2 Multivariate Group Analysis Through Partial Least Squares

The proposed approach uses the principles of Partial Least Squares Correlation analysis (PLSC)^24,26. PLSC has been previously used in neuroimaging to jointly analyze all the voxels in the brain simultaneously^27–29. Here we apply the PLSC principles in a voxel-wise fashion to jointly analyze the different diffusion parameters at each voxel independent from the others. In a sense this voxel-wise multivariate work is a straightforward extension of univariate analysis to multi-parametric data. For the sake of completeness we present the proposed approach starting from basics without assuming any knowledge of PLSC.

Let us assume we have N subjects and for each subject there are d diffusion parameter maps and a condition-related variable, which can be either binary (e.g. diagnosis) or continuous (e.g. age). We also assume the parameter maps from different subjects are registered to the same template and measurements at each voxel can therefore be compared across the sample. This can for instance be achieved using the TBSS analysis pipeline^30,31, which aligns different subjects’ images onto a common white matter skeleton and minimizes likely confounds in group-based diffusion imaging studies. For the rest of the section we restrict our presentation to a single voxel on the common template. The treatment of each voxel is identical.

At a given voxel in the common template space we stack the different diffusion parameters of the i^th subject into vector form and represent it with x_i ∈ R^d, where R^d is the parameter space (d-dimensional Euclidean space) with each axis corresponding to a different diffusion parameter. We represent the condition-related variable for the same subject with letters in regular font, such as y_i or z_i. We remove the offsets between different diffusion parameters by removing the sample means from each parameter in isolation. We also remove differences in scales between the parameters by dividing them by sample standard deviations. This step ensures that the scale differences do not affect the results, i.e. components with larger scale would otherwise dominate the results and shadow differences in components with smaller scales. The proposed method with all the normalizations is how PLSC is widely used in neuroimaging²⁹. It might also be seen as a variation of Canonical Correlation Analysis (CCA). In the supplementary material (Appendix B) we provide the precise links between these methods. The identical normalization is also applied to the condition-related variables. To not alter notation, we will keep using x_i, y_i and z_i for the normalized variables.

In conventional univariate analysis one estimates a linear model between y and each element of x separately, keeping y as the independent variable, and determines the significance of the coefficients of the linear model. In the multivariate setting however, all the elements of x are used jointly. The covariance between y and x is defined as a function of direction in the parameter space. For a given direction v ∈ R^d (with |v|₂ = 1 where |·|₂ is the Euclidean norm), the direction-specific covariance is simply the covariance between the condition-related variable and the magnitude of the parameter vector in that direction. Mathematically, direction-specific covariance can be estimated as

$${\rho }_y(\mathbf{v})=\text{cov}[({\mathbf{v}}^{\mathrm{T}}\mathbf{x}),y]\approx \frac{1}{N-1}\sum _{i=1}^N({\mathbf{v}}^T{\mathbf{x}}_i)y_i$$

The quantities of interest of the ρ_y(v) function are its maximum value, i.e. the maximum covariance between the y and x, and the direction of maximum covariance, i.e. the v vector at which the maximum covariance is achieved. These quantities can be computed by solving the following optimization problem

$${\rho }_y=\underset{\mathbf{v}}{\text{max}}{\rho }_y(\mathbf{v}),\text{such that}{|\mathbf{v}|}_2=1{\mathbf{w}}_y={\text{arg}}_{\mathbf{v}}\text{max}{\rho }_y(\mathbf{v}),\text{such that}{|\mathbf{v}|}_2=1$$ (1)

We refer to the maximum covariance ρ_y as the effect strength and the direction of maximum covariance w_y as the effect type. The effect strength can simply be considered as the condition’s effect size on the entire set of diffusion parameters, i.e. aggregation of effect sizes on individual parameters. The effect type on the other hand is the vector of proportions indicating the relative effect size of each parameter compared to the others. While the effect strength gives a measure of how much the underlying tissue varies with the condition, the effect type provides a profile that is descriptive of the nature of the variation.

The optimization problem in (1) can be solved analytically and the solutions are given as

$${\rho }_y=\frac{1}{N-1}{\left|{\sum }_{i=1}^N{y}_i{\mathbf{x}}_i\right|}_2\text{and}{\mathbf{w}}_y=\frac{{\mathrm{\Sigma }}_{i=1}^N{y}_i{\mathbf{x}}_i}{{\rho }_y}$$ (2)

These forms have very close relationships to the diffusion footprint. Specifically, considering the diffusion footprint representation as a vector, ρ_y is the magnitude and w_y is the direction of this vector. The advantage of this novel interpretation is that it allows us to easily define different multivariate procedures, as we will describe in Sections 2.1.4 and 2.1.5.

One point to clarify is the use of categorical condition-related variables. In two-group analysis the group assignments are represented in binary, thus, the condition-related variables take the values 0 or 1 (can also be −1 or 1). For instance, when examining the effect of AD, diagnosis can be used as the condition related variable, where patients take the value 1 and non-demented controls take the value 0. In this case, the normalization across the sample and formulations in (1) and (2) are applied as if the condition-related binary variable were continuous, without any modification. In the case of 3 or more categories, the analysis described here cannot be used immediately unless the categories are ordered in the mathematical sense in which case we treat them as continuous variables.

Three points we would like to note are:

1. Both the effect strength and type depend on the condition-related variable. Different conditions might yield different values for both of these quantities. Furthermore, the analysis is done on each voxel separately; hence different locations may yield different results. As a result, both the effect strength and type can be compared between different locations and different conditions.

2. The straightforward derivation given in this section is simply the application of PLSC in the case where one of the tables is one-dimensional.

3. In previous multivariate analysis methods for neuroimaging, including applications of PLSC, localized interpretations of condition effects were not possible as Friston et al. point out in ³². The main reason is these approaches used the entire set of voxels as a single multivariate representation. Hence, the estimated correlation strength can only be attributed to the entire set of voxels and voxel-wise interpretation becomes not possible. However, the application of PLSC proposed here is multivariate in the number of parameters at a given voxel and not in the number of voxels involved in the analysis. As a result, localized interpretations are possible.

2.1.3 Statistical Inference Through Permutation Testing

Statistical inference in partial least squares analyses is mostly done using non-parametric permutation testing ^25,33. Here we follow suit. The generality of permutation testing is also useful for probing more complex questions. The inference aims to test the statistical significance of the effect strength, i.e. maximum covariance ρ_y. The null hypothesis states there is no relationship between the condition and the diffusion parameters. In the permutation-testing framework we can estimate the corresponding null distribution by permuting the condition-related variables across the sample and computing the maximum covariance for each permutation. In mathematical notation this is written as

$${\rho }_{\pi (y)}(\mathbf{v})=\frac{1}{N-1}\sum _{i=1}^N{\mathbf{v}}^T{\mathbf{x}}_{\mathbf{i}}{\mathrm{y}}_{\mathrm{\pi }(\mathrm{i})},{\rho }_{\pi (y)}=\underset{\mathbf{v}}{\text{max}}{\rho }_{\pi (y)}(\mathbf{v}),\text{such that}{|\mathbf{v}|}_2=1$$

where π is a random permutation of the subject index set {1,…, N} and the subscript π(y) represents the correspondence between the variable and the permutation π. Using the maximum covariance values obtained with permuted data one can assign a statistical significance to observed effect strength by determining the ratio of permutations that achieve higher effect strength, i.e.

$$\rho ({\rho }_y)=\frac{1}{M}\sum _{m=1}^M\delta ({\rho }_y\le {\rho }_{{\pi }^{(m)}(y)})$$ (3)

where M is the total number of random permutations computed. Following standard practice in permutation testing if there are no permuted datasets that achieve higher effect strength than observed we report p = 1/M. In the next two sections we use the PLSC-based interpretation of diffusion footprint to define two statistical procedures that are multivariate in nature. We start by describing how PLSC-based analysis and permutation testing can be used to compare the multivariate effect types between two different conditions.

Permutation testing is a generic technique that does not make distributional assumptions. However, one point to note is that, as most parametric and non-parametric techniques, permutation testing is prone to problems related to outliers, see ²⁵ Chapter 11 for a thorough treatment. In the presence of outliers the null distribution estimated via permutations is less reliable and therefore, the p-values are less reliable, which might mean higher type I errors. In addition, authors in ³⁴ point out that when the correlation is strong between different elements of x (and possibly between the elements of y in case it has multiple dimensions), the permutation tests can yield high type I errors. This is issue is most probably due to the fact that in these cases permutation testing should be implemented so to preserve the correlation structure across the elements of x. Otherwise, they might be misleading. In our case, we have not observed explicit outliers in our data. Furthermore, in our permutation scheme we make sure the correlation structure within x is preserved.

2.1.4 Comparing Multivariate Effects Types of Different Conditions

Comparing the effects of different conditions is a statistical procedure that builds upon basic group analysis. As the name suggests, it facilitates the detection of similarities and differences between conditions. A useful example of the application of this procedure is the comparison of effects of MCI and AD. Specifically, by using this procedure one can examine whether MCI’s effects are the same as AD’s only less pronounced, or whether the effects of these conditions differ. dMRI measurements are particularly important for such comparisons as they allow us to examine the differences in the alterations in the tissue microstructure, and it is currently the only way to do this non-invasively.

Univariate analysis can be used to compare effects of conditions for each parameter. However, the univariate analysis can only compare the conditions with respect to effect-sizes, it will not be possible to compare effect-types, which may possibly relate to differences in histopathology. The PLSC-based group analysis presented in Section 2.1.2 allows comparing effect-types between conditions. In this section we describe how this can be done and present the multivariate statistical procedure to test the question: at a given voxel where two conditions show effects, do they have the same effect-type, i.e. w vectors?

Let us assume there are three groups: one control and two case groups corresponding to two different conditions, which we would like to compare. We represent these three groups with two binary variables: y and z. A zero value for both of these variables means the individual is in the control group, while y = 1 indicates the individual is in the first group and z = 1 indicates the individual is in the second group. Let us also further assume that the case groups are non-overlapping, i.e. y and z are never both one for the same individual. In theory, one can have overlapping groups as well but we keep the presentation to non-overlapping groups for ease of explanation.

Using the methodology presented in Section 2.1.2, we can estimate effect-strengths and effect-types for each condition by comparing the respective case group with the control group. To compare the effects of two conditions we estimate the effect-types for each condition independently using the corresponding case group and the same control group. Since effect types are formulated as unit-norm vectors in the diffusion parameter space, a natural choice of statistic for quantifying their difference is their dot product:

$$a={\mathbf{w}}_{\mathrm{y}}·{\mathbf{w}}_z$$

Since w is normalized, the a variable is by definition in the interval [−1, 1]. a = 1 indicates that the vectors are the same while a < 1 suggests that the effect types are different between the conditions. We perform statistical inference on a using a permutation-testing framework. To formulate the specific permutation structure test let us denote the three groups with index sets I_C = {i₁,…, i_NC}, I_GY = {j₁,…, j_NY} and I_GZ = {k₁,…, k_NZ} corresponding to the subjects in the control group, group with y = 1 and group with z = 1, respectively. These indices are simply integers; we denote them with different letters to make the following permutation analysis easier to present. With these group definitions let us first re-formulate the effect type estimation presented in Section 2.1.2:

$${\mathbf{w}}_y={\text{arg}}_{\mathbf{v}}\text{max}\frac{1}{\mathit{\text{NC}}+\mathit{\text{NY}}-1}\sum _{n\in I_C\cup I_{\mathit{\text{GY}}}}{\mathbf{v}}^T({\mathbf{x}}_n-{\overline{\mathbf{x}}}_{\mathit{\text{CY}}})y_n^{\mathit{\text{CY}}},{\overline{\mathbf{x}}}_{\mathit{\text{CY}}}=\frac{1}{\mathit{\text{NC}}+\mathit{\text{NY}}}\sum _{n\in I_C\cup I_{\mathit{\text{GY}}}}{\mathbf{x}}_n{\mathbf{w}}_z={\text{arg}}_{\mathbf{v}}\text{max}\frac{1}{\mathit{\text{NC}}+\mathit{\text{NZ}}-1}\sum _{n\in I_C\cup I_{\mathit{\text{GZ}}}}{\mathbf{v}}^T({\mathbf{x}}_n-{\overline{\mathbf{x}}}_{\mathit{\text{CZ}}})Z_n^{\mathit{\text{CZ}}},{\overline{\mathbf{x}}}_{\mathit{\text{CZ}}}=\frac{1}{\mathit{\text{NC}}+\mathit{\text{NZ}}}\sum _{n\in I_C\cup I_{\mathit{\text{GZ}}}}{\mathbf{x}}_n$$

Note that these formulations are slightly different than the ones previously given. First of all, the variables of interest y and z are normalized (to zero-mean and unit variance) using only the samples in the respective computations. For instance y^CN indicates that this variable is normalized using the subjects in the control group and the subjects in the group with y = 1. The measurement vectors x on the other hand are normalized across the entire sample including all three groups. This ensures that we do not introduce any group specific bias in the normalization and the estimated vectors can be compared. However, as a result we need to include the respective means in the estimation of the covariance in the formulations.

The null hypothesis we focus on states that w_y and w_z vectors are the same and hence a = 1 (with an infinite number of samples). As a result, the group assignments between y = 1 and z = 1 samples are irrelevant in terms of the difference in effect-type. Hence, if we change these assignments across the individuals in the respective groups the value of a should only vary due to noise and finite sample size. Accordingly, to estimate the null distribution for a we randomly permute across the groups y = 1 and z = 1 while keeping the control group fixed. The permuted index sets for the groups obey the group sizes, e.g. π_GY = {j₃, k₆, k₁₄, j₇, …} with |π_GY| = NY and π_GY = {k₂, k₄, j₁, k₂₁,…} with |π_GY| = NZ. for each permutation we re-estimate the effect types with

$${\mathbf{w}}_{\pi (y)}={\text{arg}}_{\mathbf{v}}\text{max}\frac{1}{\mathit{\text{NC}}+\mathit{\text{NY}}-1}\sum _{n\in I_C\cup {\pi }_{\mathit{\text{GY}}}}{\mathbf{v}}^T({\mathbf{x}}_n-{\overline{\mathbf{x}}}_{C\pi (Y)})y_n^{C\pi (Y)},{\overline{\mathbf{x}}}_{C\pi (Y)}=\frac{1}{\mathit{\text{NC}}+\mathit{\text{NY}}}\sum _{n\in I_C\cup {\pi }_{\mathit{\text{GY}}}}{\mathbf{x}}_n{\mathbf{w}}_{\pi (z)}={\text{arg}}_{\mathbf{v}}\text{max}\frac{1}{\mathit{\text{NC}}+\mathit{\text{NZ}}-1}\sum _{n\in I_C\cup {\pi }_{\mathit{\text{GZ}}}}{\mathbf{v}}^T({\mathbf{x}}_n-{\overline{\mathbf{x}}}_{C\pi (Z)})Z_n^{C\pi (Z)}{\overline{\mathbf{x}}}_{C\pi (Z)}=\frac{1}{\mathit{\text{NC}}+\mathit{\text{NZ}}}\sum _{n\in I_C\cup {\pi }_{\mathit{\text{GZ}}}}{\mathbf{x}}_n$$

and compute the dot product as a_π = w_π(y) · w_π(z). The significance level is then computed by counting the number of permutations with lower dot products:

$$p(a)=\frac{1}{M}\sum _{m=1}^M\delta (a\ge a_{{\pi }_m})$$ (4)

While it is possible to apply this analysis to compare effect types in any voxel, it is generally only meaningful to do so in voxels where the effect strength of both conditions is significant as tested by the procedure detailed in Section 2.1.3. The reason for this is the statistic a only quantifies the angular difference between the vectors and ignores their magnitudes. In regions where the signal is mostly likely only composed of noise, the vectors will have small magnitudes but may have large angular differences. The permutation-based null distribution will most likely capture this but the test is needless since both vectors are most likely noise. On the other hand, in the regions where only one of the conditions have signal the a statistic can show large angular differences that are statistically significant based on the permutation test. It is difficult to talk about angular differences in this case since one of the conditions do not show signal on that region. We thus constrain the analysis to voxels whose effect-strength significance exceeds a threshold for both of the conditions. In order to provide intuition about the a statistic and its null distribution as estimated through permutation analysis, we provide brief analysis using synthetic dataset in the supplementary materials Appendix A.

The PLSC-based interpretation of diffusion fingerprint not only allows for comparing multivariate effect-types between conditions, but also for regressing out one effect from the other in the multivariate setting. The next section describes the procedure to accomplish this.

2.1.5 Regressing Out Nuisance Parameters in the Multivariate Setting

An important procedure in statistical analysis in neuroimaging is to “regress out” the effects of unwanted or nuisance variables in order to identify the effects that are unique to the condition of interest. An example from univariate analysis would be to regress out the effects of aging when analyzing the effects of Alzheimer’s disease on a single diffusion parameter. The PLSC-based formulation of Section 2.1.2 allows a straightforward definition of the regressing out procedure in the multivariate setting.

We will treat the regressing out procedure in two parts. Let us assume we have two condition-related variables y and z, and we are interested in regressing out the effect of z from the data to determine the “z-normalized” effect of y. In the multivariate setting the PLSC-based analysis quantifies the effect of z with the effect-strength ρ_z and the effect-type w_z, which can be combined into a single vector ρ_zw_z. We consider the regressing out procedure as determining the effect of y on the diffusion parameters in addition to the effect of z. In the multivariate setting, this additional effect has two components, one parallel and one orthogonal to w_z. The parallel component is the additional effect of y that has the same type as the effect of z. An example of parallel component is for instance the rapid aging effect of Alzheimer’s disease. In this example z becomes the age of the subject and y is the diagnosis for AD. The parallel component would quantify AD’s accelerated aging effect as seen through diffusion parameters. Conversely, the orthogonal component is y’s additional effect that is orthogonal to the effect type w_z. In the above example, the orthogonal component would quantify AD’s effect on the diffusion parameters that is structurally different than that of aging.

Both the parallel and the orthogonal components can be estimated from finite data by modifying the formulations given in Section 2.1.2. We estimate the orthogonal component by extending the optimization problem given in Equation (1). We simply add an extra constraint and solve

$${\rho }_{y\perp z}=\underset{\mathbf{v}}{\text{max}}{\rho }_y(\mathbf{v}),{\mathbf{w}}_{y\perp z}={\text{arg}}_{\mathbf{v}}\text{max}{\rho }_y(\mathbf{v}),such\text{that}{|\mathbf{v}|}_2=1\text{and}{\mathbf{v}}^T{\mathbf{w}}_z=0$$

The solution of this optimization problem can be computed using the method of Lagrange multipliers and is given by

$${\rho }_{y\perp z}=\frac{1}{N-1}\sum _{i=1}^N({\mathbf{w}}_{y\perp z}^T{\mathbf{x}}_i)y_i{\mathbf{w}}_{y\perp z}=\frac{{\sum }_{i=1}^N{\mathbf{x}}_i{y}_i-{\sum }_{i=1}^N({\mathbf{w}}_z^{\mathrm{T}}{\mathbf{x}}_i)y_i{\mathbf{w}}_z}{{|{\sum }_{i=1}^N{\mathbf{x}}_i{y}_i-{\sum }_{i=1}^N({\mathbf{w}}_z^{\mathrm{T}}{\mathbf{x}}_i)y_i{\mathbf{w}}_z|}_2}$$ (5)

w_y⊥z is the direction that maximizes the covariance with respect to y and orthogonal to the effect type of z, as given by the direction w_z. The quantity ρ_y⊥z quantifies the size of the effect in this orthogonal direction.

The parallel component captures the residual covariance between y and x in the direction of z’s effect, once z’s effect has been subtracted out. We first note that if both x and z are normalized (zero-mean and unit variance), then ρ_z is also the coefficient of the linear model $({\mathbf{w}}_z^{\mathrm{T}}\mathbf{x})={\rho }_{z}z$ that gives the least-squares error. Based on this observation, for a given subject we can estimate an effect vector z_iρ_zw_z that captures the component in x_i that is explained by z_i. To find the parallel component we subtract the effect vector from x_i and estimate the effect strength in the same w_z direction with

$${\rho }_{y\parallel z}=\frac{1}{N-1}\sum _{i=1}^N{\mathbf{w}}_z^T[{\mathbf{x}}_i-z_i{\rho }_z{\mathbf{w}}_z]y_i=\frac{1}{N-1}\sum _{i=1}^N({\mathbf{w}}_z^T{\mathbf{x}}_i)y_i-\frac{{\rho }_z}{N-1}\sum _{i=1}^N{z}_i{y}_i$$ (6)

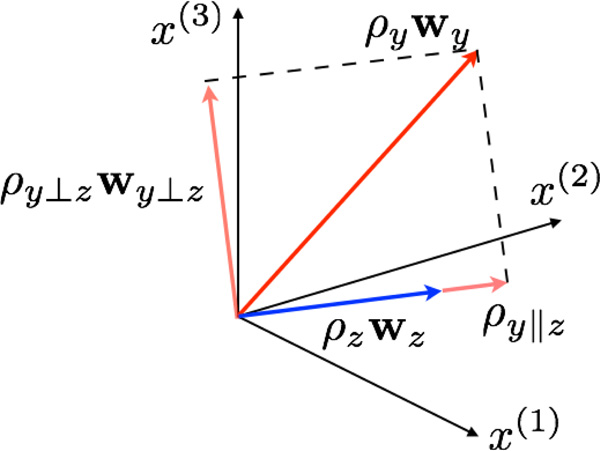
Readers familiar with Partial Least Squares Regression (PLSR) will notice the similarity between this derivation and that of PLSR. We sketch the parallel and the orthogonal components in Figure 1 in a toy example with 3 different diffusion parameters x⁽¹⁾,x⁽²⁾ and x⁽³⁾.

Figure 1.

Regressing-out procedure in the multivariate setting. The effect of z is regressed out to determine the z-normalized effect of y. The axes represent the three diffusion parameters in this toy example. The red vector is the effect of y when z is ignored and the blue vector is the effect of z when y is ignored. The parallel and orthogonal components of the z-normalized effect of y are shown in pale red.

We perform statistical inference for both ρ_y⊥z and ρ_y∥z using permutation testing. We permute the y variables across the sample, and keep both x and z fixed to preserve the covariance structure between these variables and break their statistical links with y. For the orthogonal component the significance values are assigned as before, i.e. based on the number of permutations with higher covariance values

$$p_{\perp }=\frac{1}{M}\sum _{m=1}^M\delta ({\rho }_{y\perp z}\le {\rho }_{{\pi }^{(m)}(y)\perp z})$$ (7)

For the parallel component, since the covariance values can now be also negative, we use a two-sided test as follows:

$$p_{\parallel }=\frac{1}{M}\sum _{m=1}^M\delta (|{\rho }_{y\parallel z}|\le |{\rho }_{{\pi }^{(m)}(y)\parallel z}|)$$ (8)

We also note that one could formulate the regressing-out procedure by combining ρ_y⊥z and ρ_y∥z. This approach would provide a single correlation coefficient and vector. However, to dissect the result into the parallel and orthogonal component one would have to devise a subsequent procedure. Here, our aim is to provide the procedure that focuses on analyzing the multivariate aspect. Thus we have chosen to separate the perpendicular and parallel effects from the start.

The regressing out procedure in the multivariate setting also provides a different opportunity that is decomposing the effect of a condition with respect to the other one. The parallel component quantifies the similarities between the effects of conditions while the orthogonal component quantifies their differences. Hence, this procedure can also be used to compare effect of different conditions.

In the Section 3 we apply the proposed procedures to test several different hypothesis regarding non-demented aging, MCI and AD. Before that, in the next section we would like to relate the proposed model to the previously proposed multivariate analysis techniques for analyzing diffusion data and more broadly other images in neuroimaging.

2.1.6 Links to Existing Multivariate Methods

Previous research on multivariate statistical methods in neuroimaging and diffusion image analysis, mostly focus on whole brain analysis, in which case all voxels are analyzed jointly rather than analyzing each voxel independently. Proposed techniques can be roughly categorized in two groups: exploratory and predictive. Exploratory methods mostly use variations and combinations of the fundamental decomposition techniques Principal Component Analysis (PCA), Independent Component Analysis (ICA), Canonical Correlation (Variant) Analysis (CCA), PLS and tensor decomposition. The goal of these methods is to discover “patterns” of brain regions, i.e. groups of voxels, that are affected by a condition of interest either in one image modality (or a parameter map when diffusion is considered)^{27–29,35–37} or in multiple modalities through data fusion ^38–45. Sui et al. in ⁴⁶ provides a relatively recent review of such exploratory techniques. Exploratory methods do not have to be applied to image intensities directly but can also been applied to results of initial statistical analysis, which is often done in functional MRI analysis, see for instance Krishnan et al.’s review on different use cases of PLS ²⁹. Predictive methods on the other hand use statistical learning or machine learning techniques, such as Support Vector Machines ^47–49, Linear Discriminant Analysis ⁵⁰, Deep Boltzmann Machines⁵¹ or other techniques⁵². These methods combine information coming from different modalities and parametric maps derived from diffusion data with the aim to predict the condition of interest, such as diagnosis or age. The derived maps do not necessarily have to be voxel-wise information but can also be connectivity matrices, from which features are extracted and fed to the predictive modeling.

The proposed method falls within the exploratory group. However, it is a “voxel-based” multivariate approach and not a multi-voxel one. Arguable the biggest advantage of multi-voxel multivariate approaches is that they do not make the “independent voxels” assumption univariate approaches make. They take into account the empirical correlation structure between voxels, thus do not suffer from the multiple comparisons problem related to testing millions of voxels independently, a great advantage.

Similar to the method proposed here, multi-voxel approaches can also fuse different imaging modalities or diffusion-derived parametric maps, where the underlying idea is to identify patterns of changes correlated across modalities and to the condition of interest. However, multi-voxel multivariate approaches have one important drawback that limits their application in population-wide studies: localized interpretations are not possible ^32,36. The analyses result in spatial patterns that span a group of voxels or the entire set of voxels in some cases. Currently, there is no way to break such maps apart and interpret various regions locally. The pattern has to be interpreted as a whole. For instance, if a factor shows positive values on one region and negative on the other, one cannot interpret these two regions in isolation and the only plausible way would be to interpret the two regions jointly. Although resampling techniques can quantify the reliability of this pattern at each voxel²⁸, the reliable set of voxels still need to be interpreted jointly. This limits the application of multi-voxel multivariate models.

How important is this limitation? Being able to perform localized interpretations allow more precise characterization of regional changes due to pathologies and disorders. This is crucial to build the bridges between the observed changes and the underlying anatomy, and eventually to get a better understanding of the neurobiological underpinnings of various diseases. Multi-voxel multivariate approaches may achieve higher global sensitivity than voxel-wise methods, however, due to their limitations they cannot be used to characterize regional changes; they have lower regional specificity than voxel-wise approaches. The approach proposed in this article extends voxel-wise univariate approach by adding specificity to the effect type. Since the resulting method is still voxel-wise, it maintains the desired regional specificity and allows localized interpretations.

The closest existing work to the proposed method is Naylor et al.’s voxel-wise multivariate analysis proposed in ⁵³. Similar to our work this method combines information from different parametric maps derived from different imaging modalities at each voxel using multivariate regression between modalities (dependent variables) and subject variables (independent variables). Multivariate regression is not different than applying univariate regression to each modality independently⁵⁴. However, authors in this work define multivariate contrast matrices and an appropriate unified statistical test to leverage the higher statistical power arising from using all the modalities jointly instead of applying univariate tests to each modality in isolation. The main point is that one has to apply multiple comparisons correction when testing different modalities in isolation and combining results. The joint test does not need such a correction and according to the results in ⁵³ may lead to higher statistical power in certain cases, especially when the parameters are strongly correlated. The resulting formulation is very similar to the proposed multivariate effect strength. The method proposed here extends the work of Naylor et al. and additionally allows computations of multivariate effect-types, comparisons of effect types and multivariate regressing out that disentangles the effects into orthogonal and parallel components.

3 Experiments

In all the experiments we used the publicly available dataset from the Alzheimer’s Disease Neuroimaging Initiative (ADNI, http://adni.loni.usc.edu). Below, we present three different experiments with the ADNI dataset to demonstrate the proposed multivariate statistical analysis procedures. In the supplementary material (Section C) we present additional experimental results with synthetically generated dataset and empirical quantitatively analysis of the proposed procedures.

3.1 Participants and MRI acquisition

We constructed a sample from the ADNI dataset that included 74 controls, 97 participants with MCI and 48 participants with AD. All subjects were scanned with a 3T GE Medical Systems scanner and had sagittal T₁-weighted 3D spoiled gradient echo images and diffusion-weighted images (b = 1000 s/mm², 41 directions) available at the time of download. The scans were acquired using ADNI Core MRI and DTI protocols⁵⁵. Group designation of control, MCI and probable AD was determined by ADNI based on the criteria of the National Institute of Neurological Disorders and Stroke — Alzheimer’s Disease and Related Disorders Association⁵⁶. Subjects with Clinical Dementia Rating⁵⁷ of 0 were grouped together into the control group. Participants enrolled as early and late MCI were combined into one MCI group (see ADNI 2 Procedures Manual on www.adni-info.org for more information). Demographics are provided as part of Table 1.

Table 1.

Demographics for all participants. All significant p-values are bolded. Standard errors are shown in parentheses. (MMSE: Mini-Mental State Exam; CN: control; MCI: mild cognitive impairment; AD: Alzheimer’s disease). a. Information missing for 16 CN, 20 MCI, 11 AD.

	All ADNI, n = 219
	CN	MCI	AD	p-value
Participants (female)	74 (47)	97 (36)	48 (17)	0.0007
Age in years	73.06 (0.84)	73.82 (0.73)	74.73 (1.04)	0.4607
Education in years	16.32 (0.32)	16.14 (0.28)	15.27 (0.40)	0.1045
MMSE (-)a	28.69 (0.25)	27.86 (0.21)	23.16 (0.31)	0.0001
Translation motion in mm	1.33 (0.07)	1.34 (0.06)	1.32 (0.08)	0.9869
Rotation motion in degrees	0.0063 (0.0003)	0.0063 (0.0003)	0.0066 (0.0004)	0.7900

3.2 Diffusion data pre-processing

The diffusion dataset was corrected for 3D head motion and eddy current distortion using FSL (http://www.fmrib.ox.ac.uk/fsl), and translation and rotation motion estimates were obtained from the registration matrices⁵⁸. For individuals from the ADNI sample with multiple available scans, we picked the one with the least average translation motion. The motion parameters for the groups are given in Table 1. The diffusion tensor imaging (DTI) model was fit to the diffusion dataset using FSL, and three diffusion parameters were extracted for each voxel: axial diffusivity (λ₁), radial diffusivity (λ_R) and fractional anisotropy (FA). Parametric maps of each diffusion metric were registered to a common FA template in MNI152 space using the FSL Tract-Based Spatial Statistics procedure (TBSS)^30,31. All parameter maps were registered using a single deformation field that was estimated using the FA maps. Statistical analyses were limited to voxels with mean FA values higher than 0.2 on a standard tract skeleton in order to minimize partial volume and registration confounds, as described previously in ^30,31.

3.3 Details on Analyses

We experimented with three different analyses.

1. In the first analysis we examined: (i) the multivariate effects of aging in the control group (min age = 63, max age = 89, mean age = 73.06, std = 5.53), (ii) the effect of Alzheimer’s disease by comparing AD and control groups, and (iii) the effect of mild cognitive impairment by comparing MCI and control groups. In each comparison we computed the multivariate effect-strength and effect-type based on the formulations given in Section 2.2. Statistical inference was performed using permutation testing as described in Section 2.3. The analyses were performed at each voxel independently resulting in voxel-wise maps of multivariate effect strength and type. We also performed univariate analysis on each diffusion parameter in isolation as is typically done in the literature. For each parameter we computed the sample correlation coefficient and performed inference using permutation testing. The results of the univariate analysis obtained this way are directly comparable to the multivariate results.

2. In the second analysis we examined the effect of AD when the effect of aging was regressed out. In particular, we computed the AD effect that was orthogonal to the aging effect and the residual effect that was parallel to the aging effect as described in Section 2.4. The analysis was based on comparing the AD and the control groups.

3. Our last analysis examined the difference of effect-type between AD and MCI as compared to the control group. This analysis used the results of the first analysis to identify regions where both conditions showed significant effects. The comparison study was restricted to these regions. The analysis and inference was performed based on the method described in Section 2.5.

In all the statistical tests the level of significance was set at p < 0.05 (uncorrected). The analyses and the statistical tests were applied to each voxel in the white matter skeleton independently. For all analyses 10,000 permutations were computed to estimate the null-distribution. P-value maps were thresholded at p<0.05, binarized, dilated using the FSL “tbss_fill” function and presented on an MNI152 T₁-weighted template for ease of visualization.

In this preliminary work we did not correct for multiple comparisons problem to show the results below. The reason for this is the lack of an appropriate correction method that would take into account the spatial correlation structure for skeleton based analysis, the multivariate nature of the resulting statistics and the symmetry characteristics of the final maps. We refrained from applying Bonferonni correction, as it is extremely conservative, and False Discovery Rate (FDR) correction because it does not take full advantage of the spatial content. However, FDR as well as enhancing techniques such as Threshold-Free-Cluster-Enhancing (TFCE)⁵⁹ can be applied to the results as commonly done with univariate analysis. We provide FDR corrected results in the supplementary materials (Appendix E) for completeness. In addition, we also used TFCE to enhance the statistical maps, i.e. covariance strength maps, and then compute p-values over the enhanced statistics maps using permutation testing, as often done in neuroimaging studies⁶⁰. We later correct the TFCE enhanced p-value maps using FDR. The FDR corrected and TFCE enhanced and then FDR corrected maps are provided in the supplementary materials (Appendix E). We would like to emphasize the need for an appropriate correction method for the multiple comparisons problem and set this as a future research project.

3.4 Multivariate Analysis of the Effect of Aging, AD and MCI

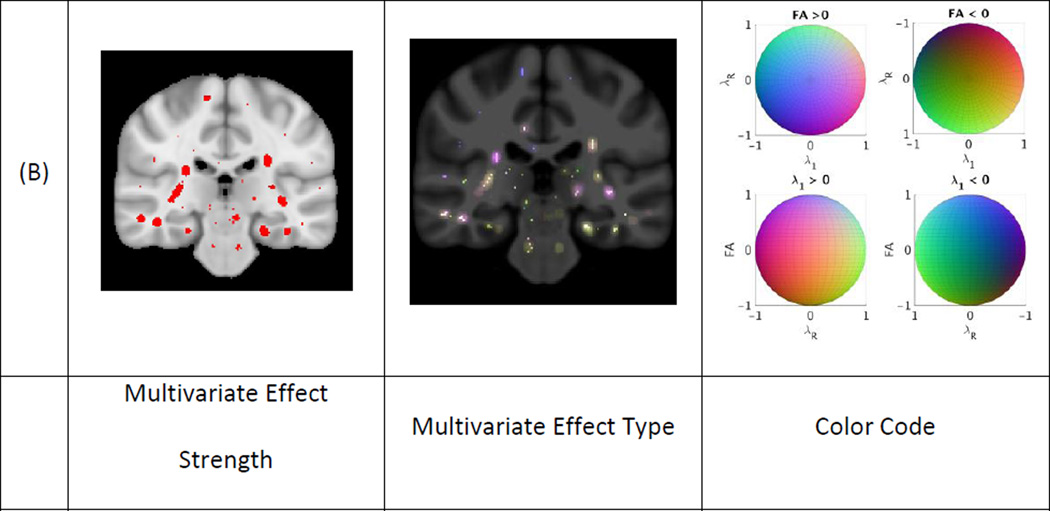
Figures 2, 3 and 4 present the results of the univariate and multivariate analyses of the effect of aging, AD and MCI, respectively. Figures 2A, 3A and 4A show the p-value maps resulting from univariate analyses. The maps display the areas on the white matter skeleton where each diffusion parameter was significantly related to the respective conditions. Figures 2B, 3B and 4B show the p-values maps for the multivariate effect-strength (computed using Equation 3) and the effect-types obtained with the multivariate PLSC-based method (w_y computed using Equation 2). The effect types are only shown for voxels that had significant multivariate effect strength. The effect-type vectors are unit-norm vectors, where each element can take positive or negative values. To map such vectors we compute the RGB vectors as w_RGB = (w_y + 1)/2. In each figure we provide the color code for interpreting the multivariate effect types. Since the effect types are formulated as unit norm vectors, the color code is drawn on a sphere and the figures show 4 projections of the sphere. In the 4 projections view the first row shows the colors where FA shows increase and decrease, and the second row shows the colors where λ₁ shows increase and decrease respectively. The existence of blue hue indicates the condition is related to increasing FA values while the lack of it to decreasing values. Similarly red hue indicates increasing and its lack decreasing λ₁ values. Lastly, green hue indicates increasing and its lack decreasing λ_R values. We also present additional images showing different slices of effect-type maps are shown in Supplementary materials Appendix D.

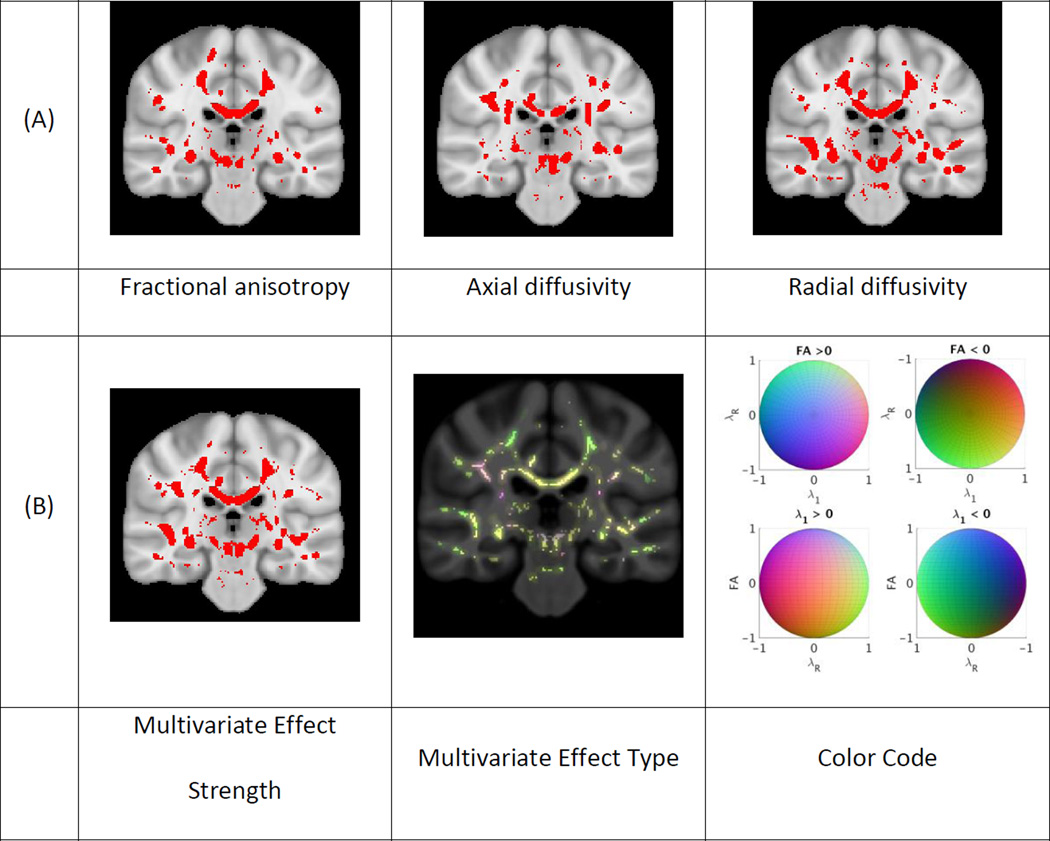
Figure 2.

Effects of aging on white matter: (a) Univariate and b) multivariate analyses of the effect of aging in the control group. P-value maps show significant effects for univariate analyses and the multivariate effect strength on the white matter skeleton in red (p < 0.05). These effects were dilated to surrounding areas in red for easier visualization. The multivariate effect type is shown at each point where the effect-strength was significant and the corresponding color code is given on a sphere as the effect-types are given as unit vectors. For visualization purposes, four views of the color code sphere are shown.

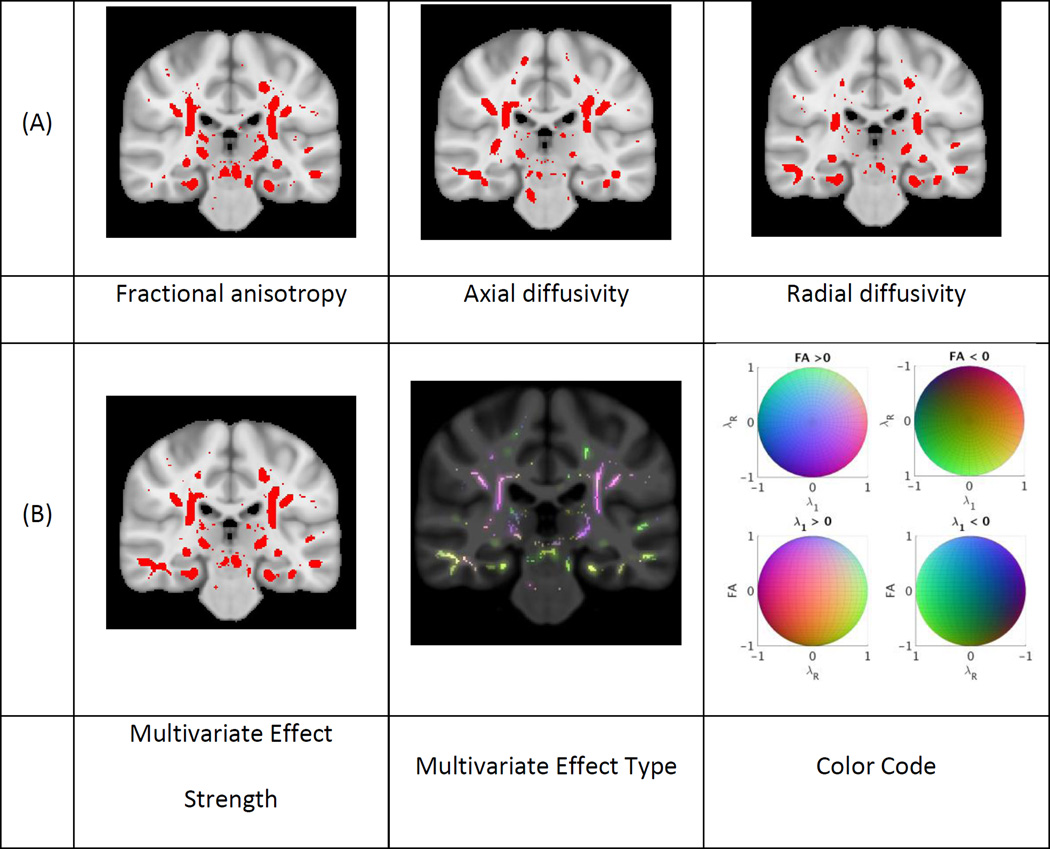
Figure 3.

Effects of Alzheimer’s disease on white matter: a) Univariate and b) multivariate analyses of the group difference between individuals with Alzheimer’s disease and non-demented controls. The same visualization as Figure 2 is used. P-value maps show significant effects for univariate analyses and the multivariate effect strength on the white matter skeleton in yellow (p < 0.05). The multivariate effect types are only shown on regions with significant effect.

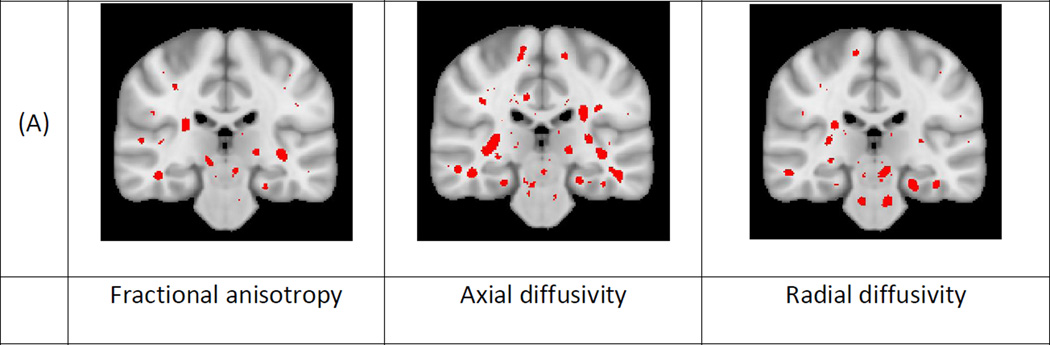
Figure 4.

Effects of mild cognitive impairment on white matter: a) Univariate and b) multivariate analyses of the group difference between individuals with mild cognitive impairment and non-demented controls. The same visualization as Figure 2 and 3 is used.

The three conditions varied in the spatial extent of their significant effects. Aging showed effects in most of the white matter, while AD effects were more constrained and MCI effects were even further constrained. The univariate effects were similar to those described in prior studies ^1,4,7,11. The significant areas for the multivariate effect-strength contained almost all the regions that were present in the different univariate analyses. Comparing the multivariate map with each univariate map independently, we observe that multivariate analysis detects effects on larger areas than each univariate map. This is expected because the multivariate analysis captures the effect-related variations in all components jointly and therefore, the effect strength map can be seen as a “statistical union” of univariate analyses maps of individual metrics. Conversely, there are some regions in each univariate map (different regions for different maps) that show effect in the univariate analysis and not in the multivariate. This is explained by the lack of correction for multiple corrections when testing several univariate hypotheses. The univariate analyses are not corrected for multiple comparisons related to testing 3 diffusion measures, while the multivariate analysis has implicit correction for this comparison. If the univariate maps are corrected they may detect smaller areas, as also demonstrated in⁵³ . To illustrate this point for the AD versus control group comparison we present an image in the supplementary material (Appendix D, Fig. D8) where we corrected the univariate maps using Bonferroni correction (for testing 3 components).

There was also great spatial variation in effect-type for all of the conditions. Even though the effects of aging and AD show overlap in the regions where they are significant for the effect strength, the effect-types in these regions differed. Slight differences between the effect-type maps for AD and MCI were also observed. These differences motivate the following analyses presented below.

Lastly, the colors in the effect-type maps were mostly in between colors, such as yellow, green and purple-mauve. Essential colors, i.e. red, blue and green, are not strongly represented. There are two reasons for this. First, the mapping between the effect-type vectors and the RGB vectors would already result in intermediate colors when only one of the components has an effect, e.g. when only λ₁ is decreasing the color would be cyan and when only FA is decreasing it would be yellow. In addition, due to correlation between different parameters the effect-type vectors include multiple non-zero components for most regions, which leads to intermediate colors.

3.5 Multivariate Effects of Alzheimer’s Disease Regressing Out Age

Figure 5 shows the results from the second experiment, where the effects of Alzheimer’s disease were analyzed while regressing out the effects of aging using the procedure described in Section 2.1.4. The procedure subtracts the effect of aging from the data and computes the AD effect in the remaining in two components: the orthogonal component in the orthogonal direction to aging effect type (computed using Equation 5) and the parallel component in the same direction as the aging effect type (computed using Equation 6). The first two images in the top row show the p-value maps for these components (Equations 7 and 8). In the parallel component map the effect can be either positive (accelerated aging) or negative (decelerated aging) and these are shown in red and blue respectively. The orthogonal component map shows the areas where Alzheimer’s disease effect has a significant component that is orthogonal to that of aging, and thus the overall effect is different than aging. The observed difference in these areas might indicate possible differing structural variations related to AD compared to non-demented aging. Almost half of the voxels showed effects both in the parallel and in the orthogonal components. However, there were regions where AD effect did not have an orthogonal component. To identify these areas we removed the regions that had a significant orthogonal component from the map of parallel components. Third image in the top row in Figure 5 shows this purely parallel map. In these areas AD’s estimated effect-type was identical to that of aging. While the regions in the orthogonal map correspond to areas where AD’s effect might structurally differ from that of aging, the regions in the purely parallel map correspond to areas where AD’s effect might be the same as aging but in different magnitude. In the second row we render the regions with purely parallel and orthogonal components in blue and red respectively. We further, render orthogonal and purely parallel component in 3D and visualize it in a glass brain in Figure 5. These 3D renderings demonstrate the symmetric characteristics and extents of the differences in effects.

Figure 5.

Multivariate analysis of group differences between individuals with Alzheimer’s disease and non-demented controls regressing out age with the multivariate procedure. The results are presented in three parts: parallel component (left), orthogonal component (middle) and purely parallel component (right). Left: P-value maps show significant effects for the parallel component on the white matter skeleton in red and blue, respectively corresponding to effects significantly greater and lower than the effect of aging in the same type (p < 0.05). Middle: P-value maps show the significant effects for the orthogonal component in red. Right: P-value map shows the significant effects that only have a parallel component. The 3D renderings in the second row visualize the orthogonal (red) and purely parallel (blue) components. The effects were dilated to surrounding areas in red and darker blue for easier visualization. In the 3D renderings very small clusters (size less than 20 voxels) have been removed and the remaining clusters have been smoothed for visualization. These areas display the regions where AD’s effect on the diffusion parameters was the same type as aging and different than aging.

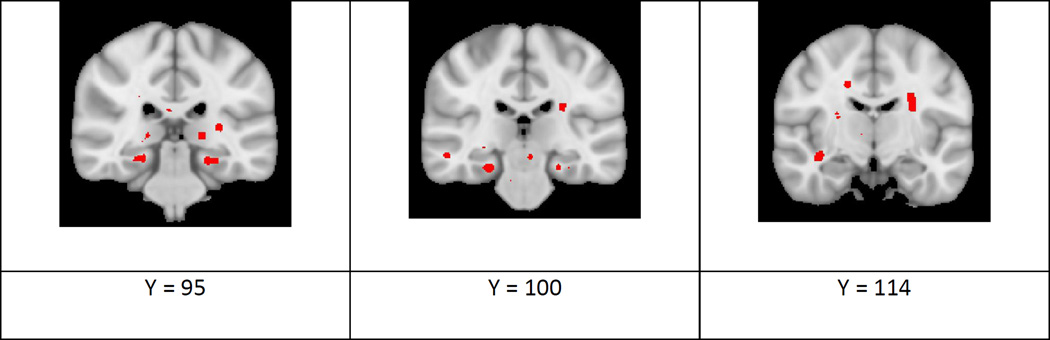
Additional images of the p-value maps of the parallel and orthogonal components are provided in Supplementary materials Appendix D, Figures D4, and D5. In the same Appendix Figure D6 we show additional slices of the purely parallel map. The supplementary figures demonstrate the similarity of AD’s effect-type to aging around the parahippocampal regions and the broad areas in which a significant effect-strength with an orthogonal effect-type to aging was found, including large bilateral portions of the internal capsule.

3.6 Differences in the effect-types of MCI and AD

Figure 6 presents the results of comparing the effect types between AD and MCI, using the procedure in Section 2.1.5. The analysis was constrained to the regions where both MCI and AD showed significant effects, as presented in section 3.4. The images show p-value maps corresponding to the angle difference between effect types computed using Equation 4. There were multiple areas where the effect-types of these conditions differed. While some areas may arise due to the lack of voxel-wise correction for multiple comparisons, regions that show symmetric differences across hemispheres, such as bilaterally in the parahippocampal area, may represent real differences in effect-type. Images of additional slices of the difference in effect-type between MCI and AD are provided in Supplementary Figure C7.

Figure 6.

Multivariate analysis comparing the effect type of the group difference between individuals with Alzheimer’s disease and non-demented controls to the effect-type of the group difference between individuals with MCI and non-demented controls. P-value maps show significant effects for the multivariate effect strength on the white matter skeleton in red (p < 0.05). These effects were dilated to surrounding areas in red for easier visualization. MNI coordinates are also provided for each image.

4 Discussions

The statistical multivariate analysis procedure presented in this study is based on Partial Least Squares Correlation analysis and extends the work of ²³. The main advantages of the proposed procedure are to allow voxel-wise quantification of effect-types and through this quantification to enable testing sophisticated multivariate hypotheses, which were not possible with previous approaches. In this article we presented two such multivariate procedures. The first is formal statistical testing of differences in type of effects within a region across conditions, such as mild cognitive impairment (MCI) and Alzheimer’s disease (AD). The results given in Section 3.6 demonstrated this point for the MCI - AD example. The observed differences between effect types of MCI and AD could be based on differing histopathology in these populations; for instance, a demyelinating effect may be observed in MCI while more significant pathology in AD may involve a substantial reduction in fiber density, leading to a different effect on the set of diffusion parameters. Future work in comparing conditions more distinct in histopathology, such as differentiating AD from Lewy body dementia, will be of great interest.

The second procedure extended the regressing nuisance parameters to the multivariate setting. The proposed approach through the regressing-out procedure allows for removing the effects of a nuisance condition in the multivariate setting through decomposing the effects of a condition with respect to another one. In the example we used in our experiments the regressing out procedure decomposed the effects of AD with respect to the effects of aging into two components: one that is parallel to the effect of aging and therefore has a similar effect-type, and one that is orthogonal and therefore suggestive of a different underlying histopathological mechanism. This enabled the statistical determination that there is a stronger aging type of effect in AD patients in some areas such as the parahippocampal region, in addition to showing other regions that display a different type of effect due to the condition. While it is not possible to ascribe a specific biophysical mechanism to these differing effects, and it is also possible that certain effects are related not only to the pathological changes but also to the initial baseline/premorbid anatomy (e.g. natively highly anisotropic regions may behave differently than regions with greater crossing fibers due to similar pathology), it is likely that the multivariate profile and the proposed procedures would have a greater specificity for a single mechanism compared to any individual measure. Future work will continue to advance the procedures demonstrated here, and work towards gaining a better understanding of the distinct effects of various conditions e.g. aging and AD.

In addition to the multivariate procedures regarding effect-types, as a secondary advantage the proposed method removes the need for correcting for multiple comparisons problem related to testing multiple parametric maps from one or multiple modalities. The statistical significance maps of multivariate effect-strength can be loosely interpreted as the statistical union of univariate tests. The correction for the related multiple comparisons problem is implicit and in certain cases and leads to higher statistical power than performing univariate tests for each parameter independently and then correcting for the multiplicity. This property has been analyzed thoroughly by Naylor et al. in ⁵³ for their voxel-based multivariate model, which in essence provides similar quantification to the effect-strength we propose. A major finding in their simulation studies was that when the different parameters are highly correlated the multivariate method improves statistical power. Our method enjoys this characteristic in theory as well. Similarly in this study, our proposed multivariate method demonstrated equivalent or superior statistical results compared to univariate testing.

In the results, it was observed that the multivariate effect strength and effect type of aging and AD were largely symmetric across hemispheres. This symmetric behavior also exists in the effect-type map of MCI but is less prominent. This symmetric behavior is not an artifact induced by the method considering that all the voxels are treated independently during the statistical analysis, and might instead reflect the underlying biological and microstructural symmetry of the brain and the pathological processes of AD and aging. This is particularly valid in the case of aging and AD where asymmetries in degenerative effects are minimal or not particularly noted in comparison to other conditions such as semantic dementia ^61–63.

Previous studies have suggested regionally varying effects of AD compared to cognitively healthy older adults when examining multiple diffusion parameters^1,64. However, these effects were not statistically integrated and therefore could not qualitatively distinguish among effects measured. The results here further demonstrate statistical differences in effect type within regions across group, for example, in the parahippocampal region in AD compared to MCI. Two possible explanations exist for these differences. First, considering MCI as an initial stage for AD, the pathology might be changing its alteration type on the tissue structure during its progression. Second, the MCI group might be composed of several sub-groups some of which show similar effect-type as AD and others not. These results provides the motivation for future work where we will investigate the use of clustering within the multivariate analysis procedures to dissect the MCI group and investigate the existence of sub-groups. They also provide motivation to investigate whether the multivariate effect-type or more simply a ratio of diffusion parameters may track the disease better than any single diffusion parameter, providing potentially differentiation of individuals with MCI who progress to AD from those who do not.

Results suggested that parahippocampal white matter exhibits a type of change due to AD that is similar to the type of effect seen in aging in the same region. That is, the residual effect of AD after regressing out the effects of aging was similar in type to aging. This was somewhat contrary to expectations given that damage of the parahippocampal white matter is presumed to be related and/or secondary to the medial temporal degeneration that occurs in the early stages of AD. However, while it was possible to dissect the AD effect and find a stronger age-like component than is normally seen in non-demented aging, there remains a possibility that a different histopathological mechanism than the one observed in non-demented aging may be responsible by having an effect on diffusion parameters that is not intrinsically orthogonal to the effect of aging and may have a stronger effect than aging in the same direction of the aging effect-type.

In this initial work we used the tensor-model to extract parameters from the diffusion imaging data. Despite its shortcomings, the tensor model is widely used for population-wide studies in the neuroimaging literature. In particular, disease-related and aging-related studies heavily rely on metrics derived from the tensor-model, such as Fractional Anisotropy (FA). However, we would like to emphasize that the proposed method is generic and can be applied to different multi-parametric diffusion signals including the entire tensor extracted in the DTI model and other more realistic diffusion imaging models including diffusion kurtosis imaging and possibly an entire orientation distribution function (ODF) representation. In this study, we focus our experiments on the tensor-model and in particular on the metrics derived from this model to demonstrate the advantages of the proposed method for a wide range of studies, including retrospective studies, which might only have limited diffusion imaging data, as well as to prospective studies that plan to implement state-of-the-art diffusion acquisitions to support more realistic diffusion models. Furthermore, although we apply the proposed method on diffusion imaging data, the method is not specific to diffusion data. The proposed analysis can be easily extended to other multi-parametric imaging data, which might include images coming from different modalities or MR spectroscopy.

In terms of computational burden of the presented work, the main bottleneck is the permutation testing. Our experiments included 219 study participants and each of them had 116474 data points on the TBSS skeleton, with each data point represented by three diffusion metrics. The analysis that took the longest time was the regression procedure with 1500 permutations and it took 92 minutes on a single core of an Intel Xeon X5482 CPU at 3.20 GHz. Although this is a substantial computational load, we believe it is tolerable for statistical analysis in neuroimaging studies. The computational load can be decreased significantly if one replaces the permutation testing with parametric tests, which need to be derived specific to each procedure. In this work we aimed to take a generic approach and used permutation testing that can be applied to all the different procedures.

The proposed procedure also has limitations. First of all, the analysis does not explicitly account for the dependencies between the diffusion parameters. For instance, fractional anisotropy is closely related to the radial and axial diffusivities. From a technical perspective there are no limitations caused by such dependencies. However, as the dependence increases, the contributions of the additional dependent dimensions will decrease in the multivariate analysis. In the extreme case where all variables are affine transformations of each other, the proposed multivariate method will reduce to univariate analysis and therefore the procedures will not be relevant. Modeling existing dependencies and possibly reducing the dimension of the parameter space should ideally provide higher specificity for differentiating between conditions because lower dimensionality will yield higher statistical power. In the current work, we preferred not to perform such dimensionality reductions on the diffusion parameters. The motivation behind this choice was to allow for interpretations of the effect-types in terms of parameters that are intuitive and well understood in the literature. We would also like to note that the dependency between parameters is taken into account in the statistical tests through appropriate permutation schemes.

The second limitation is that the proposed method does not take into account the spatial context and the empirical correlation structure of the parametric maps across voxels. In this first work, we present a voxel-wise approach to facilitate localized interpretability. This approach can be extended by post-hoc clustering or using unsupervised multi-voxel approaches as a preceding step. In particular, as is commonly done in analyzing functional MRI, one can use an unsupervised decomposition technique to define data-driven regions of interest. The proposed analysis can then be performed on these predefined regions. Both of these extensions are subjects of our future research.

The third limitation is the lack of appropriate voxel-wise correction for multiple comparisons. In the main text we provide results without any correction and in the supplementary materials we present results with FDR both on the raw p-value maps and on the TFCE enhanced maps. However, currently we do not have an ideal method to deal with this problem that arises due to performing statistical tests in thousands of voxels on the white matter skeleton. In future work we intend to devise an appropriate correction method that would take into account spatial correlations and the symmetry across the hemispheres.

Finally, it is currently difficult to directly relate the diffusion parameters and how conditions affect them to the underlying biological changes, and therefore more studies correlating histology with MRI are needed. The RGB visualization used in the article is helpful in appreciating the spatial variations and also for visually comparing effect-types across conditions. However, we acknowledge that this method is not ideal and cannot be easily extended to studies with higher number of parametric maps. Furthermore, when parameters are strongly correlated to each other, the resulting effect-type maps will have intermediate colors, which might make visual interpretations more challenging. Our future research focuses on better visualization techniques for such multivariate analyses.

The presented study was cross-sectional. Application of the proposed multivariate approach in longitudinal studies may be useful in better characterizing the progression of the Alzheimer’s disease as well as other pathologies. Furthermore, we constrained our study to the white matter. As the dMRI acquisition technologies evolve the proposed multivariate techniques can be useful for characterizing changes of the gray matter. Lastly, in the current article we presented regressing out one variable as the initial step. The natural extension of the regressing out procedure would be to include multiple nuisance variables. The PLSC roots of the proposed method and the optimization framework that we based regressing-out procedure on allows for such extensions. This is the focus of our future research.

Highlights.

• Voxel-wise multivariate statistical method is proposed.

• The method allows sophisticated multivariate hypotheses to be tested.

• Results with diffusion imaging are demonstrated.

• Method is applied to study effects of AD, MCI and aging.