Neuromusculoskeletal Model Calibration Significantly Affects Predicted Knee Contact Forces for Walking

Abstract

Though walking impairments are prevalent in society, clinical treatments are often ineffective at restoring lost function. For this reason, researchers have begun to explore the use of patient-specific computational walking models to develop more effective treatments. However, the accuracy with which models can predict internal body forces in muscles and across joints depends on how well relevant model parameter values can be calibrated for the patient. This study investigated how knowledge of internal knee contact forces affects calibration of neuromusculoskeletal model parameter values and subsequent prediction of internal knee contact and leg muscle forces during walking. Model calibration was performed using a novel two-level optimization procedure applied to six normal walking trials from the Fourth Grand Challenge Competition to Predict In Vivo Knee Loads. The outer-level optimization adjusted time-invariant model parameter values to minimize passive muscle forces, reserve actuator moments, and model parameter value changes with (Approach A) and without (Approach B) tracking of experimental knee contact forces. Using the current guess for model parameter values but no knee contact force information, the inner-level optimization predicted time-varying muscle activations that were close to experimental muscle synergy patterns and consistent with the experimental inverse dynamic loads (both approaches). For all the six gait trials, Approach A predicted knee contact forces with high accuracy for both compartments (average correlation coefficient r = 0.99 and root mean square error (RMSE) = 52.6 N medial; average r = 0.95 and RMSE = 56.6 N lateral). In contrast, Approach B overpredicted contact force magnitude for both compartments (average RMSE = 323 N medial and 348 N lateral) and poorly matched contact force shape for the lateral compartment (average r = 0.90 medial and −0.10 lateral). Approach B had statistically higher lateral muscle forces and lateral optimal muscle fiber lengths but lower medial, central, and lateral normalized muscle fiber lengths compared to Approach A. These findings suggest that poorly calibrated model parameter values may be a major factor limiting the ability of neuromusculoskeletal models to predict knee contact and leg muscle forces accurately for walking.

1. Introduction

Disorders affecting walking ability (e.g., osteoarthritis and stroke) are prevalent in society. Worldwide each year, approximately 15 million individuals suffer a stroke [1] and 250 million individuals are diagnosed with knee osteoarthritis [2]. Walking dysfunction from these and other disorders leads to a decreased quality of life and other serious health conditions such as heart disease and diabetes, thereby increasing the risk of death as well [3]. Unfortunately, current clinical interventions are largely ineffective at reversing walking impairments [4,5]. Even total joint replacement frequently does not achieve full normalization of walking function [6]. Improved clinical treatment methods are therefore needed to address this important societal problem.

Researchers have begun to explore using computational walking models to develop improved clinical interventions for walking impairments [7]. One of the primary challenges with this approach is indeterminacy of model-predicted muscle forces, since more muscle actuators exist than degrees-of-freedom (DOFs) in the skeleton. Researchers have explored several computational approaches to address the muscle redundancy problem. The most common approach found in the literature is static optimization, where a cost function is minimized one time frame at a time to find muscle forces that reproduce experimental joint moments calculated via inverse dynamics [8–11]. Musculoskeletal models used in this process are typically scaled versions of generic models available in the literature [12,13]. While this approach can be computationally efficient, it does not take advantage of experimental electromyographic (EMG) data when available, and the correct physiological form of the cost function to be minimized is unknown. An alternate approach is to use an EMG-driven model whose muscle excitation inputs are taken directly from experimental EMG measurements [14–16]. With this approach, no assumptions are required about the form of the cost function being minimized, plus model parameter values are often calibrated to match the subject's experimental joint moments from inverse dynamics. However, “flexibility” still remains in the solution process, since the absolute amplitude of each muscle excitation is difficult to determine, the number of EMG measurements is often limited, and EMG data are typically unavailable from large deep muscles (e.g., psoas). Regardless of which approach is used, the estimated muscle forces remain sensitive to both the computational method used to resolve muscle force indeterminacy and the parameter values used in the neuromusculoskeletal model.

One way to address the dual problem of indeterminate muscle force solutions and unmeasurable model parameter values is to identify additional types of experimental data that could limit muscle force solutions and the model calibration process further. Neural control studies have shown that a large number of muscle EMG signals (8–32) collected during walking can be decomposed into three to six independent time-varying basis signals called “neural commands” [17–20]. Recent work has also shown that neural commands extracted from a subset of experimentally measured EMG signals can reconstruct the shapes of the omitted EMG signals accurately [21]. Thus, it may be physiologically reasonable to use experimentally derived neural commands as basis functions to construct all model-predicted muscle activations [22]. In addition, instrumented knee studies performed using force-measuring knee replacements have provided internal force data that permit at least two additional inverse dynamic knee loads to be used as constraints in the muscle force estimation and model calibration process [23,24]. While synergy-derived neural commands can limit only muscle activation shapes, knee contact force measurements can limit both the amplitudes and shapes of predicted activations.

This study investigated how knowledge of in vivo knee contact forces affects calibration of neuromusculoskeletal model parameter values and subsequent prediction of knee contact and leg muscle forces during walking. The two primary questions investigated were the following. First, can a static optimization that uses a well-calibrated neuromusculoskeletal model predict experimental knee contact forces accurately for multiple gait trials? This question addresses whether poorly calibrated model parameter values may be just as critical as an indeterminate muscle force solution in affecting predicted knee contact and leg muscle forces during walking. Second, which model parameter values change the most when experimentally measured knee contact forces are not used as part of the model calibration process? This question addresses whether particular types of parameters require more refined calibration methods to achieve accurate knee contact force predictions. The novel two-level static optimization approach used to address these questions employed muscle synergy information extracted from experimental EMG signals to limit predicted activations, thereby accounting for subject-specific neural control characteristics.

2. Methodology

2.1. Experimental Data.

Experimental data for this study were obtained from the Fourth Grand Challenge Competition to Predict In Vivo Knee Loads [23]. Surface marker, ground reaction, EMG, knee contact force, and single-plane fluoroscopic knee motion data were available from a subject (gender: male, age: 88 yrs, mass: 65 kg, and height: 166 cm) implanted with a force-measuring tibial prosthesis (right knee). The prosthesis possessed four uniaxial load cells located in the four quadrants of the tibial tray [25]. Six normal overground gait trials performed at a self-selected speed (1.26 ± 0.03 m/s) were selected for analysis. Available data included trajectories of 53 surface markers, ground reactions from three force plates, knee contact forces from the instrumented implant, and EMG data from ten muscles (adductor magnus—addmag; biceps femoris longhead—bflh; gastrocnemius lateralis—gaslat; gastrocnemius medialis—gasmed; peroneus longus—perlong; semimembranosus—semimem; soleus—sol; tibialis anterior—tibant; tensor fascia latae—tfl; and vastus lateralis—vaslat).

The experimental data were processed using standard methods. The EMG data were high-pass filtered (fourth-order zero phase-lag Butterworth at 30 Hz), full-wave rectified, demeaned, and low-pass filtered (fourth-order zero phase-lag Butterworth at 6 Hz). Each processed EMG signal was resampled to 101 data points and normalized to its maximum value over all movement trials from the Fourth Grand Challenge Competition, including trials from other walking conditions (e.g., medial thrust gait). Ground reaction and knee contact force data were also low-pass filtered in a consistent manner (fourth-order zero phase-lag Butterworth at 6 Hz) [26].

2.2. Muscle Synergy Analysis.

Experimental neural commands were calculated by performing muscle synergy analysis on the ten processed muscle EMG signals after they were passed through an activation dynamics model. Activation dynamics was modeled using a first-order ordinary differential equation [27], where the activation and deactivation time constants for each muscle were taken from the literature [28]. Muscle synergy analysis was then performed on the experimental activations using a non-negative matrix factorization algorithm [22,29,30]. The analysis decomposed the ten experimental activations into a predefined number of synergies (<10), where each synergy consisted of a single time-varying neural command with a corresponding set of time-invariant weights (called a “synergy vector”) describing how the neural command contributed to each experimental activation. The weights in each synergy vector were normalized to a maximum value of one, and the associated neural command was scaled such that the product of the synergy vector and neural command did not change. The analysis was performed iteratively with the predefined number of synergies incremented by one each time until the total variance accounted surpassed 90%, which required five synergies. Muscle synergies were calculated for all six gait trials together. The five neural commands varied from trial-to-trial, while the five synergy vectors remained constant across all trials.

2.3. Musculoskeletal Model Analyses.

A subject-specific musculoskeletal model of the pelvis and right leg (femur, patella, tibia/fibula, and foot) [23] was constructed in opensim [31] and used to calculate joint kinematics and inverse dynamic loads for the six normal walking trials. The model incorporated subject-specific bone and implant geometry and possessed 23 DOFs: three translations and three rotations defining the position and orientation of the pelvis with respect to ground, three rotations (flexion, adduction, and rotation) for the hip, three rotations (flexion, adduction, and rotation) and three translations (superior–inferior, anterior–posterior, and medial–lateral) for the knee, three rotations (flexion, adduction, and rotation) and three translations (superior–inferior, anterior–posterior, and medial–lateral) for the patella relative to the femur, and two rotations (flexion and eversion) for the ankle. A published opensim lower-body model possessing 44 muscle-tendon actuators (see Supplemental Table S.1, which is available under the “Supplemental Materials” tab for this paper on the ASME Digital Collection) on each leg [12] was scaled to match the subject-specific bone geometry, and muscle origins, insertions, and wrapping surfaces were transferred to the subject-specific skeletal model. Patellar flexion was coupled with the knee flexion angle, while the remaining patellar DOFs were locked at constant values of zero. The one exception was patellar height, which was locked at a nonzero value such that patellar motion relative to the femoral component was visually similar to that observed fluoroscopically. No ligaments were included in the model. Each head of the quadriceps was modeled as two muscles: one that inserted into the patella which was used for muscle-tendon length and velocity calculations, and one that wrapped around the patella and inserted into the tibia which was used only for muscle moment arm calculations.

Tibiofemoral kinematics (three rotations and three translations) consistent with the knee contact force and surface marker measurements from each gait trial were calculated in matlab using an elastic foundation contact model of the subject's femoral component and tibial insert [32]. First, initial opensim inverse kinematic analyses were performed with all tibiofemoral DOFs locked except for flexion. These analyses provided an initial estimate of the knee flexion time history for each gait trial. Next, for each time frame of each gait cycle, the pose of the femoral component on the tibial insert was estimated by performing a nonlinear least squares optimization. The optimization locked three DOFs (flexion angle from inverse kinematics, internal–external rotation and anterior–posterior translation from fluoroscopy data collected in an earlier test session) and adjusted three DOFs (superior–inferior translation, medial–lateral translation, and varus–valgus rotation) to match the experimentally measured medial and lateral compressive contact forces and a medial–lateral shear contact force of zero. The 6 DOF tibiofemoral kinematics found for each gait trial were used for both optimization approaches. A more detailed description of this process can be found in Ref. [22].

opensim analyses were performed to calculate joint kinematics, inverse dynamic loads, muscle-tendon lengths and velocities, and muscle moment arms as required for the subsequent muscle force optimizations. For each gait trial, a second opensim inverse kinematic analysis was performed where all tibiofemoral DOFs except flexion were prescribed to match their values from the pose estimation optimizations. The resulting joint kinematics were filtered (four-order zero phase-lag Butterworth at 6 Hz) prior to performing an opensim inverse dynamic analysis that calculated net loads for three hip, six knee, and two ankle DOFs. The filtered joint kinematics were also used in an opensim muscle analysis that calculated muscle-tendon length and muscle moment arm time histories for all muscles in the model. Muscle-tendon velocities were calculated by differentiating muscle-tendon lengths.

Muscle force generation was modeled in matlab using a custom Hill-type model with a rigid tendon. The model possessed normalized force–length and force–velocity characteristics and included both active and passive force generation. Peak isometric strength values were taken from Ref. [33], while pennation angles were taken from Ref. [12]. To avoid infeasible initial guesses, we scaled the initial values of optimal muscle fiber lengths and tendon slack lengths taken from the literature [12] following an approach similar to Ref. [34]. Muscle-tendon model inputs included activation, optimal muscle fiber length, and tendon slack length values guessed by the two-level optimization described below and muscle-tendon length and velocity information provided by the final opensim inverse kinematic analyses.

2.4. Optimization Problem Formulations.

We formulated a two-level optimization problem in matlab to calibrate neuromusculoskeletal model parameter values to data from the six selected gait trials (Fig. 1). The outer-level optimization used a nonlinear least squares algorithm to adjust design variables related to time-invariant model parameter values (optimal muscle fiber length scale factors, tendon slack length scale factors, muscle moment arm deviations, activation scale factors for muscles with associated experimental EMG data, and synergy vector weights for muscles without associated experimental EMG data). The outer-level cost function minimized a weighted sum of squares of terms that included passive muscle forces, moment arm deviations, optimal muscle fiber length and tendon slack length changes, activation deviations away from synergy-based activation estimates (i.e., linear combinations of experimental neural commands), and reserve activations (from reserve actuators with a strength 0.5 Nm) required to balance six commonly used inverse dynamic loads (three hip, one knee for flexion only, and two ankle). Each reserve actuator torque was constructed by multiplying its reserve activation by the reserve actuator strength of 0.5 Nm. The strength of the reserve actuators was chosen such that all reserve activations remained between 0 and 1. Sixteen of the 44 muscle bundles were associated with one of the ten experimental EMG signals (see Supplemental Table S.2 in the “Supplemental Materials”). For muscles with associated experimental EMG data, minimizing activation deviations away from synergy-based estimates is similar to tracking scaled experimental activations directly. In addition, the outer-level cost function included penalty terms raised to a higher power that enforced physiologically realistic bounds. These terms bounded optimal muscle fiber length and tendon slack length scale factors to remain within 20% of 1 while also remaining within 20% of each other, activation scale factors to remain between 0.1 and 1, synergy-based activation estimates to remain between 0 and 0.7, average values of normalized muscle lengths for related muscles (see Supplemental Table S.3 in the “Supplemental Materials”) to remain within 10% of each other, and moment arm deviations for related muscles (see Supplemental Table S.4 in the “Supplemental Materials”) to remain within 5 mm (for moments) or 0.015 (for knee superior–inferior force) of each other.

Fig. 1.

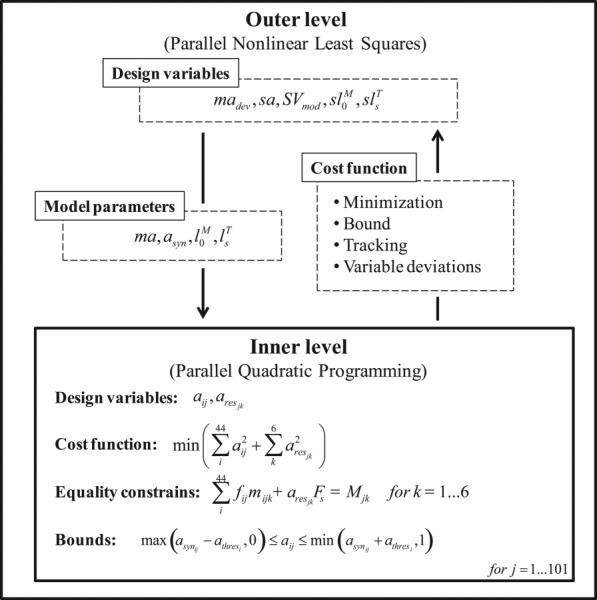
Block diagram of the two-step optimization formulation. a_syn stands for activations reconstructed from synergy components, ma and ma_dev for moment arm and moment arm deviations, respectively, sa for activation scale factors for muscles with experimental EMG data, SV_mod for synergy vectors for muscles without experimental EMG data, $l_0^M$ and $s{l}_0^M$ for optimal fiber lengths and their scale factors, $l_s^T$ and $s{l}_s^T$ for tendon slack lengths and their scale factors, a for model activations, a_res for reserve activations, F_s for reserve actuator strength values (which are 0.5 Nm), a_thres for half-range of allowable activation variation (0.01 for muscles with associated experimental EMG data and 0.05 for all other muscles), f for muscle forces, and M for inverse dynamic moments. i is the muscle (44 muscles), j is the time frame (101 frames), and k is the tracked joint moment (six loads).

The inner-level optimization used a fast quadratic programing algorithm applied to one time frame at a time of all six gait trials to adjust design variables for time-varying muscle activations given the current guess for model parameter values from the outer-level optimization. The inner-level cost function minimized the sum of squares of muscle and reserve activations [35] subject to equality constraints that the same six inverse dynamic loads be matched and bound constraints that predicted activations be within ±0.05 of synergy-based activation estimates and also remain between a small positive value (to prevent a singularity in the Hill-type muscle model) and 1.

To explore how the knowledge of knee contact forces affects model calibration and estimated knee contact and leg muscle forces, we formulated the outer-level cost function two ways. The first way (henceforth called “Approach A”) introduced additional weighted terms that minimized the sum of squares of errors in medial and lateral knee contact forces. Experimental medial and lateral knee contact forces were calculated from the four load cell measurements using a validated regression relationship [23]. Model medial and lateral knee contact forces were calculated by subtracting muscle contributions to the superior–inferior force and varus–valgus moment from inverse dynamics and then converting the superior–inferior contact force and varus–valgus contact moment into an equivalent medial and lateral force via an additional validated regression relationship [23]. Since no terms existed in the inner-level cost function that tracked medial and lateral knee contact forces, close matching of these quantities by the inner-level optimization could only occur through proper calibration of model parameter values by the outer-level optimization. The second way (henceforth called “Approach B”) did not track experimental knee contact forces in the outer-level cost function and thus did not use any experimental contact force information during the model calibration process. Both approaches used an identical inner-level problem formulation.

2.5. Data Analysis.

We evaluated how knowledge of knee contact forces affected calibration of model parameter values and subsequent prediction of knee contact and leg muscle forces using several quantitative measures. These measures fell into two categories: (1) accuracy measures for when model predictions from both approaches could be compared to experimental data, and (2) similarity measures for when model predictions could be compared between the two approaches. Accuracy measures were calculated for knee contact force predictions relative to experimental data and muscle activation predictions relative to activations constructed from experimental neural commands. Similarity measures were calculated for knee contact force predictions, muscle force predictions, model parameter values, normalized muscle length predictions, and muscle activation predictions for Approach B relative to Approach A. Accuracy and similarity measures included mean difference MeanD as a measure of magnitude differences, the coefficient of determination R² as a measure of magnitude and shape differences, root mean square difference (RMSD) as a measure of magnitude differences, and the correlation coefficient r as a measure of shape differences. Wherever possible, measures from the two approaches were compared statistically for the six gait trials using either a two-tailed paired t-test (default) or a two-way ANOVA (measures calculated for multiple muscles). Knee contact force measures were calculated for medial, lateral, and total forces, while leg muscle force and activation measures were calculated for medial, central, lateral, and all muscles (see Supplemental Table S.1 in the “Supplemental Materials” for description of muscle groupings).

To determine to which types of model parameters the predicted knee contact forces were most sensitive, we also performed two sensitivity analyses. Each sensitivity analysis performed four inner-level optimizations involving changes in only one of four types of model parameters: (1) optimal fiber length and tendon slack length scale factors, (2) moment arm deviations, (3) activation scale factors (for muscles with associated experimental EMG data), and (4) synergy vectors (for muscles without associated experimental EMG data). In the first sensitivity analysis, all model parameter values were set to those from Approach A, and then, one type at a time was changed to the values from Approach B. In the second sensitivity analysis, the same process was followed except all parameter values started with those from Approach B with one type at a time changed to values from Approach A.

3. Results

3.1. Knee Contact Forces.

Accuracy of predicted knee contact forces relative to the experimental measurements was significantly higher for Approach A than for Approach B (Table 1; Fig. 2). This result was expected, since the outer-level cost function for Approach A tracked experimental contact forces during calibration, though not guaranteed, since the inner-level cost function for Approach A did not make use of experimental contact force information. For every quantity calculated (MeanD, R², RMSE, and r) for medial, lateral, and total contact force, predictions from Approach A (average MeanD = 0.7 N, R²= 0.94, RMSE = 67 N, and r = 0.97) were statistically better (p < 0.05) than those from Approach B (average MeanD = 245.8 N, R²= −1.23, RMSE = 410 N, and r = 0.51). For Approach A, the medial, lateral, and total contact force predictions matched the amplitudes and shapes of the experimental forces well. For Approach B, the medial contact force was overpredicted but maintained a similar shape to the experimental forces, while the lateral contact force had peaks in the beginning of stance and swing phases that were not present in the experimental forces. Similarity between predicted knee contact forces from the two approaches was low (Table 2). Mean medial, lateral, and total contact force were statistically higher (p < 0.05) for Approach B by an average of 245 N, the average RMSD between the two approaches was 392 N, and the average r value between approaches was 0.58, consistent with the accuracy results for the two approaches.

Table 1.

Accuracy of knee contact force predictions for the two approaches. Accuracy was quantified using mean ± standard deviation of MeanD, R², RMSE, and r values for each approach relative to the experimental measurements. Statistically significant differences (p < 0.05) in each quantity are indicated by an asterisk (*).

Quantity	Approach	Medial	Lateral	Total
MeanD (N)	A	−0.3 ± 12.4*	1.3 ± 20.4*	1.1 ± 23.3*
B	223.6 ± 45.5*	145.1 ± 44.7*	368.7 ± 65.7*
R2	A	0.97 ± 0.01*	0.88 ± 0.05*	0.96 ± 0.02*
B	0.10 ± 0.28*	−3.43 ± 1.74*	−0.36 ± 0.24*
RMSE (N)	A	52.6 ± 16.4*	56.6 ± 9.5*	92.8 ± 26.0*
B	322.8 ± 63.9*	347.8 ± 33.1*	559.9 ± 32.1*
r	A	0.99 ± 0.01*	0.95 ± 0.02*	0.98 ± 0.01*
B	0.90 ± 0.03*	−0.10 ± 0.10*	0.74 ± 0.07*

Fig. 2.

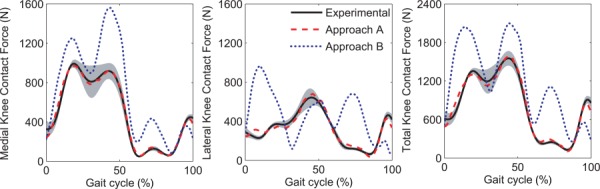
Experimental knee contact forces and mean knee contact force predictions for approaches A and B. The gray area corresponds to the mean ± standard deviation for the experimental forces.

Table 2.

Similarity of knee contact force predictions between the two approaches. Similarity was quantified using mean and standard deviation of MeanD, RMSD, and r values for Approach B relative to Approach A. Statistically significant differences (p < 0.05) in MeanD are indicated by an asterisk (*).

Quantity	Medial	Lateral	Total
MeanD (N)	223.9 ± 50.2*	143.8 ± 38.8*	367.7 ± 80.3*
RMSD (N)	315.2 ± 60.3	330.5 ± 25.7	530.5 ± 30.7
r	0.91 ± 0.02	0.05 ± 0.04	0.79 ± 0.09

3.2. Leg Muscle Forces.

Similarity of predicted leg muscle forces between the two approaches was also low (Fig. 3). When muscle forces were considered on a muscle-by-muscle basis, 29 of 44 muscles exhibited statistically different (p < 0.05) mean force values. Of the 13 muscles with the largest mean force differences ( > 40 N), eight were lateral muscles (bflh, bfsh, gaslat, glmed1, glmed2, glmed3, tfl, and vaslat). When mean force differences were analyzed for different muscle groupings, the lateral muscles and all muscles together had statistically higher (p < 0.05) forces for Approach B (Table 3). For the same groupings, the average RMSD in muscle forces was on the order of 65–85 N, while average r values were between about 0.60 and 0.70. Passive muscle forces were lower than 40 N for most muscles in both approaches.

Fig. 3.

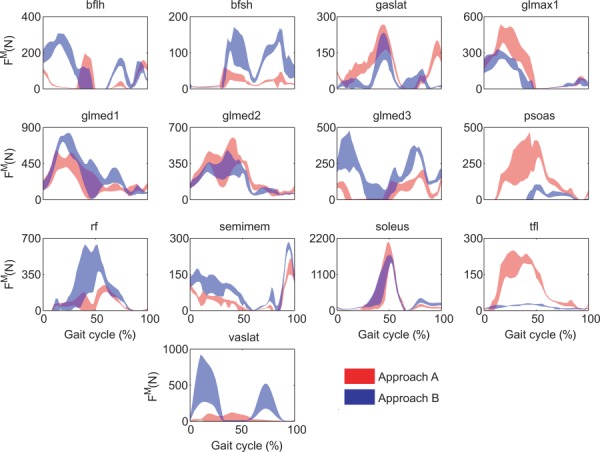
Muscle forces for muscles with the greatest mean differences between approaches A and B. The plotted area corresponds to the mean ± standard deviation for all six gait cycles.

Table 3.

Similarity of muscle force, normalized muscle fiber length, and muscle activation predictions between the two approaches. Similarity was quantified using mean and standard deviation of MeanD, RMSD, and r values for Approach B relative to Approach A. Statistically significant differences (p < 0.05) in MeanD are indicated by an asterisk (*).

	Quantity	Medial	Central	Lateral	All
Muscle forces	MeanD (N)	−3.1 ± 34.9	13.9 ± 39.2	24.4 ± 70.6*	9.6 ± 51.8*
	RMSD (N)	64.5 ± 51.5	86.7 ± 55.0	79.8 ± 77.8	73.6 ± 62.05
r	0.71 ± 0.26	0.63 ± 0.17	0.59 ± 0.34	0.66 ± 0.28
Fiber lengths	MeanD	−0.031 ± 0.109*	−0.047 ± 0.152*	−0.063 ± 0.165*	−0.045 ± 0.136*
	RMSD	0.075 ± 0.084	0.125 ± 0.088	0.128 ± 0.120	0.102 ± 0.100
r	1 ± 0.00	1 ± 0.00	1 ± 0.00	1 ± 0.00
Muscle activations	MeanD	−0.000 ± 0.056	0.004 ± 0.050	0.021 ± 0.078*	0.009 ± 0.064*
	RMSD	0.08 ± 0.05	0.09 ± 0.06	0.09 ± 0.07	0.09 ± 0.06
r	0.70 ± 0.26	0.67 ± 0.21	0.52 ± 0.45	0.63 ± 0.34

3.3. Model Parameter Values.

Model parameter values from the two approaches were different for some parameter types but not others (Table 4). Optimal muscle fiber lengths for Approach B were statistically larger (p < 0.05) by 13.0% for lateral muscles and 8.5% for all muscles together, with 33 of 44 muscles having larger values for Approach B. In addition, activation scale factors for Approach B were statistically larger (p < 0.05) by 0.31 for medial muscles and smaller by 0.05 for central muscles. Given that activation scale factors were limited to be between 0 and 1, between-approach variability of 0.59 for lateral muscles was high. No other parameter types exhibited statistically significant differences between approaches when grouped according to medial, central, lateral, and all muscles. Though tendon slack lengths were not statistically different between the two approaches for any muscle grouping (i.e., no bias), large differences still existed for many muscles. A similar situation was found for moment arm deviations, where large differences existed between approaches despite the lack of any statistically significant results. However, when differences were analyzed on a joint-by-joint basis (see Supplemental Table S.7 available in “Supplemental Materials”), knee flexion–extension moment arm deviations were statistically larger (p < 0.05) for Approach A for medial and all muscle groupings by an average of 10–14 mm. The only other statistically significant difference (p < 0.05) in moment arm deviations was for hip internal–external rotation, which was higher in Approach A only for the all muscles grouping.

Table 4.

Similarity of model parameter values between the two approaches. Similarity was quantified using the mean and standard deviation of values for Approach B relative to Approach A. Similarities are reported as percent differences for optimal muscle fiber lengths $l_0^M$ and tendon slack lengths $l_s^T$ and as absolute differences for activation scale factors sa and moment arm deviations ma_dev. Statistically significant differences (p < 0.05) in each quantity are indicated by an asterisk (*).

Quantity	Medial	Central	Lateral	All
$l_o^M$ (%)	4.90 ± 12.78	9.23 ± 17.81	13.00 ± 15.49*	8.54 ± 14.76*
$l_s^T$ (%)	1.41 ± 11.00	−1.47 ± 4.80	−0.86 ± 11.59	0.13 ± 10.39
sa	0.31 ± 0.25*	−0.05 ± 0.01*	−0.07 ± 0.59	0.12 ± 0.43
madev (mm)	−1.9 ± 10.1	−1.9 ± 14.1	−0.7 ± 9.3	−1.5 ± 10.4

3.4. Other Relevant Quantities.

Normalized muscle lengths possessed nearly identical shapes but different mean values between the two approaches (Table 3). Mean normalized fiber lengths were statistically lower (p < 0.05) for Approach B by 0.045 for all muscles together, while the shapes of the normalized fiber length curves were basically the same for the two approaches (r = 1.00 for medial, central, lateral, and all muscles). The RMSD in normalized fiber lengths between the two approaches was on the order of 0.1 for each muscle grouping (medial, central, lateral, and all). For both approaches, all muscles operated primarily on the ascending regions of their normalized force–length curves (Fig. 4) [36,37], consistent with the low amount of passive force generated by most muscles.

Fig. 4.

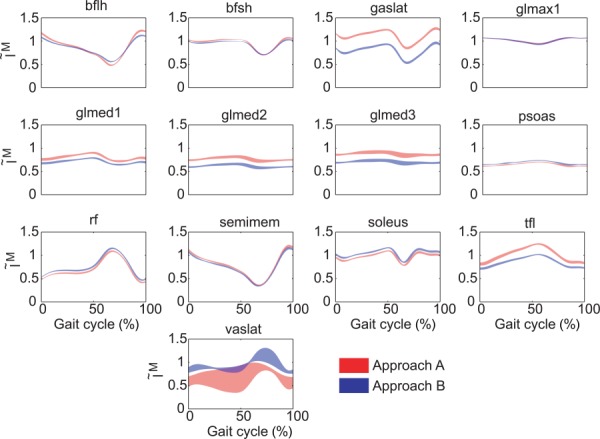
Normalized muscle fiber lengths for muscles with the greatest differences in mean muscle forces between approaches A and B. The plotted area corresponds to the mean ± 1 standard deviation for all six gait cycles.

Shape accuracy of predicted muscle activations relative to experimentally derived activations was generally higher for Approach B than for Approach A (Table 5; Fig. 5). For muscles with associated experimental EMG data, Approach B activation shapes were statistically closer to experimental activation shapes (p < 0.05) for lateral and all muscle groupings, while for muscles without associated experimental EMG data, they were statistically closer (p < 0.05) to activation shapes constructed from experimental neural commands for medial, central, and all muscle groupings. Similarity between predicted muscle activations from the two approaches was high for amplitude and moderate for shape (Table 3). Though statistically different (p < 0.05) for lateral and all muscle groupings, mean activation differences between the two groups were small, always being less than 0.03. Corresponding RMSD for each muscle grouping was less than 0.1. In contrast, mean r values between approaches ranged from 0.52 to 0.70 for the different muscle groupings.

Table 5.

Accuracy of muscle activation predictions for the two approaches for the 16 muscles with associated experimental EMG data (top rows) and the 28 muscles without associated experimental EMG data (bottom rows). Accuracy was quantified using mean ± standard deviation of r values for each approach relative to activations constructed from experimental neural commands. Statistically significant differences (p < 0.05) in each quantity are indicated by an asterisk (*).

Muscles	Approach	Medial	Central	Lateral	All
With EMG data	A	0.37 ± 0.24	0.55 ± 0.32	0.28 ± 0.50*	0.36 ± 0.35*
B	0.43 ± 0.25	0.57 ± 0.33	0.44 ± 0.61*	0.45 ± 0.40*
Without EMG data	A	0.42 ± 0.33*	0.47 ± 0.14*	0.64 ± 0.31	0.51 ± 0.31*
B	0.57 ± 0.31*	0.71 ± 0.17*	0.56 ± 0.45	0.59 ± 0.34*

Fig. 5.

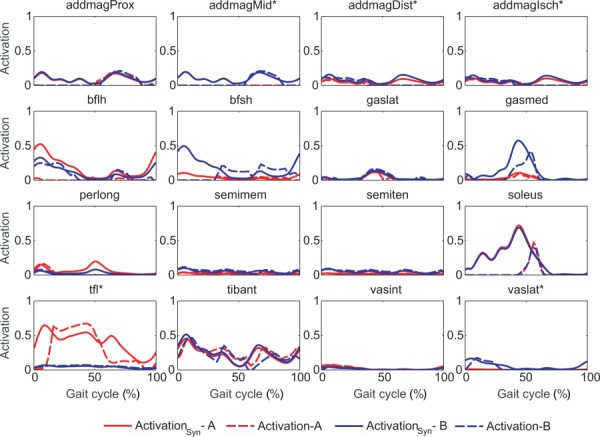
Activations reconstructed from synergy components (activation_Syn in solid lines) and model activations (activation in dashed lines) for muscles with associated experimental EMG data in one representative gait cycle. Asterisks (*) indicate statistically different r values between approaches A and B.

3.5. Sensitivity Analyses.

The two sensitivity analyses revealed that medial contact force predictions were most sensitive to moment arm deviations and activation scale factors while lateral and total contact force predictions were most sensitive to optimal fiber length and tendon slack length scale factors (Table 6). These findings held whether model parameter values started from the Approach A solution and were changed toward the Approach B solution or vice versa. In addition, when starting from the Approach A solution, the lateral and total contact force predictions were moderately sensitive to moment arm deviations, while starting from the Approach B solution revealed moderate sensitivity to activation scale factors. Overall, the contact force predictions were not very sensitive to the synergy vectors found for muscles without associated experimental EMG data.

Table 6.

Sensitivity of knee contact force predictions to changes in each type of model parameter values, starting from the Approach A solution (top) and the Approach B solution (bottom). Only one type of parameter was changed at a time, keeping all other types at the values from the original approach. Highlighted rows in gray contain original results obtained from Approach A (top) and Approach B (bottom). Numbers highlighted in bold indicate largest changes from original approach.

Starting from approach A	Quantity	Medial	Lateral	Total
Original approach A solution	R2	0.97	0.88	0.96
RMSE	52.62	56.63	92.80
Changed $l_o^M$ and $l_s^T$ scale factors	R2	0.84	−1.02	0.44
RMSE	136.45	239.47	358.78
Changed moment arm deviations	R2	0.61	-0.19	0.78
RMSE	209.48	170.52	222.50
Changed activation scale factors	R2	0.65	0.09	0.86
RMSE	201.15	156.03	174.70
Changed SV weights	R2	0.94	0.78	0.91
RMSE	84.13	76.53	132.77

Starting from approach B	Quantity	Medial	Lateral	Total
Original approach B solution	R2	0.10	−3.43	−0.36
RMSE	322.73	347.78	559.95
Changed $l_o^M$ and $l_s^T$ scale factors	R2	0.38	−0.33	0.41
RMSE	260.80	189.92	362.62
Changed moment arm deviations	R2	−0.46	−1.78	−0.08
RMSE	413.12	283.15	499.97
Changed activation scale factors	R2	0.53	−1.53	0.20
RMSE	232.28	267.10	430.10
Changed SV weights	R2	0.45	−3.87	−0.10
RMSE	255.20	363.38	503.18

4. Discussion

The goal of this study was to investigate how knowledge of in vivo knee contact forces affects calibration of neuromusculoskeletal model parameter values and subsequent prediction of knee contact and leg muscle forces during walking. The prediction method utilized a two-level synergy-based optimization that calibrated model parameter values such that the predicted activations would be close to a linear combination of experimental neural commands and would also reproduce the experimental contact forces [22]. The most significant result was that when experimental contact force tracking was included in the outer-level cost function (Approach A), one set of model parameter values was identified that allowed the inner-level static optimization to predict the medial and lateral knee contact forces with high accuracy in terms of both magnitude (average RMSE = 52.6 N medial and 56.6 N lateral) and shape (average r = 0.99 medial and 0.95 lateral). This accuracy for six gait trials was achieved despite the lack of experimental contact force information in the inner level and was similar to or higher than that of other published unblinded predictions for a single gait trial [22,38]. As expected, when knee contact force tracking was not used in the outer-level cost function (Approach B), the contact force predictions were poorer. The medial contact force was overpredicted (average RMSE = 322.8 N and r = 0.90) and the lateral contact force had a significantly different shape (RMSE = 347.8 N and r = −0.1). These results suggest that use of experimental muscle synergy information to limit the shapes of the predicted activations may not be sufficient to obtain accurate knee contact force predictions when knee contact force measurements are not used to calibrate the model. Furthermore, they suggest that poorly calibrated model parameter values may be a major factor limiting the ability of neuromusculoskeletal models to predict knee contact (and by implication, leg muscle) forces accurately for walking.

While one could argue that Approach A matched the knee contact forces by design, there was no guarantee that a single set of model parameter values could reproduce the experimental medial and lateral knee contact forces accurately for multiple gait trials [39]. The most obvious way of creating a model that can match the experimental knee contact forces is to develop a single-level optimization problem that calibrates model parameter values while also matching the knee contact forces in the cost function [22]. However, such an approach does not guarantee that the optimization will predict the correct knee contact forces when they are not tracked in the cost function. In fact, if the knee contact forces are removed from the cost function, it is likely that they will not be matched closely. In contrast, our two-level problem sought to identify a single set of model parameter values that allowed the inner-level optimization to predict knee contact forces well even though they were not included in the inner-level cost function (i.e., a true prediction). The fact that our two-level optimization was able to identify one such set of model parameter values does not guarantee that we found the correct parameter values or the correct inner-level cost function, but it does demonstrate that our existing model structure and inner-level cost function are at least capable of predicting knee contact forces accurately for multiple gait cycles, which was not known before performing this study. It also demonstrates how critical the calibration of model parameter values is for developing accurate predictions of knee contact forces—and by implication leg muscle forces, since muscle forces are the primary determinants of joint contact forces [40].

A unique aspect of this study was calibration of subject-specific neural control parameter values. The typical approach for calibrating musculoskeletal model parameter values is to start with a generic model and then scale it to match the physical dimensions of the subject being studied. Muscle-tendon and muscle moment arm parameter values are scaled automatically based on the required scaling of the skeletal model. Most musculoskeletal models do not calibrate any neural control model parameter values to account for the unique way that a particular subject activates his or her muscles during the tasks being simulated. In our study, construction of activations from experimental neural commands using unknown activation scale factors and synergy vector weights provided a form of neural control model calibration. Nonetheless, use of subject-specific neural commands alone was insufficient to produce accurate knee contact force predictions, despite contrary results in a previous study [22]. However, that study used a different optimization formulation, different design variables, and data from a different instrumented knee subject. Further research is therefore needed to determine whether use of subject-specific neural commands to limit activation shapes can help improve knee contact force predictions.

Observed differences in predicted knee contact and leg muscle forces between the two approaches were due to differences in calibrated model parameter values. The use of knee contact force information for calibration led to different muscle moment arms, especially for knee flexion and hip rotation moments, with moment arms being lower in Approach B. Optimal muscle fiber lengths for lateral muscles were statistically higher when no contact forces were used during calibration. Scale factors of muscle activations for muscles with associated experimental EMG data also had differences between approaches. These observations suggest that improved model calibration methods are needed if knee contact and leg muscle forces are to be predicted accurately for individual subjects.

Differences in predicted leg muscle forces between the two optimization approaches can also be viewed from the perspective of muscle force changes needed to match the experimental knee contact forces. The largest differences in predicted knee contact forces occurred at three points in the gait cycle (13%, 43%, and 71%, Fig. 2), and these differences can be traced back to changes in how the individual muscles contributed to knee contact forces (see Supplemental Fig. S.5 in the “Supplemental Materials”). For medial knee contact force, vasmed was primarily responsible for changes in the first peak near 17% and gasmed for changes in the second peak near 43%. For lateral knee contact force, bflh and vaslat were the main contributors to changes in the first peak, bflh, bfsh, gaslat, and tfl to changes in the second peak, and vaslat and vasmed to changes at the third location. For total contact force, bfsh, rf, semimem, and vaslat were mainly responsible for changes in the first peak, bfsh, gasmed, and tfl for changes in the second peak, and vaslat and vasmed for changes at the third location. In most cases, Approach A caused muscles to have a smaller contribution to knee contact forces except for bflh, gaslat, and tfl at the second peak.

Because six of the nine muscles noted above are biarticular (bflh, gasmed, gaslat, tfl, rf, and semimem), changes in the forces produced by these muscles had a “domino effect” on the muscle forces produced by uniarticular muscles acting at the hip and ankle joints. For example, as shown in Supplemental Fig. S.4 (available in the “Supplemental Materials”), uniarticular hip flexor muscles pect and psoas had very different muscle forces between the two approaches, as did uniarticular hip extensor muscles glmax1 and glmed3. Forces in these uniarticular hip muscles had to change between the two approaches to balance the different forces produced by biarticular hip–knee muscles tfl, bflh, rf, and semimem.

The main differences between approaches came from muscle activations and forces for lateral muscles. Of the 13 muscles with greatest differences in tendon forces, eight of them were from the lateral side. It is possible that the use of alternate motion patterns (especially ones that preferentially excite lateral muscles) in the calibration process could improve the similarity of calibrated model parameter values. We would hypothesize that activities requiring large hip adduction and subtalar moments would improve calibration of parameter values for lateral muscles.

Comparing our results with those of other studies, we observed that the muscle forces obtained from Approaches A and B (see Supplemental Fig. S.4 in the “Supplemental Materials”) were generally within the ranges reported by others. Gaslat, gasmed, sart, and sol forces had magnitudes and shapes similar to those in other studies [41–44]. Hamstrings (bflh, bfsh, semimem, and semiten) force, which is usually reported for all heads combined, was also generally within previously reported ranges [42–48]. In contrast, the vastus force, which is also usually reported for all heads together [42,44,48], was negligible for vaslat in Approach A, which is not in agreement with other studies [46]. This finding may suggest incorrect force sharing between tfl and vaslat.

The sensitivity analysis revealed which model parameters had the greatest influence on medial and lateral knee contact force predictions. For medial contact force, EMG scale factors for muscles with associated experimental EMG data and moment arm deviations had the greatest influence. The latter were dependent on other model parameter values, as suggested by the fact that when starting from the solution of Approach B and using moment arm deviations from Approach A, medial knee contact force predictions got worse. For lateral and total knee contact force, scale factors for optimal muscle fiber lengths and tendon slack lengths had the greatest influence. These results are in agreement with Ref. [49]. Thus, future research should focus on improving the calibration of these parameters when knee contact force data are not used during the calibration process [50,51].

The most important limitations of this study involved the use of data from only a single elderly subject and for only normal walking trials. Since knee contact forces cannot currently be measured in vivo from young subjects with healthy knees, it is unknown how the measured knee contact forces and estimated leg muscle forces would differ for younger healthy individuals. Analysis of additional instrumented knee subjects performing a wider variety of tasks, especially those involving lateral muscles, would be valuable for evaluating the two-level optimization formulation more broadly. Possible additional movement tasks worth analyzing include crouch gait, trunk sway gait, and one-legged squats. Future work could also investigate whether identification of additional physiological constraints could improve knee contact force predictions when no contact force data are used during calibration. For example, use of fewer neural commands could lead to a decrease in the amount of indeterminacy in muscle activation predictions.

Another limitation involved omission of knee ligaments (especially the collaterals) from the model. To investigate whether ligament contributions to knee contact forces may have affected our muscle force predictions, we examined the medial and lateral knee contact forces measured during a passive knee motion trial performed by the subject on a Biodex isokinetic dynamometer (Biodex Medical Systems, Shirley, NY). The selected trial covered a 0–60 deg flexion arc with only minimal knee muscle EMG activity. Medial contact force was approximately constant at 100 N over the range of motion, while lateral contact force was near 100 N at full extension and quickly dropped to almost 0 N as the knee flexed. Near full extension, passive hamstring muscle force likely contributes to knee contact forces, and during stance phase, ligaments will be less strained since the knee is compressed. Thus, during stance phase, we estimate that ligaments contribute roughly 50 N of contact force on the medial and lateral sides, and during swing phase, roughly 100 N on the medial side and close to 0 N on the lateral side. Consequently, omission of ligaments from the model may have had a small effect during swing phase on muscles that contributed significantly to medial contact force. It would be valuable for future studies to perform a detailed investigation of how knee ligament forces contribute knee contact forces.

A key limitation of our two-level optimization approach is that accurate prediction of knee contact forces requires knowledge of the quantities being predicted. Ideally, we would like to identify an outer-level cost function where knowledge of experimental knee contact forces is not required to find model parameter values that allow the inner-level optimization to predict knee contact forces accurately. When the experimental contact forces were not tracked in the outer-level, the medial and lateral knee contact forces predicted by the inner-level optimization were generally too large. This observation suggests that the minimization, tracking, and bounding terms used in our current out-level cost function are not adequate to produce well-calibrated model parameter values, and that further research will be needed to identify an appropriate outer-level cost function. Furthermore, there is no guarantee that the inner-level cost function is physiologically correct, as the ability to predict knee contact forces accurately for six gait trials using a single calibrated model is a necessary but not sufficient requirement.

In conclusion, this study demonstrated that a single set of well-calibrated muscle-tendon, moment arm, and neural control model parameter values was capable of predicting medial and lateral knee contact forces accurately over six walking trials using a standard static optimization approach with slight modifications. However, when knee contact force measurements were not available to the calibration process, use of experimental synergy information alone to limit muscle activations was insufficient to achieve accurate contact force predictions, especially for the lateral compartment. Given the importance of using a properly calibrated model when predicting knee contact (and by implication, leg muscle) forces for movement tasks performed by a specific subject, future work should explore finding improved methods for calibrating muscle-tendon, moment arm, and neural control model parameter values uniquely and accurately for individual subjects.