Which Diameter and Angle Rule Provides Optimal Flow Patterns in a Coronary Bifurcation?

Abstract

The branching angle and diameter ratio in epicardial coronary artery bifurcations are two important determinants of atherogenesis. Murray’s cubed diameter law and bifurcation angle have been assumed to yield optimal flows through a bifurcation. In contrast, we have recently shown a $\frac{7}{3}$ diameter law (HK diameter model), based on minimum energy hypothesis in an entire tree structure. Here, we derive a bifurcation angle rule corresponding to the HK diameter model and critically evaluate the streamline flow through HK and Murray-type bifurcations. The bifurcations from coronary casts were found to obey the HK diameter model and angle rule much more than Murray’s model. A finite element model was used to investigate flow patterns for coronary artery bifurcations of various types. The inlet velocity and pressure boundary conditions were measured by ComboWire. Y-bifurcation of Murray type decreased wall shear stress-WSS (10%–40%) and created an increased oscillatory shear index-OSI in atherosclerosis-prone regions as compared with HK-type bifurcations. The HK-type bifurcations were found to have more optimal flow patterns (i.e., higher WSS and lower OSI) than Murray-type bifurcations which have been traditionally believed to be optimized. This study has implications for changes in bifurcation angles and diameters in percutaneous coronary intervention.

INTRODUCTION

The large epicardial coronary artery bifurcations are predisposed to atherosclerosis (Nichols and O’Rourke, 1998; Asakura and Karino, 1990; Debakey et al., 1985) and restenosis after percutaneous coronary intervention (PCI) (Tanabe et al., 2004; Sharma and Kini, 2006) because of abnormal biomechanical stimuli (e.g., low wall shear stress-WSS and high oscillatory shear index-OSI) (Moore et al., 1994; Thubrikar and Robicsec, 1995; Malek et al., 1999; Kleinstreuer et al., 2001; Cheng et al., 2006; Suo et al., 2007; Huo et al., 2007; 2008; 2009a). The branching angle (between the two daughter vessels) and diameter ratio (large to small daughter vessels) are two important factors that affect the hemodynamic parameters at bifurcations (Ku, 1997).

Eighty-five years ago, Murray first derived a cubed diameter expression (Murray, 1926a) as ${\text{D}}_{\text{m}}^3={\text{D}}_{\text{l}}^3+{\text{D}}_{\text{s}}^3$ (where D_m, D_l, and D_s are the diameters of mother and large and small daughter vessels) and a corresponding bifurcation angle model (Murray, 1926b) as a consequence of minimum energy hypothesis in a single bifurcation. Murray diameter model has support for small arteries (50 < diameter < 500 μm) of rat cardiovascular system (Zamir et al., 1983) and arterioles (diameter < 100 μm) of swine heart (VanBavel and Spaan, 1992; Kaimovitz et al., 2008). In large epicardial coronary artery bifurcations, however, a smaller exponent has been validated for swine (VanBavel and Spaan, 1992; Kaimovitz et al., 2008) and patients (Hutchins et al., 1976; Finet et al., 2008). The epicardial coronary artery bifurcations agree well with the prediction of HK diameter model ( ${\text{D}}_{\text{m}}^{\frac{7}{3}}={\text{D}}_{\text{l}}^{\frac{7}{3}}+{\text{D}}_{\text{s}}^{\frac{7}{3}}$), which is derived from minimum energy hypothesis in a tree structure (Huo and Kassab, 2009b; 2012). Consequently, the bifurcation angle corresponding to HK diameter model should be different from Murray angle rule (Murray, 1926b). In the present study, a bifurcation angle rule (HK angle rule) is derived to complement the HK diameter model (see Appendix A), based on blood volume conservation and minimum energy hypothesis, and is validated by computed tomography (CT) measurements (Wischgoll et al., 2009).

The objective of the study is to investigate the distribution of WSS and OSI at coronary bifurcations of various branching angles and diameter ratios. We hypothesize that a bifurcation obeying HK diameter and angle models has higher WSS and lower OSI at atherosclerosis-prone sites than Murray models. To test the hypothesis, we compare the flow patterns computationally in large epicardial coronary artery bifurcations according to HK and Murray diameter models and their respective angle rules. A detailed hemodynamic analysis is first carried out in coronary artery bifurcations obtained from coronary casts, which conform to the HK diameter model and angle rule. The Y-type bifurcation is also made to comply with Murray diameter model and angle rule for further analysis. A 3-D finite element (FE) model is used to solve the continuity and Navier-Stokes equations with inlet flow boundary condition and outlet pressure boundary conditions. The time-averaged WSS and OSI are analyzed and computed for different cases. The implications and limitations of the model simulations are discussed in relation to coronary intervention that may alter the bifurcation angles and diameter ratios.

MATERIALS AND METHODS

Animal Preparation

To compare various bifurcation diameter models and angle rules, studies were performed on five normal Yorkshire porcine of either sex with body weight of 34.3–42.1 kg. The experimental procedures of the animal preparation were described previously (Kassab et al., 1993; 2009). The animal protocols were approved by the Institutional Animal Care and Use at Indiana University-Purdue University, Indianapolis.

Briefly, the coronary pressure and flow waves in the main trunk of LAD (left anterior descending) epicardial arterial tree were measured by the ComboMap system (Model 6800, Volcano Corporation). The LAD artery, right coronary artery (RCA) and left circumflex (LCx) artery were cannulated for construction of arterial cast with a polymer (Microfil, Flow Tech, Carver, MA) (Choy and Kassab, 2008). After Microfil was allowed to harden for ~60 min, the hearts were kept in the refrigerator in saline solution until the day of CT scan. Scans were made axially (120 mAs, 120 kV, 0.6 × 0.6 × 1.0 mm) on a 16-slice scanner (Siemens Somatom Sensation 16), resulting in ~200 slices of 512 × 512 pixels each (Wischgoll et al., 2009).

Bifurcation Angles

Based on blood volume conservation and minimum energy hypothesis (see the derivation in Appendix A), a bifurcation angle rule (HK angle rule) as a function of diameter ratio ( $\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}$) is given as:

$$\{\begin{array}{l}cos(a)=\frac{{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{12}{7}}-\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4\right)}{2{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2}\hfill \\ cos(\beta )=\frac{{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{12}{7}}+\left(1-{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4\right)}{2{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{6}{7}}}\hfill \\ cos(\gamma )=\frac{{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{12}{7}}+\left({\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4-1\right)}{2{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{6}{7}}{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2}\hfill \end{array}$$ [1]

where α, β, and γ are the angle between daughter vessels, the angle between mother and larger daughter vessels, and the angle between mother and smaller daughter vessels, respectively. If angle α is < 60° or ≥ 60°, a bifurcation is defined as Y or T bifurcations (see Appendix A), respectively; as shown in Figs. 1a and b. The morphometric data of coronary artery bifurcations were extracted from CT images of porcine casts (Wischgoll et al., 2009), based on which we evaluated the HK bifurcation angle rule (see Appendix A).

Figure 1.

(a–b) Coronary bifurcations with angle α of (a) 44° (Y bifurcation) and (b) 71° (T bifurcation) obtained from casts of porcine LAD arterial tree. The bifurcation angles α, β, and γ refer to the angles between daughter vessels, between mother and larger daughter vessels, and between mother and smaller daughter vessels, respectively. Bifurcation angles obey the angle rule (Eq. 1) and diameters comply with the HK diameter model as ${\text{D}}_{\text{m}}^{2\frac{1}{3}}={\text{D}}_{\text{l}}^{2\frac{1}{3}}+{\text{D}}_{\text{s}}^{2\frac{1}{3}}$, where D_m, D_l, and D_s are the mother, large and small daughter vessel diameters, respectively. (c) In vivo pulsatile flow velocity waveform measured at the inlet of porcine LAD arterial tree, which serves as inlet boundary condition for the flow simulation.

Geometrical Models

We generated FE meshes for bifurcations of HK, Murray, and Finet types in the LAD arterial tree, as shown in Table 1, where HK-type refers to a bifurcation whose vessel diameters and bifurcation angles obey HK diameter model (Huo and Kassab, 2009b) and angle rule (Eq. 1) and are consistent with morphometric data from casts in Fig. 1. Murray-type refers to an artificial Y bifurcation whose vessel diameters and bifurcation angles obey Murray’s cubed law (Murray CD, 1926a) and angle rule (Murray CD, 1926b). Finet-type refers to an artificial T bifurcation whose vessel diameters and bifurcation angles obey Finet diameter model (Finet et al., 2008) and angle rule (Eq. A6 in Appendix A). There is negligible difference between HK and Finet models for Y-type bifurcation and between HK and Murray models for T-type bifurcation. Numerical simulations were carried out in comparison between bifurcations of the three types.

Table 1.

Morphometric parameters for Y and T bifurcations in the LAD epicardial arterial tree

Morphometric parameters	Y bifurcations		T bifurcations
	HK	Murray	HK	Finet
Mother diameter (mm)	3.63	3.63	3	3
Larger daughter diameter (mm)	2.89	3.12	2.89	2.89
Smaller daughter diameter (mm)	2.42	2.61	1.27	1.53
Angle α (degrees)	44	75	71	81
Angle β (degrees)	18	30	10	15
Angle γ (degrees)	26	45	61	66

HK-type refers to a bifurcation whose vessel diameters and bifurcation angles obey HK diameter model (Huo and Kassab, 2009b) and angle rule (Eq. 1), which is consistent with morphometric data from casts (Figs. 1a and b). Murray-type refers to an artificial Y bifurcation whose vessel diameters and bifurcation angles obey Murray’s cubed law (Murray CD, 1926a) and angle rule (Murray CD, 1926b). Finet-type refers to an artificial T bifurcation whose vessel diameters and bifurcation angles obey Finet diameter model (Finet et al., 2008) and angle rule (Eq. A6).

3-D FEM Model

The governing equations were formulated for bifurcations, each vessel of which was assumed cylindrical with rigid and impermeable wall. The equations of continuity and Navier-Stokes can be written as:

$$\nabla ·\overrightarrow{\text{v}}=0$$ [2]

$$\rho \frac{\partial \overrightarrow{\text{v}}}{\partial t}+\rho \overrightarrow{\text{v}}·\nabla \overrightarrow{\text{v}}=-\nabla P+\nabla ·\mu \left(\nabla \overrightarrow{\text{v}}+{(\nabla \overrightarrow{\text{v}})}^T\right)$$ [3]

where v⃗ = uê_x + vê_y + wê_z, P, ρ, and μ represent velocity, pressure, blood mass density, and viscosity, respectively.

Numerical Method

The Navier-Stokes and continuity equations were solved using Galerkin FE method (Huo et al., 2009a). A FORTRAN program was used to implement the FE method. A mesh dependency was conducted such that the relative error in two consecutive mesh refinements was < 1% for the maximum velocity of steady state flow with inlet flow velocity equal to the time-averaged velocity over a cardiac cycle. A total of almost 300,000 linear tetrahedral finite elements (element edge of 0.2 mm) and 55,000 nodes were necessary to accurately mesh the computational domains. The backward method was used for the time integration. Three cardiac cycles were required to achieve convergence for the transient analysis. A constant time step was employed, where Δt = 0.004 s with 125 total time step per cardiac cycle. Although blood is a suspension of particles, it behaves as a Newtonian flow in tubes with diameters > 1 mm (Nichols et al., 1998). The experimentally-measured flow velocity wave, as shown in Fig. 1c, was set as the boundary condition at the inlet of mother vessel, which has a blunt velocity profile. The pressure wave was computed in each vessel of the entire LAD arterial tree (including the cast bifurcations in Figs. 1a and b) in the arrested heart in the absence of vascular tone through Womersley-type numerical analysis (Huo and Kassab, 2006). Since there is an approximate phase difference of $\frac{1}{5}$ cardiac cycle between arrested and beating hearts (Nichols et al., 1998), the pressure wave was adjusted and used as the boundary condition at each outlet of daughter vessels. The viscosity (μ) and density (ρ) of the solution were assumed as 4.0 cp and 1.06 g/cm³, respectively, to mimic blood flow with a hematocrit of about 45% in these arteries. After the velocity and pressure of the blood flow were calculated, WSS and OSI were determined from the velocity field (Huo et al., 2009a).

RESULTS

Numerical simulations are performed for Y and T bifurcations of various types, as shown in Table 1. Figures 2a and 2b show the time-averaged WSS over a cardiac cycle at Y arterial bifurcations of HK and Murray types corresponding to Table 1. Accordingly, Figures 2c and 2d show the OSI distribution. There are three surface regions (surface regions A–C in Fig. 2b) with low WSS and high OSI at the Y bifurcation: A) the surface region in the smaller daughter and mother vessels opposite to the carina of daughter vessels, B) the surface region in the larger daughter and mother vessels opposite to the carina of daughter vessels, and C) two joint surface regions (anterior and posterior) of mother and two daughter vessels lateral to the carina of daughter vessels, which penetrate into the carina of daughter vessels.

Figure 2.

(a–b) Time-averaged (over a cardiac cycle) WSS (Unit: Dynes·cm⁻²) at Y bifurcations of (a) HK and (b) Murray corresponding to Table 1. Symbol A refers to the surface region in the smaller daughter vessel opposite to the carina of daughter vessels. Symbol B refers to the surface region in the larger daughter vessel opposite to the carina of daughter vessels. Symbol C refers to the joint surface regions of mother vessel and two daughter vessels lateral to the carina of daughter vessels, which penetrates into the carina of daughter vessels. (c–d) OSI at Y bifurcations of (c) HK and (d) Murray. In Y bifurcations, HK type is similar to Finet type.

Figures 3a–d show the distribution of time-averaged WSS and OSI at T arterial bifurcations of HK and Finet types in correspondence with Table 1. Because of the small diameter ratio in T bifurcation, the smaller daughter vessel has very small effect on the surface region in the larger daughter vessel opposite to the carina of daughter vessels. Therefore, there are only two surface regions (surface regions A and B in Fig. 3b) with low WSS and high OSI at the T bifurcation: A) the surface region in the smaller daughter vessel opposite to the carina of daughter vessels and B) two joint surface regions (anterior and posterior) of mother and large daughter vessels lateral to the carina of daughter vessels, which penetrate into the carina of daughter vessels.

Figure 3.

(a–b) Time-averaged (over a cardiac cycle) WSS (Unit: Dynes·cm⁻²) at T bifurcations of (a) HK and (b) Finet corresponding to Table 1. Symbol A refers to the region in the smaller daughter vessel opposite to the carina of daughter vessels and Symbol B refers to the region in the larger daughter vessel lateral to the carina of daughter vessels. (c–d) OSI at T bifurcations of (c) HK and (d) Finet. In T bifurcations, HK type is similar to Murray type.

Figures 4a–c and 4d–f show mean ± SD values of WSS and OSI (averaged over all nodes in the corresponding region) at surface regions A–C at Y bifurcations of HK and Murray types. Regions A–C have surface areas of 0.94, 1.45, and 0.76 mm², respectively, whereas surface area in Region C only corresponds to one of two joint surface regions. At surface regions A–C, the Y bifurcation of HK type has, on average, higher WSS and lower OSI (less atherosclerosis-prone) than that of Murray type (more atherosclerosis-prone). WSS decreases on surface regions B and C of Murray bifurcation (about 40% and 20%, respectively) as compared with that in HK bifurcation. OSI has a value of 0.09 and 0.02 on surface regions B and C of Murray bifurcation, but equals to zero at proportional surfaces of HK bifurcation. There is no significant difference (relative error of WSS and OSI is < 3%) on surface region A.

Figure 4.

(a–c) Mean ± SD WSS (averaged over all nodes in the corresponding region) at (a) region A, (b) region B, and (c) region C in Y bifurcations of HK and Murray. (d–f) Mean ± SD OSI (averaged over all nodes in the corresponding region) at (d) region A, (e) region B, and (f) region C in Y bifurcations of HK and Murray. Regions A–C correspond to regions marked by symbols A–C in Fig. 2b. Regions A–C have surface areas of 0.94, 1.45, and 0.76 mm², respectively, where surface area in Region C only corresponds to one of two joint surface regions (anterior and posterior) of mother and two daughter vessels lateral to the carina of daughter vessels. OSI in regions B and C of HK-type bifurcations is zero.

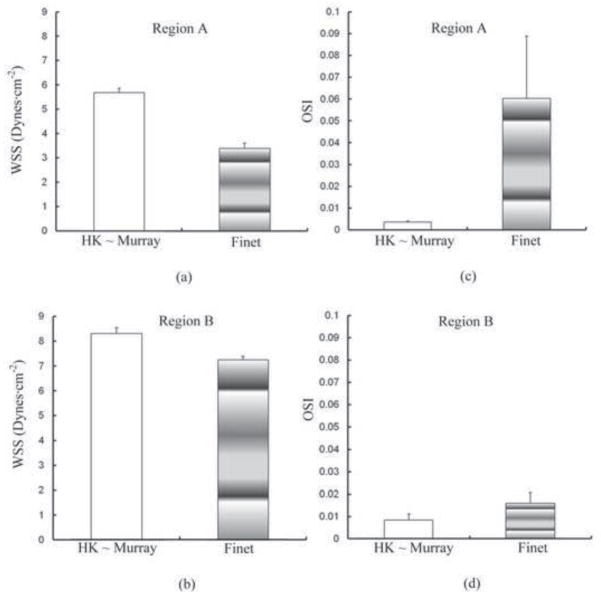
Figures 5a–b and 5c–d show comparisons of WSS and OSI (averaged over all nodes in the corresponding region) at surface regions A and B between T bifurcations of HK and Finet types. Regions A and B have surface areas of 0.43 and 0.68 mm², respectively. Similar to the Y bifurcation, the T bifurcation of HK type is less atherosclerosis-prone than that of Finet type. There is a decrease of WSS on surface regions A and B of Finet bifurcation (about 40% and 10%, respectively) from HK bifurcation. OSI increases significantly on surface regions A and B of Finet bifurcation.

Figure 5.

(a–b) Mean ± SD WSS (averaged over all nodes in the corresponding region) at (a) region A and (b) region B in T bifurcations of HK and Finet. (c–d) Mean ± SD OSI (averaged over all nodes in the corresponding region) at (c) region A and (d) region B in T bifurcations of HK and Finet. Regions A and B correspond to regions marked by symbols A and B in Fig. 3b. Regions A and B have surface areas of 0.43 and 0.68 mm², respectively, where surface area in Region B only corresponds to one of two joint surface regions (anterior and posterior) of mother and two daughter vessels lateral to the carina of daughter vessels.

DISCUSSION

The major finding of this study is that Y and T coronary artery bifurcations obeying the HK diameter model and angle rule have higher WSS and much lower OSI at atherosclerosis-prone sites (i.e., regions A–C) than those of Murray and Finet types. We elaborate on these findings as well as discuss potential implications on interventions that may alter coronary bifurcation diameters or angles.

Theory of Bifurcation Design

Murray’s cubed law (1926a) that stems from the minimum energy hypothesis is assumed to be the principles of design of fluid transport systems in zoology (LaBarbera M, 1990) and botany (McCulloh et al., 2003). In cardiovascular system, an agreement between experiments and Murray diameter model has only been found in small arteries (Zamir et al., 1983) and arterioles (VanBavel and Spaan, 1992; Kaimovitz et al., 2008). On the other hand, we reported a smaller exponent of ~2.1 for D_m ≥ 200 μm, an even smaller exponent of ~1.7 for 100 ≤ D_m < 200 μm, and a monotonic increase to ~3 as D_m decreased from 100 μm to the precapillary arterioles (Kaimovitz et al., 2008) consistent with other coronary data (VanBavel and Spaan, 1992). Since atherosclerotic lesions typically predominate around bifurcations of large epicardial coronary arterial trees (Asakura and Karino, 1990) as opposed to smaller intramyocardial vessels (Scher AM, 2000), Murray’s cubed law (1926a) may be less relevant to an optimal distribution of WSS and OSI at epicardial coronary artery bifurcations.

Murray (1926b) proposed a relationship between bifurcation angles and diameters of mother and daughter vessels, based on the minimum energy hypothesis. A similar bifurcation angle rule consistent with HK diameter model (Eq. 1) was derived in Appendix A. We also determined an angle rule based on Finet diameter model (Eq. A6 in Appendix A). In comparison with morphometric data from CT measurements (Wischgoll et al., 2009), the HK, Murray, and Finet bifurcation angle rules have a relative error of 44±17%, 115±26%, 46±17% (mean ± standard error) at bifurcations of various diameter ratios as shown in Fig. A1(b). Although Finet angle rule has a similar mean value to HK angle rule, it cannot be applied to bifurcations with diameter ratio < 0.37.

Figure A1.

(a) Schematic representation of a bifurcation with an infinitesimal perturbation of mother vessel length; (b) Relationship between bifurcation angle α (the angle between two daughter vessels) and diameter ratio D_s/D_l determined by HK, Murray, and Finet angle rules and measurements of CT scans.

Epicardial coronary artery bifurcations with diameter ratios ( $\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}$) of 0.6–1.0 are often treated in PCI. The median bifurcation angle α (diameter ratio = 0.8) predicted by HK, Murray, and Finet rules has a value of 50°, 75°, and 51°, respectively. A human study has shown a median bifurcation angle of ~50° (Dzavik et al., 2006), which agrees well with the prediction of HK and Finet angle rules as shown in Fig. A1(b). In diameter ratios of 0.6–1.0, the bifurcation angle α predicted by HK, Murray, and Finet rules has a value of 51°±1°, 75°±1°, and 54°±8° (mean ± standard deviation), respectively. The angiographic measurements for coronary bifurcations show a bifurcation angle of 60°±28° (Finet et al., 2008) or 60°±20° (Godino et al., 2010). This is also in better agreement with HK and Finet angle rules than Murray angle rule (Murray CD, 1926b). Therefore, Murray angle rule may not be suitable for investigation of the optimal angles of large epicardial coronary artery bifurcations.

Hemodynamic Parameters

There is a relationship between low WSS/high OSI and intimal hyperplasia after stenting (Chen et al., 2011). Figures 4 and 5 show the highest WSS and the lowest OSI at all sites in coronary bifurcations of HK type. Conversely, Y bifurcation of Murray type and T bifurcation of Finet type have less favorable distribution of hemodynamic parameters; i.e., lower WSS and higher OSI. It is also found that an increase of bifurcation angle decreases WSS and increases OSI significantly around the carina and an increase of daughter diameters mainly changes these parameters at surface sites opposite to the carina, as compared with coronary bifurcations of HK type.

Critique of Model

Morphometric data obtained from microscope measurements (Kassab GS, 2006; 2007) and CT scans (Fig. A1–b) show substantial scatter for individual bifurcation diameters and angles albeit the mean values tend to agree with HK diameter model and angle rule. The flow patterns in the large epicardial arterial tree comprised of bifurcations of various types need to be considered. Furthermore, the effects of vessel compliance and branching on wave propagation and reflection (Nichols and O’Rourke, 1998; Van De Vosse1 and Stergiopulos, 2011) requires a computational fluid-structure model (Huo et al., 2009a) to compare the distribution of hemodynamic parameters between HK- and Murray-type coronary bifurcations.

Implications for Coronary Interventions

Coronary artery bifurcation lesions are estimated to be 18–20% of all PCIs (Sharma and Kini, 2006). The major adverse cardiac events occur more frequently (22.7% vs. 6.2%) in patients with bifurcation angles ≥ 50° after crush stenting (Dzavik et al., 2006). An increase of bifurcation angle induces a stronger oscillatory flow velocity in the direction perpendicular to the centerline of mother vessel, which may decrease in-stent reendothelialization and promote thrombosis-occlusion at the carina of daughter vessels after bifurcation stenting (Chen et al., 2009; Nakazawa et al., 2010). The decreased WSS and increased OSI due to an increase of bifurcation angle may explain why the carina of daughter vessels is vulnerable to restenosis (Tanabe et al., 2004; Sharma and Kini, 2006). On the other hand, an increase of daughter diameters leads to flow reversal at surface regions opposite to the carina, which may cause greater intima hyperplasia (Nakazawa et al., 2010). An increase of daughter diameters can result in different types of lesions and restenosis as compared to an increase of bifurcation angle based on the Lefevre’s classification of bifurcation lesions after bifurcation stenting (Lefevre et al., 2000).

A change of bifurcation angles and diameters may be caused by coronary intervention, particularly for bifurcation stenting. If the mother diameter is unchanged, an increase of bifurcation angle (similar to a decrease of daughter diameters) leads to low WSS and high OSI near the carina while an increase of daughter diameters (similar to a decrease of bifurcation angle) affects surface regions opposite to the carina. An increase of both angle and diameter (e.g., Y bifurcation of Murray type and T bifurcation of Finet type vs. HK-type bifurcation) induces even worse hemodynamic conditions at bifurcations.

APPENDIX A

Theory of Bifurcation Angles

Figure A1(a) shows a bifurcation, whedL_m ) is added to L_m L_l (and L_s are at positions indicated by the dashed lines). If we assume blood volume conservation over a bifurcation (i.e., $\frac{\pi }{4}{\text{D}}_{\text{m}}^2{\text{L}}_{\text{m}}+\frac{\pi }{4}{\text{D}}_1^2{\text{L}}_1+\frac{\pi }{4}{\text{D}}_{\text{s}}^2{\text{L}}_{\text{s}}=\text{constant}$) or mass conservation for a constant blood density, an infinitesimal increase of volume in mother vessel ( $\frac{\pi }{4}{\text{D}}_{\text{m}}^2{\text{dL}}_{\text{m}}$) should be equal to a decrease of volume in daughter vessels $\left(\frac{\pi }{4}{\text{D}}_1^2{\text{dL}}_{\text{m}}cos(\beta )+\frac{\pi }{4}{\text{D}}_{\text{s}}^2{\text{dL}}_{\text{m}}cos(\gamma )\right)$, which can be written as:

$$\frac{\pi }{4}{\text{D}}_{\text{m}}^2{\text{dL}}_{\text{m}}=\frac{\pi }{4}{\text{D}}_{\text{l}}^2{\text{dL}}_{\text{m}}cos(\beta )+\frac{\pi }{4}{\text{D}}_{\text{s}}^2{\text{dL}}_{\text{m}}cos(\gamma )$$ [A1]

Applying the same principle of volume conservation to an infinitesimal increment of the two daughter vessels, we obtain:

$$\frac{\pi }{4}{\text{D}}_{\text{l}}^2{\text{dL}}_{\text{l}}=-\frac{\pi }{4}{\text{D}}_{\text{s}}^2{\text{dL}}_{\text{l}}cos(a)+\frac{\pi }{4}{\text{D}}_{\text{m}}^2{\text{dL}}_{\text{l}}cos(\beta )$$ [A2]

$$\frac{\pi }{4}{\text{D}}_{\text{s}}^2{\text{dL}}_{\text{s}}=-\frac{\pi }{4}{\text{D}}_{\text{l}}^2{\text{dL}}_{\text{s}}cos(a)+\frac{\pi }{4}{\text{D}}_{\text{m}}^2{\text{dL}}_{\text{s}}cos(\gamma )$$ [A3]

Solving Eqs. [A1–A3], we obtain:

$$cos(a)=\frac{{\text{D}}_{\text{m}}^4-{\text{D}}_{\text{l}}^4-{\text{D}}_{\text{s}}^4}{2{\text{D}}_{\text{l}}^2{\text{D}}_{\text{s}}^2};cos(\beta )=\frac{{\text{D}}_{\text{m}}^4+{\text{D}}_{\text{l}}^4-{\text{D}}_{\text{s}}^4}{2{\text{D}}_{\text{m}}^2{\text{D}}_{\text{l}}^2};cos(\gamma )=\frac{{\text{D}}_{\text{m}}^4+{\text{D}}_{\text{s}}^4-{\text{D}}_{\text{l}}^4}{2{\text{D}}_{\text{m}}^2{\text{D}}_{\text{s}}^2}$$ [A4]

From the HK diameter model (Huo and Kassab, 2009b), ${\text{D}}_{\text{m}}^{\frac{7}{3}}={\text{D}}_{\text{l}}^{\frac{7}{3}}+{\text{D}}_{\text{s}}^{\frac{7}{3}}$ at a bifurcation so that Eq. [A4] is written as:

$$\{\begin{array}{l}cos(a)=\frac{{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{12}{7}}-\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4\right)}{2{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2}\hfill \\ cos(\beta )=\frac{{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{12}{7}}+\left(1-{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4\right)}{2{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{6}{7}}}\hfill \\ cos(\gamma )=\frac{{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{12}{7}}+\left({\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4-1\right)}{2{\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^{\frac{7}{3}}\right)}^{\frac{6}{7}}{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2}\hfill \end{array}$$ [A5]

Equation [A5] represents bifurcation angles as a function of diameter ratio ( $\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}$) (HK angle rule). Hence, for a given diameter ratio, the optimal angles are constrained by Eq. [A5], which is clearly different than those provided by Murray (Murray CD, 1926b). Furthermore, from the Finet diameter model (Finet et al., 2008), D_m =0.678 =D_l +D_s = at a bifurcation so that Eq. [A4] can be written as:

$$\{\begin{array}{l}cos(a)=\frac{{0.678}^4{\left(1+\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4-\left(1+{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4\right)}{2{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2}\hfill \\ cos(\beta )=\frac{{0.678}^4{\left(1+\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4+\left(1-{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4\right)}{2\times {0.678}^2{\left(1+\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2}\hfill \\ cos(\gamma )=\frac{{0.678}^4{\left(1+\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4+\left({\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^4-1\right)}{2\times {0.678}^2{\left(1+\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2{\left(\frac{{\text{D}}_{\text{s}}}{{\text{D}}_{\text{l}}}\right)}^2}\hfill \end{array}$$ [A6]

which leads to Finet angle rule. When the area-preservation model (i.e., ${\text{D}}_{\text{m}}^2={\text{D}}_{\text{l}}^2+{\text{D}}_{\text{s}}^2$) is considered, cos (α) = 1 in Eq. [A4], i.e., α = 0° or 180° which is non-physical. Therefore, the area-preservation model is not included in the study.

Figure A1(b) shows a comparison between HK (Eq. A5), Murray (1926b), Finet (Eq. A6) angle rules and CT measurements obtained from a previous study (Wischgoll et al., 2009). There is a relative error (|α_actual − α_theory|/α_actual) of 44 ± 17%, 115 ± 26%, 46 ± 17% (mean ± standard error) at bifurcations of various diameter ratios when α_theory corresponds to HK, Murray, and Finet angle rules, respectively. Finet angle rule only applies to bifurcations with diameter ratio > 0.37 because the absolute value of the right-hand term in Eq. [A6] is > unity when diameter ratio is ≤ 0.37.

The bifurcation angle α has a value of 60° ± 28° (mean ± standard deviation), based on angiographic measurements for coronary bifurcations in which mother vessel diameters vary from 1.8 to 6.2 mm (Finet et al., 2008). Hence, it is reasonable to define a coronary bifurcation as Y or T bifurcations If angle α is < 60° or ≥ 60°, respectively.