A moving ParA gradient on the nucleoid directs subcellular cargo transport via a chemophoresis force

Abstract

DNA segregation is a critical process for all life, and although there is a relatively good understanding of eukaryotic mitosis, the mechanism in bacteria remains unclear. The small size of a bacterial cell and the number of factors involved in its subcellular organization make it difficult to study individual systems under controlled conditions in vivo. We developed a cell-free technique to reconstitute and visualize bacterial ParA-mediated segregation systems. Our studies provide direct evidence for a mode of transport that does not use a classical cytoskeletal filament or motor protein. Instead, we demonstrate that ParA-type DNA segregation systems can establish a propagating ParA ATPase gradient on the nucleoid surface, which generates the force required for the directed movement of spatially confined cargoes, such as plasmids or large organelles, and distributes multiple cargos equidistant to each other inside cells. Here we present the critical principles of our diffusion-ratchet model of ParA-mediated transport and expand on the mathematically derived chemophoresis force using experimentally-determined biochemical and cellular parameters.

Abbreviations

ATP

adenosine triphosphate

DNA

deoxyribonucleic acid

Par

partition

Sop

stability of plasmid

RD

reaction diffusion

Introduction

Subcellular cargo transport and positioning has long been thought to be mainly carried out by classical motor proteins, e.g. myosins and kinesins, and cytoskeletal elements, e.g., actin filaments or microtubules.¹ However, it has recently become apparent that protein gradients on biological surfaces, such as condensed DNA, can be used to transport and position a wide variety of large cargoes in bacteria including chromosomes, plasmids, and protein machineries.^2,3 The most common microbial transport scheme for both chromosome and plasmid segregation, or ‘partitioning’, is the self-organizing Par system. Par systems are minimal, encoding only 2 proteins: a deviant Walker-type ATPase, ParA that forms dynamic protein gradients on the nucleoid upon interacting with its stimulator, ParB, which binds to a centromere-like site on the plasmid or chromosome and forms a ‘partition complex’ that demarcates the DNA as cargo.⁴ Despite the apparent simplicity and ubiquity of ParA-type systems, how nucleoid-bound ParA gradients are generated, and how, in turn, they provide the driving force to segregate, transport, and position ParB-bound cargo over the nucleoid remains unknown and controversial.

ParA-type systems are the principal segregation pathways of most low-copy plasmids, making them excellent models to study bacterial DNA segregation. ParA and ParB equidistantly disperse plasmids over the long-axis of the bacterial nucleoid so that at least one copy is inherited by the 2 daughters following cell division. In the absence of Par, plasmids and other large cargoes, such as bacterial organelles, occupy the cytosolic space at the poles or between nucleoids.³ In other words, large bodies in bacteria are nucleoid excluded without active positioning. Therefore, the nucleoid acts as a formidable diffusion barrier for large cargoes. How ParA-type systems overcome this barrier and allow large cargoes to occupy, and/or travel across, the narrow cytosolic gap between the nucleoid surface and inner membrane of the cell remains unclear.

Two of the first Par systems to be identified, considered paradigms for the study of ParA-mediated DNA segregation, are the ParABS and SopABC systems of Escherichia coli plasmids P1 and F, respectively.^5,6 In the F Sop system, SopA is the ParA-type ATPase and SopB is the ParB-type stimulator that binds to the plasmid centromere site, sopC (or parS in other systems).⁴ P1 ParA and F SopA have very weak intrinsic ATPase activity.^7,8 We have shown that the ATP-activated dimers can non-specifically bind and undergo hop diffusion across a DNA-carpeted flowcell without hydrolyzing ATP,^9,10 indicating they are not statically bound to the nucleoid in vivo. Rather, ParA dimers dynamically associate and diffuse on the nucleoid surface. ParB and non-specific DNA synergistically stimulate the ATPase activity of ParA,^7,8 and significantly increase the rate of ParA release from DNA, indicating that ATP hydrolysis is obligatorily coupled to DNA release.^9,10 After ParB-stimulated ATP hydrolysis, ParA must release its hydrolysis products, dissociate to monomers, rebind ATP, dimerize, and undergo slow ATP-dependent transitions before rebinding DNA.¹¹ ParA-ATP dimers can therefore rapidly bind and unbind the nucleoid until contact with plasmid-bound ParB renders ParA temporarily incapable of rebinding in the vicinity of the cargo. The diffusion-ratchet model we developed posits that the ParA depletion zone and associated concentration gradient generated by plasmid-bound ParB is utilized for active and directional transport of cargo over the nucleoid.^9-12 Here we summarize our recent cell-free reconstitution of ParA-mediated plasmid motion, highlight the key aspects of our diffusion-ratchet model for cargo transport, and demonstrate via simulations how a ‘chemophoresis’ force can produce directed motion of large bodies in bacteria over the nucleoid surface.

Reconstituting ParA-mediated cargo transport in vitro

To directly test the diffusion-ratchet model, we reconstituted and visualized the P1 Par and F Sop plasmid partition systems using purified and fluorescent-labeled components inside a DNA-carpeted flow cell, which acted as an artificial nucleoid surface.^9,10 The cell-free dynamics recapitulated several features observed in vivo. ParA-ATP associated with the DNA-carpet and tethered ParB-bound plasmid clusters, which stimulated the local removal of ParA to form depletion zones on the DNA-carpet. However, plasmid tethering was transient and formation of a ParA gradient on the perimeter of the depletion zone was not followed by robust and directed plasmid motion as shown in vivo for several ParA-mediated partition systems.^13-15 Instead, the plasmids diffused away from the carpet once all tether points were released. We reasoned that our flow cell, with a depth of 25 μm, lacked the surface confinement needed to maintain contact between the plasmid and the DNA carpet. We proposed that the narrow cytosolic space between the nucleoid and the inner membrane in vivo is critical to the diffusion-ratchet mechanism as it promotes frequent associations between plasmid-bound ParB and nucleoid-bound ParA – a requirement for sustained plasmid motion.

To mimic surface confinement on the nucleoid, we recapitulated the F Sop system using magnetic beads, coated with centromere DNA (sopC), that were artificially confined to the DNA-carpet by a magnet placed above the flow cell (Fig. 1A; Vecchiarelli et al.¹²). Like the plasmid substrate, sopC-coated beads bound by SopB were tethered to SopA-ATP on the DNA-carpet. As SopA was rapidly released, a depletion zone formed around the beads on the DNA-carpet and the beads began to diffuse randomly once the SopA anchor points were released. Strikingly however, when beads with robust SopA depletion zones drifted into the SopA gradient, forward motion continued toward the perimeter of the depletion zone (Fig. 1B and Movie 1). ¹² The depletion zone then continued to propagate along with the bead, which traveled in a directed manner that persisted for many microns. The depletion zone in the wake of bead movement slowly refilled with SopA molecules diffusing from the nearby surface and from solution. Our results demonstrate that physical confinement of cargo to the nucleoid surface is a key requirement for cargo transport and perhaps other forms of subcellular organization mediated by ParA.

Figure 1.

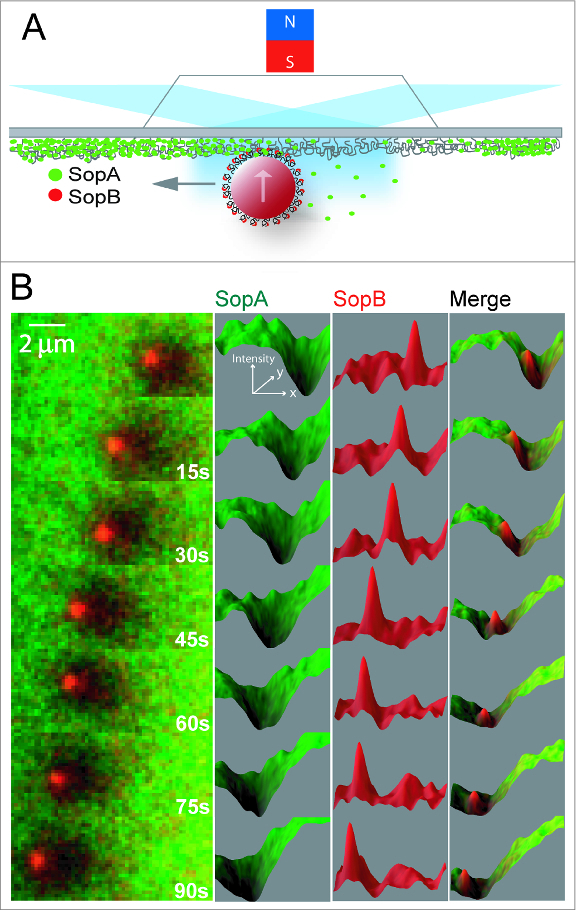
ParA-type cargo transport on a DNA-carpet. (A) Schematic of the reconstitution setup, where a magnet above the flowcell confined sopC-coated magnetic beads on to the DNA-carpet. Fluorescent labeled components of the system were visualized by TIRFM. (B) A freeze-frame image series of SopA (green) on the DNA-carpet and SopB (red) on a bead traveling from right to left. Figure panels with permission from Vecchiarelli et al. ¹²

The diffusion-ratchet model for ParA-mediated transport

Together with previous biochemical and in vivo cytological observations, our cell-free reconstitution provides strong evidence of ParA-mediated transport via a diffusion-ratchet mechanism, which can be split into 2 key components – ParA gradient formation by reaction-diffusion (RD) and motive force generation by “chemophoresis”.¹² To form a gradient of ParA concentration that decreases toward the cargo, many ParB dimers concentrated on a macroscopic element, such as a plasmid, interact with ParA dimers on the nucleoid and stimulate their local release to form a depletion zone around the cargo. A biochemically imposed delay in nucleoid rebinding by ParA is central to forming the gradient as it prevents immediate rebinding to the nucleoid in the vicinity of the cargo. We identified one such delay in the ATPase cycle for P1 ParA,¹¹ and we anticipate a similar biochemical delay in the F SopA ATPase cycle, which has a similar intrinsic timing mechanism for nucleoid rebinding.

We propose that the ParA gradient results in a chemical potential gradient that provides the chemophoresis force, which drives the directed motion of a macroscopic element, the plasmid, bound by a large number of ParB molecules that weakly bind ParA. The cumulative effect of the individual ParA–ParB interactions directs cargo motion toward regions of increased binding, that is, the cargo moves up the gradient toward higher ParA concentrations. Directed motion is promoted by the lowered free energy state provided by (i) the decrease in free energy associated with an increase in the number of ParB-ParA contacts within the increasing ParA gradient and (ii) the relative decrease in free energy of the system as ParA is bound by ParB at locations with increasing chemical potential, i.e, concentration. The resulting change in free energy with distance is a force – the chemophoresis force. Individual ParA-ParB contacts are weak and transient, but multiple ParB dimers interacting with multiple ParA dimers would allow the cargo to probe its contact density within the ParA gradient via local Brownian motion. Moreover, surface confinement of the cargo further promotes frequent interactions between cargo-bound ParB and surface-bound ParA.

Simulations of cargo movement driven by a ParA gradient via the chemophoresis force

From measurements of the bead-based reconstitution experiments, we estimated the chemophoresis force exerted on the bead with a simplified theoretical formulation proposed by Sugawara and Kaneko.¹⁶ The model was sufficient to obtain a rough estimate of the force for a static SopA concentration gradient, but it contains several simplifying assumptions that likely do not accurately reflect the experimental conditions. Here we address some of these shortcomings and extend the calculations to encompass the generation and propagation of the SopA gradient as well as the motion of the bead interacting with the gradient. The Sugawara and Kaneko chemophoresis model assumes that ParA molecules are freely diffusing,¹⁶ but for ParA-mediated cargo motion, the relevant ParA-ParB interactions are relegated to the nucleoid surface. This reduction in dimensionality leads to 2 modifications of the original model. First, the SopA-SopB binding isotherm must be modified to take into account the limited amount of surface-bound SopA that can interact with cargo-bound SopB, which leads to a more general form of the binding isotherm that takes into account the depletion of “free” SopA as it binds SopB. Second, the diffusion of SopA that is responsible for the gradual refilling of the depletion zone is dominated by the relatively slow hop diffusion of surface-bound SopA rather than the 3 dimensional diffusion and rebinding of SopA from solution. With these 2 modifications the equation of motion (Equation 9 from Suguwara and Kaneko ¹⁶) for the bead becomes:

$$\gamma \dot{\zeta }=b_n{k}_{B}Tf\left(b_c\right)\frac{\nabla u\left(\zeta ,t\right)}{u\left(\zeta ,t\right)}+\eta \left(t\right)$$ (1)

$${\displaystyle f\left(b_c\right)=\frac{\left(b_c+u\left(\zeta ,t\right)+K_{eq}\right)-\sqrt{{\left(b_c+u\left(\zeta ,t\right)+K_{eq}\right)}^2-4\left(b_{c}u\left(\zeta ,t\right)\right)}}{2b_c}}$$

Where γ is the drag on the bead, which can be estimated from the diffusion constant D_b, ζ is the position of the center of the bead, ${\displaystyle \dot{\zeta }}$ is the time derivative of the bead position, b_n is the number of SopB molecules on the bead that can interact with surface-bound SopA, k_BT is the thermal energy, ${\displaystyle u(\zeta ,t)}$ is the total concentration of SopA at the bead position, ${\displaystyle ▿u(\zeta ,t)}$ is the spatial derivative of the total concentration profile of SopA evaluated at the position of the bead, and η(t) is the Brownian noise term. The binding isotherm, f(b_c), represents the fraction of SopB bound to SopA, where b_c is the concentration of SopB that can interact with SopA and K_eq is the equilibrium binding constant.

For the reaction-diffusion (RD) process that generates the SopA depletion zone, in the absence of a complete mechanistic framework, we use a simplified equation in which SopA molecules are irreversibly released from the DNA-carpet by the bead-bound SopB. The localized SopA depletion is counteracted by slow surface diffusion of carpet-bound SopA. The 1-dimensional version of the RD equation can be expressed as (derived from Equation 9 from Suguwara and Kaneko¹⁶):

$${\displaystyle \partial u_t\left(x,t\right)=D_a{▿}^{2}u\left(x,t\right)-k{b}_{c}f\left(b_c\right)\delta \left(x-\zeta \right)}$$ (2)

Where D_ɑ is the surface diffusion constant of SopA, k is the SopB-stimulated SopA off rate, and δ(x-ζ) is the Kronecker delta function that is 0 unless x = ζ, which imposes the condition that the unbinding of SopA by SopB occurs only in the vicinity of the SopB-coated bead. Whereas this simplified model of the RD process does not faithfully reproduce the details of the experimentally observed SopA depletion zone, it recapitulates the sustained and directed motion of the bead (Figs. 2 and 3, Movies 1 and 2).

Figure 2.

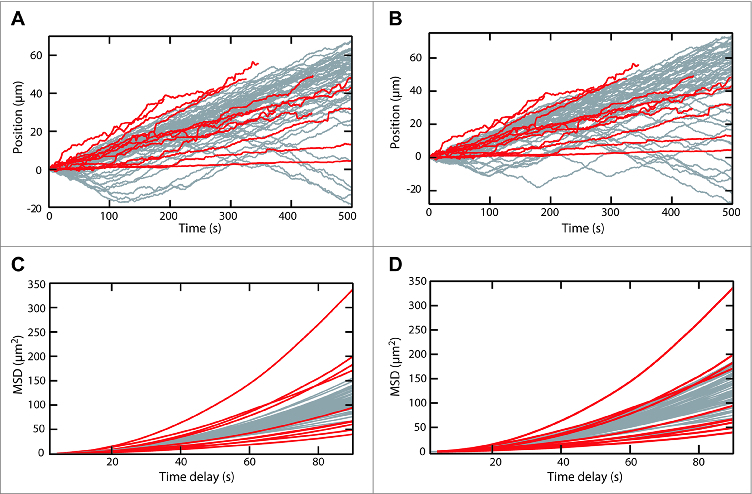
Comparison of experimental and simulated SopA-SopB driven motion. (A) Position as a function of time for SopB coated beads moving on a random DNA surface with bound SopA from Vecchiarelli et al. ¹² (red lines) and 50 simulated trajectories (gray lines) based on the chemophoresis force (Equation 1) and the reaction diffusion expression (Equation 2) for parameters listed in Table 1 (Simulation 1) for which the average velocity of the simulated traces (0.09 ± 0.01 μm s⁻¹ (SEM)) was the same as the experimental traces (0.1 ± 0.02 μm s⁻¹ (SEM)). The experimental trajectories correspond to the maximum projection of the motion, which was highly directional. The simulated trajectories were oriented so that the average velocity for each trajectory was positive. Note the frequent reversals in the direction of motion of the simulated trajectories. (B) Same as in (A) except that the SopB density was 5-fold less (parameter set 2 in Table 1). The average velocity of the simulated traces was 0.089 ± 0.005 μm s⁻¹ (SEM). (C) The mean square displacements (MSD) of the trajectories in panel (A) plotted as a function of the time interval. (D) The mean square displacements (MSD) of the trajectories in panel (B) plotted as a function of the time interval.

Figure 3.

Simulations resemble experimentally-observed ParA-mediated cargo dynamics. Time-lapse sequence of the simulated 2-dimensional motion of a SopB-coated particle on a SopA-coated surface. Scale bar = 10 μm. Also see Movie 2 and SI Methods for simulation details.

All the parameters for the 2 equations, with the exception of the SopA-SopB equilibrium binding constant (K_eq), can be directly estimated from experimental measurements of the bead-based motion (Table 1). A suitable choice of K_eq results in bead motion that largely recapitulates the experimentally measured bead motion (Fig. 2 and 3, Movies 1 and 2). Given that the equations are largely governed by products of the parameters, the value of K_eq that reproduces bead motion likely compensates for errors in estimating the other parameters. For example, we ignored the presence of bead-bound SopA and carpet-bound SopB, which would decrease the number of SopB-SopA interactions contributing to the force on the bead by as much as one order of magnitude. This potential overestimate of the number of SopB-SopA interactions is compensated by the higher K_eq, which effectively decreases these interactions. To illustrate this point, 1- and 2-dimensional simulations run with a 5-fold change in the effective SopB concentration on the bead approximately reproduced the average velocity and mean squared displacement curves of the experimental data for suitable choices of K_eq (Fig. 2 and 3, Movies 1 and 2).

Table 1.

Simulation parameters. All parameters were estimated from the bead-based experiments 12 except Keq, which was adjusted so that the simulation results matched the experimental results. The experimentally measured velocity, diffusion constant (from the linear term of the mean square displacement fit), and quadratic term of the mean square displacement fit are listed in the Parameter column under the Measured parameters heading. The measured parameters for the simulations are obtained from fits to the 1-D simulations in Figure 2 See main text for descriptions of the simulation parameters.

Parameter	Simulation 1	Simulation 2
u(0,x) (μM)	10	7
Da (μm2 s−1)	0.05	0.05
k (s−1)	0.01667	0.01667
Db (μm2 s−1)	0.02	0.02
bc (μM)	10	2
bn	4800	960
Keq (μM)	40	0.3
Measured parameters
Velocity 0.10 ± 0.02 μm s−1	0.089 ± 0.005 μm s−1	0.09 ± 0.01 μm s−1
Db 0.03 ± 0.02 μm s−1	0.026 ± 0.001 μm2 s−1	0.030 ± 0.001 μm2 s−1
Quadratic MSD term 0.012 ± 0.003 μm2 s−2	0.016 ± 0.002 μm2 s−2	0.019 ± 0.001 μm2 s−2

Comparing experimental and simulated ParA-mediated cargo dynamics

One-dimensional simulations are reasonable approximations of the experimentally observed motion, since the direction of bead motion was remarkably persistent and individual trajectories consisted of essentially one-dimensional motion.¹² Results from 1-D simulations were used to compute the average velocity and mean square displacement curves for 2 different effective SopB densities (Fig. 2). Representative trajectories were also generated with a 2-dimensional generalization of the simulations (Fig. 3, Movie 2). However, the relatively frequent spontaneous direction reversals in the 1-D simulated trajectories, and lack of directional persistence in the 2-D simulated trajectories, were not observed in the experimental trajectories, suggesting the simple chemophoresis model encompassed in Equations 1 and 2 is missing subtle mechanistic details of the actual process observed in the experiment. The simulations therefore do not allow us to directly probe this surprising directional persistence of bead motion. The persistence may result from one or more aspects of the motion that are not represented in the model such as the fact that while SopB is bound to SopA the bead is constrained, undergoing tethered Brownian motion rather than diffusive or biased motion. The effective averaging of the force over the lifetime of the SopB-SopA tethers may reduce spatial fluctuations and contribute to the highly persistent directional motion.

The experimentally estimated motive force on the bead was roughly 5-10 fN.¹² In order for this small force to generate directed motion of the bead without being quickly randomized by thermal fluctuations, there must be a time-averaging process that effectively reduces the random force fluctuations. We believe 2 factors contribute to this time-averaging process: (i) slow cargo diffusion (in this case, the bead plus the attached SopB-sopC complexes) dominated by viscoelastic interactions with the DNA-carpet, and (ii) the slow diffusion (tens of seconds) of SopA that refills the depletion zone. If either of these time scales were too fast, we would predict the chemophoretic force would become insufficient to overcome random thermal motion. On the other hand, too large a number of stable ParA-ParB interactions bridging the cargo to the DNA-carpet would prevent cargo motion altogether, which we have experimentally observed at high ParA densities on the DNA-carpet. ^9,10

Finally, we cannot rule out the potential influence of the applied magnetic field on the beads in establishing the highly persistent directional motion. Although the magnet was aligned to minimize forces on the beads in the plane of the flowcell, or perpendicular to the intended pulling direction, a small but non-negligible force may nonetheless have existed in the plane of motion. Control experiments where free magnetic beads were tracked in parallel with directed beads in the same field of view established that the lateral forces were substantially less than the chemophoresis forces on the beads. But we cannot rule out the possibility of a small residual force sufficient to bias the direction and persistence of bead motion.

Conclusion

To refine the ParA-mediated transport model, several technical improvements of the in vitro reconstitution are being implemented. First, micro-confinement chambers are being used to spatially confine multiple copies of cargo without externally applied forces and the potential associated artifacts. This passive confinement scheme permits the study of bidirectional segregation and equidistant cargo positioning – hallmark functions of ParA-type systems that have not been recapitulated in vitro.

Centromere-coated beads are different from plasmid cargo in many respects. However, a variety of protein and DNA-based cargos use Par systems for active transport,^2,3 suggesting cargocomposition is not a critical factor in the mechanism. Nevertheless, plasmids and other physiologically relevant cargos will certainly be useful in studying ParA-type systems in the chambers discussed above. Also, it is likely that many DNA-binding proteins, such as nucleoid-associated proteins (NAPs), influence the system dynamics in vivo. Adding these proteins to the cell-free setup may unveil further details of chromosome dynamics in general.

Finally, one of the many exciting features of this transport mechanism is the use of the nucleoid as a matrix for transport, which raises a number of questions with respect to the nature of the nucleoid surface. It's a jungle in there! Is the cargo rolling over the forest canopy, swinging from branch to branch through the DNA trees, or penetrating even further down and rolling along the forest floor? These questions can be addressed by changing the length and topology of the DNA making up the carpet in the flowcell. We anticipate that cell and cell-free imaging, combined with genetics and biochemical approaches, will soon provide the details necessary for a comprehensive explanation of the mechanism governing ParA-mediated segregation, transport, and positioning of large bodies in bacteria.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Acknowledgments

Supported by the intramural research fund for NIDDK (K.M.) and NHLBI (K.C.N.), NIH US Dept of HHS, and the Nancy Nossal Fellowship (A.G.V.).

Supplemental Material

Supplemental Material may be downloaded here: publisher's website