DanQ: a hybrid convolutional and recurrent deep neural network for quantifying the function of DNA sequences

Abstract

Modeling the properties and functions of DNA sequences is an important, but challenging task in the broad field of genomics. This task is particularly difficult for non-coding DNA, the vast majority of which is still poorly understood in terms of function. A powerful predictive model for the function of non-coding DNA can have enormous benefit for both basic science and translational research because over 98% of the human genome is non-coding and 93% of disease-associated variants lie in these regions. To address this need, we propose DanQ, a novel hybrid convolutional and bi-directional long short-term memory recurrent neural network framework for predicting non-coding function de novo from sequence. In the DanQ model, the convolution layer captures regulatory motifs, while the recurrent layer captures long-term dependencies between the motifs in order to learn a regulatory ‘grammar’ to improve predictions. DanQ improves considerably upon other models across several metrics. For some regulatory markers, DanQ can achieve over a 50% relative improvement in the area under the precision-recall curve metric compared to related models. We have made the source code available at the github repository http://github.com/uci-cbcl/DanQ.

INTRODUCTION

The recent deluge of high-throughput genomic sequencing data has prompted the development of novel bioinformatics algorithms that can integrate large, feature-rich datasets. Deep learning algorithms are attractive solutions for such problems because they are scalable with large datasets and are effective in identifying complex patterns from feature-rich datasets (1). They are able to do so because deep learning algorithms utilize large training data and specialized hardware to efficiently train deep neural networks (DNNs) that learn high levels of abstractions from multiple layers of non-linear transformations. DNNs have already been adapted for genomics problems such as motif discovery (2), predicting the deleteriousness of genetic variants (3), and gene expression inference (4).

There has been a growing interest to predict function directly from sequence, instead of from curated datasets such as gene models and multiple species alignment. Much of this interest is attributed to the fact that over 98% of the human genome is non-coding, the function of which is not very well-defined. A model that can predict function directly from sequence may reveal novel insights about these non-coding elements. Over 1200 genome-wide association studies have identified nearly 6500 disease- or trait-predisposing single-nucleotide polymorphisms (SNPs), 93% of which are located in non-coding regions (5), highlighting the importance of such a predictive model. Convolutional neural networks (CNNs) are variants of DNNs that are appropriate for this task (6). CNNs use a weight-sharing strategy to capture local patterns in data such as sequences. This weight-sharing strategy is especially useful for studying DNA because the convolution filters can capture sequence motifs, which are short, recurring patterns in DNA that are presumed to have a biological function. DeepSEA is a recently developed algorithm that utilizes a CNN for predicting DNA function (7). The CNN is trained in a joint multi-task fashion to simultaneously learn to predict large-scale chromatin-profiling data, including transcription factor (TF) binding, DNase I sensitivity and histone-mark profiles across multiple cell types, allowing the CNN to learn tissue-specific functions. It significantly outperforms gkm-SVM (8), a related algorithm that can also predicts the regulatory function of DNA sequences, but uses a support vector machine instead of a CNN for predictions. To predict the effect of regulatory variation, both gkm-SVM (9) and DeepSEA use a similar strategy of predicting the function of both the reference and allele sequences and processing the score differences.

Another variation of DNNs is the recurrent neural network (RNN). Unlike a CNN, connections between units of an RNN form a directed cycle. This creates an internal state of the network that allows it to exhibit dynamic temporal or spatial behavior. A bi-directional long short-term memory network (BLSTM) is a variant of the RNN that combines the outputs of two RNNs, one processing the sequence from left to right, the other one from right to left. Instead of regular hidden units, the two RNNs contain LSTM blocks, which are smart network units that can remember a value for an arbitrary length of time. BLSTMs can capture long-term dependencies and have been effective for other machine learning applications such as phoneme classification (10), speech recognition (11), machine translation (12) and human action recognition (13). Although BLSTMs are effective for studying sequential data, they have not been applied for DNA sequences.

Hence, we propose DanQ, a hybrid framework that combines CNNs and BLSTMs (Figure 1). The first layers of the DanQ model are designed to scan sequences for motif sites through convolution filtering. Whereas the convolution step of the DeepSEA model contains three convolution layers and two max pooling layers in alternating order to learn motifs, the convolution step of the DanQ model is much simpler and contains one convolution layer and one max pooling layer to learn motifs. The max pooling layer is followed by a BLSTM layer. Our rationale for including a recurrent layer after the max pooling layer is that motifs can follow a regulatory grammar governed by physical constraints that dictate the in vivo spatial arrangements and frequencies of combinations of motifs, a feature associated with tissue-specific functional elements such as enhancers (14,15). Following the BLSTM layer, the last two layers of the DanQ model are a dense layer of rectified linear units and a multi-task sigmoid output, similar to the DeepSEA model.

Figure 1.

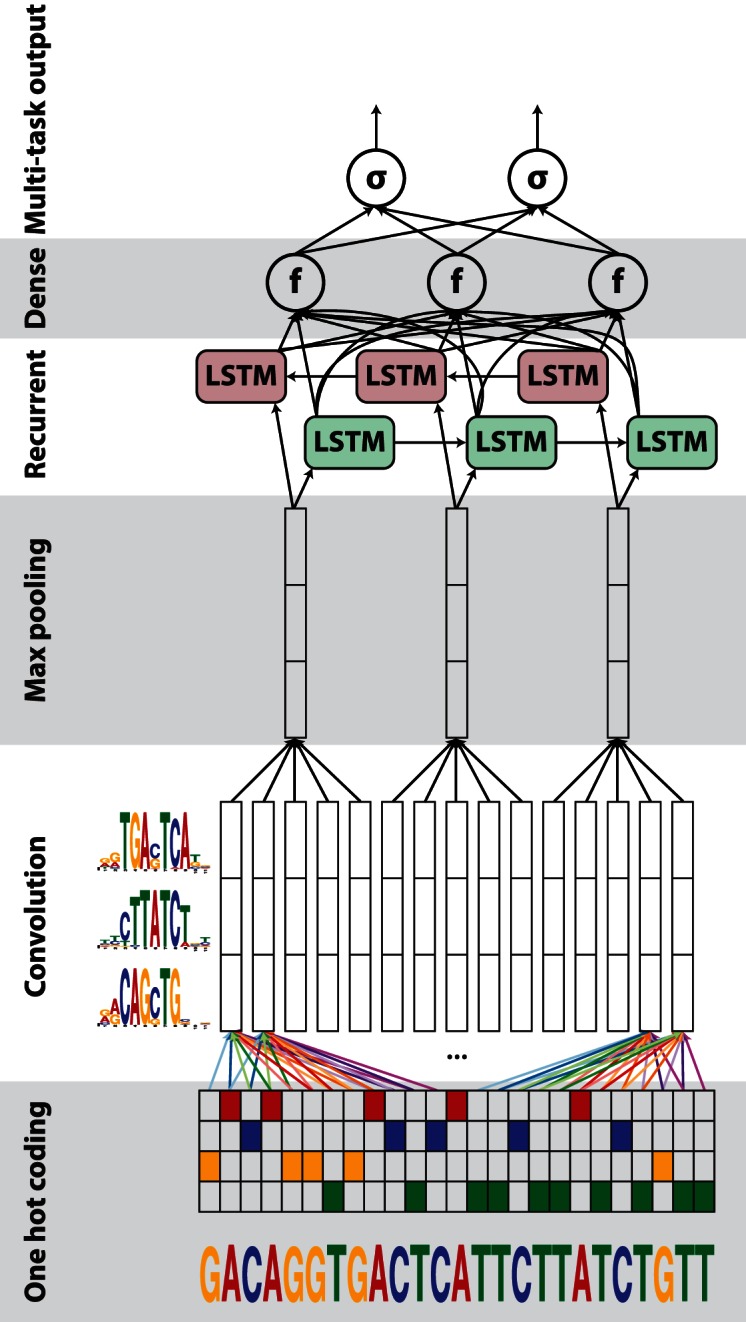
A graphical illustration of the DanQ model: an input sequence is first one hot encoded into a 4-row bit matrix. A convolution layer with rectifier activation acts as a motif scanner across the input matrix to produce an output matrix with a row for each convolution kernel and a column for each position in the input (minus the width of the kernel). Max pooling reduces the size of the output matrix along the spatial axis, preserving the number of channels. The subsequent BLSTM layer considers the orientations and spatial distances between the motifs. BLSTM outputs are flattened into a layer as inputs to a fully connected layer of rectified linear units. The final layer performs a sigmoid non-linear transformation to a vector that serves as probability predictions of the epigenetic marks to be compared via a loss function to the true target vector.

DanQ surpasses other methods for predicting the properties and function of DNA sequences across several metrics. In addition, we show that the convolution kernels learned by the model can be converted to motifs, many of which significantly match known motifs. We expect DanQ to provide novel insights into non-coding genomic regions and contribute to understanding the potential functions of complex disease- or trait-associated genetic variants.

MATERIALS AND METHODS

Features and data

The DanQ framework uses the same features and data as the DeepSEA framework. Briefly, the human GRCh37 reference genome was segmented into non-overlapping 200-bp bins. Targets were computed by intersecting 919 ChIP-seq and DNase-seq peak sets from uniformly processed ENCODE (16) and Roadmap Epigenomics (17) data releases, yielding a length 919 binary target vector for each sample. Each sample input consists of a 1000-bp sequence centered on a 200-bp bin that overlaps at least one TF binding ChIP-seq peak, and is paired with the respective target vector. Based on this information, we expected that each target vector would contain at least one positive value; however, we found that about 10% of all target vectors were all negatives. Each 1000-bp DNA sequence is one-hot encoded into a 1000 × 4 binary matrix, with columns corresponding to A, G, C and T. Training, validation and testing sets were downloaded from the DeepSEA website. Samples were stratified by chromosomes into strictly non-overlapping training, validation and testing sets. The validation set was not used for training or testing. Reverse complements are also included, effectively doubling the size of each dataset.

For evaluating performance on the test set, the predicted probability for each sequence was computed as the average of the probability predictions for the forward and reverse complement sequence pairs, similar to DeepSEA's evaluation experiments.

DanQ model and training

For detailed specifications of the architectures and hyperparameters used in this study, see Supplementary Note. Dropout (18) is included to randomly set a proportion of neuron activations from the max pooling and BLSTM layers to a value of 0 in each training step to regularize the DanQ models.

All weights are initialized by randomly drawing from unif(−0.05,0.05) and all biases are initially set to 0. In addition to random initialization, an alternative strategy is to initialize kernels from known motifs: a random subsection of a kernel is set equal to the values of the position frequency matrix minus 0.25 and its corresponding bias is randomly drawn from unif(−1.0,0.0). We tried both in our implementation.

Neural network models are trained using the RMSprop algorithm (19) with a minibatch size of 100 to minimize the average multi-task binary cross entropy loss function on the training set. Validation loss is evaluated at the end of each training epoch to monitor convergence. The first model we trained contains 320 convolution kernels with random initial weights, referred to as DanQ, took 60 epochs to fully train and each epoch of training takes ∼6 h. The second model we trained, which we designated as DanQ-JASPAR because half of the kernels are initialized with motifs from the JASPAR database (20), contains 1024 convolution kernels, took 30 epochs to fully train, and each epoch of training takes ∼12 h.

Our implementation utilizes the Keras 0.2.0 library (https://github.com/fchollet/keras) with the Theano 0.7.1 (21,22) backend. An NVIDIA Titan Z GPU was used for training the model.

Logistic regression

For benchmark purposes, we also trained a logistic regression (LR) baseline model. Unlike the DanQ and DeepSEA models, the LR model does not process raw sequences as inputs. Instead, the LR model uses zero-mean and unit variance normalized counts of k-mers of lengths 1–5 bp as features. The LR model was regularized with a small L2 weight regularization of 1e-6. Similar to the training of the DanQ models, the LR model was trained using the RMSprop algorithm with a minibatch size of 100 to minimize the average multi-task binary cross entropy loss function on the training set. Validation loss is evaluated at the end of each training epoch to monitor convergence. We note that this method of training is equivalent to training 919 individual single-task LR models.

Functional SNP prioritization

The DanQ functional SNP prioritization framework shares the same datasets, features and training algorithm as the DeepSEA functional SNP prioritization framework, essentially exchanging DeepSEA chromatin effect predictions with DanQ chromatin effect predictions. Briefly, we downloaded positive and negative SNP sets for training and testing. We also downloaded DeepSEA functional SNP scores for these variants for benchmarking purposes. Positive SNPs include expression quantitative trait loci (eQTLs) from the genome-wide repository of associations between SNPs and Phenotypes (GRASP) database (23) and non-coding trait-associated SNPs identified in GWAS studies from the US National Human Genome Research Institute (NHGRI) GWAS Catalog (24). Negative SNPs consist of 1000 Genomes Project SNPs (25) with controlled minor allele frequency distribution in 1000 Genomes population. The negative SNPs are further split into training and testing sets, the former consisting of 1,000,000 randomly selected non-coding 1000 genomes SNPs with minor allele frequency distribution matched with the eQTL or GWAS positive standards and the latter consisting of negative SNPs of varying distances to positive standard SNPs. We trained two boosted ensemble classifier models, one for the GRASP set and one for the GWAS set, using the XGBoost implementation (https://github.com/tqchen/xgboost). For a detailed specifications of the hyperparameters, see Supplementary Note. Features were computed as in Zhou and Troyanskaya (7), replacing DeepSEA chromatin effect predictions with DanQ chromatin effect predictions. All features were standardized to mean 0 and variance 1 before training. Unequal positive and negative training sample sizes were balanced with sample weights. The performance of each model was estimated by 10-fold cross-validation and across several negative groups.

RESULTS

We first train a DanQ model containing 320 convolution kernels for 60 epochs, evaluating the average multi-task cross entropy loss on the validation set at the end of each epoch to monitor the progress of training. To regularize the model, we also include dropout to randomly set a proportion of neuron activations from the max pooling and BLSTM layers to a value of 0 in each training step. For detailed specifications of the hyperparameters and model architecture, see Supplementary Note.

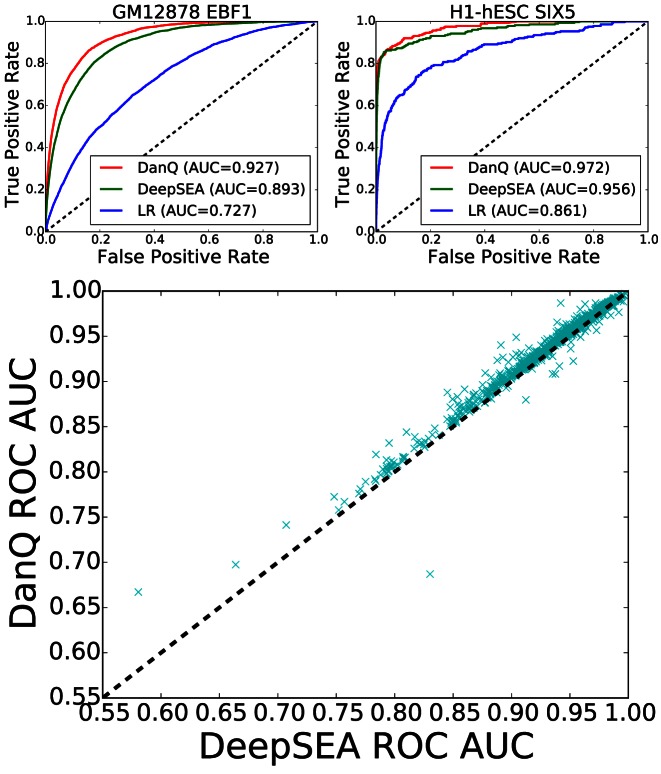
For benchmarking purposes, we compare a fully trained DanQ model to a LR baseline model and the published DeepSEA model. To compare performance among models, we first calculated the area under the receiver operating characteristics curve (ROC AUC) for each of the 919 binary targets on the test set (Figure 2). In terms of the ROC AUC score, DanQ outperforms the DeepSEA model for two of the targets as shown in the examples at the top of Figure 2, although this performance difference is relatively small. This pattern extends to the remaining targets as DanQ outperforms DeepSEA for 94.1% of the targets, although the difference is again comparatively small with an absolute improvement of around 1–4% for most targets. Despite the simplicity of the LR models, the ROC AUC statistics suggests that LR is an effective predictor, with ROC AUC scores typically over 70%. Given the sparsity of positive binary targets (∼2%), the ROC AUC statistic is highly inflated by the class imbalance, a fact overlooked in the original DeepSEA paper.

Figure 2.

(Top) ROC curves for the GM12878 EBF1 and H1-hESC SIX5 targets comparing the performance of the three models. (Bottom) Scatterplot comparing DanQ and DeepSEA ROC AUC scores. DanQ outperforms DeepSEA for 94.1% of the targets in terms of ROC AUC.

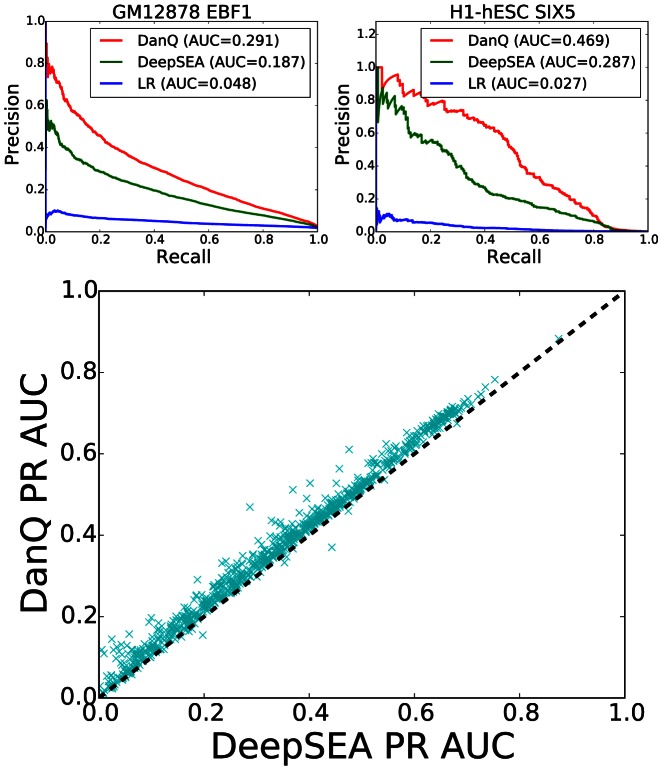
A better metric to measure the performance is the area under precision-recall curve (PR AUC) (Figure 3). Neither the precision nor recall take into account the number of true negatives, thus the PR AUC metric is less prone to inflation by the class imbalance than the ROC AUC metric is. As expected, we found the PR AUC metric to be more balanced, as demonstrated by how the LR models now achieve a PR AUC below 5% for the two examples at the top of Figure 3, far below the performance of the other two models. Moreover, the performance gap between DanQ between DeepSEA is much more pronounced under the PR AUC statistic than under the ROC AUC statistic. For the two examples shown, the absolute improvement is over 10% and the relative improvement is over 50% under the PR AUC metric and 97.6% of all DanQ PR AUC scores surpass DeepSEA PR AUC scores. These results show that adding recurrent connections significantly increases the modeling power of DanQ.

Figure 3.

(Top) PR curves for the GM12878 EBF1 and H1-hESC SIX5 targets comparing the performance of the three models. (Bottom) Scatterplot comparing DanQ and DeepSEA PR AUC scores. DanQ outperforms DeepSEA for 97.6% of the targets in terms of PR AUC.

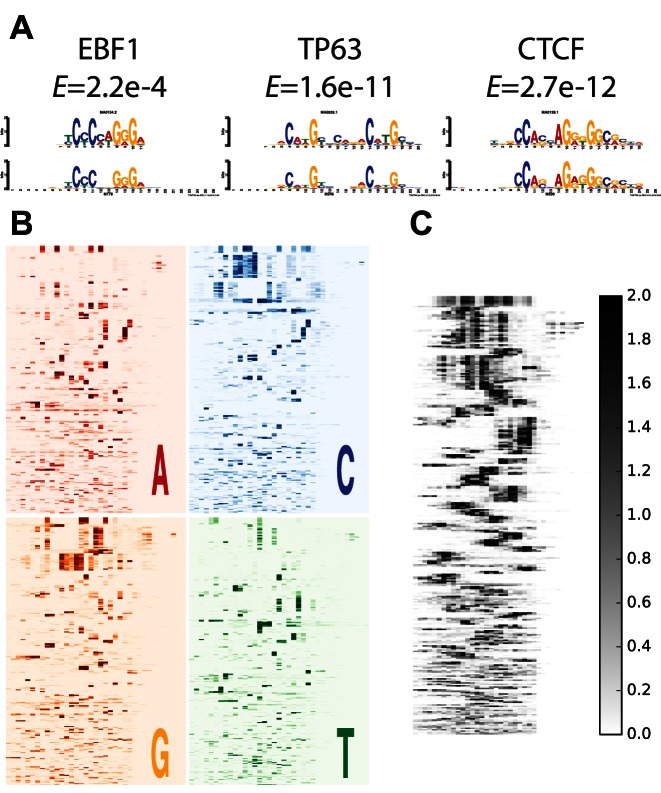
Using a similar approach described in the DeepBind method (2) we converted the kernels from the convolution layer of the DanQ models to position frequency matrices, or motifs. Then, we aligned these motifs to known motifs using the TOMTOM algorithm (26). Of the 320 motifs learned by the DanQ model, 166 significantly match known motifs (E < 0.01) (Figure 4A, Supplementary Figure S1 and Supplementary File). Next, we aligned and clustered the 320 motifs together into 118 clusters using the RSAT matrix clustering tool (27), and confirmed that the model learned a large variety of informative motifs (Figure 4B and C; Supplementary Figure S2).

Figure 4.

(A) Three convolution kernels (bottom) visualized and aligned with EBF1, TP63 and CTCF motif logos (top) from JASPAR using TOMTOM. Significance values of the match are displayed below motif names. (B) All 320 convolution kernels are converted to sequence logos and aligned with RSAT. The heatmaps are colored according to the information content of the respective nucleotide at each position. (C) Same as (B), except the heatmap is colored by the sum of the information content of each letter.

Given the large scope of the data, we conjectured that our current model did not exhaust the entire space of useful motif features despite the large variety of motifs learned. Moreover, weight initialization is known to play crucial role for the performance neural networks (28) and we hypothesized that a better initialization strategy can further improve the performance of our neural network. Therefore, we trained a larger model containing 1024 convolutional kernels of which about half are initialized with known motifs from JASPAR (20) and found this alternative way of initialization can further improve the performance of DanQ (Supplementary Table S1 and Figure S3).

Finally, we extended DanQ to prioritize functional SNPs based on differences of predicted chromatin effect signals between reference and allele sequences. Specifically, we downloaded training and testing SNP sets (7) that we used to train and evaluate boosted ensemble classifiers. The positive SNPs are annotated ‘functional’ non-coding positive SNPs are eQTL SNPs from the GRASP database (23) and non-coding trait-associated SNPs identified in GWAS studies from the US NHGRI GWAS Catalog (24). Negative ‘non-functional’ variant standards consist of 1000 Genomes Project SNPs (25) with controlled minor allele frequency distribution in 1000 Genomes population. These variant sets are the same sets used by the DeepSEA functional SNP prioritization framework for training and testing. The DanQ framework outperforms the DeepSEA framework across most of the testing sets, with the performance difference being 0.5–2% in terms of the ROC AUC metric (Supplementary Figure S4).

DISCUSSION

In conclusion, DanQ is a powerful method for predicting the function of DNA directly from sequence alone, making it a valuable asset for studying the function of non-coding DNA. Its hybrid architecture allows it to simultaneously learn motifs and a complex regulatory grammar between the motifs. The additional modeling capacity afforded by the recurrent connections allows DanQ to significantly outperform DeepSEA, a pure CNN model that lacks recurrent modeling. This performance gap is demonstrated across several metrics, including a direct comparison of AUC statistics between the two models. We argue that the PR AUC statistic is a much more balanced metric than the ROC AUC statistic to assess performance in this case due to the massive class imbalance. In fact, the performance gap can be quite drastic under the PR AUC statistic, reaching well over a 50% relative improvement for some epigenetic marks. Despite the significant improvement in performance, there is still much room for improvement because most of the PR AUC scores are below 70% for either model. Furthermore, the significant improvement in chromatin effect prediction does not immediately translate to an equally large improvement in functional variant prediction. One factor that may limit performance in this regard is that while the GRASP eQTL and GWAS catalog SNPs we label as positive variants are associated with phenotypes, these SNPs may not be the causal variants. Instead, the causal variants are likely in linkage disequilibrium with these SNPs. Thus, we hypothesize that extending our framework to study the link between phenotypes and haplotypes instead of phenotypes and individual SNPs may improve prediction performance. Nevertheless, the improved capability of DanQ to predict chromatin effects means it can better predict the epigenetic changes caused by genetic variants, which is useful information for prioritizing the causal variant among a group of tightly-linked variants and predicting the phenotypic outcomes of genome editing, the latter of which is beneficial for several fields including synthetic biology and transgenic animal studies.

There are several avenues of future interest to explore. First, the model can be made fully recurrent so it can process sequences of arbitrary length, such as whole chromosome sequences, to generate sequential outputs. In contrast, our current setup can only processes sequences of constant length with static output. A fully recurrent architecture may also benefit our effort to study variants since it would allow us to explore the long-range consequences of genetic variants, as well as the cumulative effects of SNPs that are in linkage disequilibrium with each other. Second, we are interested in incorporating new ChIP-seq and DNase-seq datasets from more cell types as they become available. Incorporating other types of data, such as methylation, nucleosome positioning and transcription may also yield novel results and improve functional variant prioritization. Finally, we are committed to updating and improving the DanQ model. As our results have shown, the model architecture and weight initialization can influence performance. Previously, we manually selected model parameters. For example, the DanQ model contains 320 kernels because the DeepSEA model also contains 320 kernels in its first convolutional layer, making the two models somewhat more comparable at the architectural level. Interestingly, although our first model contains fewer free weights than DeepSEA, our first model still significantly outperforms DeepSEA. In addition, the choice of 1024 kernels in the JASPAR-based model was made to accommodate 519 motifs in the JASPAR database in addition to an approximately equal number of randomly initialized kernels. One interesting prospect is to utilize distributed computing-based hyperparameter tuning algorithms to automatically find the optimal combination of model architecture, initial weights and hyperparameters. We will commit to providing regular updates as the model improves. Also, our motif analysis has shown that neural network training is an effective motif discoverer. Hence our updates will include motifs from the model in MEME minimal format, a flexible format compatible with most motif-related programs, as a resource to the community. To the best of our knowledge, this is the first application of a hybrid convolution and recurrent network architecture for the purpose of predicting function de novo from DNA sequences. We expect this hybrid architecture will be continually explored for the purpose of studying biological sequences.

Disclaimer: Any opinion, findings and conclusions or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the National Science Foundation.

FUNDING

National Institute of Biomedical Imaging and Bioengineering; University of California, National Research Service Award [EB009418]; Irvine, Center for Complex Biological Systems; National Science Foundation Graduate Research Fellowship [DGE-1321846]; National Institute of Health [HG006870]. Funding for open access charge: National Institutes of Health; National Science Foundation.

Conflict of interest statement. None declared.