Structure and dynamics of DNA loops on nucleosomes studied with atomistic, microsecond-scale molecular dynamics

Abstract

DNA loop formation on nucleosomes is strongly implicated in chromatin remodeling and occurs spontaneously in nucleosomes subjected to superhelical stress. The nature of such loops depends crucially on the balance between DNA deformation and DNA interaction with the nucleosome core. Currently, no high-resolution structural data on these loops exist. Although uniform rod models have been used to study loop size and shape, these models make assumptions concerning DNA mechanics and DNA–core binding. We present here atomic-scale molecular dynamics simulations for two different loop sizes. The results point to the key role of localized DNA kinking within the loops. Kinks enable the relaxation of DNA bending strain to be coupled with improved DNA–core interactions. Kinks lead to small, irregularly shaped loops that are asymmetrically positioned with respect to the nucleosome core. We also find that loop position can influence the dynamics of the DNA segments at the extremities of the nucleosome.

INTRODUCTION

Nucleosomes are the fundamental building blocks of eukaryotic chromatin. They consist of a protein core of eight histones (two copies of H2A, H2B, H3 and H4), surrounded by 147 base pairs (bp) of double-stranded DNA. Electrostatic interactions between the dominantly cationic histones and the anionic DNA overcome the bending strain of the double helix and the electrostatic repulsion between adjacent turns (or ‘spires’), enabling DNA to be wrapped around the core, forming a left-handed superhelix with an average radius of 41.4 Å and an average pitch of 22.2 Å (using the helical axis calculated with Curves+ (1) and the PDB structure 1KX5 (2,3)). The principal DNA–histone contacts occur in phase with the helical pitch of DNA (roughly every 10 bp within the nucleosome), where cationic arginine side chains penetrate the minor groove of DNA. These 14 contact points are numbered +1 → +7 and −1 → −7 in opposite directions leading away from the pseudodyad of the nucleosome (corresponding to the position of the central base pair of the wrapped DNA, see Supplementary Figure S1). The 147 base pairs are similarly numbered −73 → 0 → +73.

Since nucleosome-wrapped DNA is not easily accessible to proteins, nucleosome positioning within eukaryotic chromatin is a crucial element of gene regulation. Under normal physiological conditions, nucleosomes are relatively stable, although they will spontaneously migrate on the timescale of hours, and considerably faster at higher temperatures, or at lower salt concentrations (4–6). Such spontaneous movement (at least of some nucleosomes) may explain the intrinsic ‘fuzziness’ in mapping nucleosome positioning within chromatin (7). However, to carry out controlled nucleosome movements, cells contain chromatin remodelers, multi-protein complexes that bind and move nucleosomes, while consuming large quantities of ATP (8–11). Although the detailed mechanism of spontaneous, or controlled, nucleosome repositioning is not clear, global rotation of the histone core or global screw rotation of DNA around its superhelical axis can be excluded due to the large activation energies involved in simultaneously breaking all DNA–histone contacts (12). In the case of the SWI/SNF and RSC family of remodelers, there is strong evidence in favor of DNA loop formation during remodeling (13,14). Recent experiments have notably shown that RSC can release stable intermediates, termed ‘remosomes’, that are nucleosomes containing 30–40 bp of additional DNA, drawn into the nucleosome symmetrically from both ends (15). Remosomes have irregular shapes compatible with the formation of loops at various positions around the histone core. DNA loops are also probably involved in spontaneous nucleosome migration, and can be induced by superhelical stress (16).

Until now, DNA loops on nucleosomes have been studied with uniform elastic rod models of DNA that cannot treat breakdowns in elastic behavior and also require some assumptions about how DNA–histone interaction energy is distributed around the nucleosome core (17–19). These models try to limit the elastic deformation of DNA by avoiding small radii of curvature while, at the same time, minimizing the loss of stabilizing DNA–histone interactions. While long loops, typically beyond the persistence length of DNA (≈ 500 Å, 150 bp), can preferentially form plectonemic (interwound) structures, short loops involving a few turns of DNA cannot. These loops, which are our current target, are termed planar loops. In passing, we note that Wiggins et al. have included the notion of local breakdowns in uniform elastic behavior (i.e. kink formation) (20), but, to our knowledge, these models have not yet been applied to studying nucleosome loops.

Here, we use atomistic molecular dynamics (MD) simulations to investigate the detailed structure and dynamics of loops containing either two- (21 bp) or four- (42 bp) helical turns of inserted DNA, increasing the nucleosome-wrapped DNA from 147 bp to either 168 or 189 bp. The lengths of the DNA inserts were chosen to minimize any torsional stress within the looped DNA (given an average helical pitch in solution of 10.5 bp).

MATERIALS AND METHODS

Simulation protocol

MD simulations were performed using the GROMACS 5 package (21–24) with the Amber 99SB-ILDN force field for proteins (25–27) and the recent PARMBSC1 modifications (28) that have been specifically developed for DNA and shown to accurately reproduce its conformational and dynamic behavior. The modified nucleosomes, IN21 and IN42, were placed in a truncated octahedral box, solvated with SPC/E water molecules (29) to a depth of at least 10 Å and neutralized with potassium cations. K⁺Cl⁻ ion pairs (30) were then added to reach a physiological salt concentration of 0.15 M. After energy minimization of the solvent, and careful thermalization of the system, following a standard protocol described elsewhere (31), we began simulations under controlled temperature (298 K) and pressure (1 bar) conditions using the Bussi thermostat (32) and the Berendsen barostat (33), both with a 5 ps coupling constant. Long-range electrostatic interactions were treated using the particle mesh Ewald method (34) with a real-space cutoff of 10 Å. Bond lengths involving hydrogen atoms were restrained using P-LINCS (35,36), allowing a time step of 2 fs. Translational movement of the solute was removed every 5000 steps to avoid any kinetic energy build up (37). Simulations were carried out typically using between 240 and 480 computer cores depending on the system size, which allowed a production rate of ∼50 ns/day for both systems. The solvated system with the 21 bp insert (IN21) contained 256 K atoms, while the system with the 42 bp insert (IN42) contained a total of 470 K atoms.

Conformational analysis

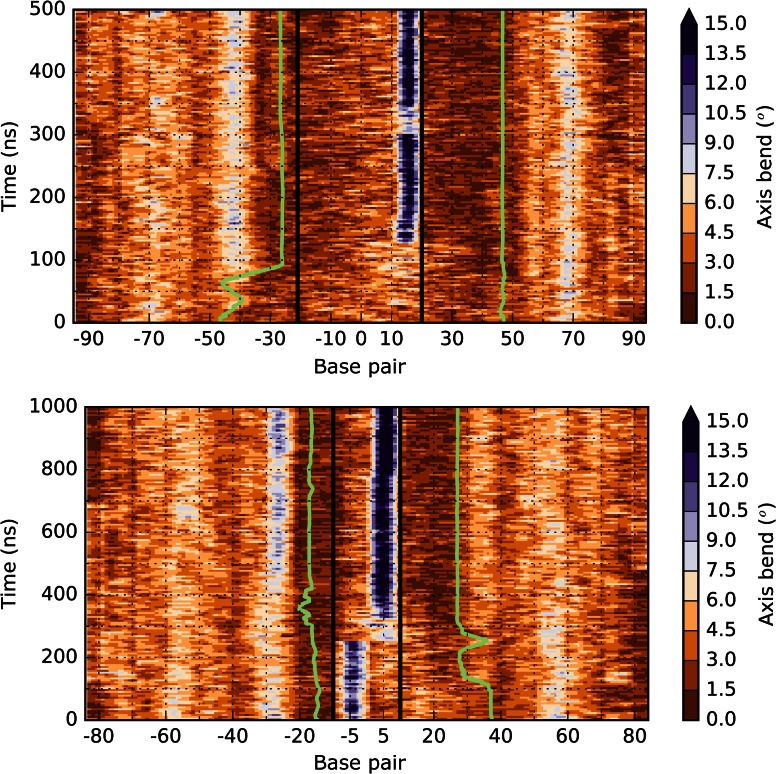
Conformations were extracted from the MD simulation every ps and DNA conformations were analyzed using Curves+ (1). As well as defining helical, backbone and groove variables, this analysis also determines an optimal curvilinear helical axis. DNA bending was subsequently described with the variable ‘axis bend’ that quantifies the angle between the helical axis segments associated with successive base pairs. The time evolution of axis bend during the simulations (see Figure 3) provides a concise picture of the changing conformation of the DNA loops, and notably makes it easy to identify the appearance and the location of the local conformational disruptions termed kinks. Although the exact nature of DNA kinks is still actively studied (38), molecular dynamics simulations currently suggest that they can adopt different structures including unstacking at a single step (termed Type I and originally proposed by molecular model building in 1975 (39)) or unstacking at two consecutive steps with a central broken base pair (Type II) (40,41). However, we should stress that the kinks discussed here are major local disruptions of the double helix, well beyond the smaller ‘kinking’ seen within DNA bound to unperturbed nucleosomes (3,42,43). We locate kinks, as in our earlier work, by using the inter-BP variables roll and propeller. These variables are presented in Supplementary Figures S2 and S3 of the supplementary material accompanying this article. Average axis bend values also enable us to quantify the overall bending within the DNA loops. Such averages exclude any broken base pairs within the kinks and one flanking base pair on either side (see panels D and E of Figure 2).

Figure 3.

Time evolution of the DNA axis bend. Axis bend values at each base-pair step along the MD trajectories of IN42 (top) and IN21 (bottom). Black lines delimit the DNA inserts and green lines indicate loop DNA that is detached from the protein core. White and blue regions indicate increasing DNA bending.

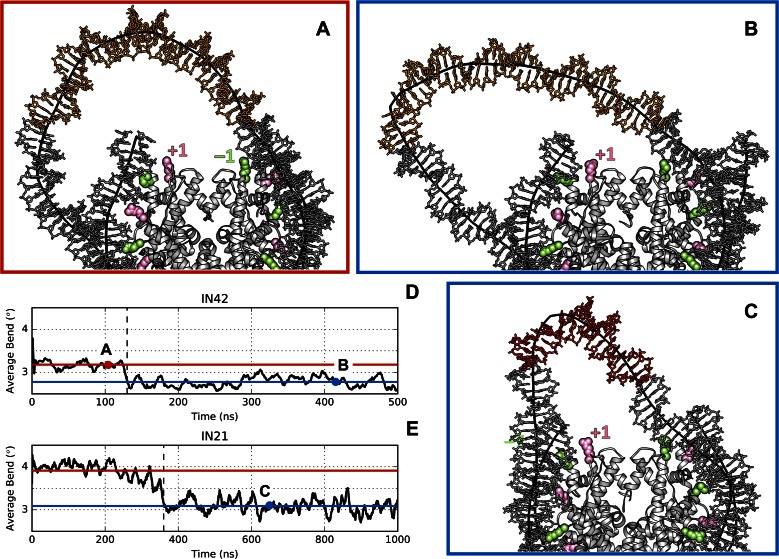
Figure 2.

Kink formation and average DNA bending. Snapshots along the MD trajectories of IN42 (A and B) and IN21 (C). Plots (D) and (E) show 10 ns sliding-window averages of the DNA axis bend for IN42 and IN21 respectively (calculated excluding 1 bp on either side of DNA kinks). The red and blue horizontal lines show the average axis bend before and after kink formation (indicated by the vertical dashed lines). The position of the snapshots (A), (B) and (C) are indicated by the letters on the time axis. See the Supplementary Information for further details of the analyses.

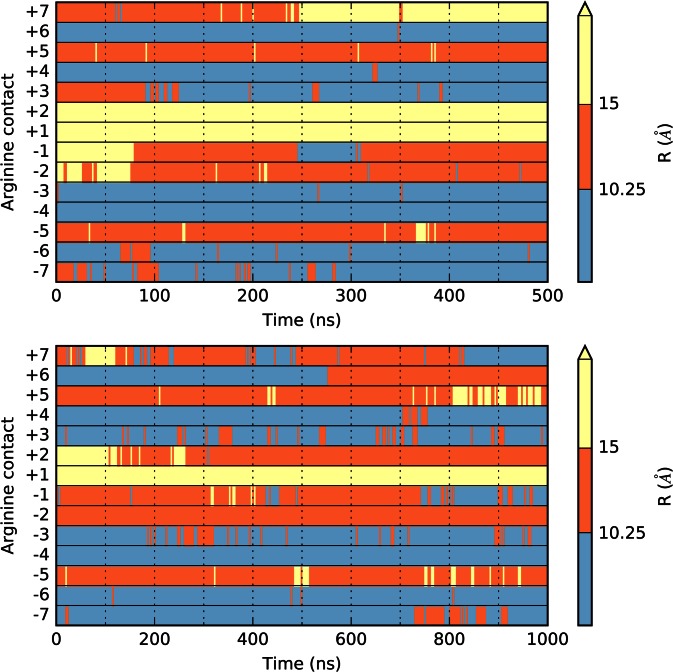
In order to define which segment of DNA belongs to the loop at any given moment, we rely on the interactions between DNA and the 14 arginine side chains that are distributed regularly around the histone core and that usually bind in the minor groove once every turn of the double helix (see Supplementary Figure S1). In order to locate each arginine side chain with respect to DNA, we use the curvilinear helicoidal coordinate analysis recently developed for locating ions around DNA (44,45). This enables us to calculate the distance R between the central carbon of each arginine head group and the helical axis of DNA. We have analyzed the distance R in MD simulations of an unperturbed nucleosome (28) (data kindly provided by P.D. Dans and F. Battistini, IRB Barcelona). The results presented in Supplementary Figure S5 show that, in this case, the arginine head groups lie either within the DNA minor groove at R ≤ 10.25 Å or at the level of the backbone phosphate groups at 10.25 < R ≤ 15 Å (which also corresponds to the distance for an optimal salt bridge between phosphate and arginine). We have consequently chosen R > 15 Å as a cutoff to indicate unbound arginine side chains and indeed unbound arginines in our loop simulations typically occur around R = 25 Å. In analyzing the extent of the loop region during simulations (Figure 4), short-lived binding/unbinding events were filtered out by using 25 ns sliding-window averaging.

Figure 4.

Time evolution of minor groove arginine contacts. Distance R of the 14 arginine head groups from the DNA helical axis along the MD trajectories of IN42 (top) and IN21 (bottom). Each row refers to one of the 14 arginines contact points, numbered −7 → +7. Distances are color-coded according to whether the arginine is within the groove (R ≤ 10.25 Å), bound to phosphates (10.25 Å < R ≤ 15 Å) or unbound (R > 15 Å).

Elastic rod calculations

We use the worm-like chain (WLC) loop model proposed by Schiessel et al. (17). This model describes the total loop length L as the sum of the length of the inserted DNA ΔL and the length of DNA detached from the nucleosome core L*,

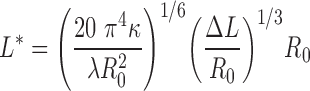where κ = l_Pk_BT, l_P is the persistence length of DNA (taken as 500 Å), k_B is Boltzmann's constant and T the temperature is taken as 300 K. R₀ is the radius of DNA on the nucleosome (41.1 Å) and the λ is the adsorption energy of DNA on the nucleosome core per unit length (taken as the upper limit of the experimental estimates, 0.1 kcal mol⁻¹ Å⁻¹) (17,46–48). Using these criteria, and taking the average rise/bp of DNA to be 3.4 Å, for ΔL = 21 bp, L* = 62 bp and L = 83 bp, while for ΔL = 42 bp, L* = 78 bp and L = 120 bp.

Graphics

All molecular graphics were obtained using Chimera v1.11 (49,50). Raw data was analyzed using numpy v1.10 (51) and pandas v0.15, and visualized using matplotlib v1.5 (52) within IPython v4.0 (53).

RESULTS AND DISCUSSION

Loop construction

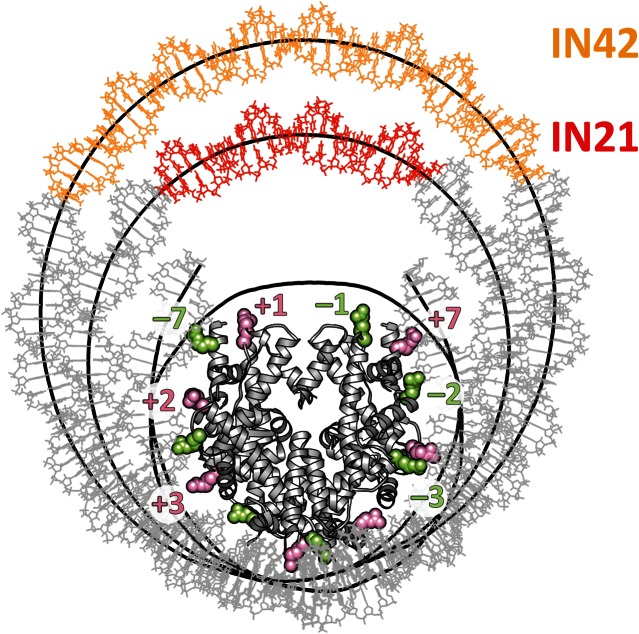
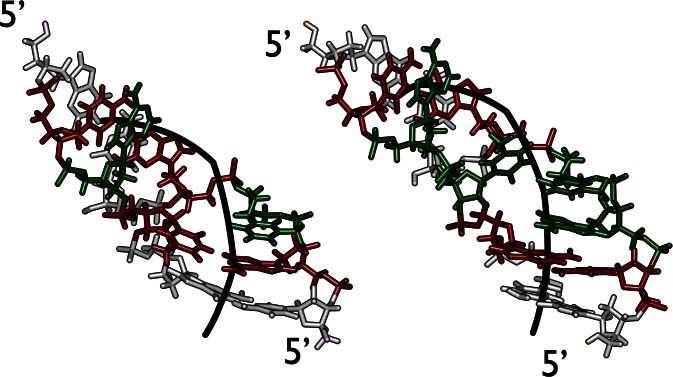
The DNA to be inserted into the nucleosome was built with a repeating tetranucleotide sequence ATGC. This sequence was chosen to have a balanced AT/GC content and to be free of backbone conformational oscillations observed with some other sequences (31). To construct the initial loops with either 21 or 42 bp inserts (termed hereafter IN21 and IN42), we began with a high-resolution structure of the nucleosome from the Protein Data Bank 1KX5 (2,3). The unstructured histone tails were removed since they cannot be correctly conformationally sampled on the timescale of our simulations. We chose to insert the loops at the pseudodyad position of the nucleosome. In line with earlier coarse-grain loop models, we assumed that sharp DNA bending should be avoided. This was achieved by removing an entire superhelical turn of DNA, centered on the pseudodyad position, building a new superhelical turn incorporating the extra base pairs and then linking this turn back into the nucleosome structure with energy minimization, using the internal coordinate program JUMNA (54). Energy minimization used the same force field as the subsequent MD simulations, coupled with a simple continuum solvent and salt model. The resulting structures contain large epicyclic loops, namely loops that are tangential to the nucleosome core (Figure 1). This initial conformation favors low curvature (large radius of curvature), at the cost of lost DNA–histone contacts.

Figure 1.

Epicyclic DNA loop constructions on the nucleosome core. Superposed structures of the IN42 and IN21 loops (with inserted DNA in orange and red, respectively). The helical axes of the loops and of the native nucleosome are shown as thick black lines. Histones are shown in grey and the arginines contacting the DNA minor groove are shown as green spheres (−1 → −7) and pink spheres (+1 → +7). Following the numbering of PDB entry 1KX5, arginines, from +1 to +7 are H4.R45, H3.R63, H3.R83, H2A.R42, H2A.R29, H2A.R77, H3.R49. See also Supplementary Figure S1.

Molecular dynamics simulations

Simulations were performed using the GROMACS 5 package (21–24) with the recent PARMBSC1 force field (28). Trajectories of the IN21 and IN42 nucleosomes were obtained in an aqueous environment, with a physiological salt concentration (yielding a total of 256 K atoms for IN21 and of 470 K atoms for IN42), for durations of 1.0 and 0.5 μs, respectively. See the Materials and Methods section for further details of the simulation and conformational analysis protocols.

We begin by considering the larger IN42 structure (Figure 1). Creating the initial epicyclic loop involved cutting the nucleosomal DNA at positions −37 and +37 (opposite the pseudodyad) and replacing the existing 73 bp superhelical turn with a 115 bp fragment containing the centrally positioned 42 bp insert. This leads to a change in superhelical radius from 41.4 to 72.6 Å. The creation of this loop results in breaking six minor groove arginine contact points, −3 → +3. As soon as the MD simulation begins, the loop begins to distort, losing its regular superhelical shape and moving towards the closest contact points. After a few nanoseconds (ns) of simulation, histone contacts −3 and +3 are reestablished (Figure 2a), thanks to an increase in DNA bending at symmetric positions −69 and 69, respectively towards the minor and major grooves (see Figure 3 top and Supplementary Figure S2). This effectively reduces the loop size to 95 bp. By 30 ns, contact −2 is transiently reformed and around 80 ns, contacts at −2 and −1 are both stably reestablished (Figure 4 top). Beyond this point, the distortion of the 74 bp remaining in the loop results in the formation of a kink toward the minor groove within the 42 bp insert (Figure 3 top). This kink belongs to the family termed Type II (Figure 5, left), implying a strong roll at two adjacent base pair steps (i.e. bending of the double helix towards the minor groove, see Supplementary Figure S2) and disruption of the central base pair (40,55,56). The appearance of a localized kink allows the rest of the DNA loop to relax, as evidenced by a decrease in the average axis bend (Figure 2d). Note that a 1° decrease in average axis bend with respect to its average value for the nucleosome (4.7°) corresponds to an increase in radius of 11 Å. After 0.5 μs of simulation, the IN42 loop has adopted a ‘V-like’ shape with the kink at its apex, flanked by weakly curved DNA arms (Figure 2b). Note that because kinks involve sharp bending in a fixed direction (toward the local minor groove), the kink location will reflect the need to avoid further straining the loop by induced writhe (40).

Figure 5.

Kinked structures. Structures of Type II (left) and Type III (right) kinks extracted from the simulation of the IN21 structure. DNA is shown as grey sticks; base pairs are colored green if they are broken and red if they are intact but feature large negative values of roll with one of their neighbors. The Curves+ helical axis is shown as a thick black line.

We now consider the smaller IN21 insert. The nucleosomal DNA is again cut out between positions −37 and +37 and the intervening 73 bp are replaced with a 94 bp superhelical fragment containing the centrally placed 21 bp insert, leading to a superhelical radius of 59.7 Å. However, this loop remains close enough to the histone core to only truly break minor groove histone contacts −2 → +2, reducing the effective loop size to 73 bp. During energy minimization the loop again becomes asymmetric, leaning towards the histone core on the side of the negative contact points and early in the MD trajectory contacts −2 and −1 are reformed, reducing the effective loop to 53 bp (Figure 4 bottom). This distortion is accompanied by the formation of a Type II kink within the 21 bp insert (Figure 3 bottom, Figure 2c). After 170 ns, the +2 contact is recovered, while the 45 bp remaining in the loop continue to distort and the kink moves one turn towards the positive contact points around 300 ns (Figure 3 bottom). After 800 ns, the kink moves again slightly and leads to two successive broken base pairs. The two purines from these base pairs stack on the flanking base pairs, while the pyrimidines form an unusual, offset pairing interaction (Figure 5). We term this previously unseen kink conformation Type III. As in the case of IN42, kink formation reduces the bending strain in the rest of the loop (Figure 2e).

A last interesting point concerns the ends of the nucleosomal DNA that, both experimentally (57) and during simulations (58–60), have been shown to sporadically detach from the histone core. During the IN42 simulation, this only occurs for the end held by the +7 histone contact and only after 250 ns when the IN42 loop has reformed the −1 and −2 contacts in the neighboring spire (Figure 4 top and Supplementary Figure S5). Similarly, we see a brief detachment of the +7 contact at the beginning of the IN21 simulation when this loop has also formed the −1 and −2 contacts (see Figure 4 bottom and Supplementary Figure S5). These observations suggest that inter-spire electrostatic repulsion is an important factor in destabilizing the DNA termini of nucleosomes.

CONCLUSIONS

Atomistic, microsecond-scale MD trajectories, using the latest BSC1 DNA force field, have been used to study two differently sized DNA loops formed on the nucleosome core. Despite building both loops with smooth ‘epicyclic’ conformations, our study shows that nucleosomal DNA loops attempt to establish maximal contacts with the histone core. This leads to small effective loop sizes with high bending strain that can only be relaxed by localized kink formation. We have modeled loops involving the insertion of either two or four helical turns of DNA into a native nucleosome. Restablishing DNA–histone contacts reduces the final lengths of loop DNA to only two to three turns more than the length of the insert, namely 45 and 74 bp respectively, with the loss of only one or two DNA–arginine interactions in the minor groove compared to native nucleosomes. This finding is compatible with the observed stability of isolated ‘remosomes’ (nucleosomes containing three to four turns of additional DNA) created and then released by the RSC remodeler. It could also explain the accessibility of the DNA in remosomes to attack by restriction enzymes (DNase I and ExoIII) (15), if we assume that loops can occur at any position around the histone core. Although the limited timescale of our simulations may preclude any observation of spontaneous movement of loops around the core once they are formed, kink formation coupled with extensive DNA–core interactions suggests these movements may not occur easily.

The small loops that result from atomistic simulations can be compared with a simple worm-like chain (WLC) model of DNA loops (17), although, as it has been pointed out (61), WLC models are likely to overestimate elastic bending energy for small loops. Such a model indeed predicts much larger loop sizes, with 83 bp for IN21 and of 120 bp for IN42 (see Materials and Methods section). These loops are somewhat larger than our initial epicyclic loop constructions and would imply that either six or eight DNA–core contacts would be broken.

In contrast to smoothly curved elastic rod models, the kinked DNA loops adopt very irregular shapes and are asymmetrically positioned with respect to the histone core. An analysis of the kinks shows that the longer 74 bp loop of the IN42 insert contains a kink (Type II) that involves perturbing the stacking at two consecutive base pair steps and breaking the intervening base pair. This type of kink has already been seen in earlier simulation studies of small minicercles (40,62). In contrast, the final state of the smaller and, consequently, more strained 45 bp loop of the IN21 insert brings to light a new kink (now termed Type III) involving two broken base pairs and the formation of an unusual offset pyrimidine-pyrimidine base pairing interaction. While a number of experimental studies support the formation of kinks in strongly bent DNA (38,63,64), their exact structure remains unclear. This uncertainty may in part be due to the existence of a number of distinct kink families such as those found here. It should also be remarked that kinks can affect not only local bending, but also, as a function of their type, put different constraints on bending direction (40), a fact that is worth considering when developing more sophisticated rod models of DNA.

Finally, these simulations suggest that electrostatic repulsion between the adjacent spires of DNA wrapped around the nucleosome core is a significant factor in facilitating the detachment of the DNA termini, since no detachment occurs when the position of a DNA loop increases the distance separating the spires.

FUNDING

Agence Nationale de la Recherche (ANR) Project CHROME [ANR-12-BSV5-0017-01]. Funding for open access charge: Project CHROME [ANR-12-BSV5-0017-01]

Conflict of interest statement. None declared.