Spatial scale modulates the strength of ecological processes driving disease distributions

Significance

For four decades, ecologists have hypothesized that biotic interactions predominantly control species’ distributions at local scales, whereas abiotic factors operate more at regional scales. Here, we demonstrate that the drivers of three emerging diseases (amphibian chytridiomycosis, West Nile virus, and Lyme disease) in the United States support the predictions of this fundamental hypothesis. Humans are contributing to biodiversity loss, changes in dispersal patterns, and global climate change at an unprecedented rate. Our results highlight that common single-scale analyses can misestimate the impact that humans are having on biodiversity, disease, and the environment.

Abstract

Humans are altering the distribution of species by changing the climate and disrupting biotic interactions and dispersal. A fundamental hypothesis in spatial ecology suggests that these effects are scale dependent; biotic interactions should shape distributions at local scales, whereas climate should dominate at regional scales. If so, common single-scale analyses might misestimate the impacts of anthropogenic modifications on biodiversity and the environment. However, large-scale datasets necessary to test these hypotheses have not been available until recently. Here we conduct a cross-continental, cross-scale (almost five orders of magnitude) analysis of the influence of biotic and abiotic processes and human population density on the distribution of three emerging pathogens: the amphibian chytrid fungus implicated in worldwide amphibian declines and West Nile virus and the bacterium that causes Lyme disease (Borrelia burgdorferi), which are responsible for ongoing human health crises. In all three systems, we show that biotic factors were significant predictors of pathogen distributions in multiple regression models only at local scales (∼10²–10³ km²), whereas climate and human population density always were significant only at relatively larger, regional scales (usually >10⁴ km²). Spatial autocorrelation analyses revealed that biotic factors were more variable at smaller scales, whereas climatic factors were more variable at larger scales, as is consistent with the prediction that factors should be important at the scales at which they vary the most. Finally, no single scale could detect the importance of all three categories of processes. These results highlight that common single-scale analyses can misrepresent the true impact of anthropogenic modifications on biodiversity and the environment.

Humans presently are contributing to unprecedented rates of infectious disease emergence (1, 2), climate change (3, 4), and biodiversity loss and homogenization (5, 6). The ramifications and interdependences of these environmental changes represent some of the most important and challenging scientific problems of today. However, a fundamental but undertested hypothesis in ecology—that the influence of biotic and abiotic drivers on species distributions is scale dependent (7–10)—poses a serious challenge to addressing these daunting problems.

It has long been understood that three processes generally dictate the distribution of all organisms: environmental filtering (abiotic conditions), species interactions (biotic conditions), and dispersal limitations (11). Because climate mostly varies regionally (<10⁴ km² according to the Intergovernmental Panel on Climate Change) with relatively minor variation at smaller, local scales (12), it has been widely hypothesized that environmental filters operate mostly at larger, regional scales (>10⁴ km²) (Fig. 1) (7–10, 12). In contrast, because there can be considerable variation in species composition locally, biotic processes, such as competition, predation, mutualism, and parasitism, are thought to influence distributional patterns primarily at smaller scales (Fig. 1) (7–10). A result of these hypotheses is that the outcomes of single-scale analyses might misrepresent the true consequences of natural and human-induced changes to the environment. For example, analyses across geographic areas of different sizes can produce differently shaped elevation–richness curves (10), give contrasting richness–productivity relationships (13), alter the perceived importance of competition and predation on biodiversity (11), and change the factors found to influence community assembly (14).

Fig. 1.

How does spatial scale affect processes in ecology? Three processes are typically found to control the distribution of organisms: biotic interactions, environmental filtering, and dispersal. However, the extent to which each of these processes is relevant is expected to vary with spatial scale. The thickness of the blue bars represents the hypothesized importance of each process at different scales (horizontal axis). Biotic interactions are hypothesized to be important at local scales, and climate and dispersal are expected to be relevant at larger, regional scales. The question mark denotes that there are no established hypotheses regarding how scale affects the detection of human population density on distribution patterns. (Adapted from ref. 9.)

Although there have been many calls to test these scale-based hypotheses (1, 7–10, 15, 16), there are several reasons why they have not been tested at a broad spectrum of scales (but see ref. 17). First, it can be logistically difficult to repeat experiments at multiple scales, and it often is challenging to determine which scales are most important for a given system (7, 10, 18). Most importantly, however, only recently have the necessary computing power and large-scale, spatially explicit datasets of species occurrence and abiotic factors become available. Therefore, although we have contemporary tests of theory for how deterministic and stochastic processes associated with environmental filtering, biotic processes, and dispersal affect species distributions on relatively small spatial scales (e.g., ∼100 km²) (10, 13, 17), the lack of tests showing how these factors influence distributions when scaled up to larger (regional to global) areas can be an impediment for identifying generalities in ecology. For example, it has been suggested that controversy surrounding the hypotheses that infectious diseases are being increased by anthropogenic climate change and biodiversity loss (i.e., the dilution effect) is at least partly a product of the scale dependence of these abiotic and biotic factors on disease risk (1, 15, 16).

Here, we use species distribution models and multimodel inference approaches to examine the influences of biotic and abiotic processes and human population density (which can have impacts on dispersal) on the distributions of three emerging pathogens across seven spatial scales (quadrupling in area at each step; Fig. S1) spanning nearly five orders of magnitude. Two of these pathogens, West Nile virus (WNV) and Borrelia burgdorferi, the bacterium that causes Lyme disease, are responsible for ongoing human health crises (19, 20). The third pathogen, the chytrid fungus Batrachochytrium dendrobatidis (Bd), is considered one of the deadliest organisms on the planet because of its association with hundreds of amphibian extinctions in the last half century (21, 22). We chose to model the spatial factors affecting these pathogens because (i) spatially explicit datasets of their distributions were available (but were not available for other pathogens or other organisms in general; see Methods); (ii) they span a diversity of taxa (a virus, bacterium, and fungus) and transmission modes (WNV and Lyme are mosquito- and tick-borne, respectively, and Bd is a directly transmitted, water-borne pathogen), and infect various types of hosts (endothermic and ectothermic), increasing the generality of our findings; (iii) they are widespread generalists throughout the United States, providing a spatial extent great enough to conduct large-scale analyses; (iv) their abundances or prevalences appear to be partially controlled by a common biotic factor, the richness of potential hosts (19, 21, 23, 24), and by common abiotic factors, including climate and vegetation (20, 25, 26); and, finally, (v) understanding emerging diseases is of critical importance to biodiversity conservation and human health. Our goal was not to develop and put forth the best possible model to explain the spread of these diseases but rather to test whether spatial scale influences which types of ecological processes are important.

Fig. S1.

Rasters of varying grain sizes were used in models. Shown are sample rasters of amphibian richness across scales with the following grain (cell) sizes: (A) 0.0625 × 0.0625 degree; (B) 0.25 × 0.25 degree; (C) 1 × 1 degree; (D) 4 × 4 degrees. Green cells represent high richness, yellow indicates moderately high richness, orange indicates moderately low richness, and white indicates low richness. Amphibian richness was used as a predictor in our Bd models. Rasters were scaled up by taking the mean of the values in 2 × 2 grids of cells.

Because the abundance of all three pathogens has been shown previously to be affected by a common biotic factor, the richness of potential hosts (defined as the richness of all species that receive either successful or failed transmission attempts from a generalist pathogen or vector) (19, 21, 23, 24), we chose to use this factor in our models to represent the subset of biotic interactions that drive the processes causing dilution or amplification effects (5). We used total amphibian richness to predict the spread of Bd, avian richness for WNV, and mammalian richness for Lyme disease (we also initially tested the richness of other taxa for B. burgdorferi; see Methods). Additionally, for WNV we also tested models that included mosquito richness given that many mosquitoes can vector this virus (Supporting Information). In contrast, Lyme disease in the eastern United States is known to be vectored by only a single tick species, Ixodes scapularis, found in every county where thorough sampling has been performed (Supporting Information). Thus, we did not include vector richness, prevalence, or abundance in our Lyme disease models. Importantly, because humans generally cannot be infected with WNV or B. burgdorferi unless they are bitten by an appropriate vector, modeling the distribution of these pathogens in humans implicitly integrates the effects of ecological processes on the pathogen as well as the vector. For our biotic factors, we hypothesized that potential host species richness would have the highest relative importance at local scales, inhibiting or promoting pathogen prevalence because of dilution and amplification effects (a negative or positive association between host richness and infections per host, respectively) (19). In contrast, we predicted that abiotic factors (climatic variables, altitude, and the normalized vegetation index; Table S1) would have the highest relative importance at regional scales.

Table S1.

Loadings from a factor analysis of eight abiotic variables: mean, minimum, and maximum monthly temperature, precipitation, diurnal temperature range, annual temperature range, altitude, and NDVI and associated variation accounted for by each factor

Variable	Factor one	Factor two	Factor three	Factor four
Altitude	−0.478	−0.372	0.674	0.335
Annual temperature variation	−0.449	−0.442	0.072	−0.640
Diurnal temperature variation	0.075	−0.376	0.909	−0.149
NDVI	0.085	0.900	−0.246	0.079
Precipitation	0.158	0.773	−0.423	0.194
Mean temperature	0.984	0.114	−0.076	0.107
Maximum temperature	0.990	0.039	0.103	0.077
Minimum temperature	0.941	0.183	−0.248	0.133
SS loadings	3.302	1.931	1.603	0.623
Proportion variation	0.413	0.241	0.200	0.078
Cumulative variation	0.413	0.654	0.855	0.932

Variables were condensed into four factors. Factors one–three were used to predict the distribution of all three diseases across scales. Factor one was highly correlated with temperature, factor two represents NDVI and precipitation, and factor three correlated with temperature variability and altitude. Scores shown are from a factor analysis of climate variables across the extent of the United States used to predict the spread of Bd. However, the factor analysis performed for WNV and Lyme disease using only climate data in the eastern United States produced nearly identical factors, each representing the same abiotic variables.

Although biotic and abiotic variables have traditionally been the central focus of species-distribution models (11, 27), much attention recently has turned toward modeling the importance of human impacts on species distributions. Human activities can alter the dispersal of organisms (even for species not expanding their ranges; see Supporting Information) (25) both by facilitating long-distance movements of nonnative species (28) and emerging pathogens (25, 29) and by impeding spread by reducing habitat connectivity through habitat destruction and the construction of roads, canals, and buildings (30). Indeed, the distributions of all three pathogens have been reported to be affected by humans (20, 25, 29). Thus, we used human population density to represent the ways in which humans can affect pathogen transmission (e.g., through dispersal). We hypothesized that human impacts might be most important at regional scales because humans can homogenize biodiversity across large spatial scales.

Results and Discussion

For all three parasites, host richness was a statistically significant predictor of prevalence at local scales when controlling for the other factors in the model, and its relative importance declined as spatial scale increased (Fig. 2 and Bd in Table 1 and WNV and Lyme disease in Table S2). Hence, as hypothesized by several researchers (15, 16), the slope between host richness and prevalence became shallower as scale increased, suggesting that the controversy surrounding the relationship between host diversity and parasite abundance (i.e., the dilution effect) might partly be a product of the variation in the scales at which studies have been conducted (15, 16). In the multivariate WNV models, mosquito richness was not predictive of WNV distribution at any scale (Table S3), suggesting that the richness of hosts is more important than the richness of vectors in regulating WNV transmission.

Fig. 2.

Different processes control species distribution at different scales. Predictors for Bd (A), WNV (B), and Lyme disease (C) varied in their relative importance scores depending on the spatial scale of analysis (roughly 37–150,000 km²; horizontal axes). Blue lines represent host richness (a biotic process), green lines are abiotic factors (importance scores for abiotic factors that were statistically significant at any scale were averaged), and orange lines are human population density, a proxy for anthropogenic influences on organisms (e.g., effects on dispersal). Points with black circles indicate significance (P < 0.05) of a process at a given scale; gray points indicate significance for some but not all abiotic factors.

Table 1.

Results of multimodel inference analyses predicting the prevalence of Bd

Scale/predictor	Estimate	SE	P value
0.0625 degree
Intercept	0.599	0.025	<0.001
Richness	−0.164	0.028	<0.001
Factor one	−0.011	0.020	0.575
Factor two	−0.021	0.029	0.470
Factor three	0.019	0.025	0.450
Population	0.002	0.010	0.782
0.5 degree
Intercept	0.060	0.026	<0.001
Richness	−0.021	0.049	0.646
Factor one	−0.083	0.031	0.008
Factor two	−0.095	0.033	0.004
Factor three	0.070	0.033	0.035
Population	0.002	0.002	0.993
4 degrees
Intercept	0.587	0.021	<0.001
Richness	−0.002	0.015	0.928
Factor one	−0.005	0.015	0.720
Factor two	−0.006	0.017	0.739
Factor three	0.013	0.028	0.646
Population	−0.177	0.034	<0.001

Models used host richness, three abiotic factors, and human population density as predictors in the analysis. The scales shown are the smallest, intermediate, and largest scales used. See the legend of Table S1 for interpretation of the factors and Table S2 for results for WNV and Borrelia burgdorferi. Statistically significant (P < 0.05) predictors are in bold.

Table S2.

Results of multimodel inference analyses (with shrinkage) predicting the prevalence of WNV and Borrelia burgdorferi

Predictor	Coefficient	SE	Z value	Pr(>|z|)
WNV
0.0625 degree
Intercept	0.0060	0.0006	10.13	<0.001
Richness	0.0018	0.0009	2.04	0.042
Factor one	0.0006	0.0008	0.80	0.422
Factor two	0.0011	0.0007	1.51	0.132
Factor three	0.0001	0.0004	0.30	0.765
Population	<0.0001	0.0002	0.21	0.831
0.125 degree
Intercept	0.0060	0.0006	10.30	<0.001
Richness	0.0014	0.0010	1.32	0.189
Factor one	0.0008	0.0008	0.96	0.338
Factor two	0.0011	0.0007	1.46	0.144
Factor three	0.0004	0.0007	0.56	0.574
Population	≤0.0001	0.0002	0.22	0.829
0.25 degree
Intercept	0.0060	0.0006	10.45	<0.001
Richness	0.0010	0.0011	0.89	0.372
Factor one	0.0009	0.0009	1.00	0.315
Factor two	0.0010	0.0008	1.20	0.231
Factor three	0.0007	0.0009	0.83	0.407
Population	−0.0005	0.0006	0.75	0.456
0.5 degree
Intercept	0.0062	0.0006	10.50	<0.001
Richness	0.0001	0.0005	0.24	0.808
Factor one	0.0016	0.0008	2.03	0.043
Factor two	0.0004	0.0006	0.66	0.507
Factor three	0.0009	0.0008	1.08	0.279
Population	−0.0009	0.0008	1.08	0.280
1 degree
Intercept	0.0062	0.0006	10.56	<0.001
Richness	≤0.0001	0.0003	0.17	0.986
Factor one	0.0019	0.0007	2.64	0.008
Factor two	0.0002	0.0004	0.40	0.688
Factor three	0.0004	0.0006	0.59	0.554
Population	−0.0011	0.0009	1.29	0.196
2 degrees
Intercept	0.0066	0.0006	10.50	<0.001
Richness	0.0001	0.0004	0.26	0.794
Factor one	0.0019	0.0007	2.60	0.009
Factor two	<0.0001	0.0004	0.26	0.797
Factor three	0.0003	0.0006	0.46	0.645
Population	−0.0020	0.0009	2.16	0.031
4 degrees
Intercept	0.0067	0.0007	9.08	<0.001
Richness	0.0005	0.0009	0.57	0.567
Factor one	0.0012	0.0009	1.31	0.190
Factor two	0.0002	0.0006	0.37	0.712
Factor three	0.0010	0.0012	0.85	0.398
Population	−0.0021	0.0013	1.53	0.127
Lyme disease
0.0625 degree
Intercept	2.848	1.143	2.49	0.013
Richness	0.815	0.344	2.37	0.018
Factor one	−0.844	0.725	1.16	0.245
Factor two	0.246	0.376	0.65	0.513
Factor three	0.010	0.115	0.09	0.929
Population	−0.193	0.132	1.46	0.145
0.125 degree
Intercept	8.533	11.463	0.74	0.457
Richness	0.625	0.437	1.43	0.153
Factor one	−1.043	0.888	1.17	0.240
Factor two	0.109	0.301	0.36	0.716
Factor three	0.096	0.252	0.38	0.703
Population	−0.409	0.132	3.08	0.002
0.25 degree
Intercept	6.884	9.434	0.73	0.466
Richness	0.120	0.256	0.47	0.638
Factor one	−0.366	0.723	0.51	0.613
Factor two	0.002	0.267	0.01	0.995
Factor three	0.188	0.295	0.64	0.524
Population	−0.648	0.161	4.03	<0.001
0.5 degree
Intercept	6.572	8.913	0.74	0.461
Richness	0.016	0.147	0.11	0.916
Factor one	−0.192	0.635	0.30	0.762
Factor two	−0.035	0.248	0.14	0.889
Factor three	0.287	0.340	0.84	0.399
Population	−0.529	0.278	1.90	0.058
1 degree
Intercept	6.253	8.103	0.77	0.441
Richness	−0.141	0.261	0.54	0.590
Factor one	0.260	0.587	0.44	0.658
Factor two	−0.169	0.309	0.55	0.585
Factor three	0.009	0.177	0.05	0.959
Population	−0.144	0.260	0.56	0.578
2 degrees
Intercept	4.467	6.550	0.68	0.496
Richness	−0.013	0.177	0.08	0.940
Factor one	0.552	0.864	0.64	0.523
Factor two	−1.412	0.553	2.70	0.007
Factor three	0.006	0.149	0.04	0.969
Population	−0.770	0.526	1.46	0.143
4 degrees
Intercept	5.803	7.657	0.76	0.449
Richness	0.082	0.323	0.54	0.588
Factor one	1.478	0.901	2.43	0.015
Factor two	−0.893	0.602	2.28	0.023
Factor three	0.004	0.208	0.05	0.961
Population	0.131	0.358	0.92	0.360

Models used host richness, three abiotic factors, and human population density in the analysis. Statistically significant (P < 0.05) values are in bold.

Table S3.

Effect of mosquito richness on WNV distribution across scales

Scale in degrees2	Estimate	SE	Adjusted SE	Z value	Pr(>|z|)
0.0625	−2.92E-04	7.328E-04	7.33E-04	0.398	0.6905
0.125	−2.87E-04	7.723E-04	7.73E-04	0.372	0.710
0.25	−3.79E-05	4.128E-04	4.13E-04	0.092	0.927
0.5	1.713E-05	3.919E-04	3.92E-04	0.044	0.9652
1	2.833E-05	3.645E-04	3.65E-04	0.078	0.938
2	−1.97E-05	3.769E-04	3.77E-04	0.052	0.9584
4	−0.00025	0.0010168	0.001017	0.243	0.808

Different abiotic factors were important for different host–parasite systems (see Bd in Table 1 and WNV and Lyme disease in Table S2). Nevertheless, for all three parasites and when controlling for the other factors in the model, abiotic factors were statistically significant and of high relative importance only at scales larger than those at which biotic factors were important. Finally, human population density was significantly (negatively) related to all three parasites at scales much larger than the scales at which host richness was important (Table 1 and Table S2)—this generally was at regional spatial scales (∼10⁴–10⁵ km²) but at intermediate to regional scales (∼10³–10⁴ km²) for Lyme disease. This result was not surprising, because Bd and WNV are found throughout the United States, whereas Lyme disease is, for the most part, restricted to a comparatively narrower geographic range because of habitat requirements (26), limiting the influence of humans to smaller scales (31). When significant, different abiotic factors were generally important at the same scales as one another (Supporting Information).

Importantly, several supplemental analyses support the robustness of our results. First, single regions of the country did not tend to influence the results of our Bd models heavily (Fig. 3), although we did see some variation in space for WNV and Lyme models (Fig. S2), possibly because of extreme predictor values in specific areas (Supporting Information). Second, null model randomization tests (Supporting Information and ref. 18) confirmed that our results were not a statistical artifact of the structure of the predictor data (Fig. S3). Moreover, our findings were consistent across a bacterium, virus, and fungus, invasive (WNV and Bd) and native species, pathogens that infect endothermic and ectothermic hosts, and pathogens that are and are not transmitted by vectors. Despite the robustness of these results, they should not be taken to suggest that abiotic factors or richness cannot predict species distributions at local or regional scales, respectively; rather, they only show that at these scales these factors are generally less important than the other factors considered.

Fig. 3.

Generality of scale-dependent processes in space. The maps indicate the contribution of each of three processes as predictors of Bd distribution in models. Points represent physical locations with Bd prevalence data and are colored based on the magnitude of the change in their residual after the given process was added to a model predicting Bd distribution. Blue, white, and red points indicate the process decreased, had no effect, or increased the magnitude of the residuals, respectively. Maps with many colored points indicate that a given process was highly important at a given scale; maps with mostly white points signify that it was unimportant. See Fig. S2 for equivalent maps for WNV and Lyme disease.

Fig. S2.

Generality of scale-dependent processes in space. As in Fig. 3, maps depict the contribution of processes at varying spatial scales to models predicting county-level Borrelia burgdorferi (A) and WNV (B) data. The counties are colored based on the change in their residuals after the given process was added to a model predicting parasite distribution. In blue counties the magnitude of the residuals was decreased (the change helped the model); in red counties the magnitude of the residuals increased them (the change hurt the model); in white counties the change did not affect the model. The color strength indicates the magnitude of the change in residual. Maps with many colored counties represent scales at which a given process was highly important; maps with mostly white counties signify that a process was not relevant at a given scale.

Fig. S3.

Null-model randomizations. Results of the randomization procedures conducted on Bd prevalence data. Predictors were randomized 500 times. The average MuMIn relative importance score after 500 iterations is shown on the y axis, and scale is on the x axis. Blue represents richness, green is the average of the abiotic factors, and human population density (a potential proxy of dispersal) is shown in orange. None of the points is statistically significant, but importances are nonzero because their values are relative to the other predictors. Because no predictor was ever significant during the randomizations, we did not run randomization models with response data from the other two diseases.

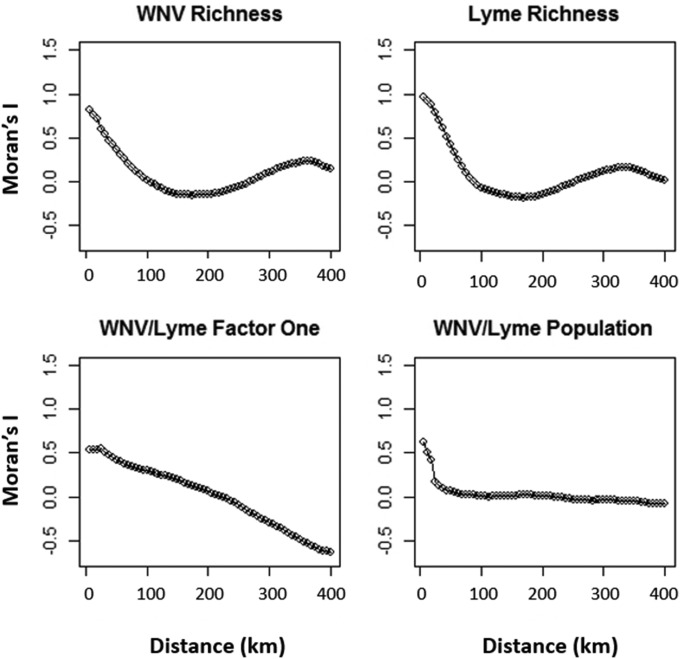
We conducted several additional analyses to provide insights into the statistical and ecological mechanisms for our findings. Univariate models revealed that biotic factors were significant only at local scales, climate was generally scale independent, and human population density was significant only at regional scales, providing a statistical explanation for the pattern observed in relative importance scores (Supporting Information and Fig. S4). Correlograms of spatial autocorrelation revealed that biotic factors varied most at local scales, whereas climatic factors varied more at regional scales (Supporting Information and Fig. S5). These results support the traditionally hypothesized ecological mechanism for scale-dependent variation in the importance of biotic and abiotic variables: Factors should be most important at the scales at which they vary the most, because it will be difficult to find a statistically significant correlation when independent variables have low variance (8).

Fig. S4.

Results of univariate GLS models. The absolute value of the coefficient (±SE) is given at each scale for all three diseases. Blue points and lines represent the coefficients for host richness, orange points and lines represent human population density, and green points and lines represent abiotic factor one (mainly consisting of mean, minimum, and maximum temperature), the factor significant in most of the multivariate models. These patterns are mostly consistent with those observed in the multivariate analyses; the coefficient for host richness is always largest at the smallest scale, and human population always peaks at the largest scale, suggesting that these predictors were important at these scales because they were truly the best predictors. Conversely, the abiotic factor coefficient mostly remains constant (except for Lyme disease), so the observed importance of abiotic factors at moderate to large scales in multivariate models may have been influenced by the significance of the other variables.

Fig. S5.

Spatial correlograms. Correlograms of spatial autocorrelation (Moran’s I) as a function of distance (degrees) for host richness, abiotic factor one (mainly representing temperature), and human population data used in the GLS models. Autocorrelations for Bd predictors should be interpreted with caution because geographic points were not evenly distributed in space. Human population was moderately autocorrelated at first but quickly became uncorrelated at short distances. Although host richness was initially highly autocorrelated, within about a degree it became uncorrelated (except for Bd). Factor one, which was the most commonly significant factor in our models, remained autocorrelated for long distances. These correlograms suggest that richness is highly variable (low autocorrelation) at smaller scales, whereas abiotic factors remain nonvariable (autocorrelated), possibly providing an ecological explanation for our model results.

Intermediate scales are commonly used in an attempt to minimize scale effects by accounting for both ends of the scale spectrum (8, 18), with the assumption that significant processes at either small or large scales will also be detectable along the spectrum. However, in our analyses, host species richness was never significant at the same scale as abiotic factors or human population density. Therefore, our results add to existing evidence (discussed in ref. 18) that rarely is there a single scale at which all three processes are important. Rather, our results support domains or sections of the scale spectrum at which processes operate stably (independent of scale), separated by abrupt transitional regions in which variables rapidly gain or lose importance. For instance, for all three parasites, host richness was relatively important below 150 km², declined abruptly in importance thereafter, and remained unimportant at all higher spatial scales (Fig. 2). Identifying domains could improve predictions and management at untested scales and simplify the selection of scales for future analyses (8).

One of the most important challenges in ecology is to determine what dictates the abundance and distribution of species. Here we show that biotic factors vary most and seem to drive distributional patterns at more local scales, whereas abiotic factors vary most and seem to drive patterns at regional scales, providing support for a long-held but undertested hypothesis in spatial ecology. Importantly, multiple regression models at a single scale almost always would have shown only one ecological process to be important, erroneously implying that the others were of low relevance. As humans continue to modify species composition, dispersal, and climate across scales, it is critical that we understand the full spectrum of consequences of these changes. Without thorough multiscale analyses, scientists are likely to misestimate the impacts of anthropogenic modifications on biodiversity and the environment.

Methods

Predictor Data.

We used the total species richness of amphibians, birds, and mammals to predict the distribution of Bd, WNV, and B. burgdorferi, respectively. Richness of potential hosts was used instead of richness of known hosts because noncompetent hosts can dilute pathogen prevalence in the area by wasting bites from a vector or infection attempts from a parasite, resulting in failed transmission events. Geographic ranges for all species within each taxon were downloaded from the International Union for the Conservation of Nature Red List website (www.iucnredlist.org) as polygons and were used to create richness rasters (Supporting Information). We considered using the richness of birds and reptiles to predict the distribution of Lyme disease as well, but these factors were not significant in preliminary models. We used a human population density grid from the Center for International Earth Science Information Network’s Global Rural-Urban Mapping Project (GRUMPv1). We log-transformed population data because they were right-skewed. Rasters containing data for the following abiotic variables were downloaded from WorldClim (www.worldclim.org): 50-y means of precipitation; mean, minimum, and maximum monthly temperatures; diurnal temperature range; annual temperature range; and altitude. We also collected the average monthly Normalized Difference Vegetation Index (NDVI) data from the National Oceanic and Atmospheric Administration (www.ospo.noaa.gov/Products/land/gvi/NDVI.html). We reduced our eight abiotic variables to three (>90% of the total variation) using a factor analysis (factanal function in statistics package, R 3.0.1, fitting four factors; Table S1). Factor one was heavily influenced by mean, minimum, and maximum temperatures. Factor two was primarily based on precipitation and the NDVI. Factor three consisted mainly of temperature variability (diurnal temperature range) and altitude data. Given that Bd is a freshwater pathogen and mosquitos require freshwater to breed, we also tested whether water as a fraction of land cover was predictive of these two pathogens. It was not a significant positive predictor in preliminary models and thus was not included in our final models (see Supporting Information for additional details). In addition, we tested whether species richness for vectors (mosquitos) was predictive of WNV prevalence (Supporting Information). We chose not to examine the temporal dispersal of the pathogens because temporal resolution was insufficient for a robust examination of temporal dynamics.

Creation of Rasters at Multiple Scales.

All Geographic Information Systems data processing was done using the raster package in R v. 3.0.1 unless otherwise indicated. To produce rasters at each of our targeted resolutions, we first masked, or cropped, rasters to the United States or the eastern United States (mask function, raster package), depending on the pathogen, as discussed below. The smallest scale we could achieve with all available predictors was 0.0625 × 0.0625 degree (∼37 km²), so we adjusted all rasters up to this size and removed any geographic projections (aggregate and projectRaster functions, raster package). This scale served as the smallest in our analyses. From there, we up-scaled rasters (aggregate function) to take the mean (abiotic factors and human density) or sum of unique values (richness) of each 2 × 2 group of cells in the smaller scale, forming one new cell at the larger scale and quadrupling the area at each step. This process was repeated six times until we had rasters with cell sizes of 4 × 4 degrees (∼1.5 × 10⁵ km²).

Species ranges were clipped (i.e., cropped using the clip function, raster package) to the border of the United States or eastern United States using ArcMap 10.2 and were converted from spatial polygons to rasters in R (SI Methods). All predictors were again standardized via conversion to z-scores so that predictors had a mean of zero and SD of one at every scale. See Table S4 for correlations between predictors at all scales.

Table S4.

Correlations between predictors across spatial scales

	Factor one	Factor two	Factor three	Richness	Population
Bd
0.0625 degree2
Factor one	1	0.369	−0.029	0.664	0.432
Factor two	0.369	1	0.146	0.494	0.153
Factor three	−0.029	0.146	1	−0.304	−0.421
Richness	0.664	0.494	−0.304	1	0.409
Population	0.432	0.152	−0.421	0.409	1
0.125 degree2
Factor one	1	0.361	−0.039	0.663	0.451
Factor two	0.361	1	0.116	0.497	0.207
Factor three	−0.039	0.116	1	−0.318	−0.468
Richness	0.663	0.497	−0.318	1	0.460
Population	0.451	0.207	−0.468	0.460	1
0.25 degree2
Factor one	1	0.345	−0.052	0.669	0.476
Factor two	0.345	1	0.075	0.506	0.231
Factor three	−0.052	0.075	1	−0.328	−0.514
Richness	0.669	0.506	−0.328	1	0.524
Population	0.476	0.231	−0.514	0.524	1
0.5 degree2
Factor one	1	0.335	−0.066	0.674	0.511
Factor two	0.335	1	0.037	0.523	0.290
Factor three	−0.066	0.037	1	−0.324	−0.586
Richness	0.674	0.523	−0.324	1	0.599
Population	0.511	0.290	−0.586	0.599	1
1 degree2
Factor one	1	0.313	−0.093	0.660	0.510
Factor two	0.313	1	−0.062	0.493	0.362
Factor three	−0.093	−0.062	1	−0.330	−0.584
Richness	0.660	0.493	−0.330	1	0.632
Population	0.510	0.362	−0.584	0.632	1
2 degrees2
Factor one	1	0.207	−0.168	0.693	0.498
Factor two	0.207	1	−0.157	0.478	0.371
Factor three	−0.168	−0.157	1	−0.358	−0.621
Richness	0.693	0.478	−0.358	1	0.673
Population	0.498	0.371	−0.621	0.673	1
4 degrees2
Factor one	1	0.097	−0.227	0.638	0.518
Factor two	0.097	1	−0.257	0.484	0.437
Factor three	−0.227	−0.257	1	−0.422	−0.721
Richness	0.638	0.483	−0.422	1	0.743
Population	0.518	0.437	−0.721	0.743	1
WNV
0.0625 degree2
Factor one	1	0.042	−0.004	0.332	0.025
Factor two	0.042	1	−0.118	−0.404	−0.211
Factor three	−0.004	−0.118	1	0.524	0.111
Richness	0.332	−0.404	0.524	1	0.074
Population	0.025	−0.211	0.111	0.074	1
0.125 degree2
Factor one	1	0.035	−0.002	0.333	0.018
Factor two	0.035	1	−0.128	−0.433	−0.271
Factor three	−0.002	−0.128	1	0.517	0.117
Richness	0.333	−0.433	0.517	1	0.112
Population	0.018	−0.271	0.117	0.112	1
0.25 degree2
Factor one	1	0.045	−0.008	0.331	−0.028
Factor two	0.045	1	−0.137	−0.480	−0.368
Factor three	−0.008	−0.137	1	0.521	0.121
Richness	0.331	−0.480	0.521	1	0.197
Population	−0.028	−0.368	0.121	0.197	1
0.5 degree2
Factor one	1	0.097	0.001	0.300	−0.044
Factor two	0.097	1	−0.149	−0.496	−0.406
Factor three	0.001	−0.149	1	0.513	0.095
Richness	0.300	−0.496	0.513	1	0.264
Population	−0.044	−0.406	0.095	0.264	1
1 degree2
Factor one	1	0.189	0.047	0.259	−0.091
Factor two	0.189	1	−0.172	−0.477	−0.390
Factor three	0.047	−0.172	1	0.502	0.035
Richness	0.259	−0.477	0.502	1	0.309
Population	−0.091	−0.390	0.035	0.309	1
2 degrees2
Factor one	1	0.260	0.100	0.226	−0.124
Factor two	0.260	1	−0.166	−0.430	−0.349
Factor three	0.100	−0.166	1	0.544	−0.055
Richness	0.226	−0.430	0.544	1	0.317
Population	−0.124	−0.349	−0.055	0.317	1
4 degrees2
Factor one	1	0.362	0.223	0.227	−0.189
Factor two	0.362	1	−0.184	−0.161	−0.368
Factor three	0.223	−0.185	1	0.513	−0.157
Richness	0.227	−0.161	0.513	1	0.293
Population	−0.190	−0.368	−0.157	0.293	1
Lyme disease
0.0625 degree2
Factor one	1	0.047	−0.006	−0.107	0.023
Factor two	0.047	1	−0.115	0.455	−0.206
Factor three	−0.006	−0.115	1	−0.641	0.109
Richness	−0.107	0.455	−0.641	1	−0.065
Population	0.023	−0.206	0.109	−0.065	1
0.125 degree2
Factor one	1	0.040	−0.004	−0.110	0.015
Factor two	0.040	1	−0.125	0.463	−0.265
Factor three	−0.004	−0.125	1	−0.648	0.115
Richness	−0.110	0.463	−0.648	1	−0.075
Population	0.015	−0.265	0.115	−0.075	1
0.25 degree2
Factor one	1	0.045	−0.008	−0.102	−0.028
Factor two	0.045	1	−0.137	0.472	−0.368
Factor three	−0.008	−0.137	1	−0.657	0.121
Richness	−0.102	0.472	−0.657	1	−0.116
Population	−0.028	−0.368	0.121	−0.116	1
0.5 degree2
Factor one	1	0.097	0.001	−0.083	−0.044
Factor two	0.097	1	−0.149	0.492	−0.406
Factor three	0.001	−0.149	1	−0.664	0.095
Richness	−0.083	0.492	−0.664	1	−0.103
Population	−0.044	−0.406	0.095	−0.103	1
1 degree2
Factor one	1	0.189	0.047	−0.081	−0.091
Factor two	0.189	1	−0.172	0.523	−0.390
Factor three	0.047	−0.172	1	−0.628	0.035
Richness	−0.081	0.523	−0.628	1	−0.024
Population	−0.091	−0.390	0.035	−0.024	1
2 degrees2
Factor one	1	0.260	0.100	−0.104	−0.124
Factor two	0.260	1	−0.166	0.546	−0.349
Factor three	0.100	−0.166	1	−0.518	−0.055
Richness	−0.104	0.546	−0.518	1	0.178
Population	−0.124	−0.349	−0.055	0.178	1
4 degrees2
Factor one	1	0.362	0.223	−0.169	−0.189
Factor two	0.362	1	−0.184	0.435	−0.368
Factor three	0.223	−0.184	1	−0.446	−0.157
Richness	−0.169	0.435	−0.446	1	0.400
Population	−0.189	−0.368	−0.157	0.400	1

Parasite Data.

On March 21, 2014 we downloaded a compilation of spatially explicit chytrid data from Bd Maps (www.bd-maps.net) containing records obtained by swabbing animals for infection in the field. We calculated arcsine-transformed prevalence at each location where amphibians were tested. We obtained WNV and B. burgdorferi data through the county-level disease monitoring program (diseasemaps.usgs.gov) of the Centers for Disease Control and Prevention (CDC). Total human cases were averaged across years for B. burgdorferi (1992–2011) and WNV (2001–2012 beginning with the first year in which cases were reported in a particular county to account for the rapid spread) and were adjusted to prevalence per 10,000 people using 2010 US county-level census data (www.census.gov). If we did not adjust the Lyme and WNV data by population density, the distribution simply would match the human population distribution. Any significant effects of human population density for these pathogens thus indicate that the effect of humans is greater or less than a linear proportional function. To produce spatial points for our analysis, we converted the centroid of each county to a point containing that county’s data (gCentroid function, rgeos package). However, because counties in the western United States often were larger than the cells in our fine-grain rasters (∼37 km²), we limited our analysis of these two pathogens to the states east of the Mississippi River (Fig. S2). All response data were in the form of spatial points. We attempted to find spatially explicit prevalence data for other pathogens as well, but could not (Supporting Information).

Generalized Least Squares Models.

We fit generalized least squared (GLS) multiple regression models (gls function, nlme package, full maximum likelihood fit, accounting for spatial autocorrelation using corExp function) (32) using extracted values (extract function, raster package) of the five continuous predictors (pathogen-specific host richness, population density, and three abiotic factors) for each pathogen data point in space. We did not test for interactions between predictors, as explained in Supporting Information. GLS models were fit for the same response data at every scale for each pathogen by using predictors generated for that scale.

Multimodel Inference.

We did not want to rely on any single model for our conclusions. Therefore we used multimodel inference (MuMIn package), a procedure that fits models using all possible combinations of predictors and weights them by Akaike Information Criterion (AIC) (dredge function). This procedure entailed generating AIC values and Akaike weights for each candidate model (which were limited to three predictors or less). We then computed relative importance scores by summing the Akaike weights of all of the models in which each predictor appeared (33, 34). Next, we computed model-averaged parameter estimates with and without shrinkage using all possible models. We considered all possible models with three or fewer predictors because models with large ΔAIC contribute extremely little to the model-averaged parameter estimate because they have very small Akaike weights (33, 34) and because models with four or all five predictors would have overwhelmed the averaged models and swamped out relative importance scores.

Randomization Tests.

We tested whether the observed changes in the importance of biotic, abiotic, and human density variables across scales were spuriously driven by correlations among these predictors using a randomization test (500 iterations). For each iteration, we randomly reshuffled chytrid prevalence data among the observations (thus preserving the correlation structure of the predictors) and repeated our statistical analysis.

Univariate Models.

For all pathogens, we ran univariate GLS models with every predictor at each scale to test whether predictors changed in importance across scales (in multivariate models) on their own or because of changes in importance for other predictors.

Spatial Correlograms.

To test the hypothesis that biotic factors were more variable at smaller scales than climate factors, we created correlograms [Moran’s I vs. distance plots; ncf package, correlog function; 0.0625° scale (∼37 km²)] to evaluate spatial autocorrelation as a function of distance, with the expectation that at small scales biotic factors would have smaller Moran’s I values than climatic factors.

The root mean square errors (RMSE) for the model-averaged predictions for each parasite at each scale are shown in Table S5. The lists of models incorporated into each averaged model, along with their respective weights, are presented in Table S6. In addition, we have presented model averaged outputs without shrinkage in Table S7.

Table S5.

RMSE of each model output for every other scale in our analyses and RMSE standardized to the range of values in the response variables

Scale	RMSE			Standardized RMSE
	Bd	WNV	Lyme disease	Bd	WNV	Lyme disease
0.0625 degree2	0.4215	0.0746	0.0517	0.268	0.037	0.0005
0.25 degree2	0.4226	0.0744	0.0740	0.269	0.037	0.0007
1 degree2	0.4237	0.0745	0.0716	0.270	0.037	0.0007
4 degrees2	0.4260	0.0743	0.0718	0.271	0.037	0.0007

The RMSE represents the mean deviation between the observed and predicted values of the statistical model; thus smaller values indicate better overall fit of the model to the data. There were no scale-dependent patterns of RMSE across disease systems. RMSE units for Bd, arcsine-transformed prevalence and for WNV and Lyme disease are cases per 10,000 people. Standardized RMSE values are unitless proportions.

Table S6.

Complete list of models used in model averaging with their ΔAkaike scores

	Scale in degrees2
	0.0625	0.125	0.25	0.5	1	2	4
Chytrid
Intrc,Factor3,Factor2,Rich	0	0.87	3.85	5.68	12.1	9.46	13.59
Intrc,Factor1,Factor3,Rich	1.29	1.09	0.75	6.96	10.97	7.91	12.78
Intrc,Factor2,Rich	1.71	1.82	6.91	8.31	17.94	23.95	31.29
Intrc,Rich	1.86	3.55	7.51	12.31	24.6	24.56	31.23
Intrc,Factor1,Rich	1.99	1.36	3.98	8.93	17.81	23.95	31.94
Intrc,Factor1,Factor2,Rich	2.09	0	3.47	4.61	10.78	22.05	30.51
Intrc,Factor3,Rich	2.26	4.62	6.76	12.25	20.85	10.39	12.82
Intrc,Factor3,Rich,Pop	3.08	6.24	8.42	13.66	21.92	1.81	2.87
Intrc,Factor1,Rich,Pop	3.12	2.93	5.9	10.83	17.2	2.47	3.5
Intrc,Factor2,Rich,Pop	3.47	3.81	8.88	10.3	16.51	2.72	3.52
Intrc,Rich,Pop	3.52	5.52	9.5	14.32	22.33	2.29	1.96
Intrc,Factor1,Factor3,Factor2	11.71	3.64	0	0	0	4.53	11.42
Intrc,Factor1,Factor3,Pop	27.84	20.89	14.14	20.61	17.11	0	2.11
Intrc,Factor1,Factor3	28.86	20.47	13.53	19.5	15.72	12.12	16.18
Intrc,Factor1,Factor2	31.73	18.98	18.38	14.16	14.49	27.45	35.13
Intrc,Factor1,Factor2,Pop	33.66	20.74	19.32	15.13	11.51	0.12	2.78
Intrc,Factor3,Factor2,	37.55	31.11	30.26	26.65	26.42	23.65	21.73
Intrc,Factor3,Factor2,Pop	39.5	32.8	31.32	27.83	23.24	2.8	2.44
Intrc,Factor1,	42.66	31.14	28.42	31.15	31.09	39.19	48.39
Intrc,Factor1,Pop	44.61	32.65	28.71	30.44	22.72	1.47	1.49
Intrc,Factor2,Pop	57.27	44.39	42.3	34.19	25.98	3.21	1.5
Intrc,Factor2	61.88	50.31	52.73	44.32	44.19	53.5	54.56
Intrc,Factor3,Pop	79.97	69.89	60.91	60.48	43.01	4.99	1.08
Intrc,Factor3	81.48	74.28	67.27	70.35	61.37	37.55	27.21
Intrc,Pop	86.52	72.53	64.22	60.19	42.57	4.8	0
Intrc	96.24	86.48	84.67	85.13	81.88	75.05	71.38
WNV
Intrc,Factor1,Factor2,Rich	0	0	0.73	4.58	5.18	8.23	7.89
Intrc,Factor2,Rich	0.72	0.78	1.11	7.17	10.42	13.49	10.79
Intrc,Factor2,Pop,Rich	2.22	2.61	0.58	5.93	8.25	7.11	4.46
Intrc,Factor3,Factor2,Rich	2.68	2.33	2.25	7.93	11.53	14.47	6.74
Intrc,Factor1,Rich	4.12	5.21	8	8.41	5.19	7.95	7.36
Intrc,Factor1,Factor3,Factor2	4.45	1.7	0.49	1.76	3.39	6.71	3.24
Intrc,Factor1,Factor3,Rich	4.88	4.64	6.16	6.08	4.56	7.86	5.67
Intrc,Factor1,Factor3	5.06	3.34	4.16	4.79	4.1	6.87	3.74
Intrc,Rich	5.22	6.44	9.23	12.54	12.6	15.87	12.26
Intrc,Factor1,Pop,Rich	6	6.44	4.91	4.74	2.11	1.44	0.43
Intrc,Factor3,Rich	6.83	7.22	9.17	12.39	13.35	16.5	9.58
Intrc,Factor1,Factor2	6.92	5.08	4.4	3.98	3.19	6.28	6.6
Intrc,Factor1,Factor3,Pop	7.04	4.11	0	0	0	0.57	0
Intrc,Pop,Rich	7.05	7.76	6.02	8.45	8.45	7.45	3.3
Intrc,Factor1	7.45	6.54	7.57	6.42	3.47	6.04	5.81
Intrc,Factor1,Factor2,Pop	8.34	6.97	4.41	3.33	1.57	1.74	3.6
Intrc,Factor3,Pop,Rich	8.73	8.24	5.04	7.82	9.28	9.02	3.65
Intrc,Factor1,Pop	9.17	8.08	5.56	3.28	0.13	0	1.7
Intrc,Factor3	12.02	9.38	8.92	10.57	11.34	14.49	7.59
Intrc,Factor3,Factor2	12.31	8.84	6.48	8.19	10.12	12.9	4.75
Intrc	13.78	11.98	11.84	11.93	10.9	14.35	12.17
Intrc,Factor3,Pop	13.85	10.59	5.54	6.71	7.75	8.33	3.68
Intrc,Factor3,Factor2,Pop	13.95	10.47	5.21	6.88	8.59	9.02	3.44
Intrc,Factor2	14.12	11.57	9.81	10.1	10.19	13.38	11.14
Intrc,Pop	15.23	13.75	10.42	9.6	8.15	8.59	7.83
Intrc,Factor2,Pop	15.25	13.53	10.02	9.87	9.22	9.62	8.79
Lyme disease
Intrc,Factor1,Rich,Pop	0	0	1.27	4.36	1.58	7.09	5.01
Intrc,Factor2,Rich,Pop	1.68	2.95	2.88	5.47	1.25	2	6.84
Intrc,Factor2,Rich	4.39	10.21	15.47	8.47	1.25	5.72	5.06
Intrc,Factor1,Rich	4.43	10.03	15.95	7.51	0.97	7.42	5.34
Intrc,Factor1,Factor2,Rich	5.24	11.58	17.43	9.45	2.94	5.09	0.89
Intrc,Factor3,Rich,Pop	5.69	2.68	0.42	1.78	3.12	16.38	11.09
Intrc,Factor1,Factor3,Rich	6.06	11.2	17.28	9.28	2.98	9.35	7.17
Intrc,Factor3,Factor2,Rich	6.23	11.91	17.48	9.31	3.08	7.38	7.01
Intrc,Factor1,Pop	6.69	3.63	0.3	2.35	1.21	7.34	3.91
Intrc,Rich,Pop	7.76	6.77	1.68	3.51	1.23	14.54	9.08
Intrc,Factor1,Factor2,Pop	8.13	5.59	1.61	2.86	1.99	0.01	1.43
Intrc,Factor2,Pop	8.21	6	1.83	3.45	0	0	4.93
Intrc,Factor1,Factor3,Pop	8.41	5.65	1.69	1.99	2.19	7.26	5.64
Intrc,Factor3,Factor2,Pop	9.91	6.25	1.8	1.97	1.88	2.01	6.94
Intrc,Factor2	10.95	12.98	14.19	6.47	0.09	3.94	3.5
Intrc,Factor1	11.29	13.46	14.96	5.5	0.37	8.29	3.65
Intrc,Factor1,Factor2	11.74	14.62	16.19	7.45	1.96	3.32	0
Intrc,Factor1,Factor3	11.94	14.07	16.01	7.31	2.08	9.34	5.25
Intrc,Factor3,Rich	12.29	16.31	18.69	7.99	1.88	15.75	12.14
Intrc,Rich	12.54	16.88	17.02	7.63	0.19	14.36	10.41
Intrc,Factor3,Factor2	12.96	14.89	16.21	7.34	2.1	5.77	5.51
Intrc,Factor1,Factor3,Factor2	13.02	15.9	18.02	9.31	3.91	5.31	1.98
Intrc,Factor3,Pop	15.11	7.33	0	0	3.32	20.59	11.04
Intrc,Pop	15.8	10.44	0.89	1.5	1.34	18.82	9.91
Intrc	20.84	20.36	16.23	5.65	0.04	19.46	10.02
Intrc,Factor3	21.59	20.35	17.99	6.21	2.05	21.46	10.9

Intrc, intercept; Pop, population; Rich, richness.

Table S7.

Model averaged outputs without shrinkage

	Chytrid		WNV		Lyme disease
	Estimate	SE	Estimate	SE	Estimate	SE
0.0625 degrees2
(Intercept)	0.59897	0.02518	0.005954	0.000587	2.8476	1.1431
Factor three	0.03774	0.02279	0.000657	0.000807	0.114	0.3664
Factor two	−0.04428	0.02681	0.001331	0.000552	0.6954	0.2958
Richness	−0.16387	0.0277	0.002047	0.000693	0.8609	0.2913
Factor one	−0.03221	0.02191	0.001248	0.00071	−1.2954	0.4731
Population	0.01565	0.01989	0.000255	0.000415	−0.2416	0.1004
0.125 degrees2
(Intercept)	0.6029	0.02816	0.00603	0.000585	8.5334	11.4639
Factor one	−0.04791	0.02453	0.001408	0.000714	−1.5729	0.5968
Factor two	−0.05407	0.02874	0.001358	0.000567	0.5381	0.4643
Richness	−0.13988	0.02965	0.001848	0.000725	0.7923	0.3325
Factor three	0.03941	0.02697	0.001111	0.000746	0.4725	0.3667
Population	0.00887	0.02014	−0.0003	0.000471	−0.4144	0.1239
0.25 degrees2
(Intercept)	0.58405	0.027387	0.006149	0.000588	6.8836	9.4349
Factor one	−0.078	0.028254	0.001498	0.000673	−0.9976	0.893
Factor three	0.071878	0.029836	0.00143	0.000697	0.4409	0.3048
Factor two	−0.07785	0.030451	0.001499	0.000605	0.0068	0.5432
Richness	−0.11828	0.031421	0.001837	0.000768	0.3715	0.3301
Population	0.005455	0.022396	−0.0011	0.000562	−0.6482	0.16
0.5 degrees2
(Intercept)	0.600056	0.025625	0.006153	0.000586	6.5718	8.9133
Factor one	−0.08917	0.022474	0.001764	0.000618	−0.659	1.0358
Factor three	0.079372	0.022955	0.001346	0.000621	0.512	0.3009
Factor two	−0.09939	0.026935	0.001126	0.000589	−0.1445	0.4895
Richness	−0.11178	0.031444	0.000718	0.000946	0.0738	0.3142
Population	0.002044	0.02523	−0.00144	0.000626	−0.5856	0.2293
1 degree2
(Intercept)	0.59527	0.02388	0.006207	0.000587	6.25332	8.10282
Factor one	−0.09717	0.0184	0.001963	0.000632	0.72918	0.79049
Factor three	0.0906	0.02237	0.000948	0.00066	0.03594	0.35137
Factor two	−0.09491	0.02261	0.000693	0.000637	−0.4161	0.3645
Richness	−0.07604	0.02968	−3.4E-05	0.000818	−0.36364	0.30804
Population	−0.05145	0.02576	−0.00154	0.000669	−0.35687	0.30119
2 degrees2
(Intercept)	0.60158	0.02548	0.00664	0.000632	4.46738	6.55022
Factor one	−0.05069	0.02347	0.002003	0.000641	1.30635	0.88405
Factor three	0.05807	0.03519	0.000889	0.000731	0.03606	0.36851
Population	−0.13511	0.03268	−0.00219	0.000775	−0.95509	0.40791
Factor two	−0.0447	0.02547	0.000507	0.000727	−1.47287	0.44334
Richness	−0.04954	0.03013	0.00052	0.000771	−0.07892	0.42442
4 degrees2
(Intercept)	0.58735	0.021208	0.006747	0.000743	5.80359	7.65677
Population	−0.17725	0.033129	−0.00254	0.001047	0.50565	0.55191
Factor three	0.038727	0.037242	0.001974	0.000997	0.02379	0.48549
Factor one	−0.01927	0.023562	0.00161	0.000684	1.73403	0.71411
Factor two	−0.02039	0.026687	0.000997	0.00089	−1.08988	0.47805
Richness	−0.00594	0.030468	0.001458	0.000984	0.30624	0.56466

We caution that parameter estimates with shrinkage are most appropriate. In multiple regression analyses, estimates with shrinkage are preferable because they reduce model selection bias. Please see SI Results for additional details.

SI Discussion

Human-Assisted Dispersal.

Humans may have a variety of effects on the distribution of organisms, including effects on their dispersal. Dispersal is an important factor controlling species distributions even when those distributions appear stable, because species are always in dynamic disequilibrium (35). For example, continuous disturbances to the landscape, community composition, or microclimate caused by humans can result in perpetual mismatches between a species’ current and potential distribution (36). Therefore, we tested whether human population density affected the distributions of Bd, WNV, and Lyme disease despite controversy surrounding whether their ranges are expanding or are stable.

Heterogeneity of Residuals in Space.

In the Bd models, at the scales in which predictors in our models influenced the residuals, residuals were mostly altered homogenously in space (Fig. 3). However, spatial heterogeneity among residuals was observed in the WNV and Lyme models (Fig. S2). Very high or low residuals may be observed at the highest or lowest latitudes on abiotic maps because predictors may act most strongly where they are most limiting to disease ranges. Alternatively, the residuals may be high in these areas because the underlying predictor values are more extreme. For example, Florida often has high residuals on the abiotic maps because it has very high temperatures. In addition, clustering of similar residuals may be especially profound in human population density maps because of extreme human density values. Finally, our models generally did a poor job in predicting the incidence of Lyme disease in Wisconsin, which has a very high incidence of this disease.

Consideration of Vectors.

It is important to consider the conditions favoring the vector when attempting to understand the distribution of a vector-borne pathogen. We considered adding information about the vectors as predictors into our primary statistical analyses of WNV and Lyme disease but chose not to do so for several reasons. First, our analyses already consider vectors implicitly, because our response data are human disease cases. Humans cannot be infected unless they are bitten by the appropriate vector, and thus the distribution of the pathogen in humans importantly integrates the effects of abiotic, biotic, and propagule pressure factors on the pathogen, intermediate hosts, and the vectors. Therefore, the conditions that can support disease already reflect those that can support the pathogen, vector, and host, and it should not be necessary to examine the vector independently.

Nevertheless, we did consider the possibility that accounting for the vector distribution could reduce the amount of error variance and thus increase our statistical power to detect the effects of interest. We obtained geographic distribution maps for the vectors of WNV (Culex sp. and other mosquito species) (37) and Lyme disease (Ixodes scapularis) (CDC), but these maps showed that these vectors are spread throughout the entire spatial extent of our statistical analyses (the United States east of the Mississippi river). Thus, we could not use the presence/absence of the vector as a predictor in our models, because the range maps for the primary vectors showed no variation in presence/absence of these vectors among the counties in the eastern United States. However, we collected presence/absence maps of individual mosquito species (VectorMaps, ref. 32), generated vector richness rasters for the eastern United States, and included these rasters in preliminary WNV models; this predictor was not significant at any scale. Additionally, we included the abundance of bodies of water in our model for WNV because mosquitoes require water to breed; including these data did not change our results.

Importantly, many studies do not include every possible variable that affects disease, and the not including a predictor can present a third-variable problem. That is, a researcher could conclude that a relationship is causal when in fact the correlated third variable that was not included is the real causal factor. However, we are not suggesting that each of the variables we tested is the cause of a change in the focal disease. Rather, we are suggesting that biotic factors in general (whether or not they are truly causal) are more predictive on small scales and that abiotic factors (whether or not they are truly causal) are more predictive at larger scales. That we consider vectors implicitly rather than explicitly should in no way invalidate this general conclusion. For all of the reasons above, we decided against explicitly incorporating vector presence, abundance, or suitability into our models; however, to reiterate, the vector still is included indirectly or implicitly as component of our models.

Consideration of Interactions Between Predictors.

We chose not to test for interactions between vectors for several reasons, some of which are explained in the main text; the other explanations provided here. (i) Interactions cannot be classified as biotic predictors, abiotic predictors, or human population effects because they always would have predictors from at least two of these categories. Hence, because they cannot be categorized according to the focal hypothesis of our paper, they prevent us from addressing the main goal of the paper, to test whether biotic and abiotic predictors are relatively important at the same or at differing spatial scales. (ii) We lack any a priori hypotheses regarding the spatial scales at which interactions may be relevant, or even which interactions may be important. (iii) Conducting a single analysis on one parasite across all seven scales, controlling for spatial auto-correlation with multimodel inference and limiting the model to only three predictors or fewer, takes approximately 1 wk. Adding in interactions increases the number of models exponentially, would require us to consider models with more than three predictors (because a single two-way interaction alone requires three variables because the two main effects must be included), and thus quickly makes the analyses intractable. With five predictors, there would be 32 possible interactions per model, resulting in hundreds of millions of possible models for MuMIn to evaluate per parasite per scale. Even on a super computer, this computation currently would present an intractable problem. (iv) Finally, this exercise is not an attempt to generate a model that maximizes our ability to predict prevalence. That model would require considering interactions and other candidate variables. Our goal was to assess whether the importance of classes of predictors varies across spatial scales in a consistent and predictable manner across different types of host–parasite systems. We are not downplaying the importance of interaction or of improving the fit of statistical models. Indeed, interactions might be very important and also might depend on scale. However, these considerations are not crucial to our hypotheses and, just as, until recently, computing limitations at least partially prevented researchers from testing many scales hypotheses, computing limitations still make it challenging to consider interactions across scales thoroughly when spatial autocorrelation and multimodel inference approaches are used.

SI Assessing Model Predictability.

We computed the RMSE for the model-averaged predictions for each parasite at each scale (Table S5). The RMSE is a well-established criterion for evaluating predictive capability, and it has several advantages for our analysis. First, it allows us to compare the predictive performance for each parasite across each scale. Second, it retains a valid interpretation for models that incorporate spatial autocorrelation, unlike R² or pseudoR² values. Third, it can be computed from our completed analysis, rather than via resampling analyses, which we found would take months. Last, it has a simple interpretation: It represents the mean deviation between the observed and predicted values, so smaller values indicate better overall performance. Analyses based on RMSE can indicate whether our predictions changed in accuracy across scales, contributing to our understanding about working with data across spatial scales in ecology.

SI Methods

Conversion of Species Range Polygons to Richness Rasters.

We could not convert polygons directly to rasters while calculating the number of unique host species per cell because the rasterize function counts a polygon as being present in a cell only when it passes through the center of the cell rather than when it overlaps any part of the cell. In many studies, failing to calculate unique species per cell accurately may not be an issue, but it would have prevented us from obtaining equally reliable richness estimates across scales because host geographic ranges are less likely to cross the center of a cell when the cells are larger. To work around this problem, we converted the geographic range of each individual host species to a raster (rasterize function) and then converted the raster to spatial points (rasterToPoints function). Points for all species within a taxon (i.e., amphibians) then were combined into one dataset and combined with a blank raster template to create one raster (rasterize function) at each of our scales. This process was repeated for each taxon. For unknown reasons, some small, relatively isolated areas had extremely low polygon coverage (such as Long Island for bird polygons), so richness values in these areas were adjusted to the general minimum in areas with proper coverage.

Pathogen-Specific Abiotic Predictors.

In addition to the eight general abiotic variables summarized into factors, we also tested whether water as a fraction of land cover predicted Bd and WNV prevalence, hypothesizing that water cover may promote Bd and mosquito abundance. We downloaded 2011 edition land cover rasters from the National Land Cover Database (www.mrlc.gov/nlcd2011.php) and masked them to the United States or to the eastern United States for Bd and WNV, respectively. We categorized raster values as either land or freshwater and then aggregated the values into cell sizes based on our seven scales as outlined in Methods. The percent of wetland cover was used as a predictor in trial models alongside the three other abiotic factors, richness, and human population density. Because this variable was not a significant positive predictor of WNV or Bd distribution at any scale, we did not include it in any reported models.

Vector Richness.

We collected range maps for individual mosquito species from VectorMaps (vectormap.si.edu/Mosquito_Metadata.htm) as rasters. Rasters were adjusted to have a common projection (projectRaster function, raster package) and spatial extent (extent function) and were overlaid (summed) to generate counts of species across space. Rasters then were upscaled and standardized as done in generating other richness rasters. We included mosquito richness rasters in preliminary multivariate GLS and MuMIn models along with our other predictors and found that they were never significant at any scale (Table S3), so we did not include this predictor in the models reported in the main text.

Other Diseases or Pathogens.

We attempted to find spatially explicit occurrence data for other widespread diseases, including rabies and avian malaria. Although rabies data are collected and maintained by the CDC, it is not freely provided and can be obtained by only contacting each individual state. Unfortunately, only a few states agreed to provide us with these data, preventing us from obtaining a spatial extent large enough to test our hypotheses across a scale gradient. MalAvi (mbio-serv2.mbioekol.lu.se/Malavi/), the largest database of avian malaria occurrence in the world, has a few dozen records in the United States at only a handful of locations, so we could not examine the distribution of this disease either. We found no other spatially explicit disease databases of sufficient extent to test our hypotheses.

Correlations Between Predictors.

We tested for bivariate correlations among the predictors using the cor function in the stats package of R statistical software.

SI Results

Randomization Tests.

When the response data were randomized, none of the predictors was significant at any scale, and all importance scores were small and equivalent across scales (Fig. S3). Thus, our results are not driven by unknown statistical artifacts but rather appear to be a function of variation in spatially dependent ecological processes that dictate species distributions (see ref. 18 for another example of a scale-dependent–null model).

Univariate Models.

Effects of human population and richness were consistent with the results of multivariate models. For all three diseases, the magnitude of coefficient for richness peaked at the smallest scale, and the coefficient for human population peaked at the largest scale (Fig. S4). Therefore, richness and human population were important at these scales in the multimodel inferences because they became better predictors on their own. The abiotic factor coefficients were mostly consistent across scales (although they peaked at large scales for Lyme disease; Fig. S4), suggesting that their high relative importance at moderate to larger scales may have been a result of the changing significance of the other predictors.

Spatial Correlograms.

Although the univariate models provide a statistical mechanism for our results, the spatial correlograms provide an ecological mechanism for our results. Traditionally, researchers hypothesized that variables should be important at the scales at which they vary the most. That is, biotic factors should be important at small scales, and abiotic factors should be important at larger scales because each of these factors is thought to be more variable at these scales. To test this hypothesis, we focused on WNV and Lyme because we had prevalence data evenly distributed across the entire extent of the eastern United States (i.e., for every county), whereas the data for Bd were highly clumped, making it challenging to obtain reliable estimates of autocorrelation. Autocorrelation among host richness predictors for both WNV and Lyme decreased quickly, reaching zero within approximately 1 degree (Fig. S5). In contrast, factor one (representing mostly temperature), the abiotic factor consistently relevant in our relative importance results, remained autocorrelated for 2 to 4 degrees (Fig. S5). Hence, as predicted, the correlograms demonstrate that richness was more variable (low autocorrelation) than climate at small scales and that abiotic factors became variable (high autocorrelation) only large scales, consistent with the hypothesis that variables should be relatively important at the scales at which they vary the most.

Predictions for scale-dependent dispersal limitations always have been less certain than scale-dependent predictions for biotic and abiotic factors; moreover, our proxy for dispersal limitations, human population density, does not capture dispersal only, making the findings for human population density more difficult to interpret. Nevertheless, human population density became uncorrelated within 0.50 degrees of distance (Fig. S5).

Correlations Between Predictors.

Predictors were not highly correlated to one another at any scale, although for some diseases there was moderate correlation between richness and some abiotic factors (Table S4); however, this correlation is expected, given that richness decreases from tropical to temperate zones. O’Brien et al. (38) and several other authors emphasize that the rule of thumb for multicollinearity between two variables is an r² ≥ 0.9 (or r ≥ 0.949), and even then they discourage researchers from eliminating or consolidating variables. The precision of parameter estimates is extremely robust to correlations less than 0.9. Our highest correlation coefficients were nowhere near these thresholds. Finally, our approach of model-averaged parameter estimation has been shown to reduce the variance-inflating effects of collinearity among predictors, especially when all predictors do not have strong effects simultaneously or correlations are not extreme.

Assessment of Model Error.

We found that RMSE did not vary substantially across scales for any disease (Table S5), suggesting that changing the scale of our analysis did not affect overall predictive power but only affected which predictors were influential. Additionally, the raw and standardized RMSE values in Table S5 are quite small for both B. burgdorferi and WNV (<0.038 for standardized RMSE), the two parasites for which we had the greatest amount and coverage of data (data for every county across the United States). Hence, the deviations between the predicted and observed values were small for these models, indicating that the models were good fits to the data. Not surprisingly, the RMSE values for Bd are higher, presumably because of fewer data and worse spatial coverage for Bd than for B. burgdorferi and WNV. However, even the RMSE values for Bd are relatively small (<0.271 for standardized RMSE), indicating that the deviations between the predicted and observed values were not very substantial and that the model was a reasonable fit to the data. We emphasize that we obtained relatively good fits despite intentionally (i) not testing for interactions that could improve model fits (as explained above) and (ii) not considering predictor variables exhaustively.

Model Averaging.

The lists of models incorporated into each averaged model, along with their respective weights, are presented in Table S6. In addition, we have presented model averaged outputs without shrinkage in Table S7. However, we caution that parameter estimates with shrinkage are most appropriate. In multiple regression analyses, estimates with shrinkage are preferable because they reduce model selection bias (33, 34). By definition, shrinkage acknowledges that the absence of a predictor in a model implies that its coefficient is zero. By including these zeros in the model-averaging process, shrinkage reduces the upward bias that can be caused by using only a single (or few) top model(s), and it drastically reduces the chance of type I error.