The relationship between oscillatory EEG activity and the laminar-specific BOLD signal

Significance

In this study, we demonstrate that α-, β-, and γ-oscillations can be related to activity in different cortical layers in the human brain. These cortical layers are believed to instantiate feedforward and feedback information streams. Electrophysiological oscillations in α- (8–12 Hz), β- (15–30 Hz), and γ- (40–100 Hz) bands have also been associated with different roles in feedforward and feedback processes and to different cortical layers in nonhuman animals. By simultaneously recording laminar functional MRI (fMRI) and EEG, we could directly link oscillatory signals to activity in cortical layers in humans. This research provides an important neural basis for noninvasive research into the role of cortical layers in information processing using laminar fMRI alone or combined with EEG.

Abstract

Electrophysiological recordings in animals have indicated that visual cortex γ-band oscillatory activity is predominantly observed in superficial cortical layers, whereas α- and β-band activity is stronger in deep layers. These rhythms, as well as the different cortical layers, have also been closely related to feedforward and feedback streams of information. Recently, it has become possible to measure laminar activity in humans with high-resolution functional MRI (fMRI). In this study, we investigated whether these different frequency bands show a differential relation with the laminar-resolved blood-oxygen level-dependent (BOLD) signal by combining data from simultaneously recorded EEG and fMRI from the early visual cortex. Our visual attention paradigm allowed us to investigate how variations in strength over trials and variations in the attention effect over subjects relate to each other in both modalities. We demonstrate that γ-band EEG power correlates positively with the superficial layers’ BOLD signal and that β-power is negatively correlated to deep layer BOLD and α-power to both deep and superficial layer BOLD. These results provide a neurophysiological basis for human laminar fMRI and link human EEG and high-resolution fMRI to systems-level neuroscience in animals.

The different cortical layers have distinct anatomical connections with subcortical, upstream, and downstream cortical regions (1). Intracranial electrophysiological recordings in animals have linked neuronal oscillations in different frequency bands to the cortical feedforward and feedback information flow and to cortico-subcortical interactions (2–5). In line with these findings, electrophysiological recordings in animals have also demonstrated that changes in α-, β-, and γ-bands can be localized to specific cortical layers (6–12).

These findings are almost exclusively based on nonhuman animal research. Although a recent study explored the feasibility of measuring laminar-specific activity with magnetoencephalography (MEG) (13), most recent advances in measuring laminar activity in humans have been made using high-resolution functional MRI (fMRI) (14–18). In this study, we make use of these recent developments to investigate the relationship between electrophysiology and the laminar-specific blood oxygen level-dependent (BOLD) signal. By simultaneously measuring EEG and high-resolution fMRI in humans performing a visual attention task, we demonstrate that changes in specific frequency bands in the EEG can be related to changes in the BOLD signal measured at different cortical depths.

The BOLD signal is thought to be closely related to variations in local field potentials (19–21). A wide variety of features in the local field potential (LFP) or EEG, related to several cognitive processes, have now been found to correlate with the BOLD signal (19, 20, 22–26). Most relevant for this study, α- and β-power changes in EEG correlate negatively with the BOLD signal whereas γ-band changes have a positive relation (20, 22–24, 27). Moreover, we and others have demonstrated that neuronal dynamics underlying changes in power in the γ-range contribute independently to the BOLD signal from those in the α- and β-bands (22, 27).

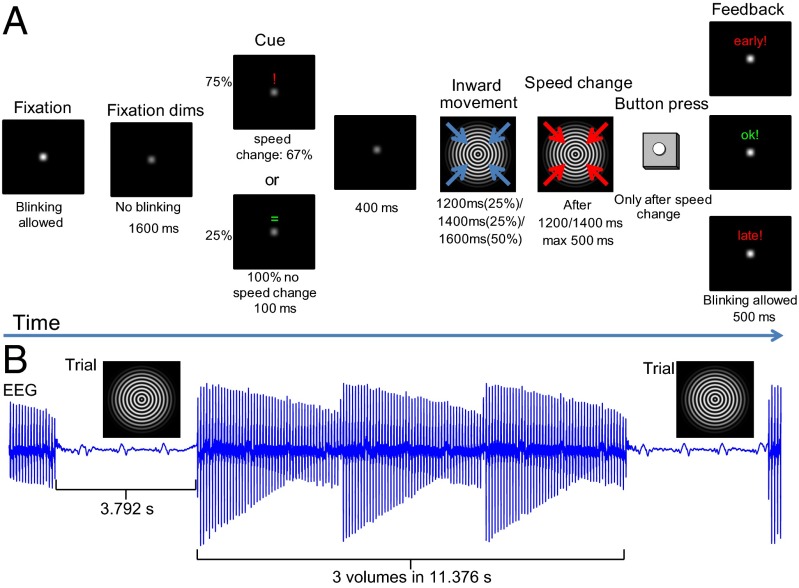
The visual attention paradigm we use in this study was adapted from an earlier study in which we observed that the neural processes related to γ-band and α-/β-band EEG power independently contribute to the BOLD signal (27). In this paradigm (Fig. 1A), subjects are presented with a cue that indicates whether a speed increase in a subsequent inward contracting circular sinusoid grating, lasting maximally 1,600 ms, is likely to occur (“attention-on,” 75% of trials), or will not occur (“attention-off,” 25%). In two thirds of the attention-on trials, a speed increase requiring a button press occurred after either 1,200 ms or 1,400 ms. This contracting grating reliably induced decreases in α- and β-band power and an increase in γ-band power at single subject level in both EEG and MEG (27, 28). From MEG source analysis and intracranial recordings in monkeys using this paradigm or similar paradigms, we know that these changes in α-, β-, and γ-band activity originate from early visual cortices (28–30) and overlap with fMRI activation (28). This paradigm therefore links findings across species and measurement modalities (31). These earlier findings make this task well-suited to investigate how variations in EEG power in the different frequency bands relate to the BOLD signal measured at varying cortical depths.

Fig. 1.

(A) The paradigm. Each trial starts with the dimming of a fixation point instructing the subject to stop blinking. After 1,600 ms, a cue (100 ms) is presented informing subjects whether or not a speed change is likely to occur. When cued (75% of the trials), a speed change followed in 66.7% of the trials. A speed change never occurred when not indicated (25%). After a cue, there is a 400-ms pause, after which the fixation point is replaced by a contracting grating. When cued, a speed increase could occur after 1,200 ms (33.3% of these trials) or 1,400 ms (33.3%) from the start of the contracting grating. Subjects were instructed to push a button as soon as they detected it. The grating stopped contracting as soon as the button was pressed, or otherwise after 500 ms. Visual stimulation lasted for 1,600 ms in trials without a speed change in either condition. Feedback was given for 500 ms. (B) The timing of the trials relative to fMRI data acquisition. The trial was presented after every third echo-planar imaging (EPI) volume (acquisition time, 3.792 s per volume) in a scan-free period that also lasted for 3.792 s.

During the task, EEG and high-resolution fMRI (0.75 mm isotropic) were measured in an interleaved fashion (EEG was measured in between the acquisition of fMRI volumes), making use of the fact that the BOLD response lags neural activity by several seconds (Fig. 1B). This approach avoids large artifacts related to MR gradients in the EEG during the trial that will strongly affect the γ-band. The setup allowed us to correlate trial-by-trial fluctuations in power for frequencies up to 120 Hz with trial-by-trial fluctuations in the laminar-specific BOLD signal in the early visual cortex (V1, V2, and V3). The attention manipulation consisted of attention-on versus attention-off conditions. This simple manipulation modulated not only attention but also other factors, like the expectation or predictability of the speed change. It was chosen to maximally modulate the α-, β-, and γ-band responses and consequently increase the likelihood of observing laminar-specific correlations over subjects.

Results

Basic Task Effects.

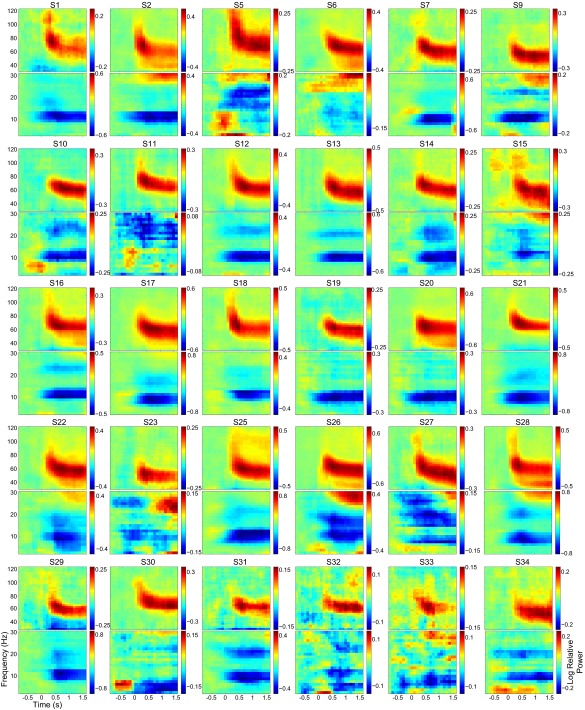
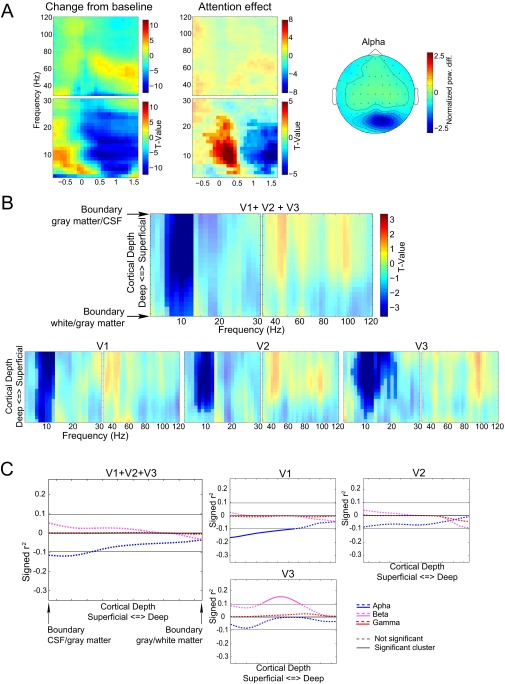
We first describe the basic task effects that formed the basis for our integrated EEG–fMRI analysis. Our experimental paradigm is depicted in Fig. 1 (Supporting Information). Analysis of the behavioral data obtained showed that subjects correctly responded or withheld their response on average in ∼93% of the trials, indicating a good compliance with the task. The full behavioral results are described in Fig. S1. Previous electrophysiological studies using this task (27, 28, 32) have demonstrated stimulus-induced power changes in the α-, β-, and γ-bands over the occipital cortices. In the current experiment, we were able to replicate these results after applying a denoising strategy in which independent component analysis (ICA) unmixing weights were estimated on data bandpass-filtered in the γ-band (Supporting Information). The results of this strategy are depicted in Fig. 2A and demonstrate a clear power increase in the γ-band and decreases in the α- and β-bands when combining over attention conditions. These effects were present in 30 of 34 subjects (Fig. S2). The topographical representation in Fig. 2B demonstrates that the γ-band modulation dominated in posterior electrodes consistent with a source in the early visual cortex. For comparison, we repeated the analyses with an ICA denoising approach applied to 3- to 30-Hz bandpass-filtered data. As also reported in our previous work (27), this approach yielded similar results for the α-band, but not for the β- and γ-frequency bands (Fig. S3).

Fig. S1.

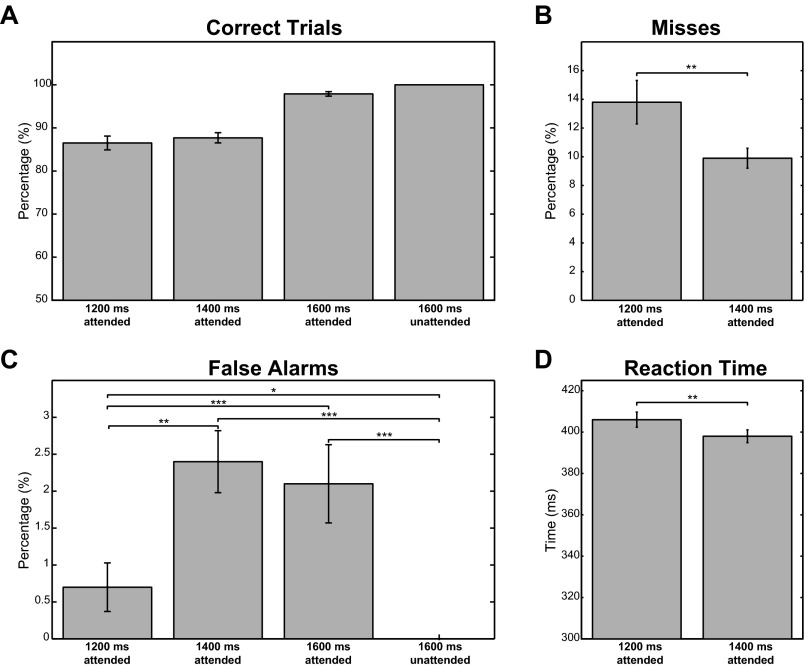
Behavioral results for the visual attention task. (A) Percentage correct trials for the four conditions determined by the length of visual stimulation and attention condition. (B) Percentage of misses for the attended trials of 1,200 ms and 1,400 that had a speed change. (C) Percentage of false alarms for all four conditions. (D) Reaction time to speed increases after 1,200 ms and 1,400 ms visual stimulation. Error bars for all panels indicate the SE of the mean. For misses and false alarms, the ranked sign test was used to test differences between conditions. For the difference in reaction time, significance was assessed by a dependent samples t test. *P < 0.05; **P < 0.01; ***P < 0.001.

Fig. 2.

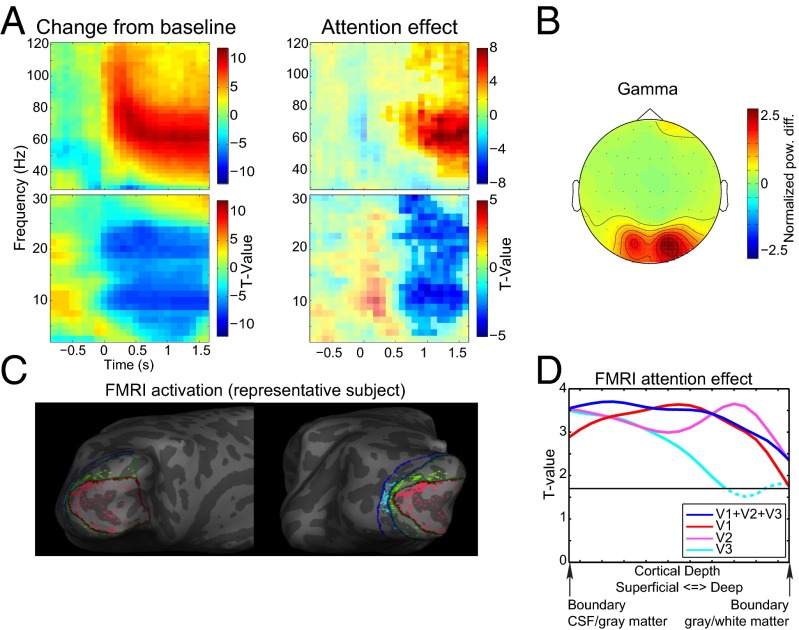
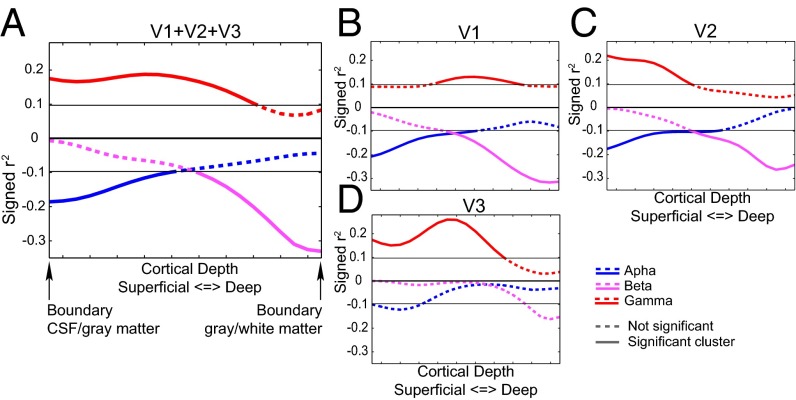
Task-related EEG and fMRI effects. (A) Time-frequency representations of power relative to a pretrial baseline collapsed over the two attention conditions and as a contrast between the attention-on and attention-off conditions. Only trials with 1600-ms visual stimulation without a speed change were used for this representation. Separate time-frequency representations are shown for low (2.5–30Hz) and high (30-120 Hz) frequencies. (B) Average topography over subjects of the change in the γ-band from baseline. For each subject, the average power change from baseline in the range from 55 to 85 Hz during the visual stimulation period was computed and subsequently root-mean-square normalized over channels before averaging. (C) The 10% strongest activated vertices within the left hemisphere for V1 (red), V2 (green), and V3 (blue) for a representative subject. (D) Laminar-specific attention effect for the selected voxels over all subjects for V1, V2, and V3 combined, and separately.

Fig. S2.

Individual time-frequency representations of power. For each subject, the log-ratio change from a precues baseline was computed separately for low (2.5–30 Hz) and high (30–120 Hz) frequencies collapsed over the two attention conditions. Only trials with 1,600-ms visual stimulation without a speed change were used. S, subject.

Fig. S3.

Results for EEG and the laminar-specific EEG–BOLD relation after low frequency-based ICA denoising of the EEG data. (A) Frequency-specific changes in EEG power compared with baseline and as a result of the attention manipulation similar to A and B of Fig. 2. (B) Laminar- and frequency-resolved trial-by-trial relation between BOLD and EEG, similar to Fig3. (C) Laminar-specific correlation between the EEG and laminar-resolved fMRI, similar to Fig 4. In A and B, significant clusters (P < 0.05 corrected) are highlighted; in C, significant clusters are indicated with a solid line. To facilitate comparison, scaling is the same as in the main figures.

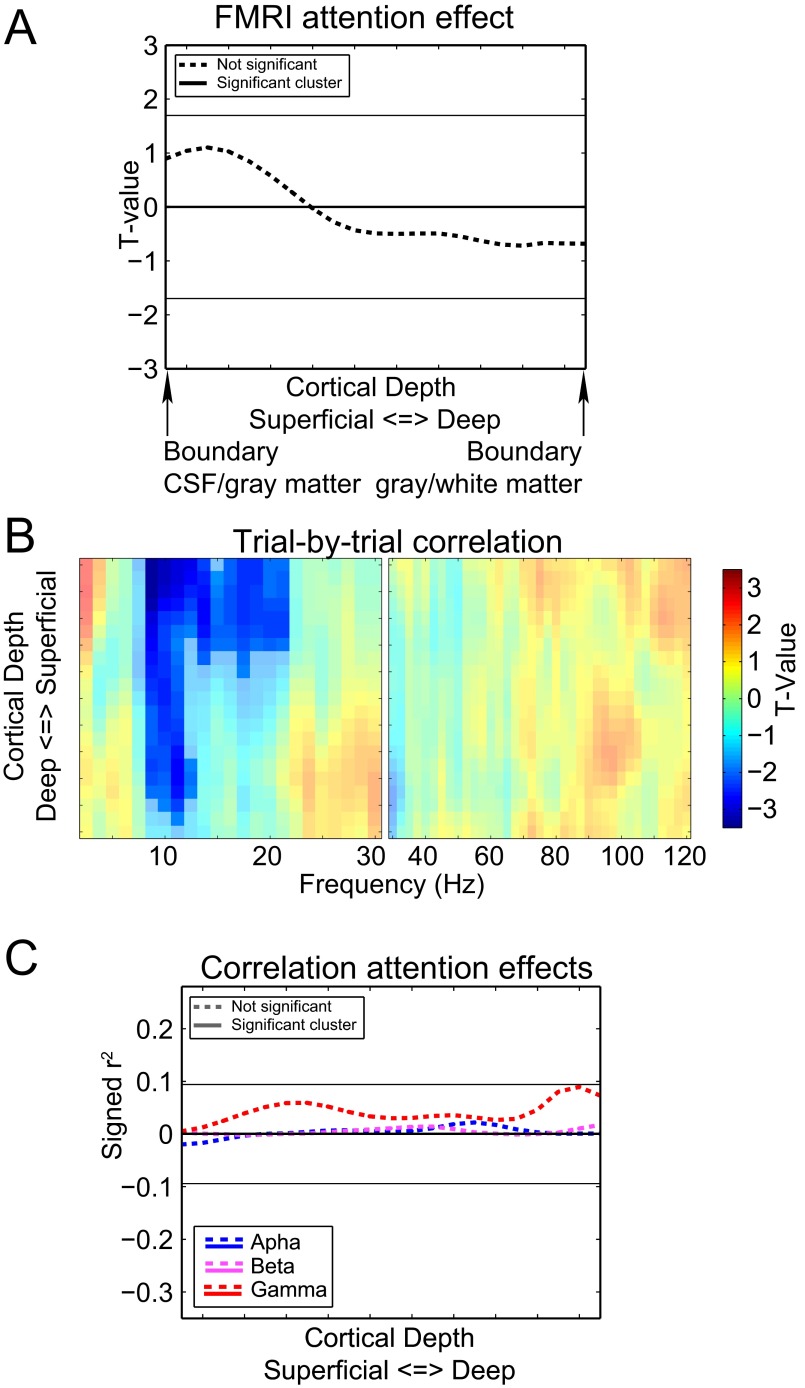
We also considered the attention modulation to correlate the attention effects in EEG power with the laminar-resolved BOLD signal over subjects in a frequency-specific manner. For this strategy to yield interpretable results, these attention effects should be present in both the electrophysiological and BOLD measurements. In the EEG data (Fig. 2A), we observed significant clusters 600 ms after onset of the visual stimulation until the end in the γ- (∼50–80 Hz) frequency band (P < 0.0001, corrected) (33) and in the low frequency range (P < 0.0001, corrected) extending over both the α- and β-bands. Within this large cluster, two regions of relatively strong effects, in terms of t values, were observed in the α-range (7.5–12.5 Hz) and the high β-range (22.5–26.25 Hz).

The laminar-resolved fMRI data consisted of 21 resampled laminar depths averaged over a cortical region. The laminar depths were equivolume linear interpolations between vertices indicating cerebrospinal fluid (CSF)–gray matter and white matter–CSF surfaces. We selected the 10% most-activated vertices from V1, V2, and V3 collapsed over the cortical depths (see Fig. 2C for an example subject). Fig. 2D clearly demonstrates that an attention effect at varying cortical depths can be observed for these selected vertices, which is a prerequisite for computing the correlation with the attention effects in EEG power. For the three visual regions combined (Fig. 2D, blue), there is a significant cluster including all cortical depths (P = 0.001). This result can also be observed for V1 (Fig. 2D, red) (P = 0.001) and V2 (Fig. 2D, pink) (P = 0.001). For V3 (Fig. 2D, cyan), the significant cluster includes only superficial and middle cortical depths (P = 0.010) although the effect is close to the cluster threshold for the deep layers.

Eye movements have been directly linked to visual LFP activity in the δ-/θ- and γ-bands (34) and across all cortical depths (35) whereas pupil dilation has been found to correlate negatively with the BOLD signal in the visual cortex (36). We recorded eye movements and pupil dilation to include these as possibly confounding or nuisance variables in the EEG–fMRI analysis. The full analyses of the eye movements and pupil dilation are described and discussed in Supporting Information and are shown in Figs. S4 and S5.

Fig. S4.

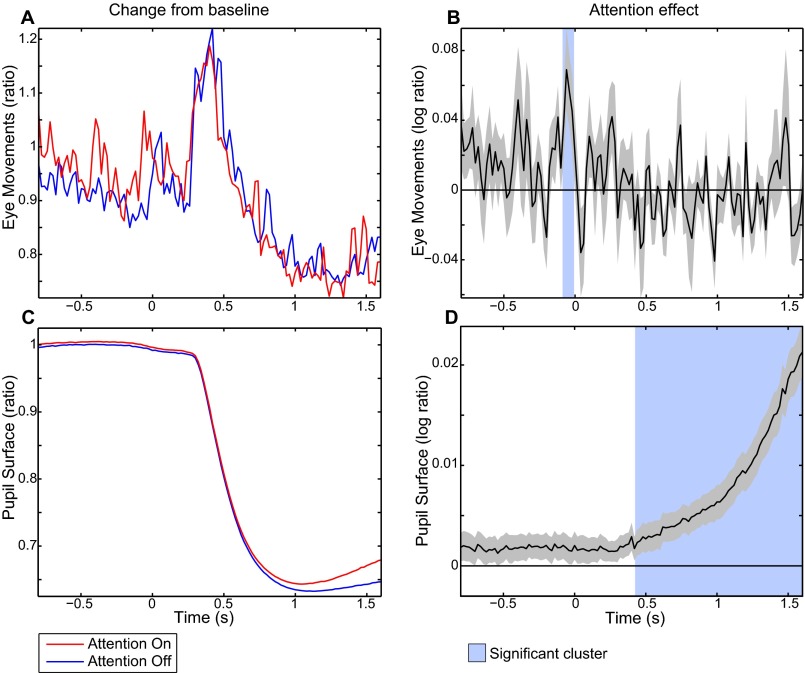
Task-related eye movement and pupil size effects. (A) Change from baseline for the for eye movements computed as the absolute of the derivative of the eye position relative (ratio) to a prestimulus baseline for the attention-on and -off conditions. (B) Attention effect for the eye movements computed as a log-ratio between the two conditions. (C) Similar as in A, but for pupil surface. (D) Similar as in B, but for pupil surface. Shaded areas show significant attention effects corrected for multiple comparisons (P < 0.05).

Fig. S5.

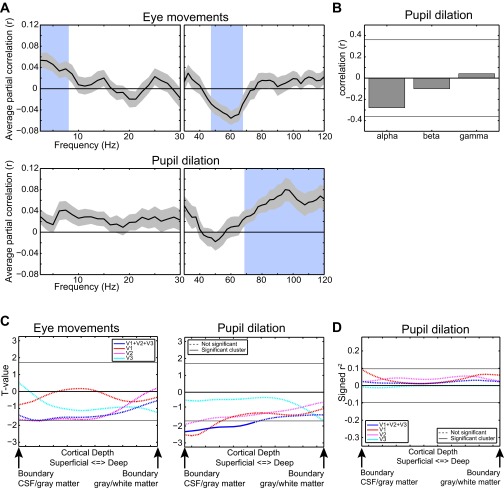
Relation of eye movements and pupil dilation with EEG power and laminar-resolved fMRI. (A) Partial correlation (corrected for all other regressors) of eye movement- and pupil dilation-based confound regressors, with EEG power-based regressors of all frequencies with the associated SE. (B) Correlation of the pupil dilation attention effect with the EEG power attention effect in the α-, β-, and γ-bands. The horizontal line indicates the P = 0.05 uncorrected level. (C) Laminar-resolved relation of eye movements and pupil dilation with the BOLD signal for all three regions combined and separately. (D) Laminar-resolved relation between the attention effect in pupil dilation and fMRI for all three regions combined and separately. Horizontal lines in C and D indicate the required cluster threshold for the cluster-based nonparametric test of significance.

Integrated EEG and fMRI Analyses.

Trial-by-trial EEG–BOLD relation.

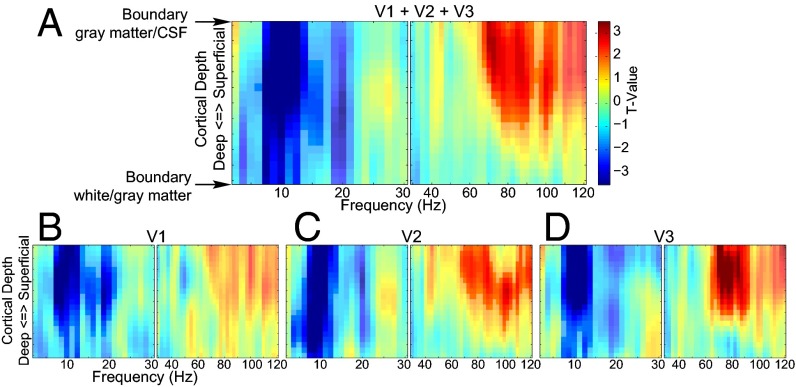
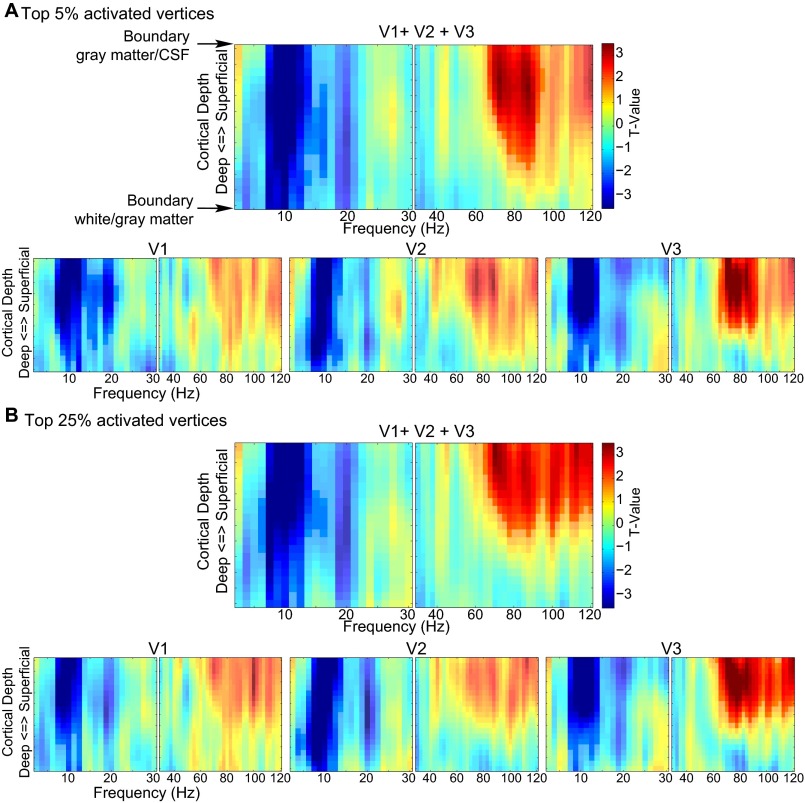
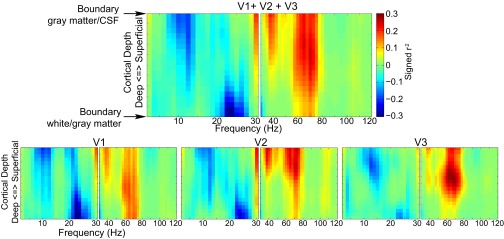
We investigated the relationship between EEG power and the laminar-resolved BOLD signal by correlating the trial-by-trial variations in power with variations in the laminar-specific BOLD signal from the early visual cortex (V1, V2, and V3) (Fig. 3). We did this investigation in the context of the general linear model (GLM) in which we estimated a separate model for each cortical depth by frequency combination. The dependent variable was the laminar-specific BOLD signal. The first regressor in the design matrix consisted of an EEG power regressor that varied over frequencies. The other regressors in the design matrix that were fixed for all frequencies modeled the main task effects, task performance, pause-related T1 effect, eye movements, pupil dilation effect, and head motion. The EEG power regressor was derived by extracting single-trial power time courses for all correct artifact-free trials and convolving these with the standard hemodynamic response function implemented in SPM12. In the context of the task and confound regressors, this explains the variance in the BOLD signal related to trial-by-trial EEG power variations. The parameter estimates for the EEG power regressors in these GLMs form two (separate for low and high frequencies) frequency-by-cortical depth representations of how EEG power relates to the BOLD signal. In a first analysis, we combined the three early visual regions (Fig. 3A) and observed a cluster primarily in the α-range (7.5–12.5 Hz), stretching across all cortical depths showing a negative relation with the BOLD signal (P = 0.001), and a cluster in the γ-range (67.5–105 Hz) showing a positive relation with the BOLD signal at superficial and middle cortical depth (P = 0.017). For V1 (P = 0.001), V2 (P = 0.002), and V3 (P = 0.003), we observed the same effect for the α-band extending across all cortical depths whereas, for the γ-band, we observed a significant cluster at middle and superficial cortical depths only for V2 (P = 0.021) and V3 (P = 0.009) (Fig. 3 B–D). For V1, no significant cluster was observed (P = 0.301 for the largest cluster). These results clearly indicate a different profile over cortical depths of the EEG-power BOLD relation for α- and γ-band activity. These findings did not critically depend on the arbitrary percentage (5%, 10%, or 25%) of vertices selected (Fig. S6) and did not systematically differ between the attention conditions (Fig. S7).

Fig. 3.

Frequency by laminar depth representation of the relation between trial-by-trial variation in BOLD and EEG power. The results for V1, V2, and, V3 combined (A) and separately (B–D) are shown. High and low frequencies are depicted separately. The t values are based on single-sample t tests of the β-weights over subjects. Highlighted clusters are significant after correcting for multiple comparisons (P < 0.05).

Fig. S6.

Frequency by laminar depth representation of the relation between trial-by-trial variation in BOLD and EEG power for the top 5% and top 25% activated vertices. (A) Results for the top 5% activated vertices. (B) Results for the top 25% activated vertices. The results for V1, V2, and, V3 combined and separately are shown. High and low frequencies are depicted separately. The t-values are based on single sample t tests of the β-weights over subjects. Highlighted clusters are significant after correcting for multiple comparisons (P < 0.05).

Fig. S7.

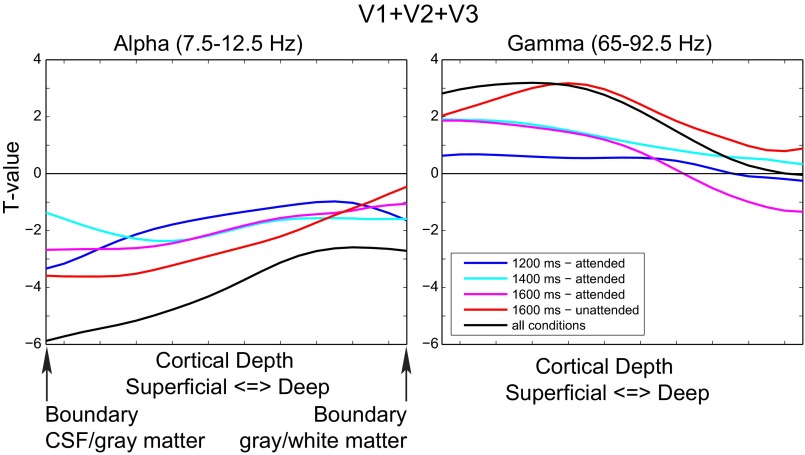
Laminar-specific BOLD–EEG power relation for the four task conditions separately and pooled over the four conditions. In contrast to the main analysis, separate EEG-based regressors modeling trial-by-trial variation in power for the four conditions were included in the GLM here. The laminar EEG–fMRI relation was here calculated by pooling the parameter estimates for these regressors over the three visual regions and separately within the α- and γ-bands. For α-power, negative values can be observed for all conditions for all cortical depths. This finding is in line with the significant negative relation observed in the main analysis that is also apparent when the results are pooled over the four condition-specific regressors. Similarly, for the γ-band, a positive relation was observed for all conditions only at superficial depths, mirroring the main result that is also observed after pooling over the four conditions here.

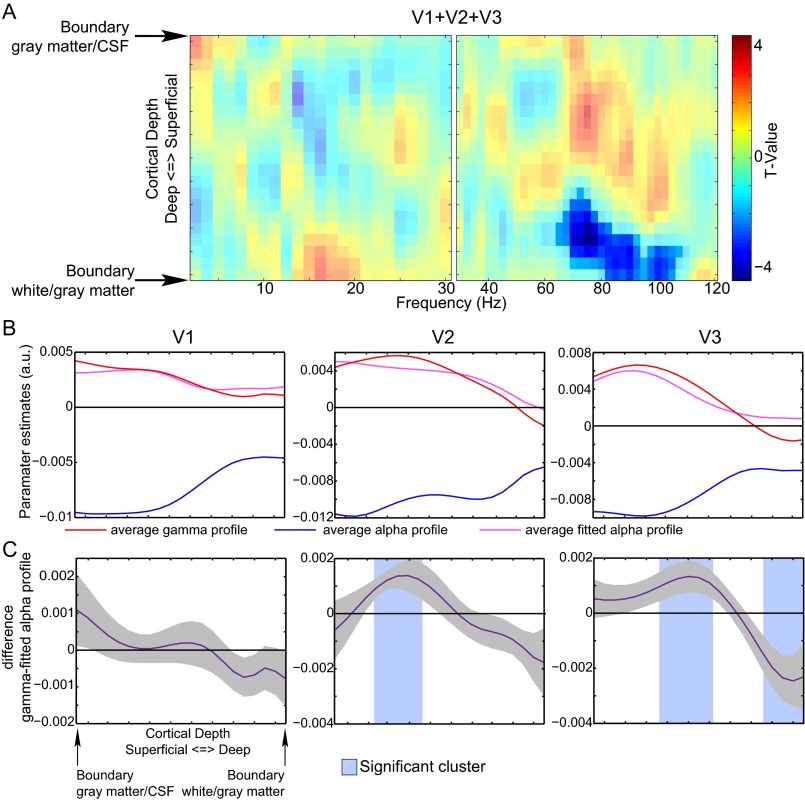
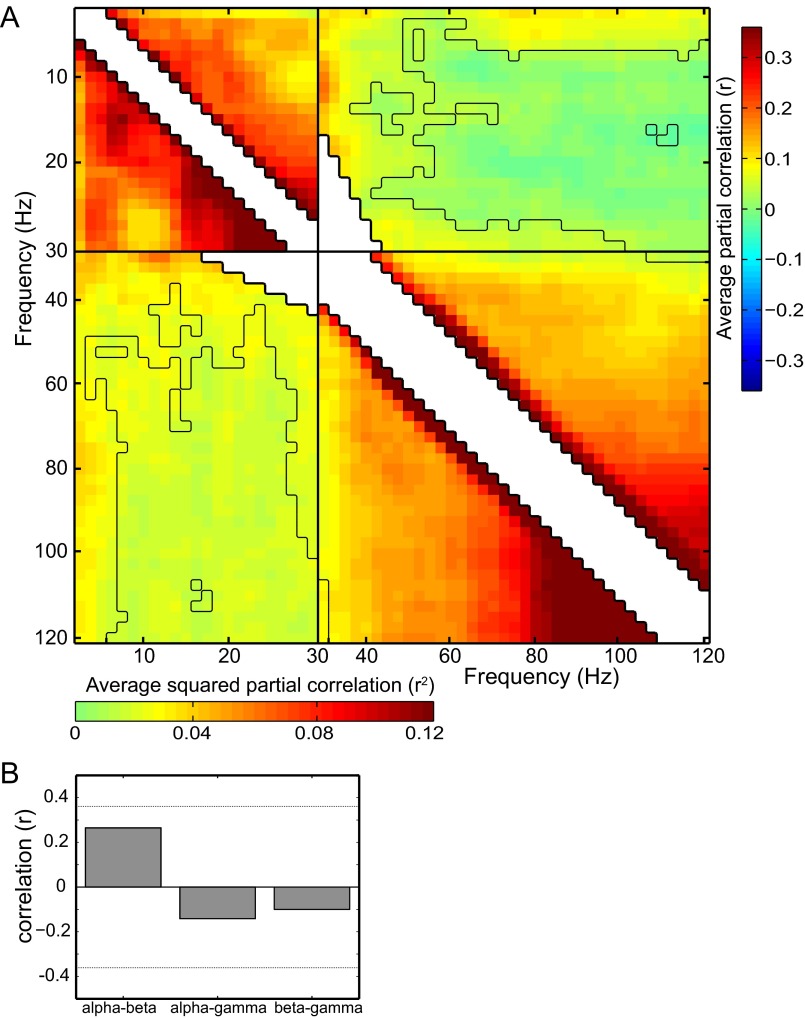
We tested for a frequency-by-depth interaction in the EEG–BOLD relation, by assessing whether the profile for the α-band EEG–BOLD relation deviated from that from other frequencies (see Supporting Information for a more details). We observed (Fig. S8) that the α-profile significantly differed from the profile in the γ-range (65–107.5 Hz; P = 0.004) for the three regions combined and V2 (P = 0.016) and V3 separately (P = 0.033). As in our previous work (27), we found that the regressors for α- and γ-frequencies were uncorrelated (Fig. S9). The frequency by cortical depth interaction demonstrates that this absence of a correlation is related to different layer-specific neural processes and provides direct evidence for laminar-level sensitivity of high-resolution fMRI in relation to electrophysiological activity.

Fig. S8.

Frequency by laminar depth interaction effect for trial-by-trial relation between EEG power and the BOLD signal. (A) For V1, V2, and V3 combined, the interaction effect is computed by fitting the average profile of parameter estimates of the α-band to each frequency separately for high and low frequencies for each subject individually by linear regression (SI Materials and Methods). These two spectra of actual and α-band–fitted profiles are compared using a cluster-based randomization test (SI Materials and Methods). Significant clusters indicate a frequency range for which the profile of parameter estimates for the EEG power regressors systematically differs from the fitted α-profile. In this case, a cluster in the γ-range is observed, which means that the laminar profile of the α–BOLD relation is different from that in the γ-range. (B) The interaction effect as computed in A for the three regions separately. Here, the interaction effect was tested only for the γ-frequency range that showed an effect in A. For this profile, the average γ-profile was computed over this frequency range. Shown are the average α, average γ, and fitted α-profiles over subjects. (C) Shown is the difference between the γ- and the fitted α-profiles with the associated SE. A shaded area indicates a significant cluster corrected for multiple comparisons (P < 0.05). If a significant cluster is observed, it indicates that the fitted α- and γ-profiles for that region are not the same.

Fig. S9.

Dependence between EEG regressors and EEG attention effects. (A) Pearson correlation and squared correlation between the EEG-based regressors for all frequencies. The black line indicates the P < 0.05 uncorrected threshold based on a ranked sign test. Note that the correlations between low (5–25 Hz) and high (>45 Hz) frequencies mostly do not pass this threshold. Correlations between center frequencies with overlapping frequency ranges are not shown. (B) Pearson correlations between the EEG attention effect in the α-, β-, and γ-bands over subjects. The horizontal lines indicate the correlation corresponding with P = 0.05 uncorrected.

Attention effect.

In the EEG, we observed attention effects in the α-, β-, and γ-bands, which were correlated with the attention effect in the BOLD signal across cortical depth for the three regions combined and separately. To correct for the potential confounding effect of the observed attention modulation in pupil dilation, we removed it from variations in both the EEG and fMRI attention effects by means of linear regression. The results are depicted in Fig. 4. For the three visual regions combined (Fig. 4A), the α-attention effect (Fig. 4, blue) significantly correlates with the BOLD attention effect at superficial depths (P = 0.038). For the β-band (Fig. 4, pink), a significant cluster is observed at lower depths (P = 0.027) whereas a significant cluster is observed at middle and superficial depths for the γ-band (Fig. 4, red) (P = 0.015).

Fig. 4.

Correlation of the attention effects in EEG power with the laminar-resolved attention effects in fMRI. The results for V1, V2, and, V3 both combined (A) and separately (B–D) are shown. The signed r² values plotted on the y axis are computed by multiplying the squared correlation with the sign of the correlation. Clusters significant after correcting for multiple comparisons (P < 0.05) are indicated with a solid line.

For the individually tested regions (Fig. 4 B–D), we observed that the α-band correlations were strongest at superficial depths in all three regions. A significant cluster was found in superficial layers in V1 (P = 0.033) and V2 (P = 0.031). The cluster observed for V3 was not significant (P = 0.071). The β-band EEG attention effect correlated significantly with the laminar-specific attention effect of the BOLD signal at deeper cortical depths in V1 (P = 0.019) and V2 (P = 0.022). A cluster at the same depth for V3 was not significant (P = 0.075). For the γ-band, we observed no substantial difference in the correlation over cortical depths in V1: A significant cluster was observed for this region at middle cortical depths (P = 0.010), but it was close to the cluster threshold for all cortical depths. For V2 (P = 0.026) and V3 (P = 0.012), we observed robust correlations only for middle and superficial depths. In line with the different laminar profiles for the three frequency bands, no significant correlation between the attention effects was observed (Fig. S9).

Because these correlations were carried out on preselected frequency ranges, they could in theory be due to variations in wider frequency ranges (e.g., broadband changes) overlapping with the preselected frequency ranges where the attention effect was observed in the EEG. The analyses depicted in Fig. S10 show, however, that the observed correlations were limited to the frequency ranges that showed an attention effect in EEG power.

Fig. S10.

Frequency by cortical depth representation of the correlation over subjects between the laminar-resolved fMRI attention effects and the frequency-resolved attention effects in EEG power. The results for V1, V2, and V3 combined and separately are shown. High and low frequencies are depicted separately. We calculated the (signed squared) correlation between the attention effect for each frequency, separately for the low and high frequency ranges for the three regions combined and individually (Fig. S4). Similar to the trial-by-trial correlation between EEG power and the BOLD signal that we previously demonstrated, this calculation resulted in a frequency-by-depth representation of how the attention effects in the two modalities are related. We observed that the patterns of correlations for the α-, β-, and γ-power were largely confined to the frequency ranges for which the attention effect was also observed, with the exception of a positive correlation at superficial depths around 40 Hz. This frequency corresponds to a second band limited γ-power increase effect that can be observed for several subjects (Fig. S1). Together, these results indicate that the effects depicted in Fig. 4 reflect a true covariation over subjects of the attention effects in EEG power and BOLD.

Control region.

To test whether the patterns observed for the trial-by trial correlations and the attention effects were specific to visual regions, we performed the same analysis for nonactivated parts of the frontal cortex (Fig. S11). For this region, we observed a significant cluster with negative correlations covering all superficial depths only when considering the trial-by-trial analysis in the α-band. No other effects that were observed for early visual regions were found in the frontal cortex.

Fig. S11.

Results for the nonactivated frontal control region. (A) Laminar-resolved fMRI attention effect, similar to D from Fig 2. (B) Laminar- and frequency-resolved trial-by-trial relation between EEG power and BOLD, similar to Fig. 3. Significant clusters (P < 0.05 corrected) are highlighted. (C) Correlation of attention effects over subjects. Horizontal lines in A and C indicate the required cluster threshold for the cluster-based nonparametric test of significance.

Discussion

In this study, we combined laminar-resolved fMRI and simultaneously recorded EEG in human subjects to investigate how BOLD activity measured from different cortical layers relates to frequency-specific power changes in the EEG. We observed an interaction between frequency and cortical depth in how trial-by-trial variation in EEG power relates to the BOLD signal. Although variation over trials in α-band power was related to the BOLD signal in both deep and superficial layers, γ-band activity showed a relation to the BOLD signal only at middle and superficial layers. This finding demonstrates that the BOLD signal at different cortical depths relates to different underlying neuronal dynamics. It supports our previous conclusion that the neural processes underlying α- and γ-band power variations independently contribute to changes in the BOLD signal (27). The observation that EEG power in different frequency bands is related to the BOLD signal at different cortical depths is strengthened by the correlation over subjects of the attention effects in EEG power and the cortical depth-resolved BOLD signal. This analysis shows clear laminar specificity in the three early visual regions for the attention effects observed in the α-, β-, and γ-bands. This work demonstrates that it is possible to link neuronal activity in different frequency bands as recorded by the EEG to laminar-resolved neural activity as measured by high-resolution fMRI. For laminar-level fMRI, our results strengthen the neurophysiological basis for conducting such studies.

Neuronal Basis of the BOLD Signal.

Previous research on the neural basis of the BOLD signal has indicated that it is coupled to the power variations in the LFP (19–21). EEG, which we use here, as well as MEG and electrocorticography (ECoG), can be regarded as spatially macroscopic versions of the LFP. Human EEG and ECoG recordings combined with hemodynamic measurements have demonstrated that signals in the θ-, α-, and β-ranges are generally anticorrelated to the BOLD signal and that the γ-band signal is positively correlated with BOLD (22–24, 27, 32), which is in line with BOLD–LFP correlations in animals (20). In the current study, we extend these findings by quantifying the laminar contributions.

It is tempting to interpret the cortical depths at which EEG power correlates with the BOLD signal as the source location of the EEG rhythm. Because our results are correlational and the underlying sources of the observed EEG rhythms measured here are not known at the laminar level in advance, such a conclusion cannot be made directly. Any neuronal process that correlates with frequency-specific variation in EEG power and also results in a local (cortical depth-resolved) change in the BOLD signal can give rise to the results presented here. These processes are therefore not necessarily confined to the laminar source location of the EEG rhythm. The BOLD signal is thought to be primarily driven by excitatory (glutaminergic) synaptic activity in a voxel (37–39). Assuming that this activity is the cause of the BOLD signal, the results here can be interpreted as the relation between variation in frequency-specific EEG power originating from early visual cortex and laminar-specific changes in excitatory synaptic activity.

There are, however, some caveats to this interpretation. First, venous blood flows from deep to superficial layers in the cortex (40). As a result, BOLD activity and consequently EEG–BOLD relations observed in deeper layers can also spread to more superficial layers: like, for instance, the correlations we find in deep layers for α- and β-power. It is currently infeasible to measure the spatial point spread function of the BOLD response for activation of a single layer, because of the difficulty of stimulating a layer in isolation. Simulations have, however, shown that the BOLD response will peak in the stimulated layer and then exhibits a relatively flat tail of activation extending from the activated layer to the pial surface, with an amplitude of 20–25% of the peak activation (41). Significant activation is therefore most likely to be recorded in the activated layer and may be measured in more superficial layers depending upon the strength of the activation and the degree to which other layers also contribute; this is well-illustrated by the correlation of the attention effect over subjects in the β-band, which is strong in deep layers (∼30% shared variance for V1), but close to zero for superficial depths.

Although we cannot claim that the cortical depths at which we find BOLD–EEG power correlations are the source of the observed EEG signals, we can compare the results with laminar-resolved electrophysiological recordings. In general, the correlation profiles for γ-band activity in the three regions combined (V1, V2, and V3) and also singly for V2 and V3 correspond well with laminar recordings in animals that have observed γ synchronization predominantly in the granular and supragranular layers of early visual regions (6, 7, 42). However, the correlations of the attention effects in V1 resulted in a flat profile over all cortical depths. Because studies mentioned above showed that γ-band synchronization in V1 is predominantly a supragranular effect, this finding suggests that neural processes reflected in the BOLD signal in all layers of V1 are related to the attention effect observed in γ with sources in superficial layers. A possible explanation for this result is that γ-band activity is coupled to excitatory bottom-up input from the lateral geniculate nucleus (LGN). Although the majority of these projections terminate in layer 4, some of these projections project to infragranular layers (1, 43). Furthermore it has been demonstrated that attention effects can be observed in the LGN in both animals (43–45) and humans (43, 46).

For the α-band, the correlations of variation over trials of BOLD and EEG power yielded a different picture than the corresponding correlation of the attention effects. Whereas the correlation over trials showed a significant negative correlation for all cortical depths, the correlation of the attention effects was observed only at superficial depths. This difference suggests multiple neural processes related to α-activity within the visual cortex as measured at the scalp with EEG. Although some studies have demonstrated multiple α-sources in the early visual regions in both supra- and infragranular layers (9, 12), others suggested a predominance of α-activity in deep layers (6, 11, 31). The results here are in line with multiple α-sources in both supra- and infragranular layers, in which, in our task, only the α-source or sources in more superficial layers are modulated by attention.

For the high β-band, we observed negative correlations over subjects of the attention affects only in deep layers. For the trial-by-trial correlation, we did not observe a correlation in the same frequency range. The results for this frequency band were, however, in line with previous findings that β-band EEG power is anticorrelated to the BOLD signal (24, 27) and is predominantly measured in the LFP recorded from infragranular layers in nonhuman animals (8). The deep layers are therefore also a likely source for the β-attention effect in the EEG measured here.

Eye movement-induced artifacts in the EEG have directly been linked to spurious γ-band power changes in the EEG (47). The results here, however, cannot be related to this artifact, and also an indirect route through neural activity related to eye movements or pupil dilation is unlikely. We discuss this theory in more detail in Supporting Information and Fig. S5.

Implications for Electrophysiological Research.

Because the cortical layers have specific functions and connections with other cortical and subcortical brain regions, the technique described herein potentially allows us to link electrophysiological features measured by EEG to specific feedforward, feedback, and cortical–subcortical streams of information. We tentatively link the results for the different frequency bands in this experiment to laminar-specific electrophysiological and anatomical research.

The relationship we observed between the BOLD signal at middle and superficial depths and γ-band activity is in line with the notion that γ-oscillations are related to a bottom-up flow of information from lower to higher order cortical regions (2–4, 48). This bottom-up flow of information is thought to be mainly carried by intra- and interarea connections in granular and supragranular layers (2). In line with this theory, γ-oscillations are observed predominantly in granular and supragranular layers (6, 7, 10) and are thought to originate through an interaction of interneurons and pyramidal cells located in granular and supragranular layers (49, 50). For the β-band, we observed a negative correlation in deep layers that is particularly strong in V1 and V2. This finding corresponds with laminar recordings in animals that find the strongest β-band synchronization in deep layers (8). Furthermore, β-activity in early visual regions has been associated with top-down streams of information from higher order regions (2, 3, 48, 51).

We observed evidence for separate neural processes at deep and superficial cortical depths related to α-power. This finding is supported by laminar recordings in animals reporting both supra- and infragranular sources (9, 12) and relating α-activity to feedback projections that target both supra- and infragranular layers (4). Consistently, laminar fMRI work has linked feedback processes to both superficial (17) and deep layers (18). Interestingly, the attention modulation in the α-band is coupled to BOLD only in superficial layers. These layers are implicated in the bottom-up flow of information to higher order cortical regions. We have recently demonstrated that α-power in the early occipital cortex is also related to the routing of information to relevant higher order cortical regions (25) by inhibiting irrelevant information streams. This inhibition, reflected in lower α-power, is reduced for relevant information streams. The α-attention effect that is related to the BOLD attention effect in superficial layers might therefore reflect attentional control of the routing of information to downstream regions.

Our finding that α-oscillations are related to activity in deep layers agrees well with various laminar studies reporting α-activity in infragranular layers (6, 7, 9, 12). However, we did not find a relation between the attention effects in BOLD and α-power in the deep layers. Interestingly, we observed the inverse trial-by trial relation across all cortical depths also for the frontal cortex, which is likely not a generator of the measured α-activity. This result might therefore speak to a general effect throughout the cortex that is not modulated by our task. From intracranial animal work, we know that the phase of infragranular layer α can modulate supragranular γ-amplitude (11). This modulation has been linked to temporal coding and prioritizing visual processing (52) and might relate to visual sampling at roughly 10 Hz (53), supported by α-band synchronization between cortical regions. α-Band activity has been closely linked to thalamo-cortical loops (54), and α-band synchronization between regions is thought to be mediated through the pulvinar (43, 55). The trial-by-trial relation of α with BOLD across all layers might be observed throughout larger parts of the cortex through its dependence on loops involving through thalamic nuclei like the pulvinar.

General Conclusions

The integrated analysis of laminar-level fMRI and simultaneously recorded EEG is a previously unused methodological approach, and laminar level fMRI in humans is still a relatively young research field. As a consequence there are no standard analysis pipelines available yet for our approach. We therefore used the best techniques we had available at the time of writing.

The main aim of this study was to investigate whether EEG power from different frequency bands is differentially related to the cortical depth-resolved BOLD signal. In our opinion, this aim is convincingly demonstrated by the collection of results for the α-, β-, and γ-bands for both the correlation over trials as well as the correlation of the attention effect over subjects. With these results, we provide a neurophysiological basis for using high-resolution fMRI as a tool to investigate laminar processing in humans. These results also demonstrate that an accurate understanding of the neural activity underlying the cortical BOLD signal requires a detailed understanding of the cortical microcircuitry (56). In general, our findings correspond also well to what is known from laminar electrophysiological work in animals (6, 7, 9, 10, 12). Combining EEG and laminar fMRI therefore might prove a useful technique to link human cognitive neuroscience using fMRI and EEG/MEG to systems-level neuroscience approaches using animal models. The interpretations we provide for the laminar BOLD correlates of the different frequency bands warrant verification using other measurement modalities (e.g., intracranial and laminar recordings), brain regions, and experimental paradigms.

Materials and Methods

Thirty-four right-handed subjects (29 female, 5 male, mean age 21.6 y, range 18–26 y) without a history of known psychiatric or neurological disorders participated in the simultaneous EEG/fMRI session. Before the start of the experiment, written informed consent was obtained from each subject. The experiment was approved by the local ethical committee [Commissie Mensgebonden Onderzoek (CMO), region of Arnhem/Nijmegen, The Netherlands]. The results are based on thirty subjects with good quality EEG. Subjects performed a visual attention task (Fig. 1A) in three blocks of 72 trials. During the main task, we measured high-resolution fMRI data (3T; volume acquisition time, 3.792 s; 48 slices; resolution, 0.75 mm isotropic; 3.792 s pause after each third volume) and 64-channel EEG.

We estimated the cortical depth-resolved BOLD signal at 21 points in the gray matter between the boundaries with CSF and white matter for V1, V2, and V3. The average cortical depth-resolved signal per region was computed by averaging over the top 10% activated vertices (collapsed over cortical depth). To obtain clean estimates of power changes over a wide frequency range, we used an ICA-based denoising approach (27). Time-frequency analysis was carried out separately for a lower (2.5–30 Hz) and a higher (30–120 Hz) frequency window using a multitaper approach. Spectral changes in power relative to baseline, and between attention conditions, were computed.

We investigated the relationships between single trial variations in the cortical depth-resolved BOLD signal and EEG power, and between the cortical depth-resolved fMRI attention effect and the frequency-resolved EEG attention effect. For the analysis using single trial variations, separate general linear models were constructed for each frequency-cortical depth combination, resulting in a 2D depiction of the EEG–BOLD relation. We correlated the attention effects in power observed for the α-, β-, and γ-bands with the laminar-resolved attention effect in BOLD for the three visual regions. Statistical significance was assessed using a cluster-based randomization procedure (33).

The full methods section can be found in Supporting Information.

SI Results

Eye movements have been directly linked to visual LFP activity in the δ-/θ- and γ-bands (34) and across all cortical depths (35) whereas pupil dilation has been found to correlate negatively with BOLD in the visual cortex (36). Therefore, we recorded eye movements and pupil dilation to include these as possibly confounding or nuisance variables in our integrated EEG–fMRI analysis (Fig. S4). For all trials types, a short increase in eye movements relative to baseline after stimulus onset was followed by a decrease until the end of the trial. We observed for a brief moment stronger eye movements in the attention-on compared with the attention-off condition just after the cue, but not during visual stimulation. Pupil size decreased during visual stimulation for all conditions. However, a substantially larger pupil size for the attention-on compared with the attention-off condition was observed from ∼400 ms after visual stimulation onset until the end of this period.

Although eye movements were found to correlate with positively θ- and negatively γ-band EEG power, we did not observe a significant correlation with the laminar BOLD signal. For pupil dilation, we did observe a negative correlation with superficial layer BOLD only in V1, but a positive relation with high γ-band oscillations. The attention effect in pupil dilation was, however, not correlated to those in EEG. These results are depicted in Fig. S5.

SI Discussion

Eye movement-induced EEG artifacts have been directly linked to spurious γ-band power changes in the EEG (47). The narrow band sustained γ-response observed here is also reported in human MEG and animal LFP recordings (31), and, furthermore, it is markedly different from the short-lived broad spectrum of (micro) saccades. Furthermore, there is substantial evidence from source analysis that this narrow band response in this task or similar tasks originates from the early visual cortex (28, 31, 57–59) and also overlaps well with fMRI activation (28). In addition, the fMRI data could not directly be affected by eye movements during the trial or later because fMRI volumes were not recorded during the trial and the eyes were outside the field of view. Therefore, our EEG–BOLD relation could not directly be related to artifacts in either modality. It is possible however that eye movements, and also pupil dilation, indirectly affected the BOLD–EEG coupling. Eye movements, which inherently occur at a δ-/θ-frequency, have directly been linked to δ-/θ- and γ-band activity (34) and affect activity in all cortical layers (35) whereas pupil dilation has been found to correlate negatively with BOLD in visual regions (36). To account for these effects, we included eye movement-based and pupil dilation-based regressors as confounds and also investigated how these regressors relate to the laminar-specific BOLD signal and frequency-specific EEG power regressors. In line with previous reports, we found coupling between eye movements and δ-/θ- (positive) and γ- (negative) range EEG regressors. We did not observe EEG–BOLD coupling in the θ- range, demonstrating that EEG power coupled to δ-/θ-frequency eye movements is not (strongly) reflected in the BOLD response. An indirect effect of the negative relation with γ-band power possibly could have affected our results through the coupling between this γ-band effect and BOLD; because the eye movements themselves did not correlate significantly with BOLD and we used them also as a confound regressor, it is, however, unlikely that our results were driven by this. For pupil dilation, we found a positive correlation with the γ-band and a negative relation with BOLD (only for V1). Because γ correlates positively with BOLD, this coupling between pupil dilation and EEG could not account for our results. In line with this finding, also the attention effects in γ and pupil dilation did not correlate with each other.

SI Materials and Methods

The experimental paradigm and parts of the methodology described here are adapted from our previous experiment described in Scheeringa et al. (27) and are in some parts very similar. Parts of the section below are therefore taken from that article and adapted to the current experiment.

Subjects.

Because, to our knowledge, no prior study on how electrophysiology relates to the laminar-specific BOLD had been published at the time the experiment was conducted, a proper power analysis to determine the sample size could not be carried out. Furthermore, a power calculation was also not readily available for the nonparametric statistical approach carried out here (see Inferential Statistics below). For a replication of the effects observed in our previous experiment (27) that formed the basis of this study, a power analysis (1 − β = 0.8) indicated that ∼20 subjects would be needed for the data points of the clusters to exceed the cluster level threshold used here. Because the current experiment comprises fewer and shorter trials and the effects are computed separately for each cortical depth, more subjects were expected to be needed here. Ultimately, we chose to include 30 subjects that showed the desired effects in the EEG power analysis because this number corresponds to a cluster level threshold for the correlation of the attention effects over subjects of |r| ≈ 0.3 (r² ≈ 0.09) for the correlation of the attention effect; this result corresponds to what is commonly qualified as a moderate relationship.

To include 30 subjects that demonstrated the desired effects in the EEG, 34 subjects (29 female, 5 male, mean age 21.6 y, range 18–26 y) without a history of known psychiatric or neurological disorders participated in the simultaneous EEG/fMRI session. All had normal or corrected-to-normal vision. Before the start of the experiment, written informed consent was obtained from each subject. The experiment was approved by a local ethical committee (CMO Arnhem/Nijmegen region). Subjects for whom a sustained γ-band response to visual stimulation was observed (see EEG Data) were selected for further analysis. After this selection, 30 subjects (26 female, 4 male) remained. All of the results presented here are based on these 30 subjects. Subjects were paid a small fee (€35, and €5 for each half hour the experiment took over 3.5 h) or given course credits. Subjects were recruited via an online system for subject recruitment at the Radboud University Nijmegen and were mainly recruited from the student population. Subjects with a relatively small head size were requested (≤58 cm) because pilots indicated that large heads would not fit within with the relatively small field of view of the high-resolution functional scans. This decision also contributed to the relatively large proportion of female participants.

General Experimental Procedure.

Subjects came to the Donders Institute in Nijmegen 1 h and 15 min before the start of the experiment. During this time, the procedures and task were explained to them, written informed consent was obtained, the EEG electrodes were applied, and the electrode positions were recorded using a Polhemus FASTRAK. After these steps, the subjects were positioned in the MRI scanner for simultaneous EEG–fMRI registration. The head was stabilized with foam pillows underneath and at the side of the head, and a strand of paper adhesive tape was applied to the forehead to provide feedback to minimize head movements. The MRI-compatible EEG amplifiers were positioned at the right foot end of the subject. When in the scanner, first a normal (1 mm) resolution T1 anatomical scan was obtained. During this scan, subjects performed a practice version of the main task to familiarize themselves with it. This practice version was followed by a shorter blocked version of the task that allowed us to run a simple GLM analysis on the MR console, the results of which were used as a localizer in the positioning of further scans. The slices of the high-resolution (0.75 mm) 3D EPI scans were planned to coincide with the main activations in the early visual cortex, and a few test volumes were acquired, while avoiding the eyes. Subsequently, a high-resolution (0.75 mm) anatomical T1 scan and a field map were made using the same slice orientations as for the high-resolution EPI volumes. This step was followed by three main task blocks, each with a duration of roughly 20 min, during which simultaneous EEG and high-resolution fMRI data were acquired. In between blocks, subjects were allowed to rest for a few minutes. After the third block, another field map was acquired, followed by a short retinotopy measurement using a normal 2D EPI sequence. In total, subjects were in the MRI scanner for ∼1 h and 45 min.

Experimental Paradigms.

Visual attention task.

Subjects engaged in a visual attention task that is known to elicit strong, long-lasting (up to several seconds), and narrow-band γ- activity increases, as well as α- and β-band decreases in both MEG (28, 30, 31, 57–59) and EEG (27, 31, 32). Source analysis has revealed that these frequency-specific responses originate from the early visual cortex (28, 30, 31, 57–59) and overlap with task-evoked fMRI activations (28). In this task, subjects attended to circular, inward moving gratings, and were asked to detect a change in inward speed.

Each trial started with a reduction in contrast of a fixation point that was present between trials (Gaussian of 0.4°) by 40%. This contrast reduction served as a warning for the upcoming visual stimulation and instructed the subjects to stop blinking until the end of the trial. After 1,600 ms, a red “!” or a green “=” appeared just above the fixation point for 100 ms. The “!” indicated a 66.7% chance of an increase in the speed of the upcoming inward moving grating and was presented in 75% of the trials. The “=” indicated that no speed change would occur with 100% accuracy and was presented in 25% of the trials. After this attention cue was removed, the fixation point remained on the screen for 400 ms before it was replaced by a sine wave grating (diameter, 7°; spatial frequency, 2.5 cycles per degree; contrast, 100%). The sine wave grating contracted to the fixation point (1.6° per second) for one of four stimulus durations: 1,200, 1,400, or 1,600 ms. This step was followed by an increase in the contraction speed to 2.2° per second for maximally 500 ms after either 1,200 or 1,400 ms. The trials with 1,600-ms stimulation were not followed by a speed change. Therefore, trials cued with “=” were always followed by a 1,600-ms visual stimulation period whereas, for trials cued with “!”, this happened in 33.3% of the trials. An equal number of trials of the four conditions were presented (1,200-ms stimulation, attended, speed change; 1,400-ms stimulation, attended, speed change; 1,600-ms stimulation, attended, no speed change; 1,600-ms stimulation, not attended, no speed change).

Subjects were instructed to press a button with their right index finger as soon as they detected the speed change. The stimulus disappeared after a response was given, after 1,600 ms of stimulation (for catch trials), or, if no response was given, within 500 ms of the speed change. Feedback about the performance was given for 500 ms. In the case of a correct response or if a response was correctly withheld, “ok!” appeared in green above the fixation point. In case of premature or slow/no responses, “early” or “late,” respectively, appeared in red.

Subjects performed a practice version of 40 trials of the task during the low-resolution anatomical scan at the start of the session. This practice block was 5-min, 28-s long, and a trial was presented every 8.2 s. Subsequently, a localizer version of this paradigm was performed to obtain an activation map that was used to plan the slices for the orientation of the slices of the high-resolution fMRI volumes (see MRI Data Acquisition). To perform a simple activation versus “rest” analysis, 64 trials were grouped in 8 blocks of 32 s, with 8 trials each, and a trial starting every 4 s within a block of 8 trials. Each group of eight trials consisted of two trials of each condition. Within a group of eight trials, the order was randomized. This block was followed by three blocks during which EEG was combined with high-resolution fMRI (i.e., the “main task”). Each session consisted of 72 trials, 18 of each condition. Onset of a trial was triggered by every third MRI volume. The laminar resolution MRI sequence we used consisted of the acquisition of three volumes of 3.792 s, followed by a scan-free period of the same length to allow for MR gradient and RF pulse-free recording of EEG data during the presentation of the trial. The trial, starting with the dimming of the fixation point, started 330 ms before the end of the third scan. The attention cue was presented in the artifact-free period, 1,260 ms after the end of the third scan, and stimulation onset was at 1,760 ms. A trial was presented every 15.168 s. In total, each session was 18-min, 12-s long.

Retinotopy.

To separate early visual regions (V1, V2, and V3), a clock-wise rotating double (one in each hemifield) wedge-shaped red-green flickering checkerboard was used. The flicker frequency was 8 Hz. The two wedges started at the center of the visual field, had an angle of 22.5°, and were presented in opposition: i.e., at a 180° angle from each other. By simultaneously using wedges in the left and right visual fields, we were able to simultaneously map left and right early visual regions. The wedges remained stationary for 6 s, after which they skipped to the next position in a clockwise fashion. After eight displacements, all angles of the visual field were stimulated. This sequence was then repeated eight times, which resulted in a duration of 6 min and 24 s for the retinotopy measurement.

MRI Data Acquisition.

MRI data were acquired using a 3.0-T whole body MRI scanner (Magnetom Trio Tim; Siemens). A 32-channel head-coil was used to record the images. For the 1-mm isotropic T1-weighted anatomical scan, a 3D magnetization-prepared rapid gradient-echo (MPRAGE) sequence was used [inversion time (TI), 1,100 ms; repetition time (TR), 2,300 ms; 192 slices per slab; 1-mm slice thickness; generalized autocalibrating partially parallel acquisition (GRAPPA) acceleration factor, 4; field of view (FOV), 256 mm; voxel size, 1.0 by 1.0 by 1.0 mm], which took 3 min and 8 s to acquire. This anatomical scan had whole brain coverage and was used to plan the slices of the high-resolution functional scans, in combination with the results of a functional localizer scan that were overlaid on it. This overlay showed all regions that were activated by the task (threshold, t > 4.00). The acquisition of this functional localizer directly followed the acquisition of the anatomical scan. Sequence parameters were as follows: 2D EPI, 3-mm isotropic resolution; echo time (TE), 30 ms; TR, 2,000 ms; 30 slices with 10% gap, 64 matrix, and 256 volumes.

A higher resolution structural scan with limited coverage was acquired, which was later used to construct cortical surfaces that were used to assign voxels to cortical depth bins. This scan had an isotropic resolution of 0.75 mm and 80 slices, other sequence parameters being identical to the whole-brain protocol. The center of the acquisition slab was aligned with the center of the slab of the high-resolution functional scans.

The high-resolution functional scans were acquired using a 3D EPI sequence (60). Sequence parameters were as follows: TE, 30 ms; TR, 79 ms; 18° flip angle; 0.75-mm slice thickness; GRAPPA acceleration factor, 4; FOV, 192 mm; voxel size, 0.75 mm isotropic. The vendor’s default fat suppression was used. During piloting, we found that data quality improved markedly when using a large bandwidth-time product of 12 for the excitation pulse. Forty-eight slices were acquired, resulting in a volume acquisition time of 3.792 s. Slices were planned over the main activated regions in the visual cortex, based on the online analysis of the localizer task. In total, 219 functional images were recorded in each session, of which the first 3 images were discarded. To be able to measure EEG signals with as little interference as possible from the scanner, the scans were paused every three volumes for 3.792 s (i.e., one volume of pause). During this time, the stimuli were presented, and the EEG responses were recorded. The peak BOLD response had about a 6-s delay with respect to the stimulus onset. The BOLD response related to the visual stimulation therefore reached its peak approximately at the end of the first/beginning of the second volume after the pause block. The irregular excitation pattern (48 × 3 excitations spaced by 79 ms, followed by a pause of 3.792 s before the next excitation) caused the pseudo steady state of the MR signal to be perturbed. The perturbation was very regular, however, and was modeled in the GLM with an exponential sawtooth pattern that was computed from the gray matter signal (see Statistical models).

The functional scans were preceded and followed by 3-min field map measurements. The scanner shim settings were fixed after the first field map to make sure its results remained valid throughout the session. The field maps were acquired to help us perform a geometric distortion correction on the data. During the analysis stage, however, other research in our group resulted in an image-based distortion correction method for laminar analyses with superior performance, which was used instead. This method is summarized below in Laminar-Level fMRI Analysis.

The task activated a large part of the visual cortex. To be able to discriminate V1, V2, and V3, retinotopy was performed. FMRI data were acquired using a standard 2D EPI sequence with 2-mm isotropic resolution. Sequence parameters were as follows: TE, 30 ms; TR, 1,500 ms; flip angle, 70°; 2.5-mm isotropic resolution; 24 slices; 64 matrix; 260 volumes were acquired.

Laminar-Level fMRI Analysis.

The laminar fMRI analysis was performed following the strategy outlined in an earlier laminar fMRI paper (61), with the inclusion of a new method to correct geometric distortions. The high-resolution 0.75-mm structural MPRAGE data were processed in Freesurfer (62, 63) to obtain a white matter (WM)–gray matter (GM) boundary surface mesh and a GM–pial surface boundary.

These surface meshes were overlaid on the high-resolution functional data after coregistration of the anatomical and average functional volume with the spm_coreg function in SPM (64). However, differences in geometric distortion resulted in suboptimal boundary assignments in the functional data. This result was addressed using an in-house implementation of Boundary Based Registration (BBR) (65) that was modified to work recursively on ever smaller scales (66). The initial WM–GM surface mesh was fed into the BBR algorithm that calculated linear transformations of the mesh with a cost function to maximize the contrast gradient through the boundary. This contrast gradient is maximal when all white matter is on one side and all gray matter on the other. The same transformation was applied to the other surface mesh. The mesh was then split into parts, and the process was repeated for each of these to get a more optimal local transformation. This process was repeated several times such that each partition received a registration based on the local distortions. The registration of all subjects was visually inspected.

After the meshes were aligned with the functional data, sampling intervals were drawn perpendicular to the cortex from each vertex of a mesh to its corresponding vertex on the other mesh. By sampling the functional data along these lines, through-cortex profiles of the fMRI signal were created using nearest-neighbor sampling as motivated earlier in Koopmans et al. (61). During this sampling step, the cortical depth assignment was corrected for the cortical folding pattern according to the Bok principle (67–69). The resulting laminar profiles consisted of 21 bins.

To determine functional areas, retinotopy and main task GLM results were projected on the surface mesh representations, and regions of interest (ROIs) were drawn assigning each of the activated nodes on the meshes to a particular functional area. For the task activation, we first selected the 10% most activated nodes within each region in each hemisphere in terms of t values, using a regressor that modeled the visual stimulation period (see Statistical models for a description of the design matrix). For each cortical depth, a t value was computed. These t values were averaged over the cortical depth for each node. For this average, the top five bins (i.e., 25%) were not used to minimize the effect of larger veins on top of the cortex. All of the profiles for each area were averaged (500–3,000, depending on area size) to form a single profile for that area for each time point. The resulting data for each area, 21 × 216 arrays (bins × time points), were fed into a GLM containing EEG-based regressors. Because taking the top 10% activated vertices is an arbitrary selection criterion, we also calculated these region of interest signals based on the top 5% and top 25% activated vertices.

To investigate whether the patterns of observed laminar BOLD–EEG power relation were specific for the visual cortex or more general throughout the brain, we repeated the analysis above for nonactivated parts of the frontal cortex. The anterior part of the field of view did contain nonvisual regions, but, because each individual’s imaging slab was tilted at an angle determined by the task-activated regions in the early visual cortex, the anterior parts did not cover the same area in each subject. Therefore, we selected all vertices in the anterior part in the field of view for which the average t value over cortical depths for the activation contrast was between −1 and 1. For each cortical depth, the signals were averaged over all selected vertices.

EEG Acquisition.

EEG data were recorded with a custom-made MRI-compatible cap equipped with copper wired Ag/AgCL electrodes, including current limiting resistors (Easycap). Data were recorded from 63 scalp sites organized according to the international 10–20 system. One dedicated electrode was placed on the sternum to record the ECG. The reference electrode was placed at FCz. A 250-Hz low-pass analog hardware filter was placed between the electrode cap and the two MRI-compatible EEG amplifiers (BrainAmp MR plus; Brainproducts). The EEG was recorded with a 10-s time constant and continuously sampled at 5 kHz. EEG recordings were performed with Brain Vision Recorder software (Brainproducts GmbH).

EEG Data.

Preprocessing.

Downsampling of the EEG data were carried out in Vision Analyzer (Brainproducts GmbH). Further preprocessing was carried out in Fieldtrip (70), in which the data were first rereferenced to the common average. Subsequently, the data were segmented in epochs that started 1,300 ms before onset of visual stimulation and ended 400 ms after visual stimulation. These segments were visually checked for artifacts, and trials with anomalies such as eye blinks and large muscle artifacts were removed. Behaviorally erroneous trials were excluded from further analysis.

ICA-based denoising.

To denoise the data, we used a two-step independent component analysis (ICA) approach adapted from a similar approach proposed by Debener et al. (26). Each ICA step was performed with the FastICA algorithm (71).

In a first step, ICA was performed on the 50- to 90-Hz bandpass-filtered concatenated EEG trials. The time period for estimation of the independent components started 300 ms before the cue and ended at the end of the stimulation period. The unmixing matrix thus obtained was applied to the unfiltered data. The resulting component time courses therefore had a broadband spectral content and were subsequently subjected to a time-frequency analysis as described in the previous section.

For the vast majority of the subjects, we were able to observe a sustained γ-band response in some of the independent component time courses, with some interindividual variation in the peak frequency of this response. In a second step, we again applied ICA, but this time on EEG data that were bandpass-filtered with a narrow band of 20 or 25 Hz (depending on the spectral extent of each subject’s γ-response) around the individually adjusted peak of the sustained γ-response. The unmixing weights of this analysis were again applied on the unfiltered data, and a time-frequency analysis was run on the component time courses.

Components that showed a sustained γ-band response were selected (one to four components for each subject) and projected back to channel level. Finally, these channel-level data were again subjected to a time-frequency analysis, separately for the lower and the higher frequency windows, as described in the previous section. The results of this analysis constitute the basis for the construction of regressors that were used in the integrated EEG–fMRI analysis. With this strategy, we were able to denoise the EEG data across the different frequency bands that have been reported before using the same or similar paradigm (27, 28, 30, 32). In total, we were able to observe these expected effects in 30 of the 34 subjects.

This strategy based on γ-band ICA proved to be the best strategy for denoising the EEG data across the different frequency bands, as has been previously reported (27). For comparison, we also applied ICA on 3- to 30-Hz bandpass-filtered data. After applying the unmixing weights on the unfiltered data, we selected the components that demonstrated a sustained decrease in the α- and β-bands and a topography of mixing weights with a posterior focus. These components were backprojected to channel level.

Time-frequency analysis.

Time-frequency analyses of the EEG data were carried out in Fieldtrip using a multitaper approach (72). To optimize the trade-off between time and frequency resolution, we carried out separate analyses for a lower frequency window (2.5–30 Hz) and a higher frequency window (30–120 Hz). For the lower frequencies, the power was estimated for windows of 0.8 s length moved across the data in steps of 100 ms. The frequency resolution was 1.25 Hz, and the use of three tapers resulted in a spectral smoothing of ±2.5 Hz. For the higher frequencies, the power was estimated for windows of 0.4 s length moved across the data in steps of 100 ms. The frequency resolution was 2.5 Hz, and the use of seven tapers resulted in a spectral smoothing of ±10 Hz. For both high and low frequencies, power was estimated up until the end of the visual stimulation period.

Eye Monitoring.

During the experiments, eye position and pupil diameter were monitored using a 50-Hz infrared-based camera focused on the left eye through mirrors mounted on top of the head coil (IView X, version 2.8; SensoMotoric Instruments). From the position data, we derived the relative strength of the eye movement by calculating the magnitude of its derivative. The measurement of the pupil diameter allowed us to estimate the approximate surface area of the pupil. To account for outliers of short duration, a five data point-wide median filter was applied. For each of these measurements, trials were extracted starting from 500 ms before cue onset until the end of the visual stimulation period. The 500 ms before the cue was used as baseline before the average response over subjects was calculated. To test the attention effect on pupil diameter, the log ratio of the pupil surface area over the two conditions was calculated. The trial-by-trial measures for the eye movements and pupil area from cue onset until the end of the visual stimulation were the basis for two confound regressors used in our fMRI analysis. For a few subjects in some trials, the data (or parts of) were missing because the software was unable to track the pupil. These parts of the data were replaced with estimates obtained by fitting the average eye movement or pupil response to the remaining data, or the entire trial was replaced by the average if fewer than 10 data points were available for fitting the average response. For one subject, the eye-monitoring data were not usable. For this subject, the regressors were replaced by a regressor based on the average response for each trial and each block over all of the other subjects, which was done because slow adaptation effects over time were observed for most subjects, particularly for the pupil size. The regressors were constructed by convolving the eye movement and pupil area values with the canonical hemodynamic response function in SPM8 and downsampled to one value per fMRI volume.

Integrated EEG and fMRI Analysis.

Regressor construction.

For each subject, the EEG channel with the maximum γ-power increase in the average spectrum over trials (defined as the average increase across time points and trials during visual stimulation in the 55- to 85-Hz band, relative to a 400-ms precue baseline) was selected. In addition, all of the channels were selected that showed a γ-power increase of at least 25% of the γ-power increase from baseline of this channel. These selected channels were used for the construction of regressors for both the low and the high frequencies. Next, considering the analysis of the lower and higher frequency windows separately, EEG-based regressors were constructed for each frequency bin as follows. For each single correct trial, the power time course during the stimulus interval was averaged across the selected channels (no baseline correction). These power time courses were concatenated into one time series. This time series was subsequently convolved with the canonical hemodynamic response function as implemented in SPM8 and downsampled to one value for each scan, taking into account the one volume long pause after every third scan that was used for recording MR gradient-free EEG. This process resulted in one EEG-based regressor for each frequency bin, for both the analysis of the lower and higher frequency bands. Regressor construction for the analysis based on the low-frequency ICA denoising was carried out in the same way, with the exception that channels were selected for which the magnitude of the decrease in power in the 7.5- to 26.25-Hz frequency was at least 25% of the channel with the maximal decrease.

Statistical models.

For the integrated analysis, we first analyzed the three visual regions (V1, V2, and V3). For this analysis, we first converted the laminar-specific signal from left and right V1, V2, and V3 to percent changes from the mean before they were averaged over sessions, hemispheres, and regions. The analyses of the three regions combined were followed up with separate analyses for each of the three visual regions separately, collapsed over sessions and hemispheres. We did this analysis first for the region of interest signals based on the top 10% of task-activated vertices and repeated this analysis for the signals based on the top 5% and top 25%.

For relating trial-by-trial variation in frequency-specific power to variations in the laminar-specific BOLD signal, separate general linear models were constructed for each frequency–cortical depth combination. In these models, the laminar-specific BOLD signal was the dependent variable, and the EEG frequency-specific power-based regressor an explanatory variable. The β-weights of the EEG power regressors over all these models resulted in a 2D depiction of how trial-by-trial variation in EEG power relates to the laminar-specific BOLD signal. Two such representations were constructed: for the low (2.5–30 Hz in 1.25-Hz steps) and high frequencies (30–120 Hz in 2.5-Hz steps).

For each frequency bin, the regressor modeling the single-trial power estimates of that frequency bin was included in the design matrix. All of the other regressors in the design matrix were the same for all frequency bins. These regressors included: (i) four HRF-convolved box-car regressors modeling the four trial types, with the length of the box-car equal to the visual stimulation period; (ii) two regressors modeling the button presses in the two trial types with a speed change; (iii) two regressors modeling the reaction time as a parametric modulation (one for each trial type with a speed change); (iv) separate regressors for each trial type that modeled the behaviorally incorrect trials; (v) the realignment parameters, their squares and derivatives to control for possible movement artifacts; (vi) regressors modeling eye movements and pupil dilation; (vii) a regressor modeling the T1 effect related to the pause after every third scan; and (viii) six sine and six cosine waves with frequencies up to 0.006 Hz, with the skipped volumes accounted for, thus implementing a high-pass filter. In the context of the regressors modeling the task and the parametric regressors modeling the reaction time, the frequency-specific EEG power regressor accounted for the relation between single-trial variations in EEG power and the BOLD signal for the EEG frequency-laminar depth location in question. The regressor modeling the T1 effect was obtained by averaging the global gray matter signal over every first, second, and third scan after a trial separately, and appending these same three values 71 times to form a regressor of 216 data points in length. The gray matter mask was obtained using a unified segmentation approach (73) of the high-resolution anatomical scan.

To investigate the EEG–laminar BOLD relation for each of the four different trial types in our task, we constructed a design matrix with four separate EEG power regressors for these four conditions. The task and confound regressors remained the same as explained above. For this additional analysis, we analyzed only the three visual regions (V1, V2, and V3) taken together and also averaged the β-weights for the EEG regressor over the α- (7.5–12.5 Hz) and γ- (65–92.5 Hz) bands that were found significant in the previous analysis.

For the GLM that was used to compute the activation versus baseline contrast, on which we based our selection of vertices for further laminar-specific analysis, mainly the same regressors were included in the design matrix. Only the EEG power regressors and the eye movement and pupil dilation-based regressors were excluded because they indirectly also model task/attention effects. We used the same design matrix to compute the BOLD attention contrast used for the cortical depth-resolved correlation with EEG power.

We correlated the attention effects in the α- (7.5–12.5 Hz), β- (21.25–27.5 Hz), and γ- (50–80 Hz) bands with the strength of the BOLD attention effect for each cortical depth. For these bands, we averaged over the attention effect, expressed as a log-ratio of the attention-on versus attention-off condition, over all time bins from 500 ms until 1,600 ms after the onset of visual stimulation and all frequency bins within the indicated ranges. Before correlations between attention effects in the different frequency bands and the BOLD signal from the different cortical depths were computed, the attention effect observed in the pupil dilation was removed from both data types by means of linear regression. For each subject, the attention effect in the pupil surface was calculated as the log-ratio of the attention-on versus attention-off condition over the entire length of visual stimulation. This analysis was performed only for the region of interest signals based on the top 10% of activated vertices.

The statistical models described for the trial-by-trial analysis with the three visual regions combined and separately, as well as the correlation of attention effects over subjects, also apply for the control region and for the analysis based on the low frequency-based ICA denoising strategy. For the latter, we applied it only for the top 10% activated vertices.

To investigate how the eye movements and pupil dilation regressors that were included as a confound could possibly influence the EEG–BOLD relation, we calculated the partial correlation (correcting for all task and other confound regressors) of these regressors with the EEG power regressors for each frequency and with the laminar-resolved BOLD signal for the visual regions. We also correlated the attention effect in pupil dilation with the same effects in the laminar-resolved BOLD signal from these regions and with the attention effects in EEG power.

The dependency between frequencies was analyzed by computing the partial correlation and its square between the EEG power-based regressors of all frequencies. In this partial correlation, we controlled for all of the other fixed regressors in the design matrix. Additionally, we correlated the strengths of the attention effects in α-, β-, and γ-power over subjects.

Inferential Statistics.

For the analysis of the behavioral results, we used a two-sided t test to test for a difference in reaction time between the two trial types with a speed change, and the ranked sign test (74) for differences in the number of errors (false alarms and misses) made during the four different trial types and to test for a significant difference from zero of the average correlation of the EEG-based regressors. Significance at the group level for all other effects of interest was evaluated by a cluster-based randomization procedure (33). This procedure effectively controls the type-1 error rate in a situation involving multiple comparisons. This procedure allows for user-defined test statistics tailored to the effect of interest within the framework of a cluster-based randomization test.

For the laminar BOLD–EEG power relation, we first tested for which frequency–cortical depth combinations a significant correlation was observed. Our test statistic was a single-sample t-score of the average β-value compared with zero over sessions for the EEG-based regressor, giving uncorrected P values. All data points that did not exceed a preset threshold level were zeroed. Clusters of adjacent nonzero frequency–cortical depth points were computed, and, for each cluster, a cluster-level test statistic was calculated by taking the sum of all of the individual t-statistics within that cluster. This statistic was entered in the cluster-based randomization procedure. To obtain a randomization distribution to compare with the observed clusters, we randomly multiplied the β-weights for each subject with 1 or −1. For each randomization, we computed the cluster-sums of subthreshold t-values and entered the maximum value into the distribution. If no cluster was observed for a randomization, a zero was added. The randomization distribution was based on 10,000 randomizations (also for all of the other tests described here). The corrected P values for the observed clusters are given by their relative position in this distribution. The threshold used to form a cluster was based on the per-data-point permutation distribution of the t-values thus obtained. We thresholded the observed values with the 95th percentile of this distribution to obtain cluster candidates. Because for α- and β-band we can expect a negative BOLD–EEG power relation and for the γ-band a positive relation (27), the tests were carried out one-sided.

We constructed a test based on this cluster-based randomization technique for the interaction between frequency and cortical depth to examine how EEG power is related to the BOLD signal. We constructed a procedure to test whether the profile over cortical depths of how EEG power relates to the BOLD signal is different for different frequency bands. For any frequency this profile is given by the β-estimates of the EEG power-based regressors. If the way two different frequencies relate to the BOLD signal is the same, we can assume these profiles of β-weights are the same, except for a possible linear transformation. A linear transformation was allowed because a unit change in the power of one frequency (e.g., γ-power) can be related to a different change in the BOLD signal than a unit change in another frequency (e.g., α-power). Furthermore the sign of the relation between two frequency bands is known to differ for different frequency bands. The test we constructed tested whether or not the two profiles were significantly different after a linear transformation that fits the one profile onto the other by linear regression using a least-squares criterion. When the profiles are the same after allowing for this linear transformation, there should not be a systematic misfit between two profiles corresponding to two different frequencies. When the profiles do systematically differ, this difference should result in systematic overfitting or underfitting for certain cortical depths over subjects. Our test was designed to be sensitive for these differences, by first computing over subjects for each cortical depth, whether or not the fitted profile differs from the original profiles it is fitted to by means of computing a t-statistic. Cluster sums were subsequently computed by summing the t-values over points at adjacent suprathreshold cortical depths. Using the cluster-based randomization procedure explained above, we could then test whether these clusters systematically differed from zero. The randomization distribution could be obtained by randomly shuffling the labels for the fitted and not-fitted profiles. If at least one cluster for a pair of profiles of two frequencies survived this procedure, we could conclude that the two frequencies had different profiles over the cortical depth regarding how EEG-power relates to the BOLD signal. In other words, there is a significant power by cortical depth by frequency interaction in how trial-by-trial EEG power variations relate to changes in the BOLD signal.

For V1, V2, and V3 combined, we applied this procedure by fitting the average profile for the 7.5- to 12.5-Hz frequency bins to every other frequency bin for both the low- and high-frequency analyses. We chose the profile for the α-band as the reference profile because it has most often been reported to be related to the BOLD signal (23–25, 27) and also because, in our study here, it showed a negative relation with the BOLD signal in all three regions. Our fitting of the profile of this frequency to the profile of every frequency bin allowed us to cluster not only over cortical depth, but also over frequencies. Clusters here therefore indicate frequency ranges in which the profile of the relation to the BOLD signal over cortical depths deviated from that for α-power. For this analysis, we observed one significant cluster in the high-frequency range from 65 to 107.5 Hz. For the three regions separately, we repeated this step for only this frequency range by testing whether the fitted α-band profile differed from the average profile in this frequency range. Clustering was carried out only in the cortical depth dimension here. Because both overfits and underfits can occur, this test was carried out two-sided. Positive and negative cluster sums were computed from data points that exceeded the 5% most positive or negative data points of the randomization distribution.

We tested whether the strength of the attention effects observed in the α-, β-, and γ-bands in the EEG correlated with the strength of the BOLD attention effect at varying cortical depths over subjects. Clustering for this test took place over the cortical depth dimension. The randomization distribution was obtained by randomizing the pairing between the two modalities over the subjects. The tests were carried out one-sided because negative correlations were expected for the α- and β-band effects, and positive effects for the γ-band effect. Clusters were formed based on uncorrected one-sided tests of the correlation. All data points exceeding the preset uncorrected significance level of 5% were included in a cluster.

For testing the differences between the attention-on and attention-off conditions in the laminar fMRI, EEG, and eye-tracker data, the randomization distribution was obtained by randomly assigning the attention-on and -off labels within a subject. We tested the attention effect in the average time-frequency representation of power over the selected channels after back-projection of the selected independent components. For each subject, the attention effect was calculated as the log-ratio between the attention-on and attention-off conditions. Clustering was done based on adjacency in both time and frequency. The threshold was based on the 95th percentile of the randomization distribution for each data point. For the basic BOLD–attention effect, a one-sided test was performed because a positive effect of the attention modulation was expected, and clustering was done in the cortical depth dimension. For testing the attention effects in eye movements and pupil dilation effects, clustering took place in the time dimension, and the time between cue onset and visual stimulation offset was considered. Two-sided tests were carried out here. Because the ICA components were selected on the presence of a baseline change from in the γ- and α/β-frequency bands, this change was not tested. The selection was, however, not based on the presence of an attention effect.