Credit assignment in movement-dependent reinforcement learning

Significance

Thorndike's Law of Effect states that when an action leads to a desirable outcome, that action is likely to be repeated. However, when an action is not rewarded, the brain must solve a credit assignment problem: Was the lack of reward attributable to a bad decision or poor action execution? In a series of experiments, we find that salient motor error signals modulate biases in a simple decision-making task. This effect is independent of the participant’s sense of control, suggesting that the error information impacts behavior in an implicit and automatic manner. We describe computational models of reinforcement learning in which execution error signals influence, or gate, the updating of value representations, providing a novel solution to the credit assignment problem.

Abstract

When a person fails to obtain an expected reward from an object in the environment, they face a credit assignment problem: Did the absence of reward reflect an extrinsic property of the environment or an intrinsic error in motor execution? To explore this problem, we modified a popular decision-making task used in studies of reinforcement learning, the two-armed bandit task. We compared a version in which choices were indicated by key presses, the standard response in such tasks, to a version in which the choices were indicated by reaching movements, which affords execution failures. In the key press condition, participants exhibited a strong risk aversion bias; strikingly, this bias reversed in the reaching condition. This result can be explained by a reinforcement model wherein movement errors influence decision-making, either by gating reward prediction errors or by modifying an implicit representation of motor competence. Two further experiments support the gating hypothesis. First, we used a condition in which we provided visual cues indicative of movement errors but informed the participants that trial outcomes were independent of their actual movements. The main result was replicated, indicating that the gating process is independent of participants’ explicit sense of control. Second, individuals with cerebellar degeneration failed to modulate their behavior between the key press and reach conditions, providing converging evidence of an implicit influence of movement error signals on reinforcement learning. These results provide a mechanistically tractable solution to the credit assignment problem.

When a diner reaches across the table and knocks over her coffee, the absence of anticipated reward should be attributed to a failure of coordination rather than diminish her love of coffee. Although this attribution is intuitive, current models of decision-making lack a mechanistic explanation for this seemingly simple computation. We set out to ask if, and how, selection processes in decision-making incorporate information specific to action execution and thus solve the credit assignment problem that arises when an expected reward is not obtained because of a failure in motor execution.

Humans are highly capable of tracking the value of stimuli, varying their behavior on the basis of reinforcement history (1, 2), and exhibiting sensitivity to intrinsic motor noise when reward outcomes depend on movement accuracy (3–5). In real-world behavior, the underlying cause of unrewarded events is often ambiguous: A lost point in tennis could occur because the player made a poor choice about where to hit the ball or failed to properly execute the stroke. However, in laboratory studies of reinforcement learning, the underlying cause of unrewarded events is typically unambiguous, either solely dependent on properties of the stimulus or on motor noise. Thus, it remains unclear how people assign credit to either extrinsic or intrinsic causes during reward learning. We hypothesized that, during reinforcement learning, sensorimotor error signals could indicate when negative outcomes should be attributed to failures of the motor system.

To test this idea, we developed a task in which outcomes could be assigned to properties of the environment or intrinsic motor error. We find that the presence of signals associated with movement errors has a marked effect on choice behavior, and does so in a way consistent with the operation of an implicit learning mechanism that modulates credit assignment. This process appears to be impaired in individuals with cerebellar degeneration, consistent with a computational model in which movement errors modulate reinforcement learning.

Results

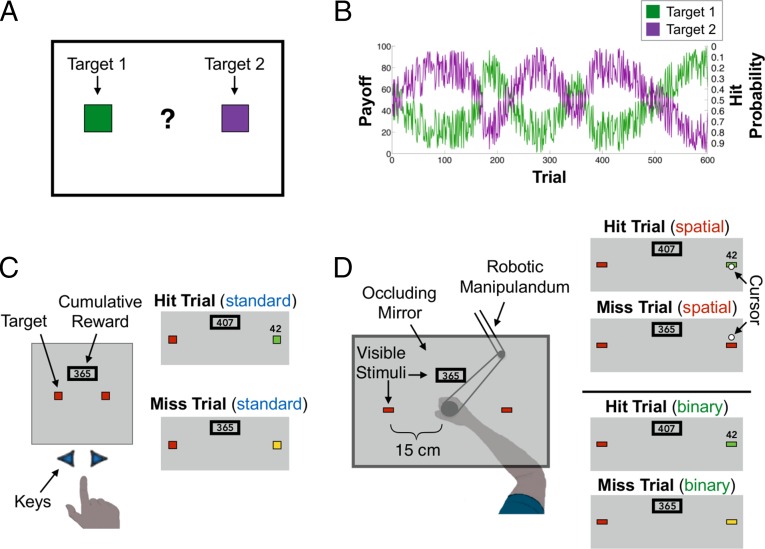
Participants performed a two-armed “bandit task” (ref. 1, Fig. 1A), seeking to maximize points that were later exchanged for money. For all participants, the outcome of each trial was predetermined by two functions: One function defined if a target yielded a reward for that trial (“hit” or “miss”), and the other specified the magnitude of reward on hit trials (Fig. 1B). The expected value was equivalent for the two targets on all trials; however, risk, defined in terms of hit probability, was not. Under such conditions, people tend to be risk-averse (2, 6).

Fig. 1.

Design. (A) Participants performed a two-armed bandit task, choosing between two targets to maximize monetary payoff. (B) Two reflected, noisy sinusoids defined the payoff value (left axis) and probability of reward (hit, right axis, inverted) for the targets. (C) In the Standard condition, participants selected targets by pressing the left or right arrow keys on a keyboard. Example hit and miss trials are shown on the right. (D) In the Spatial and Binary conditions, participants reached to the selected target using a robotic manipulandum. Vision of the hand was occluded. In the Spatial condition, a small cursor appeared after the hand passed the target. On hit trials, the cursor overlapped with the target; on miss trials, the cursor appeared outside the target. Feedback in the Binary condition matched the Standard condition.

We manipulated three variables: The manner in which participants made their choices, the feedback on “miss trials,” and the instructions. In experiment 1, participants were assigned to one of three conditions (n = 20/group). In the Standard condition, choices were indicated by pressing one of two keys, the typical response method in bandit tasks (1, 2). Points were only earned on hit trials (Fig. 1C). The participants were instructed that they had no control over whether a given trial was a hit or miss.

In the Spatial condition, participants made reaching movements to indicate their choice on each trial, allowing us to assess the effect of perceived movement errors. A cursor indicated the terminal position of the reach (Fig. 1D). Participants were informed that they would earn a reward only when the cursor landed on the target. Unbeknownst to them, the visual feedback was occasionally perturbed to impose a predetermined outcome schedule (Fig. S1). The visual feedback on trials in which the cursor landed outside the target constitutes a form of a sensory prediction error, a mismatch between a predicted and observed sensory outcome (7–9). We hypothesized that this could serve as a signal that the absence of an expected reward should be attributed to an error in movement execution.

Fig. S1.

Behavior is similarly affected by veridical and perturbed feedback. In keeping with standard bandit tasks in the human neuroscience literature, we used a fixed outcome schedule for all participants. This required us to occasionally present false feedback in the reaching conditions, sometimes indicating that an accurate reach missed the target and sometimes indicating that an inaccurate reach had hit the target. This was accomplished by subtly displacing the feedback cursor in the Spatial condition or giving the opposite color cue in the Binary condition. We conducted a series of pilot studies to identify factors that minimized the likelihood that participants would become aware of these manipulations. One factor was the inclusion of a bounded zone within which reaches had to be executed to receive outcome feedback: If the subject deviated more than 2 cm from a straight-line path to the target during any portion of the reach, the trial was terminated and restarted, and the participant received a “Too Far” feedback message. Furthermore, to make the movement more challenging, reaches had to be rapid, completed within 400 ms. Thus, the reaching conditions were designed so that the feedback “felt” veridical given the limited range of final hand and cursor positions. We obtained survey data at the end of each session, and there was little indication that the participants were aware of the feedback manipulation. Moreover, participant’ responses on questions assessing control showed no differences between the Spatial and Binary conditions (Kruskal−Wallis rank sum test on Likert scale responses, P = 0.49). Nonetheless, it is possible that altered feedback produces implicit changes in behavior, relative to trials in which the feedback was veridical. This concern is especially relevant for the Spatial condition in which the exact position of the cursor is frequently manipulated. However, the direction of this effect is not clear: Would contrived feedback increase the likelihood that a participant would revisit a given target or decrease that likelihood? We sought to conduct an analysis that was agnostic to any a priori predictions about behavior. We conducted an analysis on the effect of contrived feedback for the data from the Spatial condition using an expanded TD model. Here we used a version of our gating model with four learning rate parameters to allow for separate learning rates depending on both the outcome of the trial (hit versus miss, as in the basic credit assignment model) and the veridicality of the feedback (perturbed versus veridical, denoted with *),

$$\begin{array}{l}{V}_{t+\mathit{1}}\left(x|hi{t}_t\mathit{;FBveridical}\right)=V_t\left(x\right)+{\alpha }_{hit}{\delta }_t\\ V_{t+\mathit{1}}\left(x|mis{s}_t\mathit{;FBveridical}\right)=V_t\left(x\right)+{\alpha }_{miss}{\delta }_t\\ V_{t+\mathit{1}}\left(x|hi{t}_t\mathit{;FBperturbed}\right)=V_t\left(x\right)+{\alpha }_{hit\ast }{\delta }_t\\ V_{t+\mathit{1}}\left(x|mis{s}_t\mathit{;FBperturbed}\right)=V_t\left(x\right)+{\alpha }_{miss\ast }{\delta }_t\end{array}$$

Using the fitting procedure described in Modeling Analysis, we found no difference between optimized parameter values for α_hit and α_hit* [t_(1,38) = 0.49, P = 0.62] nor α_miss and α_miss* [t_(1,38) = 0.03, P = 0.97], suggesting comparable learning following perturbed versus veridical feedback. Moreover, this model, after a complexity penalty, performed worse than the original gating model (BIC difference = 1,223). Thus, we believe that the use of occasional perturbed feedback did not distort the results of the current experiments.

In a third, Binary condition, participants also reached to indicate their choices but were not provided with cursor feedback; thus, they received the same feedback as participants in the Standard condition (Fig. 1D). Eliminating cursor feedback should yield a less salient sensory prediction error, one limited to proprioception.

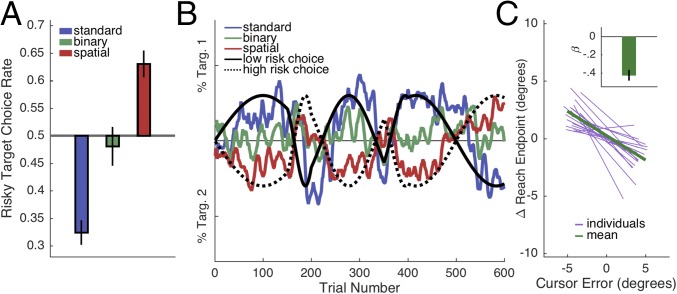
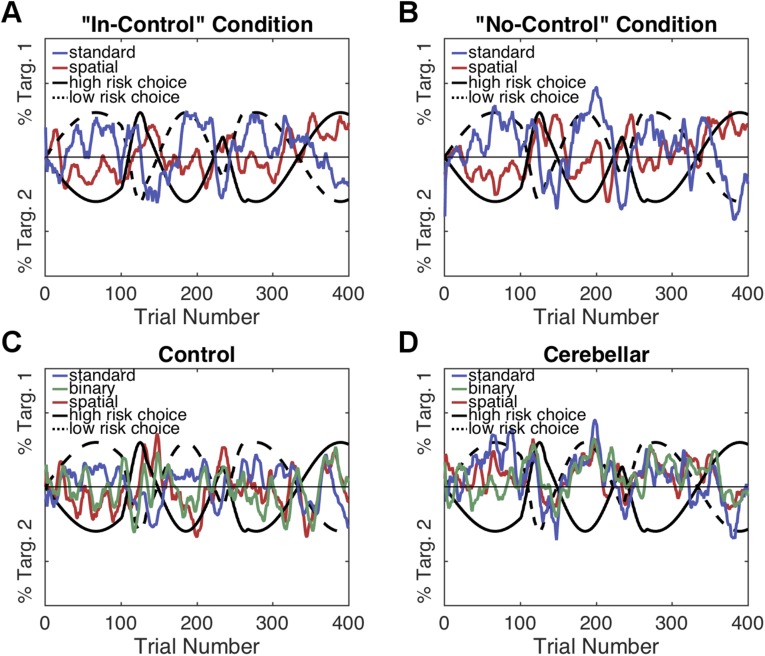
There was no optimal behavior in this task, because the expected values of each option were matched on every trial. Nonetheless, we observed significant choice biases that varied dramatically across the conditions [Fig. 2A; F_(2,57) = 30.10, P < 0.001, all paired comparisons, P < 0.01]. Consistent with previous work (2), the Standard group exhibited a strong risk-averse bias that was significantly different from the neutral bias value of 0.5 [t_(1,19) = −7.88, P < 0.001], preferring choices with high hit probabilities over large rewards. In contrast, the Spatial group exhibited a markedly different pattern, preferring choices with high rewards over high hit probabilities [t_(1,19) = 5.33, P < 0.001]. The opposing biases in the Standard and Spatial groups were consistent throughout the session, with participants tracking the safer and riskier targets, respectively (Fig. 2B). The attenuation of risk aversion observed in the Spatial group did not require a visual error signal: The bias in the Binary condition was not significantly different from chance [t_(1,19) = −0.55, P = 0.59].

Fig. 2.

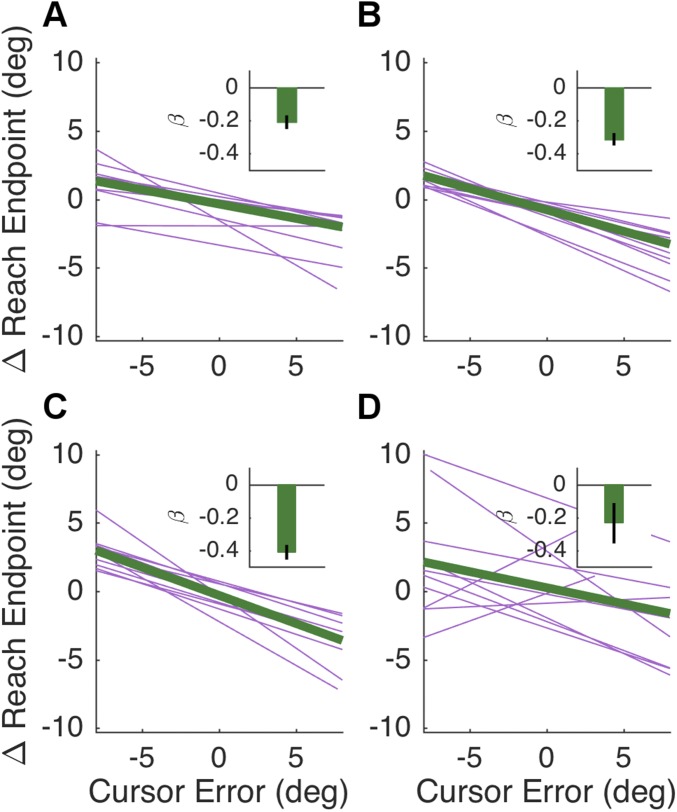
Experiment 1. (A) Risky target choice rate was calculated by dividing the number of risky choices (choosing the target with the lower hit probability on that trial) by the total number of trials. (B) Group-averaged target preferences over time. Choices were backward-smoothed with a 10-trial bin. (C) Mean change in reach direction, relative to error direction, calculated on a trial-by-trial basis in the Spatial condition. The data here are restricted to pairs in which the first trial was a miss trial due to false feedback. The mean function (green) is a line given by the average of the group’s regression coefficients, and the purple lines are individual regression functions, bounded by each participant’s maximum cursor error in both directions. (Inset) Group mean regression weights (β). Error bars depict 1 SEM.

These results are consistent with the hypothesis that movement-related error feedback can signal when negative outcomes should be attributed to failures of the motor system. Before considering how this hypothesis can be incorporated in a computational model of choice behavior, we examined a more direct reflection of the participants’ sensitivity to the movement feedback. Motor execution errors should drive adaptation of the movements themselves, resulting in subtle trial-by-trial changes in reach direction subsequent to miss trials in the Spatial condition (10). To confirm the presence of adaptation, we analyzed how the error on trial t affected the reach direction on the next trial t + 1. We restricted our analysis to pairs of trials where, on the first trial, the participant hit the target but received false miss feedback. This was done because regression to the mean (e.g., the center of the target) would also predict a negative correlation between successive reach directions when the first reach was a true miss with veridical feedback (see Supporting Information for details). Consistent with the adaptation prediction, movement direction on trial t + 1 following miss trials was negatively correlated with the signed cursor error on trial t [Fig. 2C; µ of regression weights β = −0.43, t_(1,19) = −7.30, P < 0.001].

To explore how movement errors might influence choice behavior, we examined several variants of a temporal difference (TD) reinforcement learning model (1, 2, 11). Current variants treat motor-related variables as factors influencing subjective utility (4). It is unclear if such models could account for the radical change in behavior observed in our experiment. Moreover, these models do not directly address the credit assignment problem at a mechanistic level. Thus, we compared basic and subjective utility variants of the TD model (see Supporting Information for details) to two other models that offer different mechanistic accounts of how execution errors might influence choice behavior.

We developed a gating model to capture a process whereby sensorimotor error signals act to preclude, or “gate,” the updating of value representations during reinforcement learning. In the gating model, movement errors directly modulate processes involved in value updating. To implement this, we allowed value updates to occur at different rates following hit and miss trials,

$$\begin{array}{l}{\delta }_t=r_t-V_t\left(x\right)\\ V_{t+\mathit{1}}\left(x|hi{t}_t\right)=V_t\left(x\right)+{\alpha }_{hit}{\delta }_t\\ V_{t+\mathit{1}}\left(x|mis{s}_t\right)=V_t\left(x\right)+{\alpha }_{miss}{\delta }_t\end{array}$$

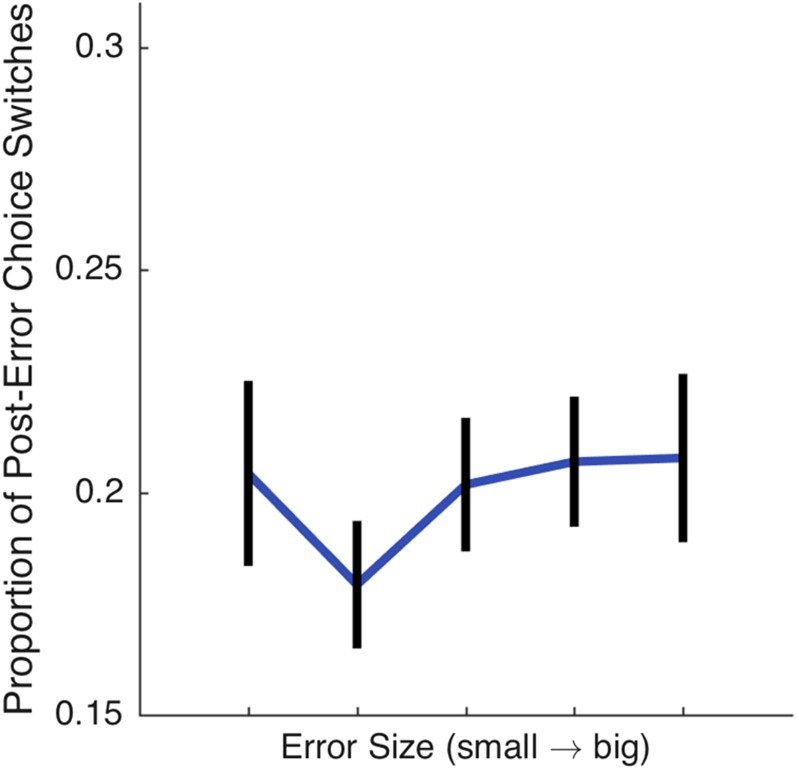
where V_t(x) is the value of target x at trial t, α is the learning rate, and δ is the reward prediction error, the difference between expected (V_t) and observed (r_t) reward. Target values were transformed into choice probabilities using the standard softmax function. By having two learning rates, the model can differentially scale the reward prediction error. When α_miss is low, the estimate of the target’s value changes minimally after a miss trial, in effect offloading “credit” for the failed outcome from the target to a different source (e.g., movement error). When α_miss is high, the value is updated at a relatively faster rate, assigning credit for the failed outcome to the target. We opted to treat hits and misses in a binary manner for simplicity, and because the size of visual errors in the Spatial group did not influence choice behavior, suggesting that decision-making was influenced by action errors in an all-or-none manner (Fig. S2).

Fig. S2.

Visual error size and choice behavior in experiment 1. For the Spatial condition of experiment 1, we examined whether the size of the visual error, the distance between the cursor and the target, affected choice behavior. To this end, we analyzed the miss trials that led to target choice switches, dividing them, for each participant, into five equally spaced bins based on the size of the observed visual cursor error (µ error ≈ 0.35 cm). An ANOVA revealed that the size of the visual feedback error on miss trials did not influence the likelihood that the participant would change their target preference after such trials [F_(4,95) = 0.49, P = 0.75].

In the probability model, the probability of reward is explicitly represented and incorporated into learning. To implement this, the probability of reward and the magnitude of reward (“payoff”) were separately tracked,

$$\begin{array}{l}{\delta }_{prob,t}=r_t^{\ast }-{\widehat{\text{p}}}_t\left(x\right)\\ {\widehat{\text{p}}}_{t+\mathit{1}}\left(x\right)={\widehat{\text{p}}}_t\left(x\right)+{\alpha }_{prob}{\delta }_{prob,t}\\ E_{t+\mathit{1}}\left(x|hit\right)=E_t\left(x\right)+{\alpha }_{payoff}{\delta }_{payoff,t}\\ V_{t+\mathit{1}}\left(x\right)={\widehat{\text{p}}}_{t+\mathit{1}}\left(x\right)E_{t+\mathit{1}}\left(x\right)\end{array}$$

where p̂_t(x) is the participants’ estimate of the probability that target x will yield a hit on trial t, and E_t(x) is the expected payoff magnitude from target x on trial t. Separate learning rates (α_payoff, α_prob) update distinct reward prediction errors, where δ_payoff is equivalent to the standard reward prediction error used in the gating model and δ_prob is a reward prediction error that uses a binary reward r*_t that takes on a value of 1 or 0 based on whether trial t was a hit or miss, respectively. Payoff estimates (E) are only updated after hits. The payoff (E) and probability (p̂) terms are multiplied to yield the total value V. It should be noted that, as framed by the instructions for experiment 1, p̂ refers to different properties of the task depending on whether the responses are made by key presses or reaches. In the Standard condition, p̂ represents the participant’s estimate of the likelihood that a target/response pair yields reward. In the Binary and Spatial conditions, p̂ represents a form of conditional probability, including both the participant’s estimated likelihood of successfully reaching the target and the target subsequently yielding a reward.

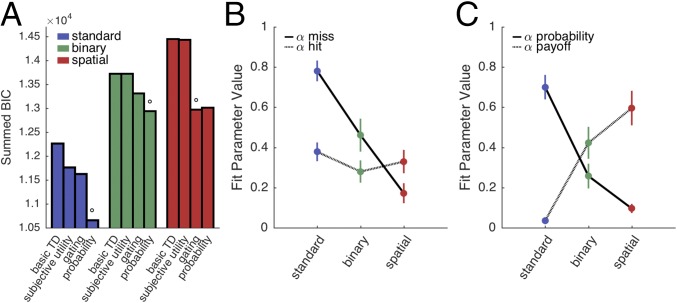
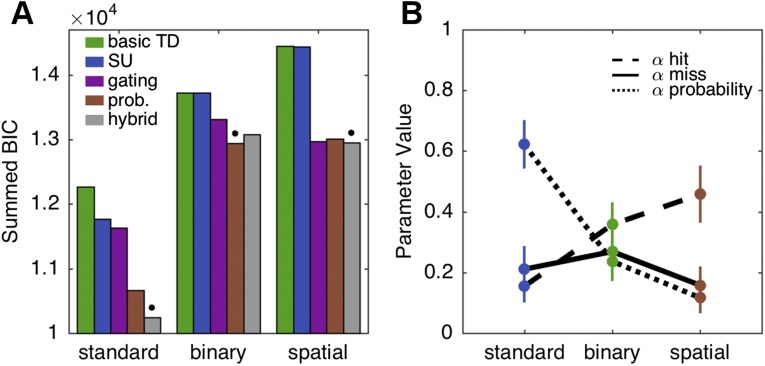
The gating and probability models both outperformed the basic and subjective utility models in all conditions (Fig. 3A). The probability model outperformed the gating model in the Standard and Binary conditions, whereas the gating model outperformed the probability model in the Spatial condition. All reported best-fitting models outperformed the next-best performing model by a summed Bayesian Information Criterion (BIC) difference of at least 40, corresponding to a significantly better fit (see Supporting Information).

Fig. 3.

Modeling analysis. (A) Summed BIC values for each model and experimental condition. Lower values imply better fits. The gating and probability models outperformed both the subjective utility and basic TD model in all conditions. Open circles specify the best-fitting model in each condition. Best-fitting models were, according to the BIC metric, significantly more likely to explain the data than the next-best-fitting model. (B) Parameter values for the gating model, indicating learning rates for value updating following miss (black line) or hit (grey line) trials. (C) Parameter values for the probability model, indicating learning rates for value probability updating (black line) and payoff magnitude (grey line). Error bars depict 1 SEM.

Parameter fits of the gating model suggest how participants assigned credit for outcome errors to either movement execution or the environment [Fig. 3B; interaction term: F_(1,19) = 13.52, P < 0.001]. In the Standard condition, the value of α_miss was high, capturing participants’ bias to penalize targets on trials in which the bandit failed to yield an expected reward. The value of this parameter was reduced in the two reaching conditions. Indeed, the mean value is quite low in the Spatial condition: In the presence of a salient signal indicating the direction of a movement error, there is minimal change in value representation because of an attenuated, or gated, reward prediction error. In contrast, fitted values of α_hit were similar across conditions, suggesting that the weight given to payoff magnitude was independent of the form of response used to obtain that reward.

The pattern of parameter fits in the probability model showed a pronounced trade-off across the three conditions [Fig. 3C; interaction term: F_(1,19) = 48.85, P < 0.001]. Execution errors and reward magnitude modulated learning in different ways as a function of the mode of response and type of feedback. The parameter values indicate that the Standard group was more sensitive to the probability of reward relative to reward magnitude, a pattern consistent with risk aversion. In contrast, the behavior of the Spatial group was most sensitive to reward magnitude, with the parameter values suggesting that these participants did not incorporate an estimate of the probability of motor success into value updating.

The above results raise the following questions: Do motor errors provide a direct, “model-free” modulation of reinforcement learning from which intelligent credit assignment is an emergent property? Or are participants explicitly representing their motor competence and incorporating this information into the value estimates? The instructions in the reaching conditions emphasized that misses were the result of execution errors, and the data suggest that our manipulation of the feedback was effective. As reported in postexperiment questionnaires, participants were unaware that the feedback had been manipulated, and, behaviorally, participants responded in a similar manner following veridical and perturbed feedback (Fig. S1). In contrast, for the key press (Standard) group, the instructions of experiment 1 emphasized that misses were due to the environment. Thus, the difference in choice biases between the key press and reaching groups may reflect a difference in how subjects explicitly perceived their degree of control over choice outcomes.

We examined this question in a second experiment, crossing two factors, response mode and instruction, in a 2 × 2 design (n = 10/group). For the key press groups, participants received either the same instructions given to the Standard condition in experiment 1 (“No-Control”) or an “In-Control” set of instructions. For the latter, it was emphasized that how they performed the key presses would determine if a trial was a hit or miss. Similarly, for the reaching groups, participants either received the same instructions given to the Spatial condition in experiment 1 (In-Control), or were informed that the trial outcome (hit/miss and position of cursor) was entirely independent of their reach endpoint (No-Control). Two markers suggest that the participants were sensitive to the instructions: First, participants in the Spatial In-Control condition displayed significantly slower movement times than those in the Spatial No-Control condition [t_(1,18) = −2.23, P < 0.05], perhaps reflecting a greater premium on movement accuracy when the participant has a sense of control. Second, participants in the Standard In-Control condition reported trying different strategies concerning a solution on how to effectively make key presses yield rewards.

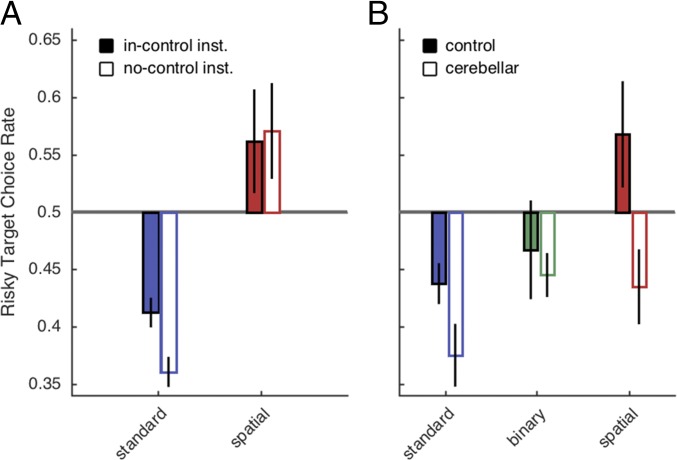
Replicating the results of experiment 1, participants in the Standard No-Control condition showed a strong risk-averse bias, whereas participants in the Spatial In-Control condition showed the opposite bias (Fig. 4A). Critically, these biases were unaffected by instructions: The risk-averse bias persisted for the Standard In-Control condition, and the opposite bias persisted in the Spatial No-Control group. These biases were stable across the experimental session (Fig. S3). There was a main effect of response mode [F_(1,36) = 31.29, P < 0.001] but not instruction [F_(1,36) = 0.44, P = 0.51], and there was no interaction [F_(1,9) = 0.89, P = 0.35]. Thus, the observed biases in choice behavior appear to be the product of an implicit mechanism, rather than arising via an explicit assessment of control. In line with this idea, our regression analysis revealed significant reach adaptation in both the No-Control and In-Control Spatial condition (Fig. S4), consistent with previous findings that adaptation is not dependent on task performance but rather is driven solely by sensory prediction error (12, 13). The trial-by-trial adaptation in the No-Control condition is especially striking given the instructions emphasized that reward outcomes and movement error feedback were not linked to movement accuracy.

Fig. 4.

(A) Choice behavior in experiment 2 for the Standard and Spatial conditions as a function of whether the instructions emphasized that the participants had either control or no control over the probability of reward. (B) Choice behavior in experiment 3 for participants with cerebellar degeneration and age-matched controls in the three response conditions: Standard (blue), Binary (green), and Spatial (red). Error bars depict 1 SEM.

Fig. S3.

Tracking behavior in experiments 2 and 3. Tracking behavior in experiments 2 (A and B) and 3 (C and D), using the same analysis as that described in Fig. 2B. Biases in both experiments were persistent over the experimental session.

Fig. S4.

Regression analysis for all subjects in the Spatial condition of experiments 2 and 3, using the adaptation metric discussed in Adaptation Analysis. As reported in Results, regression weights were significantly different from zero in both the In-Control condition [A; β = −0.21, t_(1,9) = 8.33, P < 0.001] and the No-Control condition [B; β = −0.31, t_(1,9) = 5.07, P < 0.001]. In experiment 3, regression weights were significantly different from zero in the control participants [C; β = −0.41, t_(1,9) = −9.20, P < 0.001] and the patient sample [D; β = −0.24, t_(1,9) = 1.92, P < 0.05]. The group difference was marginally significant [t_(1,18) = 1.35, P = 0.09]. Insets depict mean regression coefficients with one SEM.

We reasoned that an implicit system for signaling execution errors might depend on neural regions involved in error-based motor learning. Individuals with cerebellar degeneration often exhibit impairments in sensorimotor adaptation, a deficit that has been attributed to an inability to encode and/or use sensory prediction errors (7, 8, 13). We hypothesized that this impairment might also impact the participants’ ability to resolve, perhaps implicitly, the credit assignment problem, at least when feedback suggests that reward requires coordinated movements.

To examine this hypothesis, individuals with cerebellar degeneration and age-matched controls were recruited for a third experiment (n = 10/group), where they were tested in a counterbalanced within-subject design on the three conditions from experiment 1. Reach adaptation was observed in both groups, and adaptation was marginally attenuated in the cerebellar group [Fig. S4; t_(1,18) = 1.35, P = 0.09]. In terms of choice biases, the control group replicated, within subject, the results of experiment 1 (Fig. 4B). In contrast, the patient group showed a consistent risk-averse bias across all three conditions (Fig. 4B). A repeated measures ANOVA revealed a main effect of condition [F_(1,36) = 6.69, P < 0.01], a main effect of group [F_(1,18) = 4.69, P < 0.05], and a nonsignificant interaction [F_(1,9) = 1.54, P = 0.23]. Based on our a priori hypothesis, a planned direct comparison of the Spatial condition, the condition with the most salient sensory prediction errors, revealed a significant group difference [t_(1,18) = 2.27, P < 0.05], further suggesting that the patients failed to gate reinforcement learning when outcome errors could be attributed to motor errors.

Discussion

Laboratory studies of decision-making generally involve conditions in which choice outcomes are dependent on properties of the stimuli (e.g., stimulus A yields greater rewards than stimulus B; stimulus B has higher reward probability than stimulus A). However, in natural settings, outcomes frequently depend on the organism’s ability to execute a coordinated action: A hungry osprey not only faces the challenge of detecting the silhouette of a striped bass but must accurately execute her attack. We set out to ask how decision-making processes incorporate information about action execution and, in particular, solve the credit assignment problem that arises when an expected reward is not obtained. Execution errors strongly modified choice biases, and this effect was graded by the salience of the error feedback. The mechanism driving this behavior appears to be implicit, and is affected in individuals with cerebellar degeneration.

Previous studies have examined the impact of motor noise on choice behavior (4), focusing on how representations of motor competence influence subjective utility functions. However, such descriptive accounts do not provide a mechanism concerning how motor errors influence the representation of extrinsic value. Our gating and probability models posit a set of mechanisms by which reinforcement learning might be modified when an error is, or is not, assigned to movement execution. A sensory prediction error could gate processing within the reinforcement learning network by attenuating a negative reward prediction error signal directly and/or by attenuating the update of value representations based on negative prediction error signals. Alternatively, sensory prediction errors could be incorporated into a distributed value representation that includes an internal model of motor competence that estimates the probability of reach errors.

Central to these mechanisms is the notion that an error in motor execution is communicated to the reinforcement learning system. Although there are various ways in which this information could be signaled, the results of experiment 3 point to a potential role for the cerebellum. Computationally elegant models have been developed in which the cerebellum contributes to motor learning by using sensory prediction errors to adapt the sensorimotor system (7, 8, 14). More recently, the cerebellum has been shown to have extensive anatomical and functional connections with subcortical and cortical regions—specifically, regions strongly associated with decision-making and reinforcement learning, including the ventral tegmental area, striatum, and prefrontal cortex (15–22). To date, the functional role of these pathways has been unclear. Our findings suggest that the cerebellum may not only be essential for using movement errors to improve motor control but may also communicate this information to neural regions associated with decision-making.

How these error signals interact with value updating remains an open question. Individuals with cerebellar degeneration frequently experience execution errors in their everyday life. Thus, it is reasonable to assume they have a strong “prior” to expect motor errors (23), information which could be incorporated into action selection. This would suggest that the patients may not have a problem with trial-by-trial credit assignment per se. Rather, their low estimate of motor competence may bias them to prefer safe choices, even when no particular behavior is optimal. However, this hypothesis does not fully accord with the results of experiment 2, where an explicit sense of control was directly manipulated and shown to have no effect on choice behavior (Fig. 4A). As such, if a sense of competence impacts choice behavior, it appears to operate implicitly. An alternative hypothesis is that error signals arising from the cerebellum directly modulate reinforcement learning, and that this gating signal is disrupted in individuals with cerebellar degeneration.

It is important to recognize that the gating and competence models are not mutually exclusive. Actions may influence choice behavior via direct gating and by contributing to a sense of motor competence. We suspect that the relative reliance on these two forms of credit assignment is likely dependent on task context, motor feedback, and movement requirements. Indeed, a hybrid model, which incorporates features from both the gating and probability models, yields good fits for the Standard and Spatial conditions. Moreover, the parameter estimates are surprisingly similar to those obtained from the separate fits of the gating and probability models (Fig. S5). This hybrid model is reminiscent of reinforcement learning models that combine model-free and model-based processes (24), components that are echoed by the gating and probability models, respectively.

Fig. S5.

We developed a hybrid model that has parameters for separate updates following hits (α_hit) and misses (α_miss), as well as the probability of hits (α_prob). This hybrid model captures the ability of the gating model to discount misses by having a low value of α_miss, effectively pausing learning when a motor error is present. Additionally, the model tracks the probability of motor success with the α_prob parameter,

$$\begin{array}{l}{\widehat{p}}_{t+1}\left(x\right)={\widehat{p}}_t\left(x\right)+{\alpha }_{prob}{\delta }_{prob,t}\\ E_{t+1}\left(x|hit\right)=E_t\left(x\right)+{\alpha }_{hit}{\delta }_t\\ E_{t+1}\left(x|miss\right)=E_t\left(x\right)+{\alpha }_{miss}{\delta }_t\\ V_{t+1}\left(x\right)={\widehat{p}}_{t+1}\left(x\right)+E_{t+1}\left(x\right).\end{array}$$

We fit the hybrid model to the data in experiment 1 using the method specified in Modeling Analysis. The model provided a better fit than the gating and probability models (after correcting for the additional free parameter) in both the Spatial and Keyboard conditions but actually performed worse than the probability model in the Binary condition (A). Although the hybrid model should be able to do at least as well as the other two models (given that it contains the parameters of the other models), we used a fitting procedure that optimizes the model fit for all conditions at once to obtain a single value of the temperature parameter, β. With this procedure, it is not mandatory that the hybrid model outperform the other two models in every condition. The probability model provided a significantly better fit in the Standard (BIC difference from next best model, −414.2) and Spatial conditions (−20.70), but not the Binary condition (+139.60). In terms of mean parameter values (B) for the Spatial group, the hybrid model indicates that both the probability representation ($\widehat{p}$) after all trials, and the value representation (E_t) after a miss trial, are very weakly updated. These results further suggest that the gating mechanism may be significantly present in the Spatial case (low α_miss) whereas the probability/competence mechanism makes a modest contribution (low α_prob), a result that is consistent with that observed from the parameter estimates from the separated gating and probability models (Fig. 3 B and C). On the other hand, the Standard condition shows a relatively high value of α_prob, suggesting that the probability mechanism is driving choice behavior in this condition. Again, the Binary condition lies in the middle.

The modeling results highlight another way in which the manner of a response influences choice behavior. A consistent feature in the reinforcement learning literature is that learning rates for negative prediction errors are higher than those for positive prediction errors, regardless of the distribution of rewards in the task (25–27). The results of our Standard conditions are consistent with this pattern: In both the gating and probability models, the learning rate parameter that is operative on miss trials (α_miss, α_prob), where the prediction error is always negative, is markedly higher than the learning rates active solely on hit trials (α_hit, α_payoff), where prediction errors are primarily positive (Fig. 3 B and C and Fig. S5). For the healthy participants, this pattern was upended in the Spatial condition, consistent with the hypothesis that assigning credit for negative reward prediction errors to motor error effectively turns down the reinforcement learning rate.

In summary, the current work offers one perspective of how motor and reward learning systems interact during decision-making. To return to our coffee drinker, sensory prediction errors may not only be essential for adapting motor commands to avoid future spills but may also be useful for disclosing the underlying causes of a negative outcome in the service of resolving the credit assignment problem.

Methods

Experiment 1.

Participants in all experiments provided informed consent, approved by the IRBs at Princeton University and the University of California, Berkeley. In experiment 1, 62 healthy adults (aged 18–28, 37 female) were recruited from the research participation pool at Princeton University. Two participants were excluded, one for failure to understand the task and the other due to equipment failure. All participants were right-hand-dominant according to the Edinburgh Handedness Inventory (28).

Participants were assigned to one of three groups (n = 20 participants/group). In the Standard group (Fig. 1C), two red targets were positioned 8 cm from the center of a vertical screen. After a 1-s delay, the word “Go” was displayed. Participants selected one of the two targets by pressing the left or right arrow on a keyboard with either the index or middle finger of the right hand. Participants were told that, on some trials, the selected target would turn green (“hit”) and display points earned on that trial (1−100). On other trials, the target would turn yellow (“miss”), earning them zero points. A pleasant “ding” sounded on hit trials, and a “buzz” sounded on miss trials. Instructions emphasized that participants had no control over whether a hit or miss occurred. A cumulative score was displayed in the center of the display. Participants were instructed to maximize their total points, which would later be exchanged for money ($1−$5).

In the Spatial and Binary groups (Fig. 1D), participants indicated their choices by using their right arm to move a robotic manipulandum (Fig. S6; BKIN Technologies, sampling rate 1 kHZ). At the start of each trial, the manipulandum moved the participant’s hand to a starting point in the middle of the workspace, ∼35 cm from the participant’s body. When the hand was within 5 cm of the starting position, participants received veridical cursor feedback. After maintaining the start position for at least 500 ms, the participant made a rapid reaching movement to the target of their choice.

Fig. S6.

Depiction of the standard setup of the KINARM device used in experiment 1 (BKIN Technologies). A similar display arrangement was used in experiments 2 and 3, although a digitizing tablet was used to collect kinematic information and participants had to volitionally move their hand back to the start position.

The instructions for the two reach groups emphasized that the trial outcome (hit or miss) was dependent on reach accuracy: Points would be earned on trials in which they hit the target and withheld on trials in which they missed. The stimuli were displayed on a horizontally mounted LCD screen reflected onto a mirror that was positioned above the movement surface. As such, vision of the hand was occluded. To make the motor control requirements demanding, targets were positioned 15 cm to the left and right of the start position and limited in size (1 cm × 0.5 cm). In addition, the reach amplitude had to exceed 15 cm within 400 ms or a “Too Slow” message was displayed, and the trial was aborted and subsequently repeated.

In the Spatial group, a cursor (radius 0.5 cm) was displayed when the hand traversed the vertical axis of the target (Fig. 1D). The position of the feedback corresponded to the position of the hand (subject to the constraints described below). Hits were defined as trials in which the feedback fell within the target region; misses were defined as trials in which the feedback fell outside the target region. The position of the cursor was veridical if the actual reach outcome matched the predetermined outcome. If the actual and predetermined outcome did not match, the position of the feedback cursor was subtly shifted to induce the predetermined outcome. This was accomplished by taking the location of the hand when it crossed the vertical axis of the target and adding a small translational shift, either away from the target for predetermined misses or toward the target for predetermined hits. The size of the shift was taken from a Gaussian distribution (μ = 0, σ = 0.5 cm) relative to the location of the hand along the vertical axis. In this way, the perturbed feedback was correlated with the actual hand position. To emphasize the veracity of the feedback, trials were only valid if, during the reach, the hand stayed within an invisible 4-cm horizontal stripe centered about the target. If not, the screen displayed the message “Too Far,” and the trial was aborted and subsequently repeated. The Binary group was subjected to the same perturbation manipulations but was not provided with cursor feedback; they were only provided with color cues, indicating hit or miss outcomes (Fig. 1D). All other aspects of visual and auditory feedback for the Spatial and Binary groups matched the Standard condition.

Point values and hit probabilities for each target were established by bounded pseudosinusoidal functions (Fig. 1B). By mirroring both functions, the expected values of the two targets were matched on every trial. For all three groups, hit probability was transformed into 1s and 0s and multiplied by the rounded point value on each trial. The potential outcomes for each target were predetermined and identical for participants in all groups.

We designed the reward functions so that, during alternating phases, one target was “risky” and the other target was “safe.” For example, for the first 165 trials, target 1 was riskier, with lower hit probabilities (and higher payoffs), and target 2 was safer, with higher hit probabilities (and lower payoffs). The value/probability functions crossed paths at multiple points over the 600-trial block, creating reversals as to which target was the risky/safe choice. The locations of targets 1 and 2 were fixed for the entire session and counterbalanced across participants.

Experiment 2.

Forty healthy, right-handed adults (aged 18–22, 18 female, 12 male; we failed to retain gender data for 10 participants in one condition) were recruited from the participation pool at the University of California, Berkeley (see Supporting Information for power analysis). We used a 2 × 2 factorial design. One factor referred to the mode of the response, Standard (key press) or Spatial (reaching with cursor feedback). The other factor referred to how the instructions framed the cause of misses, No-Control (target randomly did not pay out) or In-Control (movement execution error). In the Standard/In-Control condition, the instructions emphasized that the participant controlled whether or not the key press resulted in a hit or miss: “You have control over whether a target will give you points for your response or give you nothing, but we will not tell you how to control it.” In the Spatial/No-Control condition, the instructions emphasized that the participant did not control whether or not the reach resulted in a hit or miss: “You have no control over whether the cursor lands inside or outside the target, and therefore have no control over whether a target gives you points on any given trial.”

The procedure was similar to that used in experiment 1, with the main difference being the form of the reaching movement and the visual display. Participants in the Spatial conditions held a digitizing pen and made reaching movements across a digitizing tablet (Intuos Pro, Wacom; sampling rate 100 Hz). Stimuli were displayed on a 17-inch LCD monitor, horizontally mounted 25 cm above the tablet. The task was controlled by custom software written in Python (https://www.python.org). We used a different apparatus in experiment 2 to enable a setup that was portable and available at both the Princeton and Berkeley laboratories, given our plans to test patients with a relatively rare disease (experiment 3). This also provided an opportunity to test the generality of the results observed in experiment 1.

The targets (circles, 1 cm diameter) were displayed in a “V” arrangement in front of the start point, 10 cm from the start position and separated by 60°. At the start of each trial, the participant was guided to the start position by visual feedback, initially in the form of a ring indicating the radial distance (but not direction) from the start location, and then with a cursor when the hand was within 10 cm of the start location. After maintaining that position for 500 ms, a “Go” cue signaled the participant to reach to the selected target. As in experiment 1, we imposed the same time constraints, boundary constraints, and outcome perturbations (as required by the predetermined reward schedule).

Point values and hit probabilities for each target were varied according to the same bounded pseudosinusoidal functions as experiment 1, although the length of the session was truncated to 400 trials by removing every third entry in the functions.

Experiment 3.

Twelve individuals with cerebellar degeneration (10 right-handed, two left-handed; mean age: 56, range 25–68; five female, seven male) were recruited from the Princeton and Berkeley communities. Seven individuals had an identified genetic subtype, and five were of unknown etiology (Table S1). Two patients diagnosed with spinocerebellar ataxia type 3 (SCA-3) were excluded from the final analysis given that phenotypes of SCA-3 may also show degeneration and/or dysfunction of the basal ganglia (29), a region strongly implicated in reinforcement learning (1, 2, 21, 25). (We note that the choice behavior of these two individuals was similar to that observed in the other 10 individuals with cerebellar degeneration.) Patients were screened using medical records and evaluated with the International Cooperative Ataxia Rating Scale and the Montreal Cognitive Assessments (MoCA). Seven patients scored normally on the MoCA (26+), and three of the patients had slightly below normal scores (23–25). A control group of neurologically healthy adults, matched in terms of handedness and age, was also tested (mean age 64, range 50–72; six female, four male).

Table S1.

Demographics and neuropsychological data for the individuals with cerebellar degeneration tested in experiment 3

Participant	Age, y	Gender	Diagnosis	MoCA score	ICARS score
1	68	F	Ataxia, SCA-6	27	24
2	57	M	Ataxia, SCA-4	26	22
3	68	M	Ataxia, SCA-6	26	29
4	65	M	Ataxia, unknown	26	46
5	25	M	Ataxia, unknown	26	34
6	54	M	Ataxia, unknown	27	42
7	59	F	Ataxia, unknown	29	21
8	61	M	Ataxia SCA-2	23	26
9	52	F	Ataxia, unknown	24	57
10	55	F	Ataxia, SCA-6	25	31

Diagnoses of each patient are shown, along with scores on MoCA (34) and International Cooperative Ataxia Rating Scale (ICARS; ref. 35). Individuals with SCA-3 were not included in the analyses and are thus not included in the table.

Each participant performed all three conditions (400 trials each) of experiment 1 in a single session, using the apparatus of experiment 2. Although it was not possible to fully counterbalance given the three conditions and two target-side assignments, we created a set of orders and target-side assignments that varied across individuals. Priority was given to shuffle the order of conditions, and we created patient−control pairs such that the same set of orders was used for each member of the pair.

Adaptation Analysis

Error-based sensorimotor adaptation predicts that movements after error trials (i.e., trials in which the cursor is displaced from the target) should slightly deviate in the direction opposite the error. For each participant in the Spatial conditions, a regression was conducted as follows: The signed angular cursor error at a given target on miss trial t was defined as the predictor variable for the signed change in reach endpoint angle on trial t + 1. This analysis was limited to trials in which the successive reaches were to the same target and trial t was a miss trial with false feedback. We did not include miss trials with veridical feedback, because the predicted directional change in reach angle on trial t + 1 would also be expected on these trials due to regression to the mean, given that the mean reach location was close to the center of the target (e.g., in experiment 1, the mean location was within 0.08 cm of the target). Significant negative regression weights were found for pairs in which the first trial was a miss with veridical feedback [β = −0.60, t_(1,19) = −18.97, P < 0.001] as well as for hits with false feedback, that is, pairs in which the actual reach missed the target [β = −0.45, t_(1,19) = −4.27, P < 0.001]. In the latter condition, this negative correlation is, presumably, a manifestation of regression to the mean, whereas, in the former, both regression and adaptation are potential contributors. The regression weights were not reliable for pairs in which the reach for the first trial passed through the center of the target and feedback was veridical, the condition in which regression and adaptation would not be expected to produce an observable negative correlation [β = −0.22, t_(1,19) = −1.01, P = 0.33].

Modeling Analysis

In the models tested here, value is updated by a TD error δ, the difference between the predicted (V) and received (r) reward,

$${\delta }_t=r_t-V_t\left(x\right)$$

where r_t is the number of points received on trial t, and V_t(x) is the current value V of the selected target x. Zero points were awarded on miss trials. In the basic TD model, the reward prediction error δ_t is used to update the estimated value of the selected target, weighted by the learning rate α,

$$V_{t+\mathit{1}}\left(x\right)=V_t\left(x\right)+\alpha {\delta }_t.$$

The subjective utility model is identical to the basic model with one additional free parameter, η, which exponentially transforms observed rewards r into subjective rewards R,

$$\begin{array}{l}{R}_t=r_t^{\mathit{\eta }}\\ {\delta }_{\mathit{t}}={\mathit{R}}_{\mathit{t}}-{\mathit{V}}_{\mathit{t}}\left(\mathit{x}\right)\end{array}$$

where r_t is the number of points received on trial t, and R_t is the “subjective” reward value used in the calculation of δ_t. When η > 1, the subjective utility curve is convex (risk-seeking); when 0 < η < 1, the curve is concave (risk-averse). When η = 1, subjective utility is identical to objective utility.

The gating model is an expanded form of the basic model but differentiates hits and misses with separate learning rates. The probability model is also an expanded version of the basic model, with separate update rules for learning hit probability and payoff magnitude, which are subsequently multiplied to yield choice values. Details of these models are presented in Results.

For all models, target values were converted into choice probabilities using the softmax function to simulate action selection,

$$P_t\left(x\right)=e^{\beta Vt\left(x\right)}/\left(e^{\beta Vt\left(x\right)}+e^{\beta Vt\left(y\right)}\right)$$

where P_t(x) is the probability of choosing target x on trial t rather than alternative target y. The inverse temperature parameter β scales the relative difference between target choice probabilities.

Free parameters for each model were estimated by simultaneously fitting the behavioral data for all participants in experiment 1, adjusting the parameter values to minimize the negative log posterior using the Matlab function fmincon. Free parameters (α, η) were optimized individually for each participant, and β was optimized as a single value across all participants. The latter constraint was imposed to limit the interaction between β and α, as these parameters are correlated. The values V for each target were initialized to 0 for all fits. Learning rates (α) were bounded between 0 and 1, and inverse temperature (β) was bounded between 0.05 and 10. Model fits were evaluated using the Bayesian information criterion (30), and models were compared by summing the BIC values within each condition.

Power Analysis

We performed a power analysis on the effect size obtained in experiment 1, using the choice bias (risky target choice rate) differences between the Standard and Spatial conditions (Fig. 2A). We observed a large effect size, which was approximately d = 12 between conditions. This effect size predicted a necessary power of four participants per group for a replication of the study. To be conservative, we tested 10 participants per group in experiments 2 and 3.

Statistical Tests

In experiment 1, choice biases were submitted to a one-way ANOVA to test for the effect of condition (Standard, Binary, and Spatial). Post hoc pairwise two-tailed t tests, with Bonferroni correction, were used to directly compare the conditions, and one-sample two-tailed t tests were used to determine if the bias for each condition bias differed from the neutral (no bias) value of 0.5. In experiment 2, choice biases were submitted to a 2 × 2 ANOVA with the factors of condition and instruction. In experiment 3, a 2 × 3 ANOVA was used to test for main effects of group (patient vs. control) and the three repeated conditions. Additionally, an a priori t-test (two-tailed) was used to evaluate the condition of primary interest, testing the prediction that attenuated error processing in the patient sample would alter the patients' choice behavior in the Spatial condition.

In all three experiments, the regression coefficients obtained with the metric of adaptation (see Fig. S4) were compared with zero via a one-sample one-tailed t test. This analysis was performed separately for each group.

For the modeling analysis, we used summed BICs across conditions, consistent with other work using similar reinforcement learning models (31) and work with wholly distinct modeling approaches (32). As noted in Etchells et al. (32), a summed BIC difference of ∼40 corresponds to a corrected likelihood ratio (Bayes Factor) of greater than 1,000 (33), a value that would imply a very robust difference in the model fits. Fit parameter values were statistically analyzed using two-way repeated-measures ANOVAS with the factors condition and parameter type.