Whole-exome sequencing to analyze population structure, parental inbreeding, and familial linkage

Significance

We compared the information provided by whole-exome sequencing (WES) and genome-wide single-nucleotide variant arrays in terms of principal component analysis, homozygosity rate estimation, and linkage analysis using 110 subjects originating from different regions of the world. WES provided an accurate prediction of population substructure using high-quality variants with a minor allele frequency > 2% and reliable estimation of homozygosity rates using runs of homozygosity. Finally, homozygosity mapping in 15 consanguineous families showed that WES led to powerful linkage analyses, particularly in coding regions. Overall, our study shows that WES could be used for several analyses that are very helpful to optimize the search for disease-causing exome variants.

Abstract

Principal component analysis (PCA), homozygosity rate estimations, and linkage studies in humans are classically conducted through genome-wide single-nucleotide variant arrays (GWSA). We compared whole-exome sequencing (WES) and GWSA for this purpose. We analyzed 110 subjects originating from different regions of the world, including North Africa and the Middle East, which are poorly covered by public databases and have high consanguinity rates. We tested and applied a number of quality control (QC) filters. Compared with GWSA, we found that WES provided an accurate prediction of population substructure using variants with a minor allele frequency > 2% (correlation = 0.89 with the PCA coordinates obtained by GWSA). WES also yielded highly reliable estimates of homozygosity rates using runs of homozygosity with a 1,000-kb window (correlation = 0.94 with the estimates provided by GWSA). Finally, homozygosity mapping analyses in 15 families including a single offspring with high homozygosity rates showed that WES provided 51% less genome-wide linkage information than GWSA overall but 97% more information for the coding regions. At the genome-wide scale, 76.3% of linked regions were found by both GWSA and WES, 17.7% were found by GWSA only, and 6.0% were found by WES only. For coding regions, the corresponding percentages were 83.5%, 7.4%, and 9.1%, respectively. With appropriate QC filters, WES can be used for PCA and adjustment for population substructure, estimating homozygosity rates in individuals, and powerful linkage analyses, particularly in coding regions.

Whole-exome sequencing (WES) has become the leading strategy for uncovering germ-line exome variants in humans. A number of gene- and variant-level methods have been proposed for the analysis of WES data to select candidate variants in rare Mendelian disorders and more common traits (1–13). These analyses benefit from the use of additional information, such as familial linkage, homozygosity rate, and ethnic background, which are commonly used in the study of inherited diseases (14–17). Genome-wide single-nucleotide variant array (GWSAs) are the gold standard method for linkage analysis, because they provide maximal linkage information for the whole genome (18). GWSAs are also classically used to estimate homozygosity rate in patients, confirming or sometimes, revealing parental consanguinity through the inbreeding coefficient parameter F in particular (19, 20). Population stratification can be an issue in the analysis of population-based genetic data, including WES, particularly for association studies (21–24). Population structures have been widely determined by GWSA (25, 26) in European (27), African (28, 29), Asian (30), Jewish (31), Mexican (32), and other populations (33). These analyses are mostly based on principal component analysis (PCA) (34), which can also be used to confirm or reveal the ethnicity of an individual patient (or his or her parents).

Unlike WES, which provides thorough coverage for less than 2% of the human genome for both rare and common variants, GWSAs cover the whole genome for common variants but only patchily, with a mean interval between variants of about 2–4 kb. Obtaining both WES and GWSA data in patients, kindreds, or populations is DNA-, resource-, and time-consuming. Two studies comparing WES and GWSA in linkage analyses based on real data from three families (35) or both simulated and real data from two families (36) showed that the two sets of genetic data defined linkage peaks (35) and excluded genomic regions (36) in a consistent manner. A recent study estimating homozygosity rates with both GWSA and WES data in patients born to consanguineous families provided recommendations for the detection of homozygous regions by WES (37). Finally, a method for estimating individual ancestry from a PCA map generated from data for a reference set of individuals also showed added value for a combination of single-nucleotide variant (SNV) data from exome chips or targeted sequencing with genotyping and imputed data for accurate ancestry estimation, particularly for European populations (38). We performed both GWSA and WES on 110 subjects originating from various regions of the world, including North Africa and the Middle East. Both of these regions are poorly covered by the HapMap Project and the 1000 Genomes Project and have high consanguinity rates. We compared the information provided by the two datasets for the estimation of homozygosity rate and linkage analysis by homozygosity mapping. We also defined the optimal criteria for selecting WES variants to optimize PCA and ancestry prediction for individuals of various ethnic origins.

Results

We performed genotyping with the Affymetrix GWSA 6.0 array and WES with the Agilent Sureselect All Exons V4 Kit on 110 unrelated individuals (58 male and 52 female subjects) originating from six regions of the world, including North Africa (27 subjects) and the Middle East (16 subjects) (Table 1). After the application of quality control (QC) filters (Methods), 810,914 high-quality (HQ) GWSA SNVs and 249,310 HQ WES SNVs were retained for our analyses (Fig. S1). In total, 10,598 of these SNVs, with a call rate (CR) of 100%, were common to both WES and GWSA. We checked the genotype matching rate of these common variants between WES and GWSA with the PLINK Identity by State matrix (39). The mean Identity by State genotype matching rate between WES and GWSA was 99.37% (SD = 1.02%), a value similar to that reported in previous studies (40).

Table 1.

Origin of 110 individuals included in the analysis

World region	No. of individuals
Central and South America*	5
Middle East†	16
North Africa‡	27
Sub-Saharan Africa§	6
Western Europe¶	53
Mixed origin#	3

^*Individuals from Colombia, Brazil, and Mexico.

^†Individuals from Turkey, Pakistan, Kuwait, India, Iran, Qatar, and Afghanistan.

^‡Individuals from Morocco, Algeria, Tunisia, and Egypt.

^§Individuals from Mali, Senegal, Comoros Islands, and Madagascar.

^¶Individuals from France, Italy, Spain, Portugal, and the United Kingdom.

^#Individuals with parents from sub-Saharan Africa and Europe and from the Middle East and Europe.

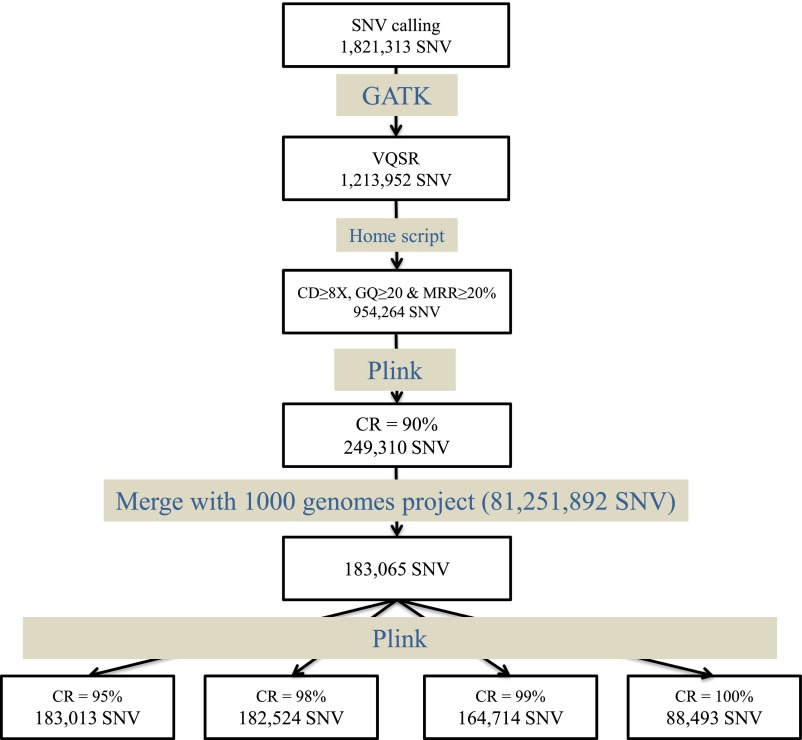
Fig. S1.

Flowchart summarizing the entire WES quality process. First, genotypes for all positions with an SNV (heterozygous or homozygous for the alternative allele) for at least one individual were called. Then, only variants passing the GATK Variant Quality Score Recalibrator (VQSR) filters were kept. Genotypes with a low coverage, genotype quality, or minor read ratio (for heterozygous) were filtered out. Finally, variants with a CR < 90% over our sample of 110 individuals were removed. After merging with the 1000 Genomes Project data, in total, 183,065 SNVs were retained for our analyses, for which we considered four levels of CR between 95% and 100%.

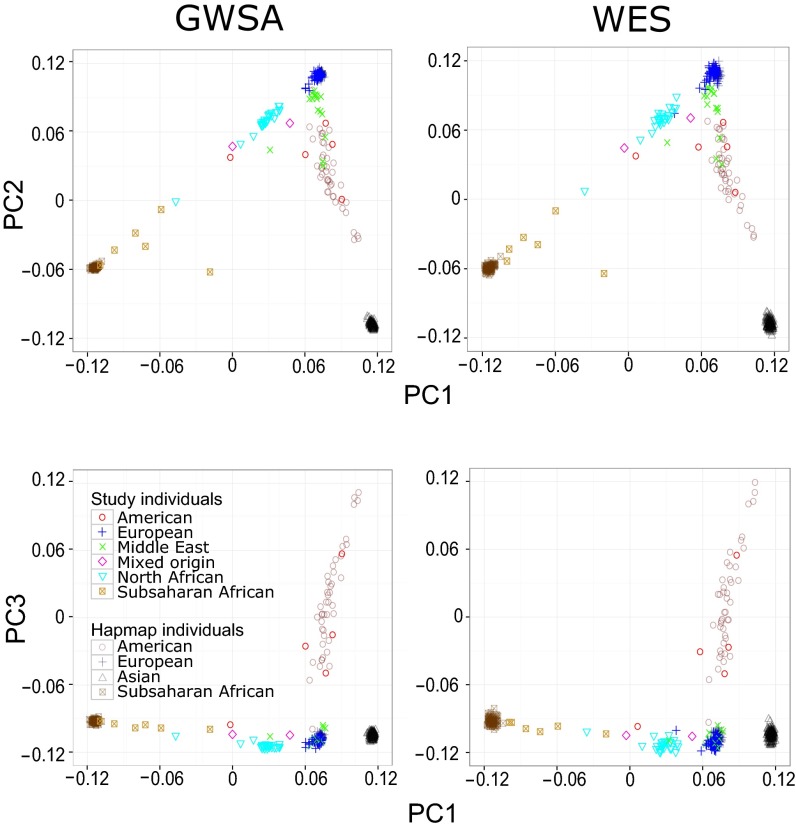
We first conducted PCA using 375 unrelated individuals from five world regions as the reference (Table S1). Data for these individuals were present in both the HapMap Project (HapMap release 3) (41) and the most recent 1000 Genomes Project phase 3 (42) database available since May of 2013. We merged our GWSA data with the HapMap data, such that all of the 810,914 HQ SNVs of our sample were present in the HapMap dataset. The resulting merged database was then used for PCA. We found that 183,065 (73.4%) of the 249,310 HQ SNVs detected in our 110 WES samples were present in the SNVs included in the 1000 Genomes Project phase 3 (Fig. S1). The difference in the number of variants in our WES data and the 1000 Genomes Project reflects the enrichment of our WES data in rare variants. We first conducted PCA on the HapMap/GWSA data (Fig. 1). Consistent with their geographic origin, the North African individuals mapped between the European and African clusters, whereas the Middle Eastern individuals mapped between the European and Asian clusters (Fig. 1). Like subjects from the Middle East, Central and South Americans were located between the European and Asian clusters for the first two principal components (PCs). However, the South American and Middle Eastern subjects were separated by the third PC.

Table S1.

Populations used as reference in our analysis

Ethnicity	Population	Abbreviation	No. of samples
African	Yoruba in Ibadan, Nigeria	YRI	86
European	Utah residents with northern and western European ancestry	CEU	81
Asian	Han Chinese in Beijing, China	CHB	84
Asian	Japanese in Tokyo, Japan	JPT	80
American	Mexican ancestry in Los Angeles, CA	MEX	44

All individuals are founders and present in both the 1000 Genomes Project phase 3 and HapMap Project release 3.

Fig. 1.

PCA was performed with smartPCA software on both (Left) GWSA and (Right) WES data. The results for WES data are presented for SNVs with an MAF > 0.03 and a CR > 98%. (Upper) The first two PCs and (Lower) the first and third PCs are plotted. We included a total of 110 individuals (colored plots) and 375 HapMap individuals (black plots) in the analysis.

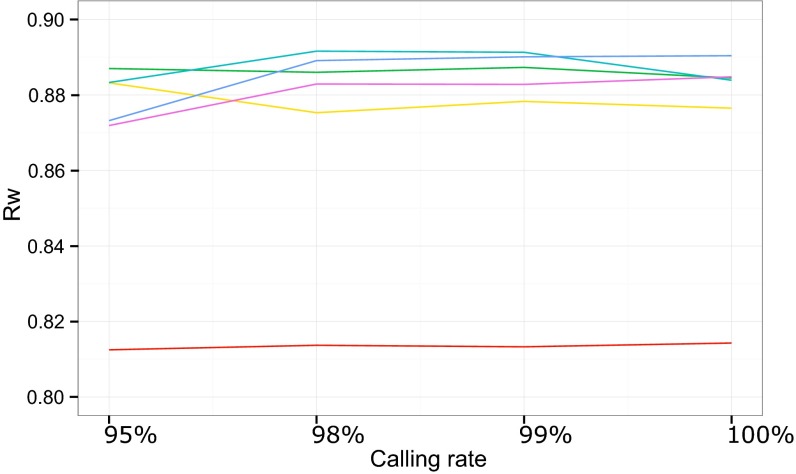
We then performed a more formal comparison of PCA between the GWSA/HapMap data used as a gold standard and the WES/1000 Genomes Project data using the R_W correlation coefficient weighted by the eigenvalues of the significant PCs (Methods). We considered different CRs (range = 95–100%) and different minor allele frequency (MAF) thresholds (range = 0–5%) for the WES SNVs, because higher CRs and MAFs would be expected to increase variant quality while decreasing the number of variants (range = 39,391–183,013) (Table S2). The R_W correlation coefficient was calculated for the 14 PCs significant at P < 0.05 (Table S3). Correlations were particularly strong (R_W > 0.98) for the four first PCs, which accounted for >85% of the scaled eigenvalues in both GWSA and WES (Table S3). Overall, we found strong correlations (range = 0.813–0.892) between the PCA coordinates obtained by GWSA and WES for our 110 subjects for all combinations of CR and MAF (Fig. 2). The exclusion of rare variants (MAF < 2%) from the PCA clearly decreased the number of variants but increased the strength of the correlation. The strongest correlations were observed with WES variants with an MAF > 2%, and for MAF values in this range, CR had very little influence. The panel of WES variants with an MAF > 3% and a CR > 98% provided the highest R_W value at 0.892, corresponding to 85,112 variants in total, whereas the corresponding value was 183,013 in the largest panel (Table S2). The results of PCA with this panel of 85,112 SNVs are shown in Fig. 1, in which the distribution of population structures is very similar to that derived from the GWSA/HapMap data.

Table S2.

Number of SNVs used in the analysis of WES data according to the MAF and the CR filter used

SNV panel	CR > 95%	CR > 98%	CR > 99%	CR = 100%
All SNVs	183,013	182,524	164,714	88,493
MAF > 1%	115,772	115,362	103,847	58,459
MAF > 2%	95,574	95,201	85,679	49,335
MAF > 3%	85,464	85,112	76,612	44,663
MAF > 4%	78,878	78,554	70,763	41,752
MAF > 5%	73,884	73,565	66,276	39,391

Table S3.

Significant PCs (P value < 0.05 based on the Tracy–Widom statistic) in the PCA using the GWSA or the WES (using SNVs with MAF > 3% and CR > 98%)

No. of significant PCs	GWSA-scaled eigenvalue	WES-scaled eigenvector	Raw correlation	Weighted correlation
1	0.499	0.497	0.994	0.495
2	0.292	0.294	0.993	0.291
3	0.0432	0.046	0.983	0.044
4	0.021	0.023	0.985	0.021
5	0.0158	0.017	0.424	0.007
6	0.0150	0.015	0.552	0.008
7	0.014	0.014	0.304	0.004
8	0.014	0.014	0.014	0.001
9	0.014	0.013	0.03	0.001
10	0.014	0.013	0.065	0.001
11	0.014	0.013	0.413	0.006
12	0.014	0.013	0.305	0.004
13	0.014	0.013	0.347	0.005
14	0.0141	0.013	0.303	0.004
Overall RW				0.891

Fig. 2.

Weighted correlation, R_W, between the PCA coordinates obtained with GWSA and WES for 110 individuals of our sample as a function of the CR (x axis) and the MAF thresholds used to filter WES SNVs: no MAF filter (red line), MAF > 1% (yellow line), MAF > 2% (green line), MAF > 3% (turquoise line), MAF > 4% (blue line), and MAF > 5% (purple line). R_W was calculated as described in Methods.

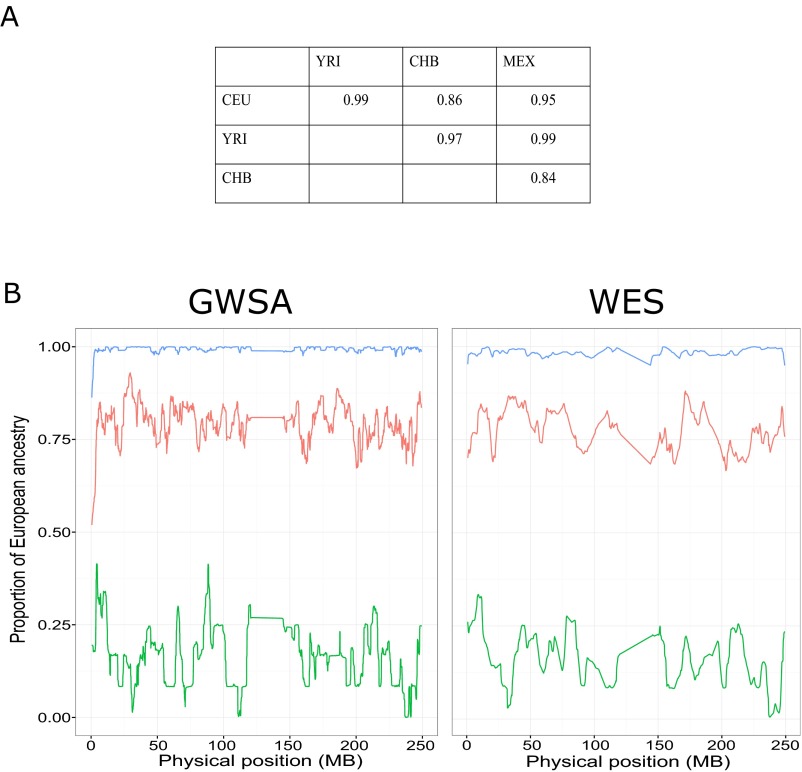
Next, we considered the prediction of coordinates for a single individual from WES data and a sample of publicly available data. Based on our previous findings, we used variants with an MAF > 3% and a CR > 98% when WES data for this single individual were merged with the 1000 Genomes Project data. Predictions were made independently for each of our 110 individuals, and the R_W correlation coefficient for the whole sample was again very strong at 0.844 (0.841 when MAF was >2% and CR was >98%). Interestingly, this correlation was also very strong when we considered only ethnic groups not represented in the reference panels of the HapMap Project and the 1000 Genomes Project, such as 16 individuals from the Middle East (R_W = 0.853), 27 individuals from North Africa (R_W = 0.829), and 3 subjects of mixed origin (R_W = 0.949). All of these results indicate that WES data based on common variants are appropriate for use in population structure analyses and inferring the ethnic ancestry of an individual. Finally, we compared the performance of WES and GWSA in terms of local ancestry inference using Hapmix (43), which can consider two ancestral populations (Methods). The correlation between the proportions of ancestry obtained by GWSA or WES data in our 110 individuals was high, varying from 0.84 to 0.99 (Fig. S2) according to the two ancestral populations considered among the four HapMap/1000 Genomes populations European (CEU), Han Chinese (CHB), Yoruba Nigerian (YRI), and Mexican (MEX). An example for the analysis using CEU and YRI as ancestral populations is shown in Fig. S2. These high correlations are consistent with our PCA results, further indicating that WES data could be used to infer local ancestry.

Fig. S2.

Local ancestry estimation. (A) Pearson correlation coefficients between the proportions of ancestry estimated in our 110 individuals using the GWSA or the WES data according to the two ancestral populations considered among the four following HapMap/1000 Genomes Project populations: CEU, YRI, CHB, and MEX. The mean local ancestry was computed over the whole autosomal genome using Hapmix (43). (B) Mean local European ancestry across chromosome 1 estimated by means of Hapmix (43) using (Left) GWSA or (Right) WES data. Represented here are the mean local European ancestries when 44 CEU and 44 YRI from HapMap/1000 Genomes Projects were taken as reference ancestry. The mean probability for each variant for having European or African ancestry is computed for three groups of our sample: 53 individuals of European origin (blue line), 27 individuals of North African origin (red line), and 6 individuals of African origin (green line).

We then estimated homozygosity rates by calculating the inbreeding coefficient F by two approaches: one based on the search for runs of homozygosity (ROHs) over a given length of the genome (20) and the other based on the use of Markov processes to model homozygous states throughout the genome by the FEstim method (19). We identified ROHs with PLINK (39), in which a sliding window of 1,000 kb is passed across the genome, with homozygosity determined at each window. We considered different numbers of SNVs within the sliding window (Methods). With GWSA data, the mean homozygosity of our sample, estimated by FEstim (F_ESTIM-GWSA), was 1.64% (SD = 3.44%; range = 0–15.50%) (Table S4). As expected, with the ROH approach, the mean homozygosity (F_ROH-GWSA) increased as the number of SNVs included in the window decreased from 1.34% (300 SNVs) to 2.27% (100 SNVs). The F_ROH-GWSA values obtained with 200 SNVs (F_ROH-GWSA200 = 1.67%) and 250 SNVs (F_ROH-GWSA250 = 1.47%) were the closest to F_ESTIM-GWSA, which could be considered the reference estimate (44). They were also strongly correlated with the F_ESTIM-GWSA estimates (r = 0.973 and r = 0.975, respectively). With WES data, the estimated F_ESTIM value was higher than that obtained with GWSA data at 2.53% (SD = 5.23%; range = 0–22.50%), and the coefficient of correlation with the F_ESTIM-GWSA estimates was 0.889. However, less than 20% of the submaps generated by the F_ESTIM-WES approach could be used for analysis in 18 subjects who were from various geographic regions (12 from Europe, 3 from sub-Saharan Africa, 2 from North Africa, and 1 from the Middle East). We noted that these 18 individuals had significantly higher missing rates of WES variants than the 92 others (3% vs. 0.9%; P = 0.0003). In addition, we found that the mean chromosomal segment lengths homozygous by descent (HBD) were significantly lower (P = 0.0004) when using WES data (mean = 1.91 Mb) than when using GWSA data (mean = 2.64 Mb), indicating that WES data may lead more often to exclusion of submaps compared with GWSA because of smaller HBD segment lengths. Overall, these findings suggest that the F_ESTIM-WES estimates may be less reliable, at least for these 18 individuals.

Table S4.

Estimation of homozygosity rates with different methods using GWSA and WES data

Method, data, and no. of SNVs in ROH windows	Average homozygosity, % (SD)	Homozygosity range, %	Correlation with FESTIM-GWSA
ROH
GWSA
100	2.27 (2.61)	0–13.91	0.963
200	1.67 (2.59)	0–13.55	0.973
250	1.47 (2.59)	0–13.37	0.978
300	1.34 (2.58)	0–13.31	0.979
WES
10*	2.97 (2.61)	0–14.43	0.937
20	1.95 (1.67)	0–9.51	0.935
30	1.87 (1.61)	0–9.42	0.936
50	1.73 (1.56)	0–9.24	0.933
100	0.80 (1.40)	0–8.02	0.958
FEstim
GWSA
—	1.64 (3.44)	0–15.50	1
WES
—	2.52 (5.23)	0–22.50	0.887

The inbreeding coefficient F was computed for 110 individuals using two approaches based on either ROHs or the use of Markov processes along the genome through the FEstim approach.

^*Corresponds to the WES optimal parameters proposed in the work in ref. 37.

When the ROH approach was applied to WES data, the mean F_ROH-WES estimates varied from 0.80% (100 SNVs) to 1.95% (20 SNVs) (Table S4). The F_ROH-WES values obtained with 50 SNVs (F_ROH-WES50 = 1.73%) and 30 SNVs (F_ROH-WES30 = 1.87%) were the closest to F_ESTIM-GWSA and also strongly correlated with F_ESTIM-GWSA (r = 0.933 and r = 0.930, respectively) and F_ROH-GWSA200 (r = 0.952 and r = 0.951, respectively) (Table S5) data. With the optimal parameters proposed in a previous study (37), the mean F_ROH-WES10 was higher at 2.97%, with correlation coefficients of 0.931 with F_ESTIM-GWSA and 0.985 with F_ROH-WES30. Thus, for both GWSA and WES data, the most appropriate number of SNVs within a 1,000-kb window for calling an ROH providing F_ROH estimates similar to F_ESTIM-GWSA was close to the mean number of SNVs per 1,000 kb (corresponding to 0.37% of the autosomal genome) from the GWSA (∼242 SNVs per 1,000 kb) and WES (∼27 SNVs per 1,000 kb) data (Methods). These results indicate that WES can be used to obtain reliable homozygosity estimates by ROH methods if the number of SNVs within a window of 1,000 kb used corresponds to about 0.37% of the total number of available autosomal HQ WES SNVs (∼30 SNVs in this analysis).

Table S5.

Pearson correlation coefficients observed between the inbreeding coefficients, F, estimated by ROHs in our sample of 110 individuals using either GWSA or WES data according to the number of SNVs considered to call an ROH

Data and no. of SNVs	No. of SNVs
	GWSA				WES
	100	200	250	300	10	20	30	50	100
GWSA
100	1	0.995	0.992	0.989	0.957	0.952	0.955	0.955	0.958
200		1	0.999	0.997	0.955	0.948	0.951	0.952	0.967
250			1	0.999	0.952	0.945	0.948	0.950	0.970
300				1	0.949	0.942	0.945	0.947	0.970
WES
10					1	0.980	0.985	0.984	0.958
20						1	0.987	0.988	0.962
30							1	0.999	0.968
50								1	0.971
100									1

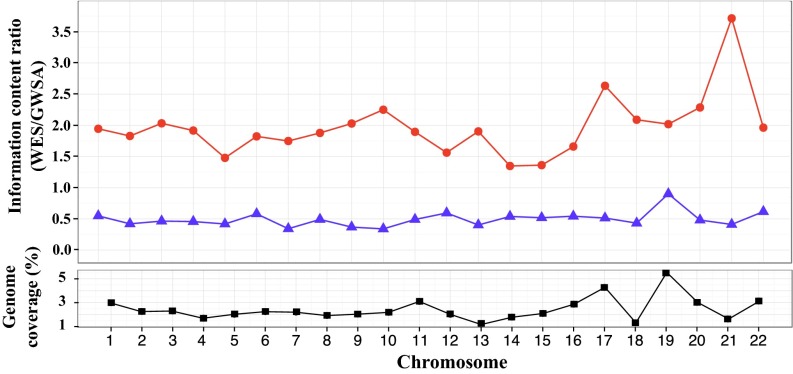
Based on the homozygosity results, we selected 15 individuals with F_ROH-GWSA250 and F_ROH-WES30 above 3% for linkage analysis by homozygosity mapping, because the offspring of first cousin marriages may have as little as 3% of their genome identical by descent (19); 11 of these 15 individuals were known to have been born to consanguineous parents. Information about consanguinity was not available for the other four subjects, although inbreeding was considered likely given their high rates of homozygosity. We also assumed that family structure was the same across families and that the patient was the only person genotyped/sequenced in each family. We performed homozygosity mapping with either GWSA or WES data (including all HQ variants with CRs > 98%). We first compared the linkage information content provided by the two methods, because this content provides some indication as to how closely the available markers approach the ideal situation of complete inheritance information concerning the segregation of the chromosomal region tested. Over the 22 autosomes, GWSA provided 51% more information, on average, than WES data. The ratio of the amount of information provided by WES to that provided by GWSA ranged from 0.41 on chromosome 21 to 0.90 on chromosome 19 (Fig. 3). This ratio was strongly correlated (Pearson’s correlation coefficient = 0.72) with the proportion of coverage by the exome kit for each chromosome defined as the number of bases covered by the probes over the total length of each chromosome (Fig. 3). For example, chromosomes 19 and 22 contain a high proportion of coding sequences. They are, therefore, more densely covered by WES data than the other chromosomes, resulting in a higher information ratio. We then restricted our linkage analysis to the regions covered by the exome kit. These regions included a total of 10,674, and 73,565 autosomal SNVs in GWSA and WES data, respectively. In these regions, the amount of information provided was 1.97 higher, on average, with WES data than with GWSA data. Indeed, the WES/GWSA information ratio ranged from 1.35 on chromosome 14 to 3.71 on chromosome 21 (Fig. 3). Thus, for the regions covered by the exome kit, WES data clearly provided more information for linkage analysis than GWSA data.

Fig. 3.

(Upper) Ratio of information content (IC) for linkage analysis performed with GWSA and WES SNPs calculated with Merlin software. Each dot represents the IC ratio (IC for WES/IC for GWSA). The IC is the mean amount of information for all SNPs per chromosome computed over all of 15 families. Blue triangles indicate the ratio at the whole-genome level; red circles indicate the ratio for the analysis conducted with SNPs located in the regions covered by the SureSelect Exome Kit. (Lower) Black squares indicate the proportion of the whole genome covered by the probes of the SureSelect Exome Kit defined as the number of bases covered by the probes divided by the total length of each chromosome.

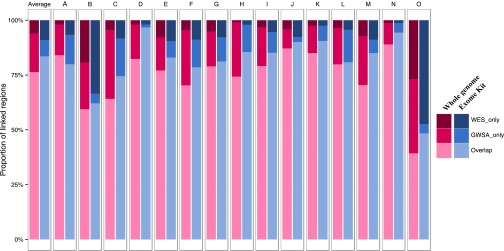
Finally, we compared the linked regions larger than 1 Mb with a logarithm of the odds (LOD) score above 1 (the maximum expected LOD score in the family structure that we analyzed was 1.2), which we identified by conducting the analysis with three different sets of SNVs from (i) GWSA, (ii) WES, and (iii) the combination of GWSA and WES data (GWSA+WES). The third set of data with the largest number of SNVs was used as the reference for the linkage results (this combined set would be expected to provide the true linked regions). From these GWSA+WES results, we were able to estimate the proportion of linked regions identified by both GWSA and WES, those identified only by GWSA, and those identified only by WES. At the genome-wide scale, 76.3% of these regions were found by both GWSA and WES in 15 families, 17.7% were found by GWSA only, and 6.0% were found by WES only (Fig. S3). The WES/GWSA information ratio was higher in the regions found by WES only (mean WES/GWSA information ratio of 1.19) than in those found exclusively by GWSA (mean information ratio of 0.48). We conducted a similar analysis restricted to coding regions covered by the exome kit. We found that 83.5% of the regions were found by both GWSA and WES in 15 families, and slightly more regions were found by WES only (9.1%) than by GWSA only (7.4%) (Fig. S3). The linked regions found by GWSA only were regions in which WES supplied less information than GWSA (mean information ratio of 0.39) because of the small number of variants in the targeted sequenced segments. Overall, WES seems to provide reasonable linkage results at the genome-wide scale, with 82.3% of linked regions correctly detected vs. 94% for GWSA. In coding regions, WES is more informative overall and more powerful, detecting 92.6% of linked regions correctly, whereas 90.9% of these regions were correctly detected by GWSA.

Fig. S3.

Proportion of linked (LOD score > 1) regions larger than 1 Mb found by homozygosity mapping (with GWSA or WES data) in the whole genome (gradient of pink colors) or the regions covered by the exome kit (gradient of blue colors). Dark colors represent regions found with both analyses (homozygosity mapping with GWSA data and homozygosity mapping with WES data). Intermediate gradient colors represent regions found with GWSA data only. Light colors represent regions found with WES data only. Each pair of bars corresponds to the homozygosity mapping results in one family (A to O), and the first pair is the average proportions over 15 families.

Discussion

PCA is usually performed on common markers provided by GWSA. We conducted the first comprehensive PCA comparison of GWSA and WES, to our knowledge, by measuring a specific correlation. We found that performing PCA on WES data with HQ variants (with a CR > 95%) with an MAF > 2% provided a distribution of population structures very similar to that obtained from GWSA data for individuals of various ethnic origins. These criteria substantially decreased (>50%) the total number of WES variants used for the analyses, but they clearly provided an optimal tradeoff for HQ PCA. WES studies can be carried out on limited numbers of individuals, sometimes a single family or a single patient (45). We also showed that WES can accurately predict the ethnic origin of a single individual when using a sample of publicly available data including individuals belonging to ethnic groups that are not directly represented in the reference panel or who are born to parents of different origins. We also found reliable estimates when using WES data to infer local ancestry by means of the Hapmix approach (43). These results indicate that WES data are appropriate for use in population structure analyses and inferring the ethnic ancestry of an individual. The extent to which rare WES variants (MAF < 1%) could be used to refine population substructures remains to be investigated in depth, because it has been shown that rare variants could show stratification patterns that are different from those captured by common variants (24, 46). It will be particularly important to assess the influence of these stratification patterns on the association studies focusing on the role of rare variants (23, 46).

Genetic data from GWSA are used to estimate the homozygosity rate in patients to predict or confirm parental consanguinity in particular. We used the two most widely used approaches to estimate F from GWSA and WES data. We searched for ROHs and used Markov processes to assess homozygous states throughout the genome by the F_ESTIM approach. Using F_ESTIM on multiple sparse maps, as recommended (47), we obtained reliable homozygosity estimates with GWSA data. With WES data, we observed that ∼16% of individuals had a high proportion (>80%) of submaps that could not be used for the estimation of F_ESTIM. Although this aspect requires additional investigation, a first analysis indicated that WES data may be more sensitive to submap exclusions with the F_ESTIM approach because of smaller HBD segments than those obtained with GWSA data, in particular in subjects who have more missing data. Using ROH methods, we found that optimal F_ROH estimates for both GWSA and WES data (compared with F_ESTIM-GWSA) were obtained by considering a number of SNVs for calling an ROH within a 1,000-kb window close to the mean number of SNVs per 1,000 kb available in the GWSA (∼250 SNVs in our study) or the WES (∼30 SNVs in our study) data. In this context, estimates of mean homozygosity from WES were very similar to those obtained with GWSA, and there was a strong correlation between the two estimates of F_ROH (r = 0.95 between F_{ROH-GWSA250SNVs} and F_{ROH-WES30SNVs}). This result is consistent with the findings of a previous study (37), although the optimal configuration for detecting ROH from WES data in this previous study included fewer SNVs (10) within the 1,000-kb window. The detection of ROHs from WES data could also be improved by adding genotyped SNVs from other family members (17). In any case, reliable homozygosity estimates could be obtained from WES data only if ROHs were identified with PLINK, considering a number of SNVs within a 1,000-kb window corresponding to ∼0.37% of the total number of available HQ SNVs.

Many linkage studies have been conducted with WES data in the context of Mendelian disorders (1–3, 6, 15), but to our knowledge, only two have formally compared their results with those obtained with GWSA data. Using real genetic data from three families as an example, Smith et al. (35) showed that accurate genetic linkage mapping could be performed with WES SNVs. Gazal et al. (36) performed a linkage study of two families with both simulated and real data. They reported similar performances for linkage analyses conducted with GWSA or WES (36). As mentioned above, the recent study by Kancheva et al. (37) was based on the detection of ROHs in patients born to consanguineous families without a formal linkage analysis. Here, we extended the analysis to 15 individuals with high homozygosity rates (>3%) in the specific context of linkage analysis by homozygosity mapping, a frequent situation in which WES data may be available for the patient only.

We first analyzed the linkage information content provided by GWSA and WES across the genome. The linkage information obtained with WES was generally only about one-half that obtained with GWSA at the genome-wide level and highest for chromosomal regions with a high density of coding regions. Consistent with this result, we found that, at the genome-wide level, WES detected a smaller proportion of linked regions than GWSA, although this proportion remained substantial at 82.3% (vs. 94% with GWSA). GWSA, nevertheless, missed 6% of the linked regions, corresponding to regions in which the information content was higher for WES than for GWSA. In the regions covered by the exome kit, the information content obtained with WES was generally twice that obtained with GWSA, and WES detected slightly more linked regions than GWSA (92.6% vs. 90.9%). However, in some coding regions, the segments sequenced by WES included only a small number of SNVs, resulting in a low information content and accounting for the small proportion of linked coding regions (7.4%) detected only by GWSA. Clearly, with the decreasing cost of whole-genome sequencing (48), optimal approaches will, in the future, involve linkage analysis together with other analyses of whole-genome sequencing data (49). However, it is currently possible to use WES data for PCA after the application of the appropriate QC filters and adjustment for population substructure to estimate homozygosity rates by ROH and perform reliable linkage analyses, particularly for coding regions.

Methods

Study Subjects.

The individuals used in the analysis were selected from samples ascertained by our laboratory and recruited with the collaboration of many clinicians. They presented a variety of severe infectious diseases and/or primary immunodeficiencies. Although these individuals do not form a random sample, they were ascertained through a number of distinct phenotypes and in different countries. Cohort-specific effects are, therefore, not expected to bias patterns of variation. Among these patients, we studied only 110 individuals who had both WES by Agilent Sureselect All Exons V4 (50 Mb) Single-Sample Capture and genotyping by the Affymetrix Genome-Wide SNV 6.0 Array. The retained 110 subjects studied (58 male and 52 female patients) originated from different regions of the world (Table 1). Written consent was obtained from all subjects included in this study, which was overseen by the Comité de Protection des Personnes (Institutional Review Board) Ile de France 2 (Institutional Review Board no. 00001072).

WES.

WES was performed on an Illumina HiSeq 2000 by Agilent Sureselect All Exons V4 (50 Mb) Single-Sample Capture at the Rockefeller core facilities and the New York Genome Center. Sequencing was performed with 2 × 100 bp paired end reads, and we pooled five samples per lane. We used the Genome Analysis Software Kit (GATK) best practice pipeline to analyze our WES data (50). Reads were aligned with the human reference genome (hg19) with the Maximum Exact Matches algorithm in Burrows–Wheeler Aligner (51). Local realignment around indels was performed with the GATK (52). PCR duplicates were removed with Picard tools (broadinstitute.github.io/picard/). The GATK base quality score recalibrator was applied to correct sequencing artifacts. Individual genomic variant call files were generated with the GATK HaplotypeCaller, and joint genotyping was performed with the GATK Genotype genomic variant call files. The calling process targeted regions covered by the WES 50-Mb Kit, including 200 bp flanking each region.

All variants with a Phred-scaled SNV quality ≤ 30 were filtered out. We then used the GATK Variant Quality Score Recalibrator (50) on the combined variant call file for 110 samples. We retained 1,213,952 SNVs that passed the Variant Quality Score (VQS) Recalibrator filter (VQS log-odds > −0.682). We filtered out sample genotypes with a coverage < 8×, a genotype quality < 20, or a ratio of reads for the less covered allele (reference or variant allele) over the total number of reads covering the position at which the variant was called in the heterozygous genotypes of <20% using an in-house script. Finally, we excluded from the analysis 704,954 variants, for which more than 10% of the genotypes were missing. A set of 249,310 HQ variants was retained for the analysis (Fig. S1).

GWSA.

In total, 110 individuals were genotyped with the Affymetrix Genome-Wide SNV 6.0 Array. Genotype calling was achieved with Affymetrix Power Tools (www.affymetrix.com/estore) for all individuals. In total, 909,622 raw SNVs were detected. We applied QC criteria similar to those used in Hapmap release 3 (41) by removing SNVs with a CR < 95% and a P value in Fisher’s exact test for Hardy–Weinberg equilibrium on 53 European individuals of <10⁻⁶. In total, 810,914 HQ SNVs passed this Hapmap filter and were retained for analysis.

PCA and Local Ancestry Inference.

PCA was carried out with the smartPCA program (53). We initially included 375 unrelated individuals from five regions of the world (Table S1) present in both the 1000 Genomes Project and the Hapmap (Hapmap release 3) Project. We used the data from the Affymetrix 6.0 array and the 1000 Genomes Project for these 375 individuals as a reference for our PCA with GWSA and WES data, respectively. We further considered four different CRs for WES SNVs (95%, 98%, 99%, and 100%) and different MAF thresholds for WES variants (0.01, 0.02, 0.03, 0.04, and 0.05), because these parameters may affect the results of the PCA (54).

We compared PCAs on GWSA and WES data using our whole sample of 110 individuals by calculating the weighted correlation, R_W, between the coordinates of our individuals obtained with GWSA or WES data. These correlations were summed over the M significant PCs and weighted by the mean eigenvalues of the corresponding GWSA and WES components as follows:

$$R_W={\displaystyle \sum }_{j=0}^M\frac{\left(P_{{\text{WES}}_j}+P_{{\text{GWSA}}_j}\right)}{2}\hspace{0.17em}{\text{cor}}_{\text{Pearson}}\left({\text{WES}}_j,\hspace{0.17em}{\text{GWSA}}_j\right),$$

where $P_{{\text{WES}}_j}$ and $P_{{\text{GWSA}}_j}$ are the normalized eigenvalues of the PC j in the analysis of WES and GWSA data, respectively; WES_j and GWSA_j are the vectors of the coordinates for PC j in our 110 individuals obtained in PCA on WES and GWSA data, respectively; M is the number of significant PCs (P value < 0.05) obtained with unsupervised Tracy–Widom statistics (Table S3); and the R_W correlation coefficient was calculated for each of 25 combinations of CRs and MAF shown in Table S2.

The local ancestry for 110 study individuals was inferred by Hapmix (43). Because Hapmix assumes two ancestral populations, we ran the software for six sets of two ancestral populations from four HapMap/1000 Genomes Projects: CEU and YRI, CEU and CHB, CEU and MEX, YRI and CHB, YRI and MEX, and CHB and MEX. Because the MEX population included only 44 independent individuals with both HapMap and 1000 Genomes data, we also used a set of 44 independent individuals for three other ancestral populations. The correlation between the proportions of ancestry estimated in our 110 individuals using the GWSA or the WES data was computed over the whole autosomal genome for each of six sets of ancestral populations.

Estimation of Homozygosity.

Several approaches have been proposed for estimating the inbreeding coefficient F from genetic data (20). Chromosomal regions that are HBD can be identified by searching for ROHs over a given length, providing an estimate of F based on the proportion of the autosomal genome in ROHs (20). For these analyses, we used the HQ autosomal SNVs with an MAF > 0.05 (654,155) identified by GWSA and 73,565 SNVs with a CR > 98% and an MAF > 0.05 identified by WES. We identified ROHs with PLINK (39), which has several advantages over other methods (37). We used the classical PLINK method with default parameters, in which a 1,000-kb window is moved across the genome, with homozygosity determined for each window. We varied the number of SNVs within the 1,000-kb window required to call an ROH using a smaller number for WES (20, 30, 50, and 100) than for GWSA (100, 200, 250, and 300) to account for the lower total autosomal SNV counts in WES than in GWSA data (37). The choice of these numbers was based on the fact that a window of 1,000 kb corresponds to ∼0.37% of the autosomal genome, giving mean numbers of available SNVs per 1,000 kb of ∼27 for WES data and ∼242 for GWSA data. We also considered the PLINK parameters reported to be optimal in a recent study (37) for the analysis of the WES data. These parameters included 10 SNVs within the 1,000-kb window. We obtained a genomic measurement of individual homozygosity (F_ROH) by determining the proportion of the autosomal genome present in ROHs (20).

Another approach for estimating F involves modeling the HBD states of the different markers of one individual along the genome as a Markov process using hidden Markov models as initially proposed in the F_ESTIM method (19). This method assumes that marker alleles are independent conditionally on HBD state, which is not true for dense SNVs (in array or exome data), for which linkage disequilibrium (LD) may occur. We used the FEstim_SUBS method to minimize LD between SNVs as recommended in a previous study (44) for the random extraction of sparse markers every 0.5 cM to create 1,000 submaps. This strategy does not require the estimation of LD scores for the data, and F is estimated by calculating the median value of the estimates obtained from the different maps. The FSuite program was used to calculate F_ESTIM for each individual from both GWSA and WES data (47).

Linkage Analysis.

We performed linkage analysis assuming autosomal recessive inheritance with complete penetrance (homozygosity mapping) on individuals found to have a high rate of homozygosity. For each individual, we created the same family structure based on a unique consanguinity loop at the first cousin level. The main goal of our study was to compare the linkage information provided by WES with that provided by GWSA using the same familial structure and the same data for all families, consisting of nine individuals with a single genotyped subject assumed to be affected (the offspring of the youngest generation). We carried out parametric multipoint linkage analysis by homozygosity mapping (55) with Merlin software (56). A population disease allele frequency of 0.0001 was specified together with a fully penetrant recessive genetic model. LOD scores were calculated for every marker (from WES or GWSA data), and 1000 Genomes Project allele frequencies were used (42). Information content was also estimated for both WES and GWSA data, because this parameter provides an indication of how closely the available markers approach the ideal situation of complete inheritance information for the segregation of the chromosomal region considered.