A statistical property of fly odor responses is conserved across odors

Significance

Although the brain has long been considered to use combinatorial codes (a defined population of neurons whose pattern of rates is specific to a particular object), in no case has the code been well-characterized. Here I characterize the fly odor code by showing it is maximum entropy; what this means is that the response to all odors is statistically the same. This characterization is a significant first step in cracking the odor code.

Abstract

I have reanalyzed the data presented by Hallem and Carlson [Hallem EA, Carlson JR (2006) Cell 125(1):143–160] and shown that the combinatorial odor code supplied by the fruit fly antenna is a very simple one in which nearly all odors produce, statistically, the same neuronal response; i.e., the probability distribution of sensory neuron firing rates across the population of odorant sensory neurons is an exponential for nearly all odors and odor mixtures, with the mean rate dependent on the odor concentration. Between odors, then, the response differs according to which sensory neurons are firing at what individual rates and with what mean population rate, but not in the probability distribution of firing rates. This conclusion is independent of adjustable parameters, and holds both for monomolecular odors and complex mixtures. Because the circuitry in the antennal lobe constrains the mean firing rate to be the same for all odors and concentrations, the odor code is what is known as maximum entropy.

The projection neurons of the fly antennal lobe present odor information to the Kenyon cells of the mushroom body in the form of a combinatorial code—each odor is specified by a particular pattern of firing rates across the population of projection neurons—and a recent paper (1), using data published in ref. 2, provided preliminary evidence that this odor code is what information theorists call maximum entropy (3). To understand what a maximum entropy code is, suppose that we record the firing rates from, say, 10 different projection neurons, each presented with, say, 10 different odors to give a total of 100 firing rates. Now make a histogram of these firing rates. If the odor code is maximum entropy, this histogram would have nearly the same shape no matter which projection neurons and which odors were chosen. Also, the larger the sample of projection neurons and/or odors, the closer the shapes of histograms would be. Remarkably, if only a single odor and many projection neurons, or a single projection neuron and many odors, are used to generate the rates, the histogram shape is always nearly the same.

Many different maximum entropy codes have been studied, and the type of code is defined by the shape of the histogram that results from a sample of rates. The histogram in each case is an approximation of a probability distribution of rates. For example, if the mean rate is always the same, the maximum entropy code is known to be associated with an exponential distribution of rates, and if both the mean and variance are always the same, a Gaussian distribution of rates is associated (3). For the fly projection neurons, the associated probability distribution of rates is proposed to be an exponential (1) (with always the same mean).

As pointed out earlier (1), a maximum entropy code would be advantageous to the fly because it would permit the most odors to be discriminated with the available number of odorant receptors.

This characterization of the odor code used by antennal lobe projection neurons makes a strong prediction about the odor responses of olfactory receptor neurons (ORNs) in the antennae that supply olfactory information to the antennal lobe. Among the computations carried out by the antennal lobe, we know an important job of this structure is to remove the odorant concentration dependence from the ORN responses (4–6)—i.e., to make the mean projection neuron rate the same for any odor at almost any concentration. The ORNs must differ from antennal lobe projection neurons insofar as the ORN mean rates depend on odor concentration, whereas projection neuron mean rates do not; otherwise, the population of ORNs is predicted to respond the same way to any odor. This difference means that the probability distribution for ORN firing rates in response to any odor should have an exponential shape, even though the mean rate varies with odor concentration, because the shape of the firing rate distribution should be maintained by the gain control between the ORNs and antennal lobe projection neurons (6).

Testing these predictions is important, because the conclusion that the fly’s antennal lobe uses a maximum entropy code was based on a histogram of firing rates constructed from a sample of only 126 projection neuron rates (2), and thus this conclusion remains unproven for at least three reasons. First, a sample of only 126 rates may be too small to detect significant departures from an exponential distribution. Second, because only a small fraction of the projection neurons types and 18 odors (of the many hundreds experienced by the fly) were used to generate the 126 rates, the small sample size raises questions about the generality of the conclusion. Finally, only monomolecular odors were used, whereas most natural odors are mixtures (often hundreds of monomolecular odors at different concentrations), and the idea that the same probability distribution describes both monomolecular odors and odor mixtures—as would be necessary if the odor code is maximum entropy—is untested.

Fortunately, two classic papers by Hallem and Carlson (7, 8) provide the data necessary to test the idea that the fly odor code is, in fact, maximum entropy. These papers reported measured firing rates of 24 ORN types (a different odorant receptor gene for each neuron type) in response to a panel of 110 monomolecular odors and extracts from nine types of fruit. The fruit fly olfactory system naturally specializes in odors from biologically relevant fruits and other odor sources. Of the 110 odors studied by Hallem and Carlson (7, 8), many were associated with fruits, but the entire panel of odors included a wide range of functional groups: amines, lactones, acids, sulfur compounds, terpenes, aldehydes, ketones, aromatics, alcohols, and esters. Despite the acknowledged importance of fruit odors to the fly, the panel of 110 odors used and the 24 ORNs sampled should provide a mostly accurate picture of the response to the odors experienced by the fly.

The goal of this paper, then, is to test, through reanalysis of the data presented in two classic papers on ORN properties (7, 8), two predictions: (i) if the measured firing rates across 24 ORNs for each odor are normalized to the same mean rate, a single distribution function should describe the response to all odors in the panel, and to all odor mixtures; and (ii) that probability distribution of firing rates should be an exponential. Below I show that the published data support these predictions.

Results

The first of the pair of papers that I consider here (7, 8) described the basic properties of the fly’s ORNs and the odorant receptor (OR) proteins expressed by these neurons. In the second paper (8), an extensive survey and analysis, the authors examined 24 of 32 ORN types (known in 2006) that project from the antenna; additional ORN types present in the adult project from the maxillary palp (9, 10). The responses of this population of 24 ORNs to a total of 119 odor types were examined by recording the firing rates electrophysiologically. Of these responses, 110 [presented in table S1 of Hallem and Carlson (8)] were produced to pure (monomolecular) odors that fall into 10 different chemical types; each of the 110 pure odors was applied at a single standard concentration, although the maximal affinity for these odors presumably varied over the population of ORNs studied. In addition to the 110 pure odors, nine fruit extract odors were studied over a six-order-of-magnitude concentration range [nine odors, each at four different concentrations presented in table S2 of Hallem and Carlson (8)]. A total of 3,504 data points are reanalyzed here (together with the results from an additional 960 data points—10 monomolecular odors at four concentrations each—presented in Fig. S2), mainly by constructing cumulative probability distributions of firing rates across the population of 24 ORNs for each odor and odor concentration.

Fig. S2.

Analysis of probability distributions for 24 ORNs with 10 monomolecular odors at four dilutions each (10⁻², 10⁻⁴, 10⁻⁶, and 10⁻⁸). The procedures here were the same as those described in the main text for fruit extracts. (A) Cumulative distributions for 10 odors and four concentrations each (24 ORNs). (B) Logarithm of mean firing rate as a function of the logarithm of relative odor concentration. The line, fitted with the least-squares method to 40 data points (mean firing rates for 10 odors, four concentrations each), has a slope of 0.12 and an intercept of 1.89 (logarithmic coordinates). The vertical bars on the data points are the SDs for the 10 odors at each concentration. (C) Superimposed cumulative probability, normalized to the same mean rate (100 Hz), as a function of rate. (D) Average of the distributions that appear in C, with an exponential distribution superimposed.

The 110 Pure Odors at a Single Concentration Each.

The mean firing rate for the population of 24 ORNs varies significantly over the 110 pure odors, with a range from 11 to 95 Hz, and with half of the odors giving mean rates below 24 Hz. Some of this variability arises because about half of the ORN types were not sampled [30 of the 54 ORN types present (11)], but much of the range reflects differences in the effective odorant concentrations used.

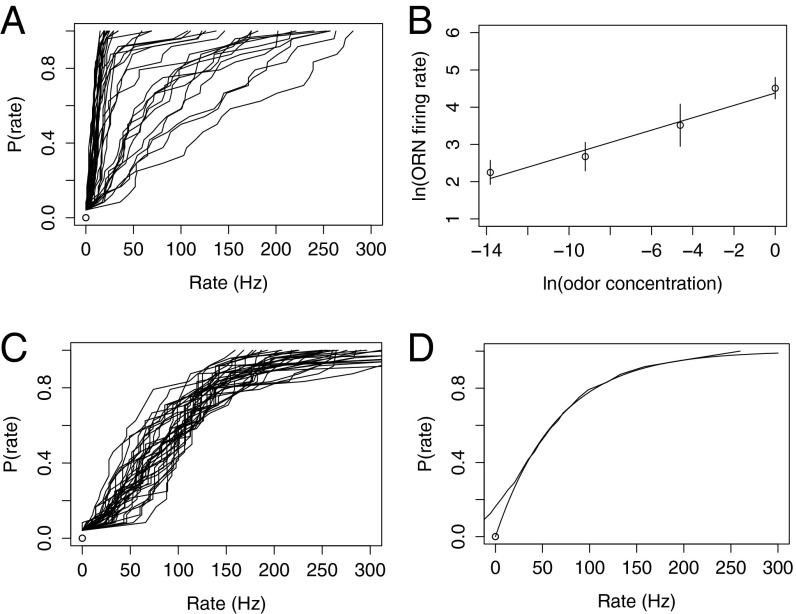
I constructed 110 cumulative probability distributions of ORN firing rates, with each distribution being based on the population of 24 ORNs and a single odor (24 measured rates). These distributions (Fig. 1A) are, as would be expected for the wide range of mean firing rates, quite different. Fig. 1A, like most of the ones that follow, plots the cumulative probability [P(rate)] as a function of ORN rate (Hz) where P(rate) gives the probability of finding an ORN rate less than or equal to the value chosen on the rate axis.

Fig. 1.

Analysis of data from 110 odors and 24 ORNs. (A) Cumulative probability distributions as a function of ORN firing rate for each odor. All 110 histograms are superimposed. (B) Normalized cumulative probability distributions for 110 odors. All probability distributions in B have been scaled to have the same mean firing rate of 100 Hz. (C) Six of the 110 cumulative probability distributions (every 18th distribution) plotted so that the individual traces can be inspected. (D) The average of the 110 scaled cumulative probability distributions exhibited in B plotted with an exponential distribution superimposed.

Because the large number of curves plotted obscure one another, the shapes of the individual distributions cannot be appreciated, but the purpose of this figure is to illustrate how different the 110 histograms are from one another.

I normalized these histograms to have the same mean (100 Hz) by multiplying the 24 ORN rates produced in response to each odor by 100/(mean rate for that odor) and replotted them superimposed. The result is shown in Fig. 1B.

The individual histograms still obscure one another, but they appear to describe what could be a single distribution, perhaps one where noise gives the broad band around a single underlying distribution (Model of ORN Properties). To gain some insight into the source of this variability, I superimposed six individual normalized histograms (mean 100 Hz for all) by arbitrarily plotting every 18th histogram from Fig. 1B—of the population of 110 total cumulative histograms—in Fig. 1C.

Two factors clearly contribute to the variability in the shapes of these normalized distributions: the first relates to the background firing of ORNs, and the second reflects random variability arising in a small sample.

First, all 24 ORNs are found to fire at an average “background” rate of 13.75 Hz (range 1–47 Hz) in the absence of any odor (see the last row in table S1 of ref. 8). Presentation of an odor usually causes ORNs to increase their firing, but this same odor inhibits some other ORNS to a rate below the background seen in the absent of odor. Thus, background firing is decreased, but not entirely eliminated, for some of the ORNs in the sample by any odor presented. This effect is variable, however, as can be seen by the behavior of the cumulative histograms in Fig. 1C where some histograms increase rapidly directly from the origin (leftmost curves in Fig. 1C) and other histograms increase very slowly from 0 Hz to a frequency between 20 and 40 Hz (right-shifted histograms). The behavior near the origin reflects differences in the background firing rates seen with different odors. For some ORNs and odors, the fast initial rise represents ORNs for which inhibition has eliminated the background firing. The right-shifted curves represent one or a few ORNs that are firing at a high background rate (little inhibition of the background) that is unchanged by the particular odor used.

Second, the population of ORNs that contributed to the cumulative histograms is a relatively small one (only 24 of a total of 54), and so random variability of the sort seen in individual histograms is what would be expected from noise in a sample of only two dozen ORNs (Model of ORN Properties).

To estimate the probability distribution underlying the histograms that appear Fig. 1B, I averaged across the 110 cumulative histograms from Fig. 1B (I simply added together all of the histograms in Fig. 1B and divided by 110, the number of histograms) and presented the average in Fig. 1D (line with an S shape at the origin). This estimate of the underlying distribution is quite smooth and seems to capture well the population of normalized histograms in Fig. 1B. The S curve at the origin is an artifact of averaging across individual histograms with different background firing and depends on the way that different odors decrease or increase the background rate.

I have also superimposed the predicted exponential distribution on the average curve in Fig. 1D. Clearly, the exponential distribution is a good description of the estimated underlying distribution function (the average across all normalized cumulative probability distributions) except for a few ORNs with lowest firing rates. Thus, the predicted behavior of the ORNs is confirmed, although the exact way the background rate is handled by the antennal lobe, where the projection neurons also have variable background firing rates (2), is not known. All (or at least most) of the 110 odors seem to give the same response as determined by the probability distribution of rates across the population of 24 ORNs.

For Fig. 1, I compiled 110 cumulative probability distributions over the 24 ORN types, one distribution for each odor. The result should be the same if I had compiled 24 distributions over the 110 odors, one distribution for each ORN type. The confirmation of this expectation is presented in Fig. S1.

Fig. S1.

Superimposed cumulative distributions for probability as a function of ORN rate. (A) Normalized (to 100 Hz) cumulative probability distributions for ORN rate calculated by compiling histograms for each of the 24 ORN types across 110 odors. Twenty-four histograms appear, each based on 110 rates (one rate for each odor). (B) The average of the 24 distributions shown in A with a cumulative exponential probability distribution (like the distributions that appear in Figs. 1E and 2D).

Nine Fruit Odors at Four Concentrations.

The preceding section examined ORN firing rates in response to 110 pure (monomolecular) odors and showed that, when the 110 probability distributions for the firing of the 24 ORNs are normalized to the same mean firing rate, the distributions can plausibly be said to have the same shape except for random fluctuations and a variable S shape rise at the origin. Furthermore, when the empirical probability distributions are averaged together, the overall estimate for the probability as a function of normalized ORN firing rate is well-fitted by an exponential probability distribution.

Because the previous section was based on only pure odors, not odor mixtures, and on only a single concentration for each odor, my analysis there leaves two main questions unanswered. First, how does the average firing rate (across the 24 ORN types studied) depend on the odorant concentration? Second, do natural odors—ones of biological significance to the fly that are combinations of many monomolecular odor components—produce probability distributions that are the same shape for all odors, and is this the shape of an exponential distribution like it is for pure odors? This section addresses these questions. The answers are that the dose–response curve is a power law with the odor concentration raised to a power well less than 1, and that the odor mixtures give the same probability distribution (an exponential) seen for the pure odors, as would be expected if the odor code is maximum entropy.

Table S2 of the Hallem and Carlson (8) paper reports the responses of the 24 ORN types to odors from nine fruit extracts (apple, apricot, banana, cherry, mango, peach, pineapple, raspberry, and strawberry). For each of these fruit extracts, three dilutions were made (at 10⁻², 10⁻⁴, and 10⁻⁶) of the undiluted extract, so that the fruit odors were presented over a six-order-of-magnitude concentration range (undiluted and three dilutions). I constructed 36 cumulative probability distributions for the firing rates of the 24 ORNs sampled (one distribution function for each fruit odor and concentration), and these distributions are displayed in Fig. 2A.

Fig. 2.

Analysis of nine complex fruit odors at four odor concentrations each. (A) Thirty-six superimposed cumulative probability distributions of ORN firing rates for nine fruit extracts, each at four concentrations. Twenty-four ORNs were used to compile each distribution for one odor and one concentration. (B) Double-logarithmic plot of mean ORN firing rate (across nine odors at a single concentration each) as a function of relative concentration (dilution of fruit extract). The least-squares fitted line has a slope of 0.166. The vertical bars on the data points are the SDs for the nine odors at each odor concentration. (C) The superimposed cumulative distributions as a function of ORN rate that appear in A, replotted after scaling each distribution to the same mean (100 Hz). (D) The average of the 36 distribution functions from C with an exponential distribution function with a mean of 100 superimposed.

The distributions for natural odors look roughly similar to those for the pure odors considered in the previous section, even though each distribution here represents the response to a complicated mixture of pure odors.

To examine how the firing rates are distributed over a million-fold odorant concentration range, I have calculated the mean ORN rate for each odor and concentration, and averaged these rates across the nine odors, with one average for each odor concentration. The logarithms of the average rates are plotted in Fig. 2B as a function of the logarithm of the relative odor concentrations to show the odorant dose–response curve over a million-fold concentration range.

What is the equation that describes this dose–response curve over a million-fold range? The straight line in the figure was fitted to the 36 data points [log(mean rate) for nine odors and four concentrations vs. log(relative concentration)] using least squares. The fit of the linear relation for the data are adequate, and is described, in linear rather than logarithmic coordinates, by the equation

$$\overline{r}=80\left(c_r^{0.166}\right),$$

where $\overline{r}$ is the mean ORN firing rate (Hz) (mean calculated across the nine fruit odors at each dilution) and $c_r$ is the relative odorant concentration expressed as dilution (e.g., 10⁻⁴); 80 is a fitted constant with the units of hertz. Thus, the dose–response curve is a power function over this concentration range. I return to this relation in Discussion to describe some of its implications.

It has been suggested (12) that the response to a complex odor mixture (like fruit extracts where many components are present in different concentrations) might be something like the sum of the responses to the individual components. This expectation would predict that the probability distribution function (formed across 24 ORN types) to a complex odor would not be a single exponential but rather something more complicated. My prediction here, however, based on the idea that the odor code is maximum entropy, is that distribution functions for the fruit odors, where different concentrations for each fruit odor (a complex mixture) have been normalized a mean ORN firing rate of 100 Hz, would have the same shape for all complex odors and concentrations; i.e., it would be a single exponential. In Fig. 2C, I present the 36 distribution functions (for nine fruit odors with four concentrations each) that have been normalized to the same mean firing rate (100 Hz). Again, the shapes of these distributions are plausibly the same, with the scatter produced by the difference in the way the background firing rate is modified by odor inhibition, and by random fluctuations in the empirical histograms.

To estimate the underlying probability distribution function that produces the histograms in Fig. 2C, I have averaged the 36 normalized distributions that appear in this figure. The estimated underlying probability of finding an ORN that fires at a particular rate for a given odor appears in Fig. 2D.

As before, I have fitted an exponential distribution function to the estimated probability distribution. Clearly, the fit is mostly a good one, so the exponential distribution describes the normalized empirical distribution function arising from complex odor mixtures presented at different concentrations; this is the predicted result.

In addition to the data on the nine fruit extracts, table S2 in ref. 8 also has data on 10 of the monomolecular odors from table S1 presented at four concentrations each that range over six orders of magnitude. Fig. S2 presents these data to show that the conclusions for the monomolecular odors at different concentrations are basically the same as those for the complex mixtures.

Model of ORN Properties.

In previous sections, the figures have shown either 36 (Fig. 2C) or 110 (Fig. 1B) superimposed histograms—ones that have been normalized to a mean rate of 100 Hz—that represent cumulative probability as a function of ORN rate. In both cases, a broad band of histograms appears, and I have claimed that this broad band arises from statistical fluctuations due to the small sample size (24) and the variable way in which various odors correct for this background firing through how much they inhibit it. To substantiate this claim, I need to show that these two effects (small sample size and variable correction of background firing) can produce superimposed histograms like those seen in Figs. 1 and 2. That is the goal of this section.

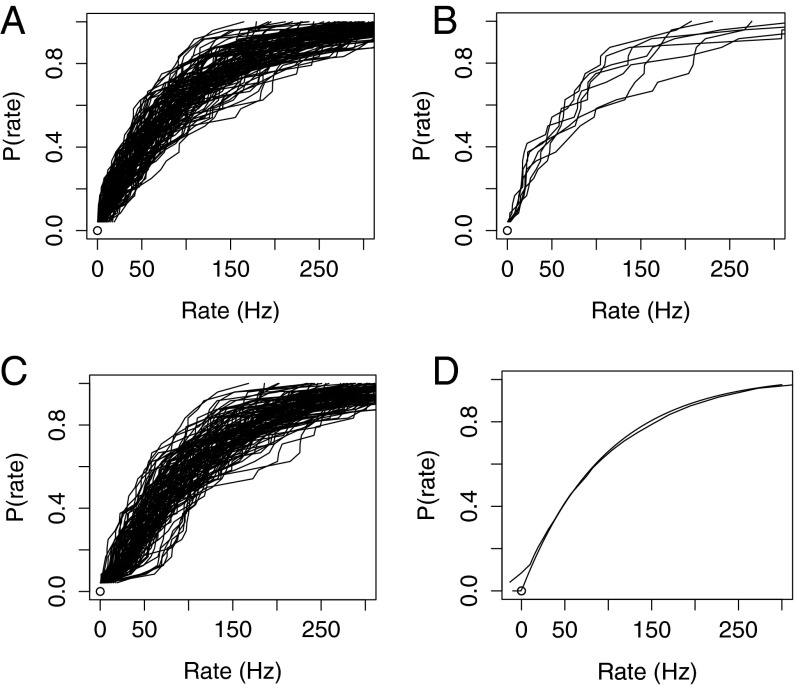
Examining the effects of the sample size (24) on variability in the shape of the histograms is easy: generating a collection of 24 random numbers according to an exponential distribution with a mean of 100 is a standard operation (see Experimental Procedures for more details). I produced 110 such collections and constructed cumulative histograms from them in the same way as I did for the actual Hallem and Carlson (8) data. The result appears in Fig. 3A, and a sample of six of the 110 histograms (every 18th) is displayed in Fig. 3B so the traces do not obscure one another. It is apparent from Fig. 3 A and B that the individual traces are about as variable as the single histograms derived as the actual data.

Fig. 3.

(A) The 110 histograms, each based on 24 rates distributed according to an exponential distribution with a mean rate of 100 Hz. (B) Six individual histograms from A (every 18th). (C) The 110 histograms generated according to an exponential distribution with the two ORNs with the slowest firing ORNs given a randomly selected background firing rate. (D) The average of the 110 histograms in C with an exponential distribution superimposed as in Figs. 1D and 2D.

In Fig. 3C, the effect of a variable correction of the background firing has been included by adding a randomly selected background rate (distributed according to exponential distributions with a means of 9 and 5 Hz for the two lowest-firing ORNs). Notice that including these background rates broadens the lower part of the band of 110 distributions and gives the characteristic slow linear rise to the point at which the histograms start to increase rapidly. Thus, the main part of the variability between individual histograms can arise from the small sample size (24), but the effect of the incomplete correction of the background rate has an important effect near the origin of the histograms.

As before, I have also averaged the histograms in Fig. 3C and presented the average in Fig. 3D, where it appears as a smooth curve. Exponential distribution has been superimposed on the simulated distribution function, and the exponential distribution is a mostly accurate description.

I conclude, then, that the random suppression of the background firing, together with the sampling fluctuations from an exponential distribution, are adequate to explain the behavior of the actual data presented in Figs. 1 and 2.

Discussion

My result here is a simple one: every odor, pure or complex, produces statistically the same output (one arising from the same probability distribution) from the fly’s population of ORNs, except that the mean rate of the population differs according to odor concentration. In detail, however, which ORN types are firing at which rates varies considerably for different odors (tables S1 and S2 in ref. 8).

No obvious exceptions to my simple conclusion are apparent in the data presented in the figures above, but I know this conclusion cannot be completely correct: at least two receptors (Gr21a and Or56a) are known to respond selectively to only CO₂ (13) and geosmin (14), respectively. How well my conclusion for the fruit fly applies across different insect species compared with the alternative “labeled-line” approximation will require further evaluation (15).

Furthermore, an entirely genetically different class of 15 odorant receptor types, the ionotropic receptors (IRs) discovered after the Hallem and Carlson work (16), are present in the fly antennae. These receptors are present in a distinct class of sensilla (coeloconic), tend to respond to acids and amines, and are related to the family of ionotropic glutamate receptors present at synapses. The IRs project to distinct glomeruli in the antennal lobe, and from there to Kenyon cells, but the responses of individual IR types to a panel of odors is, as yet, unknown (17), so the IRs responses cannot be related to the OR responses described here.

Hallem and Carlson (8) characterized odorant receptors types according to their “tuning curves,” which were constructed to appear similar to tuning curves for other sensory modalities. To construct a tuning curve, Hallem and Carlson (8) rank ordered the responses of the 24 ORNs to a specific odor (from largest to smallest firing rates), plotted the largest rate on the y axis at x = 0, and then the even-numbered rates in the positive x direction and the odd rates in the negative x direction. The result is a graph of 24 rates on the y axis, one for each ORN, with the largest in the center ($x=0$) and the other 23 rates decreasing in both directions away from the origin of the x axis. If the odor studied activated only a few ORNs strongly, the tuning is very narrow, and if many ORNs are activated more strongly, the tuning curve is very broad. A wide range of tuning widths was found, and the tuning for various odors ranged from narrow to broad for the odors studied.

How does this description of tuning curves relate the description here in terms of cumulative probability distributions of firing rates for 24 ORNs measured for each odor (Fig. 1A; Cumulative Histograms)? I have also rank ordered the 24 firing rates (but from small to large rather than large to small), and have plotted these rank-ordered rates on the x axis and the fraction of rates less than or equal to a given rate on the y axis (the cumulative probability). The rates for all odors were found to be exponentially distributed, but with different mean rates for each odor (Fig. 1A). Thus, the Hallem–Carlson tuning width is related to the mean firing rate of the present analysis, and Fig. 1A would exhibit the distribution of Hallem–Carlson tuning widths (8).

According to my analysis of the nine fruit extracts, each at four concentrations, the relation between mean ORN rate and odor concentration follows the equation $\overline{r}=a{\left(\lambda c_0\right)}^k$, where $\overline{r}$ is the mean ORN firing rate (calculated across the 24 ORNs studied), λ is the relative concentration (measured by the dilution from a specific odor concentration), $c_0$ is the odorant concentration in the dilution of the undiluted extract, a is the constant 80 (Hz), and k = 0.166, a unitless constant derived from the slope of the straight line fitted to the observed relation between odor relative concentration and measured mean ORN firing rate on a double-logarithmic plot.

Recall that normalizing the cumulative probability histograms to have the same mean rate [by multiplying all observed rates for one odor by 100/(mean rate for that odor)] gave histograms that were described by an exponential distribution (except for the lowest rates). Probability distributions that superimpose when normalized in this way are called “self-similar distributions,” and they have a remarkable property: to be self-similar, their mean (and possibly other statistics for certain distributions) must be described by a power law like the one for the mean rate $\overline{r}$ discussed in the previous paragraph [see Stevens (18) for a simple description of self-similar functions in a biological context and an explanation for why the mean rate must follow a power law]. I confirmed this prediction about the mean rate following a power law in Fig. 2B. Many functions are self-similar, but the exponential probability distribution is known to depend, according to a power law, on only its mean. Another well-known self-similar probability distribution is the Gaussian, and it depends according to power laws on both its mean and variance. Of course, the power law for $\overline{r}$ cannot be correct for all odor concentrations because saturation must occur when the concentration is sufficiently high and, as saturation occurs, the self-similarity of the probability distributions will also fail (and the shape of the distributions will change).

These observations are important for two reasons. First, my conclusions here can hold only over the low end of the odor concentration range where the odorant receptors are far from saturated. Specifically, the responses to the 110 monomolecular odors are, statistically, only the same in this low-concentration regime. Second, the self-similar behavior in this low-concentration range also explains why all odors, both monomolecular and mixtures, must be, statistically, the same. In this odor concentration range, the mean firing rate across the population of ORNs depends only on concentration and not on the type of odor (see the power law equation above for mean rate vs. odor concentration). Whenever the mean rate as a function of concentration is independent of odor type and the distribution functions are self-similar, the distribution must be an exponential as was found here.

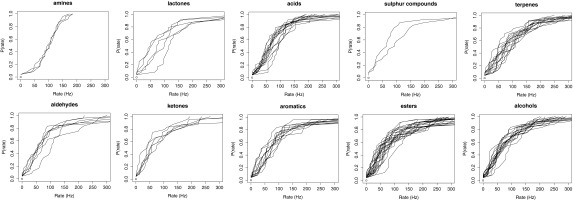
Although the Hallem and Carlson (8) study was extensive—24 ORN types, 110 monomolecular odors, and 9 fruit odor mixtures were studied—the question remains whether my conclusions would apply if more ORN types and more odors were included. The 24 ORN types represented in the analysis here is a little under half of the 52 odorant receptors expressed by ORNs (11). Although the fly repertoire of receptors is weighted toward fruit odors, the odor panel used for the experiments reanalyzed here was chosen to include 10 functional categories of chemicals (amines, lactones, acids, sulfur compounds, terpenes, aldehydes, ketones, aromatics, esters, and alcohols). Furthermore, the sensilla represented are approximately in proportion – twice as many basiconic as trichoid – to the number present in the antenna (19). Together, short of a complete survey, the Hallem and Carlson (8) work made a significant effort to provide a representative sample of the fly’s encoding of odors. The normalized cumulative probability distributions for the 10 chemical classes of odors appear in Fig. S3, so the reader can judge if the conclusions I draw represent the 10 odor classes.

Fig. S3.

Normalized cumulative probability distributions as a function of ORN rate for each of the 10 chemical classes of odors.

Although it has been proposed that combinatorial codes may be common in the brain (for two seminal papers, see refs. 20 and 21), to my knowledge, no combinatorial code has been mathematically characterized. Similarities between olfaction in insects and vertebrates (22) raise the possibility that vertebrates might also use a maximum entropy code like the fly, and it would be interesting, then, to see if other combinatorial codes share the maximum entropy property.

Materials and Methods

Experimental Procedures.

The work described here depended almost exclusively on forming cumulative probability histograms of ORN firing rates, normalizing these histograms to an arbitrary mean firing rate (selected to be 100 Hz), and estimating the underlying probability distribution function by averaging the normalized histograms. I cover these procedures in turn. All three procedures are simple and straightforward.

The cumulative histogram of ORN firing rates estimates the probability distribution of finding a rate that is less than or equal to some given rate. The probability density function (the probability of finding a rate within a narrow range around a given rate) is more intuitive but requires selecting a bin size for the rates. The cumulative histograms are chosen here because they contain the same information and do not require selecting a bin size.

Cumulative Histograms.

The procedure for forming a cumulative histogram is as follows: select an odor (one of the rows of the tables S1 or S2 of ref. 8). Each row in the table gives a list of 24 firing rates, and this list is sorted to place the rates in increasing order. Call the sorted list $f.$ Now plot f on the x axis of a graph against a list y that runs from (1–24)/24 (i.e., in even steps of 1/24th from 0 to 1). For each entry in the list $f,$ the y axis is increased by 1/24. The result is a cumulative histogram across all of the ORNs for the odor (the row) chosen.

The original tables S1 and S2 in ref. 8 presented values of the observed firing rate for each ORN with the background firing rate for that ORN subtracted, and this produced negative firing rates when the odor happened to decrease (inhibit) the rate for the ORN below its background. Although the average background firing rates are given in the last row of table S1 in ref. 8, the background firing rates varied around this average for particular experiments, so the information is unavailable to restore the table entries to their (nonnegative) observed values. To avoid having negative rates, I added the absolute value for the most negative firing rate in each list f to all of the entries in f. This choice was arbitrary, and does not materially alter the shape of the histograms.

Rather than selecting a row in the table to use for forming the cumulative histogram as just described, an alternative would have been to pick a column (a particular ORN) and construct the cumulative histogram based on the firing rates in that column, which would produce a cumulative histogram for one ORN across all odors. What we care about is the estimate of the probability distribution function of ORN rates, and this is found by averaging across all histograms (as described below). This estimate cannot depend on the order (average cumulative histograms found for each odor vs. averaging the cumulative histograms found for each ORN), and in Fig. S1, I show that the two ways of estimating the probability distribution function produce the same result.

Normalized Cumulative Histograms.

To form the cumulative histograms, I started by finding the sorted list f of ORN firing rates for a particular odor arranged in increasing order. To find the normalized cumulative histograms, it is necessary to adjust the mean firing rate $\overline{r}$ for each odor to some arbitrary value that is the same across all odors. I selected the adjusted mean firing rate to be 100 Hz. To assign this mean to each odor, I multiplied all of the entries in the list f by 100/$\overline{r}$, where $\overline{r}$ is the mean of $f.$ The normalized f is called $f_n=(100/\overline{r)}f.$ Then, I follow the procedure described in the previous section, except that I substitute $f_n$ for f.

Estimate of the Underlying Probability Distribution Function for ORN Rates.

The estimated probability distribution function is just the average across normalized cumulative histograms for all odors. To calculate this average, I find, for each entry j, $\overline{f_n}\left(j\right)=\frac{1}{N}{\displaystyle {\sum }_{i=1}^{i=N}{f}_n\left(i,j\right)}$, where $f_n\left(i,j\right)$ is the $j^{th}$ entry in the $i^{th}$ histogram (one histogram for each monomolecular odor, and one histogram for each fruit odor and each concentration), and N is the number of histograms ($N=110$ for data in table S1, and $N=36$ for fruit extract data in table S2 in ref. 8). The graph plotted then is $\overline{f_n}$ on the x axis and $1/24,2/24,3/24\cdots 24/24$ on the y axis. Note that I adjusted the first entry of $f_n$ to zero in the histograms superimposed in Figs. 1 and 2 A–C to eliminate negative firing rates, but I permitted negative firing rates for the estimates of the probability distribution functions in Figs. 1D and 2D. The cumulative exponential distribution I fitted to the estimates was $p\left(r\right)=1-exp\left(r/100\right)$, which has a value of zero when $r=0,$ and the estimates of the underlying distributions are translated along the rate axis until the rising phase of the exponentials matched.

Simulated Histograms.

The simulations were carried out with the R program (https://www.r-project.org/) running under RStudio (https://www.rstudio.com/). A 110 × 24 matrix, analogous to Hallem and Carlson’s table 1 in ref. 8, was generated by the R command rexp(24, 0.01); here, 24 (first variable) specifies the number of exponentially distributed random numbers generated each time the command is executed, and the exponential distribution has a mean of 100 = 1/0.01 (second variable). This command was executed 110 times and results collected into the 110 × 24 matrix. The first step in the analysis was to convert this 110 × 24 matrix to a new matrix, called F, by rank-ordering the entries in each row. From there on, this matrix was treated like the one from table S1 in Hallem and Carlson (8).

To produce the variable correction of the background firing, exponentially distributed random numbers were added to the second and third entries in each row.