Improved spatial accuracy of functional maps in the rat olfactory bulb using supervised machine learning approach

Abstract

Functional MRI (fMRI) is a popular and important tool for noninvasive mapping of neural activity. As fMRI measures the hemodynamic response, the resulting activation maps do not perfectly reflect the underlying neural activity. The purpose of this work was to design a data-driven model to improve the spatial accuracy of fMRI maps in the rat olfactory bulb. This system is an ideal choice for this investigation since the bulb circuit is well characterized, allowing for an accurate definition of activity patterns in order to train the model. We generated models for both cerebral blood volume weighted (CBVw) and blood oxygen level dependent (BOLD) fMRI data. The results indicate that the spatial accuracy of the activation maps is either significantly improved or at worst not significantly different when using the learned models compared to a conventional general linear model approach, particularly for BOLD images and activity patterns involving deep layers of the bulb. Furthermore, the activation maps computed by CBVw and BOLD data show increased agreement when using the learned models, lending more confidence to their accuracy. The models presented here could have an immediate impact on studies of the olfactory bulb, but perhaps more importantly, demonstrate the potential for similar flexible, data-driven models to improve the quality of activation maps calculated using fMRI data.

1. Introduction

Non-invasive measures of neural function play a critical role in the field of systems neuroscience, particularly in the area of human cognition. Of the available tools, functional MRI (fMRI) remains the most popular because of its effective balance between volumetric sampling and spatiotemporal resolution (Cohen and Bookheimer, 1994). A number of techniques exist for using fMRI to map brain function, each of which measure some aspect(s) of the vascular response to the underlying neural activity. Of these methods, blood oxygen level dependent (BOLD) contrast is by far the most common because it results from neural activity, is relatively easy to implement, and does not require the administration of contrast agents.

While the BOLD signal possesses a number of strengths, the complexity of this signal does pose significant challenges for accurately mapping the location of neural activity. At least three physiological responses are known to significantly contribute to the relative proportion of paramagnetic deoxyhemoglobin present in a given voxel, and thus impact the BOLD signal. These responses include the cerebral metabolic rate for oxygen, cerebral blood flow, and cerebral blood volume (CBV). These individual responses have competing effects on the BOLD signal and change dynamically over time with respect to the stimulus onset, and thus the largest BOLD signal changes may not co-localize with the actual sites of increased neural activity (Kim and Ogawa, 2012). Moreover, the spatial specificity of these responses is varied and some large signal changes can be induced by nonspecific processes such as draining veins, which negatively impact the accuracy of fMRI-derived activation maps (Turner, 2002).

Recently we compared the spatial accuracy of CBV- and BOLD-weighted functional images in the rat olfactory bulb (OB), and highlighted some of the limitations in using BOLD to perform fMRI experiments (Poplawsky et al., 2015). Given the highly laminar architecture in the OB, we were able to devise three unique stimuli to preferentially activate synapses in discrete layers of the circuit. Whereas the BOLD response was largest in the outer layers of the OB regardless of the stimulation (likely due to deoxyhemoglobin drainage to large surface vessels), the CBV response was well-localized to the expected layer in each case.

Given the importance of BOLD fMRI, in particular to human studies that cannot use contrast agents, there remains substantial motivation to improve the accuracy of the technique through the implementation of novel modeling strategies. In this work, we hypothesized that with the sufficient or appropriate context (e.g., distance from the surface, baseline T2* weighting, and baseline blood volume information), BOLD data can provide significantly improved spatial accuracy for reporting neural activity compared to a traditional parametric model approach. To this end, we used a supervised machine learning approach to develop a data-driven voxel-wise classifier using fMRI time-series data as the input features. We utilized data from the rat OB, where the circuit is well characterized, allowing for an accurate definition of expected neural activity to enable this supervised learning. This methodology allowed us to identify features that have significantly improved the spatial accuracy of fMRI activation maps.

2. Materials and Methods

Eight male Sprague Dawley rats (240-422 g) were used for this study. Complete methodological details on animal preparation and image acquisition have been previously described (Poplawsky et al., 2015).

2.1. Olfactory bulb circuit and stimulation paradigms

The OB circuit and stimulation pathways are summarized in Figure 1. Axons from odor sensory neurons project through the olfactory nerve layer (ONL) and form excitatory synapses with the apical dendrites of mitral cells in the glomerular layer (GL). Mitral cell dendrites propagate through the external plexiform layer (EPL) and form dendro-dendritic synapses with the apical dendrites of granule cells, whose bodies are located in the granule cell layer (GCL). Finally, output from the mitral cell body layer (MCL) exits the bulb via the lateral olfactory tract (LOT). To preferentially activate different layers, odor stimulation and electrical stimulations of LOT and anterior commissure (AC) were performed during CBV-weighted (CBVw) and BOLD fMRI. Odor stimulation preferentially evokes neural activity in the superficial GL, while LOT and AC electrical stimulations evoke activity in the middle EPL and deep GCL, respectively. Extracellular electrophysiological recordings across the depth of the bulb were used to confirm that the LOT and AC stimulating electrodes activated the EPL and GCL, respectively (Poplawsky et al., 2015).

Figure 1.

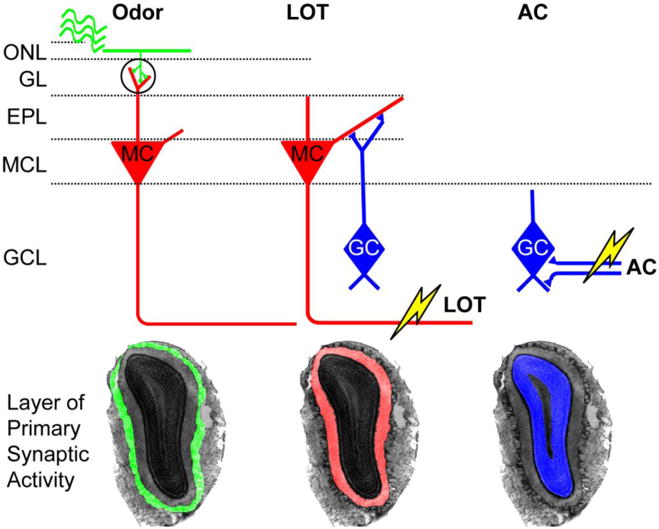
Schematic diagram of the olfactory bulb circuit and expected pattern of synaptic activity elicited by each stimulation paradigm. Odor stimulation first activates synapses in the glomerular layer (GL). Electrical stimulation of the lateral olfactory tract (LOT) stimulates primarily synapses in the external plexiform layer (EPL) via antidromic activation of dendro-dendritic synapses in that layer. Electrical stimulation of the anterior commissure (AC) primarily stimulates synapses in the granule cell layer (GCL) via orthodromic activation of the AC fibers.

2.2. Animal preparation

All experiments were performed after obtaining IACUC approval. Briefly, all rats were induced with 5% and maintained with 2% isoflurane gas during surgery. First, tungsten stimulating electrodes were located to the left AC and right LOT. Then, the right femoral artery and vein were catheterized for physiological monitoring and administration of 5% dextrose, anesthetic and contrast agent, respectively. For hemodynamic measurements, isoflurane was discontinued and switched to alpha-chloralose (45 mg/kg i.v. induction, followed by a continuous 40 mg/kg/h i.v. maintenance). Rats were freely breathing and did not require intubation. Hemodynamic recording commenced more than one hour after the switch to alpha-chloralose. The mean arterial blood pressure (BP) and heart rate (HR) were monitored through the arterial line (MP150, BioPac Systems Inc., Goleta, CA). In addition, the rat rectal temperature was maintained at 37 ± 1°C using a warm water circulator and the respiratory rate (RR) was recorded with a pneumatic pillow sensor. A 0.9% saline and 5% dextrose supplemental fluid was administered intravenously at 1.0 mL/kg/h.

2.3. Image acquisition

A home-built olfactometer gated by data acquisitions was used for odor stimulation (Poplawsky and Kim, 2014). Briefly, a flow of 0.95 L/min medical air and 0.05 L/min O₂ gases was switched between a flask containing 100% mineral oil or 5% amyl acetate in mineral oil. These two conditions were switched using solenoid pinch valves controlled by the MR acquisition computer. Each condition was delivered through prefilled, dedicated lines approximately 5-m long that converged at the rat snout for fast switching between conditions. A vacuum at the opposite end of the snout removed the odorant. For AC and LOT stimulations, a rectangular pulse train (-200 uA, 200 us pulse width, 40 Hz) was delivered to the implanted monopolar stimulation electrode tips using an isolator (Isoflex, AMPI, Israel) equipped with an electrical pulse generator (Master 8, AMPI, Israel).

All MRI experiments were performed on a 9.4-T/31-cm MR system interfaced by a DirectDrive console (Agilent Tech, Santa Clara, CA) and an actively shielded gradient coil with a 40-G/cm peak gradient strength and 120-μs rise time (Magnex, UK). The head of the rat was fixed in a non-magnetic head restraint with a bite bar and ear plugs. A custom-built 1-cm inner diameter surface coil was positioned dorsal to the olfactory bulb for radio-frequency excitation and reception. Odor, LOT and AC stimulations were interleaved in a block design experiment (120-s off, 64-s on, 120-s off), and this paradigm was repeated for 6 trials for each contrast. For CBVw fMRI, a 15-mg/kg bolus of Feraheme (ferumoxytol, AMAG Pharmaceuticals, MA) was injected following BOLD fMRI. fMRI data were acquired at 9.4 T with a compressed-sensing, gradient-recalled echo technique (Zong et al., 2014), in order to minimize the effects of susceptibility compared to an echo planar imaging pulse sequence. Imaging parameters were T_R = 125 ms, T_E = 8 ms for CBVw and 18 ms for BOLD, 110 × 110 μm² in-plane resolution, 500-μm slice thickness, reduction factor of 4, and temporal resolution = 2 s. Five slices with matching spatial location were evaluated for both CBVw and BOLD images.

2.4. Region of interest definition

Regions-of-interest (ROIs) were manually drawn on high-resolution, T2-weighted anatomical images of individual rats and corresponded to the seven layers previously verified with histological staining methods (Poplawsky et al., 2015). Briefly, ROIs were drawn on the dorsal ∼2/3 of all five BOLD fMRI slices and the corresponding five CBV fMRI slices because the ventral ∼1/3 of slices had a diminished coil sensitivity that caused a less reliable layer identification. The surface ROI included the bulb surface, midline and any pial vessels identified as signal hypo-intensities, the GL and MCL were defined by the outer and inner bands of hypo-intense signal, respectively, and core by the inner-most hyper-intense band, while the ONL, EPL, and GCL were identified by their spatial relationship to these bands.

2.5. Image preprocessing

Reconstructed images were realigned, linearly detrended and the normalized difference of the fMRI series was calculated (baseline image numbers 1-60 and 148-152) using home-written Matlab code (MathWorks, Natick, MA). Realignment was performed on a run-by-run basis by co-registering the average fMRI image of each run to the average fMRI image of the first run using a rigid-body, three degree-of-freedom transformation (translations in x and y-axes, and rotation about the z-axis). The estimated motion parameters for each run were then applied to all of the corresponding fMRI time points. Individual trials were grouped according to their stimulation type and the corresponding time series were concatenated for subsequent analysis. Mean time courses by OB layer and for each combination of contrast and stimulation paradigm are shown in Supplementary Figure 1. The time courses show signal changes that are time-locked to stimulus delivery, without evidence of systematic artifacts that would contaminate the signal.

2.6. General linear model (GLM) activation maps

After image preprocessing, maps of percent change were calculated using a general linear model (GLM) in the test animals for both CBVw and BOLD images. Each voxel was then fitted by a model with two predictors: the stimulation paradigm convolved with the canonical hemodynamic response function (HRF) and a constant term. For BOLD data, the HRF was given by SPM8 using default parameters (http://www.fil.ion.ucl.ac.uk/spm/), while the HRF for the CBVw data was previously described and implemented with in-house software (Silva et al., 2007). Percent change maps were computed by taking the ratio of these two coefficients at each voxel and then converting to a percent change by subtracting 1 and multiplying by 100.

2.7. Learned model (LM) activation maps

The general design of the learned model is to extract features of a given voxel in order to classify it as either active or inactive (Figure 2A), while providing the model no explicit information about the stimulation. Due to the large number of observations and the large feature spaces tested, we used a logistic regression to model our data, which was regularized with a penalty on the L2-norm. The model and cost function are given by

Figure 2.

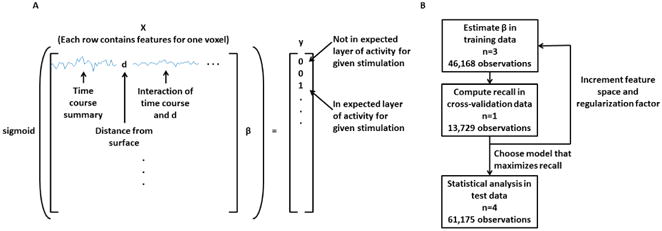
A. An illustration describing the construction of the predictor matrix. Each row contains the time course data and contextual information from one voxel, while the ground truth is a binary array equal to 1 if the voxel is expected to be active for a given layer assignment and stimulation paradigm or equal to 0 otherwise. B. Flow diagram outlining how the eight animals were used for training, cross-validation, and statistical testing.

$$f\left(x\right)=\frac{1}{1+\mathit{exp}(-X\beta )}$$

$$\mathit{\text{cost}}=\frac{1}{n}\sum _{i=1}^n[-y_i\mathit{log}(f(x_i))-(1-y_i)\mathit{log}(1-\mathit{log}(f(x_i)))]+\frac{\lambda }{2n}{\beta }^{\prime }\beta$$

where X is the predictor matrix, β are the model coefficients, n is the number of observations, y is the defined truth, and λ is the regularization factor. For the regularization term of the cost function, the constant term was not included. Each voxel accounted for up to three observations in the model (i.e., one observation for each stimulation paradigm), so the total number of observations (n) is approximately 2.5 times the number of voxels. The reason that not all voxels were included three times is that stimulation of the right LOT will only evoke a response in the right bulb, and so the left bulb was excluded for this stimulation. The defined truth was given as a binary array which was equal to 1 if that voxel was expected to be active given its laminar assignment and stimulation paradigm and 0 otherwise. For separating active and inactive voxels, the tested features included summary time course data from the voxel of interest and its neighbors, the distance of the voxel from the surface (DFS), the baseline BOLD image (BOLD₀), the baseline CBVw image (CBV₀), the interaction of these latter features and the time course data, and finally physiological conditions (i.e., BP, HR and RR). To reduce the feature space, the summary time course data were computed by first averaging over the 6 trials and then by binning the data by a factor of 4 in the time dimension to create an effective resolution of 8 s. Time courses were further normalized by dividing by the maximum absolute value in the time series. Then a given time course was summarized by the mean and standard deviation during the baseline period, while the remaining time course was provided in full to the model for fitting. To compute DFS, we calculated the cumulative sum of an OB mask following erosion after each iteration. BOLD₀ and CBV₀ images were computed by taking the average image over the entire pre-stimulus time window. Taken together, these images provide the model with information about baseline T2* relaxation parameters and baseline blood volume. Two further steps were taken to provide the model more flexibility. First, we tested the interactions between DFS, BOLD₀, CBV₀ and the time course summary data, allowing the model to account for changes in the time course related to these features. Second, we included the square and the square root of the DFS, BOLD₀ and CBV₀ features in order to better model any nonlinearity, if present. Prior to model fitting, each feature was normalized to have a mean of zero and standard deviation of one.

A flow diagram of the fitting, cross-validation, and testing is shown in Figure 2B. Functional MRI data from three animals were used in the training set, then data from a fourth animal were used for the refinement and final selection of models, and data from four more animals were used for final model evaluation. This process was completed twice, once each for CBVw and BOLD fMRI data. Model features and regularization factors were varied and each candidate model was evaluated by computing recall in the cross validation animal. A voxel was considered active if the model reported a probability greater than 0.5. Then recall was computed as TP/(TP+FN) where TP is true positives and FN is false negatives. Model evaluation began with the simplest model (single voxel time course data), and at each iteration of testing, the added features were retained for future testing if recall in the cross validation data was improved. The set of all candidate models is described in Table 1. For each set of features, we also tested 11 regularization factors including 0 and 2ⁿ for n equal to 1 through 10. The model that maximized recall was chosen for final evaluation in the test animals. To further evaluate this model we also computed precision, which is given by TP/(TP+FP) where FP are false positives.

Table 1.

List of all candidate feature sets.

		Number of Features
Feature set	Features	(not counting constant)
1	Time course	25
2	Feature set 1 (FS1) + time course of neighbors	225
3	FS2 + distance from surface (DFS)	226
4	FS3 + DFS*FS2	451
5	FS4 + DFS2 + DFS2*FS2 + DFS1/2 + DFS1/2*FS2	903
6	FS5 + BOLD0	904
7	FS6 + BOLD0*FS2	1129
8	FS7 + BOLD02 + BOLD02*FS2 + BOLD01/2 + BOLD01/2*FS2	1581
9	FS8 + CBV0	1582
10	FS9 + CBV0*FS2	1807
11	FS10 + CBV02 + CBV02*FS2 + CBV01/2 + CBV01/2*FS2	2259
12	FS11 + HR	2287
13	FS11 + BP	2287
14	FS11 + RR	2287
15	FS11 + HR + BP	2315
16	FS11 + HR + RR	2315
17	FS11 + BP + RR	2315

Once the final models were selected for each image contrast, we estimated the relative contribution of the features to the measured recall and precision in the test data set. This estimation was performed by fitting a new set of models, where each model had a subset of features excluded. For example, to investigate the impact of DFS, a new model was computed excluding DFS, nonlinear transformations of those data, and interactions between these values and the time course data. A similar procedure was repeated for BOLD₀, and CBV₀, and physiological data.

2.8. Statistical analyses

The resulting activation maps were evaluated in the test data set according to two criteria: 1. accuracy with respect to the expected site of activation; and 2. agreement between CBVw and BOLD activation maps. First, we computed the activation maps for all three stimuli, and summarized the laminar distribution of activation by computing the average image value in each OB layer and then normalizing by the maximum value. This calculation was performed separately for each animal in the test set, and then the mean across animals was computed. To test for accuracy in activation with respect to OB layer, we computed a Dice coefficient for each activation map comparing two binary maps: A) a map equal to 1 in the layer with expected activity and 0 otherwise; and B) a map equal to 1 for the n largest image values where n is equal to the number of nonzero voxels in map A. The Dice coefficient is given by $\frac{2\ast |A\cap B|}{\left|A\right|+\left|B\right|}$. This Dice coefficient was computed for the GLM and Learned Model (LM). To test for agreement between the CBVw and BOLD activation maps, we computed the spatial correlation between these maps for each stimulation paradigm. Finally, to test for accuracy in activation with respect to intralaminar glomerular organization, we computed the spatial correlation between CBVw and BOLD activation maps in the glomerular layer during odor stimulation. These correlations were tested for both GLM and LM activation maps. Differences between the GLM and LM maps were then tested with paired T-tests with P<0.05 considered significant. We report uncorrected p values since the uncorrected values are more conservative than false discovery rate corrected values.

For display, the set of 4 activation maps were averaged following normalization of all animals to the first using SPM8, using the anatomical images as the reference images. These mean images were then thresholded to display the n largest values in the activation map, where n was chosen to have the same number of nonzero voxels as the binary map of expected activity. Unthresholded mean activation maps are also included in the Supplementary material.

3. Results

3.1. Model selection

Precision and recall measured in the cross-validation set are summarized in Figure 3 with the selected models indicated by white circles. For the CBVw images, the best performance was obtained with Feature Set 14 (see Table 1 for full list of features in this set) and regularization factor λ=2. The recall in the test set was 0.202 ± 0.186 (mean ± standard deviation, n=4) and the precision was 0.398 ± 0.086. For the BOLD images, recall was maximized by Feature Set 12 (Table 1) and regularization factor λ=4. The recall in the test set was 0.186 ± 0.073 (mean ± standard deviation, n=4) and the precision was 0.410 ± 0.026. The relative contribution of these features to the observed recall and precision in the test set is summarized in Table 2, which displays the mean recall and precision across test animals normalized by the mean values provided by the full model. The largest reductions in performance occurred when leaving out features related to the baseline CBVw and BOLD images. In general, the performance of the CBVw model was more resistant to losing features compared to the BOLD model.

Figure 3.

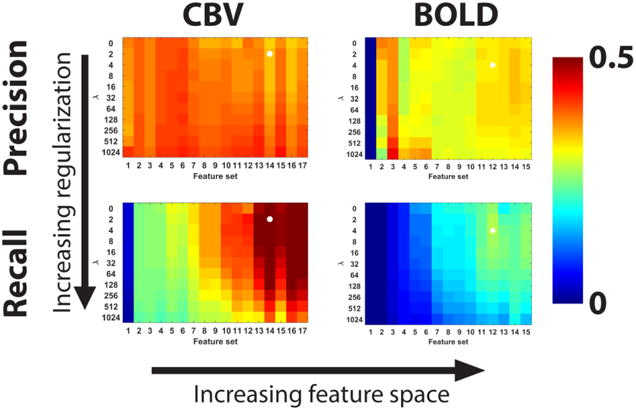
Summary of precision and recall for all tested models in the cross-validation data set. Each matrix displays the precision or recall for every candidate model, where the models were varied by altering the regularization and feature space. The optimum model was selected by maximizing recall, which is indicated by white circles in the matrices.

Table 2.

Summary of relative model performance while excluding specified portions of the feature set.

	CBVw		BOLD
	Normalized recall	Normalized precision	Normalized recall	Normalized precision
Full model	100.00%	100.00%	100.00%	100.00%
Leave out physiology	103.65%	93.31%	89.30%	100.74%
Leave out Distance To Surface	87.13%	96.33%	87.37%	90.39%
Leave out Baseline BOLD	93.10%	105.64%	89.59%	106.52%
Leave out Baseline CBV	88.37%	101.59%	69.28%	95.08%
Leave out Baseline BOLD and CBV	68.72%	107.08%	44.56%	100.11%
Time course only (voxel plus neighbors)	48.43%	105.89%	6.39%	63.55%

3.2. Activation maps in the test set

As previously described, GLM analysis of CBVw images provides a fairly accurate set of activation maps where the measured activity is largely in the expected layers (Fig. 4, bottom-left panel). When using the LM to map activity, the laminar specificity appears slightly improved, as particularly evidenced by improved separation between the laminar profiles seen in the bottom graph (Fig. 4, bottom-right panel). The difference between the GLM and LM activation maps is more pronounced in the BOLD images. The GLM activation maps indicate maximum activation in the superficial GL regardless of the stimulation paradigm (Fig. 5, bottom-left panel). By comparison, the activation maps shown in the bottom-right panel of Figure 5 show increased laminar specificity, which is particularly evident during LOT and AC stimulations.

Figure 4.

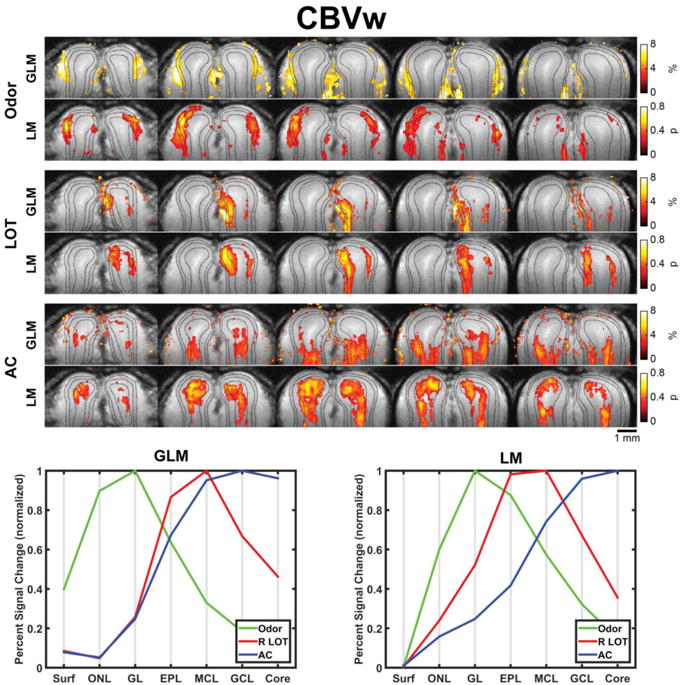
Mean activation maps and line profiles (n=4 animals) calculated using CBVw test data and either a general linear model (GLM) or the learned model (LM). Top: Each row of images shows the mean activation maps for one of the three stimulation paradigms overlaid on the mean anatomical image, with the five slices arranged from anterior to posterior positions. The activation maps are thresholded such that the largest n values are shown, where n was chosen to have the same number of nonzero voxels as the number of voxels in the expected layer of activity. Unthresholded maps are shown in Supplemtary Figure 2. Dashed lines indicate the outer and inner boundaries of GL and the outer boundary of MCL. Bottom: Summary plot showing the mean percent change or probability active in each layer for each stimulation paradigm following normalization by the maximum value and then averaging across animals.

Figure 5.

Mean activation maps and line profiles (n=4 animals) calculated using BOLD test data and either a general linear model (GLM) or the learned model (LM). Top: Each row of images shows the mean activation maps for one of the three stimulation paradigms overlaid on the mean anatomical image, with the five slices arranged from anterior to posterior positions. The activation maps are thresholded such that the largest n values are shown, where n was chosen to have the same number of nonzero voxels as the number of voxels in the expected layer of activity. Unthresholded maps are shown in Supplemtary Figure 3. Dashed lines indicate the outer and inner boundaries of GL and the outer boundary of MCL. Bottom: Summary plot showing the mean percent change or probability active in each layer for each stimulation paradigm following normalization by the maximum value and then averaging across animals.

The spatial accuracy of these maps is summarized in Figure 6. In this graph, we computed the Dice coefficient between the ROI where activity was expected and a thresholded activation map. The threshold was chosen in each case so these two binary masks had the same number of nonzero voxels. This coefficient was computed for CBVw (Fig. 6A) and BOLD (Fig. 6B) data using both the GLM and LM approaches. The overlap was either statistically not different or significantly improved using the LM approach, particularly in deeper layers (*p<0.05, paired T-test).

Figure 6.

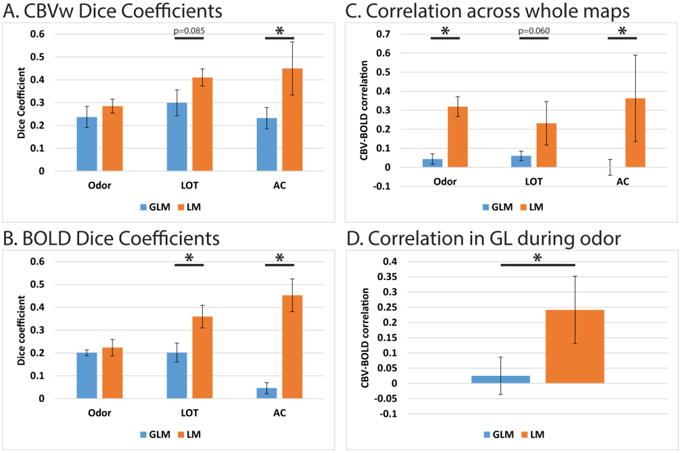
On the left are Dice coefficients comparing maps of the expected layer of activity and the thresholded activation maps for each stimulation paradigm using the general linear model (GLM) and learned model (LM), both for CBVw data (A) and BOLD data (B). Graphs on the right summarize the agreement in activation maps between CBVw and BOLD data, using either the GLM or LM. Graph C shows the Pearson correlation between CBVw and BOLD activation maps using the entire image. Graph D shows the Pearson correlation between CBVw and BOLD activation maps only within the glomerular layer during the odor stimulation. All bars and error bars represent the mean ± standard deviation (n=4 rats). Differences between the GLM and LM were tested by a paired T-test (*p<0.05)

3.3. Comparison of CBVw and BOLD activation maps

Previously we reported that activation maps computed from CBVw and BOLD images are not in strong agreement in the OB (Poplawsky and Kim, 2014), decreasing confidence in the spatial accuracy of these maps. Here we made two comparisons between the CBVw and BOLD maps, using both the GLM and the LM, which are summarized in Figure 6. In Figure 6C, we computed the Pearson correlation between CBVw and BOLD activation maps for each modeling method and each stimulation paradigm. In each case, the correlation between the maps improves when using the LM to compute activation. Finally, glomeruli within the GL have unique, concentration-dependent preferences for specific odors, and therefore a unique pattern of activity within the GL can be elicited both by different odorants (Johnson et al., 2002; Johnson et al., 1998), as well as different concentrations of those odorants (Rubin and Katz, 1999). Therefore, as the pattern of activity within the GL during odor stimulation is expected to be biologically relevant, we computed the Pearson correlation of the activation maps within this layer and under this condition. The result, shown in Figure 6D, once again demonstrates improved agreement between the CBVw and BOLD activation maps when using the LM.

4. Discussion

In this study, we used a supervised machine learning approach to design a model that provides fMRI activation maps with improved spatial accuracy with respect to the underlying neural activity in the rat olfactory bulb. Particularly when considering BOLD fMRI data, the activation maps produced by the learned model are fundamentally different than those produced by a common general linear model approach due to the flexibility afforded by the model's feature space. The results indicate that the investigated feature space can provide at least partial separation of active and inactive voxels in the rat OB, and also that the results are well-generalizable to data outside the training set. Interestingly, the learned models produced activation maps with improved agreement between CBVw and BOLD data, both across the entire activation map (Fig. 6C), and within the glomerular layer during odor stimulation compared to the GLM (Fig. 6D). These observations imply that the learned model inherently improved the spatial accuracy for not only inter-laminar BOLD responses, but also for intra-laminar responses, which were not overtly specified in the model. This point demonstrates the potential to apply a similar approach in cortical systems, where the goal is to accurately map the location of neural activity within the cortical plane.

The improvements in spatial accuracy afforded by the learned models were greater for BOLD data compared to CBVw data, and also for deeper layers of activity compared to more superficial layers. We think these trends are driven by the relative accuracy of the GLM activation maps, which performed better using CBVw data and for more superficial activity, in turn allowing less room for the learned models to improve the results. However, it may also be true that the learned models perform particularly well in regions with low baseline blood volume, particularly for BOLD data. In indirect support of this latter point, baseline BOLD and CBVw images were the largest contributors to sensitivity of the models (Table 2), with these baseline images providing the model with information about T2* relaxation and baseline blood volume. In contrast to the BOLD model, the CBVw learned model was more resistant to losing features. This result is expected given that the CBVw GLM activation maps agree well with the expected pattern of neural activity (Poplawsky et al., 2015). The accuracy of CBVw images is thought to arise from this contrast's insensitivity to certain nonspecific responses including draining veins, which likely do not dilate in response to neural activity (Kim et al., 2007; Lee et al., 2001), and large pial arteries, where the signal is diminished due to the susceptibility effects generated by the contrast agent (Kim et al., 2013). With these points in mind, one might speculate that in order to achieve improved agreement with the CBVw data, the BOLD learned model is detecting features that are also more sensitive to responses in these more specific, small vessels. Further experimental validation is necessary to test this hypothesis.

This type of application of machine learning to fMRI data is somewhat novel compared to other applications seen in the literature. Much of this previous work is focused on multi-voxel pattern analysis (Norman et al., 2006). In this type of analysis each voxel in an fMRI image acts as a feature in a model that predicts, for example, whether that sample in time occurred during a stimulus or at rest (LaConte et al., 2005). This type of analysis has even been used to estimate an image that is shown to the participant while measuring neural activity via fMRI (Cox and Savoy, 2003; Nishimoto et al., 2011). These studies are impressive demonstrations of the depth of information that can be extracted from fMRI data. However, our work has a fundamentally different goal, which was to use the fMRI time series data in order to classify the probability that a given voxel was active. In this way, the learned model represents an early step toward improved circuit mapping using fMRI data. Previous work by Song et al. has investigated similarly structured models, where the features are extracted from each voxel's time course in order to classify it as active or inactive (Song et al., 2016; Song and Wyrwicz, 2009). The major difference between their work and ours is the nature of these features. Whereas previous literature has summarized the time course by computing features such as the cross correlation function between the time course data and stimulation paradigm, our work provides the model with more freedom by including the entire time course and its interaction with supplementary contextual information. While our approach is computationally more expensive, and thus limits the complexity of the model that can be fit in a reasonable time, this more general approach is necessary to achieve activation maps that are fundamentally different from those obtained by a traditional parametric model approach.

As this work represents an early step toward the use of learned models to more accurately map neural activity from fMRI data, this study does have some limitations that will be the source of future investigations. A limitation related to the underlying data is that certain confounding factors, such as signal-to-noise ratio (SNR), may make it difficult to draw direct comparisons between the CBVw and BOLD data. However, we believe it is unlikely that differences in SNR can systematically bias our results. First, any SNR-related effects will be mitigated by our exclusion of the ventral 1/3 of the bulb. Second, as mentioned in our previous manuscript, SNR is lowest at the surface of the bulb and increases with laminar depth (Poplawsky et al., 2015). This trend in SNR opposes the trend in amplitude of the evoked signal change, where the largest signal changes are observed closer to the surface (especially true of BOLD). Finally, the main metric that this work is trying to address is the spatial accuracy of the functional maps. While we would expect a low SNR to impact the sensitivity of the activation maps, we would not expect it to systematically bias the location of the activation. The main limitation with respect to the model is its dependence on an assumed spatial pattern of activity. While a supervised approach may be well suited in the well-characterized olfactory bulb circuit, this type of approach is less suited for more complex cortical circuits and with stimuli/tasks that will elicit unknown patterns of activity. Also, the olfactory bulb represents a unique circuitry within the brain (Oswald and Urban, 2012; Shepherd, 1972), making this type of approach more difficult to apply in cortical systems. Nonetheless, we believe this study represents an important demonstration of data-driven models for improved spatial accuracy using fMRI data, particularly for images with BOLD contrast. In particular, this model may be immediately useful for studies in the rat OB. Furthermore, the feature space developed in this study should be also suitable or easily adapted to model activity in other brain systems. To train the model in other systems, the ground truth must simply be replaced, perhaps with electrophysiological measurements.

In conclusion, we used a supervised learning algorithm to develop a data-driven model in the rat OB to predict the probability a voxel was active based upon its fMRI time course data and supplementary MRI-based features (distance from the bulb surface, baseline BOLD intensity, and baseline CBV-weighted intensity). These models provided activation maps with spatial accuracy that was either improved or not significantly different from GLM-based maps (Poplawsky et al., 2015), both for CBVw and BOLD data. The models also produced activation maps with improved agreement between CBVw and BOLD data, both across the entire image and within the glomerular layer during odor stimulation. Taken together, this study demonstrates the potential for data-driven models to produce improved activation maps for mapping neural activity as compared to the models predominantly used in the literature. Based on these results, several future directions merit further investigation, including the identification of features that can improve the model and a determination of how well similar models generalize to the rest of the brain.

Highlights.

• We applied machine learning to compute activation maps in the rat olfactory bulb.

• Results from learned models were compared to results from general linear models.

• Spatial accuracy of activation maps was significantly improved with learned models.

• CBV and BOLD activation maps showed increased agreement using learned models.