Novel Methodology for Characterizing Regional Variations in the Material Properties of Murine Aortas

Abstract

Many vascular disorders, including aortic aneurysms and dissections, are characterized by localized changes in wall composition and structure. Notwithstanding the importance of histopathologic changes that occur at the microstructural level, macroscopic manifestations ultimately dictate the mechanical functionality and structural integrity of the aortic wall. Understanding structure–function relationships locally is thus critical for gaining increased insight into conditions that render a vessel susceptible to disease or failure. Given the scarcity of human data, mouse models are increasingly useful in this regard. In this paper, we present a novel inverse characterization of regional, nonlinear, anisotropic properties of the murine aorta. Full-field biaxial data are collected using a panoramic-digital image correlation (p-DIC) system. An inverse method, based on the principle of virtual power (PVP), is used to estimate values of material parameters regionally for a microstructurally motivated constitutive relation. We validate our experimental–computational approach by comparing results to those from standard biaxial testing. The results for the nondiseased suprarenal abdominal aorta from apolipoprotein-E null mice reveal material heterogeneities, with significant differences between dorsal and ventral as well as between proximal and distal locations, which may arise in part due to differential perivascular support and localized branches. Overall results were validated for both a membrane and a thick-wall model that delineated medial and adventitial properties. Whereas full-field characterization can be useful in the study of normal arteries, we submit that it will be particularly useful for studying complex lesions such as aneurysms, which can now be pursued with confidence given the present validation.

Introduction

Aortic aneurysms and dissections are biologically and mechanically complex vascular pathologies that are responsible for significant death and disability in industrialized nations. They are characterized geometrically by complex fusiform dilatations and histopathologically by a nonuniform fragmentation of elastic fibers, loss of smooth muscle cell functionality, and remodeling of fibrillar collagen [1,2]. The ultimate fate of the aortic wall is dictated by the resulting structural integrity, for dissection and rupture occur when the local wall stress exceeds local wall strength. This vulnerable situation can arise when the degradation of extracellular matrix outpaces deposition. Improvements in medical imaging and computational methods have enabled the development of patient-specific fluid–solid interaction models of aortic aneurysm and dissection biomechanics [3–5], but these models are often based on assumptions of homogeneous material properties and uniform wall thicknesses, both of which can render predictions of intramural stresses inaccurate.

Histopathological changes that occur at the microstructural level manifest at the macroscopic level as altered mechanical functionality and structural integrity. Correlations between local wall composition and mechanical properties can thus provide increased insight into conditions that render a vessel susceptible to failure or disease. Whereas regional variations in microstructure are quantified easily using standard histological and immunohistochemical methods, there is yet a pressing need for methods suitable for quantifying spatial heterogeneities in the material and structural properties of aneurysmal and dissected lesions and to correlate these heterogeneities with the underlying microstructure in order to gain increased insight into the mechanics of complex vascular pathologies.

Toward this end, we develop and apply a novel inverse method, based on the PVP, which can determine locally varying values of the constitutive parameters from full-field data acquired using a biaxial p-DIC method. By focusing first on normal vessels, the associated results can be compared with those obtained via standard biaxial extension–inflation testing and constitutive modeling [6]. Whereas both the p-DIC and the biaxial extension–inflation techniques have been separately presented and validated in previous papers [7–11], the scope of the current study is the development of a novel combination of the inverse and p-DIC methods and its validation as a combined mechanical testing procedure designed for local material characterization. Toward this end, we first detail the proposed combined method and then present illustrative results for the suprarenal abdominal aorta from two young, nondiseased, apolipoprotein-E null (ApoE^-/-) mice. Mean behaviors correspond well with those from standard testing and analysis but, in addition, regional heterogeneities in the material properties are successfully reconstructed. We submit that this novel experimental–computational approach represents another important step toward improving our ability to study complex vascular lesions as it will enable one to correlate, for the first time, regional distributions of material properties with the underlying microstructure.

Materials and Methods

Animal Model.

All the animal protocols were approved by the Yale University Institutional Animal Care and Use Committee and followed methods detailed previously [6,7]. Nondiseased control samples, as opposed to dissecting aneurysm samples, were used given the goal of validating the new inverse methodology. Briefly, two male ApoE^-/- mice were euthanized at ∼20 weeks of age (Table S1 is available under the “Supplemental Materials” tab for this paper on the ASME Digital Collection) using an intraperitoneal injection of Beuthanasia-D, and the abdominal aorta was excised en bloc. The suprarenal segment (from the final pair of intercostal branches to the right renal artery) was prepared for mechanical testing by removing excess perivascular tissue and ligating all the side branches using a single strand from braided 7-0 nylon suture.

Standard Biaxial Mechanical Testing.

The excised samples (sample A for mouse 1 and sample B for mouse 2) were cannulated with custom drawn glass pipets, secured using 6-0 silk sutures, and placed within a validated computer-controlled testing system that allowed now standard biaxial inflation–extension testing [8]. Preconditioning consisted of four cycles of pressurization from 10 to 140 mmHg at the estimated in vivo length, following previous reports [6,7]. Next, samples were subjected to three cyclic pressure–diameter (P–d) tests consisting of pressurization from 10 to 140 mmHg at fixed axial stretches of 0.95λ⁰, λ⁰, and 1.05λ⁰, where λ⁰ is the estimated in vivo axial stretch, and four cyclic axial force–length (f–l) tests consisting of loading from 0 to 35 mN at fixed pressures of 10, 60, 100, and 140 mmHg. Note that, similar to previous reports [6,12], the estimated in vivo axial stretch, λ⁰, was defined as the value that minimized variations in transducer measured axial load upon pressurization. Tests were performed at room temperature in a Hanks-buffered physiologic solution (HBSS), which yields a passive mechanical behavior [9]. As previously demonstrated [13], there are no discernible differences in the measured passive properties between room temperature (19–21 °C) and physiologic temperature (37 °C).

p-DIC System.

Following biaxial inflation–extension tests, the samples were placed in a custom p-DIC system [10] to monitor full-field surface deformations at multiple states of pressurization and axial stretch using a 45 deg concave conical mirror and known calibration target (Figs. 1(a) and 1(b)). The samples were recannulated proximally and distally on a single through-the-lumen blunt-ended needle composite with one fixed and one sliding end to allow both pressurization and axial stretch (Fig. 1(c)). The specimens were air-brushed to generate a random speckle pattern of black and white India ink, submerged in HBSS at room temperature, and placed coaxially within the conical mirror to visualize the entire lateral surface when viewed from a single vertically mounted digital camera (DALSA Falcon 4M30, cf. Fig. 1(b)). Eight rotationally symmetric images about the central axis of the conical mirror were acquired at each quasi-statically loaded configuration according to the loading protocol shown in Fig. 1(d), then analyzed using custom matlab scripts to perform the cross-correlations between unwrapped images needed to compute full-field surface deformations [11].

Fig. 1.

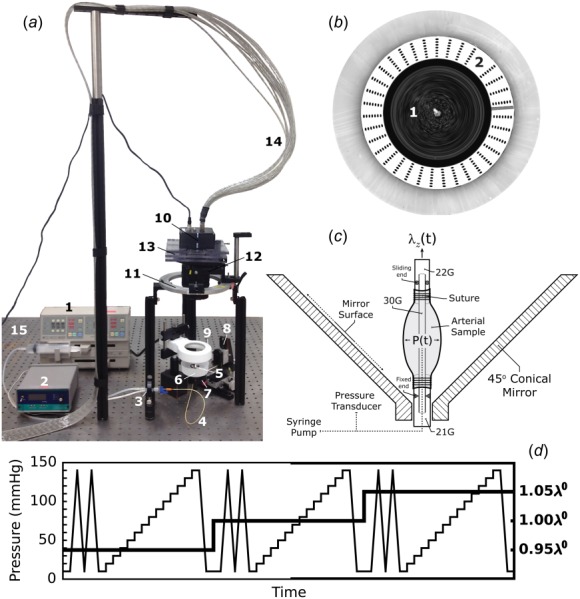
Overview of the p-DIC system. (a) Components include a syringe pump (1), pressure monitor (2), pressure transducer (3), and tubing (4) for pressure control. A 45 deg conical mirror (5) is located within a specimen bath (6) and mounted atop a small kinematic mount (7) that is attached to a three-axis translational stage (8). An annular light source (9) is used for illumination. The digital camera (10) is mounted vertically above the sample on a rotational stage (11) via a large kinematic mount (12) and custom translational stage (13). Images are acquired and sent to the computer for analysis through a camera link cable (14), and the entire system is placed on a precision optical bench (15). (b) Top-view of 45 deg conical mirror inside of the specimen bath showing the speckle pattern on the measurement surface (1) and the calibration target (2) used for 3D reconstruction. (c) Schematic of the cannulation of a pressure-distended specimen showing different gauge needles, locations of fixed and sliding ends, and methods to pressurize and axially stretch the specimen. (d) Loading protocol used for mechanical testing: for each axial stretch (bold solid line; right scale), the sample underwent two cycles of preconditioning followed by a stepwise increase in pressure from 10 to 140 mmHg in 10 mmHg increments (thin solid line; left scale for pressure).

Wall Kinematics.

A global coordinate system was defined by an origin, located on the central axis at the base of the conical mirror, and a Cartesian basis, defined by three vectors $({\mathit{e}}_x,{\mathit{e}}_y,{\mathit{e}}_z)$. Vector ${\mathit{e}}_z$ was aligned along the long axis of the needle. A cylindrical coordinate system was also defined by three locally orthogonal base vectors $({\mathit{e}}_r,{\mathit{e}}_{\theta },{\mathit{e}}_z)$. The reference configuration ($P(t=0)$ and ${\lambda }_z(t=0)$) was set at pressure $P$ = 80 mmHg and axial stretch ${\lambda }_z$ = λ⁰. For any material point represented by its position vector $\mathit{X}$, the Cartesian coordinates in the reference configuration were denoted both by the triplet $(X,Y,Z)$ and the cylindrical coordinates $(R,\mathit{\Theta },Z)$. Hence, in a deformed configuration, the coordinates for the current position $\mathit{x}(t)$ of the same material point were $(x(t),y(t),z(t))$ and $(r(t),\theta (t),z(t))$; here, $t$ denotes subsequent configurations achieved quasi-statically, not a dynamic process.

The outer wall surface of each artery $S^o$ was meshed in the reference configuration with >5000 nodes for full-field deformation measurements, but parametrically remeshed with 400 nodes for parameter estimation within small local patches. The $Z\in [0,L]$ coordinate was divided into 20 segments (where $L$ is the reference length of the sample), and the $\Theta \in [0,2\pi ]$ coordinate was divided into 20 angular sectors. For each node $n$ defined in $S^o$, the Cartesian $(X_n^o,Y_n^o,Z_n^o)$ and/or cylindrical $(R_n^o,{\Theta }_n^o,Z_n^o)$ coordinates were reconstructed using the calibration parameters of the p-DIC system. Each material point in $S^o$ was then tracked in all the deformed configurations by applying a custom serial correlation algorithm between neighboring configurations (i.e., all the pressures $P(t)$ and axial stretches ${\lambda }_z(t)$). For instance, while at λ⁰, the result of the correlation between images at 60 and 70 mmHg was used to initiate the correlation between images at 70 and 80 mmHg, respectively. In other words, the resulting correlated mesh was stored and taken as a reference to be correlated to a neighboring deformed configuration (i.e., 80–90 mmHg, 60–50 mmHg, and so forth) until all the deformed configurations had been processed. In this way, data were collected at each node $n$ of the reconstructed p-DIC point cloud: $(x_n^o(t),y_n^o(t),z_n^o(t))$ and/or $(r_n^o(t),{\theta }_n^o(t),z_n^o(t))$ for every biaxially loaded configuration (pressure $P(t)$ ranging from 10 to 140 mmHg in increments of 10 mmHg at axial stretches of ${\lambda }_z(t)$ = 0.95λ⁰, λ⁰, and 1.05λ⁰). Note, too, that the biaxial load at each configuration was held for ∼2 min to allow image acquisition, which is in contrast to the continuous cyclic loading of standard biaxial tests.

Unit vectors normal to the outer surface, denoted, respectively, by ${\mathit{n}}_n(t)$ and ${\mathit{N}}_n$ for each node $n$ in the current and reference configurations, were deduced from the geometrical reconstruction of $S^o$ based on p-DIC data. A local orthonormal basis (${\mathit{G}}_n^1$,$\hspace{0.17em}{\mathit{G}}_n^2,{\mathit{N}}_n$) was defined in the reference configuration, where ${\mathit{G}}_n^1$ and $\hspace{0.17em}{\mathit{G}}_n^2$ were aligned with directions of maximum and minimum principal curvatures of $S^o$ at node $n$, respectively. We let (${\mathit{g}}_{\mathit{n}}^1(t)$, $\hspace{0.17em}{\mathit{g}}_n^2(t),{\mathit{n}}_n(t)$) denote the local orthonormal basis, ${\mathrm{\kappa }}_n^1(t)$ denote the maximum curvature, and ${\mathrm{\kappa }}_{\mathit{n}}^2(t)$ denote the minimum curvature, for every node $n$ defined in each deformed configuration at time t.

Nodal positions across the wall $(x_n^w(t,\mathrm{\xi }),y_n^w(t,\mathrm{\xi }),z_n^w(t,\mathrm{\xi }))$ were defined as

$$(x_n^o(t)-x_n^w(t,\mathrm{\xi })){\mathit{e}}_x+(y_n^o(t)-y_n^w(t,\mathrm{\xi })){\mathit{e}}_y+(z_n^o(t)-z_n^w(t,\mathrm{\xi })){\mathit{e}}_z=(1-\xi )h(t){\mathit{n}}_{\mathit{n}}(t)$$ (1)

for every node $n$ in each configuration at each time t, where $\mathrm{\xi }\in [0,1]$ indicates the through-the-thickness position between the inner ($\mathrm{\xi }=0$) and outer ($\mathrm{\xi }=1$) radii. Assuming a constant wall volume at each loaded configuration (tissue incompressibility), a uniform thickness $h(t)$ was deduced from the average thickness measured in the unloaded configuration, denoted $H$. The average thickness in the unloaded configuration was measured using an optical coherence tomography system.

The deformation gradient tensor ${\mathit{F}}_n^w(t,\mathrm{\xi })$ at the surface was written as follows (in 2D summation notation):

$${\mathit{F}}_n^w\left(t,\mathrm{\xi }\right)=F_{ij,n}^w\left(t,\mathrm{\xi }\right){\mathit{g}}_n^i\left(t\right)\otimes {\mathit{G}}_n^j+\frac{1}{\det \left({\mathit{F}}_n^w\left(t,\mathrm{\xi }\right)\right)}{\mathit{n}}_n\left(t\right)\otimes {\mathit{N}}_n$$ (2)

where, at every node $n$ and through-the-thickness position ξ in a deformed configuration at time $t$, the components of the deformation gradient tensor $F_{11,n}^w(t,\mathrm{\xi })$, $F_{22,n}^w(t,\mathrm{\xi })$, $F_{12,n}^w(t,\mathrm{\xi })$, and $F_{21,n}^w(t,\mathrm{\xi })$ were deduced from the set of current coordinates $(x_n^w(t,\mathrm{\xi }),\hspace{0.17em}{y}_n^w(t,\mathrm{\xi }),\hspace{0.17em}{z}_n^w(t,\mathrm{\xi }))$ and reference coordinates $(X_n^w(t,\mathrm{\xi }),Y_n^w(t,\mathrm{\xi }),Z_n^w(t,\mathrm{\xi }))$ using a finite difference algorithm.

Constitutive Relations.

Similar to the prior work [14], the aortic wall was modeled as a hyperelastic material with a strain energy function, defined per unit mass, of the form

$$W_n(t,\mathrm{\xi })={\varphi }^e(\mathrm{\xi })W_n^e(t,\mathrm{\xi })+{\varphi }^m(\mathrm{\xi })W_n^m(t,\mathrm{\xi })+{\varphi }^c(\mathrm{\xi })W_n^c(t,\mathrm{\xi })+{\varphi }^a(\mathrm{\xi })W_n^a(t,\mathrm{\xi })$$ (3)

where $\hspace{0.17em}{\varphi }^e(\mathrm{\xi })$ is the mass fraction of elastin, ${\varphi }^m(\mathrm{\xi })$ is the mass fraction of circumferential collagen fibers and smooth muscle cells, ${\varphi }^c(\mathrm{\xi })$ is the mass fraction of diagonal collagen fibers, and ${\varphi }^a(\mathrm{\xi })$ is the mass fraction of axial collagen fibers. In particular, following previous histological reports of wall composition in the murine suprarenal abdominal aorta [15], we assigned the layer-specific mass fractions for each constituent to be

$${\varphi }^e\left(\mathrm{\xi }\right)=0.49,\hspace{1em}\hspace{0.17em}\hspace{0.17em}{\varphi }^m\left(\mathrm{\xi }\right)=0.49,\hspace{1em}{\varphi }^c\left(\mathrm{\xi }\right)=0.01,\hspace{1em}{\varphi }^a\left(\mathrm{\xi }\right)=0.01,\hspace{1em}\text{for}\hspace{1em}0\le \mathrm{\xi }\le \frac{h_{\text{media}}\left(t\right)\hspace{0.17em}}{h\left(t\right)}\hspace{0.17em}\left(\text{media}\right)$$

$${\varphi }^e\left(\mathrm{\xi }\right)=0.04,\hspace{1em}{\varphi }^m\left(\mathrm{\xi }\right)=0.04,\hspace{1em}{\varphi }^c\left(\mathrm{\xi }\right)=0.80,\hspace{1em}{\varphi }^a\left(\mathrm{\xi }\right)=0.12,\hspace{1em}\text{for}\hspace{1em}\frac{h_{\text{media}}\left(\mathrm{t}\right)\hspace{0.17em}}{h\left(t\right)}\le \mathrm{\xi }\le 1\hspace{0.17em}\left(\text{adventitia}\right)$$

where $h_{\text{media}}(\mathrm{t})/h(t)=0.69$ in the unloaded reference configuration. The constitutive relations used to describe the stored energy contribution of each constituent were (cf. [14])

$$W_n^e\left(t,\mathrm{\xi }\right)=\frac{c_n^e}{2}\left[\text{tr}\left({\mathit{C}}_n^e\left(t,\mathrm{\xi }\right)\right)-3\right]$$ (4)

$$W_n^m\left(t,\mathrm{\xi }\right)=\frac{c_n^m}{4k_n^m}[\left[e^{k_n^m{|{\left[{\lambda }_n^m\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}^2}-1\right]+{\alpha }_n^m\left[e^{k_n^m{|{\left[{\lambda }_n^m\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}^2}-1\right]]$$ (5)

$$W_n^c\left(t,\mathrm{\xi }\right)=\frac{c_n^c}{2{\mathit{k}}_n^c}\left[\sum _{i=1}^2\left[e^{k_n^c{|{\left[{\lambda }_n^{\mathit{c}\mathit{i}}\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}^2}-1\right]+{\alpha }_n^c\left[e^{k_n^c{|{\left[{\lambda }_n^{\mathit{c}\mathit{i}}\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}^2}-1\right]\right]$$ (6)

$$W_n^a\left(t,\mathrm{\xi }\right)=\frac{c_n^a}{4k_n^a}[\left[e^{k_n^a{|{\left[{\lambda }_n^a\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}^2}-1\right]+{\alpha }_n^a\left[e^{k_n^a{|{\left[{\lambda }_n^a\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}^2}-1\right]]$$ (7)

where $c_n^e,\hspace{0.17em}{c}_n^m,c_n^c,\hspace{0.17em}{c}_n^a,k_n^m,k_n^c,\hspace{0.17em}\text{and}\hspace{0.17em}{k}_n^a\hspace{0.17em}$ are the material parameters, and ${\alpha }_n^m,{\alpha }_n^c,\hspace{0.17em}\text{and}\hspace{0.17em}{\alpha }_n^a$ are the ratios that account for the differential contribution of fibers in compression and tension. Thus, several additional material parameters were defined as $c_n^{j,c}={\alpha }_n^j\hspace{0.17em}{c}_n^j$ for $j=m,c,a$, with superscript $c$ denoting compression. Here, the notation ${|•|}_{+}$ indicates the contribution of fibers in tension, whereas ${|•|}_{-}$ indicates the contribution of (laterally supported) fibers in compression.

Consistent with the concept that the arterial wall can be modeled as a constrained mixture consisting of multiple constituents that have different natural configurations and yet the same motions [14,16], the right Cauchy–Green tensors and associated fiber stretches for each constituent at node n assumed the following forms. The right Cauchy–Green tensor for elastin is

$${\mathit{C}}_n^e(t,\mathrm{\xi })={({\mathit{F}}_n^w(t,\mathrm{\xi }){\mathit{G}}_n^e)}^{\mathrm{T}}{\mathit{F}}_n^w(t,\mathrm{\xi }){\mathit{G}}_n^e$$ (8)

where ${\mathit{G}}_n^e$ is the unique deposition stretch tensor for elastin, namely,

$${\mathit{G}}_n^e={\mathit{G}}_n^{e1}{\mathit{G}}_n^1\otimes {\mathit{G}}_n^1+{\mathit{G}}_n^{e2}{\mathit{G}}_n^2\otimes {\mathit{G}}_n^2+\frac{1}{{\mathit{G}}_n^{e1}{\mathit{G}}_n^{e2}}{\mathit{N}}_n\otimes {\mathit{N}}_n$$ (9)

$G_n^{e1}$ is the deposition stretch of elastin in the circumferential direction, and $G_n^{e2}$ is the deposition stretch of elastin in the axial direction. Similarly, the stretch of the smooth muscle cells and the associated circumferentially oriented collagen fibers ${\lambda }_n^m(t,\mathrm{\xi })$ is defined as

$${\lambda }_n^m(t,\mathrm{\xi })=G_n^m\sqrt{{\mathit{C}}_n^w(t,\mathrm{\xi }):({\mathit{G}}_n^1\otimes {\mathit{G}}_n^1)}$$ (10)

where $G_n^m$ is the deposition stretch of the smooth muscle cells/collagen fibers and

$${\mathit{C}}_n^w(t,\mathrm{\xi })={({\mathit{F}}_n^w(t,\mathrm{\xi }))}^{\mathrm{T}}{\mathit{F}}_n^w(t,\mathrm{\xi })$$ (11)

${\lambda }_n^{\mathit{c}\mathit{i}}(t,\mathrm{\xi })$ is the stretch for the two symmetric diagonal collagen fiber families ($i$ = 1, 2) defined as

$${\lambda }_n^{\mathit{c}\mathit{i}}(t,\mathrm{\xi })=G_n^c\sqrt{{\mathit{C}}_n^w(t,\mathrm{\xi }):({\mathit{A}}_n^i\otimes {\mathit{A}}_n^i)}$$ (12)

where $G_n^c$ is the deposition stretch of each diagonal collagen fiber family, and ${\mathit{A}}_n^i$ is the fiber direction in the reference configuration which was defined as

$${\mathit{A}}_n^i=\text{cos}\hspace{0.17em}({\beta }_n^c){\mathit{G}}_n^1-{(-1)}^i\hspace{0.17em}\text{sin}\hspace{0.17em}({\beta }_n^c){\mathit{G}}_n^2$$ (13)

where $\mp {\beta }_{\mathit{n}}^c$ represents an average angle toward the axial direction, with circumferential fibers at ${\beta }_n^c$ = 0 deg and axial fibers at ${\beta }_n^c$ = 90 deg. Finally, ${\lambda }_n^a(t,\mathrm{\xi })$ is the average stretch of axial collagen fibers, namely,

$${\lambda }_n^a(t)=G_n^a\sqrt{{\mathit{C}}_n^w(t):({\mathit{G}}_n^2\otimes {\mathit{G}}_n^2)}$$ (14)

where $G_n^a$ is the deposition stretch of the axially oriented collagen fibers.

Computation of Intramural Stress.

The Cauchy stress tensor at every node $n$ and through-the-thickness position ξ in a deformed configuration at time $t$ (pressure $P(t)$ ranging from 10 to 140 mmHg at fixed axial stretches of ${\lambda }_z(t)$ = 0.95λ⁰, λ⁰, and 1.05λ⁰) was generalized as follows:

$${\mathit{\sigma }}_n^w\left(t,\mathrm{\xi }\right)=-p_n^w\left(t,\mathrm{\xi }\right)\mathit{I}+\frac{2}{\det \left({\mathit{F}}_n^w\left(t,\mathrm{\xi }\right)\right)}{\mathit{F}}_n^w\left(t,\mathrm{\xi }\right)\frac{\partial W_n\left(t,\mathrm{\xi }\right)}{\partial {\mathit{C}}_n^w\left(t\right)}{\mathit{F}}_n^w{\left(t,\mathrm{\xi }\right)}^{\mathrm{T}}$$ (15)

Using Eqs. (2), (3), and (11), the expression for the Cauchy stress could be rewritten such that

$$\begin{array}{c}{\mathit{\sigma }}_n^w(t,\mathrm{\xi })=-p_n^w(t,\mathrm{\xi })\mathit{I}+{\varphi }^e(\mathrm{\xi })c_n^e{\mathit{B}}_n^e(t,\mathrm{\xi })+{\varphi }^m(\mathrm{\xi })c_n^m{\Psi }_n^m(t,\mathrm{\xi }){(G_n^m)}^2{\mathit{g}}_n^1(t)\otimes {\mathit{g}}_n^1(t)\\ +{\varphi }^a(\mathrm{\xi })c_n^a\hspace{0.17em}{\Psi }_n^a(t,\mathrm{\xi }){(G_n^a)}^2{\mathit{g}}_n^2(t)\otimes {\mathit{g}}_n^2(t)+\sum _{i=1}^2{\varphi }^c(\mathrm{\xi })c_n^c\Psi {\hspace{0.17em}}_n^{\mathit{c}\mathit{i}}(t,\mathrm{\xi }){(G_n^c)}^2{\mathit{a}}_n^i(t,\mathrm{\xi })\otimes {\mathit{a}}_n^i(t,\mathrm{\xi })\end{array}$$ (16)

where the left Cauchy–Green tensor for elastin is written as

$${\mathit{B}}_n^e(t,\mathrm{\xi })={\mathit{F}}_n^w(t,\mathrm{\xi }){\mathit{G}}_n^e{({\mathit{F}}_n^w(t,\mathrm{\xi }){\mathit{G}}_n^e)}^{\mathrm{T}}$$ (17)

and the ${\Psi }_n$ terms for each constituent in the constrained mixture are

$${\Psi }_n^m\left(t,\mathrm{\xi }\right)={|{\left[{\lambda }_n^m\right(t,\mathrm{\xi }\left)\right]}^2-1|}_{+}{e}^{k_n^m{|{\left[{\lambda }_n^m\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}^2}+{\alpha }_n^m{|{\left[{\lambda }_n^m\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}{e}^{k_n^m{|{\left[{\lambda }_n^m\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}^2}$$ (18)

$${\Psi }_n^a\left(t,\mathrm{\xi }\right)={|{\left[{\lambda }_n^a\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}\hspace{0.17em}{e}^{k_n^a{|{\left[{\lambda }_n^a\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}^2}+{\alpha }_n^a{|{\left[{\lambda }_n^a\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}\hspace{0.17em}{e}^{k_n^a{|{\left[{\lambda }_n^a\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}^2}$$ (19)

$${\Psi }_n^{ci}\left(t,\mathrm{\xi }\right)={|{\left[{\lambda }_n^{ci}\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}\hspace{0.17em}{e}^{k_n^c{|{\left[{\lambda }_n^{ci}\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{+}^2}+{\alpha }_n^c{|{\left[{\lambda }_n^{ci}\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}\hspace{0.17em}{e}^{k_n^c{|{\left[{\lambda }_n^{ci}\left(t,\mathrm{\xi }\right)\right]}^2-1|}_{-}^2}$$ (20)

whereas the collagen fiber directions in the current configuration ${\mathit{a}}_n^i\hspace{0.17em}$ (for $i$ = 1,2) are

$${\mathit{a}}_n^i(t,\mathrm{\xi })={\mathit{F}}_n^w(t,\mathrm{\xi }){\mathit{A}}_n^i$$ (21)

Note that $p_n^w(t,\mathrm{\xi })$ is a scalar function that enforces the kinematic constraint of no local changes of volume.

In summary, the list of the 16 unknown material parameters to be identified was

• seven elastic coefficients in tension/compression: $c_n^e,\hspace{0.17em}{c}_n^m,\hspace{0.17em}{c}_n^c,\hspace{0.17em}{c}_n^a,\hspace{0.17em}{c}_n^{m,c},\hspace{0.17em}{c}_n^{c,c},\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}{c}_n^{a,c}$

• three exponential coefficients: $k_n^m,\hspace{0.17em}{k}_n^c,\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}{k}_n^a$

• five deposition stretch parameters: $G_n^{e1},G_n^{e2},\hspace{0.17em}{G}_n^m,G_n^c,\hspace{0.17em}\text{and}\hspace{0.17em}{G}_n^a$

• the average angle of diagonal fibers: ${\beta }_n^c$

Fortunately, the values of many of these parameters are well bounded (e.g., tension/compression ratios, deposition stretches, and fiber angles), which favor the estimation process. Finally, note that for all the tensor components, fiber stretches, and material parameters, the subscript $n$ indicates that they could take a different value at each node $n$ due to the possible regional variations of material properties.

The Inverse Method.

Our objective was to identify values of model parameters separately for each node $n$ (i.e., localized region). For this, we employed an inverse method where we first defined a cost function $J$ involving the computed stress (Eq. (16)) as well as the experimentally measured and theoretically predicted pressures ($P^{\hspace{0.17em}\text{exp}\hspace{0.17em}}(t)$ and $P^{\text{th}}(t)$) and axial loads ($f^{\hspace{0.17em}\text{exp}\hspace{0.17em}}(t)$ and $f^{\text{th}}(t)$). The parameters to be identified were continuously updated until we found the minimum of the cost function $J$.

As the suprarenal abdominal aorta does not have a perfectly cylindrical shape, equations of thick-walled cylinders relating the theoretically predicted pressure $P^{\text{th}}(t)$ and the computed stresses could not be used directly. A more general equation was obtained using the virtual fields method (VFM) [17–19], namely,

$$P^{\text{th}}\left(t\right)=h\left(t\right){\int }_0^1\frac{{\sigma }_{11,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{1/{\mathrm{\kappa }}_n^1\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)}+\frac{{\sigma }_{22,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{1/{\mathrm{\kappa }}_n^2\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)}d\mathrm{\xi }$$ (22)

where

$${\sigma }_{11,n}^w(t,\mathrm{\xi })={\mathit{\sigma }}_n^w(t,\mathrm{\xi }):({\mathit{g}}_n^1(t)\otimes {\mathit{g}}_n^1(t))$$ (23)

$${\sigma }_{22,n}^w(t,\mathrm{\xi })={\mathit{\sigma }}_n^w(t,\mathrm{\xi }):({\mathit{g}}_n^2(t)\otimes {\mathit{g}}_n^2(t))$$ (24)

$${\sigma }_{33,n}^w(t,\mathrm{\xi })={\mathit{\sigma }}_n^w(t,\mathrm{\xi }):({\mathit{n}}_n(t)\otimes {\mathit{n}}_n(t))$$ (25)

The details of the derivation of Eq. (22) are given in the Appendix, Proof 1. It is an extension of the traditional equations for thick-walled cylinders, where both the local circumferential and axial curvatures of the artery are accounted for to ensure equilibrium. This difference is particularly important for mouse aortas as they may be curved in their traction-free configuration and may show axial bending effects during inflation–extension testing.

A second equation involving the axial load was necessary to close the system. Again using the VFM (Appendix, Proof 2), the theoretically predicted axial load $f^{\mathrm{t}\mathrm{h}}(t)$ could be related to the computed stresses using the following equation:

$$f^{\mathrm{t}\mathrm{h}}(t)=\pi h(t){\int }_0^1[2{\sigma }_{zz,\mathit{n}}^w(t,\mathrm{\xi })-{\sigma }_{xx,\mathit{n}}^w(t,\mathrm{\xi })-{\sigma }_{yy,\mathit{n}}^w(t,\mathrm{\xi })][r_{}^o(t)-(1-\mathrm{\xi })h(t)]d\mathrm{\xi }$$ (26)

where $r_{}^o(t)$ is the outer radius and

$${\sigma }_{xx,n}^w(t,\mathrm{\xi })={\mathit{\sigma }}_n^w(t,\mathrm{\xi }):({\mathit{e}}_x\otimes {\mathit{e}}_x)$$ (27)

$${\sigma }_{yy,n}^w(t,\mathrm{\xi })={\mathit{\sigma }}_n^w(t,\mathrm{\xi }):({\mathit{e}}_y\otimes {\mathit{e}}_y)$$ (28)

$${\sigma }_{zz,n}^w(t,\mathrm{\xi })={\mathit{\sigma }}_n^w(t,\mathrm{\xi }):({\mathit{e}}_z\otimes {\mathit{e}}_z)$$ (29)

Finally, using Eqs. (22) and (26), we defined the following cost function at each node n:

$$J_n=\sum _{k=1}^K{\left(\frac{P^{\text{exp}}(t_k)-P^{\mathrm{th}}(t_k)}{{\overline{P}}^{\text{exp}}(t_k)}\right)}^2+{\left(\frac{f^{\text{exp}}(t_k)-f^{th}(t_k)}{{\overline{f}}^{\text{exp}}(t_k)}\right)}^2$$ (30)

where K is the total number of experimentally measured configurations $k$, and the overbar notation denotes an average over all the data points (e.g., ${\overline{P}}^{\text{exp}\hspace{0.17em}}(t_k)={\sum }_{k=1}^K{P}^{\hspace{0.17em}\text{exp}\hspace{0.17em}}(t_k)/K$). It is important to note that, for the p-DIC data sets, pressure was measured directly in the device as it was varied incrementally in steps of 10 mmHg at each of three different axial stretches. In contrast, the associated axial force, for each prescribed pressure and axial stretch, was assumed to be the same as that measured in the standard biaxial test, which is why the same axial stretches were used. Hence, the standard biaxial tests not only provided an important comparative approach for parameter estimation but they also provided axial force data for the p-DIC data sets.

Thin-Wall Assumption.

Following many prior reports on the mechanical properties of murine aortas (cf. Ref. [7]), as a first approximation the wall may be modeled mechanically as a membrane (i.e., transmurally homogenized) under physiologic loads. Such an approach is particularly useful for fluid–solid interaction implementations (cf. Ref. [20]) where it is the structural, not material, stiffness that is of most importance. Toward this end, one can replace ${\mathit{F}}_n^w(\mathrm{t},\mathrm{\xi })$ by its average over the thickness and deduce ${\mathit{F}}_n^{}(t)$ using a simpler kinematic description. The values of stress ${\mathit{\sigma }}_n^w(t,\mathrm{\xi })$ in Eqs. (22) and (26) then become ${\mathit{\sigma }}_n^{}(t)$ (with no thickness dependence). In this case, the expressions for the theoretically predicted pressure and axial load can be reduced to

$$P^{\text{th},*}\left(t\right)=h\left(t\right)\left(\frac{\left({\sigma }_{11,n}^{}\left(t\right)-{\sigma }_{33,n}^{}\left(t\right)\right)}{1/{\mathrm{\kappa }}_n^1\left(t\right)-h\left(t\right)/2}+\frac{\left({\sigma }_{22,n}^{}\left(t\right)-{\sigma }_{33,n}^{}\left(t\right)\right)}{1/{\mathrm{\kappa }}_n^2\left(t\right)-h\left(t\right)/2}\right)\hspace{0.17em}$$ (31)

$$f^{\text{th},*}(t)=\pi h(t)[r_{}^o(t)-h(t)/2](2{\sigma }_{zz,n}^{}(t)-{\sigma }_{xx,n}^{}(t)-{\sigma }_{yy,n}^{}(t))$$ (32)

Thus, minimization of a modified cost function required

$$J_n=\sum _{k=1}^K{(\frac{P^{\text{exp}}(t_k)-P^{\mathrm{th}}(t_k)}{{\overline{P}}^{\text{exp}}(t_k)})}^2+{(\frac{f^{\text{exp}}(t_k)-f^{th}(t_k)}{{\overline{f}}^{\text{exp}}(t_k)})}^2$$ (33)

Resolution of the Inverse Problem.

The requisite minimization and material parameter identification are achieved in two steps, namely:

Step 1: Minimize $J_n$ (or $J_n^{*}$) with respect to the material parameters $(c_n^e,\hspace{0.17em}{c}_n^m,\hspace{0.17em}{c}_n^c,\hspace{0.17em}{c}_n^a,\hspace{0.17em}{c}_n^{m,c},\hspace{0.17em}{c}_n^{c,c},\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}{c}_n^{a,c})$ using a non-negative linear least squares algorithm.

Step 2: Minimize $J_n$ (or $J_n^{*}$) with respect to the remaining parameters using a bounded genetic algorithm. The bounds that were used for the minimization procedure are consistent with Ref. [14] and are reported in Table 1.

Table 1.

Bounds used for the material parameter identification procedure

Parameter	Lower bound	Upper bound
$G_n^c,G_n^a,G_n^m$	1.01	1.15
$k_n^m, k_n^c, k_n^a$	0.001	10
$G_n^{e1}$	2	2.4
$G_n^{e2}$	1.6	2
${\beta }_n^c$	25 deg	70 deg

The stopping criteria included both a time limit (30 s for each node $n$) and a tolerance (10⁻⁶) for the improvement of the cost function from one iteration to the next. After the resolution, a coefficient of determination $R_n^2$ is computed using Eq. (22). In the case of the thin-wall assumption, $R_n^{2*}$ is computed using Eq. (31) and defined as

$$R_n^{2*}=1-\frac{\sum _{k=1}^K{\left(P^{\text{th},*}\left(t_k\right)-P^{\hspace{0.17em}\text{exp}\hspace{0.17em}}\left(t_k\right)\right)}^2}{\sum _{k=1}^K{\left({\overline{P}}^{\hspace{0.17em}\text{exp}\hspace{0.17em}}\left(t_k\right)-P^{\hspace{0.17em}\text{exp}\hspace{0.17em}}\left(t_k\right)\right)}^2}$$ (35)

Suprarenal Branch Locations.

Because all the suprarenal branches were ligated to enable pressurization during testing, several major branch locations could be identified on the reconstructed vessel surface as large deviations in local radius. Potential regions of influence around these branch locations were extracted using a modified branch splitting procedure in the open-source Vascular Modeling Toolkit (VMTK2). Briefly, seed points for centerline computations (vmtkcenterlines) were manually placed near the maximum local radius of each branch location. Branching centerline paths to each manually placed target were computed using a maximum inscribed sphere radius algorithm [21]. Additional VMTK subroutines were then used (vmtkbranchextractor and vmtkbranchclipper) to extract a region about each branch based on the locations of centerline bifurcations. Finally, the boundary of each clipped surface was extracted, converted into a cylindrical coordinate system, and overlaid on 2D representations of the full-field data, which facilitated regional comparisons. For example, Fig. 2 shows three to four potential regions of branch influence (dashed lines) located near (1) smaller suprarenal branches, (2) the celiac artery, (3) the superior mesenteric artery, and (4) the right renal artery. Following identification of several major branch locations, each reconstructed surface was rotated such that the average position of largest regions of branch influence (1 and 2) were aligned with an angle of 0 deg in cylindrical coordinates (positive x-axis).

Fig. 2.

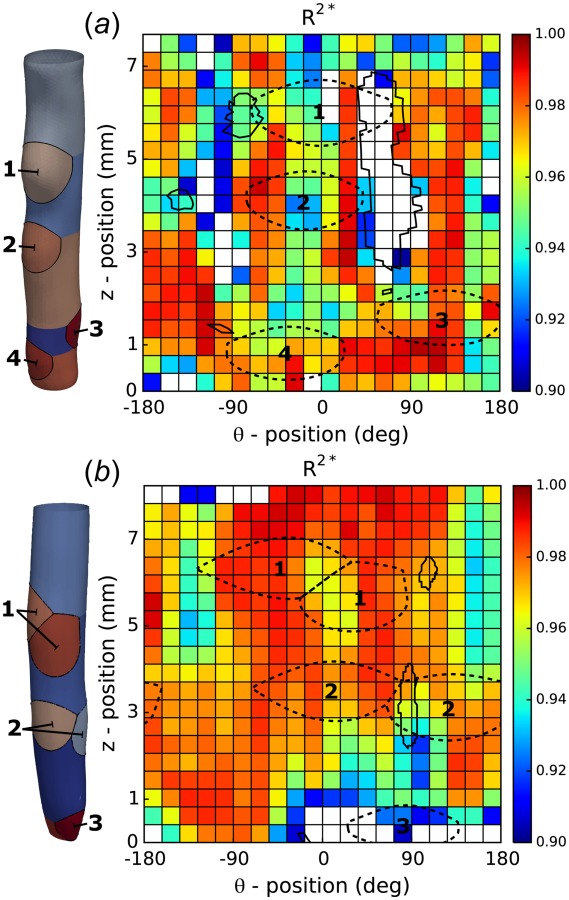
Spatial distribution of the coefficients of determination. Goodness-of-fit for (a) specimen A and (b) specimen B. Both panels show outputs from a modified branch splitting algorithm to highlight regions of influence due to specimen branches (1–4). The results are shown in both a 3D (left) and 2D (right) representation over the entire surface of each sample. Boundaries of both low mean curvature (solid enclosed regions) and regions of branch influence (dashed ellipses) are overlaid in the 2D representation to show localization with regions of low $R_n^{2*}$.

Statistical Analysis.

Notwithstanding the utility of computing quantities of interest in many different regions, 400 in our case, for purposes of illustration and statistical ease, distributions of identified material parameters, stored energy, and linearized stiffness were also divided into four larger regions for comparison: ventral-top, dorsal-top, ventral-bottom, and dorsal-bottom, with n = 100 observations per region. Regional differences were assessed both within and between samples A and B. Namely, values on the dorsal and ventral halves at the same top or bottom position and for the top and bottom halves on the same dorsal or ventral side within the same sample were compared using a one-way ANOVA followed by a post-hoc Bonferroni correction. The values from the same region for different samples were compared using a standard Student's t-test. For all the comparisons, a value of P < 0.05 was considered significant. Table S2, which is available under the “Supplemental Materials” tab for this paper on the ASME Digital Collection, summarizes all the identified values by region, with values expressed as mean ± SEM and statistical significance indicated when appropriate.

Results

Morphometric information for the two mice and their respective aortic samples is given in Table S1, which is available under the “Supplemental Materials” tab for this paper on the ASME Digital Collection. Figure 2 shows regional distributions (at 400 possible locations) of the coefficients of determination for the inverse estimation for both samples based on the thin-walled assumption. Associated distributions of representative best-fit parameters ($c_n^e$, $c_n^m$, $c_n^c$, and ${\beta }_n^c$) are shown in Figs. S1 and S2, which are available under the “Supplemental Materials” tab for this paper on the ASME Digital Collection, with mean values for the four larger regions (ventral-top, etc.) listed in Table S2, which is available under the “Supplemental Materials” tab for this paper on the ASME Digital Collection. In particular, note that Fig. 2 and Figs. S1 and S2, which are available under the “Supplemental Materials” tab for this paper on the ASME Digital Collection, show values of either $R^{2*}$ or the identified model parameters on both a reconstructed 3D surface of the aorta in its reference configuration of 80 mmHg at λ⁰ (left) and a 2D representation in a parameterized $(\theta ,z)$ space (right). All the distributions suggest regional heterogeneities, albeit to varying degrees. As revealed further by Fig. 2, however, not all the locations yielded reliable inverse estimations; regions with $R^{2*}<0.90$ are indicated with (transparent) white patches. Specifically, for sample A, only 89% of all the patches had a coefficient of determination above the threshold, with more than 72% of accepted patches having a value larger than 0.95. In contrast, results for sample B revealed a larger proportion of patches above threshold with 95% of all the patches accepted and 83% of accepted patches having $R^{2*}<0.95$; in this case, discarded patches were often close to the cannulation ligatures at the top and bottom of the sample, which may be a result of “end effects.”

There are two primary regions on the surface of sample A (centered at $z$ = 4 mm and $\hspace{0.17em}\theta$ = ±90 deg) that can be identified with low coefficients of determination (Fig. 2(a)). These areas of low $R^{2*}$ tended to localize on the lateral sides of the regions of branch influence, in particular branch locations 1 and 2. Indeed, it appeared that areas of low mean curvature (Fig. 2, solid lines) tended to colocalize with regions of low $R^{2*}$, suggesting that the local curvature of the reconstructed sample has a significant impact on the ability of the thin-walled model to fit data, as evidenced by the explicit dependence of $P^{\text{th},*}(t)$ on the principal curvatures ${\kappa }_n^1$ and ${\kappa }_n^2$ (cf. Eq. (31)). Although regions of low mean curvature may arise as a local effect of branch ligation, the ability of the p-DIC analysis to capture modes of bending upon pressurization at a fixed axial stretch may also contribute to regions of low $R^{2*}$.

Gross regional variations in material properties were analyzed by comparing distributions (which excluded nonidentified patches) for the four nonoverlapping regions: ventral-top, dorsal-top, ventral-bottom, and dorsal-bottom. Following alignment of major branch locations with the 0 deg circumferential coordinate, a straightforward definition of the ventral and dorsal halves of the sample was given by the ranges ${\theta }_v\in \left[-\frac{\pi }{2},\frac{\pi }{2}\right]$ and ${\theta }_d\in \left[\frac{\pi }{2},\frac{3\pi }{2}\right]$, respectively; top (proximal) and bottom (distal) halves were defined as all nodes above and below $Z=L/2$. Illustrative results for several identified parameters from both samples are shown in Fig. 3 using a histogram representation: black bars for sample A and white bars for sample B, with overlapping values indicated by gray shading. Note that patches containing a branch ostium are included in the histogram representation but we have verified that this does not adversely affect the results and statistical comparison between regions.

Fig. 3.

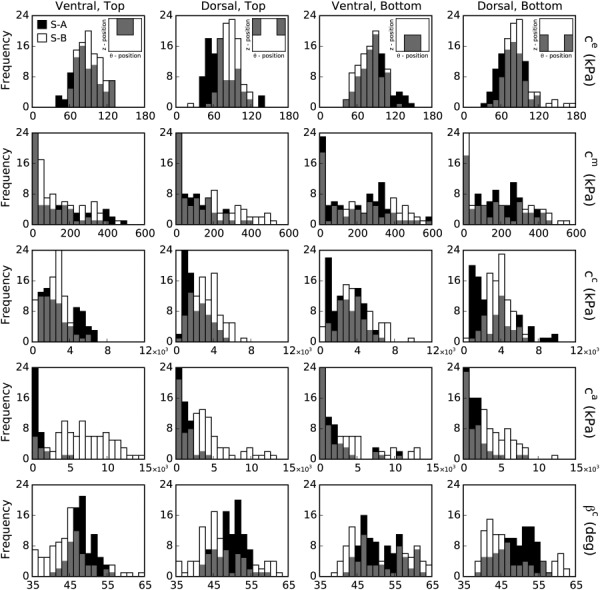
Histogram distributions of identified material parameters. The results from the identification procedure are shown for $c_n^e$ (first row), $c_n^m$ (second row), $c_n^c$ (third row), $c_n^a$ (fourth row), and ${\beta }_n^c$ (fifth row) for both sample A (S-A, black bars) and sample B (S-B, white bars). All the identified parameters are spatially varying. The results are also shown by region: ventral-top (first column), dorsal-top (second column), ventral-bottom (third column), and dorsal-bottom (fourth column). The gray bars indicate overlapping results for the two samples.

Significant differences in identified parameter values were found between regions on each sample. Specifically, for sample A the elastin parameter $c_n^e$ was significantly lower on the dorsal side independent of axial position (proximal to distal), whereas for sample B the lowest values were found in the ventral-bottom quadrant. The circumferential collagen parameter $c_n^m$ and the diagonal collagen parameter $c_n^c$ were significantly higher on the bottom half of each sample, independent of the dorsal-ventral sides; the dorsal-top quadrant showed opposite trends in $c_n^c$ between samples. The identified spatial distribution of the axial collagen parameter $c_n^a$ was opposite across samples. Namely, $c_n^a$ was highest on the bottom half of sample A and on the top half of sample B. Finally, for both samples, the fiber angle ${\beta }_n^c$ was highest in the ventral-bottom quadrant. Despite several similar trends in significance, all the identified elastic coefficients were found to be significantly larger in magnitude on sample B as compared to sample A, highlighting the utility of the inverse method in identifying distributions of sample specific properties. Although there are statistically significant differences in material parameters by region, the dispersions are wider than the average difference between the means; this is especially the case for $c_n^m$, $c_n^c$, and $c_n^a$, which may have been induced by a smaller sensitivity of the cost function to these parameters or the existence of intercorrelations between parameters. Indeed, the number of parameters for the material model is relatively large (16 total) and we note that full-field information was collected only on the outer (adventitial) surface.

Although individual material parameters are important, it is their collective contribution for modeling the material properties that is most important. Among the properties of most importance are the stored energy density $W_n$ and the circumferential and axial material stiffness [6,22]. Regional distributions (at up to 400 locations) of stored energy density were computed for two different loaded configurations for both samples (Figs. 4(a)– 4(d): pressures of $P(t)$ = 80 mmHg (left) and 140 mmHg (right), at individual values of the in vivo axial stretch ${\lambda }_z(t)$ = λ⁰). It is seen that, in contrast to distributions of individual material parameters, the regional distributions in strain energy density are relatively smooth. In addition, the dorsal halves of the samples store significantly less energy than the ventral halves upon pressurization to 140 mmHg (sample A: 107.7 ± 2.2 kPa versus 116.05 ± 2.2 kPa and sample B: 99.3 ± 1.3 kPa versus 122.3 ± 2.3 kPa; P < 0.05). The removal of perivascular support needed to enable in vitro mechanical testing, in particular the dorsal support of the spine, likely contributed to the measured differences in dorsal versus ventral energy storage capability under the action of a uniform distending pressure. Similar to $c_n^e$, the stored energy also tended to be higher in the central region (i.e., $z$ = 1.5–5.5 mm), independent of pressure. The distribution of $W_n$ corresponding to the distribution of $c_n^e\hspace{0.17em}$ is consistent with the elastic fibers being the main contributor to energy storage, the primary function of large arteries, such as the aorta.

Fig. 4.

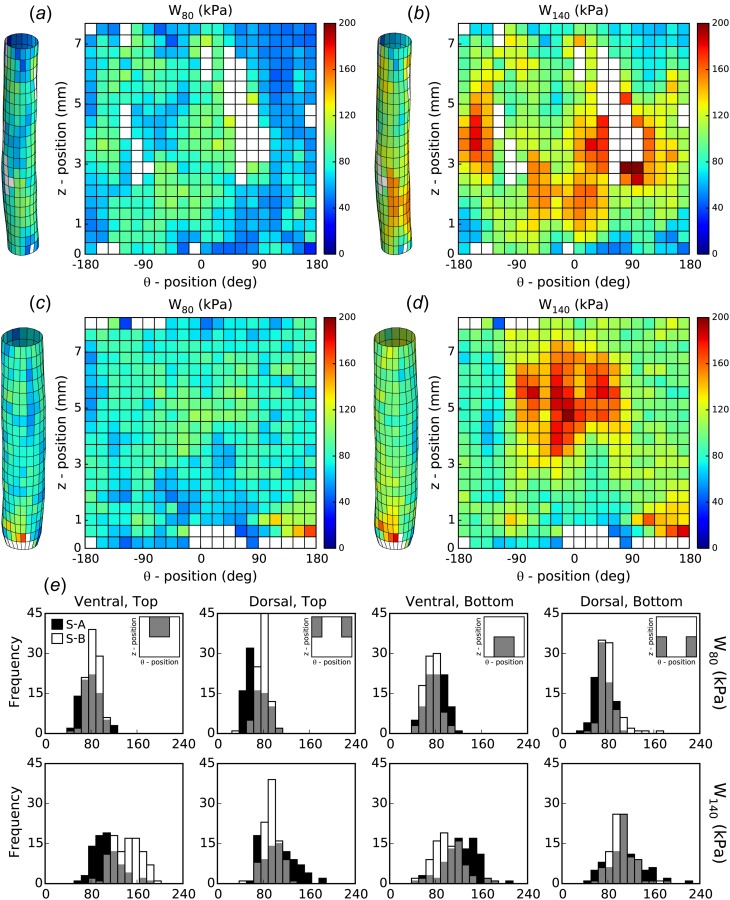
Spatial distribution of strain energy. The strain energy density was computed (Eq. (3)) using the identified material properties over the surface of ((a) and (b)) sample A and ((c) and (d)) sample B. The results are shown for two loaded configurations: ((a) and (c)) P(t) = 80 mmHg at λ_z(t) = λ⁰ and ((b) and (d)) $P(t)$ = 140 mmHg at λ_z(t) = λ⁰. (e) Histograms show the spatial distributions in each quadrant for both samples (cf. Fig. 3).

Figure 5 shows the regional distributions (at up to 400 locations) of the circumferential ($C_{1111}$, left) and axial ($C_{2222}$, right) components of the linearized material stiffness for samples A and B computed at a loaded configuration of $P(t)$ = 100 mmHg and individual value of ${\lambda }_z(t)$ = λ⁰. Histograms are shown for the four larger regions. Circumferential stiffness was significantly lower in the dorsal-top quadrants of both samples as compared to the other quadrants in their respective dorsal or top halves. Axial stiffness, on the other hand, was significantly different on both the ventral and bottom halves of each sample. Specifically, the ventral half had higher stiffness than the dorsal half independent of top or bottom location (sample A: 1.32 ± 0.03 MPa versus 1.15 ± 0.02 MPa and sample B: 1.67 ± 0.04 MPa versus 1.49 ± 0.02 MPa; P < 0.05), and the bottom half had higher stiffness than the top independent of the dorsal-ventral side (sample A: 1.35 ± 0.03 MPa versus 1.10 ± 0.02 MPa and sample B: 1.61 ± 0.04 MPa versus 1.55 ± 0.03 MPa; P < 0.05). One main structural difference between the four quadrants, of course, is the location of the major suprarenal branches. Comparison of stiffness distributions with branch sites for samples A and B (dashed lines, Figs. 5(a)–5(d)) suggests that higher values of biaxial stiffness tend to colocalize with regions of branch influence. Specifically, circumferential stiffness tends to be higher at the boundaries whereas axial stiffness is higher over the entire branch area.

Fig. 5.

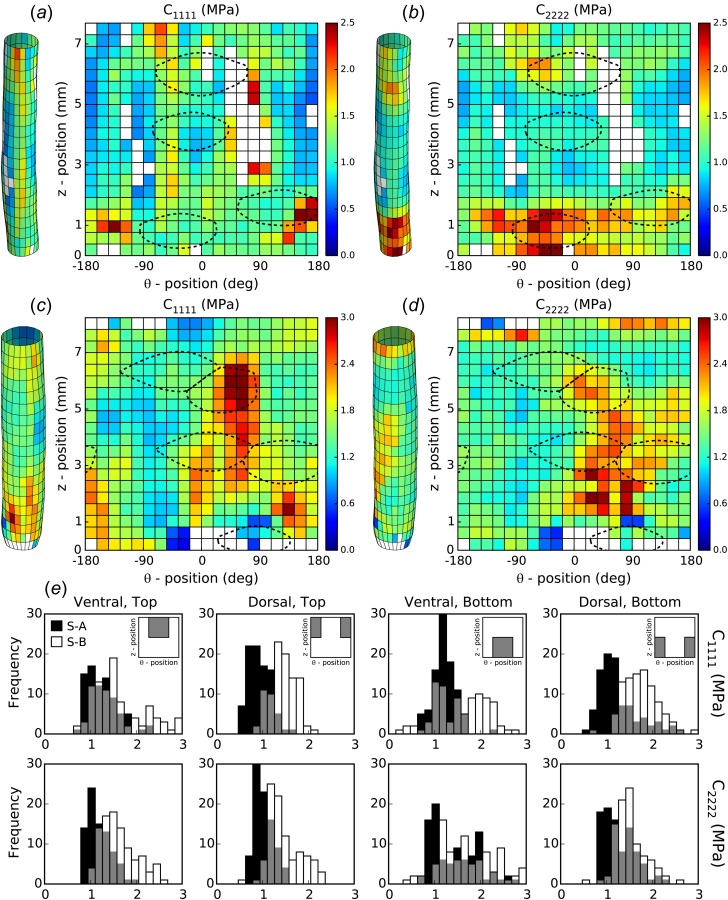
Spatial distribution of biaxial material stiffness. The biaxial material stiffness was computed using the identified material parameters over the surface of ((a) and (b)) sample A and ((c) and (d)) sample B. The results are shown for ((a) and (c)) circumferential (${\mathrm{C}}_{1111}$) and ((b) and (d)) axial (${\mathrm{C}}_{2222}$) stiffness evaluated at a loaded configuration of P(t) = 100 mmHg and λ_z(t) = λ⁰. Regions of influence due to branches (dashed lines) are overlaid to show localization near regions of high stiffness. (e) Histograms show spatial distributions in each quadrant for both samples (cf. Fig. 3).

In standard biaxial inflation–extension tests, one typically measures on-line both the outer diameter and the axial force in response to changes in pressure and axial stretch. Such data were collected for both samples prior to the biaxial p-DIC testing, and values of the constitutive parameters were estimated using traditional nonlinear regression [6]. Representative values of the estimated material parameters ($c^e$, $\hspace{0.17em}{c}^m$, $c^c$, and ${\beta }^c$) and the associated scalar metrics of goodness-of-fit or material behavior ($R^2,\hspace{0.17em}W,\hspace{0.17em}{C}_{1111}$, and $C_{2222}$) are reported in Table 2. The best-fit parameter values are generally in good agreement with the local distributions that were obtained using the p-DIC data.

Table 2.

Best-fit model parameters and associated scalar metrics estimated using nonlinear regression of standard biaxial experimental data for samples A and B

Sample	$c_{}^e$ (kPa)	$c_{}^m$ (kPa)	$c_{}^c$ (kPa)	${\beta }_{}^c$	$W$ (kPa) at 80 mmHg	$W$ (kPa) at 140 mmHg	$C_{1111}$ (MPa)	$C_{2222}$ (MPa)	$R^{2*}$
A	71	385	959	51 deg	70	93	1.78	1.18	0.98
B	65	128	1470	46 deg	61	79	1.74	0.96	0.99

Finally, as a qualitative comparison of approaches, we computed local pressure–radius curves and local circumferential stress–stretch curves for every node at which material parameters were identified (Fig. 6). Data from the standard (global) biaxial inflation–extension approach (single strings of black circles) were compared to the reconstructed pressure–radius (left) and stress–stretch (right) curves for samples A and B. Although similar curves can be generated for all the tested axial stretch values, data are shown only at ${\lambda }_z(t)$ = λ⁰, for clarity. The many sets of gray curves represent the reconstructed behavior of the inverse method based on the locally identified material parameters from all the patches above a given $R^{2*}$ value. Namely, the light-gray and dark-gray sets of curves show the behavior for all the patches with $R^{2*}>0.95\hspace{0.17em}$ and $R^{2*}>0.99$, respectively. For sample A, the light-gray curves represent 72% of all the identified patches (257/356 patches) and the dark-gray curves represent 6.5% of all the identified patches (23/356 patches). Similarly, for the better fitting sample B, the light-gray curves represent 83% of all the identified patches (316/380 patches) and the dark-gray curves represent 2.9% of all the identified patches (11/380 patches). Overall, there is a very good agreement between the standard and new p-DIC based approaches. In particular, the mean global responses fall well within the expected dispersion of the identified local responses. This overall agreement highlights both the general utility and added advantage of local measurements even in healthy aortic tissue.

Fig. 6.

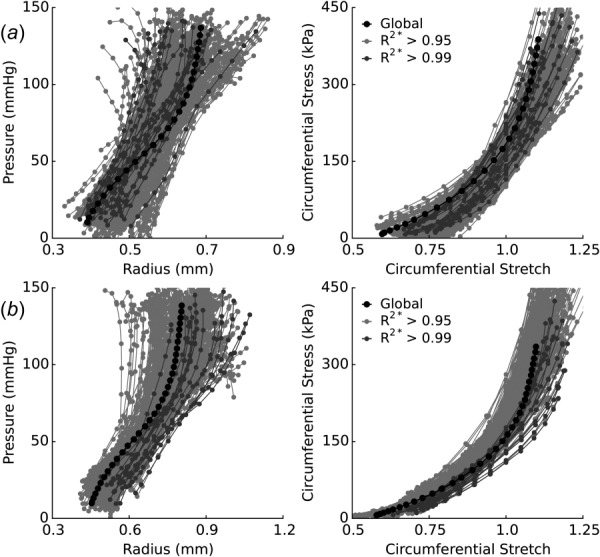
Comparison of p-DIC and standard biaxial results. The reconstructed pressure–radius (left) and circumferential stress–stretch (right) behaviors for (a) sample A and (b) sample B were compared to standard biaxial testing results (black circles). Local responses are compared for locations with an $R^{2*}$ value above 0.95 (light-gray) and 0.99 (dark-gray). Comparison is shown only for data collected at λ_z(t) = λ⁰, for clarity.

Discussion

Relevance of Inverse Methods.

Advances in medical imaging and computational biomechanics have enabled investigators to study patient-specific models of hemodynamics, wall stress, and even fluid–solid interactions. The utility of such models depends, however, on the goodness of the specified material properties and boundary conditions. With regard to the former, increasing attention is appropriately being directed toward in vivo estimations of arterial [23,24] and aneurysmal [25,26] properties. Such attempts are nevertheless complicated by the limited information that is available via in vivo measurements as well as by the existence of regional variations in properties both along the normal arterial tree and within diseased segments [15,27–30]. Indeed, because of the complexity of the constitutive behavior of the aorta in health and disease, it is inconceivable that in vivo data alone could enable both the identification of appropriate functional forms of the constitutive relations and the calculation of best-fit values of the associated material parameters. Complementary in vitro tests are essential. For example, in vitro biaxial tests on planar or cylindrical specimens allow one to perform the multiple protocols that are necessary to generate the overdetermined systems of equations that ensure robust parameter estimation. Such tests enable much more, however. They also allow a more careful evaluation of the appropriateness of specific functional forms of the constitutive relations and identification of ranges for the values of the material parameters, which provides important constraints on the estimations [31,32]; they similarly allow equal quantification of circumferential and axial behaviors and their coupling (e.g., see Ref. [33] and [34]), even if directional deformations are not equal in vivo. Given such information from in vitro tests, one can then focus in vivo on parameter estimation alone.

Notwithstanding the advantages of standard biaxial testing, there is yet a need for more advanced in vitro methods, including ones that can both delineate possible regional variations in cases of disease and better correlate such variations with the underlying microscopic composition and structure. For this reason, we developed a novel approach that combines in vitro biaxial p-DIC based mechanical testing with a nonlinear inverse material characterization method. The former has been described in detail previously [10,35,36]. The latter can be accomplished in multiple ways, but we employed a VFM that has proven useful in different applications [17,19]. This approach allows one to derive relatively simple extensions of traditional relations for thick-walled cylindrical geometries [37,38] that yet allow one to account for added complexities, including axial bending during testing and associated changes in local curvatures.

Choice of Material Model.

We used a four-fiber family model that has proven reliable in describing murine arterial behavior in multiple studies [6,7,9,14,15,20]. Although motivated by microstructural information, this model was developed primarily to capture phenomenologically the anisotropic response of blood vessels subjected to extension–inflation tests, which ultimately depends on constituent fractions, fiber orientations, cross-linking, physical entanglements, and so forth. The four-fiber model is thought to allow complexities beyond just fiber orientations and has been shown (in comparison to two- and six-) to represent a good compromise between model complexity and goodness-of-fit when applied to seven independent pressure–diameter (P–d) and axial load–axial stretch (f–l) protocols obtained during standard biaxial extension–inflation testing [6]. In particular, all of the parameters of the four-fiber family model contribute to the fitting of the data; uncertainty in the best-fit values was estimated using a nonparametric bootstrap approach, and no fundamental problem of identifiability was found [6]. When using a reduced number of protocols in the material parameter identification (e.g., only the three P–d protocols, with force measurement as in the current study, as opposed to the three P–d and four f–l protocols), the primary effect was a modest change in the identified fiber angle that tended to increase the biaxial linearized stiffness.

One recent addition to the four-fiber family model is the incorporation of deposition stretches, which permits convenient predictions of residual stresses while using an in vivo reference configuration [14]. We showed that deposition stretch values should remain within a narrow range to ensure reasonable model predictions. Hence, although their inclusion adds to the number of parameters, they are well bounded and do not compromise the identification of the standard parameters. This overall previous experience with extension–inflation tests of excised arteries supports the use of the present model to simultaneously fit P–d–f data at different extensions. Whereas all the previous analyses on this model (i.e., traditional analyses) were based on the assumption of a perfectly cylindrical geometry, herein we extended this approach to local analyses, for each position on the reconstructed surface of the blood vessel, based on full-field measurements for every applied pressure and every applied axial stretch that yield the local surface deformation gradient.

The PVP allows the model to locally adjust to data at every position instead of global adjustment based only on the measured (P–d) and (f–l) curves. For every position, the identification is based on 14 × 3 × 2 = 84 independent data points (14 pressures × 3 axial stretches × 2 independent equations). Therefore, similar to the traditional approach, at every position defined on the surface of the sample, the number of reconstructed data points is sufficient to ensure the overdetermined number of equations needed to identify the parameters in the model. As in traditional analyses, however, we note that one disadvantage of Fung-type exponential models is that there are intrinsic correlations among the parameters $c_{\mathit{n}}^i$ and $k_{\mathit{n}}^i$ (cf. Eqs. (5)–(7)). Hence, the cost function can often be minimized equally well using different combinations of the $c_{\mathit{n}}^i$ and $k_{\mathit{n}}^i$ parameters. This is one reason why we should focus more on the predicted material properties, such as energy storage or material stiffness, rather than individual material parameters.

Uncertainty of the Inverse Method.

The question of uncertainty for each material parameter holds in all the nonlinear models and associated testing. To evaluate this point, we repeated the identification after adding noise to the experimental data. White noise with a standard deviation of 0.05 was added to each component of the deformation gradient. This standard deviation was chosen to be larger than the measurement uncertainty (which was less than 0.01 for the deformation gradient) to amplify its effects on the identification. After the new identification, similar distributions of material parameters were reconstructed. Changes on the $R^{2*}$ criterion were negligible, thus suggesting that the goodness-of-fit depends more on the ability of the model to fit the data than on random noise in the data. Similarly, we tested the sensitivity of the identification procedure to the initial set of parameter values used in the nonlinear optimization. The identification was performed several times with different sets of initial values that were drawn randomly from within the defined bounds (cf. Table 1). Independent of initialization, the results again showed similar values of the material parameters and $R^{2*}$ distributions, and especially the derived material properties, thus suggesting that the observed heterogeneities are deterministic.

The results are also sensitive to other inevitable experimental uncertainties, which further complicate parameter estimation. Among the many causes of uncertainly, consistent experimental definition of a reference configuration, often taken to be the traction-free state, is challenging. Potential effects of these errors can be assessed by repeating the estimations for different values that define the reference configuration [38]. Our approach, using a near in vivo reference configuration, naturally reduces the uncertainly in comparison with measurements of traction-free configurations because of the extreme compliance of arteries at low loads.

Regional Variations in Material Properties.

Notwithstanding possible uncertainties in our characterizations, heterogeneities appeared to manifest both locally (based on nodal values) and regionally (based on the four regions so defined). In particular, steep variations appeared for some parameters, such as those meant to model the collagen fibers, whereas mild variations arose for other parameters, including those meant to model the elastic fibers. Considering the phenomenological nature of the model, however, one should not try to overinterpret the underlying reasons for these variations in parameter values, with or without knowledge of the underlying histological structure. Rather, it is best to focus on metrics such as energy storage and material stiffness (Figs. 4 and 5) when comparing material behaviors either regionally or from specimen-to-specimen. Additionally, to distinguish between uncertainty and true regional variations in material properties, regions should be defined with a significant number of data points (for local estimates) or patches (for regional estimates) to have appropriate statistical power and anatomical relevance (for instance, dorsal, ventral, top, and bottom halves).

The suprarenal aorta has significant perivascular support in vivo, namely, the spine and dorsal musculature. Interestingly, the energy stored upon pressurization in vitro was significantly lower on the dorsal than the ventral side for both tested samples. It thus seems that the capability of the dorsal side of the aorta to store energy, ultimately to be used to work on the blood during diastole, is potentially reduced throughout development due to this increased perivascular support. The values of circumferential and axial material stiffness tended to be higher near the axial boundaries and on the ventral side of the sample. Higher stiffness near the top (proximal) and bottom (distal) edge is likely an end-effect due to cannulation and pressurization of the sample at a fixed axial stretch; in contrast, the increased ventral stiffness tends to colocalize with regions of branch influence. The increased stiffness near branch locations could similarly result from the ligatures that are needed to enable mechanical testing. In particular, circumferential stiffness is often increased on the lateral sides of the branch region, consistent with the ligation at the branch ostium potentially playing a role upon pressurization. Increased axial stiffness at branch locations is likely compounded by the fact that axial stretch is influenced by the distance between the cannulation sutures. This effect can necessarily vary over the surface of the sample and lead to a reduced relative stretch at the branch locations and ultimately contribute to increasing the stiffness.

Coefficients of Determination.

Another fundamental question relates to the origin of regional variations for the $R^{2*}$ < 0.90 criterion, especially in sample A. This goodness-of-fit is related to the ability/inability of the model to capture the experimental response locally. Mismatches between model and data could be a source of bias for the identified parameters, hence we discarded patches where $R^{2*}$ is lower than 0.90. Discrepancies often localized close to cannulation ligatures or near branches (Fig. 2). Additionally, large central regions of discrepancy for sample A likely resulted, in part, from bending instabilities and associated changes in local mean curvature that occur in an inflated vessel maintained at a constant axial stretch [39]. Bending was even triggered at low pressures, for the suprarenal aorta is curved slightly upon excision. For this reason, the suprarenal abdominal aorta is probably one of the most challenging case studies for our novel identification method. Nevertheless, despite difficulties related to bending and the presence of branches, there was very good agreement between the myriad identified local behaviors and the global response of the same sample (Fig. 6). Moreover, strain energy and stiffness estimated from the standard biaxial tests (Table 2) were consistent with the center value of the regional distributions.

Recall that the biaxial loading was maintained for several minutes at each state to allow p-DIC image acquisition. Hence, in contrast to the continuous cyclic loading of the standard biaxial tests, the loading was incremental in the p-DIC tests. Direct comparisons between continuous and incremental loading protocols in separate standard biaxial tests on the same sample (not shown) revealed no difference in the measured pressure–diameter behavior, hence the difference in loading protocol did not appear to be a concern. We also checked whether a thick-wall model that delineates medial and adventitial properties would improve the coefficients of determination when compared to a membrane model. Again, however, this did not have a significant effect on the results (not shown). This finding is somewhat consistent with the wall thickness being at least 1 order of magnitude lower than radius upon pressurization (e.g., radius of 0.65 mm and thickness of 0.04 mm, on average), but also because both methods rely on measuring deformations or diameters at the outer surface and invoking incompressibility of the wall.

Conclusions

We submit that the present experimental–computational method for local arterial characterization represents another important step toward the ultimate goal of understanding better the structure–property relationships that underlie regional variations in material properties along the arterial tree and especially within many arterial lesions, including aortic aneurysms. Combining such findings with advances in growth and remodeling simulations (e.g., Refs. [40,41]) promises to improve our ability to predict subsequent mechano-adaptations or disease progression. Many challenges yet remain, however. Highly localized defects in wall structure, as, for example, localized deposits of calcium or pools of mucoid material, may play significant roles in initiating local failure processes including those that initiate intramural delamination [42,43]. Such defects could be difficult to identify even with sophisticated methods such as p-DIC and will likely require additional transmural imaging and layer-specific inverse methods. The present validation study provides a firm foundation upon which to build, however.

Appendix

The PVP is an integral expression of the equilibrium equations across a solid, which may be written quasi-statically as

$$\underset{P_{\text{int}}^{*}}{\underbrace{-{\int }_{\omega (t)}\mathit{\sigma }:(\mathbf{\nabla }\otimes {\mathit{\xi }}^{*})d\omega }}+\underset{P_{\text{ext}}^{*}}{\underbrace{{\oint }_{\partial \omega (t)}\mathit{T}.{\mathit{\xi }}^{*}ds}}=0$$ (A1)

where ${\mathit{\xi }}^{*}$ is a virtual velocity field defined across the volume of the solid (denoted $\omega (t)$), and $\mathbf{\nabla }\otimes {\mathit{\xi }}^{*}$ is the gradient of ${\mathit{\xi }}^{*}$. $\mathit{T}$ are the tractions across the boundary (surface denoted $\partial \omega (t)$), $P_{\text{int}}^{*}$ is the virtual power of internal forces, and $P_{\text{ext}}^{*}$ is the virtual power of external forces.

The PVP has been used for the identification of material properties since 1990 through the VFM, which is an inverse method based on the use of full-field deformation data [17,18]. The VFM was recently applied to the identification of uniform material properties in arterial walls [19] and will be extended herein to consider regional variations of the material properties. Hence, let us consider two virtual fields ${\mathit{u}}^{*}$ and ${\mathit{v}}^{*}$ defined across a given patch n

$${\mathit{u}}^{*}\left(\mathrm{\xi }\right)=\left[\frac{\left(1/{\mathrm{\kappa }}_n^1-h\right)\left(1/{\mathrm{\kappa }}_n^2-h\right)}{1/{\mathrm{\kappa }}_n^1-\left(1-\mathrm{\xi }\right)h}\frac{\left(1/{\mathrm{\kappa }}_n^1+1/{\mathrm{\kappa }}_n^2-2h\right)}{1/{\mathrm{\kappa }}_n^2-\left(1-\mathrm{\xi }\right)h}\right]\hspace{0.17em}{\mathit{n}}_{\mathit{n}}^{}$$ (A2)

$${\mathit{v}}^{*}=-\frac{x}{2}{\mathit{e}}_x-\frac{y}{2}{\mathit{e}}_y+z\hspace{0.17em}{\mathit{e}}_z$$ (A3)

where ${\mathrm{\kappa }}_n^1$ and ${\mathrm{\kappa }}_n^2$ are the average maximum and minimum principal curvatures, respectively. Therefore, $1/{\mathrm{\kappa }}_n^1$ is the radius of curvature on the outer surface along the direction of the maximum principal curvature, and $1/{\mathrm{\kappa }}_n^2$ is the radius of curvature on the outer surface along the direction of the minimum principal curvature. The radii of curvature at any position ξ between the inner ($\mathrm{\xi }=0$) and outer ($\mathrm{\xi }=1$) surfaces for the inner surface are then $1/{\mathrm{\kappa }}_n^1-(1-\mathrm{\xi })h$ and $1/{\mathrm{\kappa }}_n^2-(1-\mathrm{\xi })h$.

In this Appendix, we prove that Eq. (A1) written with ${\mathit{u}}^{*}$ yields Eq. (22) (Proof 1) and similarly Eq. (A1) written with ${\mathit{v}}^{*}$ yields Eq. (26) (Proof 2).

Proof 1.The gradient of ${\mathit{u}}^{*}$ may be written as follows:

$$\begin{array}{c}\mathbf{\nabla }\otimes {\mathit{u}}^{*}=\frac{\left(1/{\mathrm{\kappa }}_n^1-h\right)\left(1/{\mathrm{\kappa }}_n^2-h\right)\left(1/{\mathrm{\kappa }}_n^1+1/{\mathrm{\kappa }}_n^2-2h\right)}{\left(1/{\mathrm{\kappa }}_n^2-\left(1-\mathrm{\xi }\right)h\right){\left(1/{\mathrm{\kappa }}_n^1-\left(1-\mathrm{\xi }\right)h\right)}^2}\hspace{0.17em}{\mathit{g}}_n^1\otimes {\mathit{g}}_n^1\\ +\frac{\left(1/{\mathrm{\kappa }}_n^1-h\right)\left(1/{\mathrm{\kappa }}_n^2-h\right)\left(1/{\mathrm{\kappa }}_n^1+1/{\mathrm{\kappa }}_n^2-2h\right)}{\left(1/{\mathrm{\kappa }}_n^1-\left(1-\mathrm{\xi }\right)h\right){\left(1/{\mathrm{\kappa }}_n^2-\left(1-\mathrm{\xi }\right)h\right)}^2}\hspace{0.17em}{\mathit{g}}_n^2\otimes {\mathit{g}}_n^2\\ -[\frac{\left(1/{\mathrm{\kappa }}_n^1-h\right)\left(1/{\mathrm{\kappa }}_n^2-h\right)\left(1/{\mathrm{\kappa }}_n^1+1/{\mathrm{\kappa }}_n^2-2h\right)}{\left(1/{\mathrm{\kappa }}_n^2-\left(1-\mathrm{\xi }\right)h\right){\left(1/{\mathrm{\kappa }}_n^1-\left(1-\mathrm{\xi }\right)h\right)}^2}+\frac{\left(1/{\mathrm{\kappa }}_n^1-h\right)\left(1/{\mathrm{\kappa }}_n^2-h\right)\left(1/{\mathrm{\kappa }}_n^1+1/{\mathrm{\kappa }}_n^2-2h\right)}{\left(1/{\mathrm{\kappa }}_n^1-\left(1-\mathrm{\xi }\right)h\right){\left(1/{\mathrm{\kappa }}_n^2-\left(1-\mathrm{\xi }\right)h\right)}^2}]\hspace{0.17em}{\mathit{n}}_n\otimes {\mathit{n}}_n\end{array}$$ (A4)

Substituting in and evaluating the integral expression for $P_{\text{int}}^{*}$ (cf. Eq. (A1))

$$\begin{array}{c}{P}_{\mathrm{int}}^{*}\left(t\right)=-h\left(t\right)\left(1/{\mathrm{\kappa }}_n^1\left(t\right)-h\left(t\right)\right)\left(1/{\mathrm{\kappa }}_n^2\left(t\right)-h\left(t\right)\right)\left(1/{\mathrm{\kappa }}_n^1\left(t\right)+1/{\mathrm{\kappa }}_n^2\left(t\right)-2h\left(t\right)\right)\\ {\int }_0^1\left(\frac{{\sigma }_{11,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{\left(1/{\mathrm{\kappa }}_n^2\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right){\left(1/{\mathrm{\kappa }}_n^1\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right)}^2}+\frac{{\sigma }_{22,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{\left(1/{\mathrm{\kappa }}_n^1\hspace{0.17em}\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right){\left(1/{\mathrm{\kappa }}_n^2\hspace{0.17em}\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right)}^2}\right)A_n\left(t,\mathrm{\xi }\right)d\mathrm{\xi }\end{array}$$ (A5)

where $A_n(t,\mathrm{\xi })$ is the area of patch n at radial position ξ and may be written as

$$A_n(t,\mathrm{\xi })=(1/{\mathrm{\kappa }}_n^1(t)-(1-\mathrm{\xi })h(t))(1/{\mathrm{\kappa }}_n^2(t)-(1-\mathrm{\xi })h(t)){\Theta }_n^1(t){\Theta }_n^2(t)$$

where ${\Theta }_n^1$ and ${\Theta }_n^2$ are the two angles defining the angular sector of patch $n$ along the directions of the maximum and minimum principal curvatures, respectively. Introducing the expression of $A_n(t,\mathrm{\xi })$ into Eq. (A5), we obtain

$$\begin{array}{c}{P}_{\mathrm{int}}^{*}\left(t\right)=-h\left(t\right)\left(1/{\mathrm{\kappa }}_n^1\left(t\right)-h\left(t\right)\right)\left(1/{\mathrm{\kappa }}_n^2\left(t\right)-h\left(t\right)\right)\left(1/{\mathrm{\kappa }}_n^1\left(t\right)+1/{\mathrm{\kappa }}_n^2\left(t\right)-2h\left(t\right)\right){\Theta }_n^1\left(t\right){\Theta }_n^2\left(t\right)\\ {\int }_0^1\left(\frac{{\sigma }_{11,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{\left(1/{\mathrm{\kappa }}_n^1\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right)}+\frac{{\sigma }_{22,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{\left(1/{\mathrm{\kappa }}_n^2\hspace{0.17em}\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right)}\right)d\mathrm{\xi }\end{array}$$ (A6)

Regarding the virtual work on the boundaries, shear stresses are null so only the virtual work of the internal pressure needs to be considered

$$P_{\text{ext}}^{*}(t)=P(t)(1/{\mathrm{\kappa }}_n^1(t)-h(t))(1/{\mathrm{\kappa }}_n^2(t)-h(t)){\Theta }_n^1(t){\Theta }_n^2(t)(1/{\mathrm{\kappa }}_n^1(t)+1/{\mathrm{\kappa }}_n^2\hspace{0.17em}(t)-2h(t))$$ (A7)

So, using Eq. (A1), we have

$$P\left(t\right)=h\left(t\right){\int }_0^1\left(\frac{{\sigma }_{11,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{\left(1/{\mathrm{\kappa }}_n^1\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right)}+\frac{{\sigma }_{22,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{33,n}^w\left(t,\mathrm{\xi }\right)}{\left(1/{\mathrm{\kappa }}_n^2\hspace{0.17em}\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right)}\right)d\mathrm{\xi }$$

Proof 2. A second virtual field is required here. Indeed, even if the artery shape is not a perfect cylinder, ${\mathrm{\kappa }}_n^2$ is globally the curvature along the axis of the artery and may take very small values at most of the patches. The result is that ${\sigma }_{zz,n}^w$ has little influence in Eq. (22), leading to almost no sensitivity to a material parameter such as $c_n^a$. To address this issue, a second virtual field involving ${\sigma }_{zz,n}^w$ even in the patches where ${\mathrm{\kappa }}_n^2\cong 0$ is proposed and will involve the measured axial load $f(t)$. The simplest virtual field both satisfying these requirements and zeroing the virtual work of the hydrostatic pressure is given by ${\mathit{v}}^{*}$ (cf. Eq. (A3)). The gradient may be written as

$$\mathbf{\nabla }\otimes {\mathit{v}}^{*}=-\frac{1}{2}\hspace{0.17em}{\mathit{e}}_x\otimes {\mathit{e}}_x-\frac{1}{2}\hspace{0.17em}{\mathit{e}}_y\otimes {\mathit{e}}_y+{\mathit{e}}_z\otimes {\mathit{e}}_z$$ (A8)

We assume here that the same internal virtual work is shared along the circumferential direction

$$P_{\mathrm{int}}^{*}\left(t\right)=-{\int }_{\omega \left(t\right)}\mathit{\sigma }:\left(\mathbf{\nabla }\otimes {\mathit{v}}^{*}\right)d\omega =-\frac{1}{K}{\int }_{\text{whole}\hspace{0.5em}\text{circumference}}\mathit{\sigma }:\left(\mathbf{\nabla }\otimes {\mathit{v}}^{*}\right)d\omega$$

where $K$ is the number of patches along the circumferential direction.

Then, we have

$$\begin{array}{c}{P}_{\text{int}}^{*}\left(t\right)=-\frac{1}{K}{\int }_{z_n-b/2}^{z_n+b/2}{\int }_0^{2\pi }{\int }_{r_{}^o-h}^{r_{}^o}\left[{\sigma }_{zz,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{xx,n}^w\left(t,\mathrm{\xi }\right)/2-{\sigma }_{yy,\mathrm{n}}^w\left(t,\mathrm{\xi }\right)/2\right]drrd\theta dz\\ P_{\mathrm{int}}^{*}\left(t\right)=-\frac{\pi }{K}b\left(t\right)h\left(t\right){\int }_0^1\left[2{\sigma }_{zz,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{xx,n}^w\left(t,\mathrm{\xi }\right)-{\sigma }_{yy,n}^w\left(t,\mathrm{\xi }\right)\right]\left[r_{}^o\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right]d\mathrm{\xi }\end{array}$$ (A9)

where $r_{}^o$ is the average radius of the cross section of the considered patch, and $b$ is the length of the patch in the $z$ direction.

Regarding the virtual work across the boundaries, shear stresses are again neglected and we have only to consider the virtual work of the internal pressure on the inner surface and the virtual work of the axial stress. We assume that the external virtual work is also shared along the circumferential direction, yielding

$$P_{\text{ext}}^{*}\left(t\right)={\oint }_{\partial \omega \left(t\right)}\mathit{T}\cdot {\mathit{v}}^{*}ds=\frac{1}{K}{\oint }_{\text{whole}\hspace{0.17em}\text{circumference}}\mathit{T}\cdot {\mathit{v}}^{*}ds$$

Then, we have

$$\begin{array}{c}{P}_{\text{ext}}^{*}\left(t\right)=\frac{1}{K}\left[-\frac{P\left(t\right)}{2}b\left(t\right)2\pi {\left[r_{}^o\left(t\right)-h\left(t\right)\right]}^2+b\left(t\right)h\left(t\right){\int }_0^1{\sigma }_{zz,n}^w\left(t,\mathrm{\xi }\right)2\pi \left[r_{}^o\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right]d\mathrm{\xi }\right]\\ P_{\text{ext}}^{*}\left(t\right)=\frac{b\left(t\right)}{K}\left[-P\left(t\right)\pi {\left[r_n^o\left(t\right)-h\left(t\right)\right]}^2+\left(2\pi h\left(t\right){\int }_0^1{\sigma }_{zz,n}^w\left(t,\mathrm{\xi }\right)\left[r_{}^o\left(t\right)-\left(1-\mathrm{\xi }\right)h\left(t\right)\right]d\mathrm{\xi }\right)\right]\end{array}$$ (A10)

We recognize in the bracket of Eq. (A10) the formula of the axial load [37,38] and we eventually obtain

$$P_{\text{ext}}^{*}\left(t\right)=\frac{b\left(t\right)}{K}f\left(t\right)$$ (A11)

Thus, using Eq. (A1), we have

$$f(t)=\pi h(t){\int }_0^1[2{\sigma }_{zz,n}^w(t,\mathrm{\xi })-{\sigma }_{xx,n}^w(t,\mathrm{\xi })-{\sigma }_{yy,n}^w(t,\mathrm{\xi })][r_{}^o(t)-(1-\mathrm{\xi })h(t)]d\mathrm{\xi }$$