A Statistical Approach Reveals Designs for the Most Robust Stochastic Gene Oscillators

Abstract

The engineering of transcriptional networks presents many challenges due to the inherent uncertainty in the system structure, changing cellular context, and stochasticity in the governing dynamics. One approach to address these problems is to design and build systems that can function across a range of conditions; that is they are robust to uncertainty in their constituent components. Here we examine the parametric robustness landscape of transcriptional oscillators, which underlie many important processes such as circadian rhythms and the cell cycle, plus also serve as a model for the engineering of complex and emergent phenomena. The central questions that we address are: Can we build genetic oscillators that are more robust than those already constructed? Can we make genetic oscillators arbitrarily robust? These questions are technically challenging due to the large model and parameter spaces that must be efficiently explored. Here we use a measure of robustness that coincides with the Bayesian model evidence, combined with an efficient Monte Carlo method to traverse model space and concentrate on regions of high robustness, which enables the accurate evaluation of the relative robustness of gene network models governed by stochastic dynamics. We report the most robust two and three gene oscillator systems, plus examine how the number of interactions, the presence of autoregulation, and degradation of mRNA and protein affects the frequency, amplitude, and robustness of transcriptional oscillators. We also find that there is a limit to parametric robustness, beyond which there is nothing to be gained by adding additional feedback. Importantly, we provide predictions on new oscillator systems that can be constructed to verify the theory and advance design and modeling approaches to systems and synthetic biology.

A major challenge facing the progress of synthetic biology is the design and implementation of systems that function in the face of fluctuating cellular environments. While it is widely accepted within the field that the task of constructing and rewiring pathways is tractable, predicting in silico how an implemented system will behave in vivo under different cellular conditions remains a huge challenge.¹ Robust systems perform their function over a wide range of parameters and external influences. If we could design and build synthetic systems that are robust, then not only would the systems have a higher probability of functioning, but we would also enhance their predictability. Robustness in the context of biological systems has been intensively studied for almost two decades.²⁻⁶ Approaches to studying this in biological systems often utilize the frameworks of feedback and robust control.⁷ It is well-known that feedback mechanisms can increase the robustness of a biological system,^8,9 and there are trade-offs between robustness and performance, fragility, and efficiency.^10,11 Although some biological systems have been shown to be structurally robust—that is the underlying biochemical rate parameters have little effect on the system stability properties¹²—in general we expect system behavior to depend heavily on the biochemical parameters.¹³

Biological oscillators have been studied extensively as they form the core of many crucial biological processes such as circadian rhythms and the cell cycle. Oscillating systems also serve as a model for the understanding and engineering of complex and emergent phenomena. Various synthetic systems have been implemented both in vivo and in vitro.¹⁴⁻²⁰ More complex behaviors have been constructed, enabling synchronization over multiple scales, and entrainment by external signals.²¹⁻²³ There has been much theoretical study of biological oscillators (for reviews see refs (24−26)). Specific work has been done on noise attenuation,²⁷ motifs capable of oscillation,²⁸⁻³¹ robustness,³²⁻³⁴ and the role of positive and negative feedback.^35,36 Feedback in natural circadian oscillators has also been studied.^37,38

Despite this body of work, a comprehensive study of the robustness of transcriptional oscillators has not been performed because of the technical challenges it poses. Traditional mathematical approaches can elucidate general design principles and are of great importance²⁵ but these techniques generally simplify systems down to a handful of parameters. More contemporary methods can also explore model and phenotype space and are less restricted in model size,^31,39 but they rely on the analysis of deterministic dynamics and cannot handle the full complexity of realistic stochastic biological systems. Therefore, to develop more predictable design and modeling frameworks that can calculate realistic estimates of system properties, including robustness, requires approaches that can handle a large number of parameters, parametric uncertainty, and stochastic dynamics. This can be achieved using sequential Monte Carlo methods.^40,41 Here we extend the Monte Carlo framework to include model space exploration. The novelty in our approach is that the algorithm spends time in models and parameters in direct proportion to their robustness, and thus focuses in on interesting regions of joint model-parameter space. This avoidance of enumeration of all possibilities allows us to address more interesting questions and to assess robustness in a quantitative manner.

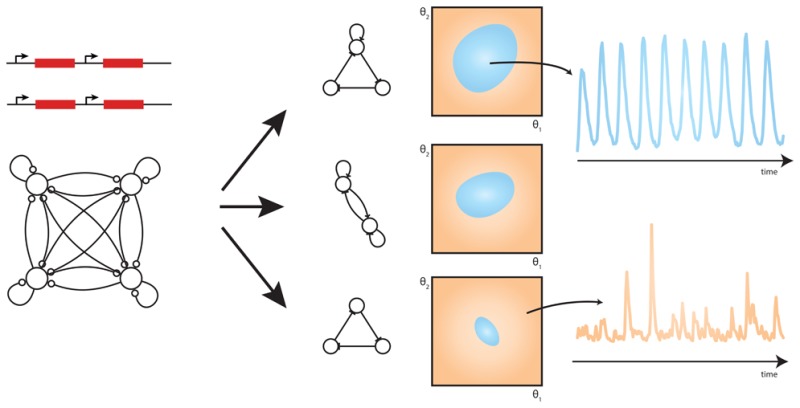
We apply this novel framework to investigate the robustness of transcriptional oscillators, an outline of which is given in Figure 1. We examine two main questions regarding the robustness of stochastic transcriptional oscillators: Can we build genetic oscillators that are more robust than those already constructed? Can we make genetic oscillators arbitrarily robust? We find that the most robust two-gene oscillators that can provide regular oscillations are of a type already constructed.¹⁷ We also examine the ring oscillator—the repressilator being the classic synthetic implementation¹⁴—and find that different activation reactions, in addition to positive autoregulation,³⁵ can increase its robustness. We also determine the topologies that give rise to the most robust three-gene systems and find that in general they are more robust than the simple two gene and ring oscillators. The frequency, amplitude, and robustness of all transcriptional oscillators, independent of topology, depend strongly on the rates of degradation of the species involved. Finally we find that the number of regulatory interactions increases oscillator robustness up to a plateau, beyond which there is no increase in robustness, which has wide implications for the construction of complex synthetic systems.

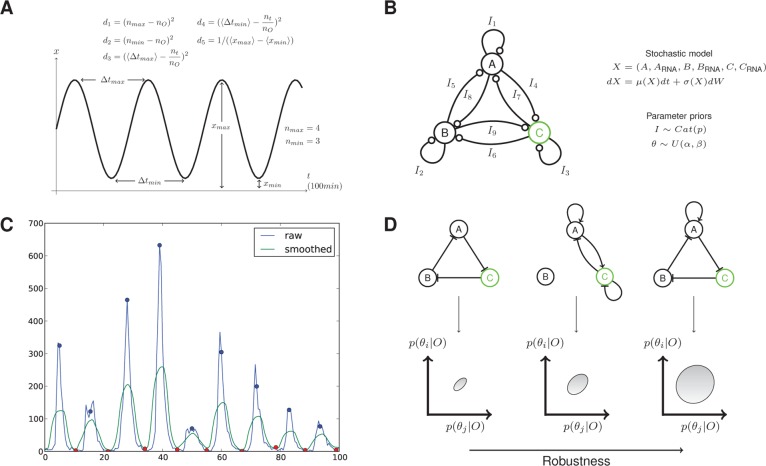
Figure 1.

Outline of the method. (A) The objective behavior is specified through a set of summary statistics and distances on the summaries (see Materials and Methods for a description of the terms). (B) Model space is defined through a fully connected network. A mapping from the graphical network to a stochastic model is defined together with a prior on the parameters and priors on the allowed networks. (C) Simple signal processing methods are used to extract features from model simulations. The blue and red circles indicate identified maxima and minima, respectively. (D) As the algorithm proceeds the (multidimensional) objective is achieved via small increments using sequential Monte Carlo. The final output of the algorithm is a set of models that satisfy the objective and maximize robustness.

Results and Discussion

The Most Robust Two-Node Oscillators Combine Positive and Negative Autoregulation

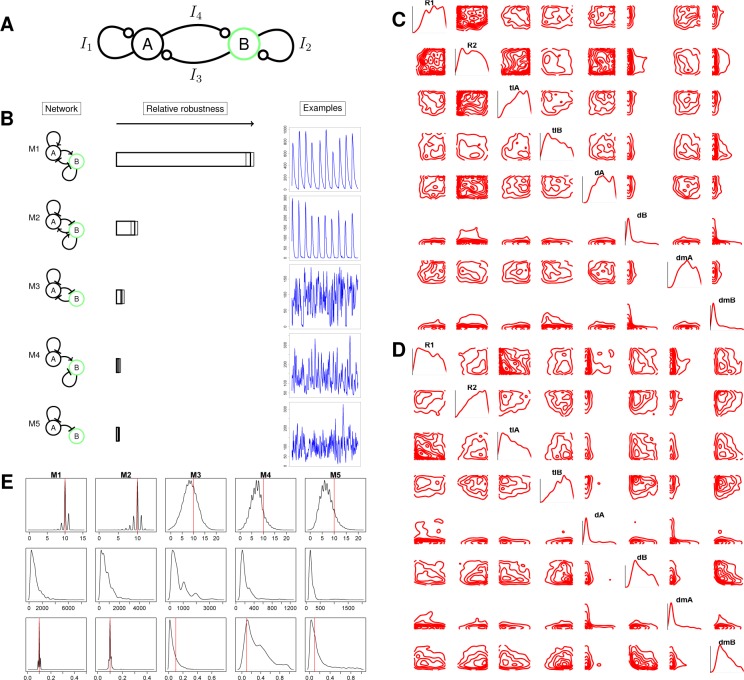
We searched model space for the most robust two-node oscillators and considered all possible regulatory interactions resulting in 3⁴ = 81 different models (Figure 2A). We found that only five models were capable of oscillations at the specified frequency (Materials and Methods), which we denote by M1–5 (Figure 2B). M1 and M2, which are mirror images, account for around 93% of the posterior model space and have the structure of an amplified negative feedback loop with negative autoregulation on the repressor and positive autoregulation on the activator. The other three systems all contain negative autoregulation of protein A (the protein that does not serve as the output), a well-known oscillatory motif, but show high levels of stochasticity. Interestingly the topology represented by M1 and M2 formed the basis for the robust oscillator constructed by Stricker et al.^17,42 We also note the absence of the delayed negative feedback oscillator with no negative autoregulation on the repressor, which is consistent with the observation that it cannot produce sustained oscillations.^15,20,43 The last oscillator system, denoted here by M5, has also been constructed and shown to produce more stochastic behavior than the amplified negative feedback topology of M1 and M2.¹⁷ These findings demonstrate that the modeling framework can reconstitute empirical findings in real synthetic oscillators.

Figure 2.

The most robust two-gene oscillators. (A) The regulatory interactions considered for the systems. The output protein, where oscillations are required, is shown in green. (B) The most robust two-node oscillators. The error bars indicate the variability in the marginal model posteriors over three separate runs (minimum, median, maximum). On the right are representative example time series of the time course behavior. (C,D) Posterior parameter distributions for the top two models, M1 and M2, for production, translation, and degradation rates of proteins A and B (R₁, R₂, tl_A, tl_B, d_A, d_B) and the degradation rates of A_mRNA and B_mRNA (d_mA, d_mB). The posteriors are plotted on their prior range of (0,10000) for the production rates and (0,10) for the decay rates. (E) Model checking of the stochastic systems by resampling and resimulation under the posterior distribution. The top, middle, and bottom plots correspond to the number of oscillations, the amplitude, and the maximal frequency of the Fourier spectrum, respectively.

Since our approach examines the dynamics of a specified protein (in this case B), we can elucidate how targeting different output nodes affects robustness. In the two-node oscillator we see that system M1 is around 8 times more robust than system M2 (Bayes factor ≈ 8) despite the fact that the only difference is the output node. This can be understood in terms of the dynamics of the relaxation oscillator. The repressor generally has slower dynamics and reaches higher numbers of mRNA and protein molecules in comparison to the activator (Supplementary Figure 4). Placing the output on the activator (M2) and requiring a minimum amplitude on the resultant oscillations forces the levels of repressor to reach a higher amplitude than is necessary when the output is placed on the repressor (M1). This can also be seen by examining the system size (total number of mRNA and protein molecules) which is larger in M2 (Supplementary Figure 4). These additional requirements on the dynamics constrains the parameters of M2. The one and two-dimensional marginal posteriors for a subset of the parameters are given for the two oscillator systems in Figure 2C,D. The parameter posterior distributions for M1 are closer to their prior distributions, with tl_A, tl_B, d_A, and d_mA appearing to be virtually unconstrained. These flat distributions indicate that a larger fraction of the parameter space in M1 can give rise to oscillations when compared to M2. We also note that M2 requires a higher promoter strength (R₂) upstream of gene B. These posterior distributions can also be used to aid the design process by providing information on the required biochemical properties to create functional and robust systems.

Defining oscillations in stochastic systems is nontrivial,¹⁷ and separating true oscillators from excitable systems can be difficult. To investigate the stochasticity of the five systems, and whether they are truly oscillators, we applied a statistical model checking procedure, whereby the posterior parameter distributions are resampled and the systems resimulated to examine the resultant performance. Figure 2E shows the results of the resampling and recalculation of the number of oscillations (top) and amplitude (middle). M1 and M2 have a large peak at ten pulses in the 100 min time period, showing a consistent and reliable performance. In contrast M3–M5 show much wider distributions indicating that they are more stochastic. There are also differences between the oscillator amplitude properties with M4 and M5 showing lower amplitude oscillations. To verify the frequency properties in an unbiased manner we also calculated the maximal frequency of the Fourier spectrum, which was not included in the objective summary statistics (Figure 2E bottom). Taken together, these results suggest that M1 and M2 have very reproducible frequency properties, both M4 and M5 are true oscillators albeit with high stochasticity and low amplitude, and M3 is most likely to be an excitable system. From an engineering point of view, we are only interested in regular oscillators, and so can exclude M3-M5 as failing our design objectives.

To examine how the robustness changes under specification of the objective behavior, we compared the two-node systems under the objectives S1 (fixed frequency) and S2 (variable frequency, regular oscillations) (Supplementary Figure 5). We found almost identical results indicating that in this particular system, and under our prior assumptions, the difference between these objectives is minimal.

Different Activation Reactions Increase the Robustness of the Ring Oscillator

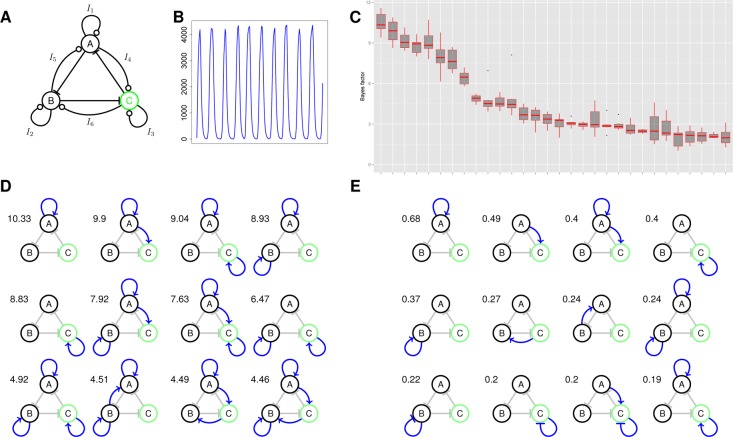
Next we examined how one can increase the robustness of the three gene ring oscillator by the incorporation of additional feedback interactions. The setup for the model is shown in Figure 3A. The three negative feedback interactions of the standard ring oscillator were fixed, with additional activating and repressing interactions allowed, giving a model space of 3⁶ = 729 models. The distribution of the Bayes factor with respect to the standard ring oscillator for the 30 most robust topologies is shown in Figure 3C. The 12 most robust networks are shown in Figure 3D. Additional positive autoregulation clearly increases the robustness of the ring oscillator by as much as an order of magnitude (Bayes factor ≈ 10 in Figure 3C). This is in agreement with previous work that showed that a ring oscillator with a single positive auto regulatory feedback loop could achieve more robust oscillatory behavior than the ring oscillator with or without a single negative autoregulatory feedback loop.³⁵ The benefit of our approach is that we can quantitatively estimate the gain in modifying the original design and judge its worth; a Bayes factor of >10 indicates strong evidence. We also find that including an additional activation from gene A to C can significantly increase robustness. This can be seen more clearly by adopting the notion of inclusion probabilities, which rank the regulatory interactions by their probability of occurring in the ensemble of systems in the posterior distribution (Figure 3E). Here we clearly see that including autoregulation on gene A has the best chance of increasing robustness, followed by activation from gene A to C. Interestingly this type of activating interaction within a ring oscillator was found in the Arabidopsis circadian oscillator.³⁷

Figure 3.

Increasing the robustness of the ring oscillator. (A) The regulatory interactions considered for the ring oscillator system. The output protein, where oscillations are required, is shown in green. (B) A representative time series from this system with an oscillation every 10 min. (C) The distribution of the 30 most robust topologies. In the box plot, the central bar indicates the median estimate and the upper and lower quartiles correspond to the top and bottom of the box. The points correspond to outliers. The y axis represents the Bayes factor with respect to the ring oscillator (here corresponding to the system with no additional feedback interactions.) (D) The most robust 12 oscillators. The number given next to each network gives the median Bayes factor compared to the basic ring oscillator. (E) The top 12 regulatory interactions ranked by inclusion probability.

We created a graph in which nodes represent autoregulatory motifs and edges connect nodes related by the addition or removal of a single autoregulatory interaction (Supplementary Figure 6). We find that positive autoregulation is associated strongly with robustness, with negative autoregulation associated with the least robust systems. Interestingly the relationship between the addition of positive autoregulatory feedback and robustness is nonmonotonic and the addition of three such interactions appears to decrease robustness significantly. Examination of the posterior parameter distributions for the production and decay rates of the ring oscillator and the ring oscillator with positive autoregulation on gene A (Supplementary Figure 7), shows that for these systems to function at this oscillator frequency, the values of the decay rates are very important. In the former, the decay rates of protein C and all mRNA species are constrained to be high. In the latter only the decay rates for C (protein and mRNA) are constrained to be high. Interestingly this is in stark contrast to the two-node oscillators which in general need to have low decay rates for the mRNA and protein species. We again examined robustness under the objectives S1 (fixed frequency) and S2 (variable frequency, regular oscillations) and obtained very similar results (Supplementary Figure 8). We also directly examined the correlation between model robustness under the two objectives, which we found to be reasonably high (Pearson correlation 0.76, Supplementary Figure 9), though the agreement increases with robustness. The posterior distributions of the species decay terms show looser requirements on the decay rates of mRNA and protein species of gene C.

A natural question that arises is how does the robustness of the two-gene and ring oscillators compare. We addressed this by using a reduced network topology and prior model space (Figure 4). We find that the two-gene oscillator is more robust than the basic ring oscillator though only weakly (Bayes factor ≈ 2). However, the addition of the positive feedback autoregulatory loop clearly out performs both with a Bayes factor of ≈ 10.8 and 5.7 compared to the ring oscillator and two-node oscillator, respectively.

Figure 4.

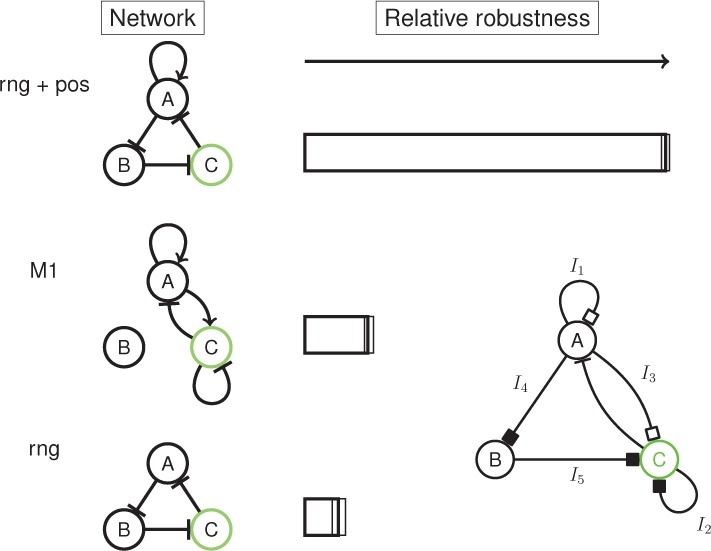
Direct comparison of the relative robustness of the hasty oscillator, the ring oscillator, and the ring oscillator with a single positive feedback. Inset: The network used for the direct comparisons. Black squares represent either none or negative regulation ({−1,0}) and white squares represent either none or positive regulation ({0,+1}).

Robustness of Three-Node Oscillators Is Achieved through Combinations of Oscillating Motifs

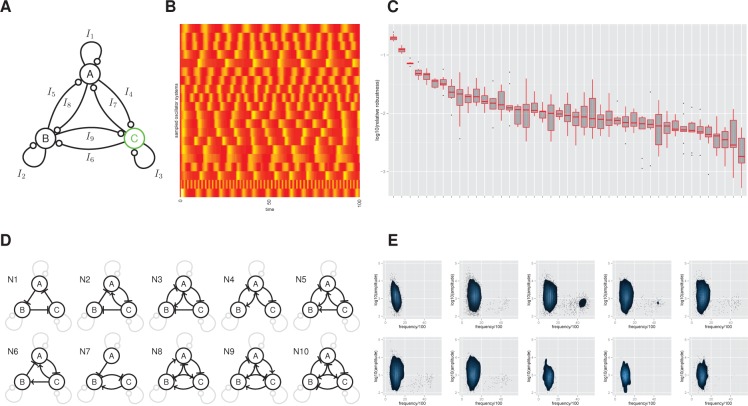
In the previous section we investigated ring oscillators, which are a particular case of the more general three-node oscillator. Here we directly addressed the question of which three gene oscillators give the most robust systems. Rather than considering individual topologies, we explored the more general landscape of possible systems by examining the core architectures. We considered the general three-node network given in Figure 5A with 48 parameters, but restricted the model prior space by setting the prior probability of half the symmetric systems to be zero, resulting in 9963 independent networks (see Supporting Information). Given the similar results between the fixed frequency objective (S1) and the regular oscillation objective (S2), we used the latter (the phenotypes are shown in the heat map in Figure 5B). The resultant systems were uniquely classified into categories dependent on the core architecture (i.e., ignoring the autoregulatory interactions). We found in total 43 out of a possible 138 architectures that were reproducible, with robustness spanning over 2 orders of magnitude. Figure 5C shows the relative robustness of these categories, scaled by the number of topologies in each category. The top ten network topologies are shown in Figure 5D and roughly span an order of magnitude in robustness (Bayes factor ≈ 10).

Figure 5.

The most robust three-gene networks. (A) The regulatory interactions considered for the three-node oscillator system. The output protein, where oscillations are required, is shown in green. (B) Example phenotypes of the resulting oscillators. Each row of the heat map represents one sampled oscillator system. The yellow and red colors depict the high and low amplitude regions, respectively. (C) Motif robustness analysis. Each network is classified into a unique category based upon its core network topology. In the box plot, the central bar indicates the median estimate of relative robustness and the upper and lower quartiles correspond to the top and bottom of the box. The points correspond to outliers. (D,E) The 10 most robust three-node core topologies together with their frequency-amplitude properties.

We find that the ring oscillator core architecture is the most robust, which is a form of delayed negative feedback oscillator. This is followed by topology N2 that can be referred to as an incoherently amplified negative-feedback loop (IANF),²⁵ and then N3, which is a combination of a delayed negative feedback (ring) oscillator and two amplified negative feedback oscillators. The N10 system can be considered as as a ring oscillator with additional delayed negative feedback; a design principle that has been shown to be at the core of the mammalian circadian oscillator.^44,45 More generally, we observe that the motif of mutual activation and repression X → Y −| X is an important feature of these high frequency oscillators.

Upon examination of the number of regulatory interactions within each category (Supplementary Figure 10) we can see that the top network, N1, contains the least number of edges (or low complexity). This topology scores highly because our definition of robustness automatically takes into account complexity, and essentially scores the robustness per biochemical reaction. In contrast, networks N8–N10, contain a maximal six interactions in their core, plus contain further autoregulatory loops taking the total number of interactions to nine, indicating a fully connected network. These are penalized for containing a high number of interactions. Since our categories represent averages over the autoregulatory interactions we examined how negative, positive, and mixed autoregulation featured within a topology by counting the number of motifs in which these occurred (Supplementary Figure 10). We found that practically every topology contains some form of autoregulation. In particular, positive autoregulation dominates in N1 and N2 as expected. However, N3–N7 contain varying amounts of mixed autoregulatory interactions in addition to pure positive autoregulation, while in N8–N10, mixed and pure negative autoregulation dominate. These differences between categories are expected since some core topologies, for example N4, are not expected to oscillate without any additional autoregulatory interactions.

To investigate how the frequency and amplitude properties of the robust oscillators depend on the core architecture we resampled the posteriors for the top 10 core topologies and resimulated the dynamics (Figure 5E). We found high reproducibility in the stochastic dynamics (Supplementary Figure 11). No correlations between amplitude and frequency were apparent, indicating there are no explicit trade-offs within these categories. There appears to be a natural frequency range with these parameter priors that gives oscillations with a time period of between 5 and 20 min, and an amplitude range spanning 2 orders of magnitude. Interestingly, although we required an average amplitude greater than 100 protein molecules, most oscillators have an amplitude much higher than this. This implies that the frequency and amplitude are related, and that requiring a specific frequency implies a specific amplitude range. Here the oscillators are constrained by their frequency properties, which gives rise to oscillators with amplitude properties that easily satisfy our constraints. In topologies N3–N5, and to a lesser extent N2, N6, and N7, we did observe high variability in the frequency, which implies a high frequency tunability. This is obtained through the addition of positive feedback within the core topology, which effectively speeds up the amplified negative feedback. We investigated this phenomenon further by performing a regression of all the parameters on oscillator frequency and found that the most significant parameters were the degradation rates for the mRNA and protein species of B and C, plus the edges I₇ and I₉ (Supplementary Figure 12). The highest frequency oscillators are formed from a combination of high degradation rates and positive (activating) I₇ and I₉

Both the Robustness and the Phenotype of the Oscillators Depend on Degradation Rates

Given the strong dependence of frequency on degradation rates we decided to investigate how changing the prior assumptions on degradation rates affected our analysis of the three-node categories. We changed the prior so that protein and mRNA degradation rates were reduced by an order of magnitude with prior distribution of U(0, 1) min^–1. Figure 6A,B shows the distribution of relative robustness and the ten most robust topologies. Interestingly, the ring oscillator is much less robust under this scenario and is ranked 21st, which verifies the observation that this topology requires very high degradation rates to function robustly. We see a corresponding increase in positive feedback within the core topologies which can counteract the smaller degradation rates.

Figure 6.

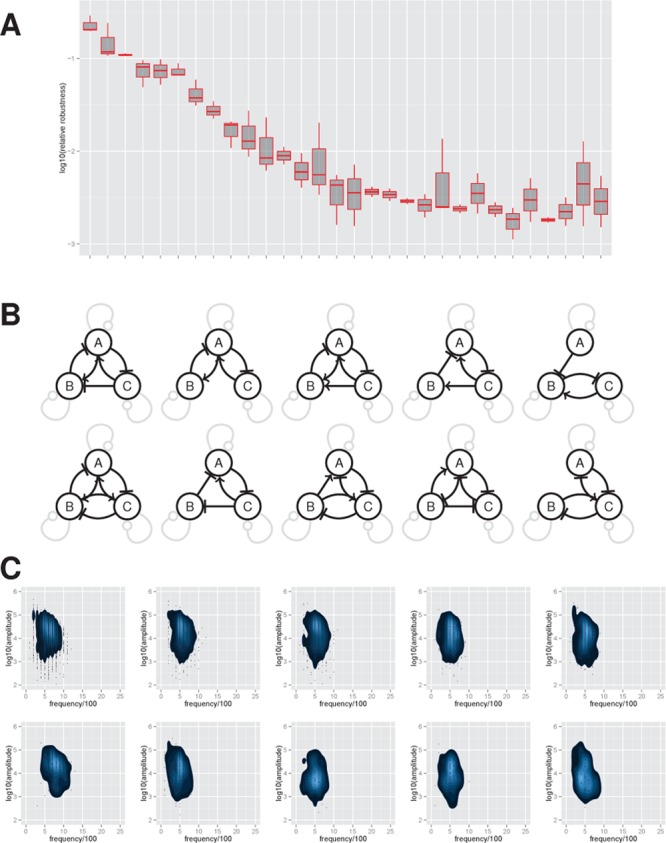
Low frequency oscillators. Reanalysis of the three-node networks with a reduced prior on the decay rates of the mRNA and protein species. (A) The distribution of the 30 most robust topologies. In the box plot, the central bar indicates the median estimate and the upper and lower quartiles correspond to the top and bottom of the box. (B,C) The 10 most robust three-node core topologies together with their frequency–amplitude properties.

The frequency and amplitude properties of these oscillators are shown in Figure 6C. We see a doubling in oscillator time period, accompanied by an increase in species number, albeit with a similar amplitude range of 2 orders of magnitude (see Supplementary Figure 13). We also note the oscillators that previously showed a large variation in frequency no longer demonstrate this behavior. The frequency and amplitude properties of four different oscillator systems (two-node, ring, three-node, and four-node) show no significant differences in oscillator frequency and amplitude (see Supplementary Figure 13). These findings suggest that degradation rates are key in defining the frequency and amplitude properties of general oscillators and also that reducing frequency generally implies an increase in amplitude.

That robustness and phenotype of oscillators are affected by degradation rates should come as no surprise. Wong et al. showed that the robustness of their gene-metabolic oscillator depended on the nature of protein degradation,⁴⁶ and Stricker et al. added ssrA tags to construct their robust two-gene oscillator.¹⁷ What we have shown is that this dependence applies to a large class of transcriptional oscillators. It also demonstrates the importance of engineering protein degradation in real systems,⁴⁷ which could be applied to the construction of robust oscillators and synthetic circuits more generally.

Increasing the Number of Regulatory Interactions Increases Robustness

While it is known from quantitative biology that feedback interactions can increase robustness,^8,9,35,38 these studies have mostly focused on a small number of regulatory interactions. Here we examined directly how the robustness of the oscillator systems change as the number of regulatory interactions increases (Figure 7). To do this we examined oscillators formed from a four node interconnected network with 76 parameters (Figure 7A). Again we precomputed the prior on the model space by removing mirror images (transforming only one node) and removing unconnected networks (topologies where the output node was unconnected), which resulted in 7 559 460 networks (see Supporting Information). We calculated the relative robustness by taking the ratio of the model posterior probability and the induced prior due to the number of topologies with the given number of interactions (Supplementary Figure 14).

Figure 7.

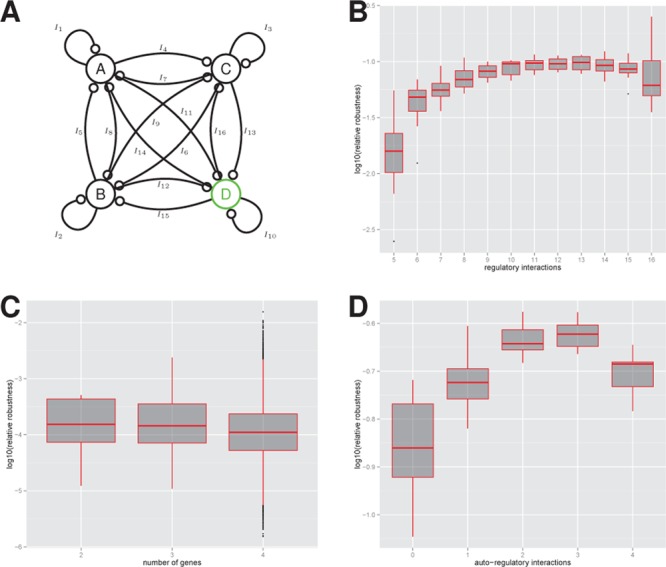
Analysis of robustness and system topology. (A) The regulatory interactions considered for the four-node oscillator system. Oscillator robustness as a function of (B) total number of regulatory interactions, (C) the number of genes and (D) the number of autoregulatory interactions. In the box plots, the central bar, top and bottom of the box indicates the median, upper, and lower quartiles, respectively. The points correspond to outliers.

We find that robustness increases with the number of regulatory interactions but only up to around 10 or 11 where it reaches a plateau (Figure 7B). The Bayes factor between 5 interactions and 11 interactions is around 6.5 indicating a substantial increase in robustness. After the plateau is reached, any increase in robustness by adding regulatory interactions approximately equals the increase in the (multidimensional) volume of parameter space. Another way to express this is that the robustness per biochemical parameter is constant. The implications of this are that while increasing the number of interactions above 11 will possibly produce systems that have an increased level of robustness, the increase in robustness will be directly proportional to the complexity (number of interactions). If we assume that increased complexity comes at a high price (as is generally the case in synthetic biology) then we may conclude that systems with 10 or 11 interactions provide a best case scenario (when constrained to a maximum of four genes). We may also speculate that a similar trade-off could apply to naturally evolved systems and could be investigated further. Interestingly we do not see a strong dependence of robustness on the number of genes in the system (Figure 7C). We also split the regulatory interactions into those that comprise the core topology and those that comprise autoregulatory interactions (Supplementary Figure 14, Figure 5D). We see a similar plateau in the number of core regulatory interactions but see a drop in robustness in the four node system with four autoregulatory interactions, although the Bayes factor indicates this is not a strong effect. Although we can conclude that increasing the number of genes from two to four does not seem to give any increase in robustness, we cannot rule out that systems with five or more genes show a stronger increase in robustness, and also that the relationship between robustness and regulatory interactions is different in that case.

Conclusion

We have presented a mathematical framework for the modeling and analysis of robustness in stochastic biological systems and applied it to the case of stochastic transcriptional oscillators. This framework can be used for the design of systems for synthetic biology in order to predict the most robust systems to construct. It can also be used to gain understanding of natural biological systems. Our analysis of transcriptional oscillators has provided a number of insights. We have shown that the oscillator constructed by Stricker et al.¹⁷ is the most robust two gene system and more robust than the ring oscillator, a fact alluded to but never directly shown.²⁰ In addition, we verified the increase in robustness of ring oscillators by the addition of positive feedback,³⁵ but also show how this can be achieved in a number of ways and how each of these affects robustness. We searched model space for the most robust three gene systems possible and arrived at systems comprising known and novel oscillator topologies. Our results also indicate that once the structure of the system is fixed, it is the degradation of the species, rather than the regulatory parameters, that determine oscillator phenotype and robustness. Finally we show that increasing the number of regulatory interactions increases the robustness of the oscillator systems up to a certain level of complexity (number of regulatory interactions). This provides evidence that natural systems should display high levels of interconnectedness to increase robustness, but also that there is a natural limit, beyond which adding further feedback makes no difference. This also suggests that the future of synthetic gene networks lies in the creation of systems comprising additional connectivity to ensure their function across a wide range of conditions. We have highlighted interesting network topologies for further study in order to gain a deeper understanding of their dynamics (stochastic behavior, robustness, chaos²⁵), but also made quantitative predictions on the robustness of different designs, which will be tested in real systems in future work. Realizing these oscillating systems and testing the predictions of the framework will further our knowledge of the intricate details of biological systems and allow us to generate accurate but efficient model descriptions.

We believe that our approach has wide applicability across quantitative and synthetic biology, however there are a number of limitations. Our conclusions depend on the modeling assumptions, and here we have tried to find a balance between simplicity and explanatory power with as much biological detail as possible. We did not explicitly include time delays in our model although it is known to be important for oscillating systems.^17,45 Despite this, the model recapitulates known results, suggesting that our model of mRNA dynamics with large parameter priors causes sufficient delay in the system, although this is not expected to be generally valid²⁵ and is also dependent on other parameter values.³¹ A related issue is the prior parameter distributions which we generally treat as uniform over a biologically plausible range. As our quantitative knowledge improves, for example, with high throughput measurement of biochemical parameters,⁴⁸ this information can be incorporated into our prior, which should be seen as an advantage of the Bayesian approach. The algorithm is computationally intensive and requires high performance computing to explore the kinds of model spaces that are of interest. While the SMC algorithm has desirable properties regarding convergence to the true target distribution in the limit of number of particles, there is still the possibility of falling into local minima. This can be alleviated by running multiple replicates and increasing the number of particles, as in this study, but there is always the possibility that some part of the space was not explored. Finally it is worth emphasizing that our framework is probabilistic in nature and its predictions can be interpreted as an average over implementations (specific promoters, genes). Any particular implementation of a single system may possess properties that make it more or less robust than predicted (for example due to temperature dependence⁴⁹).

Future developments of our framework will be to incorporate contextual effects—known to strongly influence gene network dynamics—such as coupling with growth dynamics⁵⁰ and competition for resources.⁵¹⁻⁵³ Eventually, this type of approach could be combined with whole cell models.^54,55 The framework will also be used to investigate the design principles of more general pulsatile systems,^56,57 investigate systems that provide robust sensing, and also devices for the robust delivery of therapeutic molecules.

Predictive mathematical modeling is at the core of engineering principles and forward design. Currently we lack the tools and knowledge to achieve this in biological systems. Our statistical framework is a significant step in this direction and can provide an engineer with the most robust systems achieving a particular design objective, together with novel and testable predictions. We believe that because of the uncertainty inherent in biological systems, which arises from their complexity and stochasticity, coupled with our lack of detailed knowledge of both their structure and underlying parameters, probabilistic modeling will have a major part to play in the future engineering of biological systems.

Methods

Defining and Calculating Robustness

Intuitively we can think of robustness as a measure of the average performance of a system over some space of perturbations.⁶ Generally speaking, perturbations can be applied at the mutational level, which change the structure of the system, or at the parametric level through changes in rates due to internal and environmental interactions. Consider a model of a system that is required to perform some objective behavior, O. We define an evaluation function or measure of performance, D(x, O), under the effect of a perturbation 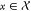with probability distribution given by p(x). We can then define a general form for the robustness as

1

In the case of systems and synthetic biology the model often takes the form of a biochemical reaction system, M, with an associated set of reaction rate constants θ ∈ Θ_M. Here we will focus on robustness to changes in the biochemical parameters and, as in previous studies, will assume that changes to the parameters, θ, occur through processes such as the changing of cell size, temperature variations, and cellular contexts.⁵⁸ Once this mapping has been applied, the probability distribution of perturbations, p(x) becomes the probability distribution of reasonable, or physically constrained, parameter values over the range of fluctuations and contexts, p(θ|M), which in Bayesian statistics is known as the prior distribution (note we have kept the explicit dependence on M). In principle we are free to choose any evaluation function for D(θ, O), however a particularly useful choice is the probability of observing the objective behavior given the value of θ, denoted p(O|θ, M). Taken as a function of θ this is known as the likelihood. The definition of robustness can then be expressed as

2

which is precisely the model evidence (or marginal likelihood) from Bayesian statistics, p(O|M). Note this quantity is also the normalization constant of the posterior distribution, p(θ|O, M), which is the probability distribution of the parameters that give rise to the objective behavior, p(θ|O, M) ∝ p(θ)p(O|θ, M). It is this adoption of the likelihood as our evaluation function that allows us to interpret our results in a probabilistic manner and also provides us with established methods to calculate both p(θ|O, M) and R. One advantage in defining R as the integral over Θ is that increasing the size of a model (also known as its complexity) increases the size of Θ. This automatically penalizes model complexity unless there is a corresponding increase in performance (likelihood) (see Supporting Information).

For a typical biochemical system of interest Θ is high dimensional. This makes analytical calculation of eq 2 impossible for all but the simplest systems. In more realistic examples one must use Monte Carlo methods such as Markov chain Monte Carlo (MCMC) or sequential Monte Carlo (SMC) to either calculate R directly, or indirectly through first calculating the posterior p(θ|O, M). A further complication arises when the biochemical system is stochastic and represented by either a continuous time Markov process or a system of stochastic differential equations (SDEs). In these cases, p(O|θ, M) generally cannot be written in closed form and we must evaluate R using approximate methods, known collectively as approximate Bayesian computation (ABC), which use simulations to match model output to data.⁵⁹⁻⁶²

The Bayesian framework allows us to calculate a numerical value for the difference in robustness between two systems, which is expressed through the Bayes factor.⁶³ The Bayes factor for how well two models M₁ and M₂ can achieve an objective behavior is given by

3

Generally speaking, the value of BF₁₂ provides evidence that M₁ satisfies the objective behavior better than M₂, across the parameter space defined by the prior distribution. A BF₁₂ < 3 indicates weak evidence, BF₁₂ ≈ 3–10 indicates substantial evidence, and a BF > 10 indicates strong evidence.⁶³

Finally it is worth noting that in principle one could use a frequentist model selection framework to calculate robustness, such as the Akaike Information Criterion (AIC).⁶⁴ However, it has been shown previously that this method does not always perform well when applied to the case of discriminating network motif models.⁶⁵

Representation of Network Topologies

A given network topology is modeled by a set of reactions describing the interactions of the different mRNA and protein species. Each node in the network represents transcriptional and translational processes, and each edge represents a regulatory interaction. While we expect the conclusions about the robustness of networks to depend strongly on the specific modeling assumptions, in order to create a predictive framework, we must make some modeling decisions that represent some generalities of synthetic gene networks. In the following, we assume that the biochemical system is spatially homogeneous, that transcription rates follow Hill-type functions with regulatory proteins acting as dimers, and that protein and mRNA species degrade through first order processes. In reality, the kinetics can be more complex and can include time delays and Michaelis–Menten kinetics for active enzymatic degradation, though in principle these could also be included.

From this set of reactions, and assuming homogeneous spatial conditions, a Markov jump process (MJP) governed by the master equation can be formed, which models the probability of each species in the system as a function of time.^66,67 In principle, this is the most appropriate formalism since it correctly accounts for the probabilistic nature of the dynamics. However, there exists an approximation to the master equation, known as the diffusion approximation, which allows the derivation of stochastic differential equations (SDE), also known as the chemical Langevin equation.^67,68 We chose to use this formalism since their simulation is more amenable to parallelization on Graphics Processing Units and is therefore much more efficient when simulating ensembles of systems with different parameters.⁶⁹ Although one assumption underlying the SDE representation is a large system size (number of molecules), we found a high correlation between summaries generated from SDEs and the MJP under the same parameters (Supplementary Figure 15). Since we are working in a stochastic modeling setting we use the convention that species amount is measured in numbers of molecules rather than concentrations.

Given a node X, we represent the numbers of mRNA and protein molecules as X_mRNA and X, respectively. Both species have production and decay terms, giving rise to the following SDEs

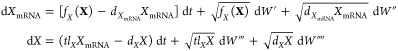4

where d_XmRNA, tl_X, d_X are the rate constants for mRNA degradation, translation, and protein degradation, respectively (all units of min^–1), and the W represents the stochastic nature of the reactions (independent Wiener processes). Therefore, the model of a n node network consists of a system of 2n SDEs.

In eq 4 the regulatory interactions are encoded in the function f_X(X), which represents the binding of proteins to the promoter region upstream of the coding region of X. Here X represents all the proteins in the network so, for example, in a two-node network with nodes A and B, X = {A, B}. To model the probability that a promoter is in the open configuration we utilize the Shea–Ackers formalism, which adopts a thermodynamic argument under equilibrium.⁷⁰ We assume that the regulatory proteins form dimers, which coarsely models commonly used promoter interactions in existing prokaryotic synthetic gene networks, and is important for capturing the nonlinearity present in genetic systems.^17,71 We further assume that the dimerization process is in equilibrium

which allows the identification X₂ = X²/K_d where K_d = k_r/k_f N is the dissociation constant (where the notation, N, corresponds to the integer number of molecules). As an example, given two edges A → B and C −| B, the expression for f_B(A, B, C) is given by

5

where k₁, σ, and δ are parameters for the relative affinity of RNAP (baseline expression, dimensionless), the affinity of activator A₂ in units N^–2 and the affinity of repressor C₂ in units N^–2, respectively (see Supporting Information). The strength of the promoter is represented by R_B and is measured in units of N min^–1. The advantages of this modeling formalism is that multiple protein bindings can be handled in a straightforward manner, and these parameters are often measured when promoters are characterized, and are therefore available in the literature.⁷²

The prior parameter distributions are specified through uniform distributions to reflect the wide range of possible biochemical parameters. Translation and decay rates are given prior distributions of U(0, 10) min^–1. The promoter parameters for transcription factor binding (corresponding to σ and δ in eq 5) are given priors of U(0, 1 × 10⁶) N^–2. The parameters representing baseline expression (corresponding to k₁ in eq 5) are given priors of U(0, 500). Promoter strengths are given priors of U(0, 10000) N min^–1 to reflect variations seen in real synthetic promoters.⁷² The initial conditions of the network must also be specified, which themselves can be treated as parameters. We assign a prior of U(0, 100) N on the initial conditions of all mRNA and protein molecules.

Defining the Objective for Stochastic Oscillations

Oscillatory behavior in deterministic dynamical systems can be specified in various ways including objective functions minimizing squared deviations at regular intervals, Fourier spectra, and through the eigenvalues of the Jacobian matrix of the linearized system near the (unstable) steady state.^28,40,41,73 Quantifying stochastic oscillations presents a challenge since in general the behavior can range from periodic with constant amplitude to pulsatile with varying time period and amplitude, depending on the level and nature of the noise.¹⁷

Here we take a signal processing approach to identifying stochastic oscillations. All systems were simulated for t = 100 min. The raw signal for the protein of interest is smoothed by applying to the time series a mean filter via convolution (Figure 1C). The signal is then differentiated and maxima and minima are identified above a signal-to-noise threshold. The locations of these stationary points are used to define the summary statistics n_max, n_min, which are the number of maxima and minima respectively, and x_max,i, x_min,k, which are the signal level at maxima i and minima k, respectively. The objective behavior is then specified via distances defined on the summary statistics. For example, in the case in which a fixed number of regular pulses is desired, we use the following vector valued distance

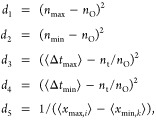6

where n_O is the number of desired pulses (here we set n_O = 10), ⟨Δt_max⟩, ⟨Δt_min⟩ are the mean number of time points between the maxima and minima, respectively, n_t is the total number of time points and ⟨x_max, i⟩, ⟨x_min, k⟩ are the average amplitude of the maxima and minima, respectively. The distances d₁ and d₂ quantify how close the observed number of peaks are to the objective, d₃ and d₄ quantify the average distance between pulses, and d₅ quantifies the amplitude. The algorithm minimizes all distances simultaneously. In this work we assume that the objective is reached when d < ϵ where ϵ = (0, 1, 0.1, 0.1, 0.01). This gives rise to regular oscillations with an amplitude of >100 molecules and a frequency of 0.1 oscillations per minute. We refer to this objective as S1.

In addition to the objective behavior defining a fixed number of pulses, as above, we also developed an alternative objective defining regular oscillations. In this case the number of desired pulses is free to change

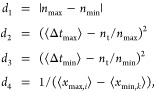7

where the main difference is that the number of maxima and minima are constrained to be equal through d₁. In this case, the objective is reached when ϵ = (1, 0.1, 0.1, 0.01) giving rise to regular oscillations with an amplitude of >100 and a variable frequency. We refer to this objective as S2.

Maximizing Robustness Simultaneously in Model-Parameter Space

To search jointly through topologies and parameters that satisfy the objective behavior we developed an extension to the ABC SMC algorithm,^59,60 inspired by variable selection in a linear regression setting, and implemented within the existing tool ABC-SysBio^61,62 The total space of possible models is specified through a connected network that contains within it all possible models (Figure 1B). Each edge has an associated integer valued parameter, I_j ∈ {−1, 0, +1}, representing a repressing, missing, and activating regulation, respectively. The set of I_j are treated as parameters to be inferred from the objective behavior in an analogous manner to the biochemical rate constants. Our approach differs from other implementations of ABC for network inference,⁷⁴ because we approximate the joint model parameter space as a product, p(M,θ) = p(M)p(θ|M) ≈ p(θ)p(M) (see Supporting Information).

The algorithm proceeds through a series of intermediate distributions defined by a decreasing distance to the objective behavior. Each new weighted population of parameters is obtained from the previous one by resampling, perturbing, and performing ABC with a new distance threshold calculated from the previous distribution of distances. Biochemical parameters are perturbed using a uniform distribution while edges in the network are perturbed using a categorical distribution. It is precisely this structure that allows the exploration of model and parameter space simultaneously. The algorithm terminates when the desired distance threshold, ϵ, is reached. The relative evidence of each model present within the posterior distribution is calculated by summing all the corresponding weights. Because the algorithm explores models in direct proportion to their robustness, it focuses in on systems where robustness is high and ignores models where the robustness is negligible.

The Bayesian framework allows us to place priors on model space; we can set the priors for particular models to be zero and therefore reduce the size of the search space. For example, the space of all possible three-node networks contains 3⁹ = 19683 models. However, if the output is fixed on one node, say node C, then nodes A and B, are interchangeable. There are 243 networks that are invariant under this symmetry operation with 19440 containing a mirror image, leaving 9963 possible nonredundant networks (see Supporting Information). This situation is handled in a straightforward manner by precomputing the prior over model space. In principle, topologies could also be weighted according to other information rather than simply included and excluded.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acssynbio.5b00179.

• Additional methods and results (PDF)

The authors declare no competing financial interest.