Gibbs Ringing in Diffusion MRI

Abstract

Purpose

To study and reduce the effect of Gibbs ringing artifact on computed diffusion parameters.

Methods

We reduce the ringing by extrapolating the k-space of each diffusion weighted image beyond the measured part by selecting an adequate regularization term. We evaluate several regularization terms and tune the regularization parameter to find the best compromise between anatomical accuracy of the reconstructed image and suppression of the Gibbs artifact.

Results

We demonstrate empirically and analytically that the Gibbs artifact, which is typically observed near sharp edges in magnetic resonance images, has a significant impact on the quantification of diffusion model parameters, even for infinitesimal diffusion weighting. We find the second order total generalized variation to be a good choice for the penalty term to regularize the extrapolation of the k-space, as it provides a parsimonious representation of images, a practically full suppression of Gibbs ringing, and the absence of staircasing artifacts typical for total variation methods.

Conclusions

Regularized extrapolation of the k-space data significantly reduces truncation artifacts without compromising spatial resolution in comparison to the default option of window filtering. In particular, accuracy of estimating diffusion tensor imaging and diffusion kurtosis imaging parameters improves so much that unconstrained fits become possible.

INTRODUCTION

A Fourier series lacking an adequate number of high frequency terms will result in an imperfect approximation of sharp edges. As a result, spurious ringing near sharp edges, e.g., boundaries of tissues, appears in the reconstructed images any time the Fourier space is truncated during acquisition or compression. This phenomenon was initially discovered by H. Wilbraham in 1848 (1), but his paper was overlooked, and the phenomenon was rediscovered by J.W. Gibbs in 1898 (2).

Magnetic resonance (MR) images that are obtained via the inverse Fourier transformation (FT) of a finite k-space acquisition represent a classic case of Gibbs ringing (3,4). Because of scan time and SNR limitations, the outer parts of the k-space that contain the high frequency information of the image, are generally not recorded.

Although ringing is a feature of all MRIs obtained via inverse FT, it becomes increasingly significant for low resolution and/or quantitative modalities such as diffusion MRI (dMRI). While introducing a bias of at most 9% of the intensity step in the individual “weighted” images in agreement with Refs. (1) and (2), here, we show that the Gibbs effect is amplified tremendously in the derived parametric maps, e.g., of diffusion and kurtosis tensor components, Fig. 1. The amplification occurs because the Gibbs oscillation pattern depends on the diffusion weighting. Likewise, a similar amplification should occur in T₂ and $T_2^{\ast }$ mapping, with the echo time playing the role of the weighting (5).

FIG. 1.

The over- and undershoots of the apparent diffusion (D) and kurtosis (K) coefficients, and of axonal water fraction (AWF) depend on the location x and greatly exceed the 9% variation observed in the simulated DW signals, which represent realistic parameter values on the border between CSF and Corpus Callosum (CC). At the red position, S(0) is underestimated, whereas S(b)|_b=1,2 get overestimated due the Gibbs artifacts, resulting in a concave log S(b), whereas the blue position shows the opposite trend (see bottom left where log S(b) is shown as function of b for both locations). In both cases, the estimated diffusion parameters show biased and unphysical values, often orders of magnitude different from the ground truth (black).

A dramatic effect happens when oscillations in the non-diffusion weighted (DW), i.e., b=0, and finite-b images are out of phase due to relative difference in DW signal intensities S(b) at different b-values (Fig. 1). In this case, ln S(b) may become concave, which causes unphysical negative diffusion and/or kurtosis values, cf. notorious “black voxels” in windowed mean kurtosis maps (as we discuss later, see Fig. 9) (6,7). Those physically implausible diffusion parameters bias statistical analysis, modeling and interpretation of dMRI data.

FIG. 9.

Non-DW, MD, and MK map of an axial slice of clinical data for the different reconstruction techniques. Zoomed details of the maps (red square) are shown as well to highlight the distinct features of the different techniques. Gibbs ringing, blurring, and staircasing can be observed for ZF, GF/LF, and TV reconstruction respectively. Although the staircasing is most pronounced in the non-DW image, it is also clearly present in the parametric maps.

Here, we prove analytically that, unexpectedly, Gibbs-induced bias is pervasive, i.e., it affects the dMRI parameters even in the b → 0 limit. This makes the effect more dangerous, as while it is not easily spotted by the naked eye, it biases practically all diffusion metrics. Due to its nonlinearity, this bias generally cannot be cured by averaging of the parametric maps over a region of interest.

The appearance of nonpositive definite diffusion tensors in tissue surrounding the cerebrospinal fluid (CSF) has been tied to Gibbs ringing by Barker et al. as early as in 2001 (8). This observation was only brought to the attention of the diffusion community again in 2011 by Tournier et al. (9). Figure 7 in their paper indicates how dominant the effect can be in important white matter structures such as the corpus callosum (CC).

Despite those observations, the problem has so far been largely ignored or overlooked. Representatively, the Gibbs artifact was not included in the comprehensive overview of pitfalls in dMRI processing and analysis by Jones and Cercignani (10). The most common strategy to suppress the artifact has been spatial smoothing of the MR data, often using an isotropic smoothing kernel. Nowadays, spatial smoothing is widely accepted (6,11) as a necessary step in the processing pipeline of diffusion kurtosis imaging (DKI) (12). Indeed, smoothing and even additionally imposing positivity constraints on the DKI fit are the current practice to clean up the parametric maps (6,7). However, spatial smoothing inherently lowers the spatial resolution of the image (blur) and introduces additional partial volume effects (13–16) that lead to complications in further quantitative analyses (17,18) or to biases in microstructural modeling (19). Furthermore, constrained parameter fitting is time consuming and, more importantly, may bias the estimator (6,7,20,21).

Inspired by previous work (22–27), here we present a comprehensive framework of a regularized extrapolation of the k-space beyond its measured part to avoid the sharp cut-off, by adopting a physically reasonable representation of the image. In the approach of Block et al. (26), which was later adopted by Perrone et al. (27) in the context of diffusion MRI, total variation (TV) regularization was used to stabilize the ill-posed estimation problem (28). The main benefit of TV models is their suitability to remove spurious variations while preserving edges in the image. However, TV regularization (L₁ norm of the image gradient) describes the object as a piecewise constant function, which leads to the typical staircase artifact in the reconstructed images (see e.g., arrow “b” in Fig. 4) (29).

FIG. 4.

(Top) Detail of the reconstruction of the MPRAGE image, i.e., the periventricular white matter. TGV outperforms all others since it features (I) high spatial resolution (v. filtering), (II) full suppression of Gibbs ringing (v. Gaussian filtering) and (III) the absence of the staircasing artifact (v. TV; arrows “b”). LR and ZF are both shown. Despite the different voxel size, they have the same information content as they represent identical data. (Bottom) Image magnitude |ℱu| in the k-space corresponding to the reconstructions whose details are shown left. Attenuation of the higher frequency components near the cutoff frequency (red squares) results in image blur. In contrast to window filtering, TV and TGV extrapolate the k-space beyond the cutoff frequency, while maintaining high data fidelity. Fine anatomical details that are lost by the LR acquisition cannot be recovered by TV or TGV (arrows “a”).

The need for regularization terms for imaging problems that go beyond the TV framework inspired Bredies and coworkers to introduce the concept of Total Generalized Variation (TGV) (30,31). Much like TGV¹ ≡ TV does not penalize a constant intensity, TGVⁿ does not penalize intensity described by a polynomial of degree n − 1. Since TGV features piecewiseness imposed by the L₁ norm, it is equivalent to TV in terms of edge preservation. However, the application of higher order TGV in MRI is far less restrictive (31). Indeed, TV is only optimal for truly flat objects like numerical phantoms, whereas the TGV family has more potential in real world objects. The technique has, e.g., already been shown to be powerful in non-Cartesian image reconstruction and image denoising (31–37).

By comparing different regularization functions, we demonstrate that TGV₂, the second order TGV minimization, which assumes piecewise linearity, achieves a good balance in parsimoniously representing images without staircasing, yet preserving edges and remedying the bias on diffusion metrics due to the Gibbs ringing artifact.

THEORY

Qualitative Considerations

The Gibbs ringing artifact arises because the Fourier series cannot represent a discontinuity with a finite number of harmonics. A sharp cut-off or truncation in the k-space is equivalent to a convolution in spatial domain with a sinc function. In the discrete FT reconstruction of MR images, the cut-off frequency, k_c, equals the frequency of the sinc function that is convolved with the image. The oscillating lobes of the sinc function result in the ringing pattern around sharp edges with a maximal over- or undershoot of approximately 9% of the step amplitude, depending on the sampling location. If the resolution of the image is not artificially increased by zero-filling (ZF), then the period of the ringing is twice the voxel size.

The Gibbs effect is amplified in the diffusion metrics. In Fig. 1, we show that a moderate signal over- and undershoots can lead to severe bias in parametric maps. Qualitatively, strong amplification occurs because the Gibbs oscillations in the b=0 and finite-b images can differ in phase due to relative difference in DW signal intensities at different b-values. This most prominently occurs at the border between tissue with low S(0) but slow diffusion, such as CC, and water, such as CSF with high S(0) but fast diffusion. For the finite b values, the value of the mismatch S_CC(b) − S_CSF(b) changes sign between, say, b=0 and b = 1ms/μm². The corresponding shift in Gibbs pattern between the b=0 and finite-b images will create a concave, rather than convex ln S(b), leading to extreme and/or unphysical diffusion model parameters.

Figure 1 demonstrates this for simulated DW signal with realistic parameter values on the border between CSF and CC, assuming as ground truth a monoexponential S_CSF(b) = S_CSF(0)e^−bD_CSF with D_CSF = 3 μm²/ms, and a two-compartment model for CC,

$$S_{\text{CC}}(b)=S_{\text{CC}}(0)\left[f{e}^{-{bD}_{\perp }^{\text{ias}}}+(1-f)e^{-{bD}_{\perp }^{\text{eas}}}\right],$$

with $D_{\perp }^{\text{ias}}=0$ transverse to white matter fibers. The effect of Gibbs ringing is observed in (i) apparent diffusion and kurtosis coefficients estimated by a cumulant expansion, and (ii) parameters of the above biexponential model nonlinearly fit to the artifact-corrupted data to extract the axonal water fraction (AWF) f. Note that the mathematical lower bound −2 on kurtosis, and the physical lower bound (zero) on diffusivity and AWF, are heavily violated due to the Gibbs ringing.

Exact Relations for the Bias in Signal Moments

The qualitative picture developed above, consistent with the previous empirical observation (8), does not address the following question: If we use very low b-values, should the Gibbs effect in dMRI metrics disappear? One could indeed think that, as signal intensity at b → 0 approaches that for b=0, the normalization onto S(0) would cure the problem, i.e., the Gibbs bias is a finite-b artifact. Here, we show that this intuition is incorrect, and there is no threshold in b for the bias in dMRI metrics to occur. In other words, the bias, possibly severe (such as negative apparent diffusion coefficient and kurtosis) can occur already for infinitesimal b-values, making the Gibbs effect unexpectedly ubiquitous and easily overlooked.

For a sharp boundary between tissue types 1 and 2, the ideal signals S_1,2(b) become the apparent ones, S̃_i,j = S_i + β(S_i − S_j), i, j = 1, 2, where |β| ≤ β_max ≈ 0.09. Using S̃₁ + S̃₂ = S₁ + S₂ and S̃₁ − S̃₂ = (1 + 2β)(S₁ − S₂), we can relate the Taylor expansion coefficients

$$S_i=\sum _{n=0}^{\infty }\frac{{(-b)}^n}{n!}{M}_i^{(n)},{\stackrel{\sim }{S}}_i=\sum _{n=0}^{\infty }\frac{{(-b)}^n}{n!}{\stackrel{\sim }{M}}_i^{(n)}$$

up to any order n:

$${\stackrel{\sim }{M}}_i^{(n)}=(1+\mathrm{\beta })M_i^{(n)}-\mathrm{\beta }{M}_j^{(n)},$$ [1]

for i = {1, 2} and the complementary j = {2, 1}, respectively.

In particular, the coefficients

$$\{\begin{array}{l}{M}_i^{(0)}=S_i^0\hfill \\ M_i^{(1)}=S_i^0{D}_i\hfill \\ M_i^{(2)}=S_i^0{D}_i^2(1+K_i/3)\hfill \end{array}$$ [2]

are tied to signal intensities $S_i^0$, diffusivities D_i, and kurtoses K_i (and similar for the apparent ones). Analogous relations can be derived for higher-order metrics.

Relations (1) can be easily inverted:

$$M_i^{(n)}=\frac{1+\mathrm{\beta }}{1+2\mathrm{\beta }}{\stackrel{\sim }{M}}_i^{(n)}+\frac{\mathrm{\beta }}{1+2\mathrm{\beta }}{\stackrel{\sim }{M}}_j^{(n)}.$$ [3]

In principle, knowing β, Eq. [3] can be used to correct the signal up to arbitrary order n; this correction affects all signal’s moments determined at b → 0, proving that there is no threshold in b for the bias to occur. In practice, we do not know β near a particular sharp boundary (as it depends on the exact position of the boundary relative to the voxels), but it is still instructive to see what the effect of β is on the normalized Taylor coefficients $m_i^{(n)}=M_i^{(n)}/S_i^{(0)}$ that are proportional to molecular displacement moments of the order 2n (in a given direction). For that, using Eqs. [1] and [2], we relate apparent to ideal signal intensities

$${\stackrel{\sim }{S}}_i^0=S_i^0\left[1+\mathrm{\beta }(1-s_j)\right],$$ [4]

where $s_j=S_j^0/S_i^0=1/s_i$, and find the ratios between apparent and ideal displacement moments in terms of

$$\frac{{\stackrel{\sim }{m}}_i^{(n)}}{m_i^{(n)}}=1+\frac{{\mathrm{\gamma }}_j}{1-{\mathrm{\gamma }}_j}\left[1-\frac{m_j^{(n)}}{m_i^{(n)}}\right],{\mathrm{\gamma }}_j=\frac{\mathrm{\beta }{s}_j}{1+\mathrm{\beta }}$$ [5]

In particular, for the (directional) diffusivities $D_i=m_i^{(1)}$ in tissue i we obtain

$$\frac{{\stackrel{\sim }{D}}_i}{D_i}=1+\frac{{\mathrm{\gamma }}_j}{1-{\mathrm{\gamma }}_j}\left(1-{\mathrm{\zeta }}_j\right),{\mathrm{\zeta }}_j=\frac{D_j}{D_i}.$$ [6]

The apparent D̃_i changes sign when ζ_j > 1/γ_j. Likewise, Eq. [5] for $m_i^{(2)}=D_i^2\left(1+\frac{1}{3}{K}_i\right)$ yields the bias

$${\stackrel{\sim }{K}}_i-K_i=-{\mathrm{\gamma }}_j·\frac{{(1-{\mathrm{\zeta }}_j)}^2(K_i+3)+{\mathrm{\zeta }}_j^2(1-{\mathrm{\gamma }}_j)(K_j-K_i)}{{(1-{\mathrm{\gamma }}_j{\mathrm{\zeta }}_j)}^2}$$ [7]

in the (directional) kurtosis. The first term in Eq. [7] is the correction due to Gibbs pattern depending on the contrast in diffusivities, (1 − ζ_j)² ∝ (D_i − D_j)², and is always negative. The second term is more subtle and originates from the Gibbs pattern depending on the mismatch in curvatures of S_i(b), and can change sign, Fig. 2.

FIG. 2.

Apparent ${\stackrel{\sim }{D}}_2^{\perp ,\Vert }$ and ${\stackrel{\sim }{K}}_2^{\perp ,\Vert }$ as function of γ₁ for ζ₁ = ζ_⊥ and ζ_||. The respective ground truth values $D_2^{\perp ,\Vert }$ and $K_2^{\perp ,\Vert }$ are shown by the dashed lines. The apparent ${\stackrel{\sim }{K}}_2^{\perp }$ has a singularity for ${\stackrel{\sim }{D}}_2^{\perp }=0$.

The overall effect scales ∝ γ_j proportional to the relative Gibbs mismatch β for small β, as expected. Eqs. [6] and [7] show for the first time that the Gibbs effect does alter the observed diffusivity and kurtosis, i.e., it affects the signal already in the b → 0 limit. However, we can see that the relevant parameter for the Gibbs effect in diffusion metrics is not β, but γ_j which can be strongly amplified by the mismatch s_j in signal intensities.

To illustrate the above exact results, consider our previous example by assigning 1 to CSF and 2 to surrounding tissue such as CC. We take realistic values for D₁ = 3μm²/ms, K₁ = 0, and s₁ = 4 = 1/s₂. We consider axial and radial diffusion in the CC with following parameters: $D_2^{\perp }=0.25\mathrm{\mu }{\mathrm{m}}^2/\text{ms},D_2^{\Vert }=2\mathrm{\mu }{\mathrm{m}}^2/\text{ms},K_2^{\perp }=3$, and $K_2^{\Vert }=0.5$ Figure 2 shows the dependence of D̃₂ and K̃₂ as function of γ₁, given ${\mathrm{\zeta }}_{\perp }=D_2^{\perp }/D_1$ and ${\mathrm{\zeta }}_{\Vert }=D_2^{\Vert }/D_1$.

In connection to our exact results, we can offer a few qualitative remarks. First, despite a smooth, monotonic decrease of D̃₂ with γ₁, K̃₂ over– and undershoots the the respective K₂ by several orders of magnitude, especially in the negative direction. Those extreme values are the result of the division by a number (1 − γ_jζ_j)² that can become arbitrarily close to zero. Therefore, they are a result of reparameterization of the cumulant expansion, when going from the apparent fourth-order cumulant $~{\stackrel{\sim }{K}}_i{\stackrel{\sim }{D}}_i^2$ to the (dimensionless) apparent kurtosis K̃_i (6). The division by zero occurs when ζ_j = 1/γ_j, corresponding to D̃_i ≡ 0, Eq. [6]. Second, the simultaneous observation of negative kurtosis and positive diffusion coefficients showcases that the apparent concavity of S(b) does not solely come from DW signals exceeding the non-DW signals, as alluded previously (8,9). Neither is the bias due to a finite or an ill-conditioned b-matrix. Finally, removing the bias by averaging the metrics within an region-of-interest (ROI) is not possible because of the nonlinearity of D̃₂ and K̃₂ as function of β.

Given Eqs. [6] and [7], one can find when the apparent D̃₂ and K̃₂ become negative as function of other variables. Taking above CSF values for D₁, K₁, s₁, the apparent WM diffusivity sign change, from ζ₁ = 1/γ₁ ≈ 3 for β = β_max, will occur at D₂ < 0.98μm²/ms. Furthermore, taking typical (ideal) CC diffusivities $D_2^{\perp }=0.25\mathrm{\mu }{\mathrm{m}}^2/\text{ms}$ and $D_2^{\Vert }=2\mathrm{\mu }{\mathrm{m}}^2/\text{ms}$ transverse and parallel to WM tracts, the directional kurtosis will become negative if the ideal $K_2^{\perp }<179$ and $K_2^{\Vert }<0.37$, respectively. These examples show that diffusion transverse to the fiber direction is much more prone to negative diffusion and kurtosis coefficients than the axial diffusion. Indeed, in Fig. 2, ${\stackrel{\sim }{D}}_2^{\perp }$ and ${\stackrel{\sim }{K}}_2^{\perp }$ show zero-crossings, whereas ${\stackrel{\sim }{D}}_2^{\Vert }$ and ${\stackrel{\sim }{K}}_2^{\Vert }$ are strictly positive.

METHODS

L₁ Regularization

Here, we assume that the limited k-space data is only corrupted by thermal noise, i.e., we are not alleviating any other artifacts in this work.

Our goal is to reconstruct the image u = u(x) in d dimensions x = (x₁, …, x_d) on a finer spatial grid than the original image by extrapolating the k-space beyond the measured part; in all our dMRI examples below, d=2 (EPI acquisition). Reconstruction of u based on the truncated (low-resolution) and noisy k-space measurement ũ_k = ũ_k(k) with |k_i| ≤ k_c, i = 1, …, d, requires employing prior knowledge of the functional shape of possible u(x). This can be formulated as a following constrained estimation problem:

$$\widehat{u}=\underset{u(x)}{\text{argmin}}\mathcal{R}(u),\text{subject}\text{to}{\Vert \stackrel{\sim }{\mathcal{F}}u-{\stackrel{\sim }{u}}_k\Vert }_2^2\le \mathrm{\epsilon },$$ [8]

where the functional ℛ(u) is a penalty term to regularize the ill-posed estimation problem, forcing u(x) to conform to a desired class of functions. The data fidelity constraint ${\Vert \stackrel{\sim }{\mathcal{F}}u-{\stackrel{\sim }{u}}_k\Vert }_2^2\le \mathrm{\epsilon }$ ensures that the experimental data ũ_k can deviate from the corresponding “ideal” low-k image ℱ̃u by the amount ε = Nσ² connected to the number of degrees of freedom (imaging voxels) N and noise variance σ²; here, ℱ̃ is the windowed FT, which is, here, defined as the forward FT followed by nullification of all |k_i| ≥ k_c to mimic the measurement. We will refer to the full reconstructed k-space as û_k = ℱû.

The constrained problem in Eq. [8] is practically solved by recasting it in an unconstrained form

$$\widehat{u}-=\underset{u}{\text{argmin}}\{{\Vert \stackrel{\sim }{\mathcal{F}}u-{\stackrel{\sim }{u}}_k\Vert }_2^2+\mathrm{\lambda }\mathcal{R}(u)\},$$ [9]

where λ > 0 is the regularization parameter that has to be found self-consistently. The parameter 1/λ is often referred to as the Lagrange multiplier.

The result of image reconstruction is determined by the choice of ℛ(u); this choice is empirical and depends on the nature of the problem. For our purposes of Gibbs ringing suppression, the penalty term must be (i) edge-preserving, (ii) convex to allow efficient numerical optimization, (iii) parsimonious, and, finally, it must (iv) suppress local signal perturbations of the Gibbs ringing shape, i.e., high-frequency oscillations. These features are captured by the L₁ norm of a well-chosen sparsifying transform Ψ(u) of the image. Note that L₁ norm serves as a convex analogue for the literal L₀ norm sparsity count. Given the observation that “ideal” high-resolution images typically do not have high frequency oscillations, a sparsifying transformation that meets condition (iv) is given by the finite difference of the image, i.e., Ψ (u) = ∇u. This approach is well known as TV minimization (28) and it has previously been used to suppress undesired local variations in the context of denoising and/or Gibbs correction (26–28). The penalty term of the TV function is given by:

$${\mathcal{R}}_{\text{TV}}(u)=\int {\Vert \nabla u\Vert }_1\mathrm{d}x,$$ [10]

with the rotationally-invariant L₁ vector norm

$${\Vert \nabla u\Vert }_1=\sqrt{\sum _{i=1}^d{({\partial }_{i}u)}^2}.$$ [11]

Here, ∂_i is the finite-difference partial derivative of the image with respect to its ith dimension, which corresponds to ∂₁u = u(x₁ + 1, x₂) − u(x₁, x₂) and ∂₂u = u(x₁, x₂ + 1) − u(x₁, x₂) in 2d.

Recently, second order TGV has been introduced as an extension of TV (30,31):

$${\mathcal{R}}_{{\text{TGV}}^2}(u)=\underset{V(x)}{min}\left\{{\mathrm{\alpha }}_1\int {\Vert \nabla u-v\Vert }_1\mathrm{d}x+{\mathrm{\alpha }}_0\int {\Vert \mathrm{\xi }(v)\Vert }_1\mathrm{d}x\right\},$$ [12]

where the auxiliary vector field v is meant to capture the linear variations of u(x). The components of v are bounded by 0 and the respective component of ∇u. The penalty is added for its symmetrized derivative $\mathrm{\xi }(v)=\frac{1}{2}\left(\nabla v+\nabla v^T\right)=\frac{1}{2}\left({\partial }_i{v}_j+{\partial }_j{v}_i\right)$, since the antisymmetric part ∂_iv_j − ∂_jv_i vanishes when v ∝ ∇u as a curl of a gradient. For our 2d example, using the norm [11],

$${\Vert \mathrm{\xi }(v)\Vert }_1=\sqrt{{({\partial }_1{v}_1)}^2+{({\partial }_2{v}_2)}^2+\frac{1}{2}{({\partial }_1{v}_2+{\partial }_2{v}_1)}^2}.$$ [13]

Empirical parameters α₀ and α₁ in Eq. [12] are set to 1 and 2, respectively (cf. Ref. 31). Optimization is done by a MATLAB implementation of the first-order primal-dual algorithm as such algorithms have been shown to be a good choice for large-scale convex optimization problems (38).

The second order TGV tends to represent an image by a piecewise linear, yet not constant, function. (Piecewiseness is ensured for the edge preservation via L₁ norm, similar to the case of TV.) The reduced penalty term for linear functions leads to the absence of the staircasing effect which is often observed in TV regularization. For further details of the TGV framework and its implementation, we refer the interested reader to Refs. (30) and (31), respectively.

Note that within the compressed sensing (CS; (39)) theory, similar L₁ norm minimization problems are used to fully recover a signal that has a sparse representation in some domain from far fewer samples (40). Indeed, it has been shown that undersampled signals can be fully recovered if (i) a sparse representation of the signal exists and (ii) the windowed Fourier operator ℱ̃ is incoherent with the sparsifying transformation. If both conditions are met, use of the L₁ norm of a sparsifying transform of the targeted object as penalty term will result in full recovery of the unmeasured k-space points (40). Typical examples of sparsifying transformations used in MRI are wavelet transformations (briefly discussed in Fig. 6) or the TV function (41). Unfortunately, it can be shown that a highly regularly sampled k-space violates the incoherence condition and, as such, full recovery of the k-space in our case is not possible. Hence, the recovery of missing fine anatomical details is impossible given our sampling scheme and is not aimed here.

FIG. 6.

Same detail of the reconstruction of the MPRAGE image as in Fig. 4. Using the Haar and D6 wavelet transformations result in unphysical spurious checkered patterns and oscillations.

Regularization Parameter λ

Rewriting the inequality constrained optimization problem into an unconstrained optimization problem, i.e., Eq. [9], comes with the introduction of a regularization parameter λ. Choosing λ is trading off between data fidelity and imposing the constraint. Assuming that thermal noise with standard deviation (SD) σ is the only source of disturbance within the original acquisition window, the optimal solution should only slightly diverge from the measured data to remove the noise while preserving the low frequency content of the data, cf. denoising. As already mentioned after Eq. [8], we can allow the data fidelity term to be of the order Nσ². Here, we choose to determine λ by fixing

$${\Vert \stackrel{\sim }{\mathcal{F}}\widehat{u}-{\stackrel{\sim }{u}}_k\Vert }_2^2=N{\mathrm{\sigma }}^2,$$ [14]

with N = n_xn_y for our 2d examples, where n_x and n_y are the numbers of rows and columns of the image matrix. The choice (14), which is an expected value of the L₂ norm of data fidelity in the case of Gaussian noise, has been suggested by Morozov in the 1960s (42,43).

As we can see, the choice of λ depends on the noise level σ that should be estimated separately. In this work, we use the global noise estimation method based on a wavelet decomposition of the MR image, which was proposed by Coupé et al. (44) to estimate the average noise level σ within a single 3d MR image.

Default Option: Window Filtering

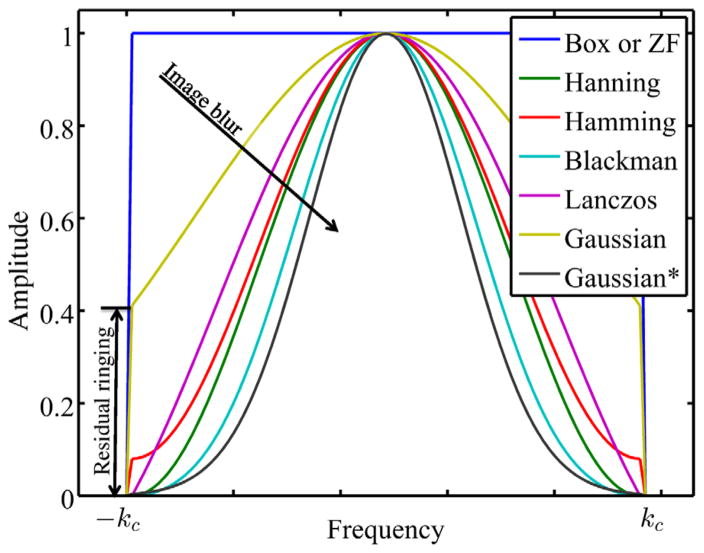
The conventional way to alleviate the ringing artifact is windowing with an apodizing filter. Indeed, many 2d radially symmetric filters with a smooth window have been designed to yield a smooth transition at the cutoff frequency. Examples of those low-pass filters are the Hanning, Hamming, Blackman, Lanczos, and Gaussian filter with FWHM=3 × voxel size in the image domain (Gaussian* in Fig. 3). Because of the lack of a discontinuity, these windows attenuate the higher-frequency components near the cutoff frequency k_c of the signal. This results in the widening of the point spread function. Hence, those filters blur the signal and, as such, reduce spatial resolution. Based on Fig. 3, we opt to use ZF reconstructions with and without filtering (Lanczos filter and the Gaussian filter with FWHM=1.25 × voxel size in the image domain) throughout this work for comparison purposes. This Gaussian filter is not expected to fully suppress the Gibbs ringing, but it maintains the spatial resolution more than the Lanczos filter. Note that the Lanczos filtering is a multiplication of the recorded k-space with a sinc function whose width is selected such that the sinc-function’s first null coincides with the border of the measured k-space.

FIG. 3.

Window functions in frequency domain. Only windows without an abrupt discontinuity will fully suppress Gibbs oscillations. Choosing a filter is a trade-off between the degree of suppression of the Gibbs artifacts and image blur. Gaussian and Gaussian* are Gaussian filters with FWHM=1.25 and 3 × voxel size in the image domain, respectively.

Diffusion and Kurtosis Tensor Imaging

As shown before, diffusion parameters can be highly biased due to Gibbs ringing. To assess the effectiveness of artifact correction, here, we use the standard model-independent representation of the dMRI signal via the cumulant expansion (45). It should be obvious at this point that an improvement in recovering dMRI signal cumulants should directly translate into the corresponding improvement of microstructural parameters determined via concrete signal models (such as our two-compartment example in Fig. 1). Because the choice of biophysical models is far from being settled (19), it is wise to stay at the level of the cumulant series. Estimation of cumulants is a linear problem

$$lnS(B,{\mathit{\vartheta }}_L)=B{\mathit{\vartheta }}_L,$$ [15]

with S(B, ϑ_L) the N DW signals given B, an acquisition-specific design matrix covering all diffusion gradient information, i.e., unit-length diffusion gradient directions ({[ĝ_ix, ĝ_iy, ĝ_iz]^T: i = 1 ⋯ N}) and diffusion strengths ({b_i : i = 1 ⋯ N}). The design matrix is typically called the b-matrix (46). Furthermore, ϑ_L is the vector that includes the cumulants to describe the DW signal up to the Lth order. Diffusion tensor imaging (DTI; L=2) (47) and DKI (L=4) (12) are well known members of this generic framework.

Consider a set of N noisy diffusion-weighted signals S̄. Given that S̄ can be modeled as:

$$ln\overline{S}=B{\mathit{\vartheta }}_0+\mathrm{\varsigma },$$ [16]

with ς being an N dimensional error term, the model parameters can be estimated using following closed-form estimator, i.e., the weighed linear least squares estimator (48):

$$\widehat{\mathit{\vartheta }}={\left(B^{T}WB\right)}^{-1}{B}^{T}W\text{ln}\overline{S},$$ [17]

with W being a diagonal weight matrix, which is chosen according to Veraart et al (48). After estimation of the tensor elements, the widely used parameter maps of DTI and DKI are calculated, including mean diffusivity (MD), fractional anisotropy (FA), and mean kurtosis (MK) (49,50).

During the DTI and DKI analysis, DW images with b > 1 μm²/ms and b > 2 μm²/ms, respectively, were excluded. Indeed, the applicability of cumulant expansions is limited by the radius of convergence of the cumulant series (51). Although the actual radius of convergence in the case of human brain structures still needs to be addressed, a theoretical estimation of the radius of convergence based on a biexponential function indicates that b ≈ 2.5 – 3 μm²/ms might be an upper bound to be considered when expanding the DW signals in cumulants.

Data

MPRAGE

A 3D T1-weighted axial MPRAGE scan was acquired on a 3T PET/MRI scanner (Biograph mMR, Siemens Healthcare) using a 12-channel receiver head coil. Imaging parameter were: matrix size=256 × 256; TR/TE : 2300/2.98 ms; inversion time : 900ms, in-plane resolution: 1.5× 1.5mm²; slice thickness: 2.5mm; number of partitions 105 for a nominal slice thickness of 1.5 mm(no gap).

Human Connectome Project

We used a randomly chosen single subject from the unprocessed Q3 release of the Human Connectome Project (HCP) dMRI data for this study. While the diffusion acquisition is covered in detail in (52,53), a brief summary is given here. Whole-brain EPI acquisitions were acquired with a 32 channel head coil on a modified 3 T Siemens Skyra with TR=5520 ms, TE=89.50 ms, flip angle=78°, BW=1488 Hz/Px, in-plane FOV=210×180 mm, 111 slices, 1.25 mm isotropic voxels, with a multi-band acceleration factor of 3. Diffusion weighting was applied along 90 DW gradient directions for each out of 3 b-shells (b = 1, 2, and 3 ms/μm²). Additionally, 18 nondiffusion-weighted images were acquired. Two runs of that diffusion protocol were acquired, one with a right-to-left and the other with a left-to-right phase encoding. Data has been corrected for eddy current distortion and subject motion (53). The SNR of this HCP data largely exceeds the SNR of the typical clinical protocols. To enable translation of our results to the more typical clinical dataset, we omitted all right-to-left data, there by reducing the SNR by $\sqrt{2}$.

Clinical Data

A diffusion-weighted dataset was acquired on a Siemens Prisma (3T) MR scanner, using a 64-channel receiver head coil. Diffusion weighting was applied along 60 isotropically distributed gradient directions with b = 1 ms/μm² as well as b = 2ms/μm². Additionally, 6 nondiffusion-weighted images were acquired. Other imaging parameters were: TR/TE : 3500/74 ms, in-plane resolution: 2.5 × 2.5mm²; NEX: 1; slice thickness: 2.5mm; axial slices: 22; and parallel imaging: GRAPPA with acceleration factor 2. The diffusion-weighted data were corrected for motion, eddy currents, and EPI distortions (53).

RESULTS

Gibbs Ringing Correction of Structural MRI

Truncating a high-resolution (HR; 256 × 256) MPRAGE image in k-space generated a simulated image that mimics a low-resolution acquisition (LR; 96 × 96).

Figure 4 (left) shows a qualitative comparison of the different filtering (Gaussian [GF] and Lanczos [LF]) and reconstruction techniques, i.e., ZF, TV, and TGV, applied on the single slice of the simulated LR image. Gibbs ringing can be strongly reduced by extrapolation of the k-space using second order TGV without the introduction of the staircasing artifact (arrows “b”) or loss of spatial resolution compared to LR acquisition. However, fine anatomical details lost during LR acquisition cannot be recovered (arrows “a”). This is expected, as we are not sensing the full HR k-space. Moreover, we are not aiming to resolve all HR details, only to cure the ringing artifact. Both the Lanczos and Gaussian filters show significant spatial ZF resolution loss.

The magnitude |ℱu| of the corresponding high-resolution image in k-space is shown in Fig. 4; the loss of resolution translates to strong suppression of |ℱu| beyond the acquisition edge k_c.

To study the k-space recovery in greater detail, we introduce the k-space filling, defined as the square root of the differential k-space energy density (integrated over a narrow square shell in 2d), as function of the distance to the k-space center, δk. Given our discrete k-space grid with frequency resolution Δk, the k-space filling is computed as ||û_k(Ω(nΔk))||₂ for n=1 to min(n_x, n_y), with δk = nΔk, and Ω(nΔk) being the 2d square shell centered around the k-space center. The width of the square is 2nΔk, and the thickness of the shell equals Δk. This normalized quantity, Fig. 5, shows that in contrast to window filtering, both TV and TGV hardly affect the actually measured k-space data, k < k_c. Furthermore, we observe good recovery of k-space filling beyond k_c for both TV and TGV. Note that the broad peak at k ≈ 2k_c (harmonic doubling) is a signature of the nonlinear reconstruction (9) employing the L₁ norm; we also observed peaks at 3k_c in our simulations when we tried to extend the reconstructed k-space further. TV’s overestimation of high frequencies compared to the HR data explains the staircase artifact observed in the corresponding image, as it represents the image as a piecewise constant function.

FIG. 5.

Square root of the k-space energy density, normalized by the HR energy density, as function of the distance to the k-space center. TGV closely approximates the HR data, whereas TV overshoots the high frequency content (cf. staircasing artifact). Window filtering destroys measurements resulting in spatial resolution loss. The broad peak at k = 2k_c is a signature of the nonlinear reconstruction (harmonic doubling).

In Fig. 6, the importance of choosing a physically reasonable representation of the high-resolution image u(x), corresponding to the choice of the penalty term ℛ(u) in Eqs. [8] and [9], is demonstrated by showing two wavelet-based reconstructions. The Haar and Daubechies (D6) wavelet functions served as sparsifying transformations Ψ(u) in the penalty term ℛ(u) ∝ ||Ψ(u)||₁. The oscillating nature of those functions not only hampers full suppression of the Gibbs artifact, but might also introduce spurious features in the reconstructed images. Indeed, checkerboard patterns and oscillations characterize the reconstruction using the Haar and D6 wavelets, respectively.

Gibbs Ringing Correction of Diffusion MRI

Human Connectome Project

The criterion (14) was used to determine the value of λ for each individual DW image. In Fig. 7, the dimensionless data fidelity ratio ${\Vert \stackrel{\sim }{\mathcal{F}}\widehat{u}-{\stackrel{\sim }{u}}_k\Vert }_2^2/N{\mathrm{\sigma }}^2$, is shown as function of dimensionless λ/σ for all images of the DW dataset. Curves were color encoded according to the corresponding b-value. The global, or average, noise variance σ² was determined by applying the method of Coupé et al. (44) to the b = 2 μm²/ms images (high-b images are expected to yield the least bias due to insufficient decoupling of noise and edges by the wavelet decomposition (54)); we assumed all DWIs to have the same σ. For the different b-values, the optimal λ is given by λ_b = τ_b σ with τ₀=0.72, τ₁= 0.83, and τ₂=0.88. Varying the diffusion direction has even a smaller effect on the ratio τ_b. We believe that the minor quality improvement of the reconstruction by tuning each λ individually does not compensate for the much increased computation cost. Therefore, we fix λ throughout this HCP experiment to λ = 0.83 σ.

FIG. 7.

Finding the regularization parameter λ from the condition (14). Tuning λ for all DW images shows that the variations of the ratio λ/σ are practically negligible. Curves were color encoded according to the corresponding b-value.

Figure 8 shows the non-DW, MD, and MK maps of a single axial slice of the HCP data, which was downsampled to 96 × 96 by truncation of the k-space and subsequently reconstructed to the original 144 × 168 resolution using ZF (with and without filtering), TV, and TGV. The initial downsampling was done to mimic clinical data. MD was calculated with diffusion tensors estimated with both the DTI and DKI model, but only the DTI-based parameter map is shown. Without smoothing and constraining the tensor fit, extreme negative MK values (black voxels) and/or unexpected heterogeneity in MD is observed in regions of interest such as the CC, i.e., alternating brighter and darker rims are visible. These maps show similar trends as Ref. (9). Smoothing the data results in spatial resolution loss, observed as image blur. Both TV and TGV result in a more robust fit as they minimize the Gibbs effect and the noise without manipulation of the resulting statistics and loss of spatial resolution. Violations of physical assumptions such as positive diffusion or positive kurtosis were observed in the HR, ZF, GF, and LF maps, whereas TV and TGV were clear from those unphysical values without constraining the fit. Visual differences between TV and TGV were subtle in this case due to the limited upsampling factor and high number of DW images. For more obvious differences, we refer to Fig. 9.

FIG. 8.

Non-DW, MD, and MK map of an axial slice, and a zoomed detail (red square) of the HCP data for the different reconstruction techniques. Gibbs ringing is clearly visible in ZF and might result in diffusion tensors with negative eigenvalues. The MK maps often show black voxels around edges, indicating outliers in the kurtosis fit.

A more quantitative evaluation was done by means of a ROI analysis. Initially, the genu (GCC) and splenium (SCC) of the CC were manually delineated, using the HR FA and MD maps for guidance. Next, the mean and SD of parameter values within the ROIs were calculated (Table 1). Negative MK values were excluded from the ROI analysis as they would dominate the results.

Table 1.

Quantitative Comparison of Different Reconstruction Methods for HCP Data Method

Method		DTI				DKI
		MD [μm2/ms]		FA		MD [μm2/ms]		FA		MK
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
GCC	HR	0.8760	0.1336	0.6711	0.1430	1.0974	0.2243	0.6946	0.1557	1.0226	0.2773
	ZF	0.8632	0.1546	0.6624	0.1535	1.0864	0.2507	0.6817	0.1693	1.0739	0.2725
	GF	0.8892	0.1629	0.5631	0.1367	1.1261	0.2673	0.5785	0.1484	1.1454	0.1540
	LF	0.8874	0.1655	0.5687	0.1412	1.1236	0.2699	0.5841	0.1530	1.1440	0.1567
	TV	0.8521	0.1227	0.6119	0.1351	1.1016	0.1892	0.6054	0.1353	1.1834	0.1719
	TGV	0.8522	0.1233	0.6118	0.1349	1.0981	0.1907	0.6068	0.1371	1.1851	0.1702
SCC	HR	0.8342	0.1814	0.7849	0.1063	1.0221	0.2538	0.8023	0.1111	1.2296	0.3475
	ZF	0.8320	0.2030	0.7768	0.1263	1.0232	0.2878	0.7942	0.1332	1.2291	0.3339
	GF	0.8932	0.2101	0.6994	0.1198	1.1228	0.3003	0.7096	0.1268	1.3203	0.2204
	LF	0.8903	0.2164	0.7046	0.1235	1.1186	0.3106	0.7153	0.1309	1.3214	0.2258
	TV	0.8377	0.1736	0.7523	0.1070	1.0591	0.2338	0.7515	0.1061	1.3953	0.2424
	TGV	0.8372	0.1739	0.7526	0.1068	1.0552	0.2336	0.7531	0.1053	1.4019	0.2403

First, comparing the GF/LF results to ZF/HR shows that CSF infiltration introduced by window filtering lowers FA by 10–15% and increases MD by 3–9%. In line with earlier studies, DKI results in significantly increased FA and MD when compared to DTI (55). Second, TV and TGV show reduced FA (3–11%) compared to ZF/HR, whereas MK is increased with 10–14%. Since the largest offset caused by Gibbs ringing increases the calculated FA, the significantly reduced FA for TV/TGV is expected. The increase in MK is also expected because Gibbs ringing lowers MK on average (see Figs. 1 and (2)), even after exclusion of the negative values. Note that HR cannot be considered as a ground truth as it is corrupted with Gibbs ringing as well. In terms of precision, quantified by the SD of parameter within the ROIs, TGV, and TV outperform all other reconstructions. In general, window filtering is also expected to result in improved precision compared to ZF. However, for MD, the opposite is observed because of the non-uniform infiltration of CSF.

Clinical Data

Figure 9 shows the non-DW, MD, and MK maps for ZF, GF, LF, TV, and TGV reconstructions of a single axial slice (256 × 256) of the clinical dataset and for a detail of those maps to highlight differences between the techniques. On the ZF map, the Gibbs ringing is very prominent, especially in the parametric maps, in accord with our analytical predictions. For example, in the MK map, black rims are aligned with the strong edges. The effect is significantly minimized by window filtering at the cost of image blur. Both the Gibbs suppression and image blur are more pronounced in LF. TV and TGV reconstructions outperform the other methods in terms of Gibbs suppression and maintaining spatial resolution after tuning λ using the criterion (14). As indicated in Fig. 1, minimal perturbations of the DW signal due to residual ringing might corrupt the estimation of the kurtosis. Hence, in a few voxels, physically implausible solutions were observed after TGV reconstruction. In that case, constrained tensor estimation might be considered. Although the staircasing artifact is more subtle in diffusion parameter maps than in the non-DW maps, the artifact can still clearly be observed in the TV reconstruction (red arrows).

DISCUSSION

Constrained Parameter Estimation

In the absence of Gibbs ringing correction, the use of constrained estimators has been promoted to ensure physical plausibility of the estimated diffusion parameters, such as positivity of the diffusion and kurtosis coefficients (6,7,20,21). Unfortunately, explicit or implicit constraints based on physical assumptions often disregard the statistical features of estimators. For example, negative diffusivities or kurtosis values are expected based on normal variance of an estimator if the expectation value is close to zero. Hence, imposing positivity constraints skews the estimates by enforcing positive values, thereby introducing a quantitative bias. Furthermore, despite potential visual enhancement, constrained solutions are not always more likely or physical. Enabling the use of unconstrained estimators avoids this potential source of inaccuracies. We would like to highlight that all the results in this work were obtained with unconstrained estimators.

Computation Time

The idea of data extrapolation has been around for decades (22–25), but it has not been fully adopted by the dMRI community. One of the reasons might be the computational cost of these techniques. The iterative optimization is time consuming (about a minute per slice on a regular desktop computer for TV and TGV), not to mention tuning of the regularization parameter. Indeed, the proposed Gibbs correction framework is a nonsmooth, but convex optimization problem in a high-dimensional space with the number of degrees of freedom determined by the number of voxels and an upscaling factor. Efficient and robust algorithms are available for such problems. However, their computational expense is inherent. Although all our experiments were performed within MATLAB, we would like to highlight that a CUDA implementation designed to run on NVIDIA graphics processing units allows speeding up the calculations significantly (56).

Regularization Parameter

Tuning of the regularization parameter λ is important. In this work we used Morozov’s discrepancy criterion (14) for an objective selection of λ, which achieves a balance between data fidelity and noise. However, the criterion assumes that anatomical features of interest can be distinguished from noise on a single DW image level. If not, those features may be removed in the respective DW images. Lowering λ might then be suggested to promote data fidelity over suppression of local fluctuations using the proposed framework.

The Morozov’s discrepancy criterion requires an independent estimation of the noise level σ. While here we used the method of Coupé et al (44) for fast and global noise estimation, we note that the problem of noise estimation is independent from our artifact correction framework and it can be tackled by several other approaches [e.g., (54,57)].

Ideally, λ should be tuned for each individual MR image. For a dMRI study, this would be very time-consuming. Fortunately, we can suggest following practices to minimize the overhead. First, for a single DW dataset in which the noise level can be assumed to be constant (54), we observe that the optimal λ is fairly independent from the diffusion encoding. The small variations of the optimal ratio λ/σ, about 10%, that we observed in our experiment are not expected to significantly alter the quality of the reconstruction. Second, we observed that the optimal λ is always quite close to σ. Hence, σ is good starting point for tuning λ with a minimum number of iterations.

Relation to Compressed Sensing

The optimization problem solved to suppress the Gibbs artifact is formally the same as described in CS (39–41). However, we would like to emphasize that the variational methods described in this article have little overlap with CS beyond the general form of the equation. CS aims to fully reconstruct signal by exploiting the sparsity of the signal in a well-chosen basis, whereas suppression of local variation by T(G)V is motivated from the observation that natural images have limited inherent spatial variability. Basically, one can state that a user-defined signal model is being imposed during TV approaches. The accuracy of the final T(G)V reconstruction depends on the accuracy of the T(G)V representation, whereas the accuracy of CS depend on two main conditions: (i) the existence of sparsifying transformation, and (ii) incoherence between window Fourier operation and this sparsifying transformation (40,58). If both conditions are met, full recovery of the undersampled signal is possible (40). Unfortunately, for many datasets, i.e., regularly k-space sampling with omitted high frequency content, incoherence is not achieved and full recovery is not possible. However, a well-chosen signal model can suppress local spatial variations due to noise and Gibbs ringing without aiming for full recovery of unmeasured signals.

In this work, we compared two signal models: piecewise constant and piecewise linear, which are implicitly imposed by the TV and second order TGV penalty term, respectively. Given that the oscillating Gibbs pattern is incoherent to the piecewise linear TGV basis, both the TV and second order TGV basis can be used for the suppression of the Gibbs artifact. However, beyond the noise and the Gibbs artifact, TV is only optimal for truly flat objects like numerical phantoms, whereas TGV has more potential in real world objects. Hence, the final reconstructions are more accurate, or less artificial (cf. staircasing artifact).

Rician Noise Bias

The Rician noise bias is another source of inaccuracies in the estimation of diffusion metrics (54,59). Although the quantitative bias due to the skewness of a Rician distribution depends on the SNR and used estimator, it is good practice to account for it in dMRI analyses. While noise bias correction has not been covered throughout the work, we would like to share some insights. First, the proposed Gibbs suppression framework alters the data distribution. Next to Gibbs ringing, local variations due to thermal noise are being suppressed and, as such, the signal variation will significantly drop (denoising) (26,28), and the precision of parameter estimators will increase. Unfortunately, the Rician noise bias tends to elevate the measured signal. Basically, the reconstructed signal approximates the expectation value, or mean, of the measured signal instead of the signal itself. In case of a Rice distribution, the expectation value is always larger than its underlying signal (60). However, this signal elevation can easily be undone given the analytical expression of the expectation value of a Rice distributed variable (60,61). Approximations of these computation expensive functions are described (60). Correcting the signal before tensor estimation (linear or nonlinear) will improve the accuracy of tensor estimation. We refer to recent literature for more in depth discussions of this topic (11,54,59,61).

Microstructural Modeling

Note that despite our focus on empirical metrics derived from the cumulant expansion throughout this work, similar conclusions will apply for all microstructural parameters (e.g., AWF, compartment diffusivities, myelin fraction, etc), regardless (regardless) of the complexity of the model. Indeed, Gibbs ringing is an artifactual feature of the signal that will corrupt all metrics derived from it. For example, Fig. 1 shows that a simple biexpontial one-dimensional model might result in negative AWFs under the influence of Gibbs ringing. We believe that the significance of the quantitative bias due to factors such as Gibbs ringing will only increase with going to more specific microstructural diffusion models. Indeed, the quantitative biases will interfere with the analysis and interpretation of those specific metrics, often in an unpredictable manner. Moreover, the artifact is mainly dominant in white matter structures of wide interest such as the CC.

CONCLUSIONS

We have shown that the Gibbs ringing effect on the diffusion signal metrics is unexpectedly strong compared to the 9% alterations in the DW images. The bias occurs even for low b-value acquisitions, due to the general dependency of the ringing pattern on the b-value. To cure this problem without resolution loss, we here described a comprehensive framework of extrapolating the k-space beyond truncation frequency by adopting physically reasonable representation of the image that is imposed by the second order TGV function. We showed that diffusion model parameters are estimated much more robustly and accurately, i.e., without violating physical constraints, using the TGV-based Gibbs correction.