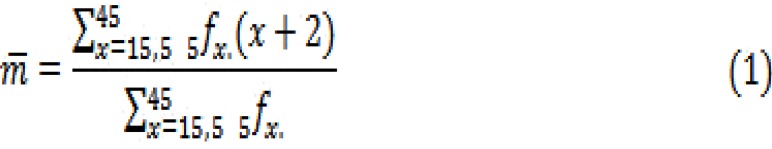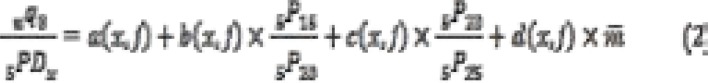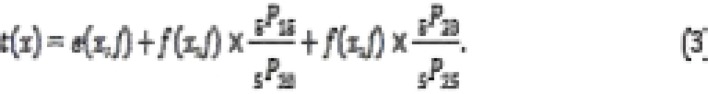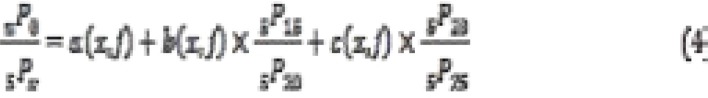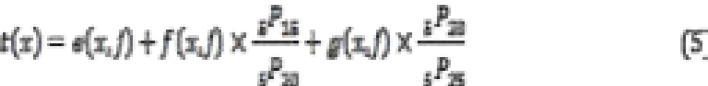Indirect child mortality estimation technique to identify trends of under-five mortality in Ethiopia

Abstract

Background

In sub-Saharan African countries, the chance of a child dying before the age of five years is high. The problem is similar in Ethiopia, but it shows a decrease over years.

Methods

The 2000; 2005 and 2011 Ethiopian Demographic and Health Survey results were used for this work. The purpose of the study is to detect the pattern of under-five child mortality overtime. Indirect child mortality estimation technique is adapted to examine the under-five child mortality trend in Ethiopia.

Results

From the result, it was possible to see the trend of under-five child mortality in Ethiopia. The under-five child mortality shows a decline in Ethiopia.

Conclusion

From the study, it can be seen that there is a positive correlation between mother and child survival which is almost certain in any population. Therefore, this study shows the trend of under-five mortality in Ethiopia and decline over time.

Introduction

The risk of a child dying before reaching five years of age is highest in the WHO African Region which is about 7 times higher (90 per 1000 live births) than that in the WHO European Region (12 per 1000 live births)^1,2. Regardless of different strategies taken to reduce under-five mortality, the threat is highest for most of the sub-Saharan countries. The proportion is above 100 deaths per 1000 live births^3,4.

The current Demographic and Health Survey that was conducted in Ethiopia has wide coverage. The survey has different demographic, socio-economic and geographic variables which could help to indicate the means to reduce the possibility of child deaths. Currently, under-five child mortality cases have shown considerable decline in Ethiopia. There has been a progressive and consistent decline in all regions of Ethiopia. This has possibly been due to the consistent implementation of health interventions since 1960⁵. As indicated by various official sources, child mortality declined by 35 per cent in Ethiopia through the years. Similarly, in Ethiopia, infant and under-five children mortality has also declined by 21 per cent and 26 per cent respectively. Nevertheless, despite all those gains under-five rates of child death is still high in Ethiopia. Furthermore, crude death rates have also significantly dropped over the past ten years^6–9. As the record shows, infant and under-five mortality in Ethiopia has showed a sustained decrease over the past 25 years. But, in the last ten years there is a more pronounced reduction^8,10. Therefore, to identify socio-economic and demographic factors which affect child mortality, survival analysis has been used.

To find trends of under-five child mortality, direct or indirect methods of estimation can be used. In 1968, Brass and Coale developed indirect methods of estimation¹¹. This method uses statistics on total numbers of children ever born and children alive or dead reported by women. This is categorized by age group to access under-five mortality. The level of under-five child mortality can be reflected by the proportion of dead children born to women by age. Similarly, under-five mortality can also be affected by the age distribution of child birth and the age distribution of child mortality^11,12.

Furthermore, the assessed probabilities of dying reveal the mortality rates that have occurred at a range of ages and dates. This can be achieved if mortality changed over time. Therefore, the probabilities of dying estimate can be found from different age groups of women. This estimated value can be interpreted into a common index of mortality. The estimated statistics value will refer to different dates. Therefore, this predictable value can be used to comprehend the wide trend in mortality over time.

The objective of this research is to estimate trends of under-five child mortality using 2000; 2005 and 2011 Ethiopian Demographic and Health Surveys.

Materials and methods

The Ethiopian Demographic and Health Surveys (EDHS) were conducted in 2000; 2005 and 2011 in Ethiopia. These are cross-sectional surveys which are conducted every five years and administered at the household level. These surveys were used in the current paper. The survey consists of 540 (2000 and 2005) and 624 (2011) selected enumeration areas. Complete household listing was done in each of selected EAs. The 2000, 2005 and 2011 EDHS sample was planned to deliver evaluations for the health and demographic factors of concern for Ethiopia for 11 geographical areas classified by urban and rural areas^6–8.

Data required for the analysis is number of women classified into five-year age groups, period of marriage, number of alive children within the five-year age group, number of children born alive that have died before or at the time of the survey within the five-year age group, and number of births before the survey within the fiveyear age group. To perform the analysis, there are important assumptions to consider. These assumptions are population age trends of fertility and under-five mortality and are sufficiently denoted by the model trend used in developing the technique. In any time period, death of children does not differ by five-year group of mothers; the relationship between mortality risks of children and survival of mothers in the population indicates that no correlation exists. Therefore, this sufficiently shows the appropriately defined cohort outlines of childbirth. The first step for the analysis is to calculate the proportion of children deceased for all five-year groups 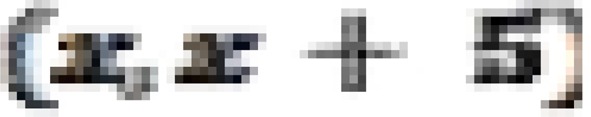of women. This can be obtained by dividing the number of children deceased by the number of children ever born. The mean numbers of children ever born to women in all five-year groups can be calculated for all five-year groups of women. This value can be calculated by dividing the reported number of children born by the number of women 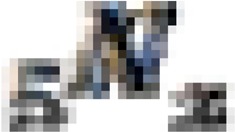in the group¹³.

Selecting the life table family model is important. To translate the proportion dead from a standard 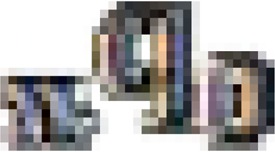, into a common index such as Under-five mortality rate (U5MR) the age pattern of a child is used. The appropriate model can be obtained based on the idea of the family birth history (FBH) by plotting estimates of 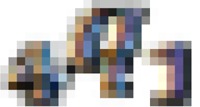against those of 1q0. Based on the graph, a model from Coale-Demeny and United Nations model life tables can be selected. But this choice depends on the availability of appropriate FBH estimates. For such cases, the choice of a model can be on the base of child mortality trend in an adjacent population. In most of the cases, the appropriate fit of the data to any model might not be found. For such cases, the model that appropriately defines the range of observations available must be selected^14,15.

The age-specific fertility can be estimated using United Nations model life tables for developing countries. This value can be estimated from age-specific fertility rates 5f_x as follows:

In the numerator (x+2) denotes the mid-point of the age group x to x+5 at the time of the occurrence of births. This assumes that age-specific fertility rates are obtained from births in the year before the survey grouped by age of woman at the time of the survey¹¹.

After identifying the model life table, it is important to find appropriate parameters estimates for ⁹. Therefore, the equation for UN model life table is given by

Here, the value of exists only for UN Model Life Tables. In the equation for each value of age group 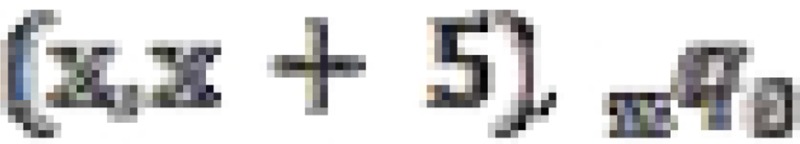is obtained by multiplying the right-hand side of the equation by the empirically-observed , where PD is proportion dead^16–18.

The percentage dead of total children ever born by women of exact age x, PD(x), can be defined as birth-weighted average of cohort probabilities of dying. It is given by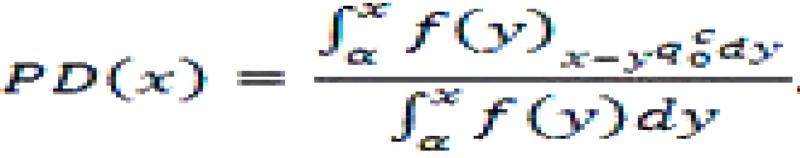

In the equation, f(y) represents the fertility rate at age y, _x-yq^co the probability of dying by age (x-y) for the cohort born (x-y) years earlier, the earliest age of childbearing. Proportions deceased for five-year age is obtained by averaging point PD. The estimate is weighted for expected population distributions. Moreover, it is expected that the population can be considered as unchanging, with a growth rate appropriate for the demographic parameters¹¹.

The time reference 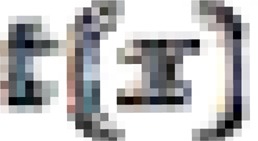for each can be estimated can be estimated using parameters 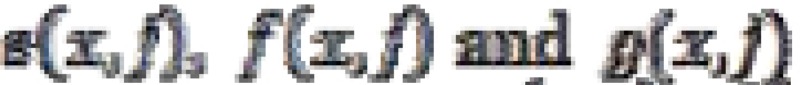can be estimated using parameters 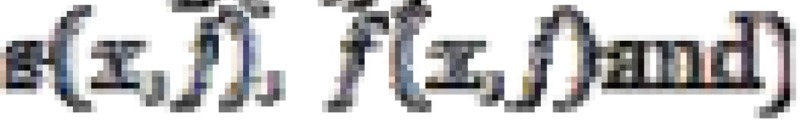for model life table. The value can be obtained as follows

Similarly, the parameters 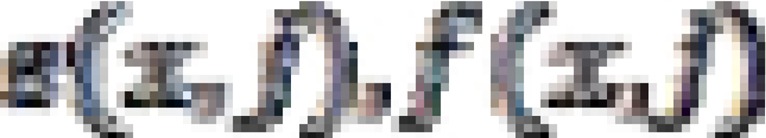and 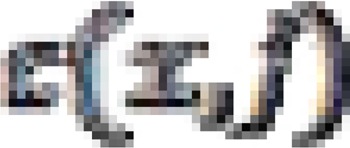can be substituted and be written as

Therefore, or all age group 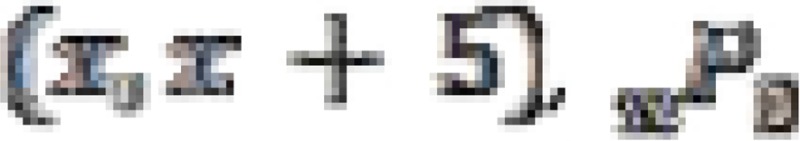is estimated by multiplying the right-hand side of the equation by .

The next step of the analysis is to estimate the time reference 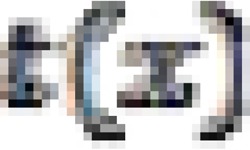for each estimated 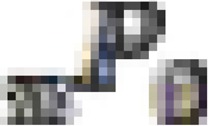. Therefore, for the model life table, parameters 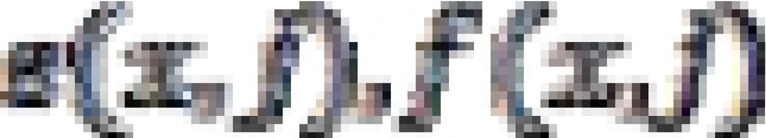and 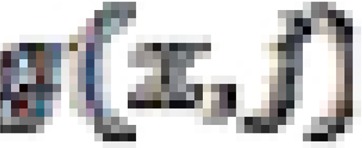can be substituted to form the following equation, which is given as:

For all age groups, 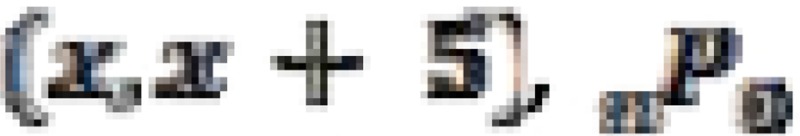is estimated by multiplying the right-hand side of the equation by ¹⁹.

After estimating the required parameters, the next step is to change all estimates of 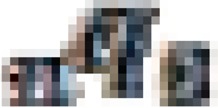into an estimate . For the indirect child mortality estimation method, each of the probabilities of dying by exact ages of childhood, 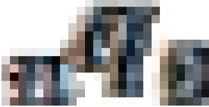, is converted into a value of . Moreover, represents the level parameter for relational logit model life tables. The value is useful to estimate the corresponding probability of dying between birth and exact age 5, . Therefore,

where the estimates of 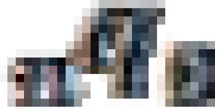come from equation 2 and the 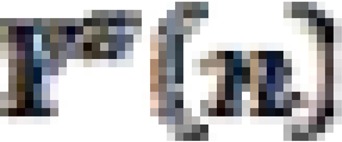are logit transformations of the standard life table. For the probabilities of dying, a sequence of values can be estimated from data for the different age groups of respondents. Therefore, for each

Choosing the appropriate standard life table is important to apply relational model approach. Identifying the appropriate model helps to use the indirect estimation procedure²⁰.

Data analysis

This analysis uses the information on total children and children surviving by age of mother from the 2000, 2005 and 2011 Ethiopian Demographic and Health Survey (EDHS).

The first step is to calculate proportions dead of children 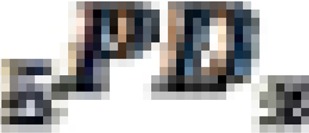. Table 1 displays the mean of total children, mean of children surviving and proportion dead by five-year age group of mother from the 2000, 2005 and 2011 EDHS. The proportion dead of children ever born 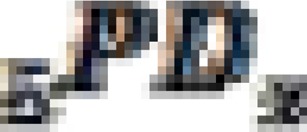is obtained by dividing the number of surviving children by the number of total children, and subtracting the result from 1.

Table 1.

Children ever born (CEB), children surviving and proportion dead (PD) for EDHS 2000, 2005 and 2011

Age of mother	2000			2005			2011
	Mean CEB	Mean children surviving	PD	Mean CEB	Mean children surviving	PD	Mean CEB	Mean children surviving	PD
15–19	0.462	0.387	0.163	0.718	0.645	0.101	1.638	1.407	0.141
20–24	1.740	1.459	0.162	1.816	1.592	0.123	2.545	2.185	0.142
25–29	3.099	2.512	0.190	3.192	2.808	0.120	3.898	3.406	0.126
30–34	4.774	3.719	0.221	4.735	4.018	0.151	5.432	4.581	0.157
35–39	5.901	4.407	0.253	6.007	4.886	0.187	6.727	5.530	0.178
40–44	7.256	5.358	0.262	6.699	5.460	0.185	7.907	6.378	0.193
45–49	6.990	5.124	0.267	7.471	5.610	0.249	8.642	6.655	0.230

The proportion dead (PD) of children ever born 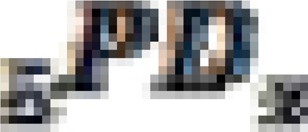, is given by 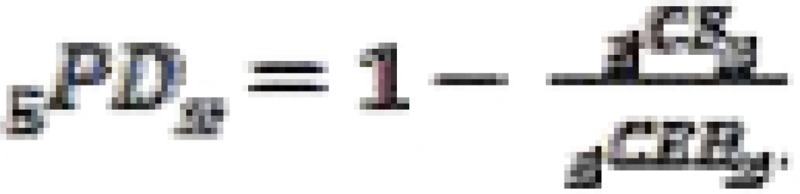. As the table indicates, for 2000, 2005 and 2011 the children ever born and children surviving increases as age increases. For the analysis, it is important to calculate the average numbers of children ever born to women in each five-year group 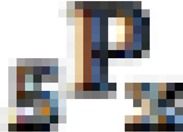. This average value is obtained by dividing number of total children by the number of women in the age group, i.e; 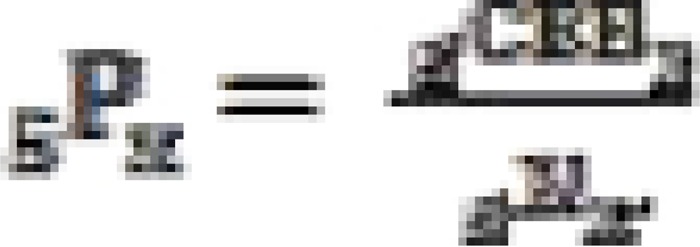. Based on the result from Table 2, it is possible to calculate parity. Parity is the number of times a female has given birth (multiple births as one birth) and includes still births. The parity ratio can be calculated for each age group. For example, for age group 20 – 24, the estimate is given by

and the rest are calculated likewise.

Table 2.

Parity ratio of the mother for 2000, 2005 and 2011 EDHS

Age Group	2000	2005	2011
15–19	-	-	-
20–24	0.2657	0.3953	0.6437
25–29	0.5615	0.5688	0.6530
30–34	0.6492	0.6742	0.7176
35–39	0.8090	0.7882	0.8074
40–44	0.8133	0.8966	0.8508
45–49	1.0380	0.8968	0.9150

The parity ratio for all age groups for 2000, 2005 and 2011 is displayed in Table 2. In the analysis, estimation of the time reference t(x) for each estimated is important. This value can be obtained using equation 3. Table 3 presents the estimate of time reference for 2000, 2005 and 2011 Ethiopian Demographic and Health Survey. The estimated reference date can be calculated by subtracting t from year of the survey. The month of the survey can be represented as the decimal. To find the final required result, it is important to convert each estimated into an estimate of the common index .

Table 3.

Estimates of time reference t(x) for each estimates in years 2000, 2005 and 2011 EDHS

Age Group	x	2000		2005		2011
		t(x)	Time location	t(x)	Time location	t(x)	Time location
15–19	1	1.4418	1998.65	2.1364	2002.95	1.0921	2008.67
20–24	2	2.8686	1997.22	3.5666	2001.52	1.3207	2007.65
25–29	3	4.7513	1995.34	5.1237	1999.96	1.5996	2006.63
30–34	5	6.8872	1993.20	6.7244	1998.36	2.0779	2001.59
35–39	10	9.2062	1990.88	8.3650	1996.72	2.7705	1996.57
40–44	15	11.6989	1988.39	10.2538	1994.83	4.1520	1991.54
45–49	20	14.4717	1985.62	12.8154	1992.27	6.9650	2011.09

The estimated index will be valuable to associate estimates through age groups. Each is transformed into its logit 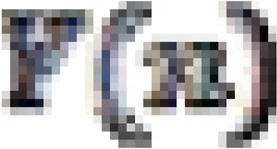by means of the identity 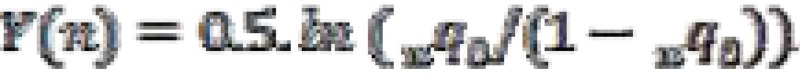The value of is then found by subtracting the standard 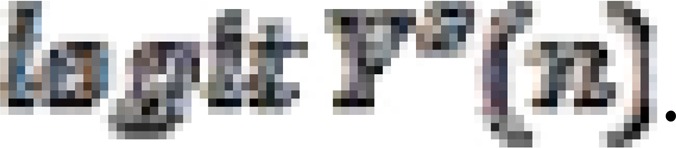. Each is used with the standard 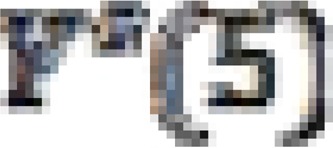to get the estimated . The estimated logit life table parameter for all estimates and developing a set of 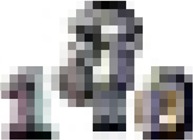and is presented in Table 4.

Table 4.

Estimating the logit life table parameter α for each estimate

Age group	2000			2005			2011
	alpha		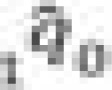	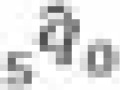alpha		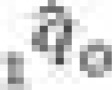	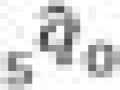alpha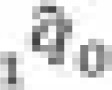
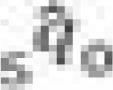15–19	0.389	132.094	197.417	−0.206	44.308	69.706	0.100	82.329	125.811
20–24	0.344	122.139	183.580	0.129	82.945	127.535	0.055	72.374	111.974
25–29	0.382	130.613	195.368	0.120	81.609	125.578	0.126	82.542	126.946
30–34	0.439	144.114	213.916	0.229	99.650	151.734	0.266	106.398	161.376
35–39	0.495	158.374	233.201	0.327	118.526	178.519	0.328	118.808	178.916
40–44	0.467	151.211	223.552	0.273	107.766	163.323	0.335	120.191	180.854
45–49	0.416	138.402	206.104	0.396	133.804	199.779	0.372	128.272	192.124

Based on Table 4, the estimated under-five and under-one mortality over time for 2000, 2005 and 2011 EDHS can be represented using graphs. These graphs are presented in Figures 1–3.

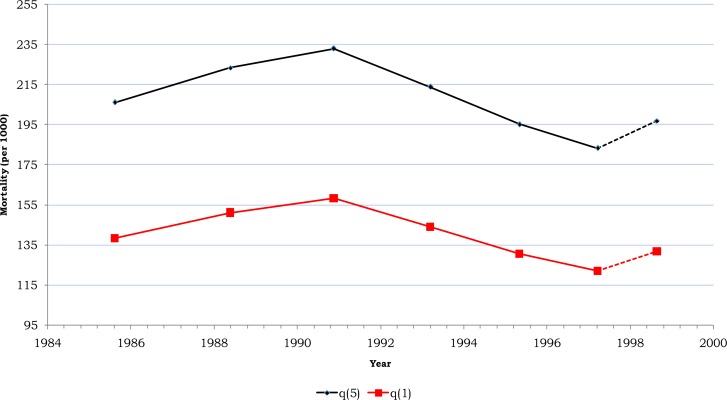
Figure 1.

Estimated under-five and under-one mortality over time, 2000 EDHS

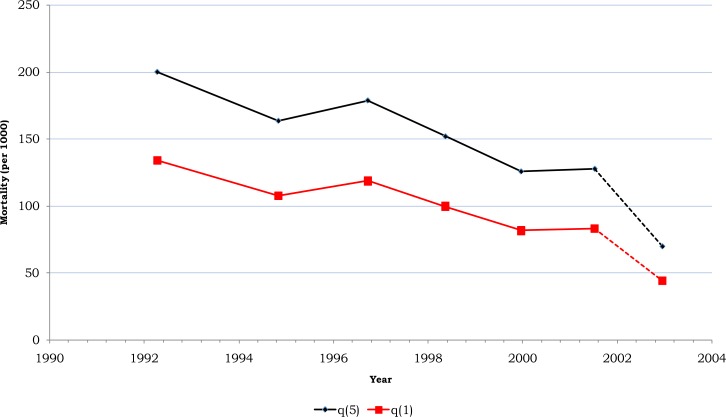
Figure 3.

Estimated under-five and under-one mortality over time, 2011 EDHS

Figure 1 represents all estimates of and with the corresponding reference date. The figure shows an increasing tendency in under-five child mortality over time, from early 1980s up to early 1990s and starts to decline up to the end of 1990s. After this, it shows an increase up to 2000. The apparent increase in child mortality at the end of 1990s is to be overlooked owing to the possible overestimation of mortality estimated from very young mothers.

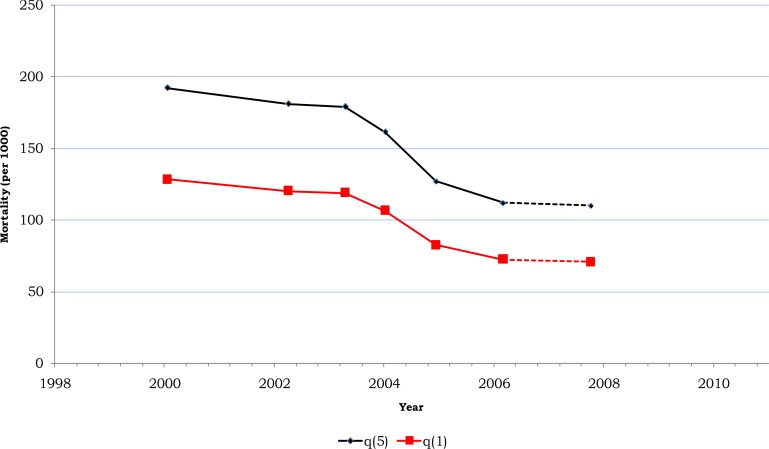
Figure 2 represents each estimate of and against the corresponding reference date for 2005 EDHS. The figure shows a declining trend in under-five mortality over time, from around 130 per 1000 and 200 per 1000 for under-five and under-one child mortality respectively.

Figure 2.

Estimated under-five and under-one mortality over time, 2005 EDHS

Similarly, Figure 3 represents each estimate of and against the corresponding reference date for 2011 EDHS. The result shows a decreasing tendency in under-five mortality over time.

Discussion

For any data generated, it is important to check for its quality. The collected data have to be checked for the quality of the data. Even though the data have been collected carefully, data sets may have errors. These errors can be as a result of many sources; for instance an interviewer error, sampling error, data entry or editing errors, etc. The threats for children of women aged 15–19 and the indirect estimate of child mortality constructed on children ever born (CEB) and children dead (CD) for this age group are repeatedly high. But sometimes the population average is also high. There are similar patterns to a minor degree for the children of mothers aged 20–24. Therefore, to check the validity of a data, it is important to check first birth information. This is because first births are recognised to be at higher threat of dying than higher-order births. Similarly, the children born to younger women contain an above-average percentage of first births. The other important factor is women having children at young ages and socio-economic factors. To check validity, it is important to check whether women having children at young ages come from below-average socio-economic groups. Because of this the children will be exposed to above-average mortality risks²⁰.

When interpreting the results, it is essential to study two characteristics. The first characteristic is that there is no evidence about specific dates or ages in the basic data. Here, for the number of total children by women, the time point is births which happened at some point between first birth and age at the time of the survey. Similarly, evidence on children that have died is very limited. Because age ranges can be determined by the time of distributions for births it is difficult to draw decisions about the short-term situation of child mortality. Therefore, results for two women of the same age reporting the same numbers of total children born and died could show dissimilar mortality situations. Therefore, using summary birth history gives a suggestion of an average past tendency. Therefore, based on 2000, 2005 and 2011 EDHS results, under-five mortality show a decrease in Ethiopia. A similar study was conducted by Ayele et al. (2015) using the 2011 EDHS. The result from this study shows a decline in under-five mortality²¹. Similarly there are numerous cross-sectional studies on under-five mortality in Ethiopia^9,22,23. These studies are restricted in their ability to show effective inferences over time using the 2000, 2005 and 2011 EDHS surveys.

On the other hand, information is given only for surviving women who were still living during the survey. The survey did not include information for dead women before the survey took place. This creates respondent selection bias. Therefore, this analysis does not include the mortality situation of children born whose mothers died before the survey. But, if information for these children is included in the survey, then it will be possible to capture the full tendency of child mortality because these children have higher mortality than those born to mothers who do still live. Therefore, from the result it is possible to see that certain positive correlation between mother and child survival is almost certain in any population. This study shows the trends of under-five mortality in Ethiopia. The next step is to investigate other factors which affect the under-five mortality. For this purpose, different statistical models, such as Bayesian methods, and generalized mixed models which incorporate random effects, will be employed.

Ethical clearance

Ethical clearance for the survey was provided by the EHNRI Review Board, the National Research Ethics Review Committee (NRERC) at the Ministry of Science and Technology, the Institutional Review Board of ICF International, and the CDC.

Competing interests

The authors declare that they have no competing interests.