Comparison of methods for auto-coding causation of injury narratives

Abstract

Manually reading free-text narratives in large databases to identify the cause of an injury can be very time consuming and recently, there has been much work in automating this process. In particular, the variations of the naïve Bayes model have been used to successfully auto-code free text narratives describing the event/exposure leading to the injury of a workers’ compensation claim. This paper compares the naïve Bayes model with an alternative logistic model and found that this new model outperformed the naïve Bayesian model. Further modest improvements were found through the addition of sequences of keywords in the models as opposed to consideration of only single keywords. The programs and weights used in this paper are available upon request to researchers without a training set wishing to automatically assign event codes to large data-sets of text narratives. The utility of sharing this program was tested on an outside set of injury narratives provided by the Bureau of Labor Statistics with promising results.

1. Introduction

The National Institute for Occupational Safety and Health (NIOSH) maintains a database from the Ohio Bureau of Workers’ Compensation (OHBWC) containing over 1 million workers’ compensation (WC) claims from 2001 to 2011. For tracking, trending and prevention purposes, it is crucial to identify the event or exposure leading to the injury for each claim. For example, an intervention program attempting to prevent back strains would benefit from the knowledge of the leading cause of this injury (i.e. overexertion, bodily reaction to slip/trip/fall, etc.). In the OHBWC database however, event/exposure was captured in a free-text field, usually filled out by the injured worker, describing the events leading to the accident. Categorizing these claims into standardized event/exposure categories, such as the Occupational Injury and Illness Classification System (OIICS) developed by the Bureau of Labor Statistics (BLS), would require manually reading each claim and assigning an event/exposure code.

Recently, researchers (Wellman et al., 2004; Lehto et al., 2009; Marucci-Wellman et al., 2011; Bertke et al., 2012; Taylor et al., 2014) demonstrated that computer learning algorithms using variations of the naïve Bayes model can auto-code injury narratives into different causation or event/exposure groups efficiently and accurately. In addition, a webinar (CWCS, 2014) was held by the NIOSH Center for Workers’ Compensation Studies with participation by experts from the Liberty Mutual Research Institute for Safety (Helen L. Corns and Helen Marucci-Wellman), NIOSH (Stephen J. Bertke), Bureau of Labor Statistics (Alexander Measure), and Purdue University (Mark R. Lehto) presenting work on the topic of auto-coding workers’ compensation narratives. The presenters demonstrated that the algorithms could code thousands of claims in a matter of minutes or hours with a high degree of accuracy by “learning” from claims previously coded by experts, referred to as a training set. Furthermore, these algorithms provided a score for each claim that reflected the algorithm’s confidence in the prediction and, therefore, claims with low confidence scores could be flagged for manual review.

The majority of recent research into auto-coding injury narratives has focused on variations of the naïve Bayes models (Vallmuur, 2015) and while these models have been shown to be highly effective and intuitive, alternative machine learning approaches have been shown to out-perform them in many applications (Measure, 2014). One method in particular is referred to as regularized logistic regression and evaluating its performance in comparison to the naïve Bayes model is one focus of this study.

Another purpose of this study is to explore the features used by these auto-coders. Previously, the main features considered were the occurrence or nonoccurrence of certain individual words. However, in natural language, words do not generally occur individually and often sequences of words commonly appear together. For example, common key words of interest for coding event/exposure are “FELL” and “OFF” and these words are helpful in identifying an injury caused by a slip, trip, or fall. However, the occurrence of the sequence “FELL OFF” is also common and could provide further evidence of a slip, trip, or fall. An example of the utility of considering two word sequences can be seen in the claim narrative “DRIVER FELL ASLEEP WENT OFF RIGHT SIDE OF ROAD INTO DITCH.” This narrative contains both “FELL” and “OFF” but does not contain the sequence “FELL OFF,” so identification of (or lack of) this feature could provide more evidence for a non-fall event/exposure.

The use of two-word sequences is not a new concept in the computational linguistics field. In fact, within the field of coding injury narratives, Lehto et al. (2009) and Marucci-Wellman et al. (2011) have considered two-word (and longer) sequences in a separate model referred to as “Fuzzy Bayes.” Also, Grattan et al. (2014) and Marucci-Wellman et al. (2015) used two-word sequences within the Naïve Bayes framework, however, single-word and two-word sequences were used in separate models, not in a single model. Measure (2014) provides a more exhaustive investigation into which features optimize various auto-coder models and found that both the Naïve Bayes and logistic event auto-coders benefit from including single word and two-word features along with the North American Industry Classification System (NAICS) code of the employing establishment in a single model.

Finally, not all researchers or public health practitioners have access to a set of previously coded records to use as a training set on their un-coded data and most privacy agreements would prohibit providing/publishing workers’ compensation claims. However, each of these auto-coding methods involve calculating a table of “weights” (coefficients) associated with each feature by event/exposure code. The weights table has all the necessary information from the training set needed to auto-code additional claims and can be easily be constructed in a way that has all personally identifiable information removed. As a result, the tables from this study are available upon request to the public (cwcs@cdc.gov). Since this table of weights has been optimized on the data from this study (OHBWC claims), we tested the feasibility of using these weights to auto-code other injury narratives by sharing it with BLS and asking them to evaluate its ability to assign event/exposure codes to Survey of Occupational Injuries and Illnesses (SOII) cases that had been previously manually coded.

In short, this paper will: (1) investigate the performance of a naïve Bayes model vs a logistic model, (2) investigate the performance of adding two word sequences into a single model, (3) demonstrate the feasibility of sharing an auto-coder pre-trained with OHBWC claims with an outside researcher.

2. Methods

2.1. Auto-coding procedures

Two general auto-coding procedures were compared for this study: Naïve Bayes and regularized logistic regression. Details of these procedures can be found in the Appendix. In short, both procedures attempt to calculate the probability a given claim is the result of a particular injury or illness event/exposure by considering the relevant features of the claim. The event/exposure with the highest probability is assigned to the claim and the associated calculated probability is retained as a score value representing the confidence that the auto-coder assigned the correct category.

For this study, relevant features included: (1) the occurrence/nonoccurrence of a list of keywords in the narrative, (2) the occurrence/nonoccurrence of a sequence of two keywords in the narrative, (3) the resulting injury diagnoses categorized into 57 groupings. We defined keywords as any word that occurred in at least 3 claims of the training set and did not appear in a list of so-called “stop-words” (common, less informative words such as “the”, “a”, “an”, etc.). A sequence of two keywords was defined as any two keywords that occurred consecutively in a given narrative, after stop-words were removed. Finally, the 57 resulting injury categories were based on the International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) code for the “optimal return to work” (i.e. most severe) diagnosis (Beery et al., 2014) listed on the claim, which OHBWC defines as the injury that most likely will keep the injured worker off of work for the longest period of time and is assigned via a proprietary OHBWC algorithm. Details for the injury category variable have been previously described (Bertke et al., 2012) and inclusion of this additional field previously showed a substantial improvement on the auto-coding performance, namely raising the overall accuracy by about 5%.

2.2. Event/exposure categories

The auto-coding methods used in this study were used to code claims to a 2-digit OIICS event/exposure category. The OIICS system is a hierarchical sequence of numbers, where each digit indicates a further level of detail describing the event leading to the injury. For example, a claim coded as a 4 represents a Slip, Trip, or Fall and this can be further specified with a second digit as a slip or trip without fall (41), falls on same level (42) or falls to lower level (43). The full list of event/exposures can be found at: http://www.bls.gov/iif/oiics_manual_2010.pdf.

The OIICS coding system has a code of 9 indicating a claim that is un-classifiable and this is either due to a vague narrative or a narrative that is completely missing. In addition, when coding to the 2-digit event/exposure level, sometimes it was possible to identify the first digit (division) but there was not enough information to assign a more detailed category. In this instance, a zero is used as the second digit to signify “unspecified” claims within a specific division.

2.3. Evaluation

The test data used for this study consist of 7200 manually coded claims from a stratified random sample of allowed claims from 2001 to 2009 in the OHBWC database. The database contains a narrative for each claim answering the following the question: Description of accident (Describe the sequence of events that directly injured the employee, or caused the disease or death.) Claims were stratified to produce an equal number of medical-only and lost-time claims and equal numbers of claims per calendar month. All claims were manually coded by an experienced coder and coded to the 2-digit event/exposure OIICS code level. To estimate inter-coder reliability, one third of the claims were randomly assigned to a second experienced coder and manually coded.

To evaluate each method, the 7200 claims were randomly split into a training set consisting of 6200 claims and a prediction set of the remaining 1000 manually coded claims. All claims with a code of 9 and codes with a second digit of 0 were removed from the training set, since these claims were determined to be un-classifiable or not further classifiable beyond the first digit (division). These claims were not removed from the prediction set, however, so that the prediction set would be a representative sample of un-coded claims. As a result, the auto-coder will assign its “best guess” to a two-digit level and hopefully claims with a manual classification of 9 or second digit of 0 will be flagged for manual review due to insufficient evidence.

Each auto-coding method was used, and the auto-coded results of the 1000 claims in the prediction set were compared to the manual codes. Overall percent agreement was calculated as well as the sensitivity and positive predictive value (PPV) for each individual event/exposure category. The process of randomly splitting the 7200 claims into a training set of 6200 and a prediction set of 1000 claims was repeated 25 times and the overall percent agreement, and event/exposure specific sensitivities and PPVs were averaged across the 25 iterations. McNemars test was used to compare the overall accuracy between two methods as well as the accuracy of causation specific classifications.

To assess the effectiveness of including two-word sequences, claims were coded considering only the single keywords, and then considering both single keywords and two-word keyword sequences in addition to the injury category.

Two additional performance measures were considered. First, the accuracy of the calculated score value calculated by the auto-coder for each model was evaluated by plotting the score value versus the probability the claim was coded correctly. Second, the coding of event/exposure division (first digit only) was evaluated because in some public health settings this level of specificity is sufficient. To evaluate the effectiveness of auto-coding by OIICS event/exposure division, the claims were first auto-coded to 2-digits then the first digit of the auto-code was compared to the first digit of the manual code and the overall accuracy as well as the cause specific sensitivity and PPV were calculated.

Finally, the weights from the logistic regression model considering single and sequences of keywords only were provided to BLS to test on a set of 1000 randomly selected and previously manually coded cases of work related injuries or illnesses collected through the 2011 Survey of Occupational Injuries and Illnesses. Each case in the BLS database contains four text narratives describing the characteristics and circumstances of an incident of work related injury or illness (additional details of the format of BLS cases can be found in Measure, 2014). Briefly, the four narrative fields are responses to the following questions:

• “What was the employee doing before the incident occurred?”

• “What happened?”

• “What was the injury or illness?”

• “What object or substance directly harmed the employee?”

To make these narratives compatible with the OHBWC auto-coder, these four narratives were combined into a single narrative field and then auto-coded using the weights calculated from the 7200 BWC claims. Again, the auto-coded results were compared to the manual codes and overall percent agreement as well as event/exposure specific sensitivities and PPVs were calculated.

3. Results and discussion

Table 1 presents the average of the sensitivity and PPV of the 25 iterations using the Naïve Bayes and logistic models to code to 2-digits for common event/exposures. Overall, the logistic model performed significantly better than the Naïve Bayes model (p-value = <0.001) by coding about 5% more claims correctly. Even by event/exposures, the logistic model generally outperformed the Naïve Bayes model with the exception of Overexertion Involving Outside Sources (71) in which case the naive Bayes model had a larger PPV (a difference of +5%). The naive Bayes model was more conservative with this outcome, coding fewer claims as 71 while maintaining a high level of sensitivity.

Table 1.

Performance of naive Bayes model and logistic model with single keywords and injury categories (Single + Inj) considered as features and single keywords, two-word sequences and injury categories (Single + Seq + Inj) as features. The results are the average of 25 iterations.

Cause	N true	Naive Bayes						Logistic
		Single + Inj			Single+ Seq +Inj			Single + Inj			Single+ Seq +Inj
		N pred	Sen	PPV	N pred	Sen	PPV	N pred	Sen	PPV	N pred	Sen	PPV
Overall	1000	1000		65.3%	1000		65.6%	1000		69.4%	1000		70.8%
Intentional injury by person (11)	13	9	33.1%	46.6%	11	36.8%	45.3%	6	24.5%	54.8%	5	25.5%	66.4%
Injury by person- unintentional/unknown (12)	13	9	32.7%	46.2%	11	35.2%	41.6%	5	21.1%	56.3%	5	22.0%	58.3%
Animal and insect related (13)	13	13	75.6%	74.3%	14	75.3%	69.0%	11	72.6%	82.9%	11	72.0%	82.8%
Pedestrian vehicular incident (24)	5	1	7.2%	26.5%	2	7.2%	19.1%	1	2.4%	20.0%	1	2.4%	17.6%
Roadway Incident involving motorized vehicle (26)	28	38	92.3%	69.2%	40	93.5%	65.7%	29	83.0%	80.5%	29	84.2%	81.4%
Slip/trip without fall (41)	45	41	36.6%	40.7%	48	42.7%	40.0%	44	66.7%	68.0%	43	67.5%	71.0%
Falls on same level (42)	107	118	73.3%	66.4%	107	70.4%	70.5%	113	77.3%	73.1%	112	78.0%	74.3%
Falls to lower level (43)	66	80	73.7%	61.0%	79	74.6%	62.6%	61	68.2%	74.1%	61	69.0%	74.5%
Exposure to temperature extreme (53)	18	22	88.9%	75.7%	21	88.3%	75.7%	21	86.3%	74.9%	21	85.9%	75.7%
Exposure to other harmful substance (55)	24	29	84.4%	69.2%	30	83.0%	65.5%	21	71.4%	80.8%	22	72.0%	78.2%
Needle stick without exposure to harmful substance (61)	6	6	81.1%	72.5%	6	79.7%	74.5%	5	81.1%	88.6%	5	79.7%	88.4%
Struck by object/equip. (62)	195	206	68.9%	65.3%	193	67.6%	68.5%	242	79.6%	64.4%	237	80.8%	66.7%
Struck against object/equip. (63)	85	74	48.1%	55.6%	84	55.1%	55.5%	85	53.3%	53.2%	90	61.6%	58.5%
Caught in or compressed by object/equip. (64)	53	69	75.6%	57.7%	70	77.7%	58.3%	54	72.6%	70.4%	54	73.1%	71.4%
Rubbed or abraded by friction/pressure (66)	7	4	17.1%	27.5%	5	27.4%	36.1%	1	5.7%	38.5%	1	6.9%	50.0%
Overexertion involving outside sources (71)	194	222	89.8%	78.8%	214	87.9%	79.9%	244	94.7%	75.3%	248	95.4%	74.8%
Repetitive motions (72)	15	22	81.1%	55.8%	24	81.6%	51.4%	13	64.1%	72.4%	13	63.0%	72.0%
Other exertions or bodily reactions (73)	43	30	36.1%	50.6%	32	37.7%	49.8%	37	52.4%	59.8%	37	53.1%	61.7%
Not classifiable (99)	14	0	0.0%	-	0	0.0%	-	0	0.0%	-	0	0.0%	-

Sen = Sensitivity; PPV = Positive Predictive Value; N_true = number of claims manually coded as each category; N_pred = number of claims auto-coded as each category.

Consideration of two-word sequences of keywords marginally improved the performance of both models. The Naïve Bayes Model slightly improved by 0.3% and the logistic model improved by about 1.4% overall. Results varied by event/exposure category. There were large improvements in coding Struck by object or equipment (62) and Struck against object or equipment (63) with both sensitivity and PPV improving for the logistic model when two-word sequences were considered. In fact, 32% of Struck against object or equipment (63) claims incorrectly coded as Struck by object or equipment (62) were correctly switched to Struck against object or equipment (63) when two-word sequences were considered for the logistic model. Similarly, there were improvements in coding Slip or trip without fall (41), Falls on same level (42) and Falls to lower level (43) claims with the logistic model.

The modest improvement in the Naïve Bayes model with consideration of both single-word and two-word keywords is noteworthy because the motivation for the Naïve Bayes model contains an assumption of independence of features. The Naïve Bayes model “naively” assumes that the features occur independently, however this assumption is blatantly violated when considering both single and two-word sequences. For example, if a claim does not contain “FELL” then it most certainly does not also contain “FELL OFF.” This independence assumption was not made in the logistic model, which may be why the improvement in adding two-word sequences of keywords for the logistic model was a bit larger.

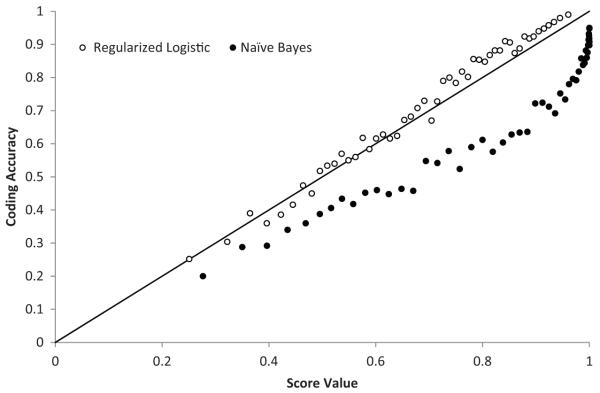
The effect of ignoring the independence assumption can also be seen when considering the score value reflecting the confidence of the auto-coded event/exposure for a given claim. The claims were evenly divided into 50 groups, based upon their score value, and the percent correctly coded in each group is graphed versus the median score of the group in Fig. 1. The score values for the logistic model were much closer to the actual accuracy, meaning that a claim with a score value of 80% is in fact coded correctly about 80% of the time. The score value for the Naïve Bayes model are optimistic, as has been shown before (Bertke et al., 2012; Lehto et al., 2009), meaning that a claim with a score value of 80% was coded correctly much less than 80% of the time (in this study, it was correct about 60% of the time).

Fig. 1.

Comparison of logistic model’s score value and Naïve Bayes model’s score value and actual coding accuracy.

Score values were useful for flagging claims for manual review for both models. However, another method used to flag claims would be to run two models and flag the claims where the models disagree (Marucci-Wellman et al., 2011; Grattan et al., 2014). In this study, the naive Bayes and logistic model disagreed on average 25.2% of the time when considering both single word and two-word sequences. Table 2 compares the effect of flagging these claims and assigning the manual code to these claims versus simply running the logistic model and flagging/manually coding the bottom 25.2% of the claims with the lowest score values. These two sets of flagged claims overlapped on only 12.5% of all claims. Both methods of flagging claims improved the overall accuracy of the set to close to 85%, with simply coding the lowest score value claims performing marginally better. By event/exposure, each method performed similarly.

Table 2.

Comparing the effect of manually coding about 25% of the claims where the Naïve Bayes model and logistic model disagreed (~25% Naïve + Log) versus simply manually coding the claims with the lowest score value from the logistic model (~25% Lowest Log). Both models used single keywords, two-word sequences and the injury category as features.

Cause	N true	~25% Naïve + Log			~25% Lowest Log
		N pred	Sen	PPV	N pred	Sen	PPV
Overall	1000	1000		84.5%	1000		84.8%
Intentional injury by person (11)	13	9	62.0%	89.4%	10	68.1%	91.7%
Injury by person-unintentional/unknown (12)	13	9	61.6%	87.5%	9	64.2%	94.9%
Animal and insect related (13)	13	13	88.1%	86.5%	12	87.8%	99.3%
Pedestrian vehicular incident (24)	5	2	40.8%	94.4%	2	36.8%	95.8%
Roadway Incident involving motorized vehicle (26)	28	32	97.6%	87.7%	30	95.8%	91.0%
Slip/trip without fall (41)	45	43	81.6%	86.0%	45	83.7%	85.0%
Falls on same level (42)	107	109	90.5%	88.6%	112	89.3%	85.2%
Falls to lower level (43)	66	66	86.5%	86.2%	63	85.2%	89.3%
Exposure to temperature extreme (53)	18	21	94.6%	82.1%	21	97.2%	86.6%
Exposure to other harmful substance (55)	24	25	88.0%	85.5%	22	88.9%	96.7%
Needle stick without exposure to harmful substance (61)	6	5	88.1%	92.6%	6	91.6%	92.9%
Struck by object/equip. (62)	195	212	88.7%	81.8%	217	89.5%	80.6%
Struck against object/equip. (63)	85	86	80.9%	79.9%	87	79.2%	77.7%
Caught in or compressed by object/equip. (64)	53	60	89.2%	78.9%	54	86.8%	84.6%
Rubbed or abraded by friction/pressure (66)	7	3	40.0%	88.6%	3	37.1%	97.0%
Overexertion involving outside sources (71)	194	224	97.8%	84.9%	228	98.0%	83.6%
Repetitive motions (72)	15	16	86.2%	79.8%	14	80.1%	87.2%
Other exertions or bodily reactions (73)	43	37	72.8%	84.6%	37	73.6%	85.6%
Not classifiable (99)	14	7	48.9%	100.0%	8	57.1%	100.0%

Sen = Sensitivity; PPV = Positive Predictive Value; N_true = number of claims manually coded as each category; N_pred = number of claims auto-coded as each category.

When flagging claims for manual review, the auto-coded event/exposure results could further be useful to a manual reviewer since the true event/exposure was in the top three of the auto-codes 89% of the time, and this was true 76% of the time in the bottom quarter of claims flagged for manual review.

Next, in a given study it may not be necessary to code event/exposure to the more specific 2-digit event/exposure level, but rather the simpler event/exposure division (7 categories) may suffice. Table 3 gives the accuracy of collapsing the auto-coded 2-digit results of the logistic model down to the event/exposure division level. Overall, the model auto-coded the correct division 87% of the time.

Table 3.

Accuracy of the first digit for the logistic model with single keywords, two-word sequences and the injury category used as features.

Cause	N true	N pred	Sen	PPV
Overall	1000	1000		87.0%
Violence and other injuries by person/animal (1)	39	21	49.6%	91.7%
Transportation incident (2)	39	30	68.3%	87.6%
Fires and Explosions (3)	3	0	0.0%	-
Falls, Slips, Trips (4)	222	218	86.1%	87.7%
Exposure to harmful substances or environments (5)	51	47	82.6%	89.3%
Contact with objects/equip. (6)	367	387	91.9%	87.2%
Overexertion and bodily reaction (7)	266	298	95.6%	85.3%
Not classifiable (9)	14	0	0.0%	-

Sen = Sensitivity; PPV = Positive Predictive Value; N_true = number of claims manually coded as each category; N_pred = number of claims auto-coded as each category.

Finally, the weights from our training set of 7200 manually coded claims from OHBWC were shared with BLS and used to code 1000 of their injury records. Only single and two-word sequences were considered as features since many occupational injury databases do not include medical diagnoses, which is required to assign the injury category variable. The results of testing the OHBWC weights on the BLS injury records were compared to the results from using the OHBWC training set on OHBWC claims in Table 4. Auto-coding performance was similar on both data sources and seems to suggest our results will translate well to outside researchers and practitioners wishing to use our training set on their injury data. In fact, the performance was slightly better overall on the BLS dataset than on the OHBWC data, which was initially surprising. However, this is likely due to the fact that the BLS dataset contained a larger proportion of categories that the auto-coder was accurate at coding. For example, the auto-coder accurately identifies Overexertion involving outside sources (71) narratives, likely due to the fact this event/exposure was well represented in the training set, and the BLS dataset contained a larger proportion of these event/exposure than in the OHBWC dataset (28% vs 19%). Consequently, when using the auto-coder we developed, keep in mind the event/exposure specific results. If, for example, it is important to identify Violence and other injuries by person/animal, or your dataset contains a larger proportion of these narratives, the overall results will be slightly worse than the results presented in this study, since the auto-coder was not as accurate in identifying these categories.

Table 4.

Results from using the OHBWC set of claims as a training set to code a set of 1000 BLS records compared to 1000 OHBWC claims with single keywords and sequences of keywords as features using the logistic model.

Cause	BLS					OBWC
	N true	N pred	Prob Sum	Sen	PPV	N true	N pred	Prob Sum	Sen	PPV
Overall	1000				69.2%	1000				67.8%
Intentional injury by person (11)	20	18	23	50.0%	55.6%	13	6	13	24.8%	56.6%
Injury by person-unintentional/unknown (12)	25	6	18	16.0%	66.7%	13	5	12	24.5%	64.5%
Animal and insect related (13)	7	4	1	57.1%	100.0%	13	10	1	66.5%	87.9%
Pedestrian vehicular incident (24)	9	3	6	33.3%	100.0%	5	1	5	1.6%	11.1%
Roadway Incident involving motorized vehicle (26)	21	25	23	76.2%	64.0%	28	30	29	84.6%	80.1%
Slip/trip without fall (41)	56	61	62	57.1%	52.5%	45	45	48	69.5%	69.7%
Falls on same level (42)	168	146	135	73.2%	84.2%	107	113	107	78.1%	73.9%
Falls to lower level (43)	38	47	56	71.1%	57.4%	66	61	63	67.9%	73.9%
Exposure to temperature extreme (53)	15	10	15	60.0%	90.0%	18	13	18	56.7%	80.3%
Exposure to other harmful substance (55)	18	15	16	66.7%	80.0%	24	18	24	53.4%	72.5%
Needlestick without exposure to harmful substance (61)	2	1	3	50.0%	100.0%	6	5	5	80.4%	88.5%
Struck by object/equip. (62)	118	112	114	68.6%	72.3%	195	237	208	77.6%	64.0%
Struck against object/equip. (63)	43	60	61	62.8%	45.0%	85	89	97	60.3%	57.4%
Caught in or compressed by object/equip. (64)	29	32	35	72.4%	65.6%	53	55	54	72.4%	68.9%
Rubbed or abraded by friction/pressure (66)	5	0	3	0.0%	-	7	1	6	8.0%	50.0%
Overexertion involving outside sources (71)	286	394	322	97.6%	70.8%	194	261	215	91.6%	68.2%
Repetitive motions (72)	28	13	18	46.4%	100.0%	15	12	15	58.0%	75.2%
Other exertions or bodily reactions (73)	70	48	58	38.6%	56.3%	43	35	42	47.1%	57.4%
Not classifiable (99)	3	0	0	0.0%	-	14	0	0	0.0%	-

Sen = Sensitivity; PPV = Positive Predictive Value; N_true = number of claims manually coded as each category; N_pred = number of claims auto-coded as each category.

Also in Table 4 are results from summing event/exposure specific probabilities across narratives. Since the calculated probabilities of the logistic model accurately reflect the probability a given narrative belongs to a given category, instead of selecting one category (the category with the highest probability) for a narrative, summing the category specific probabilities across all narratives will give an accurate estimate of the overall expected number of narratives belonging to each category. This is often sufficient since it is generally not necessary to uniquely identify the category of a specific narrative, but rather to describe the overall distribution of the number of narratives belonging to each category. Selecting a single category for a given claim ignores all the available information calculated by the auto-coder for the other categories and also ignores the uncertainty of the selected category. Summing the probabilities more fully captures the likelihood of all possible event/exposures for each narrative.

In general, Table 4 shows that the summation of the probabilities more accurately represents the true distribution of the categories in general. This can be seen by comparing the difference between the number predicted by the program and the summation of the probabilities with the true number in the set. For example, the auto-coder predicted 237 narratives as struck by object/equip. (62) whereas the sum of the probabilities for this category was 208 which is much closer to the true count of 195. Overall, when the auto-coder was used on the OHBWC set, the average difference between the true count and the predicted count for an event/exposure category was about 4 when the probabilities are summed, as opposed to an average difference of about 11 between the true count and auto-coded count. This improvement is smaller when the auto-coder was used on the BLS narratives, likely due to a reduction in the accuracy of the calculated probabilities from coding BLS claims with the OHBWC training set. For similar reasons, this approach would not work well for Naïve Bayes models, since the calculated probabilities do not accurately reflect the true probability as was shown in Fig. 1.

4. Conclusion

In this study, we found the logistic model performed better than the Naïve Bayes model and inclusion of two-word sequences marginally improved the overall accuracy of the auto-coder, reaching an overall accuracy of 71% for coding to the 2-digit OIICS event/exposure classification system while coding the first digit correctly 87% of the time. Furthermore, when the bottom 25% of narratives with the lowest score value were removed for manual review, the accuracy of the remaining set was 80% for 2-digit OIICS event/exposure classification system.

The programs used in this study, as well as the weights from this study’s training set are available upon request so that a set of un-coded injury record narratives can be auto-coded without a separate training set. Our limited evaluation of sharing weights with BLS demonstrated that outside researchers may observe similar performance using our weights and thus relieving the burden of manually coding a training set of records from their database. Nevertheless, some sort of quality control check is recommended to evaluate individual effectiveness. A basic power calculation shows that a random sample of 1000 claims will give an overall accuracy estimate within 3%.¹ Furthermore, it is likely that the success seen with the auto-coder on the OBWC data and BLS is in large part due to the fact that these databases have a narrative field(s) that are quite descriptive. The median word count per narrative was 17 and less than .1% of claims had a blank narrative. A database with less descriptive narratives or a higher rate of blank narratives will likely have lower success with the auto-coder and this should be evaluated.

Appendix

The auto-coding procedures developed for this study were based on processes referred to as Naïve Bayes and regularized logistic regression. The implementation of both models began the same. First, a list of keywords of interest was compiled. This list of keywords was comprised of all words that occurred in the narrative of at least 3 claims in the training set and that did not appear in a list of stop words (i.e. a list of words with little predictive value such as “the”, “a”, “an”, etc.). Little effort was made to correct misspellings and grammatical errors (of which, there appeared to be many) to evaluate the effectiveness of this model even in the situation of very “noisy” narratives.

The next step involved representing the narrative field of each claim as a vector of “features.” The features of a narrative are the occurrence (represented by a 1) and non-occurrence (represented by a 0) of the keywords or sequence of keywords after stop-words have been removed in the text narrative. As an illustrative example, suppose features of interest, consisting of single keywords and two-word sequences, are (fall, fell, off, hit, lift, trip, over, fell off, trip over). In reality, the list of features used in our program consisted of thousands of features as opposed to the nine used in this example. With this small list of keywords, the narrative “IN COOLER, CAR-RING CRATE TRIP OVER CASE OF BEER HIT CEMENT FLOOR” would then be represented as (0 0 0 1 0 1 1 0 1). All other words in the narrative would be ignored since they are not in the list of features. Once this vector of features is formed, the two models take different approaches to make a prediction.

A.1. Naïve Bayes

The Naïve Bayes model then attempts to calculate the probability of each event/exposure category given the vector of features using Bayes’ Rule. That is, given the vector of features v = (v₁ v₂… v_f), of 1’s and 0’s, the probability this claim belongs to event/exposure category c is:

$$P\left(c\mid \mathit{v}\right)=\frac{P\left(c\right)P\left(\mathit{v}\mid c\right)}{P\left(\mathit{v}\right)}\propto P\left(c\right)P\left(\mathit{v}\mid c\right)$$ (1)

where P(c) denotes the probability a claim belongs to event/exposure category c, P(v) denotes the probability a claim has vector of features v and P(v∣c) denotes the probability a claim known to belong to event/exposure category c has vector of features v. The term P(v) is not calculated directly in practice since it does not depend on each event/exposure category and will thus not affect the resulting decision as to which event/exposure category the claim should be assigned.

The term P(c) can be estimated in the obvious way by calculating the proportion of claims in a training set assigned to event/exposure category c. Estimating P(v∣c) is less obvious. To make this estimation, each of the features of the claim are naively assumed to be conditionally independent and therefore $P\left(v\mid c\right)={\prod }_{i=1}^{f}P\left(v_i\mid c\right)$. The term P(v_i∣c) is then estimated in the following manner:

$$P\left(v_i\mid \mathrm{c}\right)=\frac{\mathit{count}\left(v_i\mid c\right)+\alpha \ast \mathit{count}\left(v_i\right)}{\mathit{count}\left(c\right)+\alpha \ast N}$$ (2)

where count(v_i∣c) is the number of claims with feature v_i assigned to event/exposure category c, count(v_i) is the number of claims with feature v_i, count(c) is the total number of claims assigned to event/exposure category c, and N is the total number of claims in the training set. This estimation of P(v_i∣c) attempts to reduce the effects of noise in the narrative and the α term is a smoothing constant that was assigned a value of 0.05 for this study as was used by Lehto et al. (2009). Other values of α were also tested, and it was found that the algorithm performed optimally at this value. Therefore, for each claim with vector of features v = (v₁ v₂ … v_f), the following score is calculated for each event/exposure category, c:

$$\left(\frac{\mathit{count}\left(c\right)}{N}\right)\prod _{i=1}^f\frac{\mathit{count}\left(v_i\mid c\right)+0.05\ast \mathit{count}\left(v_i\right)}{\mathit{count}\left(c\right)+0.05\ast N}$$ (3)

The event/exposure category with the highest score is assigned to the claim. The scores of each category for a given claim can then be normalized so that the sum across event/exposure categories totals to one. The normalized scores then have the interpretation of being an estimate of the probability that a given claim belongs to a particular category.

The assumption of conditional independence of features is not verified, and is most likely not valid. For example, if the word “fell” occurs in a text narrative then the word “off” is more likely to occur in the same text. Attempts have been made to improve the model by relaxing the independence assumption; however this had modest improvements in performance but severe computational cost (Koller and Sahami, 1997; van Rijsbergen, 1977).

A.2. Regularized logistic regression

Once the vector of features, v, is formed, logistic regression is performed to calculate the probability of each event/exposure where:

$$P\left(c\mid \mathit{v}\right)=\frac{e^{\beta v}}{1+e^{\beta v}}$$ (4)

where β = (β₀ β₁ β₂ … β_f) is a vector of weights/parameters to be estimated associated with each of the f features. The β vector is estimated by minimizing the following cost function:

$$\sum _{i=1}^N\left[c^{\left(i\right)}\beta v^{\left(i\right)}-\ln \left(1+e^{\beta v^{\left(i\right)}}\right)\right]+\frac{\alpha }{2}\sum _{j=1}^f{{\beta }_j}^2$$

where c⁽ⁱ⁾ takes on the value 0 or 1 if claim i, from the training set of size N, belongs to event/exposure c and α is a parameter that restricts β. For this study, α was set to 1, and this value was chosen after testing a handful of alternative values that differed by orders of magnitude (0.01, 0.1, 1, 10, 100). The above cost function was optimized through the method of gradient descent.

The algorithms described above were written and executed in SAS® version 9.2 (SAS Institute Inc., Cary, NC).