Commensurate Priors on a Finite Mixture Model for Incorporating Repository Data in Clinical Trials

Abstract

Docosahexaenoic acid (DHA) is a good source of fat that can be taken up through food, such as fish, or taken as a supplement. Evidence is building that DHA provides a high yield, low risk strategy to reduce preterm birth and/or low birth weight. These births are great costs to society. A recently completed phase III trial revealed that higher birth weight and gestational age were associated with DHA dosed at 600 mg/day. In this paper we take a posterior predictive approach to assess impacts of these findings on public health. Simple statistical models are not adequate for accurate posterior predictive distribution estimation. Of particular interest is a paper by Schwartz et al. (2010) who discovered that the joint distribution of birth weight and gestational age is well modeled by a finite mixture of three normal distributions. Data from our own clinical trial exhibit similar features. Using the mean and variance-covariance matrices from Schwartz et al. (2010) and flexible commensurate priors (Hobbs et al., 2012) for the mixing parameters, we estimate the effect of DHA supplementation on the over 20,000 infants born in hospitals demographically similar to the hospital where the clinical trial was conducted.

Introduction

National hospital costs for infant admissions are much higher for preterm birth/low birth weight infants versus uncomplicated births (Russell et al., 2007). Using 2001 dollars, it is estimated that preterm (< 37 weeks gestation) or low birth weight (<2.5 kg) infants cost an average of $14,500 more and have, on average, hospital stays that are 11 days longer than for normal birth weight infants. Using a 3% annual escalation rate, the current relative cost is $20,071 per infant. The Institute of Medicine estimates the cost per infant born preterm to be $51,600, not including costs beyond early childhood (Behrman et al., 2006). Russell et al. (2007) report that the costs for preterm birth/low birth weight represent 47% of the costs for all infant stays and 27% for pediatric hospitalizations. Evidence of a cost effective solution to this medical problem has financial as well as public health implications.

Efforts to increase gestation and birth weight have medical and economic significance as well as significance for infant development. It is well known that low birth weight (<2.5 kg) and preterm birth (<37 weeks) contribute to poor developmental outcomes in infants (Hack et al., 2002). Docosahexaenoic acid (DHA) is a good source of fat that can be taken up through food, such as fish, or taken as a supplement. Evidence is building that DHA provides a high yield, low risk strategy to reduce preterm birth and/or low birthweight. A recently completed phase III trial (called Kansas University DHA Outcomes Study, KUDOS) (Carlson et al., 2013) revealed that higher average birth weight and gestational age were associated with DHA supplementation of 600 mg/day in the second and third trimesters (see also Helland et al., 2001; Makrides et al., 2010; Smuts et al., 2003). This paper uses outcomes from the KUDOS clinical trial and other data to estimate the effects of cost-effectiveness of paying for the KUDOS level of DHA supplementation dosed at 600 mg/day.

The original KUDOS trial was powered using a one-sided two-sample t-test for the continuous variables gestational age and birth weight. The study was not powered for estimating differences in the categorical low birth weight and preterm birth. Therefore, to better estimate the implications of DHA, we utilize more sophisticated modeling and additional data sources beyond KUDOS outcomes, to improve the efficiency of estimating the effect of DHA on low birth weight and preterm birth. This paper extends both the medical and statistical literatures by:

1. Providing statistically efficient estimates of the effect of paying for DHA for the estimated 20,000 newborn infants/year in demographically and geographically similar U.S. hospitals. This is articulated in a cost-effectiveness calculation in U.S. dollars invested per infant to reduce joint preterm (<37 weeks) and low birth weight (<2.5 kg).

2. Extending the work of Peacock et al. (2012) that dichotomizes continuous data (<37 weeks and <2.5 kg) but preserves the statistical power of its continuous parent. Specifically, we extend their methodology to include the important case of non-normal data (through the use of mixtures of multivariate normal distributions).

3. Extending the work by Hobbs et al. (2012) to include commensurate priors for the case of a finite mixture of normal distributions.

A systematic review of the available evidence for DHA and related fish oil is presented in a Cochrane paper (Makrides, Duley, Olsen, 2012). In this paper results are shown for up to six trials for outcomes such as birthweight (<2.5 kg), preterm birth (<37 weeks), and early preterm birth (<34 weeks). A meta-analysis (not shown) indicates a favor towards marine oil (e.g., DHA) as being effective. Three trials were ongoing and one was not listed. We did not use these studies in the current paper for two reasons: (1) the Cochrane study provides only cut-point data while we require raw data to fit the mixture model; and (2) the Cochrane data have different entry criteria and doses of DHA/fish oil, in general, than our study which was very broad with a specific dose of 600mg/day. Our broad inclusion criteria and the registry data combined are much more appropriate for the inclusion in this paper.

Data Sets

KU Hospital Data from Five Years (Historical)

The University of Kansas Hospital (KUH) recorded birth weights for infants during the same time period of the main clinical trial enrollment phase. This medical informatics project HERON (Waitman et al., 2011) has at least three clinical research functions: support retrospective studies, plan future studies, and build participant registries. We use the HERON rather innovatively to improve the prediction utility of the clinical trial. This historical data set is large as it contains n₀=6,830 births at KUH between January 2006 and just before January 2011. We emphasize that gestational ages are currently not available in this database at this point. Few demographics are available; however among births reporting, 37% are black race and 44% are male, similar to the KUDOS data.

KUDOS Data (Experimental)

During the same time (2006-2011) a Phase III randomized, double-blind, placebo-controlled clinical trial compared supplements in n = 301 women (Carlson et al., 2013). Participants in the first group received placebo (n₁= 147). The second group received 600 mg/day of DHA (n₂= 154) during their second and third trimesters. In the placebo control group (DHA group is very similar), participant characteristics were reported as either averages with standard deviation (SD) or percentages: 46% were black race; 54% births male, the mean maternal age was 24.8 years (SD=4.7 years); 22% used an iron supplement; 38% smoked during pregnancy; and 2% reported drinking alcohol during pregnancy. Almost all of the mothers took prenatal supplements (99%), and had an average number of years of education of 13.4 years (SD=2.7), and a median income of $43,572 (SD=$19,201). The study was powered for two primary outcomes: birth weight and gestational age. Among the primary outcomes, a one-sided two-sample t-test indicated that compared to placebo, DHA had longer mean gestational age (2.87 days, p - value = 0.041) and increased mean birth weight (172 g, p-value = 0.004).

North Carolina Detailed Birth Record (NCDBR) Database

To inform the structure of a mixture model (i.e., mixture of bivariate normal, three components), we use information from the NCDBR data that had 371,924 singleton births from 2004-2006 (Schwartz et al., 2010). The investigators (Schwartz et al., 2010) specifically found that a mixture of three components of bivariate normal distributions is an excellent fit to the joint distribution of birth weight and gestational age. We will use the component means and covariances from this study. Specifically, for the multivariate formulation described above we specify component means as

$${\mu }_1=\left[\begin{array}{cc}\hfill 39.59,\hfill & \hfill 3.514\hfill \end{array}\right],$$ (1)

$${\mu }_2=\left[\begin{array}{cc}\hfill 38.26,\hfill & \hfill 3.103\hfill \end{array}\right],\text{and}$$ (2)

$${\mu }_3=\left[\begin{array}{cc}\hfill 33.29,\hfill & \hfill 1.899\hfill \end{array}\right].$$ (3)

Associated component covariance matrices are

$${\Sigma }_1=\left[\begin{array}{cc}\hfill 0.960\hfill & \hfill 0.098\hfill \\ \hfill 0.098\hfill & \hfill 0.175\hfill \end{array}\right],$$ (4)

$${\Sigma }_2=\left[\begin{array}{cc}\hfill 2.480\hfill & \hfill 0.305\hfill \\ \hfill 0.305\hfill & \hfill 0.127\hfill \end{array}\right],\text{and}$$ (5)

$${\Sigma }_3=\left[\begin{array}{cc}\hfill 13.230\hfill & \hfill 1.091\hfill \\ \hfill 1.091\hfill & \hfill 0.132\hfill \end{array}\right].$$ (6)

The specific values of μ₁, μ₂, μ₃, Σ₁, Σ₂, and Σ₃ come from posterior estimates obtained from the three components discovered from the model of the birth registry data (Schwartz et al., 2010).

Historical Priors

The use of historical priors in the design and analysis of clinical trials began with Pocock (1976). Chen and Ibrahim (2006) developed power priors that were later modified to obey the likelihood principle (Neuenschwander et al., 2009; Gajewski, 2010). Unfortunately, modified power priors borrow information too conservatively (Berry et al., 2010). To address this, Hobbs et al. (2011) and Hobbs et al. (2012) developed commensurate priors that offer pre-posterior admissible estimators for general and generalized mixed regression models.

Let's first consider the two-sample design with one historical study (Hobbs et al., 2012). Let y = (y₁, y₂,.., y_n) represent n subjects such that y_i ~ f(y_i|θ + d_iω), where d_i =0 or 1 for patients in the control or treatment, respectively. θ is the control's parameter and ω is the additional treatment effect. The historical data are y₀ = (y₀₁, ... , y_0n0) such that y_0j ~ f(y_0j|θ₀). Let η = (ω, θ, θ₀). The joint posterior of given η given (y, y₀) is proportional to

$$q(\eta \mid \tau ,\mathbf{y},{\mathbf{y}}_0)\propto N(\theta \mid {\theta }_0,1∕\tau )p\left({\theta }_0\right)\stackrel{\text{historical}}{\overbrace{\prod _{j=1}^{n_0}f(y_{0j}\mid {\theta }_0)}}\stackrel{\text{experimental}}{\overbrace{\prod _{i=1}^{n}f(y_i\mid \theta +d_i\omega )}}$$

Hobbs et al. (2012) refer to θ~N (θ₀, 1/τ) as the commensurate prior, where τ is the “commensurability parameter.” Larger τ represents “increased commensurability” and induces increased borrowing of strength from the historical data.

Commensurate Prior for Mixture of Normal Distributions

In this section, we extend the commensurate prior model to the mixture of bivariate normal distributions.

Historical Data Model

Let Y_0j be the joint variables for gestational age and birth weight of the j^th birth from the historical data. Specifically, let

$${\mathbf{Y}}_{0\mathbf{j}}\mid {\Delta }_0\sim {\Delta }_{01}\varphi ({\mathbf{Y}}_{0\mathbf{j}}\mid {\mu }_1,{\Sigma }_1)+{\Delta }_{02}\varphi ({\mathbf{Y}}_{0\mathbf{j}}\mid {\mu }_2,{\Sigma }_2)+(1-{\Delta }_{01}-{\Delta }_{02})\varphi ({\mathbf{Y}}_{0\mathbf{j}}\mid {\mu }_3,{\Sigma }_3),$$

where ϕ(Y_i|μ_k, Σ_k) is the multivariate normal pdf for k=1, 2, 3 and

$${\Delta }_0=({\Delta }_{01},{\Delta }_{02},1-{\Delta }_{01}-{\Delta }_{02})$$

is the vector of mixing parameters. Recall, the mean and covariance for component k (μ_k, Σ_k) are derived from separate studies as detailed in Schwartz et al. (2010). While these parameters are fixed in our model, we allow the mix of the components to be unknown and modeled with the new datasets. Specifically, our implementation uses a parameterization of the mixing parameter of the form

$${\Delta }_{0k}=\frac{\exp \left({\theta }_{0k}\right)}{{\sum }_{k=1}^3\exp \left({\theta }_{0k}\right)},$$

where we constrain θ₀₃ ≡ 0. Thus θ₀ = (θ₀₁, θ₀₂) is the two-vector parameter of interest. After rearrangement of terms, the historical data model is expressed as

$$\mathit{f}({\mathbf{Y}}_{0\mathbf{j}}\mid {\theta }_0)=\sum _{k=1}^2\frac{\exp \left({\theta }_{0k}\right)}{{\sum }_{m=1}^3\exp \left({\theta }_{0m}\right)}\{\varphi ({\mathbf{Y}}_{0\mathbf{j}}\mid {\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})-\varphi ({\mathbf{Y}}_{0\mathbf{j}}\mid {\mu }_3,{\Sigma }_3)\}+\varphi ({\mathbf{Y}}_{0\mathbf{j}}\mid {\mu }_3,{\Sigma }_3).$$

Y_0j in general contains birth weight and gestational age. However, our historical data only have birth weight, therefore after integrating missing gestational age, we only have the univariate birth weight y_0j:

$$\mathit{f}(y_{0j}\mid {\theta }_0)=\sum _{k=1}^2\frac{\exp \left({\theta }_{0k}\right)}{{\sum }_{m=1}^3\exp \left({\theta }_{0m}\right)}\left\{\varphi \left(y_{0j}\mid {\mu }_{\mathbf{k}}^{\left(2\right)},{\Sigma }_{\mathbf{k}}^{(2,2)}\right)-\varphi \left(y_{0j}\mid {\mu }_3^{\left(2\right)},{\Sigma }_3^{(2,2)}\right)\right\}+\varphi \left(y_{0j}\mid {\mu }_3^{\left(2\right)},{\Sigma }_3^{(2,2)}\right),$$

where ${\mu }_{\mathbf{k}}^{\left(2\right)}$ and ${\Sigma }_{\mathbf{k}}^{(2,2)}$ represent the mean and variance for the k^th component's birth weight. An attractive feature of this model is that we still gain a meaningful posterior distribution of θ₀ even without gestational age in the historical data.

Experimental Data Model

Let Y_i be the joint variables for gestational age and birth weight of the i^th birth from the clinical trial. Let θ be the parameter vector of mixture parameters for placebo and ω be the effect comparing placebo to DHA. Using the same logic as the historical model, we get the following model for the experimental data:

$$\mathit{f}({\mathbf{Y}}_{\mathbf{i}}\mid \theta ,\omega )\sim \sum _{k=1}^2\frac{\exp ({\theta }_k+d_i{\omega }_k)}{{\sum }_{m=1}^3\exp ({\theta }_m+d_i{\omega }_m)}\{\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})-\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3)\}+\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3).$$

Bringing it Together

To perform estimation we employ mixture parameters to mitigate the strength of borrowing from the historical data. Then the joint posterior distribution using the commensurate prior model is proportional to

$$\pi (\omega ,\theta ,{\theta }_0\mid \tau ,\mathbf{Y},{\mathbf{y}}_0)\propto MVN(\theta \mid {\theta }_0,\mathrm{diag}{\left\{\tau \right\}}^{-1})p\left({\theta }_0\right)p\left(\omega \right)\times \prod _{j=1}^{n_0}\left\{\sum _{k=1}^2\frac{\exp \left({\theta }_{0k}\right)}{{\sum }_{m=1}^3\exp \left({\theta }_{0m}\right)}\left\{\varphi (y_{0j}\mid {\mu }_{\mathbf{k}}^{\left(2\right)},{\Sigma }_{\mathbf{k}}^{(2,2)})-\varphi (y_{0j}\mid {\mu }_3^{\left(2\right)},{\Sigma }_3^{(2,2)})\right\}+\varphi ({\mathbf{y}}_{0\mathbf{j}}\mid {\mu }_3^{\left(2\right)},{\Sigma }_3^{(2,2)})\right\}\times \prod _{i=1}^n\left\{\sum _{k=1}^2\frac{\exp ({\theta }_k+d_i{\omega }_k)}{\sum _{k=1}^3\exp ({\theta }_m+d_i{\omega }_m)}\{\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})-\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3)\}+\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3)\right\}.$$ (7)

Consistent with Hobbs et al. (2012), we refer to MVN(θ|θ₀, diag{τ}^–1) as the commensurate prior, and p(θ₀) as the initial prior, which we set to be proportional to unity. We also set p(ω) to be proportional to unity. The parameter vector τ represents the between-study precision, with larger values indicating increased commensurability and an increase in the borrowing of strength from the historical trial.

In the next section we comprehensively describe the computational algorithms for the Bayesian implementation. Here we briefly describe the estimation of τ. Hobbs et al. (2012) point to a number of approaches for estimation, including empirical Bayes and full Bayes. They describe a number of prior structures for the fully Bayesian approach; however, we follow Hobbs et al. (2012) by adopting their gamma prior approach. This leads to a conditional posterior distribution for τ of

$$p(\tau \mid \theta ,\omega ,{\mathbf{y}}_0,\mathbf{Y})\propto {\sum }_{k=1}^2\Gamma ({\tau }_k\mid c_k{\tilde{\tau }}_k+0.5,{({\theta }_k-{\theta }_{0k})}^2∕2+c_k),$$ (8)

where ${\tilde{\tau }}_k>0$ is the prior estimate of τ_k; and c_k > 0 is the confidence in that estimate, with smaller values representing less prior weight. Sparse versions of the prior structure can be incorporated as in Carvalho et al. (2010), and we consider other priors in the sensitivity analysis.

Computation and Posterior Predictive Distributions

We employ standard successive substitution Markov chain Monte Carlo (MCMC) (Gelman et al., 2004). Specific to our implementation are multivariate versions of the Metropolis algorithm in two of the steps outlined in Appendix B. The other complete conditionals are of semi-conjugate form (Gelman et al., 2004). Inspection of mixing plots for all parameters indicates no reasonable contrary evidence of convergence to the stationary distribution after 1,000 iterations; and we use the next 100,000 for inferential purposes. We select three different statistical values and calculate R̂ (Gelman et al., 2004) and summarize it for each column of θ, ω, θ₀, and τ (each of these has two vectors for a total of eight): 1.03, 1.00, 1.00, 1.01, 1.00, 1.01, 1.01, and 1.00, respectively (all below the recommended 1.1). MATLAB code can be provided upon request. The form of the complete conditional distributions can be found in Appendix B.

In general, for the b^th iteration, MCMC provides us a straightforward calculation for anything we desire. Since we are interested in the joint probabilities of <2.5 kg and <37 weeks, we define y* = (2.5,37) and can easily get what we desire from these draws: for placebo $p(Y_1<2.5,Y_2<37\mid )={\sum }_{k=1}^2\frac{\exp \left({\theta }_k^{\left(b\right)}\right)}{{\sum }_{m=1}^{3}exp\left({\theta }_k^{\left(b\right)}\right)}\{\Phi ({\mathbf{y}}^{\ast }\mid {\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})-\Phi ({\mathbf{y}}^{\ast }\mid {\mu }_3,{\Sigma }_3)\}+\Phi ({\mathbf{y}}^{\ast }\mid {\mu }_3,{\Sigma }_3)$, and DHA $p(Y_1<2.5,Y_2<37)={\sum }_{k=1}^2\frac{\exp ({\theta }_k^{\left(b\right)}+{\omega }_k^{\left(b\right)})}{{\sum }_{m=1}^{3}exp({\theta }_m^{\left(b\right)}+{\omega }_m^{\left(b\right)})}\{\Phi ({\mathbf{y}}^{\ast }\mid {\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})-\Phi ({\mathbf{y}}^{\ast }\mid {\mu }_3,{\Sigma }_3)\}+\Phi ({\mathbf{y}}^{\ast }\mid {\mu }_3,{\Sigma }_3)$, where Φ(·|μ_k, Σ_k) is the bivariate normal cumulative distribution function for k=1,2,3. For comparison purposes we calculate the posterior distribution that DHA has a lower risk than placebo control p(DHA ≥ Placebo) which is estimated the proportions of times p(Y₁ < 2.5, Y₂ < 37|θ^(b)) is larger or equal to p(Y₁ < 2.5, Y₂ < 37|θ^(b) + ω^(b)).

Generally speaking, suppose we have the posterior distributions θ|Y, y₀ and ω|Y, y₀, and now desire the predictive distribution for the number of infants < 2.5 kg and < 37 weeks among the 20,000 regionally similar births. The “what if” scenario is as follows: how many infants would be at risk under placebo, and how many would be at risk under full DHA? Further, if there is a savings in the number of infants at risk, what would be the cost per infant taken out of the at risk category? Calling S the number of infants in the at risk category, we can get predictions under placebo and control for the b^th iteration:

$$S_{placebo}^{p\left(b\right)}\sim Bin\left(20000,p(Y_1<2.5,Y_2<37\mid {\theta }^{\left(\mathbf{b}\right)})\right),\text{and}$$ (9)

$$S_{DHA}^{p\left(b\right)}\sim Bin\left(20000,p(Y_1<2.5,Y_2<37\mid {\theta }^{\left(\mathbf{b}\right)}+{\omega }^{\left(\mathbf{b}\right)})\right).$$ (10)

All parameters are conditioned on the “data.” Note that for the “flat prior” case, we set τ_k =0 which says that Equations (11) and (12) are skipped in the MCMC shown in Appendix B, and the second part of Equation (13) (MVN(θ|θ₀, diag{τ}^–1)) is dropped.

We also perform a cost analysis that is a continuous function of the univariate gestational age. For these purposes we take the simulated posterior parameters and simulate posterior predictive distributions of gestational age for placebo and control, which are

$$y_{1,placebo}^{p\left(b\right)}\sim {\sum }_{k=1}^2\frac{\exp \left({\theta }_k^{\left(b\right)}\right)}{{\sum }_{m=1}^3\exp \left({\theta }_m^{\left(b\right)}\right)}\left\{\varphi \left(y_{1,placebo}^p\mid {\mu }_{\mathit{k}}^{\left(1\right)},{\Sigma }_{\mathit{k}}^{(1,1)}\right)-\varphi \left(y_{1,placebo}^p\mid {\mu }_3^{\left(1\right)},{\Sigma }_3^{(1,1)}\right)\right\}+\varphi \left(y_{1,placebo}^p\mid {\mu }_3^{\left(1\right)},{\Sigma }_3^{(1,1)}\right)\text{and}$$

$$y_{1,DHA}^{p\left(b\right)}\sim {\sum }_{k=1}^2\frac{\exp \left({\theta }_k^{\left(b\right)}+{\omega }_k^{\left(b\right)}\right)}{{\sum }_{m=1}^3\exp \left({\theta }_m^{\left(b\right)}+{\omega }_m^{\left(b\right)}\right)}\left\{\varphi \left(y_{1,DHA}^p\mid {\mu }_{\mathbf{k}}^{\left(1\right)},{\Sigma }_{\mathbf{k}}^{(1,1)}\right)-\varphi \left(y_{1,DHA}^p\mid {\mu }_3^{\left(1\right)},{\Sigma }_3^{(1,1)}\right)\right\}+\varphi \left(y_{1,DHA}^p\mid {\mu }_3^{\left(1\right)},{\Sigma }_3^{(1,1)}\right)+\varphi \left(y_{1,DHA}^p\mid {\mu }_3^{\left(1\right)},{\Sigma }_3^{(1,1)}\right).$$

We also respectively simulated 20,000 births for each iteration.

Dichotomizing Continuous Data and Retaining Efficiency of Continuous Data

Dichotomizing continuous data is a huge problem because of the potential reduction in precision. For example, comparing the means from two normal distributions is statistically more powerful than dichotomizing these two continuous variables with a threshold and then comparing proportions (Peacock et al., 2012). Despite the reduced precision in the comparison of two proportions, clinicians prefer a threshold for clinical and policy decision making. Peacock et al. (2012) addressed this by using an approach that directly uses the integral of the normal distribution to get estimates of the proportions. It turns out that this approach preserves the precision of the original normal data. We describe their approach by supposing that in the continuous normal case, clinicians are interested in the proportion of infants under a certain threshold (e.g., < 2.5 kg). With this formulation there are two approaches to the problem. One is to count the number of subjects in a sample less than the threshold and use a Binomial likelihood for inference. Another approach is to estimate mean and variance parameters and plug them into a normal model, then integrate the normal model for an estimate of the proportion. Both approaches provide unbiased estimation, but the latter retains the statistical precision of the continuous model. In short, if the data are truly sufficiently normal, the Peacock approach outperforms the dichotomous approach. We develop in this paper a non-normal extension to Peacock's original normality assumption and apply it to our problem.

Application

For an application of the commensurate prior approach, we present an analysis of the KUDOS data with the prior distributions derived from historical data. We first compare two models on the entire KUH (historical data only) population of n₀=6,830 infants using posterior distributions. We first fit a traditional Beta-Binomial model on dichotomized data (<37 weeks and <2.5 kg) with a Beta(0,0) prior. The probability of this event in the Beta-Binomial model is labeled p_0,β and the mixture model analog is p_0,mix. The posterior mean for p_0,β and p_0,mix is 0.0814 and 0.0842 respectively. To assess the fitness of the model, we employ Bayesian model assessment of Gelman et al. (2004). In particular, we calculate a posterior predictive distribution using mix, then S^p, the predictive number of infants that are 2.5kg or less. The proportion of times that the predictive statistics are larger than the observed

$${\left(\frac{s_0^p}{n_0}-p_{0,\mathrm{mix}}\right)}^2>{\left(\frac{s_0}{n_0}-p_{0,\mathrm{mix}}\right)}^2,$$

is calculated via simulation to be 0.5961, indicating a good fit of the model to the data. The mix approach is more efficient as the ratio of posterior variances of Beta (0.33%²) and mix (0.32%²) is 1.072. Thus, the Beta variance is 7.2% larger than that of mix. A comparison using an MCMC approach to mix with 100,000 draws results in the same posterior variance (.32%²), and a normal plot that overlaps the asymptotic normal approximation. Therefore, the 7.2% larger variance of Beta is not due to approximation or simulation error.

Results

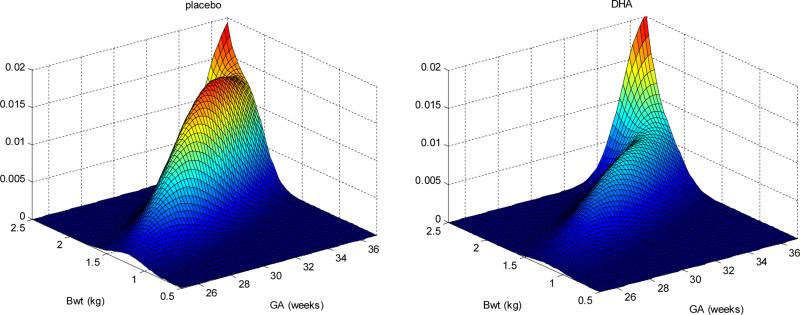
In Figure 1 we show the plots of placebo and DHA after fitting the mixture model. Zeroing in on the third component, where heights of the two figures are the same, tells us the impact in lowering the risk of joint preterm birth and low birth weight with placebo relative to DHA.

Figure 1.

Three-dimensional plot of fitted mixture model for both placebo and DHA. Back two walls represent 2.5 kg and 37 weeks cutpoints. Zeroing in on the third component, heights on the two figures are the same tells us the impact in lowering the risk of joint preterm birth and low birth weight with placebo relative to DHA.

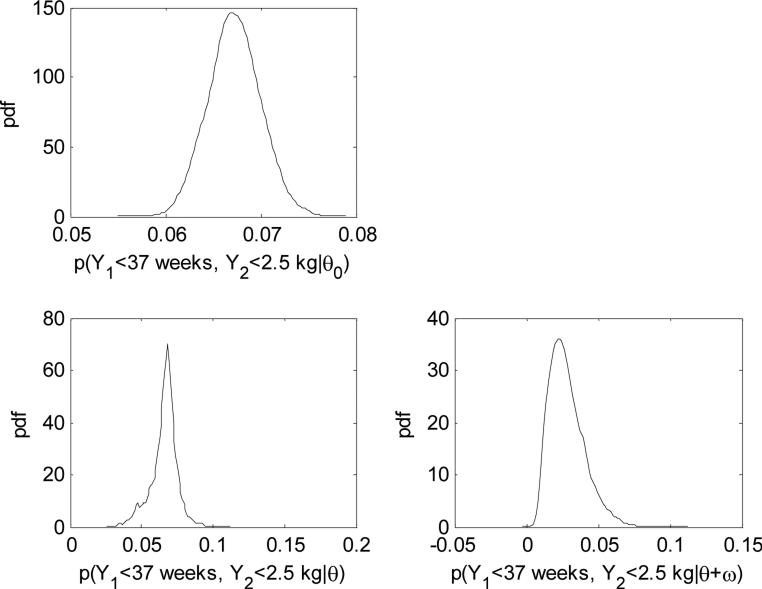
Under the full commensurate prior model, the point estimates (posterior median) and 95% credible intervals (CI) for the two components of θ₀ are 2.24 (2.13–2.34) and 1.34 (1.20–1.48), respectively. For θ the corresponding posterior median and 95% CIs are 2.27 (1.96–2.76) and 1.27 (0.0323–1.56) for the two components. The Pr(θ_0k < θ_k) are (0.6150, 0.3108) for i=(1,2), indicating that the difference between the initial prior and posterior is not significant. Additional evidence for the lack of difference is contained in the estimation of the inverse of the square root of the precision $(1∕\sqrt{{\tau }_k})$, which are 0.10 (0.01–3.17) and 0.16 (0.01–6.91), respectively. Such posterior estimates suggest that component one is more commensurate than component two, since E(τ₁) > E(τ₂) (larger average commensurate parameters). We make this clearer with the joint probabilities of <2.5 kg and <37 weeks inference described in Table 1 and their posterior densities in Figure 2. First, the Beta-binomial model shows that Pr(DHA ≥ Placebo)=0.0770 and the width of the 95% CIs are 0.0760 and 0.0529 for placebo and DHA respectively. Consistent with the results of the univariate model, the widths for the mixture-model with flat priors drop to 0.0718 and 0.0474. The Pr(DHA ≥ Placebo)=0.0378, halving Pr(DHA ≥ Placebo) when no mixture structure is used and thus increasing the overall precision. The commensurability of the mixed model again enjoys efficiency gains as we see a drop in the interval width for placebo to 0.0398 but a slight increase in DHA to 0.0493. The overall Pr(DHA ≥ Placebo) drops down to 0.0239.

Table 1.

Inferential results and summaries based on simulated data for three models comparing placebo and DHA for probability an infant is < 2.5 kg and < 37 weeks.

	Beta-Binomial Flat Prior Placebo	DHA	Mixture-Model Flat Prior Placebo	DHA	Mixture-Model Commensurate Placebo	DHA
2.5%-tile	0.031	0.010	0.034	0.010	0.043	0.010
50%-tile	0.062	0.029	0.064	0.027	0.067	0.027
97.5%-tile	0.107	0.063	0.105	0.058	0.083	0.059
P r(DHA ≥ Placebo)		0.077		0.038		0.024
95% Width	0.076	0.053	0.072	0.047	0.040	0.049

Figure 2.

Posterior distributions for the historical data, placebo, and DHA for probability a birth is < 2.5kg and < 37 weeks.

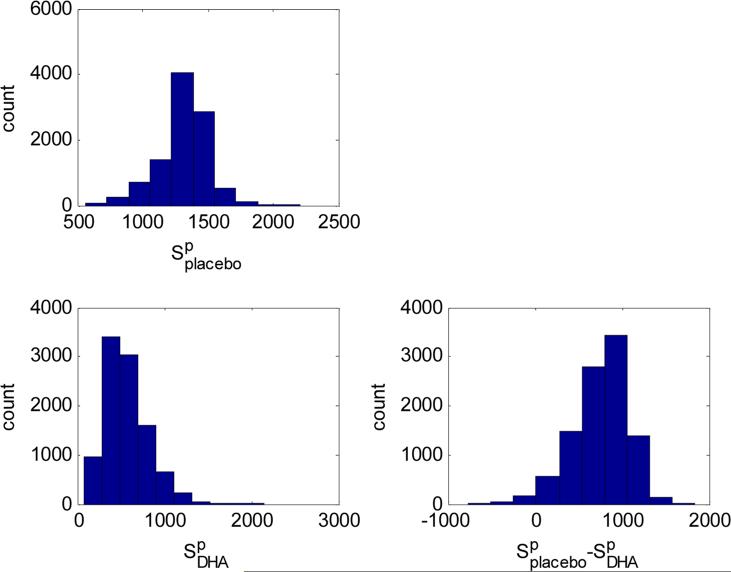
Figure 3 displays the posterior predictive distributions, along with 90% credible intervals (CIs), for 20,000 births in demographically (population) and geographically (Midwest) similar hospitals, with all mothers on either placebo or DHA. Under placebo, 1,341 (991–1,616) infants are predicted to be both preterm birth/low birth weight infants; whereas on DHA this drops to 539 (235–1,410). The estimate of the difference between placebo and DHA is 782 (194–1,200). To estimate the cost on society to prevent one infant from being preterm birth/low birth weight, we can take the total cost and divide by this last difference estimate. From the public health impact perspective, the cost of 4,200mg/week (or 600 mg/day) for 24 weeks is about $183 (http://www.enfamil.com/) per person. The cost to these hospitals for every mother (20,000) to obtain this dose would be $3.66 million/year. This DHA quote could drop with a negotiated global purchase. The cost effectiveness of a global DHA supplementation would be $4,680 ($3,050–$18,866) to prevent one infant from being both premature (<37 weeks) and born at low birth weight (<2.5 kg). Further, suppose the estimated cost differential was C for hospital stays. This cost-benefit analysis includes only the hospital stay costs and not the later development costs. Global hospital adoption of DHA in utero translates to a $3.66 million/year investment that saves 782C/year ($194C-$1200C/year) in infant medical costs. If the lower end of the interval $194C>$3.66 million, this translates into a good investment as long as C>$18, 866, which is conservative considering the $20, 071 - $51, 600 quoted in the introduction.

Figure 3.

Posterior predictive distributions for the number of infants (S) at risk if they all took placebo versus all on DHA; and their differences.

Cost Analysis as a Continuous Function of the Univariate Gestational Age

In the previous section we assume a binary cost and consider a continuous cost function (a function of gestational age), based on a detailed cost analysis from California (Phibbs and Schmitt, 2006). The binary cost assumption might be very strong and may overstate the potential benefit of DHA supplementation. Furthermore, the binary cost setup ignores the rich continuous posterior information that the probability model provides. Fitting a least squares regression to the median cost as a function of gestational age provides us a 4^th degree polynomial, cost = −30.071x⁴ + 3842.6x³ – 180,811x² + 4,000,000x – 30,000,000, where x is the gestational age in weeks and cost is in dollars, with cost=0 if x>37 weeks. As an example, births at 24 weeks cost an additional $300,000. Evaluating the cost at the simulated 20,000 births and summing the costs for each of the placebo and DHA groups, we obtain posterior predictive distributions for placebo to be a mean of $70 million (90% CI: $52-$88 million); whereas for DHA this drops to a mean of $28 million ($9-$55 million). This means that the lower 5%-tile estimate in cost per birth is $544.30, which is much greater than the $183 DHA cost per birth.

Sensitivity Analysis

The results in this paper might be very dependent on the prior, and therefore we assess the sensitivity of our prior selection. Specifically we investigate nine models, each having a different prior. We use improper (flat) priors on the mixture weight parameters, which are found to be a proper posterior after inspection of the simulations. The resulting posterior, based on improper priors, is appropriate as the mean and covariance values of the components are spread out. However, it is still necessary to assess the sensitivity of using improper priors. We approach the sensitivity analysis by changing the flat prior to something very weak, but still proper. Specifically, the flat prior model (model 1) is changed to have components with independent priors, i.e. θ_k and ω_k each with N(0,1/.001) (model 2), and is further changed to N(0,1/.01) for model 3. As shown in Table 2, the point estimates and 95% credible intervals do not change much across the first three models.

Table 2.

Results of sensitivity analyses after exploring various prior changes.

Parameter	Model	2.5%tile	Median	97.5%tile	Parameter	2.5%tile	Median	97.5%tile
ω 1	1	−0.32	0.98	2.73	θ 1	1.80	2.45	3.20
	2	−0.32	1.04	2.73		1.79	2.43	3.28
	3	−0.16	1.04	2.79		1.78	2.40	3.16
	4	−0.25	1.06	2.86		1.79	2.44	3.26
	5	−0.27	1.00	2.68		1.79	2.45	3.28
	6	−0.08	1.13	2.91		1.77	2.42	3.15
	7	−0.03	1.13	2.98		1.98	2.27	2.97
	8	0.11	1.12	2.76		2.00	2.27	2.83
	9	−0.12	1.04	2.60		1.95	2.36	3.06
ω 2	1	−0.52	1.26	3.47	θ 2	−0.49	0.87	1.92
	2	−0.39	1.38	3.38		−0.54	0.83	1.91
	3	−0.26	1.43	3.62		−0.79	0.73	1.81
	4	−0.33	1.39	3.62		−0.60	0.83	1.90
	5	−0.35	1.32	3.37		−0.57	0.84	1.93
	6	−0.20	1.47	3.69		−0.58	0.77	1.81
	7	−0.53	0.89	2.98		0.39	1.28	1.61
	8	−0.39	0.97	3.06		−0.02	1.26	1.57
	9	−0.42	1.04	2.83		0.04	1.12	1.70

We also do not estimate the means and variances in the three-part mixture, rather we assume that these are fixed and known at particular values, based on an external database in a population that is not clearly exchangeable with the population of interest. We therefore compare our results using informative priors based on this external database, rather than assuming fixed values. To that end, in model 4 we loosen the restriction on the location parameter for the components, specifically μ_k~MVN, where the means are listed in Equations (1)-(3), and the variance is diagonal and motivated from the 95% credible intervals listed in Schwartz et al. (2010). Model 5 adds uncertainty to the variance-covariance parameters from Equations (4)-(6) by multiplying a constant c_k~U(.95,1.05). The constant is further widened for model 6 such that c_k ~U(.9,1.1). This preserves positive definite for the variance-covariance parameters. Similarly, the point estimates and 95% credible intervals for models 4, 5, and 6 do not change much (Table 2).

Once historical information is added, the models exhibit big changes in the posterior distribution as shown in Table 2. Models 7, 8, and 9 use the commensurate registry and see gains with narrower 95% credible intervals. Therefore we compare distributions within this set of models using various changes on the prior. With just one historical trial, the information on the commensurability parameter is limited since it is comparable to trying to estimate a standard deviation with just two observations (Spiegelhalter, Abrams, Myles, 2004; Gelman, 2006), The prior selected for τ_k, the commensurability parameter, is a gamma distribution (model 7); however, in Hobbs et al. (2012) this prior is shown to exhibit less desirable borrowing properties than a sparsity-inducing prior, such as the spike-and-slab prior. Note that model 7 uses a Bayesian central limit theorem to approximate the likelihood for the historical part (see Appendix A). We relax this in model 8 and use its full posterior. The spike-and-slab prior is added for model 9. Specifically the prior for τ_k assumes Pr(τ_k <S_l)=0, Pr(τ_k <u)=p₀(u- S_l)/(S_u - S_l), S_l≤u≤S_u and Pr(τ_k> S_u)=Pr(τ_k=K)=1-p₀. We define p₀=.7, S_l =.05, S_u =2, and K=40. For the placebo parameters, there are some slight variations on the 95% credible interval lengths with all exhibiting shorter lengths than the models without historical data (Table 2).

Limitations

The main purpose of this paper is to efficiently measure the potential impact of 600 mg/week of DHA to the cost savings of births in similar hospitals, where such a dose comes from one randomized clinical trial. We assume that the treatment effect in the randomized trial will be exactly the same as in clinical practice.

However, it is noted that the treatment effects would vary from study to study (which is why random-effects meta-analyses would be done if we had similar doses available). Future DHA studies will allow us to address this additional uncertainty. Related to such a random-effects model, it is noted that the commensurate prior approach with one historical trial is similar to Pocock (1976), and to the meta-analytic-predictive approach (e.g., Spiegelhalter, Abrams, Myles, 2004). There is a relationship of commensurability parameter and between-trial standard deviation.

Discussion and Conclusions

We first provide a fully Bayesian extension of commensurate prior models (Hobbs et al., 2011; Hobbs et al., 2012) to include the mixture of distributions. The model is shown to increase efficiency in the case where the historical data and the current clinical trial commensurate. An added benefit is that we provide an extension of the work in Peacock et al. (2012) that dichotomizes continuous data but preserves the statistical power of its continuous parent, but for the non-normal case. However, the most important contribution of this paper is using this methodological improvement to gain efficient estimates of the potential impact that DHA supplementation has on society. Considering that premature and low birth weight infants can cost much more in medical costs, our results have shown that society paying for DHA is highly beneficial with high probability.

A concern might be with our assumption in the cost-benefit analysis where the births that are moved out of the at-risk category (low weight/preterm) have excess hospital costs that are, on average, equal to the average of all preterm/low weight births’ excess hospital costs. This assumption might be overly optimistic. If, for example, DHA exposure uniformly increases birth weights by 0.172 kg, the births that are moved out of the low weight category would be the ones whose counterfactual is close to the low/normal cutoff. Perhaps the births that would have been near 2.45 kg but moved up to 2.6 kg would incur nowhere near $20,000 less in hospital charges on average. In response to this we have reviewed our own KUH data. A recent query of the HERON database indicates that the rate of infants born in the calendar year 2008 with a length of stay of more than 7 days (to April 1, 2013) is 7/14 (95% CI:.27-.73) for infants less than 1.5 kg, and 14/66 (CI:.13-.33) for infants between 1.5 kg and 2.5 kg. For infants larger than 2.5 kg, the rate is 20/1446 (CI: .009-.021), clearly not overwhelming but trending towards differences in costs.

Future work includes looking at mixture models that incorporate estimation of the mean and covariance matrices of the mixture components. This was not necessary in our infant example but would be useful to generalize the approach to other applications. Extensions to the current approach are to include continuous covariates (e.g., dose) and incorporation of a meta analytic approach using other clinical trials from other countries with different doses of DHA but different baseline infant patterns, although this will require access to the raw birth weights and gestational ages in order to estimate the posterior distribution of the mixture parameters. We suggest a wide-spread supplementation rather than supplementation for a high-risk subpopulation only. Future work would be to identify higher-risk patients, which could improve the practical implications of our work.

Appendix A: Asymptotic Distribution

Bernardo and Smith (2007) derive posterior asymptotic normality. Adaptation of that approach leads to the following: as n₀ → ∞, ${\Delta }_0\mid {\mathbf{y}}_0\sim N({\Delta }_0\mid {\widehat{\Delta }}_0,I\left({\widehat{\Delta }}_0\right))$, where ${\widehat{\Delta }}_0$ is the limiting posterior mode and $I\left({\widehat{\Delta }}_0\right)$ is the Fisher information evaluated at the limiting posterior mode. A direct application of this approach to our model finds

$$\begin{array}{c}\hfill \frac{\partial \log \left(f_j^{\mathrm{mix}}\right)}{\partial {\Delta }_{01}}=\frac{\varphi (y_{0j}\mid {\mu }_1,{\sigma }_1)-\varphi (y_{0j}\mid {\mu }_3,{\sigma }_3)}{f_j^{\mathrm{mix}}},\text{and}\hfill \\ \hfill \frac{{\partial }^2\log \left(f_j^{\mathrm{mix}}\right)}{\partial {\Delta }_{01}^2}=\frac{(\varphi (y_{0j}\mid {\mu }_1,{\sigma }_1)-\varphi (y_{0j}\mid {\mu }_3,{\sigma }_3))}{{\left(f_j^{\mathrm{mix}}\right)}^2}.\hfill \end{array}$$

Similarly,

$$\begin{array}{c}\hfill \frac{{\partial }^2\log \left(f_j^{\mathrm{mix}}\right)}{\partial {\Delta }_{02}^2}=\frac{{(\varphi (y_{oj}\mid {\mu }_2,{\sigma }_2)-\varphi (y_{0j}\mid {\mu }_3,{\sigma }_3))}^2}{{\left(f_j^{\mathrm{mix}}\right)}^2},\text{and}\hfill \\ \hfill \frac{{\partial }^2\log \left(f_j^{\mathrm{mix}}\right)}{\partial {\Delta }_{01}\partial {\Delta }_{02}}=\frac{(\varphi (y_{0j}\mid {\mu }_1,{\sigma }_1)-\varphi (y_{0j}\mid {\mu }_3,{\sigma }_3))(\varphi (y_{0j}\mid {\mu }_2,{\sigma }_2)-\varphi (y_{0j}\mid {\mu }_3,{\sigma }_3))}{{\left(f_j^{\mathrm{mix}}\right)}^2}.\hfill \end{array}$$

These elements of the Fisher information matrix lead directly to our result. Similar calculations provide ${\theta }_0\mid y_0\sim MVN({\theta }_0\mid {\widehat{\theta }}_0,{\widehat{\mathbf{V}}}_0^{-1})$.

Appendix B: Complete Conditionals

We use MCMC to calculate the posterior distribution, which we programmed in MATLAB. This program requires complete conditional distributions (Gelman et al., 2004) to draw from the joint posterior distribution of all unknown parameters. As detailed below, we use multivariate implementations of the Metropolis algorithm in updating two sets of parameters. The other complete conditionals are of semi-conjugate (Gelman et al., 2004) form and are therefore easy to sample using existing random number generation routines in MATLAB. Inspection of mixing plots (time series line plots) for all parameters indicates a convergence to the stationary distribution (joint posterior distribution) after 10,000 iterations; we then use the next 100, 000 for inferential purposes. For plotting purposes we use a kernel density estimator for continuous distributions and histograms for discrete distributions. The MATLAB code used can be obtained by contacting the first author.

Using Equations (11)-(14), the complete conditionals for all the model parameters that provide the MCMC algorithm are

$${\tau }_k\mid \cdots \sim \Gamma \left({\tau }_k\mid c_k{\widehat{\tau }}_k+\frac{1}{2},\frac{1}{2}{({\theta }_k-{\theta }_{0k})}^2+c_k\right),$$ (11)

$${\theta }_0\mid \cdots \sim MVN({\theta }_0\mid \tilde{\theta },\tilde{\mathbf{V}}),$$ (12)

$$\begin{array}{c}\hfill \tilde{\theta }={(diag\left\{\tau \right\}+{\widehat{\mathbf{V}}}_0^{-1})}^{-1}(diag\left\{\tau \right\}\theta +{\mathbf{V}}_0^{-1}{\widehat{\theta }}_0),\hfill \\ \hfill \tilde{\mathbf{V}}={(diag\left\{\tau \right\}+{\widehat{\mathbf{V}}}_0^{-1})}^{-1},\hfill \\ \hfill \theta \mid \cdots \propto {\prod }_{i=1}^n\left\{{\sum }_{k=1}^2\frac{\exp ({\theta }_k+d_i{\omega }_k)}{{\sum }_{m=1}^{3}exp({\theta }_m+d_i{\omega }_m)}\{\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})-\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3)\}+\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3)\right\},\hfill \\ \hfill \times MVN(\theta \mid {\theta }_0,diag{\left\{\tau \right\}}^{-1}),\hfill \end{array}$$ (13)

and

$$\omega \mid \cdots \sim {\prod }_{i=1}^n\left\{{\sum }_{k=1}^2\frac{\exp ({\theta }_k+d_i{\omega }_k)}{{\sum }_{m=1}^{3}exp({\theta }_m+d_i{\omega }_m)}\{\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_{\mathbf{k}},{\Sigma }_{\mathbf{k}})-\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3)\}+\varphi ({\mathbf{Y}}_{\mathbf{i}}\mid {\mu }_3,{\Sigma }_3)\right\}$$ (14)

MCMC sampling is detailed above with Equation 11 being a draw from a Gamma distribution. The complete conditional for θ₀ (Equation 12) is also simply drawn from a multivariate normal distribution, but requires some discussion. It combines the information from the commensurate prior and the likelihood in Equation 11. Then its posterior mean ends up being a weighted average of the placebo parameter and the commensurate prior mean $\left({\widehat{\theta }}_0\right)$. The higher the precision, the more weight goes towards the placebo parameter. This result is very similar to that found in Hobbs et al. (2012), Appendix A. Unlike previous literature, the conditional posteriors for the placebo and DHA parameters in Equations (13) and (14) are more complicated and do not have analytic forms. Therefore we use Metropolis algorithms (Gelman et al., 2004) to generate draws from them. We use variations of the multivariate distribution as a candidate draw and adjust to gain around 40% rejections by multiplying the variance-covariance matrix by several constants.