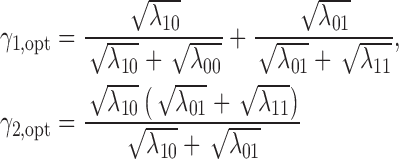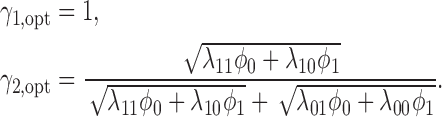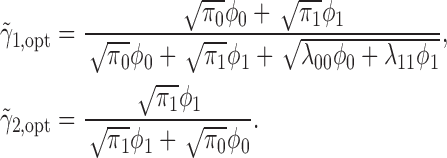Abstract
In developing targeted therapy, the marker-strategy design (MSD) provides an important approach to evaluate the predictive marker effect. This design first randomizes patients into non-marker-based or marker-based strategies. Patients allocated to the non-marker-based strategy are then further randomized to receive either the standard or targeted treatments, while patients allocated to the marker-based strategy receive treatments based on their marker statuses. Little research has been done on the statistical properties of the MSD, which has led to some widespread misconceptions and placed clinical researchers at high risk of using inefficient designs. In this article, we show that the commonly used between-strategy comparison has low power to detect the predictive effect and is valid only under a restrictive condition that the randomization ratio within the non-marker-based strategy matches the marker prevalence. We propose a Wald test that is generally valid and also uniformly more powerful than the between-strategy comparison. Based on that, we derive an optimal MSD that maximizes the power to detect the predictive marker effect by choosing the optimal randomization ratios between the two strategies and treatments. Our numerical study shows that using the proposed optimal designs can substantially improve the power of the MSD to detect the predictive marker effect. We use a lung cancer trial to illustrate the proposed optimal designs.
Keywords: Adaptive design, Clinical trial, Power, Predictive marker, Targeted therapies
1. Introduction
Owing to an improved understanding of cancer biology and rapid development of biotechnology, we have entered the era of targeted therapies for clinical oncology (Sawyers, 2004; Green, 2004; Sledge, 2005). The clinical application of a targeted therapy requires the identification of predictive biomarkers that can be used to foretell the differential efficacy of a particular therapy based on the presence or absence of the marker (Mandrekar and Sargent, 2009; Freidlin and others, 2010). For example, the estrogen receptor (ER) and human epidermal growth factor receptor 2 (HER-2) are predictive markers that are useful for choosing a targeted therapy for individuals with breast cancer. Tamoxifen is effective only for patients with a breast tumor that overexpresses ER (i.e., ER-positive status); whereas trastuzumab, a monoclonal antibody that binds to HER-2, works effectively only in patients with a breast tumor that expresses high levels of HER-2 (i.e., HER-2 positive status).
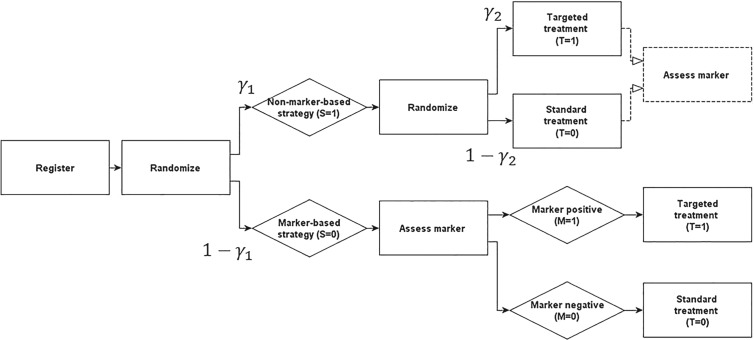
The marker-strategy design (MSD) is an important clinical trial design for identifying and validating predictive markers (Sargent and others, 2005). As shown in Figure 1, under the MSD, patients are randomized into two strategies, namely, the marker-based strategy and non-marker-based strategy. The patients randomized to the marker-based strategy are treated (deterministically) based upon their biomarker statuses (e.g., patients with a marker-positive status receive treatment A and those with a marker-negative status receive treatment B). Patients randomized to the non-marker-based strategy are randomly assigned to treatment A or B independent of their marker statuses. The MSD has drawn substantial attention from the medical community and has been used to run a number of large clinical trials (Sargent and Allegra, 2002; Sargent and others, 2005; Cree and others, 2007; Rosell and others, 2008; Mandrekar and Sargent, 2009).
Fig. 1.
Diagram of the MSD.
Surprisingly, there has been little investigation of the statistical properties of the MSD, even some fundamental properties. This is probably due to the relative newness of these designs and the fact that they were largely developed within the clinical sciences (Sargent and others, 2005; Mandrekar and Sargent, 2009). Several important questions should be answered. For example, for the MSD, in what ratio should we randomize patients between two strategies and within the (non-marker-based) strategy? The common approach is to use the equal or fixed-ratio (e.g., 1:2) randomization to assign patients between and within the two strategies. This choice is mainly driven by practical convenience without much consideration on the design properties. Ideally, the randomization ratio should be chosen to optimize the power or other utility (e.g., a tradeoff between statistical power and patient response) of the design. Furthermore, how do these randomization ratios affect the power of the design? How do we efficiently test the predictive marker effect at the end of the trial? The lack of answers to these questions has resulted in some widespread misconceptions and placed clinical researchers at high risk of using inefficient designs, which will waste research resources and miss the opportunity to discover useful predictive markers.
As an example, a trial employed the MSD to examine whether the expression level of the excision repair cross-complementing 1 (ERCC1) gene is a predictive marker for patients with non-small cell lung cancer (NSCLC) who are treated with gemcitabine (Cobo and others, 2007). A total of 444 patients with stage-IV NSCLC were randomized in a 1:2 ratio to either the non-marker-based strategy or the marker-based strategy. In the marker-based strategy, patients were treated according to their ERCC1 expression levels. The patients with low levels of ERCC1 expression received the targeted treatment (i.e., gemcitabine 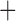 docetaxel), and the patients with high levels of ERCC1 expression received the standard treatment (i.e., cisplatin
docetaxel), and the patients with high levels of ERCC1 expression received the standard treatment (i.e., cisplatin 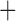 docetaxel). In the non-marker-based strategy, the trial chose an extreme randomization ratio of 0:1 and allocated all patients to the standard treatment of docetaxel plus cisplatin. At the end of the trial, as is often done in practice, the between-strategy comparison (i.e., comparing the overall response rate between the marker-based strategy and non-marker-based strategy) was used to assess whether ERCC1 expression is a predictive marker for the patient's response to gemcitabine. As we demonstrate later, this trial suffered from some design deficiencies: the between-strategy comparison actually was not a valid test to assess the predictive marker effect, and the allocation ratios adopted by the trial led to a low power to detect the predictive marker.
docetaxel). In the non-marker-based strategy, the trial chose an extreme randomization ratio of 0:1 and allocated all patients to the standard treatment of docetaxel plus cisplatin. At the end of the trial, as is often done in practice, the between-strategy comparison (i.e., comparing the overall response rate between the marker-based strategy and non-marker-based strategy) was used to assess whether ERCC1 expression is a predictive marker for the patient's response to gemcitabine. As we demonstrate later, this trial suffered from some design deficiencies: the between-strategy comparison actually was not a valid test to assess the predictive marker effect, and the allocation ratios adopted by the trial led to a low power to detect the predictive marker.
The goal of this paper is to fill these knowledge gaps and provide principled and efficient MSD designs for clinical researchers to use in evaluating the predictive marker effect. Specifically, we develop the optimal MSD, which maximizes the power for testing the predictive marker effect. We show that the typical approach of comparing the two strategies to assess the predictive marker effect has low power and is valid only under the restrictive condition that the randomization ratio between two treatments matches the marker prevalence. To address these issues, we propose a Wald test that is generally valid and uniformly more powerful than the between-strategy comparison. Based on the proposed test, we derive the optimal randomization ratios (between strategies and between treatments) that maximize the power. Through a simulation study and an application to the ERCC1 trial data, we show that the proposed optimal MSD results in a substantial improvement in statistical power.
The remainder of the article is organized as follows. In Section 2, we propose a Wald test to detect the predictive marker effect under the MSD. In Section 3, we present a numerical study to investigate the performance of the proposed design. In Section 4, we apply the proposed design to the ERCC1 trial. We conclude this article with a brief discussion in Section 5.
2. Methods
Consider an MSD consisting of a standard treatment 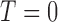 and a targeted treatment
and a targeted treatment 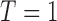 , with a binary endpoint
, with a binary endpoint 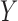 indicating whether the patient responds favorably to the received treatment (i.e.,
indicating whether the patient responds favorably to the received treatment (i.e., 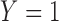 ) or not (
) or not (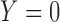 ). We assume that based on a prespecified set of markers and classification rules, patients can be classified into marker-negative (
). We assume that based on a prespecified set of markers and classification rules, patients can be classified into marker-negative (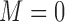 ) and marker-positive (
) and marker-positive (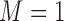 ) subgroups. Let
) subgroups. Let 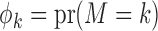 denote the prevalence of
denote the prevalence of 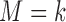 in the target population, and
in the target population, and 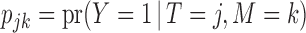 denote the response probability for patients with marker
denote the response probability for patients with marker 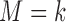 who received treatment
who received treatment 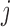 , where
, where 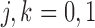 . We assume that
. We assume that 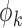 is known or can be estimated from external data, as is often the case in practice.
is known or can be estimated from external data, as is often the case in practice.
As illustrated in Figure 1, under the MSD, the enrolled patient is first randomized to either the non-marker-based strategy (denoted as 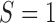 ) or the marker-based strategy (denoted as
) or the marker-based strategy (denoted as 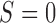 ) with probabilities
) with probabilities 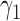 and
and 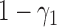 , respectively. If the patient is randomized to
, respectively. If the patient is randomized to 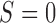 , we measure his/her marker
, we measure his/her marker 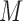 to determine the treatment assignment. If
to determine the treatment assignment. If 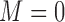 , the patient is assigned to
, the patient is assigned to 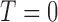 , and otherwise to
, and otherwise to 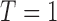 . That is, in the marker-based strategy,
. That is, in the marker-based strategy, 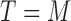 . If the patient is randomized to the non-marker-based strategy (i.e.,
. If the patient is randomized to the non-marker-based strategy (i.e., 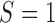 ), the measurement of
), the measurement of 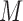 is not required. The patient is directly randomized to
is not required. The patient is directly randomized to 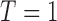 or
or  with probabilities
with probabilities 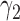 and
and 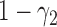 , respectively, regardless of his/her marker status. In the non-marker-based strategy,
, respectively, regardless of his/her marker status. In the non-marker-based strategy, 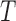 is not necessarily equal to
is not necessarily equal to  . For the moment, we assume that randomization ratios
. For the moment, we assume that randomization ratios 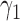 and
and 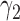 are known. In the next section, we discuss how to choose optimal randomization ratios that maximize the power of the MSD.
are known. In the next section, we discuss how to choose optimal randomization ratios that maximize the power of the MSD.
Although the measurement of  is not required for the patients randomized to
is not required for the patients randomized to  , in many practical circumstances, we still collect the marker information for these patients, prospectively or retrospectively, for other research purposes (e.g., biomarker discovery and correlation studies). Based on whether or not
, in many practical circumstances, we still collect the marker information for these patients, prospectively or retrospectively, for other research purposes (e.g., biomarker discovery and correlation studies). Based on whether or not 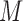 is measured for patients randomized to
is measured for patients randomized to 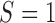 , we distinguish two versions of the MSD: the MSD with full marker information (MSD-F), under which
, we distinguish two versions of the MSD: the MSD with full marker information (MSD-F), under which 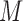 is measured for all patients; and the MSD with partial marker information (MSD-P), under which
is measured for all patients; and the MSD with partial marker information (MSD-P), under which 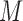 is measured only for patients with
is measured only for patients with 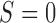 . As we describe later, the test procedures and optimization solutions are different for MSD-F and MSD-P. Because the MSD does not randomize patients to the treatments within the marker-positive and marker-negative subgroups, one limitation of the MSD is that it cannot be used to evaluate either the treatment effect within each marker subgroup or the marginal marker effect (i.e., prognostic marker effect) given a specific treatment.
. As we describe later, the test procedures and optimization solutions are different for MSD-F and MSD-P. Because the MSD does not randomize patients to the treatments within the marker-positive and marker-negative subgroups, one limitation of the MSD is that it cannot be used to evaluate either the treatment effect within each marker subgroup or the marginal marker effect (i.e., prognostic marker effect) given a specific treatment.
A primary objective of the MSD is to evaluate the predictive marker effect. According to our definition,  is the treatment effect of the targeted agent with respect to the standard treatment in the marker-positive subgroup and
is the treatment effect of the targeted agent with respect to the standard treatment in the marker-positive subgroup and  is the treatment effect in the marker-negative subgroup. Let us define
is the treatment effect in the marker-negative subgroup. Let us define 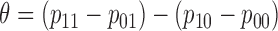 . If
. If 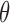 is larger (less) than 0, it means that the presence (absence) of the biomarker can predict an improvement for the treatment effect. In other words,
is larger (less) than 0, it means that the presence (absence) of the biomarker can predict an improvement for the treatment effect. In other words, 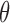 represents the predictive marker effect. Therefore, for clinical trial designs aiming to evaluate the predictive marker effect (e.g., MSD), we are interested in testing
represents the predictive marker effect. Therefore, for clinical trial designs aiming to evaluate the predictive marker effect (e.g., MSD), we are interested in testing
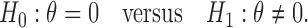 |
(2.1) |
Under the MSD, a common approach to testing the predictive marker effect relies on the two-sample t-test (or binomial test, which is asymptotically equivalent to the t-test) to compare the response rates between the marker-based and non-marker-based strategies, e.g., as in the ERCC1 trial described previously. The rationale is that a higher response rate among patients enrolled under the marker-based strategy will mean the marker is useful in guiding the treatment choice and thus the marker is predictive.
This approach, however, is problematic. First, the between-strategy comparison lacks power because of its dilution of the between-strategy difference (Simon, 2008; Freidlin and others, 2010). This dilution arises because a certain proportion of patients will receive the same treatment regardless of their assignment to the marker-based or non-marker-based strategies (e.g., some patients with a marker-positive status in both strategies will receive the targeted treatment). As a result, the MSD itself has been criticized as an inefficient design (Simon, 2008; Freidlin and others, 2010). In what follows, we show that this is not absolutely true. If we choose an appropriate test, the MSD has desirable power to detect predictive marker effects (i.e., the low power issue is caused by the between-strategy comparison, not the MSD itself). In addition, to the best of our knowledge, a more serious problem that has not been discussed in the existing literature is that the use of the t-test to compare the treatment effect between two strategies generally is not equivalent to testing the predictive marker effect, except under a restrictive condition that is described hereafter.
Theorem 1. —
Using the two-sample t-test to compare the treatment effect between two strategies is equivalent to testing the predictive marker effect only if
.
To see this, note that the hypothesis that the two-sample t-test actually evaluates is that there is no treatment difference between the two strategies, i.e.,
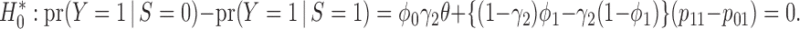 |
In general, 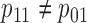 ; thus,
; thus, 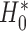 is equivalent to
is equivalent to 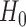 as given in (2.1) only when
as given in (2.1) only when 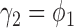 .
.
To address these issues, we propose a Wald test that is generally valid for assessing the predictive marker effect. For ease of exposition, we first consider the MSD-F, in which the value of 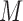 is known for all
is known for all 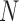 patients enrolled in the trial. Let
patients enrolled in the trial. Let 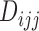 denote the number of patients who have
denote the number of patients who have 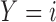 with
with 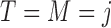 under strategy
under strategy 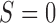 , and
, and 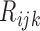 denote the number of patients who have
denote the number of patients who have 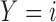 with
with 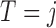 and
and 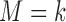 under strategy
under strategy 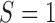 . Given the observed data
. Given the observed data 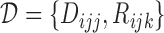 , the likelihood function for
, the likelihood function for  under the MSD-F is
under the MSD-F is
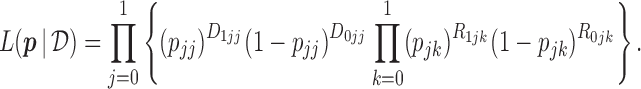 |
(2.2) |
It can be shown that the maximum likelihood estimate (MLE) of 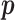 is given by
is given by
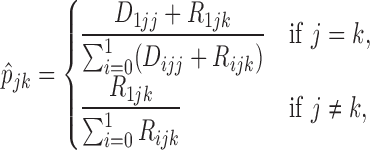 |
(2.3) |
with the corresponding information matrix
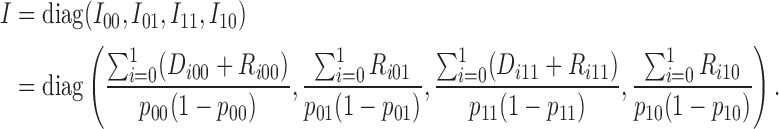 |
Therefore, the MLE and asymptotic variance of 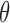 are given by
are given by
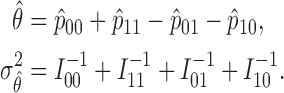 |
Substituting 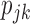 in
in 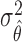 with its MLE, the Wald test statistic
with its MLE, the Wald test statistic 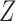 for testing
for testing 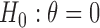 is given by
is given by
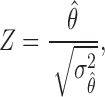 |
which asymptotically follows a standard normal distribution under 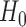 . Given a significance level of
. Given a significance level of 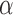 , we reject
, we reject 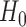 and declare that
and declare that 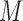 is a predictive marker if
is a predictive marker if 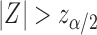 , where
, where 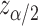 is the upper
is the upper 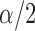 quantile of a standard normal distribution.
quantile of a standard normal distribution.
We now turn to the test of the predictive marker effect for the MSD-P, where 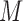 is not measured for patients with
is not measured for patients with 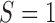 . In this case,
. In this case, 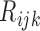 are not observed, instead we observe only
are not observed, instead we observe only 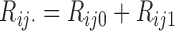 for
for 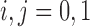 . The likelihood of the observed data
. The likelihood of the observed data 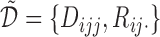 under the MSD-P is
under the MSD-P is
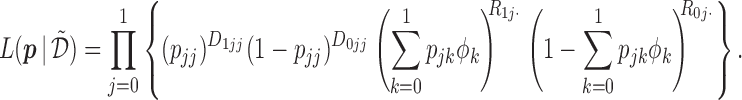 |
(2.4) |
We employ the expectation-maximization (EM) algorithm (Dempster and others, 1977) to obtain the MLE of 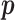 . We treat
. We treat 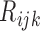 as missing data and define the complete data as
as missing data and define the complete data as 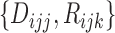 . As the likelihood of the complete data is the same as that of the MSD-F with closed-form MLEs, this is an ideal situation for using the EM algorithm, which can be described as follows:
. As the likelihood of the complete data is the same as that of the MSD-F with closed-form MLEs, this is an ideal situation for using the EM algorithm, which can be described as follows:
Initialize the starting values of
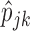 .
.
E-step: substitute the missing values of
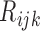 with their expectations, given by
with their expectations, given by 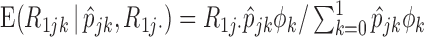 and
and 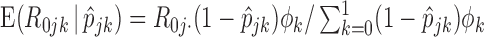 .
.
M-step: update
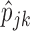 with their MLEs, as given by (2.3).
with their MLEs, as given by (2.3).
Repeat steps 2 and 3 until the estimates converge and estimate
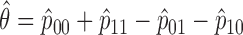 .
.
The EM algorithm does not produce the variance estimate of 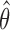 . We estimate the variance of
. We estimate the variance of 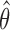 based on the information matrix
based on the information matrix 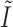 , which is derived from the observed data likelihood (2.4) and takes the following form:
, which is derived from the observed data likelihood (2.4) and takes the following form:
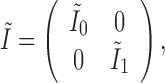 |
where
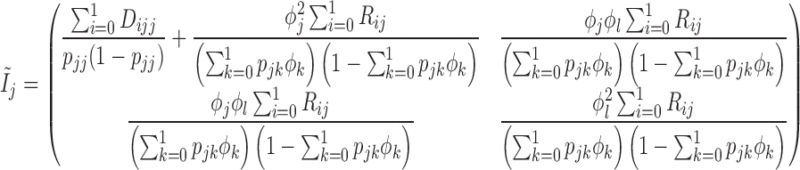 |
for  and
and 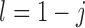 . Therefore, the variance of
. Therefore, the variance of  under the MSD-P, say
under the MSD-P, say  , is given by
, is given by
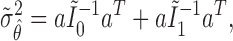 |
(2.5) |
where 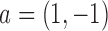 . Similarly, substituting
. Similarly, substituting 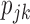 in
in 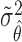 with its MLE, the Wald test statistic for the MSD-P is given by
with its MLE, the Wald test statistic for the MSD-P is given by  , which asymptotically follows a standard normal distribution under
, which asymptotically follows a standard normal distribution under 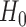 . As shown in Supplementary materials (available at Biostatistics online), compared with the two-sample t-test, the proposed Wald test has higher statistical power to detect predictive marker effects.
. As shown in Supplementary materials (available at Biostatistics online), compared with the two-sample t-test, the proposed Wald test has higher statistical power to detect predictive marker effects.
Theorem 2. —
Under both the MSD-F and MSD-P, the proposed Wald test is uniformly more powerful than the two-sample t-test.
Under the MSD-F and MSD-P, the power of the Wald test depends on the between-strategy randomization ratio, 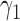 , which determines the proportion of patients to be assigned to the non-marker-based strategy, and the within-strategy randomization ratio,
, which determines the proportion of patients to be assigned to the non-marker-based strategy, and the within-strategy randomization ratio, 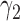 , which determines the proportion of patients to be assigned to the targeted treatment within the non-marker-based strategy. We derive the optimal MSD-F and MDS-P that maximize the power to detect the predictive marker effect by choosing the optimal values of
, which determines the proportion of patients to be assigned to the targeted treatment within the non-marker-based strategy. We derive the optimal MSD-F and MDS-P that maximize the power to detect the predictive marker effect by choosing the optimal values of 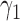 and
and 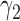 . The results are summarized in Theorems 3 and 4, and more details are provided in Supplementary materials (available at Biostatistics online).
. The results are summarized in Theorems 3 and 4, and more details are provided in Supplementary materials (available at Biostatistics online).
Theorem 3. —
Defining
, the optimal MSD-F that maximizes the power of detecting predictive marker effects is given by the following randomization ratios:
if
; otherwise,
Theorem 4. —
Define
for
and
, and
. The optimal MSD-P that maximizes the power of detecting predictive marker effects is given by the following optimal randomization ratios:
The implementation of the proposed optimal MSD requires the knowledge of 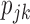 , which can be elicited from clinicians. If such information is not available, we can adopt a two-stage approach by varying the randomization ratio during the trial. At the first stage, we equally randomize a portion of patients between the two strategies and two treatments. Then, at the second stage, based on the data obtained from the patients in the first stage, we estimate
, which can be elicited from clinicians. If such information is not available, we can adopt a two-stage approach by varying the randomization ratio during the trial. At the first stage, we equally randomize a portion of patients between the two strategies and two treatments. Then, at the second stage, based on the data obtained from the patients in the first stage, we estimate 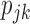 and the optimal randomization ratios
and the optimal randomization ratios 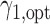 and
and 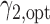 , based on which we allocate the subsequent patients.
, based on which we allocate the subsequent patients.
3. Numerical studies
We conducted simulation studies to investigate the operating characteristics of the proposed Wald test. We considered the following three cases. (1) The marker has no predictive effect, with 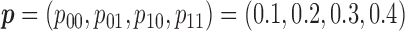 , which corresponds to the null case
, which corresponds to the null case 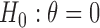 . (2) The marker has both predictive and prognostic effects. We took
. (2) The marker has both predictive and prognostic effects. We took 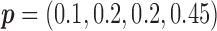 for MSD-F, under which the predictive effect
for MSD-F, under which the predictive effect 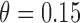 and the prognostic effect is 0.1, and
and the prognostic effect is 0.1, and 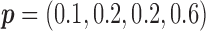 for MSD-P, under which the predictive effect
for MSD-P, under which the predictive effect 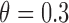 and the prognostic effect is 0.1. The reason we chose a larger predictive effect for the MSD-P is to ensure its power in the range of practical interest. (3) The marker has only a predictive effect. We set
and the prognostic effect is 0.1. The reason we chose a larger predictive effect for the MSD-P is to ensure its power in the range of practical interest. (3) The marker has only a predictive effect. We set 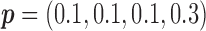 for MSD-F (i.e.,
for MSD-F (i.e., 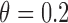 ) and
) and 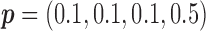 for MSD-P (i.e.,
for MSD-P (i.e., 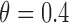 ). As we mentioned earlier, the MSD cannot be used to evaluate the prognostic effect. In the above three cases, we are interested in testing whether the marker is predictive. We considered three marker prevalence rates,
). As we mentioned earlier, the MSD cannot be used to evaluate the prognostic effect. In the above three cases, we are interested in testing whether the marker is predictive. We considered three marker prevalence rates, 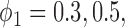 and 0.7. Under each of the simulation configurations, we conducted 10 000 simulated trials to evaluate the empirical type I error rate and the power of the proposed Wald test under the MSD-F and MSD-P with a significance level of 5%, and compared it to the conventional t-test.
and 0.7. Under each of the simulation configurations, we conducted 10 000 simulated trials to evaluate the empirical type I error rate and the power of the proposed Wald test under the MSD-F and MSD-P with a significance level of 5%, and compared it to the conventional t-test.
Table 1 shows the rejection rate of 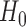 across 10 000 simulations under the MSD-F with different randomization ratios
across 10 000 simulations under the MSD-F with different randomization ratios 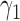 and
and 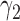 . When the predictive marker effect is zero, the rejection rate corresponds to the type I error rate. The t-test yielded reasonable type I error rates only when
. When the predictive marker effect is zero, the rejection rate corresponds to the type I error rate. The t-test yielded reasonable type I error rates only when 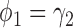 , and led to seriously inflated type I errors if
, and led to seriously inflated type I errors if 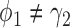 . For example, when
. For example, when 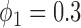 ,
, 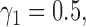 and
and 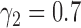 , the type I error rate of the t-test was
, the type I error rate of the t-test was 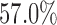 . In contrast, the proposed Wald test consistently controlled the type I error rate at around the nominal level of 5% in all cases.
. In contrast, the proposed Wald test consistently controlled the type I error rate at around the nominal level of 5% in all cases.
Table 1.
Empirical type I error rate and power of the t-test and proposed Wald test (in percentages) under the MSD-F and 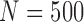
| Not predictive |
Predictive  prognostic prognostic |
Predictive only |
||||||
|---|---|---|---|---|---|---|---|---|
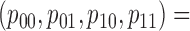 |
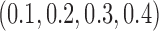 |
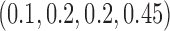 |
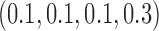 |
|||||
 |
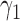 |
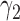 |
Wald | t-test | Wald | t-test | Wald | t-test |
| 0.3 | 0.5 | 0.3 | 5.4 | 5.2 | 35.8 | 14.3 | 72.1 | 28.2 |
| 0.5 | 5.6 | 19.8 | 38.1 | 5.0 | 73.4 | 16.3 | ||
| 0.7 | 5.5 | 57.0 | 34.4 | 10.8 | 67.0 | 8.9 | ||
| 0.7 | 0.3 | 5.3 | 5.4 | 40.3 | 11.4 | 76.0 | 21.4 | |
| 0.5 | 5.1 | 18.8 | 42.7 | 5.4 | 79.4 | 12.7 | ||
| 0.7 | 5.2 | 52.2 | 38.5 | 11.0 | 73.3 | 7.2 | ||
| 1.00 | 0.56 | 5.3 | N/A | 45.7 | N/A | 80.8 | N/A | |
| 0.90 | 0.56 | 5.2 | 19.4 | 45.2 | 7.0 | 81.1 | 6.7 | |
| 0.5 | 0.5 | 0.3 | 5.6 | 18.0 | 40.3 | 47.6 | 76.4 | 56.1 |
| 0.5 | 5.3 | 5.3 | 45.1 | 16.5 | 82.1 | 31.2 | ||
| 0.7 | 5.6 | 17.2 | 41.5 | 5.0 | 77.6 | 14.2 | ||
| 0.7 | 0.3 | 5.4 | 15.0 | 44.9 | 40.4 | 82.4 | 46.2 | |
| 0.5 | 5.5 | 5.6 | 52.0 | 13.2 | 87.6 | 24.3 | ||
| 0.7 | 5.5 | 16.5 | 48.1 | 5.3 | 84.4 | 11.3 | ||
| 1.00 | 0.56 | 4.9 | N/A | 55.2 | N/A | 89.5 | N/A | |
| 0.90 | 0.56 | 5.0 | 7.1 | 54.3 | 6.3 | 90.0 | 9.3 | |
| 0.7 | 0.5 | 0.3 | 5.5 | 52.5 | 36.5 | 80.3 | 67.9 | 80.4 |
| 0.5 | 5.4 | 17.5 | 41.6 | 42.6 | 77.0 | 49.7 | ||
| 0.7 | 5.5 | 5.4 | 40.7 | 11.2 | 76.8 | 20.9 | ||
| 0.7 | 0.3 | 5.4 | 44.6 | 40.3 | 71.1 | 75.4 | 70.8 | |
| 0.5 | 5.4 | 14.3 | 47.1 | 35.5 | 84.2 | 40.6 | ||
| 0.7 | 5.1 | 4.8 | 46.7 | 10.5 | 84.0 | 16.7 | ||
| 1.00 | 0.56 | 5.2 | N/A | 51.9 | N/A | 87.4 | N/A | |
| 0.90 | 0.56 | 5.1 | 6.8 | 51.6 | 12.3 | 87.9 | 14.0 | |
The underlined values are the optimal randomization ratios and corresponding power.
In terms of power (i.e., the rejection rate when there is a predictive marker effect), the proposed Wald test substantially outperformed the t-test, given that both tests adequately controlled the type I error rate (i.e., when 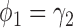 ). For example, when
). For example, when 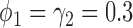 ,
, 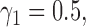 and
and 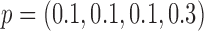 , the power of the Wald test was about
, the power of the Wald test was about 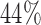 higher than that of the t-test. In addition, the optimal MSD-F when using the proposed optimal randomization ratios (underlined in Table 1) yielded substantially higher power than the MSD-F when using other randomization ratios. For example, when
higher than that of the t-test. In addition, the optimal MSD-F when using the proposed optimal randomization ratios (underlined in Table 1) yielded substantially higher power than the MSD-F when using other randomization ratios. For example, when 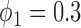 and
and 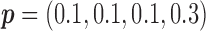 , the power of the MSD-F with
, the power of the MSD-F with 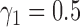 and
and  was 67.0%, while that of the optimal MSD-F with
was 67.0%, while that of the optimal MSD-F with 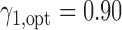 and
and 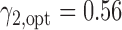 was 81.1%.
was 81.1%.
The simulation results for the MSD-P (see Table 2) were similar to those for the MSD-F. That is, the t-test yielded valid type I error rates only when 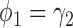 ; whereas the proposed Wald test consistently produced reasonable type I error rates and was uniformly more powerful than the t-test. In addition, using the optimal MSD-P design could substantially improve the power of the MSD-P.
; whereas the proposed Wald test consistently produced reasonable type I error rates and was uniformly more powerful than the t-test. In addition, using the optimal MSD-P design could substantially improve the power of the MSD-P.
Table 2.
Empirical type I error rate and power of the t-test and proposed Wald test (in percentages) under the MSD-P and 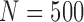
| Not predictive |
Predictive 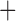 prognostic prognostic |
Predictive only |
||||||
|---|---|---|---|---|---|---|---|---|
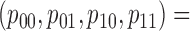 |
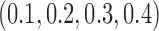 |
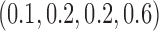 |
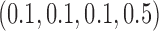 |
|||||
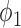 |
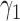 |
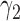 |
Wald |
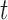 -test -test |
Wald |
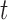 -test -test |
Wald |
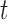 -test -test |
| 0.3 | 0.5 | 0.3 | 4.8 | 4.8 | 47.5 | 40.0 | 74.8 | 69.8 |
| 0.5 | 5.1 | 20.0 | 47.6 | 10.1 | 73.9 | 40.3 | ||
| 0.7 | 5.4 | 57.0 | 41.1 | 6.5 | 66.6 | 17.2 | ||
| 0.7 | 0.3 | 5.5 | 5.4 | 41.8 | 32.9 | 67.1 | 59.6 | |
| 0.5 | 5.3 | 19.3 | 39.9 | 8.7 | 66.4 | 32.7 | ||
| 0.7 | 5.1 | 51.1 | 38.2 | 6.1 | 61.3 | 13.8 | ||
| 0.51 | 0.37 | 5.2 | 7.2 | 48.4 | 27.0 | 74.8 | 59.1 | |
| 0.47 | 0.37 | 4.9 | 6.7 | 47.7 | 26.9 | 75.5 | 59.5 | |
| 0.5 | 0.5 | 0.3 | 5.3 | 19.0 | 45.3 | 87.3 | 72.4 | 96.3 |
| 0.5 | 5.1 | 5.1 | 52.7 | 44.9 | 79.5 | 73.8 | ||
| 0.7 | 5.3 | 17.3 | 51.5 | 9.1 | 79.9 | 33.1 | ||
| 0.7 | 0.3 | 5.4 | 15.4 | 42.0 | 80.4 | 67.1 | 92.3 | |
| 0.5 | 5.3 | 5.3 | 46.2 | 36.8 | 71.5 | 64.7 | ||
| 0.7 | 5.1 | 16.2 | 47.0 | 8.6 | 71.9 | 27.1 | ||
| 0.51 | 0.58 | 5.1 | 7.4 | 53.0 | 26.3 | 79.4 | 56.7 | |
| 0.48 | 0.60 | 5.0 | 7.8 | 52.4 | 22.5 | 80.4 | 53.6 | |
| 0.7 | 0.5 | 0.3 | 5.3 | 53.1 | 23.8 | 99.2 | 41.1 | 99.8 |
| 0.5 | 5.4 | 17.0 | 31.2 | 83.0 | 50.4 | 92.6 | ||
| 0.7 | 4.9 | 4.7 | 34.7 | 29.8 | 56.0 | 51.2 | ||
| 0.7 | 0.3 | 5.0 | 44.2 | 24.5 | 97.8 | 40.0 | 99.3 | |
| 0.5 | 5.6 | 14.1 | 28.1 | 74.1 | 46.2 | 87.1 | ||
| 0.7 | 5.4 | 5.5 | 30.5 | 25.7 | 48.7 | 43.8 | ||
| 0.51 | 0.76 | 4.9 | 5.8 | 34.9 | 17.9 | 56.9 | 35.9 | |
| 0.49 | 0.79 | 5.2 | 7.0 | 34.0 | 12.1 | 57.1 | 29.9 | |
The underlined values are the optimal randomization ratios and corresponding power.
We also conducted a simulation to evaluate the performance of the two-stage approach when the response rate  are unknown. The two-stage design equally randomized the first 100 patients to two strategies and then, based on the estimates of the response rates from the first stage, used the optimal randomization ratio to allocate the remaining 400 patients in the second stage. The simulation results show that the two-stage approach was only slightly less powerful than the optimal approach (See Figure 6 in Supplementary material available at Biostatistics online). Therefore, when
are unknown. The two-stage design equally randomized the first 100 patients to two strategies and then, based on the estimates of the response rates from the first stage, used the optimal randomization ratio to allocate the remaining 400 patients in the second stage. The simulation results show that the two-stage approach was only slightly less powerful than the optimal approach (See Figure 6 in Supplementary material available at Biostatistics online). Therefore, when 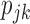 are unknown, we recommend the two-stage approach to be used in practice.
are unknown, we recommend the two-stage approach to be used in practice.
4. Application
We now turn to the ERCC1 trial (Cobo and others, 2007), in which a total of 444 patients with NSCLC were randomly assigned in a 1:2 ratio (i.e., 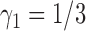 ) to either the non-marker-based strategy or the marker-based strategy. ERCC1 mRNA expression was assessed in all patients using real-time reverse transcriptase polymerase chain reaction. Relative to the housekeeping gene
) to either the non-marker-based strategy or the marker-based strategy. ERCC1 mRNA expression was assessed in all patients using real-time reverse transcriptase polymerase chain reaction. Relative to the housekeeping gene 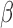 -action, ERCC1 mRNA expression was classified into a low level or a high level based on the cutoff
-action, ERCC1 mRNA expression was classified into a low level or a high level based on the cutoff 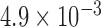 (Israel and others, 2004). In the marker-based strategy, patients were treated based on their ERCC1 mRNA levels. The patients with high ERCC1 mRNA levels (i.e.,
(Israel and others, 2004). In the marker-based strategy, patients were treated based on their ERCC1 mRNA levels. The patients with high ERCC1 mRNA levels (i.e., 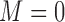 ) received the standard treatment, i.e.,
) received the standard treatment, i.e., 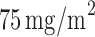 of docetaxel plus
of docetaxel plus 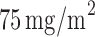 of cisplatin; whereas patients with low ERCC1 mRNA levels (i.e.,
of cisplatin; whereas patients with low ERCC1 mRNA levels (i.e., 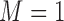 ) received the targeted agent,
) received the targeted agent, 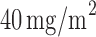 of docetaxel plus
of docetaxel plus 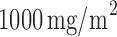 of gemcitabine. Among 296 patients randomized to the marker-based strategy, 211 patients were assessable for the treatment response, of which 122 and 89 patients had low and high levels of ERCC1 mRNA expression, respectively. In the marker-based strategy, a total of 107 patients had a favorable response to the treatments, including 65 (i.e., response rate of 53.2%) from the low ERCC1 level subgroup, and 42 (i.e., response rate of 47.2%) from the high ERCC1 level subgroup. In the non-marker-based strategy, rather than randomizing patients into the two treatments, this trial allocated all patients to the standard treatment with
of gemcitabine. Among 296 patients randomized to the marker-based strategy, 211 patients were assessable for the treatment response, of which 122 and 89 patients had low and high levels of ERCC1 mRNA expression, respectively. In the marker-based strategy, a total of 107 patients had a favorable response to the treatments, including 65 (i.e., response rate of 53.2%) from the low ERCC1 level subgroup, and 42 (i.e., response rate of 47.2%) from the high ERCC1 level subgroup. In the non-marker-based strategy, rather than randomizing patients into the two treatments, this trial allocated all patients to the standard treatment with 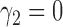 .
.
Among 148 patients randomized to the non-marker-based strategy, 135 patients were assessable and 53 of them had a favorable response to the treatment. A comparison of the response rate between the two strategies resulted in a slightly significant p-value of 0.02, based on which the investigators of the trial concluded that the ERCC1 mRNA expression level was a potential predictive marker for gemcitabine. Due to the lack of understanding of the theoretical properties of the MSD, this trial suffered from some design deficiencies. Specifically, as 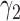 did not match the estimated marker prevalence
did not match the estimated marker prevalence 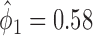 , the between-strategy comparison was not valid for testing the predictive effect of the ERCC1 mRNA, although an objective of the trial was to “confirm that ERCC1 mRNA levels predict response to platinum-based therapy in advanced NSCLC” (Cobo and others, 2007, p. 2752). Strictly speaking, the predictive effect was not identifiable in this trial (without using external data) as no patient with a high level of ERCC1 mRNA expression was treated with the targeted agent.
, the between-strategy comparison was not valid for testing the predictive effect of the ERCC1 mRNA, although an objective of the trial was to “confirm that ERCC1 mRNA levels predict response to platinum-based therapy in advanced NSCLC” (Cobo and others, 2007, p. 2752). Strictly speaking, the predictive effect was not identifiable in this trial (without using external data) as no patient with a high level of ERCC1 mRNA expression was treated with the targeted agent.
We retrospectively applied the proposed methodology to the ERCC1 trial data to demonstrate the potential power gain by using the proposed optimal designs. Based on the response data reported by the trial, we estimated response rates of 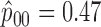 ,
,  ,
, 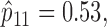 and
and 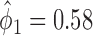 . Because no patient with a high level of ERCC1 mRNA expression was treated with the targeted agent in the ERCC1 trial, we estimated
. Because no patient with a high level of ERCC1 mRNA expression was treated with the targeted agent in the ERCC1 trial, we estimated 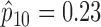 based on Burris and others (1997). Applying Theorem 3, the optimal randomization ratios for MSD-F were
based on Burris and others (1997). Applying Theorem 3, the optimal randomization ratios for MSD-F were 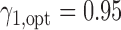 ,
, 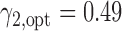 . To appreciate the potential power gain, we simulated 10 000 trials to compare the optimal MSD-F to the ERCC1 trial design (with
. To appreciate the potential power gain, we simulated 10 000 trials to compare the optimal MSD-F to the ERCC1 trial design (with 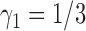 and
and 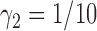 ). Note that, for the ERCC1 trial design, in order to make the predictive effect identifiable, we used
). Note that, for the ERCC1 trial design, in order to make the predictive effect identifiable, we used 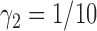 , rather than 0. The results show that the empirical power of the optimal MSD-F design was
, rather than 0. The results show that the empirical power of the optimal MSD-F design was 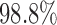 , whereas that under the ERCC1 trial design was only
, whereas that under the ERCC1 trial design was only 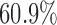 (when the proposed Wald test was used in both designs).
(when the proposed Wald test was used in both designs).
5. Discussion
We have proposed the optimal MSD for detecting predictive marker effects under two scenarios of marker measuring: when the marker is fully measured or only partially measured for the population of patients enrolled in the trial. Under the MSD, the commonly used approach to test predictive marker effects is to apply the two-sample t-test to compare the treatment effect between the marker-based strategy and the non-marker-based strategy. We have shown that such an approach has low power and is valid only under the restrictive condition that the randomization ratio between the two treatments matches the marker prevalence. To address these issues, we have proposed using a Wald test that is generally valid and uniformly more powerful than the t-test. Based on the proposed test, we have derived the optimal randomization ratios (between strategies and treatments) that maximize the power. The numerical studies have shown that the proposed optimal MSD can substantially improve the power of the MSD.
The proposed optimal designs focus on a binary outcome. In practice, other types of endpoints, such as ordinal outcomes (e.g., complete remission, partial remission, stable disease, and disease progression) and time-to-event outcomes (e.g., progression-free survival and overall survival times) are also frequently used in clinical trials. The extension of the proposed optimal design to these cases is of great practical importance and warrants further research. We consider one biomarker and two treatments in this article. The idea can be extended to multiple biomarker and treatment arms. However, the calculation is much more involved and there are typically no closed form expression for the optimal randomization ratio (Hu and Rosenberger, 2006). More recently, Zang and others (Zang and others, 2015; Zang and Guo, 2016; Zang and others, 2016) proposed several optimal biomarker-guided designs when biomarkers are measured with errors. It is also of interest to develop the optimal marker- strategy design subject to imprecisely measured biomarkers. Future research in this area is needed.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
Zang's research was partially supported by Award number R01 CA154591 from the National Cancer Institute, Liu's research was partially supported by Award number P30 CA016672 from the National Cancer Institute, and Yuan's research was partially supported by Award number R01 CA154591, P50 CA098258 and P30 CA016672 from the National Cancer Institute.
Supplementary Material
Acknowledgements
The authors thank two referees and the Associate Editor for their valuable comments and LeeAnn Chastain for her editorial assistance. Conflict of Interest: None declared.
References
- Burris H. A. 3rd, Moore M. J., Andersen J., Green M. R., Rothenberg M. L., Modiano M. R., Cripps M. C., Portenoy R. K., Storniolo A. M., Tarassoff P., and others (1997). Improvements in survival and clinical benefit with Gemcitabine as first-line therapy for patients with advanced pancreas cancer: a randomized trial. Journal of Clinical Oncology 15, 2403–2413. [DOI] [PubMed] [Google Scholar]
- Cobo M., Isla D., Massuti B., Montes A., Sanchez J. M., Provencio M., Viñolas N., Paz-ares L., Lopez-vivanco G., Muñoz M.A.. and others (2007). Customizing cisplatin based on quantitative excision repair cross-complementing 1 mRNA expression: a phase III trial in non-small-cell lung cancer. Journal of Clinical Oncology 25, 2747–2754. [DOI] [PubMed] [Google Scholar]
- Cree I. A., Kurbacher C. M., Lamont A., Hindley A. C., Love S., TCA Ovarian Cancer Trial Group (2007). A prospective randomized controlled trial of tumour chemosensitivity assay directed chemotherapy versus physicianõs choice in patients with recurrent platinum-resistant ovarian cancer. Anticancer Drugs 18, 1093–1101. [DOI] [PubMed] [Google Scholar]
- Dempster A. P., Laird N. M., Rubin D. B. (1977). Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society, Series B 39, 1–38. [Google Scholar]
- Freidlin B., McShane L. M., Korn E. L. (2010). Randomized clinical trials with biomarkers: design issues. Journal of the National Cancer Institute 102, 152–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green M. R. (2004). Targeting targeted therapy. The New England Journal of Medicine 350, 2191–2193. [DOI] [PubMed] [Google Scholar]
- Hu F., Rosenberger W. F. (2006) The Theory of Response-Adaptive Randomization in Clinical Trials. New York: Wiley. [Google Scholar]
- Israel V., Tagawa S. T., Snyder T., Jeffers S., Raghavan D. (2004). Phase I/II trial of Gemcitabine Plus Docetaxel in advanced Non-Small Cell Lung Cancer (NSCLC). Investigational New Drugs 22, 291–297. [DOI] [PubMed] [Google Scholar]
- Mandrekar S. J., Sargent D. J. (2009). Clinical trial designs for predictive biomarker validation: theoretical considerations and practical challenges. Journal of Clinical Oncology 27, 4027–4034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosell R., Vergnenegre A., Fournel P., Massuti B., Camps C., Isla D., Sanchez J. M., Moran T., Sirera R., Taron M. (2008). Pharmacogenetics in lung cancer for the lay doctor. Targeted Oncology 3, 161–171. [Google Scholar]
- Sargent D. J., Allegra C. (2002). Issues in clinical trial design for tumor marker studies. Seminars in Oncology 29, 222–230. [DOI] [PubMed] [Google Scholar]
- Sargent D. J., Conley B. A., Allegra C., Collette L. (2005). Clinical trial designs for predictive marker validation in cancer treatment trials. Journal of Clinical Oncology 23, 2020–2027. [DOI] [PubMed] [Google Scholar]
- Sawyers C. (2004). Targeted cancer therapy. Nature 432, 294–297. [DOI] [PubMed] [Google Scholar]
- Simon R. (2008). The use of genomics in clinical trial design. Clinical Cancer Research 14, 5984–5993. [DOI] [PubMed] [Google Scholar]
- Sledge G. W. (2005). What is targeted therapy. Journal of Clinical Oncology 23, 1614–1615. [DOI] [PubMed] [Google Scholar]
- Zang Y., Liu S., Yuan Y. (2015). Optimal marker-adaptive designs for targeted therapy based on imperfectly measured biomarkers. Journal of the Royal Statistical Society 64, 635–650. [Google Scholar]
- Zang Y., Guo B. (2016). Optimal two-stage enrichment design correcting for biomarker misclassification. Statistical Methods in Medical Research. In Press. [DOI] [PubMed] [Google Scholar]
- Zang Y., Lee J. J., Yuan Y. (2016). Two stage marker-stratified clinical trial design in the presence of biomarker misclassification. Journal of the Royal Statistical Society: Series C. In press. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.