Globally efficient non-parametric inference of average treatment effects by empirical balancing calibration weighting

Summary

The estimation of average treatment effects based on observational data is extremely important in practice and has been studied by generations of statisticians under different frameworks. Existing globally efficient estimators require non-parametric estimation of a propensity score function, an outcome regression function or both, but their performance can be poor in practical sample sizes. Without explicitly estimating either functions, we consider a wide class calibration weights constructed to attain an exact three-way balance of the moments of observed covariates among the treated, the control, and the combined group. The wide class includes exponential tilting, empirical likelihood and generalized regression as important special cases, and extends survey calibration estimators to different statistical problems and with important distinctions. Global semiparametric efficiency for the estimation of average treatment effects is established for this general class of calibration estimators. The results show that efficiency can be achieved by solely balancing the covariate distributions without resorting to direct estimation of propensity score or outcome regression function. We also propose a consistent estimator for the efficient asymptotic variance, which does not involve additional functional estimation of either the propensity score or the outcome regression functions. The proposed variance estimator outperforms existing estimators that require a direct approximation of the efficient influence function.

1. Introduction

Studying the effect of an intervention or a treatment is central to experimental scientists. While a randomized trial is a gold standard to identify average treatment effects, it may be infeasible, or even unethical, to conduct in practice. Observational studies are common in econometrics, social science, and public health, where the participation of intervention is only observed rather than manipulated by scientists. A typical concern for inferring causality in an observational study is confounding, where individual characteristics such as demographic factors can be related to both the treatment selection and the outcome of interest. In these cases, a simple comparison of sample averages from the two intervention groups can lead to a seriously biased estimate of the population average treatment effects.

When the treatment selection process depends entirely on observable covariates, there are two broad classes of strategies for estimating average treatment effects, namely outcome regression and propensity score estimation. When a linear model is assumed for the outcome given covariates, the coefficient for treatment status provides an estimate of average treatment effects when all relevant confounders are controlled and when there is no effect modifiers. In general, more complex regression models can be used for predicting unobservable potential outcomes, while the average treatment effects can be estimated by averaging predicted outcomes (Oaxaca; 1973; Blinder; 1973). An alternative class of strategies is based on the propensity score, which is the probability of receiving treatment given covariates. Rosenbaum and Rubin (1983) showed that adjusting the true propensity score can remove all bias due to confounding. They also showed that the true propensity score balances the covariate distributions between the two treatment arms. Propensity score can be used for subclassification (Rosenbaum and Rubin; 1984; Rosenbaum; 1991), matching (Rosenbaum and Rubin; 1985; Abadie and Imbens; 2006), and weighting (Rosenbaum; 1987; Hirano et al.; 2003). However, propensity score based methods may not be efficient in general.

To study efficient estimation, semiparametric efficiency bounds were derived independently by Robins et al. (1994) and Hahn (1998). Interestingly, the efficient influence function for the average treatment effects involves both the propensity score and the outcome regression functions. This motivated subsequent development of methods involving a combination of propensity score and outcome regression modeling (Robins et al.; 1994; Hahn; 1998; Bang and Robins; 2005; Qin and Zhang; 2007; Cao et al.; 2009; Tan; 2010; Graham et al.; 2012; Vansteelandt et al.; 2012). Recently, Chan (2013), Han and Wang (2013) and Chan and Yam (2014) considered methods that can accommodate multiple non-nested models of the propensity score and outcome regression at the same time. Many recent methods focus on improving covariate balance within the propensity score and outcome regression frameworks (Qin and Zhang; 2007; Tan; 2010; Chan; 2012; Graham et al.; 2012; Vansteelandt et al.; 2012; Han and Wang; 2013; Chan and Yam; 2014). Imai and Ratkovic (2014) argue that the estimation of propensity score parameters with a specification of outcome model does not align well with the original spirit of propensity score methodology as discussed in Rubin (2007). They proposed a covariate balancing propensity score method for the estimation of propensity score parameters, which balances covariates for an overidentified moment restriction without assuming an outcome model.

All methods mentioned so far require specification of either a propensity score model, an outcome model, or both. Consistency of the estimators requires some underlying models to be correctly specified. Since the estimand of interest is the average treatment effects, and the propensity score or the outcome models are just intermediate steps, it is natural to question whether the correctness of the intermediate models were necessary for producing correct inference. Nonparametric estimators are developed to provide valid inference in large samples without relying on parametric assumptions in the intermediate steps of estimation. Hahn (1998), Hirano et al. (2003), Imbens et al. (2006), Chen et al. (2008) have considered various nonparametric estimators for the average treatment effects. Although the validity of estimation does not rely on any parametric assumption on the propensity score and outcome models, their methods require sieve approximations of those unknown conditional functions, as these functions appear explicitly in the semiparametric efficient inference functions (Robins et al.; 1994; Hahn; 1998). An important observation has been made by Hirano et al. (2003) that the celebrated inverse probability weighted estimator of Horvitz and Thompson (1952) is globally semiparametric efficient when a sieve maximum likelihood propensity score estimator is used. Global semiparametric efficiency is more desirable than local semiparametric efficiency which requires the correct specification of parametric models. An implication of Hirano et al. (2003) is that global efficiency can be achieved by solely estimating the propensity score nonparametrically, without requiring to estimate the outcome model, which also appears in the efficient influence function. An efficient estimator is adapted from the Horvitz-Thompson estimator, a simple estimator used by decades of statisticians. Alternatively, Imbens et al. (2006) and Chen et al. (2008) showed that globally efficient estimators can be constructed from nonparametric estimators of the outcome model only. A combination of nonparametric estimators of the propensity score and outcome models can also produce globally efficient estimators (Imbens et al.; 2006; Chen et al.; 2008).

The existing globally efficient estimators do not require correct specification of propensity score or outcome regression models in large samples, but the need to specify a nonparametric approximation of either or both functions is still present. It has been shown that estimators for average treatment effects can have substantial bias when either functions are poorly estimated (Kang and Schafer; 2007; Ridgeway and McCaffrey; 2007). It is natural to question whether nonparametric estimation of these functions is even necessary, and whether they can be replaced by an alternative simple balancing criterion which is inherited from the unknown propensity score function. Although estimators that improve balance of covariate distribution are discussed in recent papers (Qin and Zhang; 2007; Tan; 2010; Graham et al.; 2012; Vansteelandt et al.; 2012; Han and Wang; 2013; Imai and Ratkovic; 2014; Chan and Yam; 2014), their methods require parametric modeling of the propensity score model or the outcome model. Nonparametric methods for improving covariate balance have been studied widely in the survey sampling literature (Deming and Stephan; 1940; Deville and Särndal; 1992; Kim and Park; 2010; Hainmueller; 2012). The recent paper of Hainmueller (2012) focused on using the implied weights of the raking estimator of Deming and Stephan (1940) to preprocess data for estimating the treatment effects on the treated. Since he focused on preprocessing, he did not study statistical inference and estimation efficiency.

There are two substantial gaps in the literature of nonparametric inference for average treatment effects that we aim to fill in this article. First, we show that a broad class of calibration estimators which solely targets on covariate balancing can attain semiparametric efficiency bound without explicitly estimating the propensity score or outcome regression functions. Compared to the seminal paper of Hirano et al. (2003) who showed that globally efficient estimation can be achieved by a nonparametric adaptation of a simple estimator by Horvitz and Thompson (1952), which has been used by statisticians for decades, we show that a globally efficient estimator can be adapted from another class of simple estimators pioneered by Deming and Stephan (1940). However, our work contains three very different conceptual aspects compared to existing survey calibration methods. The first important difference is that the proposed weights minimize a distance measure from a set of misspecified, uniform weights, whereas the original survey calibration estimators minimizes distance from the design weights, which are the unknown inverse propensity score weights for the evaluation problem. Therefore, our formulation does not involve the estimation of the unknown propensity score function. By minimizing the distance to uniform baseline weights, we improve robustness by avoiding extreme weights that typically ruin the performance of Horvitz-Thompson estimators with maximum likelihood estimated weights. The uniform baseline weights are misspecified unless the treatment is randomized, and the usual theory for survey calibration that requires a correctly specified baseline weights are therefore inapplicable. The mathematical proofs for the theorems are therefore very different from the existing results. Second, we reformulate the problem as the dual of the original calibration problem, which is a separable programming problem subject to linear constraints. The dual, as discussed in the optimization literature, is an unconstrained convex optimization problem. This reformulation allows us to provide a simple and stable algorithm for practical usage and streamlines the mathematical proofs. Third, we consider a growing number of moment conditions as opposed to a fixed number of moment conditions for survey calibration. The growing number of moment conditions is necessary for removing asymptotic bias associated with misspecified design weights while at the same time attaining global efficiency.

An equally important contribution of our paper is a novel nonparametric variance estimator for interval estimation and hypothesis testing. While there are plenty of point estimators for estimating average treatment effects, the problem of nonparametric estimation of efficient variance has received little attention because it is difficult. A consistent plugged-in estimator proposed by Hirano et al. (2003) involves the squared inverse of estimated propensity score function and can perform extremely poorly in small samples as shown in the simulation studies given in the online supplementary materials. In a local semiparametric efficiency framework, consistent variance estimation often requires both the propensity score and outcome regression models to be correctly modeled despite point estimators that are often doubly robust. Due to these difficulties, many authors proposed novel point estimators while leaving the variance estimation unattended. Bootstrapping may be used but is typically computationally intensive and may not be practical to implement for large data sets. Others have suggested that the estimated weights shall be treated as fixed weights (see for example, Section 3.4 of Hainmueller, 2012). However, statistical inference can be very misleading. The variability of the estimated weights can be substantial, and in fact we illustrate using a real example in Section 5.2 to show that the standard error of the treatment effects can be underestimated by more than five fold if the weights are treated as fixed. Our proposed variance estimator is both novel and important for statistical inference in practice. It does not require direct nonparametric estimation of either the propensity score or outcome regression models. This is in contrast to Hirano et al. (2003), whose point estimator does not require nonparametric estimation of outcome regression function but that additional functional estimation is required for interval estimation. We show that the proposed estimator is consistent to the semiparametric variance bound and its validity does not depend on any parametric models; it outperforms existing estimators which require direct approximation of the efficient influence function.

The paper is organized as follows. In Section 2, we shall introduce the notations and a class of the calibration estimators, explain the philosophical and practical differences between calibration and propensity score modeling, and study the large sample properties of the calibration estimators. A consistent asymptotic variance estimator is proposed in Section 3. In Section 4, we study three extensions of the problem: the estimation of weighted average treatment effects, treatment effects on the treated, and the estimation for multiple comparison groups. Analyses of the National Health and Nutrition Examination Survey and the famous Lalonde (1986) data for the effect of job training on income are presented in Section 5. Some final remarks are given in Section 6.

The proposed methods can be implemented through an open-source R package ATE available from the Comprehensive R Archive Network (http://cran.r-project.org/package=ATE).

2. Point Estimation

2.1. Notations and basic framework

Let T be a binary treatment indicator. We define Y (1) and Y (0) to be the potential outcomes when an individual is assigned to the treatment or control group respectively. The population average treatment effects is defined as τ ≜ (Y (1) − Y (0)). The estimation of τ is complicated by the fact that Y (1) and Y (0) cannot be observed jointly. The potential outcome Y (1) is only observed when T = 1, and Y (0) is only observed when T = 0. The observed outcome can be represented as Y = TY (1) + (1 − T)Y (0). In addition to (T, Y), we assume that a vector of covariates X is observed for everyone, and T is typically dependent on (Y (1), Y (0)) through X. We assume the full data {(T_i, Y_i(1), Y_i(0), X_i), i = 1, …, N} are independent and identically distributed, and the observed data is {(T_i, Y_i, X_i), i = 1, …, N}. The following assumption is often made for the identification of t:

• Assumption 1. (Unconfounded Treatment Assignment) Given X, T is independent of (Y (1), Y (0)).

Based on Assumption 1, the semiparametric efficiency bound for estimating t has been developed by Robins et al. (1994) and Hahn (1998). Let π(x) ≜ (T = 1|X = x) be the non-missing probability, also known as the propensity score, and m₁(x) ≜ [Y (1)|X = x], m₀(x) ≜ 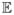[Y (0)|X = x] are the conditional mean functions. Conventional statistical methods for estimating τ involves modeling of π(X), (m₁(X), m₀(X)) or both, based on different representations of τ:

$$\tau =\mathbb{E}\left[\frac{TY}{\pi (\mathbf{X})}-\frac{(1-T)Y}{1-\pi (\mathbf{X})}\right]$$ (1)

$$=\mathbb{E}[m_1(\mathbf{X})-m_0(\mathbf{X})]$$ (2)

$$=\mathbb{E}\left[\frac{TY}{\pi (\mathbf{X})}-\frac{T-\pi (\mathbf{X})}{\pi (\mathbf{X})}{m}_1(\mathbf{X})-\frac{(1-T)Y}{1-\pi (\mathbf{X})}-\frac{T-\pi (\mathbf{X})}{1-\pi (\mathbf{X})}{m}_0(\mathbf{X})\right].$$ (3)

The inverse probability weighted estimators (Horvitz and Thompson; 1952; Hirano et al.; 2003) have been constructed based on (1); the regression prediction estimators (Oaxaca; 1973; Cheng; 1994; Imbens et al.; 2006) have been proposed based on (2); and the augmented inverse probability weighted estimators (Robins et al.; 1994; Bang and Robins; 2005; Cao et al.; 2009) have been proposed based on (3).

Based on Assumption 1, another important feature for the propensity score π(X) is that

$$\mathbb{E}\left[\frac{Tu(\mathbf{X})}{\pi (\mathbf{X})}\right]=\mathbb{E}\left[\frac{(1-T)u(\mathbf{X})}{1-\pi (\mathbf{X})}\right]=\mathbb{E}[u(\mathbf{X})].$$ (4)

Recently, many authors have proposed estimators by combining (1) and (4) in various creative manners under the propensity score framework, see Qin and Zhang (2007), Tan (2010), Chan (2012), Graham et al. (2012), Vansteelandt et al. (2012), Han and Wang (2013), Imai and Ratkovic (2014) and Chan and Yam (2014). Since (4) often defines an overidentifying set of moment restrictions, estimation is generally done within the generalized method of moments or the empirical likelihood framework. These methods require modeling and estimation of the propensity score but the proposed method does not.

2.2. A general class of calibration estimators

Let D(v, v₀) be a distance measure, for a fixed v₀ ∈ ℝ, that is continuously differentiable in v ∈ ℝ, nonnegative, strictly convex in v and D(v₀, v₀) = 0. The general idea of calibration as in Deville and Särndal (1992) is to minimize the aggregate distance between the final weights w = (w₁, …, w_N) to a given vector of design weights d = (d₁, …, d_N) subject to moment constraints. The minimum distance estimation is closely related to generalized empirical likelihood as discussed in Newey and Smith (2004). In survey applications, the design weights are known inverse probability weights. In the estimation of average treatment effects, the inverse probability weights are d_i = π(X_i)⁻¹ if T_i = 1 or d_i = (1 − p(X_i))⁻¹ if T_i = 0, for i = 1, …, N, which are unknown and need to be estimated. A recent paper by Chan and Yam (2014) discussed the calibration methods with design weights estimated by maximum likelihood approach. Here we consider a different formulation. To circumvent the need to estimate the design weights, we consider a vector of misspecified uniform design weights d^* = (1, 1, …, 1), and construct weights w by solving the following constrained minimization problem:

$$\text{Minimize}\sum _{i=1}^{N}D(w_i,1),$$

subject to the empirical counterparts of (4), that are

$$\frac{1}{N}\sum _{i=1}^N{T}_i{w}_{i}u({\mathbf{X}}_i)=\frac{1}{N}\sum _{i=1}^{N}u({\mathbf{X}}_i)\text{and}\frac{1}{N}\sum _{i=1}^N(1-T_i)w_{i}u({\mathbf{X}}_i)=\frac{1}{N}\sum _{i=1}^{N}u({\mathbf{X}}_i).$$

The choice of uniform design weights is based on a few observations. First, if the counterfactual variables are observable for everyone, we can estimate τ by the sample mean of Y (1) − Y (0) which assigns equal weights. Also, the need for estimating π(x) is not needed when the design weights are assumed to be uniform. Moreover, by minimizing the aggregate distance from constant weights, the dispersion of final weights is controlled and extreme weights are less likely to obtain. In contrast, extreme weights cause instability in Horvitz-Thompson estimators with maximum likelihood weights under model misspecification. However, the choice of uniform design weights also poses unique challenges. When the number of matching conditions is fixed, Hellerstein and Imbens (1999) showed that an empirical likelihood calibration estimator with misspecified design weights yields inconsistent estimators in general. To circumvent this theoretical difficulty, we consider matching u_K which is a K(N)-dimensional function of X, K(N) increases to infinity when N goes to infinity yet with K(N) = o(N).

The constrained optimization problem stated above is equivalent to two separate constrained optimization problems:

$$\text{Minimize}\sum _{i=1}^N{T}_{i}D(N{p}_i,1)\text{subject}\text{to}\sum _{i=1}^N{T}_i{p}_i{u}_K({\mathbf{X}}_i)=\frac{1}{N}\sum _{i=1}^N{u}_K({\mathbf{X}}_i),$$ (5)

and

$$\text{Minimize}\sum _{i=1}^N(1-T_i)D(N{q}_i,1)\text{subject}\text{to}\sum _{i=1}^N(1-T_i)q_i{u}_K({\mathbf{X}}_i)=\frac{1}{N}\sum _{i=1}^N{u}_K({\mathbf{X}}_i).$$ (6)

Furthermore, to efficiently implement the method, we consider the dual problems of (5) and (6). The reason is that the primal problems (5) and (6) are convex separable programming with linear constraints, and Tseng and Bertsekas (1987) showed that the dual problems are unconstrained convex maximization problems that can be solved by efficient and stable numerical algorithms.

Let D(v) = D(v, 1), f(v) = D(1 − v) and its derivative be f′(v), ∀v ∈ ℝ. The dual solutions are given as follows. For i such that T_i = 1, 1

$${\widehat{p}}_K({\mathbf{X}}_i)\triangleq \frac{1}{N}{\rho }^{\prime }({\widehat{\lambda }}_K^T{u}_K({\mathbf{X}}_i)),$$

where ρ′ is the first derivative of a strictly concave function

$$\rho (v)=f({(f^{\prime })}^{-1}(v))+v-v·{(f^{\prime })}^{-1}(v)$$ (7)

and γ̂_K ∈ ℝ^K maximizes the following objective function

$${\widehat{G}}_K(\lambda )\triangleq \frac{1}{N}\sum _{i=1}^N[T_i\rho ({\lambda }^T{u}_K({\mathbf{X}}_i))-{\lambda }^T{u}_K({\mathbf{X}}_i)].$$ (8)

Similarly, for i such that T_i = 0,

$${\widehat{q}}_K({\mathbf{X}}_i)\triangleq \frac{1}{N}{\rho }^{\prime }({\widehat{\beta }}_K^T{u}_K({\mathbf{X}}_i)),$$

and β̂_K ∈ ℝ^K maximizes the following objective function

$${\widehat{H}}_K(\beta )\triangleq \frac{1}{N}\sum _{i=1}^N[(1-T_i)\rho ({\beta }^T{u}_K({\mathbf{X}}_i))-{\beta }^T{u}_K({\mathbf{X}}_i)].$$ (9)

According to the first order conditions of the maximizations of (8) and (9), we can easily check that the linear constraints in (5) and (6) are satisfied. We define the proposed empirical balancing estimator for τ to be

$${\widehat{\tau }}_K\triangleq \sum _{i=1}^N\{T_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i\}.$$

The relationship (7) between ρ(v) and f(v) = D(1−v) is shown in Appendix B, where we also show that strict convexity of D is equivalent to strict concavity of ρ. Since the dual formulation is equivalent to the primal problem and will simplify the following discussions, we shall express the estimator in terms of ρ(v) in the rest of the discussions. When ρ(v) = −exp(−v), the weights are equivalent to the implied weights of exponential tilting (Kitamura and Stutzer; 1997; Imbens et al.; 1998). When ρ(v) = log(1 + v), the weights correspond to empirical likelihood (Owen; 1988; Qin and Lawless; 1994). When ρ(v) = −(1 − v)²/2, the weights are the implied weights of the continuous updating estimator of generalized method of moments (Hansen et al.; 1996), and also minimizes the squared distance function. When ρ(v) = v − exp(−v), the weights are equivalent to the inverse of a logistic function.

Despite the close connections with generalized empirical likelihood, the calibration estimator has several important differences compared to the generalized empirical likelihood literature. In econometrics, generalized empirical likelihood is often employed for estimating a p-dimensional parameter by specifying a q-dimensional estimating equation, where q > p ≥ 1. However, we are not estimating the target parameter τ by directly solving an overidentified estimating equation. The calibration conditions in (5) and (6) can be regarded as a K-dimensional moment restriction with a degenerate parameter of interest, and (8) and (9) are essentially degenerate cases of generalized empirical likelihood with only the auxiliary parameters λ and β appearing but not the target parameter τ. Even though the generalized empirical likelihood estimation problem is undefined because the moment restrictions are not functions of target parameters, implied weights can still be constructed. In econometrics, the generalized empirical likelihood estimators are usually solutions to saddlepoint problems and can be difficult to compute. In our case, λ̂ and β̂ are solutions to unconstrained convex maximization problems rather than a saddlepoint problem and can be computed by a fast and stable Newton-type algorithm. Moreover, the generalized empirical likelihood literature mainly deals with a fixed number of moment restrictions, but the dimension K of moment restrictions increases with N in our present consideration. Furthermore, the moment restrictions are misspecified for finite K in our case, but most theoretical results for generalized empirical likelihood are derived under a correct model specification and are therefore inapplicable.

2.3. Philosophical differences and practical implications

Although the calibration weights in Section 2.2 are also constructed from moment balancing conditions as in certain propensity score methodologies, there is a fundamental difference in the modeling philosophy that leads to important practical implications in the estimation of average treatment effects. Philosophically, the calibration weights are constructed without any reference to a propensity score model. It ignores the explicit link between the weights in the treated and the control groups that are present in propensity score modeling. Practically, it leads to an exact three-way balance between the treated, the controls and the combined group for finite samples as well as asymptotically, whereas finite-sample exact three-way balance is not guaranteed for propensity score modeling in general. Furthermore, calibration can be viewed as a unification of the existing globally efficient estimations that are constructed from different modeling strategies as discussed in the online supplementary material.

To illustrate the first idea, we consider a general class of weighting estimators $N^{-1}{\sum }_{i=1}^N\{T_i{w}_1({\mathbf{X}}_i)Y_i-(1-T_i)w_0({\mathbf{X}}_i)Y_i\}$. If the true propensity score π(X) is known, we set w₁(X) = (π(X))⁻¹ and w₀(X) = (1 − p(X))⁻¹, so that the corresponding weighting estimator is an unbiased estimator for τ based on (1). The propensity score setting confines the weight functions w₁(x) and w₀(x) in the following relationship:

$$w_0(x)={(1-{(w_1(x))}^{-1})}^{-1}.$$ (10)

When a propensity score model π(x; γ) is assumed, and γ̂ is an estimate of γ, the Horvitz-Thompson estimator sets w₁(x) = π⁻¹(x; γ̂) and w₀(x) = (1 − π(x; γ̂))⁻¹. It follows that (10) is satisfied. Under model misspecification, $C_1=N^{-1}\times {\sum }_{i=1}^N{T}_i{\pi }^{-1}({\mathbf{X}}_i;\widehat{\gamma })$ and $C_0=N^{-1}\times {\sum }_{i=1}^N(1-T_i){(1-\pi ({\mathbf{X}}_i;\widehat{\gamma }))}^{-1}$ can be very different from 1, therefore it has been suggested that w₁(x) = [C₁π(x; γ̂)]⁻¹ and w₀(x) = [C₀(1 − π(x; γ̂))]⁻¹ which are ratio-type inverse probability weighting estimators. However, these weight functions do not satisfy (10) unless C₁ = C₀ = 1. In fact, the ratio-type inverse probability weighting estimator is a special calibration estimator that requires propensity score modeling to be discussed in Section 6. The class of calibration estimators in Section 2.2 does not rely on propensity score modeling in the first place, and the weights w₁(x) = ρ′(γ̂^Tu_K(x)) and w₀(x) = ρ′(β̂^Tu_K(x)) do not satisfy (10) in general. We note that one of the two weights can correspond to the inverse probability weight from a propensity score model, but it is generally impossible to have both sets of weights to be consistent with a single propensity score model. Therefore, for any fixed K, the calibration estimator for the average treatment effects cannot be locally efficient. Despite this seemingly undesirable property, we shall show that τ̂ is globally semiparametric efficient when K is allowed to increase with N. Existing globally efficient estimators are all locally efficient for any fixed dimension of approximation, but the calibration estimator sacrifices local efficiency by ignoring the link (10), while achieving exact three-way balance in finite samples. Note that the true propensity score attains the exact three-way balance in (4), but the estimated propensity scores typically do not achieve exact three-way balance in finite samples. While the Horvitz-Thompson estimator with maximum likelihood weights is globally efficient and three-way balance should hold for extremely large samples, the balance can be quite poor for practical sample sizes. In our current proposal, the exact three-way balance holds for finite samples as well as asymptotically, which is a reason why our asymptotic results for the point and variance estimators hold well even for finite samples.

To further illustrate the balancing properties of estimators, suppose that π(γ^Tx) is a propensity score model. The expression (4) leads to

$$\mathbb{E}(b_1(T,\mathbf{X};\gamma ))\triangleq \mathbb{E}\left[\left(\frac{T}{\pi ({\gamma }^T\mathbf{X})}-1\right)\mathbf{X}\right]=0,$$ (11)

$$\mathbb{E}(b_2(T,\mathbf{X};\gamma ))\triangleq \mathbb{E}\left[\left(\frac{1-T}{1-\pi ({\gamma }^T\mathbf{X})}-1\right)\mathbf{X}\right]=0,$$ (12)

$$\mathbb{E}(b_3(T,\mathbf{X};\gamma ))\triangleq \mathbb{E}\left[\left(\frac{T}{\pi ({\gamma }^T\mathbf{X})}-\frac{1-T}{1-\pi ({\gamma }^T\mathbf{X})}\right)\mathbf{X}\right]=0.$$ (13)

Suppose we estimate γ by solving each of the just-identified system of estimating equations defined by moment conditions (11), (12) and (13), and denote the corresponding estimators to be γ̂₁, γ̂₂ and γ̂₃; that is, γ̂_j satisfies $N^{-1}\times {\sum }_{i=1}^N{b}_j(T_i,{\mathbf{X}}_i;{\widehat{\gamma }}_j)=0$, for j = 1, 2, 3. Note that, however, $N^{-1}\times {\sum }_{i=1}^N{b}_j(T_i,{\mathbf{X}}_i;{\widehat{\gamma }}_{j^{\prime }})\ne 0$ for j ≠ j′. The covariate balancing propensity score of Imai and Ratkovic (2014) shares the same spirit of γ̂₃, and the inverse probability tilting method of Graham et al. (2012) shares the same spirit of γ̂₁. In general, matching one set of moment conditions creates two-way balance, but does not guarantee three-way balance between the treated, the controls and the combined group. However, a lack of three-way balance can adversely affect the quality of the final estimate since the average treatment effects is defined for the combined population, and the data for Y (1) and Y (0) are only available for the treated and controls respectively. We shall further illustrate this point by the simulation studies in the online supplementary materials. On the other hand, four-or-more-way balance is not necessary because asymptotic efficiency is attained by three-way balance as shown in Theorem 1 in Section 2.4.

Since b₃ = b₁ − b₂, balancing any two systems out of (11), (12) and (13) can lead to a balance of the remaining system. Therefore, by considering an overidentified combined system of estimating functions b₁ and b₂, one can estimate γ by using generalized method of moments or empirical likelihood, and we denote the corresponding estimator by γ̂₁₂. However, it is typical that

$$\frac{1}{N}\sum _{i=1}^N{b}_j(T_i,{\mathbf{X}}_i,{\widehat{\gamma }}_{12})\ne 0,j=1,2,3,$$

because the generalized method of moment estimator does not solve that corresponding overidentified system exactly, and therefore the exact three-way balance is typically not achieved.

For the calibration estimator, however,

$$\sum _{i=1}^N{T}_i{\widehat{p}}_K({\mathbf{X}}_i)u_K({\mathbf{X}}_i)-\sum _{i=1}^N(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)u_K({\mathbf{X}}_i)=\frac{1}{N}\sum _{i=1}^N{u}_K({\mathbf{X}}_i),$$

by construction, and exact three-way balance can naturally be achieved.

Several remarks are in order. First, when the propensity score model is misspecified, which is likely in practice, γ̂_j converges in probability to ${\gamma }_j^{\ast }$, j = 1, 2, 3, which are different in general. Therefore, covariate balancing based on one of (11), (12) or (13) can lead to very different results. For balancing an over-identified system of equations using the empirical likelihood, there is no guarantee that the γ estimate is $\sqrt{N}$-consistent (Schennach; 2007) under a misspecified propensity score model. Calibration is similar to using γ̂₁ for reweighting the treated and γ̂₂ for reweighting the controls when the propensity score model is misspecified, but our proposed non-parametric calibration method does not involve propensity score estimation.

Despite the dissimilarities in the weighting aspects compared to propensity score methodologies, calibration can be viewed as a unification of the existing globally efficient estimation that are constructed from two very different strategies: weighting and prediction. Let m̃₁(X) and m̃₀(X) be weighted least square estimators for Y against u_K(X) among the treated and controls with weights p̂_K(X) and q̂_K(X) respectively. It follows that

$$\begin{array}{l}\sum _{i=1}^N{T}_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-\sum _{i=1}^N(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i=\sum _{i=1}^N{T}_i{\widehat{p}}_K({\mathbf{X}}_i){\stackrel{\sim }{m}}_1({\mathbf{X}}_i)-\sum _{i=1}^N(1-T_i){\widehat{q}}_K({\mathbf{X}}_i){\stackrel{\sim }{m}}_0({\mathbf{X}}_i)\\ =\sum _{i=1}^N{\stackrel{\sim }{m}}_1({\mathbf{X}}_i)-{\stackrel{\sim }{m}}_0({\mathbf{X}}_i).\end{array}$$

The first equality holds from the score equation of weighted least squares, and the second equality holds because of the exact three-way balance. Therefore, our proposed calibration unifies the weighting and the prediction estimators by a rather unexpected way of relaxing the estimation of propensity score and outcome regression functions.

2.4. Large sample properties of calibration estimators

To show the large sample properties, we need the following technical assumptions in addition to Assumption 1.

• Assumption 2. 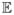[Y (1)²] < ∞ and 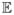[Y (0)²] < ∞.

• Assumption 3. The support 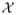of r-dimensional covariate X is a Cartesian product of r compact intervals.

• Assumption 4. π(x) is uniformly bounded away from 0 and 1, i.e. there exist some constants $\frac{1}{{\eta }_1}\triangleq \underset{x\in \mathcal{X}}{inf}\pi (x),\frac{1}{{\eta }_2}\triangleq \underset{x\in \mathcal{X}}{sup}\pi (x)$ such that

$$0<\frac{1}{{\eta }_1}\le \pi (x)\le \frac{1}{{\eta }_2}<1\forall x\in \mathcal{X}$$

• where 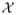is the support of X.

• Assumption 5. π(x) is s-times continuously differentiable, where s > 13r.

• Assumption 6. m₀(x) and m₁(x) are t-times continuously differentiable, where $t>\frac{3r}{2}$.

• Assumption 7. K = O (N^ν) and $\frac{1}{\frac{s}{r}-2}<\nu <\frac{1}{11}$.

• Assumption 8. ρ ∈ C³(ℝ) is a strictly concave function defined on ℝ i.e. ρ″(γ) < 0, ∀γ ∈ ℝ, and the range of ρ′ contains [η₂, η₁] which is a subset of the positive real line.

Assumptions 1–7 or their analogues also appeared in Hahn (1998), Hirano et al. (2003) and Imbens et al. (2006). Assumption 1 is required for the identification of the average treatment effects. Assumption 2 is required for the finiteness of asymptotic variance. Assumptions 3 and 4 are required for uniform boundedness of approximations. Assumption 4 is an overlap condition that is necessary for the nonparametric identification of the average treatment effects in the population. If there exists a region of X such that the probability of receiving treatment is 0 or 1, the treatment effects cannot be identified unless some extrapolatory modeling assumptions are imposed. In that case, one could define a subpopulation with a sufficient overlap so that the average treatment effects can be estimated nonparametrically within this subpopulation. Assumptions 5 and 6 are required for controlling the remainder of approximations with a given basis function. They are standard assumptions for multivariate smoothing where the order of smoothness required increases with the dimension of X. There is usually no a-priori reason to believe that the π(x), m₁(x) and m₀(x) are not smooth in x. Also the dimension of X is not restricted by the assumptions, unlike in the kernel estimation of π(x) discussed in Chen et al. (2013), in which their assumptions imply that the dimension of X cannot be greater than 4. Assumption 7 is required for controlling the stochastic order of the residual terms, which is desirable in practice because K grows very slowly with N so that a relatively small number of moment conditions is sufficient for the proposed method to perform well. Assumption 8 is a mild assumption on ρ which is chosen by the statisticians and includes all the important special cases considered in the literature. In contrast, the theoretical results for Hahn (1998), Hirano et al. (2003), Imbens et al. (2006) and Chen et al. (2008) were developed only for linear or logistic models for propensity score.

Define μ₀ ≜ 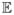[Y (0)], μ₁ ≜ 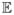[Y (1)], ${\sigma }_1^2(\mathbf{X})=\mathit{Var}(Y(1)\mid \mathbf{X})$ and ${\sigma }_0^2(\mathbf{X})=\mathit{Var}(Y(0)\mid \mathbf{X})$, which are finite by Assumption 2. We have the following theorem.

Theorem 1

Under Assumptions 1–8, we have

1. ${\displaystyle \sum _{i=1}^N}\{T_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i\}\stackrel{p}{\to }\tau$;

2. $\sqrt{N}\left({\displaystyle \sum _{i=1}^N}\{T_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i\}-\tau \right)\stackrel{d}{\to }\mathcal{N}(0,V_{\mathit{semi}})$, where

   $V_{\mathit{semi}}\triangleq \mathbb{E}\left[{(m_1(\mathbf{X})-m_0(\mathbf{X})-\tau )}^2+\frac{{\sigma }_1^2(\mathbf{X})}{\pi (\mathbf{X})}+\frac{{\sigma }_0^2(\mathbf{X})}{1-\pi (\mathbf{X})}\right]$ attains the semi-parametric efficiency bound as shown in Robins et al. (1994) and Hahn (1998).

A detailed proof of Theorem 1 will be provided in the supplementary materials. We note that our global efficiency result is substantially more general than existing results in the literature, in which global efficiency for weighting estimators has only been established for two particular estimators for the propensity score: the series least square estimator (Hahn; 1998; Chen et al.; 2008), and the maximum likelihood series logit estimator (Hirano et al.; 2003; Imbens et al.; 2006). The proof of lemma B.2 in Chen et al. (2008) relies crucially on the least square property of the projection of T on the approximation basis. The validity of the result in Hirano et al. (2003) requires a key fact about the least square projection of $-\mathbb{E}(Y(1)\mid \mathbf{X}=x){\pi }^{-1}(x)\sqrt{\pi (x)(1-\pi (x))}$ onto a transformed approximation basis $\sqrt{{\pi }^{\ast }(x)(1-{\pi }^{\ast }(x))}{u}_K(x)$, where π^*(x) is defined in terms of the limit of a maximum likelihood estimator under a logistic regression model. Their projection argument yields an asymptotically negligible residual term only when the series maximum likelihood logit estimator is used. We are able to establish the global efficiency results for any strictly concave ρ satisfying Assumption 8 because we employed a different and more delicate projection argument. We studied a weighted least square projection of − 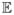(Y (1)|X = x) and − 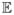(Y (0)|X = x) onto the original approximation basis u_K(x), where ρ only enters the weights of the projection, but not the approximation basis. Our projection argument yields an asymptotically negligible residual term when the weights of the projection are bounded from above and below, which was established under our regularity conditions. Theorem 1 holds even when the ρ functions used for computing p̂_K and q̂_K are different. However, we do not recommend this in practice, because each ρ(v) corresponds to a measure of distance D(v) from the unit weight, and usually there is not any justifiable reason for choosing a different measure for the two treatment groups.

3. A nonparametric variance estimator

By Theorem 1, the proposed estimator attains the semiparametric efficiency bound with the following asymptotic variance: $V_{\mathit{semi}}\triangleq \mathbb{E}\left[{(m_1(\mathbf{X})-m_0(\mathbf{X})-\tau )}^2+\frac{{\sigma }_1^2(\mathbf{X})}{\pi (\mathbf{X})}+\frac{{\sigma }_0^2(\mathbf{X})}{1-\pi (\mathbf{X})}\right]$. Since the variance involves unknown functions π(x), m₁(x) and m₀(x), plug-in estimators typically involve nonparametric estimation of functions other than π(x), as in Hirano et al. (2003). One of the advantages of our proposed point estimator is that we do not need to directly estimate those functions, and it would be nice to have a variance estimator that also does not involve any additional estimates of nonparametric functions. Moreover, existing nonparametric estimators that require estimation of π(x) often fail in practice, as illustrated in Table 4 of the online supplementary materials. A particular thorny issue is that the asymptotic variance estimators often depend on the squared inverse of estimated propensity score, and the instability caused by extreme inverse weights is even magnified. In this section, we shall study a consistent asymptotic variance estimator that can be computed easily from the point estimator and avoids the problem of extreme weights.

Define

$$\begin{array}{l}{g}_{K1}(T,\mathbf{X};\lambda )\triangleq T{\rho }^{\prime }({\lambda }^T{u}_K(\mathbf{X}))u_K(\mathbf{X})-u_K(\mathbf{X}),\\ g_{K2}(T,\mathbf{X};\beta )\triangleq (1-T){\rho }^{\prime }({\beta }^T{u}_K(\mathbf{X}))u_K(\mathbf{X})-u_K(\mathbf{X}),\\ g_{K3}(T,\mathbf{X},Y;\theta )\triangleq T{\rho }^{\prime }({\lambda }^T{u}_K(\mathbf{X}))Y-(1-T){\rho }^{\prime }({\beta }^T{u}_K(\mathbf{X}))Y-\tau ,\\ g_K(T,\mathbf{X},Y;\theta )\triangleq \left(\begin{array}{c}{g}_{K1}(T,\mathbf{X};\lambda )\\ g_{K2}(T,\mathbf{X};\beta )\\ g_{K3}(T,\mathbf{X},Y;\theta )\end{array}\right),\end{array}$$

where θ ≜ (λ, β, τ)^T. Also define θ̂_K ≜ (λ̂_K, β̂_K, τ̂_K)^T, ${\theta }_K^{\ast }\triangleq {({\lambda }_K^{\ast },{\beta }_K^{\ast },{\tau }_K^{\ast })}^T$ and ${\tau }_K^{\ast }\triangleq \mathbb{E}[TN{p}_K^{\ast }(\mathbf{X})Y-(1-T)N{q}_K^{\ast }(\mathbf{X})Y]$. Note that θ̂_K satisfies

$$\frac{1}{N}\sum _{i=1}^N{g}_K(T_i,{\mathbf{X}}_i,Y_i;{\widehat{\theta }}_K)=0.$$

Taylor series expansion on the left hand side at ${\theta }_K^{\ast }$ yields

$$0=\frac{1}{N}\sum _{i=1}^N{g}_K(T_i,{\mathbf{X}}_i,Y_i;{\theta }_K^{\ast })+\frac{1}{N}\sum _{i=1}^N\frac{\partial g_K(T_i,{\mathbf{X}}_i,Y_i;{\stackrel{\sim }{\theta }}_K)}{\partial \theta }({\widehat{\theta }}_K-{\theta }_K^{\ast }),$$ (14)

where θ̃_K = (λ̃_K, β̃_K, τ̃_K)^T lies on the line joining θ̂_K and ${\theta }_K^{\ast }$. We shall show in the supplementary materials that

$$\frac{1}{N}\sum _{i=1}^N\frac{\partial g_K(T_i,{\mathbf{X}}_i,Y_i;{\stackrel{\sim }{\theta }}_K)}{\partial \theta }=\mathbb{E}\left[\frac{\partial g_K(T,\mathbf{X},Y;{\theta }_K^{\ast })}{\partial \theta }\right]+o_p(1),$$ (15)

where

$$\mathbb{E}\left[\frac{\partial g_K(T,\mathbf{X},Y;{\theta }_K^{\ast })}{\partial \theta }\right]=\left(\begin{array}{cc}{A}_{2K\times 2K},& B_{2K\times 1}\\ C_{1\times 2K},& D_{1\times 1}\end{array}\right),$$

and

$$\begin{array}{l}{A}_{2K\times 2K}\triangleq \left(\begin{array}{cc}\mathbb{E}[T{\rho }^{″}({({\lambda }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})u_K^T(\mathbf{X})],& 0_{K\times K}\\ 0_{K\times K},& \mathbb{E}[(1-T){\rho }^{″}({({\beta }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})u_K^T(\mathbf{X})]\end{array}\right),\\ C_{1\times 2K}\triangleq (\mathbb{E}[T{\rho }^{″}({({\lambda }_K^{\ast })}^T{u}_K(\mathbf{X}))Y{u}_K^T(\mathbf{X})],-\mathbb{E}[(1-T){\rho }^{″}({({\beta }_K^{\ast })}^T{u}_K(\mathbf{X}))Y{u}_K^T(\mathbf{X})]),\\ B_{2K\times 1}\triangleq 0_{2K\times 1},D_{1\times 1}\triangleq -1.\end{array}$$

However, note that we are only interested in the limiting behavior of $\mathit{Var}(\sqrt{N}({\widehat{\tau }}_K-{\tau }_K^{\ast }))$, which is the last element of $\mathit{Var}(\sqrt{N}({\widehat{\theta }}_K-{\theta }_K^{\ast }))$ when N ↑ ∞, this leads us to consider the last row of $\mathbb{E}{\left[\frac{\partial g_K(T,\mathbf{X},Y;{\theta }_K^{\ast })}{\partial \theta }\right]}^{-1}$ which is

$$(C_{1\times 2K}·A_{2K\times 2K}^{-1},-1)=(L_K,R_K,-1),$$

where

$$\begin{array}{l}{L}_K\triangleq \mathbb{E}[T{\rho }^{″}({({\lambda }_K^{\ast })}^T{u}_K(\mathbf{X}))Y{u}_K^T(\mathbf{X})]·\mathbb{E}{[T{\rho }^{″}({({\lambda }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})u_K^T(\mathbf{X})]}^{-1},\\ R_K\triangleq -\mathbb{E}[(1-T){\rho }^{″}({({\beta }_K^{\ast })}^T{u}_K(\mathbf{X}))Y{u}_K^T(\mathbf{X})]·\mathbb{E}{[(1-T){\rho }^{″}({({\beta }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})u_K^T(\mathbf{X})]}^{-1}.\end{array}$$

Since $\mathbb{E}[g_K(T,\mathbf{X},Y;{\theta }_K^{\ast })]=0$ (the zero vector), by (3.55) in the supplementary materials we can get:

$$\begin{array}{l}\underset{K\to \infty }{lim}\mathit{Var}(\sqrt{N}({\widehat{\tau }}_K-{\tau }_K^{\ast }))=\underset{K\to \infty }{lim}(L_K,R_K,-1)\mathbb{E}[g_K(T,\mathbf{X},Y;{\theta }_K^{\ast })g_K^T(T,\mathbf{X},Y;{\theta }_K^{\ast })]\left(\begin{array}{c}{L}_K^T\\ R_K^T\\ -1\end{array}\right)\\ =\underset{K\to \infty }{lim}(L_K,R_K,-1)P_K\left(\begin{array}{c}{L}_K^T\\ R_K^T\\ -1\end{array}\right),\end{array}$$ (16)

where $P_K\triangleq \mathbb{E}[g_K(T,\mathbf{X},Y;{\theta }_K^{\ast })g_K^T(T,\mathbf{X},Y;{\theta }_K^{\ast })]$. This motivates us to define our estimator for the asymptotic variance by:

$${\widehat{V}}_K\triangleq ({\widehat{L}}_K,{\widehat{R}}_K,-1){\widehat{P}}_K\left(\begin{array}{c}{\widehat{L}}_K^T\\ {\widehat{R}}_K^T\\ -1\end{array}\right),$$

where

$$\begin{array}{l}{\widehat{L}}_K\triangleq \left[\frac{1}{N}\sum _{i=1}^N{T}_i{\rho }^{″}({\widehat{\lambda }}_K^T{u}_K({\mathbf{X}}_i))u_K^T({\mathbf{X}}_i)Y_i\right]·{\left[\frac{1}{N}\sum _{i=1}^N{T}_i{\rho }^{″}({\widehat{\lambda }}_K^T{u}_K({\mathbf{X}}_i))u_K({\mathbf{X}}_i)u_K^T({\mathbf{X}}_i)\right]}^{-1},\\ {\widehat{R}}_K\triangleq -\left[\frac{1}{N}\sum _{i=1}^N(1-T_i){\rho }^{″}({\widehat{\beta }}_K^T{u}_K({\mathbf{X}}_i))u_K^T({\mathbf{X}}_i)Y_i\right]·{\left[\frac{1}{N}\sum _{i=1}^N(1-T_i){\rho }^{″}({\widehat{\beta }}_K^T{u}_K({\mathbf{X}}_i))u_K^T({\mathbf{X}}_i)u_K({\mathbf{X}}_i)\right]}^{-1},\\ {\widehat{P}}_K\triangleq \frac{1}{N}\sum _{i=1}^N{g}_K(T_i,{\mathbf{X}}_i,Y_i;{\widehat{\theta }}_K)g_K^T(T_i,{\mathbf{X}}_i,Y_i;{\widehat{\theta }}_K).\end{array}$$

Although the construction of the proposed variance estimator did not start with a direct approximation of the influence function, the variance estimator can be written as ${\widehat{V}}_K=N^{-1}\times {\sum }_{i=1}^N{\widehat{\phi }}_{\mathit{CAL}}^2(T_i,{\mathbf{X}}_i,Y_i;\widehat{\theta })$ where

$$\begin{array}{l}{\widehat{\phi }}_{\mathit{CAL}}(T,\mathbf{X},Y)=-(L_K,R_K,-1)g_K(T,\mathbf{X},Y;\widehat{\theta })\\ =g_{K3}(T,\mathbf{X},Y;\widehat{\theta })-L_K{g}_{K1}(T,\mathbf{X};\widehat{\lambda })+R_K{g}_{K2}(T,\mathbf{X};\widehat{\beta }),\end{array}$$

which is an estimator of the efficient influence function:

$$\begin{array}{c}{\phi }_{\mathit{eff}}(T,\mathbf{X},Y)=\frac{TY}{\pi (\mathbf{X})}-\frac{(1-T)Y}{1-\pi (\mathbf{X})}-\tau +(T-\pi (\mathbf{X}))\beta (\mathbf{X}),\\ \beta (\mathbf{X})=-\left[\frac{m_1(\mathbf{X})}{\pi (\mathbf{X})}+\frac{m_0(\mathbf{X})}{1-\pi (\mathbf{X})}\right].\end{array}$$ (17)

Comparing φ_eff and φ̂_CAL, the proposed variance estimator would have a good performance if −L_Kg_K1(T, X; λ̂)+R_Kg_K2(T, X; β̂) is a good but indirect approximation of (T −π(X))β(X). This is particularly true because of approximation results that are established in the proof of Theorem 1 for the terms (29) and (30) given in Appendix A. In summary, we have the following theorem:

Theorem 2

Under Assumptions 1–8 with Assumption 2 being strengthened to 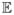(Y⁴(1)) < ∞ and 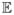(Y⁴(0)) < ∞, V̂_K is a consistent estimator for the asymptotic variance V_semi.

The proof of Theorem 2 is given in the supplementary materials. The strengthened condition in Theorem 2 is mainly used in (3.71) in the supplementary materials so as to ensure the consistency of the asymptotic variance; and this condition is mild and naturally holds for practical samples. The results illuminated the advantages of using the proposed variance estimator for statistical inference. We note that the proposed variance estimator can pair with any globally efficient estimators for valid inference, since all of them are asymptotically equivalent. However, the computation of the proposed estimator only requires intermediate input from the calibration estimation and does not require direct estimation of propensity score or outcome regression function, therefore it pairs naturally with the calibration estimators.

4. Related estimation problems

In this section we illustrate that calibration weighting can be easily extended to several related problems. All proofs of the main theorems in this section are very similar to that of Theorem 1, and they are omitted. The estimators for asymptotic variances in this section, namely $V_{\mathit{semi}}^g,V_{\mathit{semi}}^{\pi },V_{\mathit{semi}}^{\mathit{ATT}}$, and V_jl for i, l ∈ 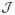= {0, …, J − 1}, J ≥ 2, and their corresponding consistent estimation results can be derived similarly by using the approach founded in Section 3.

4.1. Weighted average treatment effects

Our estimator can be easily extended to estimate a weighted average treatment effects

$${\tau }_{\mathit{WATE}}^g=\frac{\int \mathbb{E}[Y(1)-Y(0)\mid \mathbf{X}=x]g(x)dF(x)}{\int g(d)dF(x)}$$

where g is a known function of the covariates. To estimate ${\tau }_{\mathit{WATE}}^g$, we can define ${\widehat{p}}_K=N^{-1}{\rho }^{\prime }\left({\widehat{\lambda }}_K^T{u}_K(\mathbf{X})\right)$ and ${\widehat{q}}_K=N^{-1}{\rho }^{\prime }\left({\widehat{\beta }}_K^T{u}_K(\mathbf{X})\right)$, with λ̂_K and β̂_K being replaced by maximizers of slightly different objective functions:

$${\widehat{G}}_K(\lambda )\triangleq \frac{1}{N}\sum _{i=1}^N[T_i\rho ({\lambda }^T{u}_K({\mathbf{X}}_i))-{\lambda }^T{\overline{u}}_K^g]$$

and

$${\widehat{H}}_K(\beta )\triangleq \frac{1}{N}\sum _{i=1}^N[(1-T_i)\rho ({\beta }^T{u}_K({\mathbf{X}}_i))-{\beta }^T{\overline{u}}_K^g],$$

where ${\overline{u}}_K^g={\sum }_{i=1}^{N}g({\mathbf{X}}_i)u_K({\mathbf{X}}_i)/{\sum }_{i=1}^{n}g({\mathbf{X}}_i)$. Therefore, p̂_K and q̂_K satisfies

$$\sum _{i=1}^N{T}_i{\widehat{p}}_K({\mathbf{X}}_i)u_K({\mathbf{X}}_i)={\overline{u}}_K^g$$ (18)

and

$$\sum _{i=1}^N(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)u_K({\mathbf{X}}_i)={\overline{u}}_K^g.$$

Define ${\widehat{\tau }}_{\mathit{WATE}}^g={\sum }_{i=1}^N{T}_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-{\sum }_{i=1}^N(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i$. The following theorem states that ${\widehat{\tau }}_{\mathit{WATE}}^g$ is efficient.

Theorem 3

Under Assumptions 1–8, |g| is bounded from above and that 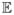[g(X)] > 0. Then we have

1. ${\widehat{\tau }}_{\mathit{WATE}}^g\stackrel{p}{\to }{\tau }_{\mathit{WATE}}$;

2. $\sqrt{N}({\widehat{\tau }}_{\mathit{WATE}}^g-{\tau }_{\mathit{WATE}})\stackrel{d}{\to }\mathcal{N}(0,V_{\mathit{semi}}^g)$, where $V_{\mathit{semi}}^g\triangleq \frac{1}{\mathbb{E}{[g(\mathbf{X})]}^2}\mathbb{E}\left[g{(\mathbf{X})}^2{(m_1(\mathbf{X})-m_0(\mathbf{X})-{\tau }_{\mathit{WATE}})}^2+\frac{{\sigma }_1^2(\mathbf{X})g{(\mathbf{X})}^2}{\pi (\mathbf{X})}+\frac{{\sigma }_0^2(\mathbf{X})g{(\mathbf{X})}^2}{1-\pi (\mathbf{X})}\right]$ attaining the semi-parametric efficiency bound as shown in Theorem 4 of Hirano et al. (2003).

4.2. Treatment effects on the treated

To estimate the average treatment effects among the treated subpopulations, we estimate

$${\tau }_{\mathit{ATT}}=\mathbb{E}(Y(1)-Y(0)\mid T=1)=\frac{\int \mathbb{E}[Y(1)-Y(0)\mid \mathbf{X}=x]\pi (x)dF(x)}{\int \pi (x)dF(x)},$$

where the last equality follows from Assumption 1. Therefore, when the propensity score is known, τ_ATT is a special case of τ_WATE with g(x) = π(x), and one can estimate τ_ATT by ${\widehat{\tau }}_{\mathit{WATE}}^{\pi }$. Following Theorem 3, we have the following results for ${\widehat{\tau }}_{\mathit{WATE}}^{\pi }$.

Corollary 4

Under Assumptions 1–8, we have

1. ${\widehat{\tau }}_{\mathit{WATE}}^{\pi }\stackrel{p}{\to }{\tau }_{\mathit{ATT}}$;

2. $\sqrt{N}({\widehat{\tau }}_{\mathit{WATE}}^{\pi }-{\tau }_{\mathit{ATT}})\stackrel{d}{\to }\mathcal{N}(0,V_{\mathit{semi}}^{\pi })$, where $V_{\mathit{semi}}^{\pi }\triangleq \frac{1}{\mathbb{E}{[\pi (\mathbf{X})]}^2}\mathbb{E}\left[\pi {(\mathbf{X})}^2{(m_1(\mathbf{X})-m_0(\mathbf{X})-{\tau }_{\mathit{ATT}})}^2+{\sigma }_1^2(\mathbf{X})\pi (\mathbf{X})+\frac{{\sigma }_0^2(\mathbf{X})\pi {(\mathbf{X})}^2}{1-\pi (\mathbf{X})}\right]$ attaining the semi-parametric efficiency bound as shown in Theorem 2 of Hahn (1998).

Note that 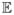(Y(1)|T = 1) is estimated by ${\sum }_{i=1}^N{T}_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i$ where p̂_K satisfies (18) with g(x) = π(x), and this estimate is more efficient than the estimator ${\sum }_{i=1}^N{T}_i{Y}_i/{\sum }_{i=1}^N{T}_i$ when π(x) is known, because one can calibrate the treated subpopulation to ${\overline{u}}_K^{\pi }$ and use the full data to improve estimation efficiency.

When π(x) is unknown, however, the weighted average treatment effects estimator cannot be used. Since we want to estimate the subpopulation of the treated, it is natural to calibrate the control group to the treated by redefining the objective function:

$${\widehat{H}}_K(\beta )\triangleq \frac{1}{N}\sum _{i=1}^N[(1-T_i)\rho ({\beta }^T{u}_K({\mathbf{X}}_i))-{\beta }^T{\overline{u}}_{1K}],$$

where ${\overline{u}}_{1K}={\sum }_{i=1}^N{T}_{i}u({\mathbf{X}}_i)/{\sum }_{i=1}^N{T}_i$. The calibration estimator for estimating the treatment effects on the treated is ${\widehat{\tau }}_{\mathit{ATT}}={\sum }_{i=1}^N{T}_i{Y}_i/{\sum }_{i=1}^N{T}_i-{\sum }_{i=1}^N(1-T_i)\widehat{q}({\mathbf{X}}_i)Y_i$. The next theorem states that τ̂_ATT is globally efficient when the propensity score is unknown.

Theorem 5

Under Assumptions 1 to 8, we have

1. ${\widehat{\tau }}_{\mathit{ATT}}\stackrel{p}{\to }{\tau }_{\mathit{ATT}}$;

2. $\sqrt{N}({\widehat{\tau }}_{\mathit{ATT}}-{\tau }_{\mathit{ATT}})\stackrel{d}{\to }\mathcal{N}(0,V_{\mathit{semi}}^{\mathit{ATT}})$, where $V_{\mathit{semi}}^{\mathit{ATT}}\triangleq \frac{1}{\mathbb{E}{[\pi (\mathbf{X})]}^2}\mathbb{E}\left[\pi (\mathbf{X}){(m_1(\mathbf{X})-m_0(\mathbf{X})-{\tau }_{\mathit{ATT}})}^2+{\sigma }_1^2(\mathbf{X})\pi (\mathbf{X})+\frac{{\sigma }_0^2(\mathbf{X})\pi {(\mathbf{X})}^2}{1-\pi (\mathbf{X})}\right]$ attaining the semi-parametric efficiency bound as shown in Theorem 1 of Hahn (1998).

4.3. Multiple treatment groups

The calibration methods can also be easily generalized to situations with multiple treatment groups. Let T_i ∈ 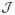= {0, …, J − 1} where J ≥ 2 is an integer. Define μ_j = 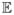[Y(j)], m_j(x) = 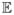[Y(j)|X = x], π_j(x) = 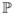(T = j|X = x), ${\sigma }_j^2(x)=\mathit{Var}(Y(j)\mid \mathbf{X}=x)$ , j ∈ 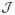, and τ_jl = μ_j − μ_l which is the average treatment effects between treatments j and l. Calibration weights can be defined for any j ∈ 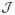by

$${\widehat{p}}_K^j({\mathbf{X}}_i)=\frac{1}{N}{\rho }^{\prime }({\widehat{\lambda }}_K^j{u}_K({\mathbf{X}}_i))$$

where ${\widehat{\lambda }}_K^j\in {ℝ}^K$ maximizes the objective function:

$${\widehat{G}}_K^j({\lambda }^j)=\frac{1}{N}\sum _{i=1}^N[I(T_i=j)\rho ({({\lambda }^j)}^T{u}_K({\mathbf{X}}_i))-{\lambda }^T{\overline{u}}_K],j\in \mathcal{J}.$$

That is, we calibrate moments of u_K(X) for each group to the full data. Estimators for μ_j, j ∈ are defined as

$${\widehat{\mu }}_j\triangleq \sum _{i=1}^{N}I(T_i=j){\widehat{p}}_K^j({\mathbf{X}}_i)Y_i,j\in \mathcal{J},$$

and the estimator for the average treatment effects between treatment j and l is τ̂_jl ≜ μ̂_j − μ̂_l.

Theorem 6

Under Assumptions 1 to 8 with π(x) and (m₁(x), m₀(x)) replaced by π_j(x) and m_j(x) for j ∈ , respectively,

1. ${\displaystyle \sum _{i=1}^N}\left\{I(T_i=j){\widehat{p}}_K^j({\mathbf{X}}_i)Y_i-I(T_i=l){\widehat{p}}_K^l({\mathbf{X}}_i)Y_i\right\}\stackrel{p}{\to }{\tau }_{jl}$;

2. $\sqrt{N}\left({\displaystyle \sum _{i=1}^N}\{I(T_i=j){\widehat{p}}_K^j({\mathbf{X}}_i)Y_i-I(T_i=l){\widehat{p}}_K^l({\mathbf{X}}_i)Y_i\}-{\tau }_{jl}\right)\stackrel{d}{\to }\mathcal{N}(0,V_{jl})$, where $V_{jl}\triangleq \mathbb{E}\left[{(m_j(\mathbf{X})-m_l(\mathbf{X})-{\tau }_{jl})}^2+\frac{{\sigma }_j^2(\mathbf{X})}{{\pi }_j(\mathbf{X})}+\frac{{\sigma }_l^2(\mathbf{X})}{{\pi }_l(\mathbf{X})}\right]$.

Estimators for the weighted average treatment effects and the treatment effects of the treated can also be easily extended to multiple treatment groups.

5. Data analysis

5.1. A childhood nutrition study

We studied the performance of various weighting estimators using the 2007–2008 National Health and Nutrition Examination Survey (NHANES), which is a study designed to assess the health and nutrition statuses of children and adults in the United States. We studied whether participation of the National School Lunch or the School Breakfast programs (hereinafter, “school meal programs”) would lead to an increase in body mass index (BMI) for children and youths aged at 4 to 17. The school meal programs are intended to address the problem of insufficient food access of children in low-income families. However, a potential unintended consequence of the program is excessive food consumption which may cause childhood obesity. We analyzed 2330 children and youth at ages between 4 and 17, with a median age of 10, with 1284 (55%) participated in school meal programs.

Covariates in the data include: child age, child gender, race (black, Hispanic versus others), families above 200% of the federal poverty level, participation in Special Supplemental Nutrition Program for Women, Infants and Children, participation in the Food Stamp Program, a childhood food security measurement which is an indicator of two or more affirmative responses to eight child-specific questions in the NHANES Food Security Questionnaire Module, health insurance coverage, and the age and sex of survey respondents (usually an adult in the family). The estimated average difference in BMI between participants and non-participants, together with standard error estimates and imbalance measures, are all given in Table 1. Direct comparison showed that the mean BMI of participants was significantly higher than that of non-participants, indicating that the program may lead to excessive food consumption. This particular finding has a policy implication in that there is a need to redesign the school meal programs to promote a healthier diet. Using a logistic propensity score model with a linear covariate specification, the Horvitz-Thompson estimators using maximum likelihood estimation and the covariate balancing propensity score estimates of Imai and Ratvokic (2014) both yielded a consistent, but opposite conclusion that the participation in school meal programs led to a significantly lower BMI and possible malnutrition. This particular finding has policy implications in that current school meal programs may fail in reducing the health disparities for poorer children. The inverse propensity score weighted estimates (IPW) were much closer to zero than the corresponding Horvitz-Thompson estimators, yielding a non-significant difference in BMI between the participants and the non-participants. The use of different propensity score weighting estimators leads to an inconclusive finding. The calibration estimators gave a consistent result that there is a negligible mean BMI difference between the participants and the non-participants. A policy implication is that the current school meal programs are implemented in an appropriate manner that provides assistance for the needed without an unintended consequence of increasing childhood obesity.

Table 1.

The difference in average BMI between participants and non-participants of school meal programs: NHANES 2007–2008 data

	Estimate	SE	95% C. I.	Imbalance ×100
				(1,0)	(1,F)	(0,F)	Total
Naive	0.53	0.21	(0.11,0.95)	103	47	57	127
HT(MLE)	−1.48	0.51	(−2.50, −0.46)	49	16	57	63
HT(CBPS)	−1.38	0.50	(−2.38, −0.38)	42	20	36	53
IPW(MLE)	−0.14	0.24	(−0.62,0.34)	7	7	26	16
IPW(CBPS)	−0.1	0.23	(−0.56,0.36)	10	11	12	17
CAL(ET)	−0.04	0.22	(−0.48,0.40)	0	0	0	0
CAL(EL)	−0.06	0.22	(−0.50,0.38)	0	0	0	0
CAL(Q)	0	0.22	(−0.44,0.44)	0	0	0	0
CAL(IL)	−0.08	0.22	(−0.52,0.36)	0	0	0	0

SE: standard error; CI: confidence interval; HT: Horvitz-Thompson estimator; IPW: inverse probability weighting estimator; CAL: calibration estimator; MLE: maximum likelihood estimator; CBPS: covariate balancing propensity score; ET: exponential tilting; EL: empirical likelihood; Q: quadratic; IL: inverse logistic. Standardized covariate imbalance between treated and controls (10), treated and full data (1F), control and full data (0F) and total imbalance are reported.

5.2. A job training study

We further demonstrate the performance of various weighting estimators by estimating the treatment impact of a labor training program data previously analyzed in Lalonde (1986) and Dehejia and Wahba (1999), among many others.

The National Supported Work (NSW) Demonstration was a randomized experiment implemented in the mid-1970s to study whether a systematic job training program would increase post-intervention income levels among workers. Both intervention and control groups were present in the original NSW study. Lalonde (1986) examined the extent to which analyses using observational data sets as controls would agree with the unbiased results of a randomized experiment. His nonexperimental estimates were based on two observational cohorts: the Panel Study of Income Dynamics (PSID) and Westat’s Matched Current Population Survey –Social Security Administration File (CPS). Detailed description of the two data sets was given in Lalonde (1986) and Dehejia and Wahba (1999).

Dehejia and Wahba (1999) and others had analyzed the data set using different propensity score methodologies. Since calibration estimators are weighting estimators, we again limit our comparison only to other weighting estimators based on propensity score modeling. We combined the three data sets and created a group variable G having four categories: G = 1 for the treated in the NSW data (N = 185), G = 2 for the controls in the NSW data (N = 260), G = 3 for the PSID data (N = 2490) and G = 4 for the CPS data (N = 15992). Categories 2, 3 and 4 all served as control data because individuals in those groups did not participate in the job training program offered in NSW. However, Categories 2, 3, 4 had substantially different covariate distributions. We considered the four categories in the combined data to illustrate that the calibration methodology can be applied to handle multiple treatment groups. We studied whether PSID and CPS can be used as the controls in the original NSW data, and we compared the estimates for the average treatment effects in the NSW study population, which was treatment effects on the treated. We noted that the treated and the control groups in the NSW data should have the same covariate distribution because of randomization. Using this information, we calibrated the weights of the four groups to the combined covariate distribution of groups 1 and 2. We also compared our results to calibration estimators with weights calibrated to the treatment group G = 1 only. Since there were four nominal group categories, we used the multinomial logit model for propensity score modeling. Two covariate configurations were considered, where the calibration estimators matched the same variables as in the propensity score models. The first (linear) specification included age, an indicator for black race (black), an indicator for Hispanic race (hisp), years of education (ed), an indicator for being married (married), an indicator for not having an academic degree (nodegr), income in 1974 (re74), income in 1975 (re75), an indicator for zero income in 1974 (u74), and an indicator for zero income in 1975 (u75). The second specification included all variables in the linear specification with the following additional higher-order variables: age², age³, ed², re74², re75², ed×re74 and u74×black. These variables were included in the final models for either PSID or CPS data in Dehejia and Wahba (1999).

We estimated the average difference of income in 1978 between the treatment group (G = 1) and the control groups (G = 2, 3, 4). We further examined the evaluation bias defined as the estimated mean difference of outcome between the NSW control group (G = 2) and the observational control groups (G = 3, 4). The results are shown in Table 2. Direct comparisons were known to be severely biased, and had a huge evaluation bias. All weighting estimators greatly reduced the estimated evaluation bias, but the Horvitz-Thompson and inverse probability weighted estimator can yield very different estimates under the same model. Also, the estimates can change dramatically in comparing the two specifications of propensity score models. The calibration estimators yielded very similar estimates for both model specifications. Calibration to the combined NSW group had lower estimated standard errors compared to calibration only to the treated group. However, the estimates for the two calibration procedures were slightly different, probably because they were referring to two slightly different populations. This was possibly due to the fact that the analysis file of Dehejia and Wahba (1999) removed observations with a missing 1974 income, and the missingness may be different in the treatment and control groups. Hence, the NSW treated and controls may not have the same covariate distribution. In general, the standard errors of the propensity score estimators were much larger than that of the calibration estimators.

Table 2.

Average treatment effects and evaluation biases for the Lalonde (1986) data.

(a) Treatment effects
Estimators	Model	NSW data		PSID data		CPS data
		Estimates	SE	Estimates	SE	Estimates	SE
Unweighted		1794	671	−15205	657	−8498	583
HT	1	1600	827	2421	917	551	862
HT	2	1936	872	2136	1018	1071	711
IPW	1	1702	734	310	1095	1515	1014
IPW	2	1287	863	−830	1207	1534	745
CAL	1	1572	667	2557	716	1233	668
CAL*	1	1712	707	2425	743	1406	675
CAL	2	1454	642	2504	699	1178	754
CAL*	2	1874	705	2285	795	1527	738
(b) Evaluation biases
Unweighted				−17000	391	−10292	349
HT	1			626	809	−1244	710
HT	2			342	998	−724	917
IPW	1			−1485	926	−279	527
IPW	2			2624	1085	−261	577
CAL	1			986	556	−338	487
CAL*	1			712	600	−306	512
CAL	2			1049	605	−276	617
CAL*	2			411	677	−347	592

SE: standard error; CI: confidence interval; HT: Horvitz-Thompson estimator with propensity score estimated from maximum likelihood; IPW: ratio-type inverse probability weighting estimator with propensity score estimated from maximum likelihood estimation; CAL: calibration with exponential tilting, moments are calibrated to the combined NSW group; CAL*: calibration with exponential tilting, moments are calibrated to the NSW treatment group. Two model specifications are considered, 1: linear in covariates; 2: linear and higher-order covariates as in Dehajia and Wahba (1999). Standard errors for HT and IPW estimators were calculated by bootstrapping with 1000 replicates.

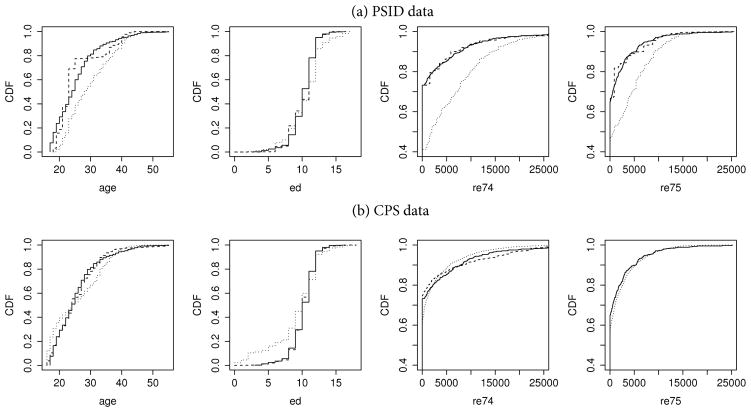
An advantage of using weighting estimators is that statisticians can graphically assess whether covariate balance is achieved. Figure 1 shows the weighted distributions of the four continuous covariates age, education (ed), income in 1974 (re74) and income in 1975 (re75). We compared the IPW and the calibration weighted distributions for the PSID and CPS data, with the empirical distributions of the combined NSW sample. Propensity score modeling and calibration were done using the non-linear model specification as in Dehejia and Wahba (1999). The calibration weighted distributions in both PSID and CPS data were close to the empirical distributions from the NSW data. However, the IPW weighted distributions showed a substantial difference for some variables, such as age, re74 and re75 in the PSID data and ed in the CPS data. Even when we matched a small number of moment constraints, the calibration weights performed well in matching the full covariate distributions between the non-experimental groups and the NSW data.

Fig. 1.

Weighted covariate distributions for the Lalonde (1986) data

Solid lines ( ): Empirical distribution from the NSW data. Dashed lines (------): Calibration weighted distributions. Dotted lines (···········): Inverse probability weighted distributions. CDF: Cumulative distribution function.

We further examined the performance of the proposed standard error estimators by comparing them to bootstrap estimates based on 1000 replications and standard error estimates that treat the weights as given and fixed. The corresponding results for the calibration estimator under the linear specification are given in Table 3. The proposed standard error estimates were very close to the bootstrap standard errors, but the standard error estimators which treated the weights as if they were fixed can greatly underestimate the variability of the calibration estimators. For instance, when we ignored the variability of the estimated weights, the standard error estimates for the CPS data were much smaller because of their large sample sizes. However, the true estimation variability can be more than 6 times larger because the weights were constructed by calibrating to the combined NSW data which had a much smaller sample size. Therefore, ignoring estimation variability of calibration weights can lead to a misleading inference. For a correct inference, one cannot rely on variance estimates that treat the weights as fixed, which was suggested in Section 3.4 of Hainmueller (2012).

Table 3.

Comparisons of standard error estimates for the Lalonde (1986) data.

(a) Treatment Effects
	NSW data	PSID data	CPS data
Proposed	667	716	668
Bootstrap	672	737	666
Fixed	643	300	111
(b) Evaluation Biases
Proposed		556	487
Bootstrap		612	500
Fixed		254	92

Bootstrap estimates were based on 1000 replicates.

6. Discussions

We studied a large class of calibration estimators for efficient inference of the average treatment effects. Calibration weights removes imbalance in pretreatment covariates among the treated, controls and the combined group. By directly modifying the misspecified uniform weights, we do not directly model or estimate the propensity score. We show that balancing covariate distribution alone can achieve global semiparametric efficiency, and we also propose a consistent asymptotic variance estimator which outperforms other estimators that involve direct approximation of the influence function.

While we considered calibration estimators that modify the uniform weights, calibration can be constructed to modify the Horvitz-Thompson weights. However, this formulation requires an additional direct modeling and estimation of propensity score. If π̂(x) is an estimated propensity score function, a class of calibration weights can be defined by

$${\widehat{p}}_K({\mathbf{X}}_i)=\frac{1}{N\widehat{\pi }({\mathbf{X}}_i)}{\rho }^{\prime }\left({\widehat{\lambda }}^T{u}_K({\mathbf{X}}_i)\right),\text{for}i\text{when}{T}_i=1,$$

where λ̂_K ∈ ℝ^k maximizes the objective function

$${\widehat{G}}_K(\lambda )=\frac{1}{N}\sum _{i=1}^N\left[\frac{T_i}{\widehat{\pi }({\mathbf{X}}_i)}\rho ({\lambda }^T{u}_K({\mathbf{X}}_i))-{\lambda }^T{u}_K({\mathbf{X}}_i)\right];$$

and

$${\widehat{q}}_K({\mathbf{X}}_i)=\frac{1}{N(1-\widehat{\pi }({\mathbf{X}}_i))}{\rho }^{\prime }\left({\widehat{\beta }}^T{u}_K({\mathbf{X}}_i)\right),\text{for}i\text{when}{T}_i=0,$$

where β̂_K ∈ ℝ^K maximizes the objective function

$$\widehat{H}(\beta )=\frac{1}{N}\sum _{i=1}^N\left[\frac{1-T_i}{1-\widehat{\pi }({\mathbf{X}}_i)}\rho ({\beta }^T{u}_K({\mathbf{X}}_i))-{\beta }^T{u}_K({\mathbf{X}}_i)\right].$$

This type of calibration procedure is discussed in detail in Chan and Yam (2014). We now focus on the special case that K = 1 and u ≜ u_K ≡ 1, together with λ and β being set as scalar parameters. The balancing equation for the treated becomes

$$\frac{1}{N}\sum _{i=1}^N\frac{T_i}{\widehat{\pi }({\mathbf{X}}_i)}\rho (\widehat{\lambda })=1.$$

Therefore, $\rho (\widehat{\lambda })={(N^{-1}\times {\sum }_{i=1}^N{T}_i{\widehat{\pi }}^{-1}({\mathbf{X}}_i))}^{-1}$ and the corresponding calibration weight is ${\widehat{p}}_K({\mathbf{X}}_i)={(\widehat{\pi }({\mathbf{X}}_i)\times {\sum }_{i=1}^N{T}_i{\widehat{\pi }}^{-1}({\mathbf{X}}_i))}^{-1}$. Similarly, ${\widehat{q}}_K({\mathbf{X}}_i)={((1-\widehat{\pi }({\mathbf{X}}_i))\times {\sum }_{i=1}^N(1-T_i){(1-{\widehat{\pi }}^{-1}({\mathbf{X}}_i))}^{-1})}^{-1}$. This yields the ratio-type IPW estimator. Therefore, the construction of IPW from HT estimators can be viewed as a calibration procedure. When π̂ is a series logit estimator, Hirano et al. (2003) and Imbens et al. (2006) show that the ratio-type IPW estimator is globally asymptotically efficient. Note that u is one-dimensional regardless of sample sizes. Therefore, when π is estimated by a series logit estimator, global efficiency can be achieved when u_K has a fixed dimension. However, our global efficiency results require u_K to have an increasing dimension with N because propensity score was not directly estimated.

In practice, we suggest to choose u_K(X) to be the first and possibly higher moments of candidate covariates. When the covariate distributions of the treated and the controls differ only by a mean shift, matching the first moment of X would be sufficient for removing imbalance. When the variances differ, one can also match the second moment. Matching moments of covariate distributions are intuitive to non-statisticians. We can also graphically check whether the choice of u_K(X) is sufficient as in Figure 1. A noticeable difference in the weighted distributions comparing the treated and the controls would suggest that additional moment conditions are needed. Furthermore, we can choose K by a graphical method or by cross-validation. Since the parameter K controls the number of moment conditions for matching to eliminate the bias from confounding, the choice of K is therefore analogous to the selection of number of confounders in regression modeling, for which a graphical method was discussed in Crainiceanu et al. (2008). Inspired by that paper, we propose the following graphical method for choosing K. From the unweighted sample, we calculate the total standardized imbalance measure for each candidate u_K(X), and rearrange them in a descending order of the imbalance measure. Then for k = 1, 2, …, we plot the point estimates and the 95% confidence intervals by matching the first k moment conditions. The bias would vanish when enough moment conditions are balanced, therefore the difference between consecutive point estimates will stabilize. Identify a region such that the the difference between consecutive point estimates is small, and within this region we can choose K such that the corresponding confidence interval is the shortest. Alternatively, K can be chosen by cross-validation. The moment conditions are matched in a training subset of the full data, while the weights are created in a complementary testing set and a total imbalance measure is calculated for the test data. This process is repeated over different partitions of data, and we choose K such that the average imbalance measure is minimized. While K can be chosen by the above methods, we would like to remark that Theorems 1 and 2 hold for a broad ranges of K and our simulation results given in the online supplementary materials show that the performance of the calibration estimators are insensitive to the choice of K when all relevant covariates are included. This is because our estimator involves the summation of linear functions of p̂_K(X_i) and q̂_K(X_i), and the summation of functions of nonparametric estimators are typically insensitive to the selection of the tuning parameter (Maity et al.; 2007), known as the double-smoothing phenomenon.

Appendix A. Asymptotic expansion of the calibration estimators

The technical proofs for the lemmas and theorems are given in the supplementary materials. Here we present an asymptotic expansion of the empirical balancing estimator, which will be the key to these proofs.

Define

$$\begin{array}{ll}\hfill G_K^{\ast }(\lambda )& \triangleq \mathbb{E}[\pi (\mathbf{X})\rho ({\lambda }^T{u}_K(\mathbf{X}))-{\lambda }^T{u}_K(\mathbf{X})]=\mathbb{E}[{\widehat{G}}_K(\lambda )],\\ \hfill {\lambda }_K^{\ast }& \triangleq arg\underset{\lambda \in {ℝ}^K}{max}{G}_K^{\ast }(\lambda )\text{and}{p}_K^{\ast }(x)\triangleq \frac{1}{N}{\rho }^{\prime }({({\lambda }_K^{\ast })}^T{u}_K(x)),\\ \hfill H_K^{\ast }(\beta )& \triangleq \mathbb{E}[(1-\pi (\mathbf{X}))\rho ({\beta }^T{u}_K(\mathbf{X}))-{\beta }^T{u}_K(\mathbf{X})]=\mathbb{E}[{\widehat{H}}_K(\beta )],\\ \hfill {\beta }_K^{\ast }& \triangleq arg\underset{\beta \in {ℝ}^K}{max}{H}_K^{\ast }(\beta )\text{and}{q}_K^{\ast }(x)\triangleq \frac{1}{N}{\rho }^{\prime }({({\beta }_K^{\ast })}^T{u}_K(x)),\\ \hfill {\mathrm{\sum }}_K& \triangleq {(G_K^{\ast })}^{″}({\lambda }_K^{\ast })=\mathbb{E}[\pi (\mathbf{X}){\rho }^{″}({({\lambda }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})u_K{(\mathbf{X})}^T],\\ \hfill {\mathrm{\Psi }}_K& \triangleq -\mathbb{E}[m_1(\mathbf{X})\pi (\mathbf{X}){\rho }^{″}({({\lambda }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})],\\ \hfill Q_K(x)& \triangleq {\mathrm{\Psi }}_K^T{\mathrm{\sum }}_K^{-1}{u}_K(x),\\ \hfill {\stackrel{\sim }{\mathrm{\Pi }}}_K& \triangleq {\widehat{H}}_K^{″}({\stackrel{\sim }{\beta }}_K)=\frac{1}{N}\sum _{i=1}^N(1-T_i){\rho }^{″}({\stackrel{\sim }{\beta }}_K^T{u}_K({\mathbf{X}}_i))u_K({\mathbf{X}}_i)u_K{({\mathbf{X}}_i)}^T,\\ \hfill {\stackrel{\sim }{\mathrm{\Omega }}}_K& \triangleq -{\int }_{\mathcal{X}}{m}_0(x)(1-\pi (x)){\rho }^{″}({\stackrel{\sim }{\beta }}_K^T{u}_K(x))u_K(x){dF}_0(x),\\ \hfill {\stackrel{\sim }{D}}_K(x)& \triangleq {\stackrel{\sim }{\mathrm{\Omega }}}_K^T{\stackrel{\sim }{\mathrm{\Pi }}}_K^{-1}{u}_K(x),\\ \hfill {\mathrm{\Pi }}_K& \triangleq {(H_K^{\ast })}^{″}({\beta }_K^{\ast })=\mathbb{E}[(1-\pi (\mathbf{X})){\rho }^{″}({({\beta }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})u_K{(\mathbf{X})}^T],\\ \hfill {\mathrm{\Omega }}_K& \triangleq -\mathbb{E}[m_0(\mathbf{X})(1-\pi (\mathbf{X})){\rho }^{″}({({\beta }_K^{\ast })}^T{u}_K(\mathbf{X}))u_K(\mathbf{X})],\\ \hfill D_K(x)& \triangleq {\mathrm{\Omega }}_K^T{\mathrm{\Pi }}_K^{-1}{u}_K(x).\end{array}$$

Now we have the following decomposition of our empirical balancing estimator in Theorem 1(b),

$$\begin{array}{l}\sqrt{N}\left(\sum _{i=1}^N\{T_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i\}-\tau \right)=\frac{1}{\sqrt{N}}\sum _{i=1}^N(\{N{T}_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-N(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i\}-{\mu }_1+{\mu }_0)\\ =\frac{1}{\sqrt{N}}\sum _{i=1}^N\left\{(N{\widehat{p}}_K({\mathbf{X}}_i)-N{p}_K^{\ast }({\mathbf{X}}_i))T_i{Y}_i-{\int }_{\mathcal{X}}{m}_1(x)\pi (x)(N{\widehat{p}}_K(x)-N{p}_K^{\ast }(x)){dF}_0(x)\right\}\end{array}$$ (19)

$$-\frac{1}{\sqrt{N}}\sum _{i=1}^N\left\{(N{\widehat{q}}_K({\mathbf{X}}_i)-N{q}_K^{\ast }({\mathbf{X}}_i))(1-T_i)Y_i-{\int }_{\mathcal{X}}{m}_0(x)(1-\pi (x))(N{\widehat{q}}_K(x)-N{q}_K^{\ast }(x)){dF}_0(x)\right\}$$ (20)

$$+\frac{1}{\sqrt{N}}\sum _{i=1}^N\left\{\left(N{p}_K^{\ast }({\mathbf{X}}_i)-\frac{1}{\pi ({\mathbf{X}}_i)}\right)T_i{Y}_i-\mathbb{E}\left[m_1(\mathbf{X})\pi (\mathbf{X})\left(N{p}_K^{\ast }(\mathbf{X})-\frac{1}{\pi (\mathbf{X})}\right)\right]\right\}$$ (21)

$$-\frac{1}{\sqrt{N}}\sum _{i=1}^N\left\{\left(N{q}_K^{\ast }({\mathbf{X}}_i)-\frac{1}{1-{\pi }_0({\mathbf{X}}_i)}\right)(1-T_i)Y_i-\mathbb{E}\left[m_0(\mathbf{X})(1-\pi (\mathbf{X}))\left(N{q}_K^{\ast }(\mathbf{X})-\frac{1}{1-{\pi }_0(\mathbf{X})}\right)\right]\right\}$$ (22)

$$+\sqrt{N}\mathbb{E}\left[m_1(\mathbf{X})\pi (\mathbf{X})\left(N{p}_K^{\ast }(\mathbf{X})-\frac{1}{\pi (\mathbf{X})}\right)\right]$$ (23)

$$-\sqrt{N}\mathbb{E}\left[m_0(\mathbf{X})(1-\pi (\mathbf{X}))\left(N{q}_K^{\ast }(\mathbf{X})-\frac{1}{1-{\pi }_0(\mathbf{X})}\right)\right]$$ (24)

$$+\sqrt{N}{\int }_{\mathcal{X}}{m}_1(x)\pi (x)(N{\widehat{p}}_K(x)-N{p}_K^{\ast }(x)){dF}_0(x)-\frac{1}{\sqrt{N}}\sum _{i=1}^N[T_i{\rho }^{\prime }({({\lambda }_K^{\ast })}^T{u}_K({\mathbf{X}}_i))-1]{\stackrel{\sim }{Q}}_K({\mathbf{X}}_i)$$ (25)

$$-\sqrt{N}{\int }_{\mathcal{X}}{m}_0(x)(1-\pi (x))(N{\widehat{q}}_K(x)-N{q}_K^{\ast }(x)){dF}_0(x)+\frac{1}{\sqrt{N}}\sum _{i=1}^N[(1-T_i){\rho }^{\prime }({({\beta }_K^{\ast })}^T{u}_K({\mathbf{X}}_i))-1]{\stackrel{\sim }{D}}_K({\mathbf{X}}_i)$$ (26)

$$+\frac{1}{\sqrt{N}}\sum _{i=1}^N[T_i{\rho }^{\prime }({({\lambda }_K^{\ast })}^T{u}_K({\mathbf{X}}_i))-1]({\stackrel{\sim }{Q}}_K({\mathbf{X}}_i)-Q_K({\mathbf{X}}_i))$$ (27)

$$-\frac{1}{\sqrt{N}}\sum _{i=1}^N[(1-T_i){\rho }^{\prime }({({\beta }_K^{\ast })}^T{u}_K({\mathbf{X}}_i))-1]({\stackrel{\sim }{D}}_K({\mathbf{X}}_i)-D_K({\mathbf{X}}_i))$$ (28)

$$+\frac{1}{\sqrt{N}}\sum _{i=1}^N\left\{[T_i{\rho }^{\prime }({({\lambda }_K^{\ast })}^T{u}_K({\mathbf{X}}_i))-1]Q_K({\mathbf{X}}_i)+\frac{m_1({\mathbf{X}}_i)}{\pi ({\mathbf{X}}_i)}(T_i-\pi ({\mathbf{X}}_i))\right\}$$ (29)

$$-\frac{1}{\sqrt{N}}\sum _{i=1}^N\left\{[(1-T_i){\rho }^{\prime }({({\beta }_K^{\ast })}^T{u}_K({\mathbf{X}}_i))-1]D_K({\mathbf{X}}_i)+\frac{m_0({\mathbf{X}}_i)}{1-\pi ({\mathbf{X}}_i)}(\pi ({\mathbf{X}}_i)-T_i)\right\}$$ (30)

$$+\frac{1}{\sqrt{N}}\sum _{i=1}^N\left(\frac{T_i{Y}_i}{\pi ({\mathbf{X}}_i)}-{\mu }_1-\frac{m_1({\mathbf{X}}_i)}{\pi ({\mathbf{X}}_i)}(T_i-\pi ({\mathbf{X}}_i))\right)$$ (31)

$$-\frac{1}{\sqrt{N}}\sum _{i=1}^N\left(\frac{(1-T_i)Y_i}{1-\pi ({\mathbf{X}}_i)}-{\mu }_0-\frac{m_0({\mathbf{X}}_i)}{1-\pi ({\mathbf{X}}_i)}(\pi ({\mathbf{X}}_i)-T_i)\right)$$ (32)

Since ${\sum }_{i=1}^N{T}_i{\widehat{p}}_K({\mathbf{X}}_i)Y_i-{\mu }_1$ and ${\sum }_{i=1}^N(1-T_i){\widehat{q}}_K({\mathbf{X}}_i)Y_i-{\mu }_0$ have a symmetric structure, we only need to consider the terms (19), (21), (23), (25), (27) and (29), and then apply the similar arguments to the terms (20), (22), (24), (26), (28) and (30). We shall show that the sum (31) + (32) asymptotically follows a normal distribution, while all the remaining terms are of order o_p(1). A key challenge of the proof is to show the asymptotic order of (29) and (30), because they link all the unknown functions (π(x), m₁(x), m₀(x)) with the calibration weights and balancing moment conditions. This is overcome by using a novel weighted projection argument.

Appendix B. Dual formulation of calibration estimators

We derive the dual of the constrained optimization problem (5) by using the methodology introduced in Tseng and Bertsekas (1987); the dual of (6) follows by a similar argument. Define E_K×N ≜ (u_K(X₁), …, u_K(X_N)), s_i ≜ 1 − T_iNp_i, i = 1, …, N, s ≜ (s₁, …, s_N)^T and f(v) ≜ D(1 − v), then we can rewrite the problem (5) as

$$\underset{\mathbf{s}}{min}\sum _{i=1}^N{T}_{i}f(s_i)\text{subject}\text{to}{E}_{K\times N}·\mathbf{s}=0.$$

For every j ∈ {1, …, N}, we define the conjugate convex function (Tseng and Bertsekas; 1987) of T_jf (·) to be

$$\begin{array}{l}{g}_j(z_j)=\underset{s_j}{sup}\{z_j{s}_j-T_{j}f(s_j)\}=\underset{p_j}{sup}\{-T_{j}N{p}_j{z}_j+z_j-T_{j}f(1-T_{j}N{p}_j)\}\\ =\underset{p_j}{sup}\{-T_{j}N{p}_j{z}_j+z_j-T_{j}f(1-N{p}_j)\}\\ =-T_{j}N{p}_j^{\ast }{z}_j+z_j-T_{j}f(1-N{p}_j^{\ast }),\end{array}$$

where the third equality follows by noting that Tf(1−TNp_j) = Tf (1 − Np_j), and $p_j^{\ast }$ satisfies the first order condition:

$$-T_j{z}_j=-T_j{f}^{\prime }(1-N{p}_j^{\ast })\Rightarrow p_j^{\ast }=\frac{1}{N}\left\{1-{(f^{\prime })}^{-1}(z_j)\right\}.$$

By defining ρ(z) ≜ f((f′)⁻¹ (z)) + z − z · (f′)⁻¹ (z), then

$$g_j(z_j)=-T_j\rho (z_j)+z_j.$$

By Tseng and Bertsekas (1987), the dual problem of (5) is

$$\underset{\lambda }{min}\sum _{j=1}^N{g}_j({\lambda }^T{E}_j)=-\underset{\lambda }{max}\sum _{j=1}^N\{T_j\rho ({\lambda }^T{u}_K({\mathbf{X}}_j))-{\lambda }^T{u}_K({\mathbf{X}}_j)\}=-\underset{\lambda }{max}{\widehat{G}}_K(\lambda ),$$

where E_j is the j-th column of E_K×N, i,e., E_j = u_K(X_j).

Since D is strictly convex, f″(v) = D″(1 − v), and hence f is also strictly convex and f′ is strictly increasing. Note that

$$\rho (v)=f({(f^{\prime })}^{-1}(v))+v-v{(f^{\prime })}^{-1}(v)\iff \rho (f^{\prime }(v))=f(v)+f^{\prime }(v)-v{f}^{\prime }(v);$$

differentiating with respect to v both sides of the latter equation yields:

$${\rho }^{\prime }(f^{\prime }(v))f^{″}(v)=f^{\prime }(v)+f^{″}(v)-f^{\prime }(v)-v{f}^{″}(v)=(1-v)f^{″}(v),$$

which also implies

$${\rho }^{\prime }(f^{\prime }(v))=1-v,$$

since f″ > 0. Further differentiating with respect to v of the above equation, we get ρ″(f′(v)) f″(v) = −1, which implies

$${\rho }^{″}(v)=-\frac{1}{f^{″}({(f^{\prime })}^{-1}(v))}<0.$$

By also working backward, the convexity of D is equivalent to the concavity of ρ.