Cross-Sectional Tracking of Particle Motion in Evaporating Drops: Flow Fields and Interfacial Accumulation

Abstract

The lack of an effective technique for three-dimensional flow visualization has limited experimental exploration of the “coffee ring effect” to the two-dimensional, top-down viewpoint. In this report, high-speed, cross-sectional imaging of the flow fields was obtained using optical coherence tomography to track particle motion in an evaporating colloidal water drop. This approach enables z-dimensional mapping of primary and secondary flow fields and changes in these fields over time. These sectional images show that 1 μm diameter polystyrene particles have a highly nonuniform vertical distribution with particles accumulating at both the air–water interface and the water–glass interface during drop evaporation. Particle density and relative humidity are shown to influence interfacial entrapment, which suggests that both sedimentation rate and evaporation rate affect the dynamic changes in the cross-sectional distribution of particles. Furthermore, entrapment at the air–water interface delays the time at which particles reach the ring structure. These results suggest that the organization of the ring structure can be controlled based on the ratio of different density particles in a colloidal solution.

INTRODUCTION

The “coffee ring effect” is a dynamic process in which colloidal particles are transported to the drop edge by thermocapillary mass convection and deposited on the substrate. The physical basis of this phenomenon, originally described by Deegan, is that colloidal particles deposit at the contact line, i.e., air–water–substrate interface, early in the evaporation process due to surface tension interactions and topological heterogeneities.^1–3 These deposited particles pin the contact line and prevent it from receding during evaporation. The evaporative flux is greatest at the contact line due to the proximal location of ambient, unsaturated gas, and internal flow is established to replenish evaporated solvent at the edge. This axisymmetric and outwardly directed current transports particles to the edge of the drop where they are deposited, resulting in the characteristic ring pattern. More than just a curiosity, these nonuniform deposits have profound effects in a wide range of industrial applications including DNA microarray manufacturing, inkjet printing, and microelectronics.^4–6

Previous reports of mitigating, reversing, or enhancing this phenomenon span a wide range of strategies including solution conditions, particle shape, and secondary flow fields. For example, Bhardwaj et al. have shown how pH-induced Derjaguin–Landau–Verwey–Overbeek (DLVO) interactions can shift particle deposition from the edge to the center of the drop,⁸ Yunker et al. have shown that the particle aspect ratio is correlated to the degree of pattern uniformity,⁹ and Hu et al. have shown that Marangoni stresses, which result from surface tension gradients, can induce internal eddies that oppose the coffee-ring effect.^10,11 Several groups have reported the effects of surfactants on Marangoni–Bénard flow in evaporating colloidal drops.^12–14 Ristenpart et al. have shown that a difference in thermal conductivities between solution and substrate can reverse the Marangoni circulation.¹⁵

Understanding the conditions that inhibit or promote deposition patterns is also of great interest in applications in which the phenomenon is manipulated for a desired effect. For example, Ho et al. recently demonstrated that the inherent size exclusion geometry present near the contact line can be used to chromatographically separate particles.¹⁶ Other groups have reported that residues from dried drops of biological fluids can potentially be used as an indication of disease.^17–19 A diagnostic assay design in which the coffee ring effect organizes surface functionalized particles in unique colorimetric patterns depending on the presence or absence of target antigen has also been recently reported.²⁰ In fact, observations made in this latter application motivated this study.

Tracking cross-sectional particle motion during drop evaporation would provide new information which is important for mapping fluid dynamics and elucidating the mechanism by which system variables affect deposition patterns. Previous studies have most commonly employed video and fluorescence microscopy to generate a top-down, two-dimensional view of particle flow during drop evaporation.^10,13,21,22 This method has proven useful for imaging the primary radial fluid fields associated with the coffee ring effect. However, as previous studies on Marangoni–Bénard flows have shown, evaporating drops can contain eddies and secondary flows under certain conditions that are difficult to resolve with two-dimensional microscopy-based techniques.^11,23 Hu et al. demonstrated cross-sectional reconstruction of 3D flows based on side-directed, out-of-focus microscopy.¹⁰ While this method enables some cross-sectional visualization of the coffee ring effect, the limited spatial and temporal resolutions of this technique limit precise mapping of 3D flow patterns. Bodiguel et al. used confocal microscopy to cross-sectionally image tracer particles in an evaporating drop.^24,25 Despite using fast scanning techniques, the imaged slice in this study was limited to a fixed distance from the substrate in order to generate a temporal resolution adequate for particle tracking. Confocal microscopy has a shallow depth of field, thereby spatially limiting the focal plane. To our knowledge, confocal microscopy is currently not capable of imaging an entire cross-section of a colloidal drop, having a maximum height of 300 μm, within a time frame that enables particle tracking during drop evaporation.

This study explores the use of optical coherence tomography (OCT) to investigate cross-sectional flow patterns in evaporating water drops. OCT is a real-time imaging modality that generates cross-sectional images of sample backscattering with micrometer-scale axial and transverse resolution and millisecond temporal resolution.²⁶ The spatiotemporal resolution of OCT is well suited for identifying and tracking movement of micrometer-sized particles. In addition, the depth-of-field of OCT is typically >1 mm, approximately 2 orders of magnitude greater than confocal microscopy and well matched to the 300 μm maximum height of sessile drops of the volumes used in this study (~1 μL). This capability enables imaging of the entire drop cross section. Unlike microscopic techniques, OCT provides accurate z-dimension information of 1 μm particles, and over time the images can directly resolve z-dimensional features of flow within the sample. OCT has been previously shown to effectively track polystyrene particle motion for other applications.^27–30 For example, Jonas et al. used OCT-based particle tracking velocimetry to image fluid flow created by oscillating cilia.²⁸ Since flow fields are axisymmetric around the drop center, particle motion captured by a single cross-sectional plane through the drop diameter provides a comprehensive depiction of flow fields in the entire drop. While the data generated from a single plane is inherently two-dimensional, three-dimensional motion can be inferred from the radial (axisymmetric) geometry of the drop. It follows that cross-sectional imaging, such as with OCT, provides 3D information about particle motion in an evaporating drop. Thus, OCT appears to be well suited for measuring particle motion and particle distribution which is necessary for obtaining a better understanding of this seemingly simple phenomenon.

In this report, OCT is used to qualitatively describe the cross-sectional motion of particles in evaporating water drops. The effect of particle density and ambient relative humidity on vertical particle distribution is quantified and shown to influence the organization of the dried ring structure. OCT-based particle tracking velocimetry using a two-frame nearest neighbor approach is also employed to quantitatively describe the motion of different particle types using an approach similar to Jonas et al.²⁸ Video sequences of OCT images recorded at 0.2 s per frame show complete particle motion under several experimental conditions.

EXPERIMENTAL METHODS

Material Preparation and Characterization

Four different particle types were used in the study, all 1 μm diameter: carboxylated polystyrene (Bangs Laboratories, Inc.), aminated polystyrene (Invitrogen), carboxylated melamine formaldehyde (Sigma Aldrich), and silica (Kisker Biotech). Physical properties of the particles are summarized in Table 1. All particles were fluorescent (polystyrene, red; melamine formaldehyde, green; silica, blue) to enable imaging of dried deposition patterns with fluorescence microscopy. Particle solutions were prepared by diluting stock particles in distilled, filtered water (MiliQ) at pH 4.1. Solutions were centrifugally washed 8×, and particles were resuspended at a volume fraction, φ, of 0.005% (or 10⁵ particles per μL) in MiliQ water at pH = 4.1. Particle surface charge was determined by measuring the zeta potential (Malvern Zetasizer) of particles suspended in a 10 mM NaCl, pH 4.1 solution. Plain glass slides (Fisher Scientific) were used as the substrate in all experiments and cleaned by washing with 100% ethanol followed by distilled water and then air dried. All particle solutions were thoroughly sonicated prior to drop deposition.

Table 1.

Physical Properties of the Four Particle Types

particle type	surface	mean diameter (μm)	density (g/cm3)	stokes sedimentation rate (μm/s)	zeta potential, ζ (mV)
polystyrene	−COOH	0.97	1.04	0.02	−23
polystyrene	−NH2	1.00	1.04	0.02	39
melamine formaldehyde	−COOH	1.00	1.50	0.27	−16
silica	plain	1.00	2.00	0.54	−13

Optical Coherence Tomography

A drop (1 μL) was deposited on a clean glass slide, and cross-sectional images were recorded using a commercial OCT system (Bioptigen, Inc.) with a laser source (860 nm center wavelength, 51 nm full-width half-max bandwidth) fixed at an angle of 9° from normal. The drop was manually positioned so the OCT laser was aligned with the diameter of the drop. This was done while imaging with OCT, and the diameter was identified as the position at which drop height was a maximum. Total evaporation time, t_f, was measured for each sample, and OCT frames were sequenced according to percent of total evaporation time. This approach allowed OCT frames from different samples to be compared on the basis of normalized evaporation time.

This experimental setup resulted in a transverse digital sampling resolution of 3 μm/pixel and an axial digital sampling resolution of 1.69 μm/pixel. The optical resolution of the system is approximately 8 μm in the lateral direction, defined as the full-width half-max of the point-spread function of the system, and 6.4 μm in the axial direction. In OCT, ballistic photons from a broad-band laser source are split between the imaging sample and a reference mirror at a known distance from the source. The light reflected from the reference mirror recombines with backscattered light from the sample and generates an interference pattern. The axial depth of a scattering object in the sample is calculated from the oscillation frequencies in this interference pattern. Axial resolution is determined by the wavelength and coherence length of the source light. All axial data at a particular position (A scan) is acquired during one integration cycle of the charge-coupled device (CCD), and transverse images are obtained by raster scanning the laser across the sample with motorized mirrors.

Interference patterns from the reference and sample arm were captured with a 2048 pixel CCD with 10 kHz integration time and approximately 700 μW on the sample. Interference data was then processed by (1) resampling the data to be linear with respect to wavenumber, (2) correcting dispersion using well-established processing algorithms, (3) subtracting the background to remove the source spectrum, and (4) generating OCT image data as a function of depth via Fourier transform.^31,32

Due to memory limitations of the instrument software, only 200 B scans could be recorded in a given sequence, which equals 40 s of recorded video at a 0.2 s time step per frame. A barrier was placed around the experimental setup to prevent ambient air currents from reaching the evaporating drop. Ambient temperature and relative humidity were recorded during evaporation. Following OCT imaging, the dried deposition pattern was imaged under phase contrast and fluorescence microscopy at 2× magnification. All drop evaporation experiments were repeated in triplicate, and blank drops (no particles) were also imaged with OCT to quantify background noise for image processing.

Image Processing and Analysis

OCT files were converted to tagged image file (TIFF) format in Matlab. ImageJ software was used to edit video sequences and image stacks. OCT images were taken of plain water drops in preliminary experiments to determine the threshold intensity in post-image processing that removed 95% of the background noise. OCT images from all subsequent experiments were thresholded at this predetermined level to ensure that remaining signal in the images is attributed to particles. Vertical particle distributions in the OCT images were quantified using a Matlab program that defined a rectangular area of interest encompassing the drop cross-section and equal to 20% of the drop diameter centered at the drop midpoint. This area was subdivided into equally sized, stacked, rectangular areas of interest each with a height of 10 pixels, or 16.9 μm, with the top area of interest vertically centered on the air–water interface (see Figure 6 inset). The Matlab program computed the average pixel intensity in each of the stacked areas of interest. Data arrays were exported to Excel, and interfacial accumulation was calculated as the average pixel intensity in the particular area of interest divided by the summed average pixel intensities for all areas of interest. Analysis was repeated for 1200 OCT frames for each data set.

Figure 6.

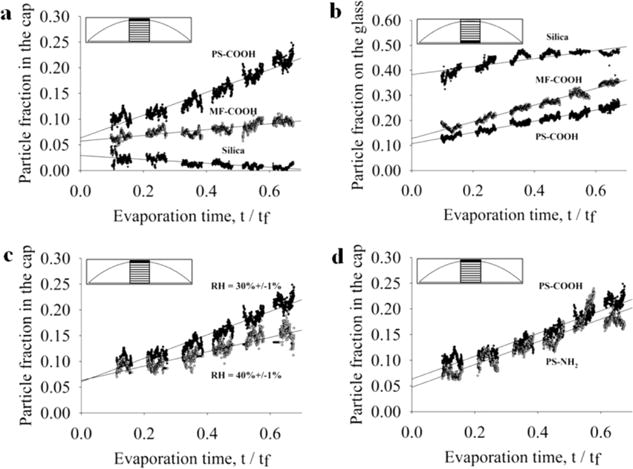
Effect of particle density, relative humidity, and particle surface charge on particle accumulation at the air–water and water–glass interfaces. Vertical distribution of particles in a region defined as 20% of drop diameter at the drop center (see inset) is measured as a function of normalized evaporation time for 1 μm particles with different densities ranging from 1.05 (PS), to 1.5 (MF), and 2.0 g/cm³ (Si) at the air–water interface (a) and water–glass interface (b). (c) Rate of accumulation of PS particles at the air–water interface in drops evaporated at 30% and 40% relative humidity, and (d) rate of accumulation of negatively charged PS–COOH and positively charged PS–NH₂ particles at the air–water interface. Each data set is the average of three samples.

OCT-based particle tracking velocimetry was performed following a method similar to that used by Jonas et al.²⁸ Each OCT frame of a 200-frame sequence, 0.2 s time step per frame, was thresholded as previously described, and pixel intensities were converted to binary values. The time step was then increased to 2 s per frame by retaining every tenth frame. Using Image-Pro Plus software (MediaCybernetics, version 7), particles were identified as any group of at least five connected pixels having an intensity value equal to one. Particles were then tracked over a sequence of frames using a nearest neighbor approach based on the center pixel of each object. Particles moving into or out of the imaged slice (i.e., B scan) were removed from the data set. Also, all particles were spatially binned, and those present at the air–water interface and water–glass interface were removed from the data set. Cartesian coordinate values for each particle per frame were exported to Excel, and average velocities, v_i, and angle of motion, θ_i relative to the substrate were calculated for each particle, p_i, as²⁸

$$v_i=\frac{\sqrt{{\left(A\mathrm{\Delta }x\right)}^2+{\left(B\mathrm{\Delta }y\right)}^2}}{\mathrm{\Delta }t}{\theta }_i={\tan }^{-1}\left(\frac{v_{iy}}{v_{ix}}\right)$$

where A and B are scaling factors equal to 3 and 1.69 μm/pixel, respectively.

This simple method of particle tracking is most applicable due to the low volume fraction of particles used in the study. As the OCT videos (Supporting Information) show, the relatively low concentration of particles enables discrete particle identification. Moreover, this method has been previously and successfully employed at similar particle velocities.²⁸ After performing the above analysis at time steps of both 0.2 and 2 s, it was determined that the latter time step was sufficient for tracking particles.

RESULTS AND DISCUSSION

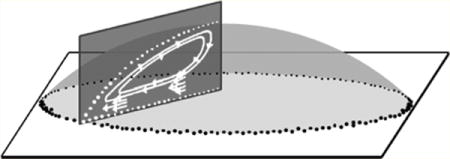
Figure 1a shows the radial fluid motion due to the coffee ring effect from a top-down view, characteristic of 2-D microscopy. Outwardly directed and axisymmetric flow fields are easily observed from this vantage point and result in the characteristic dried ring pattern shown in Figure 1b. With this technique it is difficult to resolve three-dimensional flow fields. An OCT scan through the diameter of the drop, shown in Figure 1c, enables cross-sectional mapping of these flow fields, which are often times more complex than what is represented by two-dimensional imaging methods.

Figure 1.

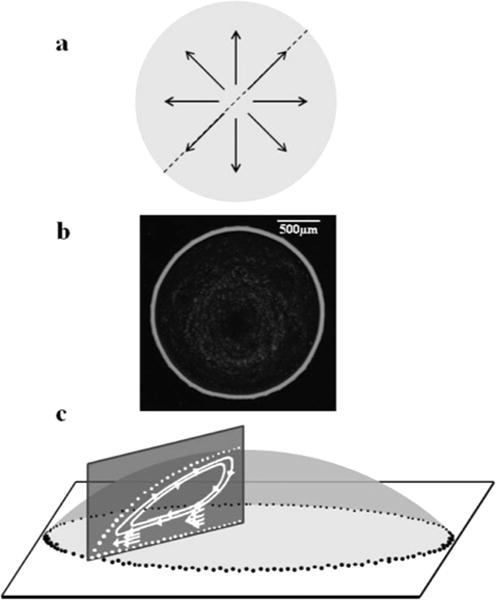
(a) Particle flow fields in an evaporating drop imaged with top-down microscopy are dominated by radial flow, (b) top-down phase contrast micrograph of a characteristic deposition pattern produced by the coffee ring effect, and (c) simplified schematic with no angular offset showing one-half of a cross-sectional slice generated by OCT that reveals three-dimensional detail of flow fields.

A single OCT frame taken through the diameter of a 1 μL drop, containing 10⁵ carboxylated polystyrene particles on a glass slide, shows the position of individual particles. In these images particles appear as white spots on a black background and, in this case, are distributed within the cross-section of the drop with particles at the interfaces outlining the drop’s shape (Figure 2a). Some particles appear smaller than others, despite being monodisperse, because they are not all aligned at the center of the imaged plane (B scan). Particles slightly off center of the B scan will appear smaller than those at the center of the B scan. For this image at the instant during evaporation (time point) corresponding to t = 0.33t_f, where t_f is the total evaporation time, particles are fairly diffuse with a small fraction collected at the air–water interface and the glass substrate. A single OCT cross-sectional scan is acquired in 0.1 s, so the particles, which travel at velocities on the order of μm/s or less,¹ appear stationary. The bottom of the drop appears slightly curved due to refraction of the incident OCT laser by the curved drop surface as well as the difference between the actual distance and the optical path length caused by the different refractive indices of air and water. This artifact decreases as the drop flattens during evaporation and is discussed in greater detail later.

Figure 2.

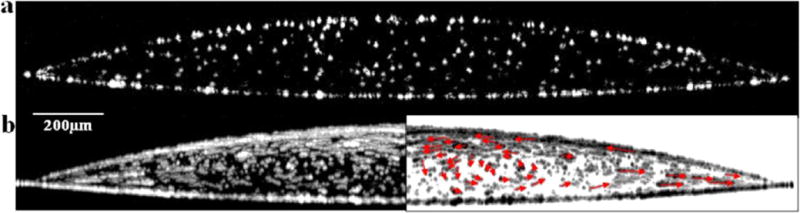
(a) Single OCT frame along the diameter of a 1 μL sessile water drop containing 1 μm diameter carboxylated polystyrene particles (10⁵ per μL) at t = 0.33t_f, where t_f is total evaporation time. Individual particles are seen as white dots. (b) Time-lapse composite of 200 consecutive OCT images of a 1 μL sessile water drop containing 1 μm diameter carboxylated polystyrene particles (10⁵ per μL) spanning 20 s of drop evaporation beginning at t = 0.33t_f. Each white track shows the trajectory of a single particle. (Right) Mirror image of the left panel but with inverted contrast and red vector lines showing particle trajectories.

The left panel in Figure 2b is a time-lapse composite image representing 20 s before and after the same evaporation time point shown in Figure 2a. The image is generated by overlaying a stack of sequential OCT frames taken at 0.1 s intervals. A track represents the distance a single particle traveled over 20 s, and the length and direction of the track indicates particle velocity. Track lengths, on average, increase with time and radial position toward the contact line. These findings are consistent with previously reported experimental findings and models of the coffee ring effect which show that capillary-induced velocity increases with evaporation time and increasing distance from the drop center.^{1,2,7,23,33–35} Radial velocity increases with evaporation time because the fluid required to replenish evaporated solution at the edge must travel through a decreasing volume as the drop height diminishes. Moreover, radial velocity increases with greater distance from the drop center due to the nonuniform evaporative flux that increases along the drop surface with greater distance from the drop center.³⁵

The right panel in Figure 2b is the same as the left panel but with reverse contrast and superimposed vector lines (red arrows) indicating particle direction. This vector plot reveals flow fields that are more complex than what would typically be observed in top-down video microscopy. A video has been provided in the Supporting Information that compares a cross-sectional sequence of OCT images to a top-down video taken with phase contrast microscopy. The dynamic particle motion is even more apparent in the video than in the time-lapse composite images. As these videos illustrate, particles near the drop’s edge are deposited at the contact line. Particles at the drop surface remain entrapped at the interface, and some are observed traveling back toward the drop center. Additionally, the time-lapse composite image in Figure 2 shows a slight circular eddy in the bulk fluid rotating counterclockwise. These observations suggest the presence of Marangoni flow, which is caused by a surface tension gradient at the air–water interface. According to theory, an interfacial region with high surface tension exerts a pulling force on neighboring regions of lower surface tension having the effect of inducing flow across the gradient. In the case of an evaporating drop, the lowest surface tension occurs at the contact line. Previous investigations have shown a nonuniform surface tension gradient arises from a nonuniform temperature gradient.¹¹ Early in evaporation, the greatest surface temperature occurs at the contact line due to the close proximity of the substrate, while the lowest surface temperature occurs at the drop center due to the greater conduction path to the substrate. Surface tension at the air–water interface is inversely proportional to temperature. This causes a Marangoni flow early in evaporation along the surface of the drop directed toward the drop center. At later time points the evaporation rate increases near the contact line and the fluid height at the drop center (conduction path to the substrate) decreases sufficiently to eliminate the surface temperature gradient which stops the Marangoni flow. Hu et al. numerically demonstrate that the temperature gradient is at or near zero when the contact angle is <14°.¹¹ In Figure 2b, the contact angle is approximately 17°, sufficiently high enough, at least theoretically, to generate Marangoni flow. These results are therefore consistent with Hu et al.’s prediction.^10,11

Weak Marangoni flow has been shown to occur in colloidal water drops.¹ However, there are conflicting reports on this issue with some groups indicating little to no Marangoni flow in colloidal water drops due to the susceptibility of aqueous interfaces to surface contaminants like surfactants that can offset surface tension gradients.^10,36 Moreover, the precise effect of surfactants on Marangoni flow in water drops is unclear. Previous reports have shown that surfactants can both induce and inhibit Marangoni flow depending on the conditions.^14,36 Great care was taken in this study to minimize residual surfactants (Tween 20) from stock particle solutions by centrifugally washing particle solutions eight times with deionized, distilled water. Nonetheless, it is possible the flow fields seen in Figure 2b are due to residual contaminants. Ambient air currents also could have affected surface flow patterns, although a rigid cardboard barrier surrounded the sample stage during all experiments to minimize air currents. All experiments were repeated in triplicate, and this weak Marangoni eddy was only observed in one trial. This lack of repeatability is consistent with these previous studies, indicating that the presence of Marangoni flow in water drops is uncommon and weak at best. The most likely explanation is that the secondary flow fields observed in Figure 2b are the result of a weak Marangoni stress.

As others have reported using 2D imaging, particle motion develops slowly and changes over time. In general, particle motion is known to accelerate toward the contact line and average particle speed increases with time. Hu et al. have shown theoretically that Marangoni flows occur early in evaporation when the height of the drop at the center is relatively large, and as the drop height falls, Marangoni flows dissipate and particle flow follows a predominantly outward trajectory. The time evolution of these flow fields in cross-section are shown in Figure 3, which shows a time-lapse composite OCT (Figure 3a) and vector plots (Figure 3b) at multiple time points during drop evaporation along with the corresponding theoretical flow fields (Figure 3c). Early in evaporation, polystyrene particle flow is mostly parallel to the substrate in a region comprising the top half of the drop and extending radially to approximately 0.25R. The distance these parallel trajectories extend down in the z-direction into the bulk drop volume decreases with time. At t = 0.3t_f (second panel in Figure 3), a Marangoni eddy becomes evident. Particles flow toward the drop center at or near the air–water interface and descend toward the substrate near the drop center. Particles then flow toward the contact line and upon reaching the eddy either ascend toward the air–water interface or continue to the contact line. By the last time point shown in Figure 3, the Marangoni eddy has dissipated and the thermocapillary mass convection becomes the dominant flow field transporting polystyrene particles to the contact line.

Figure 3.

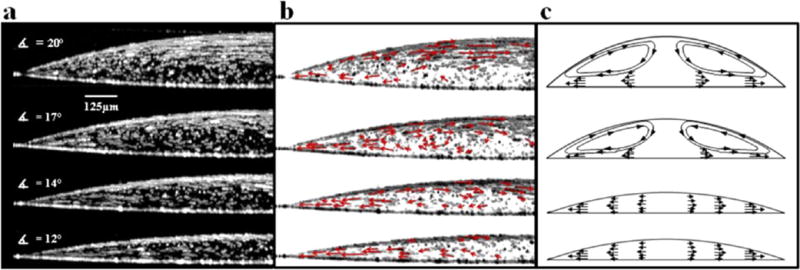
(a) Time-lapse composite of 200 consecutive OCT images of a 1 μL water drop containing 1 μm diameter carboxylated polystyrene particles (10⁵ per μL) spanning 20 s of drop evaporation at four time points during evaporation (from top to bottom): t = 0.1t_f, 0.3t_f, 0.5t_f, and 0.6t_f. (b) Same images as a but with inverted contrast and superimposed vector lines. (c) Sketch of theoretical flow fields adapted from previously reported studies.^10,11

Particle motion shown in Figure 3a and 3b does not form concentric eddies and therefore does not completely match theoretically predicted Marangoni flow fields (Figure 3c).^7,11 The reason(s) for this are unclear. It is possible that the flow fields seen early in evaporation result from a Marangoni stress are too weak to generate a Marangoni eddy. As previously mentioned, residual surfactants and/or ambient air currents could have affected surface flow patterns, which might be more dominant in cases where only weak Marangoni stresses are present.

Interestingly, Figure 3 appears to show a time-dependent accumulation of particles at the two interfaces. It should be noted that the air–water interface appears blurry due to the change in drop height that occurs during the 20 s represented in each image. Despite this artifact, it is clear that polystyrene particles accumulate at both interfaces. Previously reported studies on the coffee ring effect do not completely explain this time-dependent nonuniformity. As the drop evaporates, particles accumulate at both the air–water and the water–glass interfaces, resulting in a nonuniform distribution. At the theoretical sedimentation rate (0.022 μm/s), the polystyrene particles are expected to fall approximately 13 μm by gravitational settling, excluding the effects of other flows, during the 10 min it takes a 1 μL drop to dry at 30% relative humidity and 21 °C. Therefore, gravitational sedimentation can account at least for some of the accumulation at the water–glass interface. However, since the density of polystyrene exceeds water, the particles do not experience a net buoyant force that would cause accumulation at the air–water interface.

One hypothesis for this observation is that, holding all else equal, the ratio of the rate of change in drop height, dh/dt, to particle sedimentation rate, V_s, determines the extent to which colloidal particles accumulate at the air–water interface during evaporation. A greater ratio results in a greater particle fraction accumulating at the drop surface. Physical parameters that affect V_s or dh/dt would necessarily affect particle accumulation at the air–water interface. Two such parameters are particle density and relative humidity. A higher particle density corresponds to a faster sedimentation rate relative to dh/dt, and so a lower particle fraction is expected to accumulate at the air–water interface. As discussed previously, polystyrene particle motion at and near the drop surface is influenced by Marangoni stress at early evaporation time points, creating flow fields approximately parallel to the glass. During this time, polystyrene particle sedimentation rate is reduced and particles caught in this flow field would be more susceptible to entrapment in the retreating air–water interface than at later evaporation stages when these Marangoni flows subside and particles assume a more downward trajectory. However, it should be noted that the presence of weak Marangoni flow was observed in only one trial and particle accumulation at the interfaces in this trial was no different than that measured in the other two trials. Therefore, the presence of a Marangoni stress does not explain the interfacial accumulation of particles in this study. In fact, the OCT videos included as Supporting Information show the accumulation of particles at the interfaces with no Marangoni flow. The advancing interface provides an explanation for this behavior. Lower relative humidity causes faster evaporation and therefore a faster dh/dt. In this case, the air–water interface falls at a faster rate than in high relative humidity, resulting in more particles being caught in the air–water interface.

This hypothesis was tested by comparing the effects of particle density and relative humidity on the cross-sectional particle distribution. Figure 4a shows the cross-sectional particle distribution of drops containing three different density particles—polystyrene (“PS”, 1 μm diameter ρ = 1.04 g/cm³), melamine formaldehyde (“MF”, 1 μm diameter, ρ = 1.50 g/cm³), and silica (“Si”, 1 μm diameter, ρ = 2.00 g/cm³)—at three different time points. Physical properties of these particles are summarized in Table 1. As shown in Figure 4, at t = 0.1t_f both the PS and the MF particles appear uniformly distributed in the z direction whereas a significant fraction of the Si particles have already been deposited on the substrate. At t = 0.33t_f, there is an increase in the fraction of PS particles at the air–water interface while a greater fraction of MF particles have accumulated on the glass. The majority of Si particles are on the substrate at this time point. At t = 0.66t_f, a majority of the PS particles have collected at the two interfaces. MF particles at t = 0.66t_f are more uniformly distributed than the PS, but the largest fraction is on the substrate. Si particles at the t = 0.66t_f time point are virtually all on the substrate. These qualitative observations are consistent with our hypothesis that a low particle density and/or a low relative humidity promote nonuniform particle distribution in the drop cross-section. Despite the significant differences in cross-sectional particle distribution for PS, MF, and Si particles, the corresponding 2-D phase contrast microscopy images (Figure 4b) are nearly identical at 2× magnification. The ring structures are of comparable size, although a greater fraction of Si particles sediment in the drop center.

Figure 4.

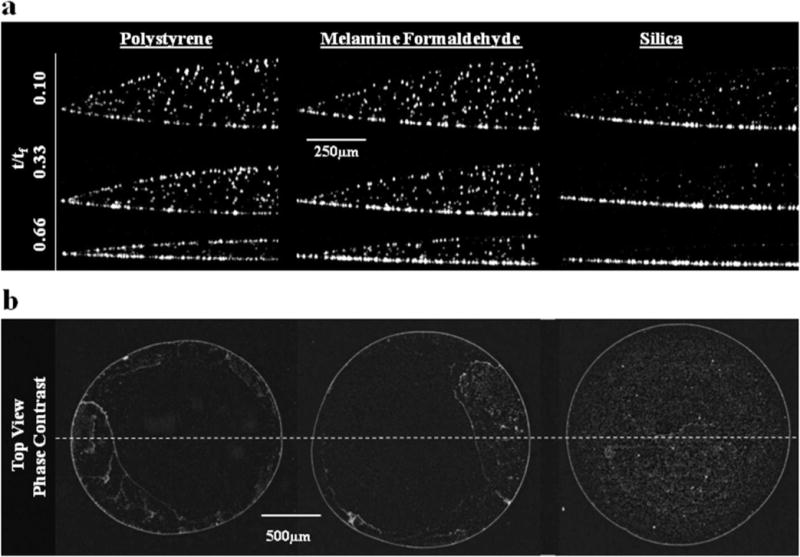
(a) Time-dependent particle accumulation at the air–water interface decreases with an increase in particle density (Si < MF < PS). (b) Corresponding top-down micrographs showing the full diameter of the same dried 1 μL drops after complete evaporation show similar outer-ring structures and changes in deposition patterns in the drop interior at 2× magnification. Dotted line indicates the orientation of the corresponding OCT slices presented in a.

The PS, MF, and Si particles, shown in Figure 4, travel in very different trajectories. Video sequences for the time points represented in Figure 4 demonstrate the difference in particle motion (Supporting Information). In contrast to the PS particles, MF particles exhibit a downward sloping vector toward the contact line. Vector slopes decrease with time and distance from both the air–water interface and the drop center. Si particles, on the other hand, sediment relatively quickly on the glass substrate.

Unlike the PS particles, the motion of the MF particles in Figure 4 does not show any Marangoni flow. This is likely due to the greater density of melamine formaldehyde (ρ = 1.50 g/cm³) versus polystyrene (ρ = 1.04 g/cm³). According to Stoke’s Law, the MF particle sediments in water at 0.27 μm/s compared to 0.022 μm/s for a PS particle of equal diameter (Table 1). This implies an approximate 10× relative contribution of sedimentation over convection on the particle trajectory for the MF particle versus the PS particle.

In theory, a high-resolution flow field in the evaporating drop could be mapped by tracking particle motion. However, in this initial report demonstrating the utility of OCT we focus on a simplified analysis in which the velocity and trajectory of low-, medium-, and high-density particles were tracked for 20 s before and after 50% evaporation. This data is shown in Figure 5. Drop volumes were divided into three sections (see inset). Particle velocity versus angle is plotted in the color corresponding to a particular volume section. This analysis shows that particles accelerate with increasing distance from the drop center, in accordance with the coffee ring effect.^1,2 Plots for all three particle types, PS (Figure 5a), MF (Figure 5b), and Si (Figure 5c), show a rightward shift in particle distributions as the volume sections approach the contact line. If particle motion perfectly tracked pure radial flow with no secondary flow fields, then all data points would be along the overlaid line in Figure 5. The standard deviation of the angles decreases and the mean angle approaches zero as the volume sections approach the contact line. This suggests that particles increasingly move with a trajectory parallel to the substrate as they approach the contact line. This particle motion is evident in Figure 3. With increasing particle density (PS < MF < Si), a greater fraction of ordinate values is negative, indicating more particles move in a downward direction. Given the time and computationally intensive process involved in generating particle tracking data, only one time point was generated in this study (t = 0.5t_f). However, a more thorough analysis of particle velocity distributions throughout the entire evaporation process may help explain the observations discussed in this study with respect to interfacial particle accumulation.

Figure 5.

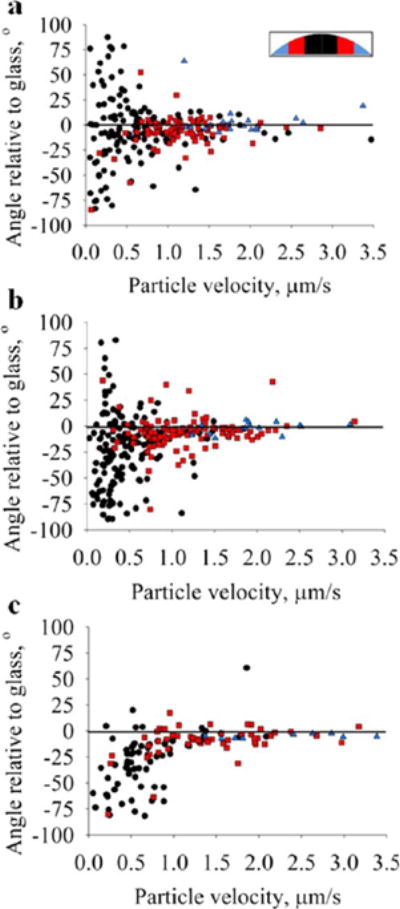
Particle velocities are plotted against direction (angle) at t = 0.5t_f for (a) polystyrene (PS), (b) melamine formaldehyde (MF), and (c) silica (Si). Each plot contains data points from three drop samples. Data points are spatially binned into three sections (inset): inner sections, ○; middle sections, □; outer sections, Δ. Si plot (c) has fewer data points because a majority of particles had reached the glass substrate by t = 0.5t_f. Particles traveling at a nonzero angle to the glass slide deviate from the pure radial flows as originally described by Deegan et al.¹ and modeled by Hu et al.⁷

One hypothesis is that interfacial particle accumulation is determined, at least in part, by parameters affecting particle sedimentation rate and the rate at which the air–water interface retreats. To test this hypothesis, z-axis particle distributions as a function of normalized evaporation time were quantified for different particle densities and relative humidities and are presented in Figure 6. Particle fraction at the interface was calculated by dividing the average pixel intensity for the top or bottom area of interest (shown in the inset) by the summation of average pixel intensities for all areas of interest. Particle fractions were calculated for each OCT frame, taken at 0.2 s intervals, and plotted against normalized evaporation time, t/t_f. Each data series is the average of three experiments, and each series is fitted with a linear regression. Plots are discontinuous because only 40 s of data could be recorded in a given sequence due to memory limitations of the Bioptigen software, and at the end of each acquisition approximately 20 s was required to save the data set and start a new sequence. The y intercept indicates the particle fraction at the interface at t/t_f = 0. If the particles are perfectly uniformly distributed at t/t_f = 0, the fraction at the interface would be ~0.08. The y intercepts for PS and MF particle fractions are ~0.06. The error is likely due to the average point spread function for particles as well as the fact that the area of interest at the air–liquid interface is rectangular while the interface is a spherical cap. As the drop dries, this interface flattens and the geometry more closely matches the area of interest.

The PS particles accumulate at the air–water interface linearly with evaporation time and at a rate approximately four times greater than the MF particles. Particle fractions at the air–liquid interface for each particle density are shown in Figure 6a. MF particles accumulate only slightly at the air–water interface, while the fraction of Si particles in the air–water interface declines with evaporation time. These results are consistent with our hypothesis that, all else equal, particle density is inversely related to accumulation at the air–water interface.

Particle density does, in fact, also affect the rate of accumulation at the drop and glass surfaces. Figure 6b shows particle fractions at the water–glass interface for each of the three particle densities. PS particles accumulate at both interfaces at approximately the same rate. MF particles accumulate at the water–glass interface at a faster rate than PS particles but at a slower rate than MF particles at the air–water interface. While the video sequences and time-lapse OCT images show that the vast majority of Si particles reach the water–glass interface within t = 0.1t_f, the particle fraction data show only 48% of particles on the glass by t = 0.6t_f. The reason for this is that so many particles are on the glass substrate that the bottom-most area of interest is not tall enough to capture all the particles. In fact, 98% of Si particles are contained within the bottom two areas of interest by t = 0.5t_f. The slope of the linear regression for the Si particle fraction on the glass is less than the other two particle types because most of the Si particles have reached the glass substrate before the first data sequence is captured.

Relative humidity also affects particle accumulation at the air–water interface. This observation is consistent with our hypothesis that particle sedimentation rate and drop evaporation rate affect interfacial particle accumulation since the evaporation rate and dh/dt are greater at lower relative humidity. PS particle fractions at the air–water interface at two different relative humidities are shown in Figure 6c. The diverging slopes of the linear regressions indicate that particles accumulate at the air–water interface more quickly at a lower relative humidity. Goniometer measurements confirm the difference in dh/dt: 0.2918 and 0.8615 μm/s for 30% RH and 40% RH, respectively (data not shown). On the basis of the reports of others that drop evaporation rate, J(t), is a linear process,^1,2 the mass flux for these cases was estimated to be 0.2918 and 0.8615 μg/s for 30% RH and 40% RH, respectively.

Particle surface charge does not appear to significantly affect the tendency of PS particles to collect at the air–water interface. Accumulation of negatively charged PS–COOH particles and positively charged PS–NH₂ particles at the air–water interface were quantified and are shown in Figure 6d. The slopes of linear regressions for the two data sets are identical, suggesting that both positively charged and negatively charged particles accumulate at the same rate at the drop surface. This result indicates that interfacial accumulation is independent of particle surface charge.

Brownian motion likely plays a role in the adsorption of particles at the air–water interface. The characteristic diffusion length of a 0.97 μm diameter particle, calculated as (Dt)^1/2, where D is the diffusion coefficient and t is time, is 0.71 μm/s compared to a dh/dt value of 0.3 μm/s (30% relative humidity). These values, being the same order of magnitude, imply that Brownian motion plays a role in the entrapment of particles at the interface but only those particles in close proximity to the interface.

The reason why colloidal PS particles remain adsorbed at the air–water interface is not entirely clear. Previous investigations suggest surface tension interactions and buoyancy force can offset particle weight to promote particle adsorption at air–liquid interfaces.^37,38 However, Aveyard et al. reported that colloidal polystyrene particles of the same size range used in this study do not penetrate the air–liquid interface but rather settle in an energy barrier just below the interface.³⁹ Another explanation, not mutually exclusive, is that interparticle electrostatic repulsive forces contribute to particle adsorption at both the air–water and the water–glass interfaces in the context of an evaporating drop. As previously discussed, convective flow fields in the drop create a nonuniform vertical distribution of particles. As the drop dries, the distance between the air–water and the water–glass interfaces decreases, which increases the interparticle electrostatic force between the two interfaces. In the case of a monodisperse water drop containing carboxylated polystyrene particles, all particles carry a negative surface charge, causing this electrostatic force to be repulsive. The distance over which Coulombic repulsive forces interact is inversely proportional to the ionic strength of the solution, which effectively screens electrostatic forces. In our studies, particles were suspended in deionized water, so the charged ions are not present to screen charge effects. The effect of electrostatic interactions on particles adsorbed at an air–liquid interface has been previously described.^39,40 To our knowledge, however, electrostatic interactions between particles at different interfaces separated by a dynamic liquid barrier less than 300 μm in height, such as that found in an evaporating drop, has not been described. Further investigation of the nature of particle adsorption at the interfaces of an evaporating drop is warranted but not investigated here.

The observation made in this report that polystyrene particles accumulate at the air–water interface in a time-dependent manner was also observed by Deegan et al.¹ He observed a 50% shortfall in ring growth compared to the predicted value from his model, which assumed a uniform vertical distribution of particles. Deegan attributed this behavior to the possibility that as particles get close to the air–liquid interface, Marangoni flow would drag particles toward the interface and flow back toward the top-center of the drop.^1,2 However, as previously discussed, Marangoni flow is not prevalent in water drops, and therefore, this explanation does not completely explain observations made in this study.

Video sequences of polystyrene particle motion taken with OCT imaging suggest that particles accumulated at the air–water and water–glass interfaces enter the ring structure in the final seconds of evaporation (Supporting Information). This may, in part, explain the deviation between Deegan’s experimental and predicted values of ring growth. One implication of this finding is that the organization of particles in the ring structure can be controlled by tuning the parameters which affect the degree of nonuniform particle distribution in the vertical direction during drop evaporation. In this initial application of OCT to study evaporating drops we have shown the effects of particle density and relative humidity. To demonstrate the effect of nonuniform, vertical particle distribution on ring structure, residue patterns of drops containing a mixture of particles with different densities were analyzed. A less dense particle like polystyrene tends to accumulate more at the air–water interface and enter the ring structure later in the evaporation process, whereas a more dense particle like melamine formaldehyde is transported to the drop edge by the coffee ring effect throughout the evaporation process. As a result, the ring structure of a drop containing both particle types is not homogeneous but rather organized by the arrival time of particles at the drop’s edge.

We tested this explanation, and our results indicate that particle density can be used to control radial deposition order. Applying these insights to control ring structure, final residue patterns of drops containing different density fluorescent particles were imaged with fluorescence microscopy (Figure 7). Figure 7a shows a fluorescence micrograph of the ring structure of a dried drop containing all three particle types, PS (red), MF (green), and Si (blue) at a ratio of 2:1:1. In Figure 7b the green MF particles have been substituted with a green PS particle, so the ring structure contains equal fractions of two different PS particles (one red and one green) and blue Si particles. A corresponding fluorescence line profile indicates the particle composition along the white line drawn through the ring structure. The line profiles of the two ring structures show a shift in the spatial distribution of particle type at the ring depending on whether or not the MF particle type is present. With all three particle types (Figure 7a), the inner region of the ring structure (away from the contact line) is mostly comprised of red PS particles while the majority of MF particles are settled at the outside region (contact line) of the ring structure. The greatest fraction of Si particles is in the middle of the ring structure. When the MF particle type is replaced with another PS particle type, all three particles (red PS, green PS, and blue Si) have almost identical distributions in the ring structure. The resulting partial separation of particles in the ring structure creates an altered color pattern because polystyrene particles (red) accumulate on the surface of the drop, enter the ring structure later in evaporation, and are deposited at the inner areas of the ring. The melamine formaldehyde particles (green) are transported to the ring by the coffee ring effect throughout evaporation and therefore are deposited at the outer areas of the ring.

Figure 7.

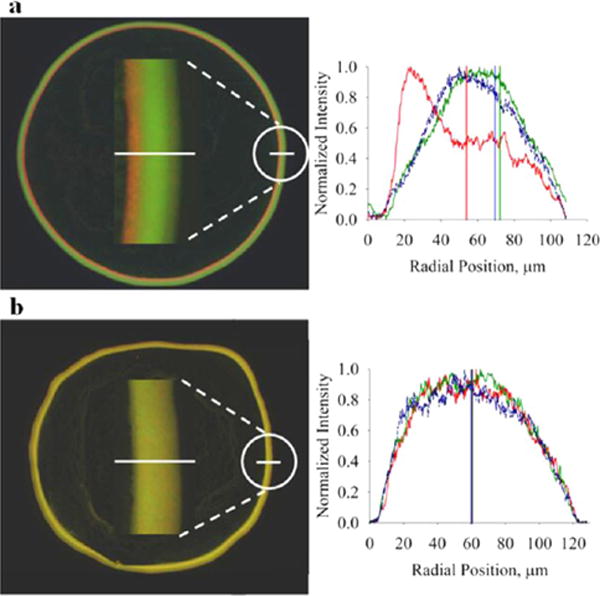
Particle density alters the final coffee ring structure in dried drops. Ring structures of dried, 1 μL water drops containing a mixture of different density particles imaged by fluorescence microscopy: (a) 1:2:1 mixture of PS–COOH (red), MF–COOH (green), and silica (blue) and (b) equal fractions of PS–COOH (red), PS–COOH (green), and silica (blue). Fluorescence profiles for the corresponding white line through the ring structure show that radial particle organization at the ring is partly determined by the densities of constituent particles. Red PS–COOH particles are shifted to the left in a because a greater fraction of these particles is trapped in the air–water interface compared to the MF–COOH and Si particles, causing them to enter the ring structure at later times compared to MF–COOH and Si particles. When the MF–COOH particle is replaced by a PS–COOH particle (green), all particles enter the ring at approximately the same time (b).

Particle tracking in evaporating drops using OCT has several experimental artifacts. First, in order to minimize specular reflectance on the drop surface, the OCT laser was adjusted to a 9° angle from the normal causing as much as 10% error in particle coordinate data. Additionally, the curvature of the drop surface refracts the incident laser causing lensing in the OCT images. This manifests as a slightly curved substrate in the OCT images that flattens with evaporation time. The greatest amount of refractive error occurs where the angle of the drop surface is greatest relative to the substrate, which occurs at the air–water–glass interface at t = 0. This error is quantified as the difference between the actual and the perceived location of a particle near the contact line assuming a worst-case contact angle of 20°. Under these conditions, the refractive error is less than 1%. No attempt is made to correct for this artifact in this study since the error that it causes appears to be negligible for the purposes of this investigation. In future studies, this artifact can likely be offset during signal processing of the OCT data. Another type of artifact that contributes to the curved appearance of the bottom of the drop in the OCT images is a mismatch in optical path length, which equals the refractive index times the actual distance. The mismatch arises from the difference in refractive index between air (n = 1) and water (n = 1.33). A maximum drop height of 300 μm can appear as large as 300 μm × 1.33 = 399 μm. This artifact, while nontrivial in appearance, is negligible in terms of particle tracking because particle velocity is calculated as the difference in particle position relative to the previous frame. The error term in this calculation is based only on the change in drop height that occurs between frames, which is ≪1 μm. This artifact exists only in the vertical direction, and most of the particle motion occurs in the radial direction. Therefore, we consider this artifact also to be negligible. The particle distribution calculations are not affected by the lensing effect or optical path length artifacts because these calculations are fractional calculations relative to average intensity summed over all areas of interest.

Another artifact arises from the optical resolution of the OCT system, approximately 8 μm in the lateral direction, being greater than the 1 μm diameter particles used in the study. As a result, a single object may in fact represent more than one particle. However, the particle solutions used in the study have a sufficiently low concentration of particles to minimize the effect of this artifact, which affects particle size not position. Another potential source of measurement variability in a system is particle concentration. The number of particles per drop was determined based on the number required to pin the contact line and provide sufficient representation of the flow fields without overcrowding the image. If there are too few particles in the water drop then the contact line will not pin and the coffee ring effect is not established.⁴¹ If too many particles are present then it is difficult to resolve an individual particle in sequential images, which is necessary for particle tracking and resolving flow fields. A particle concentration of 10⁵ per 1 μL drop was determined to sufficiently fulfill these requirements. However, the effect of particle concentration on the observations discussed in this study has not been determined. Finally, it is possible the OCT laser itself may cause temperature-induced changes in flow fields in the drop. However, the 860 nm laser used in this study with just 700 μW incident on the sample coincides with near minimal absorption by water, and so temperature effects are relatively insignificant.⁴²

CONCLUSIONS

This work demonstrates that optical coherence tomography effectively tracks particle motion in evaporating drops and provides a new experimental strategy for determining primary and secondary flow fields, interfacial particle accumulation, and dynamic changes in these flow fields. A time-dependent, nonuniform distribution of particles in the z direction was observed. In addition, low particle density and low relative humidity promote particle accumulation at the air–water interface in an evaporating drop. These insights were applied to show that the radial organization of the ring structure is partly controlled by the ratio of different density colloidal particles.

ABBREVIATIONS

OCT

optical coherence tomography

PS

polystyrene

MF

melamine formaldehyde

Si

silica