Abstract
A key issue in understanding the evolutionary and developmental emergence of numerical cognition is to learn what mechanism(s) support perception and representation of quantitative information. Two such systems have been proposed, one for dealing with approximate representation of sets of items across an extended numerical range and another for highly precise representation of only small numbers of items. Evidence for the first system is abundant across species and in many tests with human adults and children, whereas the second system is primarily evident in research with children and in some tests with nonhuman animals. A recent paper (Choo & Franconeri, 2014) with adult humans also reported “superprecise” representation of small sets of items in comparison to large sets of items, which would provide more support for the presence of a second system in human adults. We first presented capuchin monkeys with a test similar to that of Choo and Franconeri in which small sets or large sets with the same ratios had to be discriminated. We then presented the same monkeys with an expanded range of comparisons in the small number range (all comparisons of 1 to 9 items) and the large number range (all comparisons of 10 to 90 items in 10-item increments). Capuchin monkeys showed no increased precision for small over large sets in making these discriminations in either experiment. These data indicate a difference in the performance of monkeys to that of adult humans, and specifically that monkeys do not show improved discrimination performance for small sets relative to large sets when the relative numerical differences are held constant.
Keywords: Quantity classification, Enumeration, Capuchin monkeys, Analog magnitude estimation, Approximate Number System, Object File System
Two core systems of number or one? This question has pervaded the developmental and comparative literatures on numerical cognition for more than a decade. At issue is whether quantification skills that are the basis for mathematical competencies are predicated on one system or two systems for representing and judging quantity or number. There is no debate about the existence of a first core system of number, often called the approximate number system, or ANS (Brannon & Roitman, 2003; Cantlon, Platt, & Brannon, 2009; Gallistel & Gelman, 2000). In this system, quantities are represented inexactly, with increasing variance in discriminating or estimating set sizes as the true set sizes increase. This system produces the well-established distance and size effects, whereby performance in discriminating sets is best predicted by the ratio of those sets to each other (e.g., Beran, 2007), an outcome that reflects the workings of Weber's Law.
This system has been seen in a wide variety of animals including amphibians (e.g., Krusche, Uller, & Dicke, 2010), birds (e.g., Ain, Giret, Grand, Kreutzer, & Bovet, 2009; Rugani, Cavazzana, Vallortigara, & Regolin, 2013), marine mammals (e.g., Abramson, Hernandez-Lloreda, Call, & Colmenares, 2011), terrestrial non-primate mammals (Baker, Shivik, & Jordan, 2011; Perdue, Talbot, Stone, & Beran, 2012; Vonk & Beran, 2012), and many primates (Beran, 2007, 2008; Hanus & Call, 2007; Lewis, Jaffe, & Brannon, 2005; Cantlon & Brannon, 2006a, 2006b). It is also seen in the discrimination performance of children (Cantlon, Safford, & Brannon, 2010; Cordes & Brannon, 2009; Huntley-Fenner & Cannon, 2000), and adult humans who are prevented from using formal counting routines (Beran, Taglialatela, James, Flemming, & Washburn, 2006; Boisvert, Abroms, & Roberts, 2003; Cordes, Gelman, Gallistel, & Whalen, 2001; Whalen, Gallistel, & Gelman, 1999).
The second system operates very differently, and is best described as a precise but size-limited system that accurately represents small numbers but cannot accommodate numbers greater than four because of limits in attention and working memory capacity. A model of this system, often called the object file model, has been described in detail elsewhere (e.g., Feigensen & Carey, 2005; Feigenson, Carey, & Hauser, 2002; Uller, Carey, Huntley-Fennner, & Klatt, 1999), but the key point here is that a two core systems hypothesis for numerical cognition requires evidence that performance with small sets of items looks better than performance with large sets (Feigenson, Dehaene, & Spelke, 2004; Xu, 2003; also see Hyde, 2011; Hyde & Wood, 2011, for a discussion about other stimulus features that impact which of these two systems might be activated). Although there has been less evidence for this system in the comparative literature than in the developmental literature, some reports have suggested that fish may show evidence of these two systems (Agrillo, Miletto Petrazzini, & Bisazza, 2014; Agrillo, Piffer, Bisazza, & Butterworth, 2012; Gómez-Laplaza & Gerlai, 2011; Piffer, Agrillo, & Hyde, 2012; but see Gomez-Laplaza & Gerlai, 2011; Potrich, Sovrano, Stancher, & Vallortigara, 2015), as might birds (e.g., Garland, Low, & Burns, 2012; Hunt, Low, & Burns, 2008), salamanders (Krusche, Uller, & Dicke, 2010; Uller, Jaeger, Guidry, & Martin, 1996) and beluga whales (Abramson, Hernandez-Lloreda, Call, & Colmenares, 2013). Among primate studies, only one paper reported that semi-free ranging rhesus monkeys also showed the hallmark behavioral features of two core systems (Hauser, Carey, & Hauser, 2000), whereas the vast majority of the studies with primates show ratio effects indicative of the approximate number system only (e.g., Barnard et al., 2013; Beran, 2004, 2008; Evans, Beran, Harris, & Rice, 2009; Cantlon & Brannon, 2006a, 2006b; Hanus & Call, 2007; Merritt, MacLean, Crawford, & Brannon, 2011; Nieder & Miller, 2004).
A recent report with human participants suggested that enumeration of small sets was “superprecise” and reflected a specialized mechanism for representing small numbers of items as is outlined for the object file model (Choo & Franconeri, 2014). That study was based on the longstanding finding that humans are particularly fast and accurate at reporting small numbers of items (usually four or less) compared to the gradually increasing response time slope and gradually decreasing performance slope for all progressively larger numbers above four. This subitization process for small numbers (Mandler & Shebo, 1982) seemingly supports the idea of two systems for enumeration of visual items. Although alternate accounts of subitizing exist that still allow for meeting Weber's Law (Lemmon, 1927), the similarity in size limits for enumerating small numbers of items, for visual memory capacity (Luck & Vogel, 1997), and for tracking moving objects (Pylyshyn & Storm, 1988) suggests that perhaps this object file system is at work in numerical judgments. The object file system is proposed to be the second core system, and one that can be adopted for other purposes such as object tracking (see Franconeri, Alvarez & Enns, 2007).
Choo and Franconeri (2014) gave adult participants two sets of dots on a computer screen. Small set comparisons always consisted of 3 items in one set and either 1, 2, 4, or 5 items in the other, whereas large set comparisons consisted of 30 items in one set and either 10, 20, 40, or 50 items in the other. Participants had to indicate whether the second set was smaller or larger than the consistent reference set (the set with 3 or 30 items). The response times in making these decisions were faster for the small set sizes than for the large ones, and this was also true in a second experiment in which the participants judged whether the two arrays had the same number of items or differing numbers of items with faster responses for small sets compared to large sets. Choo and Franconeri suggested that these results demonstrated super-precision for small collections of items, a claim that might lend support to the idea of two separate systems for numerical and quantitative representation.
Given the ongoing debate in the comparative literature about whether small quantities are somehow “special” in terms of the precision with which they are perceived and represented, the Choo and Franconeri (2014) task could be adapted for use with nonhuman animals, and then used to assess whether those animals also showed the same pattern of greater precision for small sets compared to large sets. Such a presentation format could be used to compare nonhuman animals to humans (see Agrillo et al., 2012). In Experiment 1, we presented an adapted version of this task to capuchin monkeys in which they had to choose the larger of the two-dot arrays shown on the screen, and we used the same quantity comparisons as in Choo and Franconeri. In Experiment 2, we expanded the number of comparisons in the small range (all combinations of 1 to 9 items) and the large range (all comparisons of 10 to 90 items in 10-item increments). This allowed us to assess whether performance was similar across small and large set sizes in terms of the role of ratio effects. If this were true, this would argue against a two-system interpretation, or at least indicate that monkeys do not show the high performance for small numbers that humans showed. If monkeys instead performed relatively better with small sets compared to large sets, this could indicate a two-system interpretation and match previous results from human participants.
Critically, the six monkeys that we tested during Experiment 1 were involved in their first experimental test using the joystick-computerized apparatus that is commonly used in numerical tests and other cognitive tests with monkeys (e.g., Beran, 2008; Evans, Beran, Chan, Klein, & Menzel, 2008). This was important because it allowed us to control for any previous experience with dots, two-dimensional quantities on computer screens, or the making of relative judgments about quantities. The lack of evidence of two number systems among some comparative studies could be a result of those previous studies testing “task-savvy” animals that had experience with a number of tests of numerical cognition (e.g., Beran, 2008) and that might therefore have come to rely more heavily on the ANS (see Bisazza, Agrillo, & Lucon-Xiccato, 2014). Naïve monkeys thus allowed us to best assess any spontaneous super-precision for small sets. Previous research with naïve baboons (Barnard et al., 2013) had shown that only one core system appeared to be at work in the discriminations of those primates, and we predicted the same was likely to be true for capuchin monkeys.
Experiment 1
Methods
Participants
We tested six adult capuchin monkeys (Cebus apella) including 2 males (Benny: age 11, Mason: age 16) and 4 females (Bailey: age 15; Gonzo: age 8; Gretel: age 11; Lexi: age 6). All monkeys previously had been trained to use a joystick with their hands to control a cursor on a computer screen within the previous 6 months (see Evans et al., 2008 for training details), but this was their only prior experimental history with the joystick apparatus. However, one monkey (Mason) was trained on a touchscreen computer and had participated in several facial-recognition studies that involved discriminating conspecific faces (Pokorny & de Waal, 2009a, 2009b; Pokorny, Webb, & de Waal, 2011). The monkeys are socially housed and separate voluntarily for computer testing. The monkeys had continuous access to water. They received a daily diet of fruits and vegetables, and thus they were not food deprived for the purposes of this experiment or any other experiment. The experiment was conducted with approval of the Georgia State University Institutional Animal Care and Use Committee and followed all federal guidelines.
Apparatus
The monkeys were tested using the Language Research Center's Computerized Test System. This system consists of a personal computer, digital joystick, color monitor, and pellet dispenser (Evans et al., 2008). To engage in test trials, the monkeys manipulated the joystick with their hands and these manipulations led to isomorphic movements of a small cursor on the computer screen. When monkeys made correct responses in the task they received 45-mg banana-flavored chow pellets (Bio-Serv, Frenchtown, NJ) that were delivered by a pellet dispenser that was connected to the computer through a digital I/O board (PDISO8A; Keithley Instruments, Cleveland, OH). The task program was written in Visual Basic 6.0.
Design and procedure
The task involved quantity discriminations between two choices. Monkeys initiated trials by moving the centrally located cursor to a digital button at the top of the screen. When contacted, that button disappeared and two arrays of identical white dots (5 mm in diameter) were presented at the left center and right center of the screen, with the cursor centered between them. Both arrays were enclosed in a thin border to present them as two discrete sets, and the background was black. Monkeys could take as long as they wanted to make a response. They were rewarded with a single food pellet for selecting the array with more dots, and then a 1 s inter-trial interval occurred before the start button appeared for the next trial. Incorrect selections led to a 20 s timeout during which the screen remained blank before the start button appeared for the next trial.
There were two conditions. In the first condition (Small Magnitude), every trial presented an array of 3 dots on one randomly selected side of the screen, and 1, 2, 4, or 5 dots in the other array (also randomly selected). In the second condition (Large Magnitude), every trial presented an array of 30 dots and 10, 20, 40, or 50 dots in the other array (again, with random side presentations).
Each monkey completed as many trials as it chose to perform during the approximately 3 to 4 hour test session, during which time water was always available as was visual access to conspecifics in nearby parts of the enclosure. Half of the monkeys started with the Small Magnitude condition and half started with the Large Magnitude condition. Monkeys completed four blocks of trials where each block consisted of 200 trials in one condition and then 200 trials in the other condition. To collect the full data set required nine sessions for Bailey, five sessions for Benny, five sessions for Gonzo, three sessions for Gretel, five sessions for Lexi, and four sessions for Mason.
Results
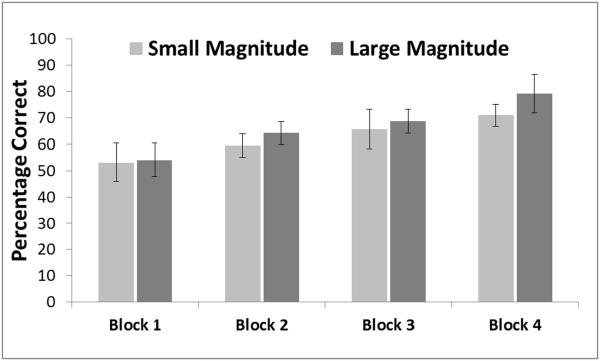
Figure 1 illustrates the accuracy of the monkeys in choosing the larger set as a function of magnitude condition (small sets or large sets) and as a function of trial block. We conducted a repeated-measures ANOVA with these two factors included. There was a significant main effect of block, F (3, 15) = 11.21, p < .001, ηp2 = .87. There was not a significant main effect of magnitude condition, F (1, 5) = 3.46, p =.12, ηp2 = .40, and there was not a significant interaction, F (3, 15) = 0.77, p = .52, ηp2 = .13. The main effect of block reflected improved performance with experience, as evidenced by a significant linear fit from the test of within-subjects contrast, F (1, 5) = 19.71, p = .007, ηp2 = .80. There was not a difference in performance as a function of magnitude condition, and capuchin monkeys did not privilege small sets over large sets.
Figure 1.
Mean accuracy for the monkeys with the small and large magnitude arrays for each trial block. Error bars indicate 95% confidence intervals using the Cousineau (2005) method for calculating confidence intervals for within-subjects designs.
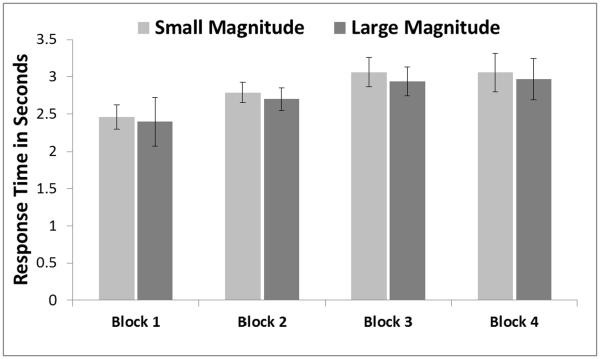
We also examined response times as a function of magnitude condition (Small or Large) and each of the four specific comparisons within each set size (Figure 3). We first removed any trials with response times that exceeded 10 s, as these were extremely rare (< 0.5% of the total trials). There was not a statistically significant effect of magnitude, F (1, 5) = 1.79, p = .23, ηp2 = .26. There was, however, an effect of block, F (3, 15) = 5.82, p = .008, ηp2 = .54. The main effect of block reflected progressively slower responding across blocks, as evidenced by a significant linear fit from the test of within-subjects contrast, F (1, 5) = 7.54, p = .04, ηp2 = .60. There was not a statistically significant interaction of magnitude and trial block, F (3, 15) = 0.07, p = .97, ηp2 = .01. The same pattern of results occurred when all trials were kept in the analysis but we recoded any trials with response times of greater than 10 s as having a response time of exactly 10 s.
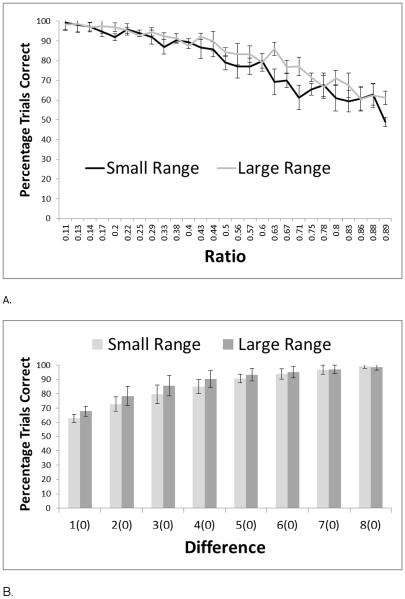
Figure 3.
The group performance of the monkeys with the small and large magnitude arrays shown as a function of the ratio between sets (A) or the difference in dot quantity between sets (B). Error bars indicate 95% confidence intervals using the Cousineau (2005) method for calculating confidence intervals for within-subjects designs.
Discussion
In the current study, experimentally-naïve capuchin monkeys were equally proficient and equally fast in discriminating small and large sets of items in a relative quantity judgment task. Crucially, there was no evidence for the “superprecision” for small sets over large sets as was documented among human adults using a similar paradigm. There also was no evidence for faster discriminations and responses toward small sets compared to large sets, unlike in human participants (Choo & Franconeri, 2014).
The comparisons used in Experiment 1 did not allow us to fully assess whether ratio effects presented similarly in these monkeys for the small range and large range of quantities. These ratio effects, calculated by dividing the small set size by the large set size, are consistently reported to best account for the performance of nonhuman primates in two-choice quantity discrimination tasks (Barnard et al., 2013; Beran, 2004, 2008; Evans, Beran, Harris, & Rice, 2009; Cantlon & Brannon, 2006a, 2006b; Hanus & Call, 2007; Merritt, MacLean, Crawford, & Brannon, 2011; Nieder & Miller, 2004). To best assess ratio effects, as well as other potential contributing factors to performance such as overall magnitude of sets, requires a wide range of comparisons. Experiment 2 presented this range, and it did so for small and large magnitude ranges.
Experiment 2
Methods
Participants
The same six monkeys participated as in Experiment 1. In the interim between Experiment 1 and Experiment 2, these monkeys completed one other study in which they made quantity judgments (Parrish, Agrillo, Perdue, & Beran, 2015). Thus, they had some additional experience in the kind of test given in Experiment 1.
Apparatus
This was the same as in Experiment 1.
Design and Procedure
The monkeys performed the same two-choice discrimination in which they compared arrays of the same dot stimuli as in Experiment 1. Now, however, there was a much greater range of quantity comparisons, and those were presented in the small magnitude and large magnitude ranges. For the small magnitude range, all possible combinations of 1 to 9 items were presented (except comparisons of equal set sizes). For the large magnitude range, all combinations of 10, 20, 30, 40, 50, 60, 70, 80, and 90 items were presented (except comparisons of equal quantities). Thus, for each magnitude range, the difference in the quantities to be compared on a given trial ranged from 1 to 8 (small range) or 10 to 80 (large range). For both ranges, the ratio of items within the possible comparisons ranged from .11 (1 vs. 9 or 10 vs. 90) to .89 (8 vs 9 or 80 vs 90). The magnitude (small or large) and specific comparison were chosen randomly on each trial, and the side of the screen with the larger array was randomly determined on each trial. Each monkey completed 3,500 trials in this experiment across a variable number of daily test sessions (Gretel – two sessions; Benny and Gonzo – four sessions; Lexi – five sessions; Mason – six sessions; Bailey – 17 sessions).
Results
Figure 3a presents the group data as a function of the ratio between sets and as a function of the relative numerical difference between sets. We compared the regression slopes for the ratio data for small and large magnitude ranges using Analysis of Covariance (with ratio as the covariate). There was a significant difference between the two magnitude ranges, F (1, 51) = 18.83, p < .001. As can be seen in the figure, performance was better for the large magnitude range, and the slope of the decreasing function was shallower for the large magnitude range. Figure 3b shows performance as a function of the difference between sets. There were differences of 1 to 8 items for the small magnitude range and differences of 10 to 90 items (in 10-unit increments) in the large magnitude range. A paired-samples t-test again showed a significant difference between the magnitude ranges, t(7) = 3.29, p = .013. Once again, this difference reflected better performance in the large magnitude range compared to the small magnitude range. This pattern of results stands in contrast to evidence of super-precision for small magnitudes among human adults (Choo & Franconeri, 2014).
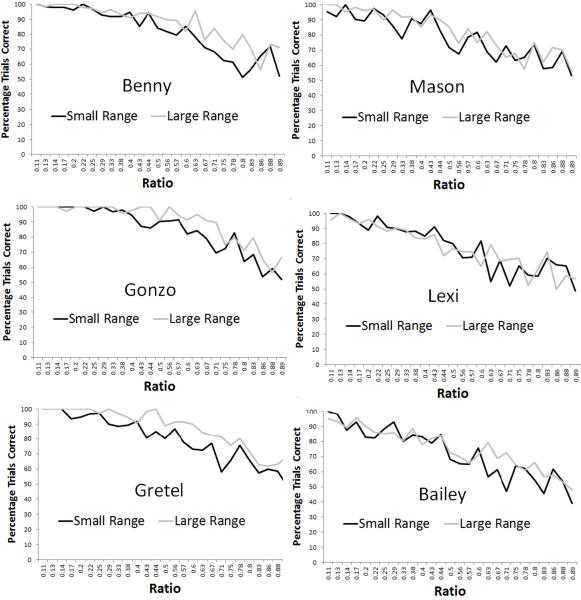
Figure 4 presented the individual monkeys' performance in each range as a function of the ratio between sets. The ANCOVAs revealed that Gonzo, F (1, 51) = 7.51, p < .01, Mason, F (1, 51) = 5.97, p =.018, Benny, F (1, 51) = 13.11, p < .001, and Gretel, F (1, 51) = 30.02, p < .001, all showed better performance for the large magnitude range. Bailey, F (1, 51) = 3.94, p = .053, and Lexi, F (1, 51) = 0.01, p = .92, showed no difference for the two magnitude ranges.
Figure 4.
Data for individual moneys with the small and large magnitude arrays shown as a function of the ratio between sets.
General Discussion
These results are valuable in light of the ongoing debate in the comparative and developmental literature over the mechanisms underlying numerical cognition. Much of the previous research had indicated strong support for a single quantity representation system among nonhuman primate species (Barnard et al., 2013; Beran, 2004, 2007; 2008; Evans et al., 2009; Cantlon & Brannon, 2006a, 2006b; Hanus & Call, 2007; Judge, Evans, & Vyas, 2005; Merritt et al., 2011; Nieder & Miller, 2004, but see Hauser et al., 2000). The present data provide similar support, and in a test that was based on one used with adult humans that had instead indicated two systems might be at work. These experimentally-naïve capuchin monkeys demonstrated the reported pattern of results from the outset of testing, suggestive of only one system at work. This was true in Experiment 1 in terms of their accuracy in choosing the larger set and in terms of comparable response times to large-magnitude sets and small-magnitude sets (but see Tomonaga & Matsuzawa, 2002, for a different test with chimpanzees in which there was evidence of faster responding to small sets). In Experiment 2, strong ratio effects were evident (as were distance effects), but these were equivalent for the small and large quantity ranges for a few monkeys, or, in the majority of cases, monkeys showed greater discrimination performance with the larger quantity range. One reason for this might be greater overall dot stimulus amount onscreen despite consistent relative amounts of dot stimuli in the two ranges. This might lead to the slight increase in performance if those sets led to more attentive discrimination. However, as illustrated in Figure 3 and Figure 4, the clearest conclusion is that performance is highly similar whether monkeys are choosing between two relatively small dot magnitudes or two relatively large ones.
It is interesting to consider why there is a difference between the treatment of small and large sets for humans (in some studies) but not often such a difference in tests with nonhuman animals (and, very rarely such a difference for nonhuman primates). Sensitivity to a wide range of quantities would clearly be advantageous among all animal species in the realms of foraging, predation, and sexual selection. A system that allowed one to generate approximate representations for telling apart important differences (e.g., 5 versus 8 pieces of food) but not for telling apart small differences in large magnitudes (e.g., 12 versus 13 predators, 21 versus 22 pieces of food) would be valuable. The approximate number system does just this, and is seen in many species.
More precise and exact representations of small quantities and numbers also could serve an adaptive function, particularly where keeping track of exactly what or who is around you is critical (e.g., as in the case of seeing two versus three predators in the vicinity). Thus, one can see why such a system might exist. But, the more precise and rapid apprehension and representation of small numbers of items is not often evident in other species (including in the present experiment) and is not always present even in tests with humans, and therefore remains elusive with regard to understanding whether it is a core system or instead may be the result of specialized learning or experience or special stimulus presentation formats (e.g., Hyde, 2011). More research is needed to clarify that issue, but the present results showed that these naïve capuchin monkeys do not show privileged capacities for dealing with small numbers of items. Such privilege may be unique to human quantity comparisons, or perhaps is the result of specific kinds of experiences or task demands in making such judgments.
Figure 2.
The mean response times for small and large magnitude arrays and each trial block. Error bars indicate 95% confidence intervals using the Cousineau (2005) method for calculating confidence intervals for within-subjects designs.
Acknowledgments
This research was supported by NIH grant HD060563.
References
- Abramson JZ, Hernandez-Lloreda V, Call J, Colmenares F. Relative quantity judgments in South American sea lions (Otaria flavescens) Animal Cognition. 2011;14:695–706. doi: 10.1007/s10071-011-0404-7. [DOI] [PubMed] [Google Scholar]
- Abramson JZ, Hernández-Lloreda V, Call J, Colmenares F. Relative quantity judgments in the beluga whale (Delphinapterus leucas) and the bottlenose dolphin (Tursiops truncatus) Behavioural Processes. 2013;96:11–19. doi: 10.1016/j.beproc.2013.02.006. [DOI] [PubMed] [Google Scholar]
- Agrillo C, Miletto Petrazzini ME, Bisazza A. Numerical acuity of fish is improved in the presence of moving targets, but only in the subitizing range. Animal Cognition. 2014;17:307–316. doi: 10.1007/s10071-013-0663-6. [DOI] [PubMed] [Google Scholar]
- Agrillo C, Piffer L, Bisazza A, Butterworth B. Evidence for two numerical systems that are similar in humans and guppies. PloS ONE. 2012;7:e31923. doi: 10.1371/journal.pone.0031923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ain SA, Giret N, Grand M, Kreutzer M, Bovet D. The discrimination of discrete and continuous amounts in African grey parrots (Psittacus erithacus) Animal Cognition. 2009;12:145–154. doi: 10.1007/s10071-008-0178-8. [DOI] [PubMed] [Google Scholar]
- Baker JM, Shivik J, Jordan KE. Tracking of food quantity by coyotes (Canis latrans) Behavioural Processes. 2011;88:72–75. doi: 10.1016/j.beproc.2011.08.006. [DOI] [PubMed] [Google Scholar]
- Barnard AM, Hughes KD, Gerhardt RR, DiVincenti LJ, Bovee JM, Cantlon JF. Inherently analog quantity representations in olive baboons (Papio anubis) Frontiers in Psychology. 2013;4:253. doi: 10.3389/fpsyg.2013.00253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beran MJ. Chimpanzees (Pan troglodytes) respond to nonvisible sets after one-by-one addition and removal of items. Journal of Comparative Psychology. 2004;118:25–36. doi: 10.1037/0735-7036.118.1.25. [DOI] [PubMed] [Google Scholar]
- Beran MJ. Rhesus monkeys (Macaca mulatta) enumerate large and small sequentially presented sets of items using analog numerical representations. Journal of Experimental Psychology: Animal Behavior Processes. 2007;33:55–63. doi: 10.1037/0097-7403.33.1.42. [DOI] [PubMed] [Google Scholar]
- Beran MJ. Monkeys (Macaca mulatta and Cebus apella) track, enumerate, and compare multiple sets of moving items. Journal of Experimental Psychology: Animal Behavior Processes. 2008;34:63–74. doi: 10.1037/0097-7403.34.1.63. [DOI] [PubMed] [Google Scholar]
- Beran MJ, Taglialatela LA, Flemming TJ, James FM, Washburn DA. Nonverbal estimation during numerosity judgements by adult humans. Quarterly Journal of Experimental Psychology. 2006;59:2065–2082. doi: 10.1080/17470210600701171. [DOI] [PubMed] [Google Scholar]
- Bisazza A, Agrillo C, Lucon-Xiccato T. Extensive training extends numerical abilities of guppies. Animal Cognition. 2014;17:1413–1419. doi: 10.1007/s10071-014-0759-7. [DOI] [PubMed] [Google Scholar]
- Boisvert MJ, Abroms BD, Roberts WD. Human nonverbal counting estimated by response production and verbal report. Psychonomic Bulletin & Review. 2003;10:683–690. doi: 10.3758/bf03196532. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Roitman JD. Nonverbal representations of time and number in animals and human infants. In: Meck WH, editor. Functional and neural mechanisms of interval timing. CRC Press; Boca Raton, FL: 2003. pp. 143–182. [Google Scholar]
- Cantlon JF, Brannon EM. The effect of heterogeneity on numerical ordering in rhesus monkeys. Infancy. 2006a;9:173–189. [Google Scholar]
- Cantlon JF, Brannon EM. Shared system for ordering small and large numbers in monkeys and humans. Psychological Science. 2006b;17:401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Platt ML, Brannon EM. Beyond the number domain. Trends in Cognitive Sciences. 2009;13:83–91. doi: 10.1016/j.tics.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon JF, Safford KE, Brannon EM. Spontaneous analog number representations in 3-year-old children. Developmental Science. 2010;13:289–297. doi: 10.1111/j.1467-7687.2009.00887.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choo H, Franconeri SL. Enumeration of small collections violates Weber's Law. Psychonomic Bulletin & Review. 2014;21:93–99. doi: 10.3758/s13423-013-0474-4. [DOI] [PubMed] [Google Scholar]
- Cordes S, Brannon EM. Crossing the divide: Infants discriminate small from large numerosities. Developmental Psychology. 2009;45:1583–1594. doi: 10.1037/a0015666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes S, Gelman R, Gallistel CR, Whalen J. Variability signatures distinguish verbal from nonverbal counting for both large and small numbers. Psychonomic Bulletin & Review. 2001;8:698–707. doi: 10.3758/bf03196206. [DOI] [PubMed] [Google Scholar]
- Cousineau D. Confidence intervals in within-subject designs: A simpler solution to Loftus and Masson's method. Tutorial in Quantitative Methods for Psychology. 2005;1:42–45. [Google Scholar]
- Evans TA, Beran MJ, Chan B, Klein ED, Menzel CR. An efficient computerized testing method for the capuchin monkey (Cebus apella): Adaptation of the LRC-CTS to a socially housed nonhuman primate species. Behavior Research Methods. 2008;40:590–596. doi: 10.3758/brm.40.2.590. [DOI] [PubMed] [Google Scholar]
- Evans TA, Beran MJ, Harris EH, Rice D. Quantity judgments of sequentially presented food items by capuchin monkeys (Cebus apella) Animal Cognition. 2009;12:97–105. doi: 10.1007/s10071-008-0174-z. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S. On the limits of infants' quantification of small object arrays. Cognition. 2005;97:295–313. doi: 10.1016/j.cognition.2004.09.010. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Hauser MD. The representations underlying infants' choice of more: Object files versus analog magnitudes. Psychological Science. 2002;13:150–156. doi: 10.1111/1467-9280.00427. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Franconeri SL, Alvarez GA, Enns JT. How many locations can be selected at once? Journal of Experimental Psychology: Human Perception and Performance. 2007;33:1003–1012. doi: 10.1037/0096-1523.33.5.1003. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Non-verbal numerical cognition: From reals to integers. Trends in Cognitive Sciences. 2000;4:59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Garland A, Low J, Burns KC. Large quantity discrimination by North Island robins (Petroica longipes) Animal Cognition. 2012;15:1129–1140. doi: 10.1007/s10071-012-0537-3. [DOI] [PubMed] [Google Scholar]
- Gómez-Laplaza LM, Gerlai R. Spontaneous discrimination of small quantities: shoaling preferences in angelfish (Pterophyllum scalare) Animal Cognition. 2011;14:565–574. doi: 10.1007/s10071-011-0392-7. [DOI] [PubMed] [Google Scholar]
- Hanus D, Call J. Discrete quantity judgments in the great apes (Pan paniscus, Pan troglodytes, Gorilla gorilla, Pongo pygmaeus): The effect of presenting whole sets versus item-by-item. Journal of Comparative Psychology. 2007;121:241–249. doi: 10.1037/0735-7036.121.3.241. [DOI] [PubMed] [Google Scholar]
- Hauser MD, Carey S, Hauser LB. Spontaneous number representation in semi–free–ranging rhesus monkeys. Proceedings of the Royal Society of London B: Biological Sciences. 2000;267:829–833. doi: 10.1098/rspb.2000.1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunt S, Low J, Burns KC. Adaptive numerical competency in a food-hoarding songbird. Proceedings of the Royal Society of London B. 2008;275:2373–2379. doi: 10.1098/rspb.2008.0702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huntley-Fenner G, Cannon E. Preschoolers' magnitude comparisons are mediated by a preverbal analog mechanism. Psychological Science. 2000;11:147–152. doi: 10.1111/1467-9280.00230. [DOI] [PubMed] [Google Scholar]
- Hyde DC. Two systems of non-symbolic numerical cognition. Frontiers in Human Neuroscience. 2011;5 doi: 10.3389/fnhum.2011.00150. Article 150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyde DC, Wood JN. Spatial attention determines the nature of nonverbal number representation. Journal of Cognitive Neuroscience. 2011;23:2336–2351. doi: 10.1162/jocn.2010.21581. [DOI] [PubMed] [Google Scholar]
- Judge PG, Evans TA, Vyas DK. Ordinal representation of numeric quantities by brown capuchin monkeys (Cebus apella) Journal of Experimental Psychology: Animal Behavior Processes. 2005;31:79–94. doi: 10.1037/0097-7403.31.1.79. [DOI] [PubMed] [Google Scholar]
- Krusche P, Uller C, Dicke U. Quantity discrimination in salamanders. Journal of Experimental Biology. 2010;213:1822–1828. doi: 10.1242/jeb.039297. [DOI] [PubMed] [Google Scholar]
- Lemmon VW. The relation of reaction time to measures of intelligence, memory, and learning. Archives of Psychology. 1927;15:5–38. [Google Scholar]
- Lewis KP, Jaffe S, Brannon EM. Analog number representations in mongoose lemurs (Eulemur mongoz): Evidence from a search task. Animal Cognition. 2005;8:247–252. doi: 10.1007/s10071-004-0251-x. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Vogel EK. The capacity of visual working memory for features and conjunctions. Nature. 1997;390:279–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- Mandler G, Shebo BJ. Subitizing: An analysis of its component processes. Journal of Experimental Psychology: General. 1982;111:1–22. doi: 10.1037//0096-3445.111.1.1. [DOI] [PubMed] [Google Scholar]
- Merritt DJ, MacLean EL, Crawford JC, Brannon EM. Numerical rule-learning in ring-tailed Lemurs (Lemur catta) Frontiers in Comparative Psychology. 2011;2 doi: 10.3389/fpsyg.2011.00023. Article 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieder A, Miller EK. Analog numerical representations in rhesus monkeys: Evidence for parallel processing. Journal of Cognitive Neuroscience. 2004;16:889–901. doi: 10.1162/089892904970807. [DOI] [PubMed] [Google Scholar]
- Parrish AE, Agrillo C, Perdue BM, Beran MJ. The elusive illusion: Do children (Homo sapiens) and capuchin monkeys (Cebus apella) see the Solitaire illusion? Journal of Experimental Child Psychology. 2015;142:83–95. doi: 10.1016/j.jecp.2015.09.021. [DOI] [PubMed] [Google Scholar]
- Perdue BM, Talbot CG, Stone AM, Beran MJ. Putting the elephant back in the herd: elephant relative quantity judgments match those of other species. Animal Cognition. 2012;15:955–961. doi: 10.1007/s10071-012-0521-y. [DOI] [PubMed] [Google Scholar]
- Piffer L, Agrillo C, Hyde DC. Small and large number discrimination in guppies. Animal Cognition. 2012;15:215–221. doi: 10.1007/s10071-011-0447-9. [DOI] [PubMed] [Google Scholar]
- Pokorny JJ, de Waal F. Face recognition in capuchin monkeys (Cebus apella) Journal of Comparative Psychology. 2009a;123:151–160. doi: 10.1037/a0014073. [DOI] [PubMed] [Google Scholar]
- Pokorny JJ, de Waal FB. Monkeys recognize the faces of group mates in photographs. Proceedings of the National Academy of Sciences. 2009b;106:21539–21543. doi: 10.1073/pnas.0912174106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pokorny JJ, Webb CE, de Waal FB. An inversion effect modified by expertise in capuchin monkeys. Animal Cognition. 2011;14:839–846. doi: 10.1007/s10071-011-0417-2. [DOI] [PubMed] [Google Scholar]
- Potrich D, Sovrano VA, Stancher G, Vallortigara G. Quantity Discrimination by Zebrafish (Danio rerio) Journal of Comparative Psychology. 2015;129:388–393. doi: 10.1037/com0000012. [DOI] [PubMed] [Google Scholar]
- Pylyshyn ZW, Storm RW. Tracking multiple independent targets: Evidence for a parallel tracking mechanism. Spatial Vision. 1988;3:179–197. doi: 10.1163/156856888x00122. [DOI] [PubMed] [Google Scholar]
- Rugani R, Cavazzana A, Vallortigara G, Regolin L. One, two, three, four, or is there something more? Numerical discrimination in day-old domestic chicks. Animal Cognition. 2013;16:557–564. doi: 10.1007/s10071-012-0593-8. [DOI] [PubMed] [Google Scholar]
- Tomonaga M, Matsuzawa T. Enumeration of briefly presented items by the chimpanzee (Pan troglodytes) and humans (Homo sapiens) Animal Learning and Behavior. 2002;30:143–157. doi: 10.3758/bf03192916. [DOI] [PubMed] [Google Scholar]
- Uller C, Carey S, Huntley-Fenner G, Klatt L. What representations might underlie infant numerical knowledge? Cognitive Development. 1999;14:1–36. [Google Scholar]
- Uller C, Jaeger R, Guidry G, Martin C. Salamanders (Plethodon cinereus) go for more: Rudiments of number in an amphibian. Animal Cognition. 2003;6:105–112. doi: 10.1007/s10071-003-0167-x. [DOI] [PubMed] [Google Scholar]
- Vonk J, Beran MJ. Bears “count” too: Quantity estimation and comparison in black bears (Ursus americanus) Animal Behaviour. 2012;84:231–238. doi: 10.1016/j.anbehav.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal counting in humans: The psychophysics of number representation. Psychological Science. 1999;10:130–137. [Google Scholar]
- Xu F. Numerosity discrimination in infants: Evidence for two systems of representations. Cognition. 2003;89:B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]