Using Diffusion Tractography to Predict Cortical Connection Strength and Distance: A Quantitative Comparison with Tracers in the Monkey

Abstract

Tractography based on diffusion MRI offers the promise of characterizing many aspects of long-distance connectivity in the brain, but requires quantitative validation to assess its strengths and limitations. Here, we evaluate tractography's ability to estimate the presence and strength of connections between areas of macaque neocortex by comparing its results with published data from retrograde tracer injections. Probabilistic tractography was performed on high-quality postmortem diffusion imaging scans from two Old World monkey brains. Tractography connection weights were estimated using a fractional scaling method based on normalized streamline density. We found a correlation between log-transformed tractography and tracer connection weights of r = 0.59, twice that reported in a recent study on the macaque. Using a novel method to estimate interareal connection lengths from tractography streamlines, we regressed out the distance dependence of connection strength and found that the correlation between tractography and tracers remains positive, albeit substantially reduced. Altogether, these observations provide a valuable, data-driven perspective on both the strengths and limitations of tractography for analyzing interareal corticocortical connectivity in nonhuman primates and a framework for assessing future tractography methodological refinements objectively.

SIGNIFICANCE STATEMENT Tractography based on diffusion MRI has great potential for a variety of applications, including estimation of comprehensive maps of neural connections in the brain (“connectomes”). Here, we describe methods to assess quantitatively tractography's performance in detecting interareal cortical connections and estimating connection strength by comparing it against published results using neuroanatomical tracers. We found the correlation of tractography's estimated connection strengths versus tracer to be twice that of a previous study. Using a novel method for calculating interareal cortical distances, we show that tractography-based estimates of connection strength have useful predictive power beyond just interareal separation. By freely sharing these methods and datasets, we provide a valuable resource for future studies in cortical connectomics.

Introduction

Tractography based on diffusion MRI (dMRI) is used widely to obtain several complementary types of information about brain anatomy and circuitry. These include characterizing trajectories of major white matter (WM) fiber bundles (Catani and Thiebaut de Schotten, 2008; Glasser and Rilling, 2008) and subdividing (parcellating) gray matter (GM) regions based on tractography-derived connectivity profiles (“connectional contrast”; Behrens et al., 2003; Johansen-Berg et al., 2004; Rushworth et al., 2006; Beckmann et al., 2009; Mars et al., 2011). Here, we focus on using tractography to estimate the presence and weight (“strength”) of long-distance connections between GM regions. This involves analysis of “parcellated connectomes”; that is, estimating connectivity between brain subdivisions (parcels) in humans or nonhuman primates (NHPs) (Sporns et al., 2005; Harriger et al., 2012; Li et al., 2013; Reid et al., 2016; van den Heuvel et al., 2015).

Tractography is an indirect method for inferring connectivity and various methodological confounds introduce noise and/or bias (Jbabdi and Johansen-Berg, 2011; Jones et al., 2013; Van Essen et al., 2014). Validation studies are needed that compare against “ground truth” data from anatomical tracer studies in laboratory animals. Previous studies in NHPs demonstrate both successes and limitations of tractography for assessing pathway trajectories (Jbabdi et al., 2015; Knösche et al., 2015) and detecting the presence of long-distance interareal connections (Jbabdi et al., 2013; Thomas et al., 2014; Azadbakht et al., 2015; Reveley et al., 2015). It is equally important to examine the accuracy of tractography-estimated connection weights given the high density of the cortical graph (Markov et al., 2014) and the fact that connection weights are fundamental to understanding cortical organization (Ercsey-Ravasz et al., 2013). A recent systematic comparison in the mouse (Calabrese et al., 2015) revealed a correlation coefficient of r = 0.46 between log-transformed, high-resolution postmortem tractography data and quantitative tracer-based connectivity data (Oh et al., 2014). In contrast, van den Heuvel et al. (2015) reported much lower correlations (r = 0.25–0.31) when comparing in vivo macaque tractography with two published tracer-based connectivity analyses. Given methodological limitations in data acquisition (e.g., coarse spatial resolution, low angular resolution diffusion scans) and analysis (e.g., a coarse cortical parcellation; see Discussion) in the latter study, this may not reflect the upper bound for tractography performance in primates.

In the present study, we used high-resolution postmortem diffusion imaging combined with complex fiber orientation modeling and probabilistic tractography to evaluate systematically tractography performance in estimating the existence and the weights of area-to-area connectivity throughout cerebral cortex in Old World monkeys. As an approximation of ground truth, we used published quantitative data generated using retrograde tracers injected into 29 cortical areas in the macaque using a 91-area atlas parcellation (Markov et al., 2014). This constitutes the most comprehensive weighted tracer-based connectivity matrix currently available for NHPs. Tractography results were generated from diffusion imaging of postmortem brains from Old World monkeys (macaque and vervet) that have very similar cortical convolutions and, likely, connectivity patterns.

Retrograde tracer interareal connection weights range over five orders of magnitude when quantified as the fraction of labeled neurons (FLNe) in each area relative to the total number of labeled neurons extrinsic to the injected area (Markov et al., 2011, 2014). We used an analogous “fractional scaling” metric for tractography based on the fraction of streamlines (FSe) connecting two areas relative to the number of streamlines extrinsic to those areas. To investigate a known tractography-path-length dependency (Basser et al., 2000; Liptrot et al., 2014), we compared two tractography seeding strategies for their impact on overall tractography performance.

Tracer-based connection weights decline approximately exponentially with interareal separation (Ercsey-Ravasz et al., 2013). Using a new tractography-based method for estimating interareal separation, we show that tractography remains modestly informative in predicting connection presence and weight after regressing out an exponential relationship with path length. These limitations of tractography likely reflect major anatomical features, such as the organization of WM bundles subjacent to sulcal fundi (Reveley et al., 2015; see Discussion).

Materials and Methods

Macaque retrograde tracer data.

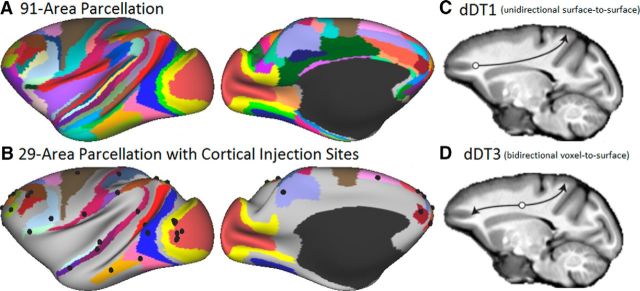
Markov et al. (2014) quantified intrahemispheric interareal connectivity in the macaque cortex using retrograde tracers and reported weighted connectivity of 29 input injection areas in an atlas of 91 cortical areas; that is, a 29 × 91 weighted and directed connectivity matrix. This 91-area parcellation, originally generated from a histologically based surface reconstruction of an individual macaque left hemisphere (M132), was registered to the macaque “F99” atlas using a landmark-constrained registration algorithm in Caret (Markov et al., 2014). We used the MSM-Sulc algorithm (Robinson et al., 2014) to register the F99 atlas to a new population average macaque Macaca mulatta atlas (“Yerkes19,” as described below). Figure 1A shows the M132 parcellation displayed on the inflated macaque Yerkes19 atlas left hemisphere. The locations of cortical area relative to gyral and sulcal landmarks on the atlas surface are similar, but not identical, to those in the original M132 surface reconstructed from histological sections. Figure 1B shows the locations of reported injection sites (Markov et al., 2014) mapped to the atlas surface.

Figure 1.

Markov et al. (2014) macaque cortical parcellation mapped to the inflated left hemisphere of the Macaque Yerkes19 atlas and diffusion tractography seeding strategies. A, The 91-area parcellation used for both retrograde tracer and tractography analyses. B, The 29 areas associated with cortical injection sites areas, with injection locations (black spheres) reported by Markov et al. (2014) projected to the cortical surface. C, dDT1, surface-to-surface tractography seeding strategy. D, dDT3, dual voxel-to-surface tractography seeding strategy. Full data are available at https://balsa.wustl.edu/RP92.

The weight of the projection from each injected area to any given source area was defined as the FLNe, the fraction of labeled neurons in a source area relative to the total number of labeled neurons extrinsic to the injected area (Markov et al., 2011, 2014). The connection weights determined by this method span five orders of magnitude and are distributed in a lognormal fashion. A 29 × 91 area connectivity matrix (“parcellated connectome”) was generated using the areal parcellation and incorporating into the data matrix the tracer connectivity values reported by Markov et al. (2014) in logarithmic (log₁₀) units. Results were represented using the Connectivity Informatics Technology Initiative data format (http://www.nitrc.org/projects/cifti/), which enables interactive visualization of connectivity maps and connectivity matrices in Connectome Workbench (http://humanconnectome.org/software/).

For the tracer injections, each injection provided information restricted to the inputs to a particular area. Therefore, a complete description of both inputs and outputs is available only for the 29 × 29 edge-complete subgraph of the larger 29 × 91 connectivity matrix. Directionality was removed by calculating the arithmetic mean of each pair of anterograde and retrograde connection weights. We refer to the 29 × 29 retrograde tracer (RT) parcellated connectivity matrix as RT_29×29, or the RT matrix for short.

dMRI data acquisition.

We analyzed dMRI scans from both the left and right hemispheres of two postmortem monkey brains (PM1 and PM2), the second of which was analyzed for two separate scans: (PM2A and PM2B). PM1 involved diffusion-weighted MRI of an immersion-fixed brain from an adult male, macaque, M. fascicularis (D'Arceuil et al., 2007). The postmortem brain was infused with a gadolinium contrast agent that enables acquisition using short TR (D'Arceuil et al., 2007). Scans were acquired using a 3D multishot, spin-echo sequence on a 4.7 T Bruker scanner with the following scan parameters: TR = 250 ms; TE = 31.7 ms; matrix size = 256 × 128 × 128; isotropic 0.43 mm voxels. Diffusion weighting was applied in 120 uniformly distributed directions with b = 8000 s/mm². Total imaging time was ∼27 h.

PM2A and PM2B were acquired from a perfusion-fixed brain of a healthy adult 32-month male vervet (Chlorocebus sabaeus) brain. The animal was obtained from the Behavioral Science Foundation, St. Kitts, and was socially housed in enriched environments. The experimental protocol was reviewed and approved by the Institutional Review Board of the Behavioral Science Foundation acting under the auspices of the Canadian Council on Animal Care. Preparation of the postmortem brain and the collection of data on a preclinical 4.7 T Agilent MR scanner (at the Danish Research Centre for Magnetic Resonance) involved the ex vivo imaging setup described previously (Dyrby et al., 2011, 2014). The scan session started with a >4 h diffusion-weighted image (DWI) dummy scan ensuring reduction of short-term instabilities introduced in the acquisition of the DWI datasets. In two separate scan sessions, the PM2A and PM2B were collected using a 2D pulsed-gradient-spin-echo sequence with single-line readout. Scan parameters for PM2A and PM2B were as follows: TR = [5100, 6500] ms; TE = [45, 35] ms; NEX = [1, 2] (averaged offline); matrix size = 128 × 256; whole brain coverage of axial slices with isotropic 0.5 mm voxels. The b-value was [4000, 7500] s/mm², 3 b = 0 s/mm² acquired in [61, 128] uniformly and noncollinear directions using the scheme files available from the Camino tool kit (Cook et al., 2006). Total imaging times for PM2A and PM2B were ∼20 and 68.5 h, respectively.

The Yerkes19 macaque atlas.

To enable accurate comparisons across results obtained in different individuals and between left and right hemispheres, tracer and MRI data were registered to a group-average “Yerkes19” macaque surface-based atlas (Van Essen et al., 2012a). This atlas was based on structural MRI scans (T1w and T2w, 0.5 mm isotropic) of 19 adult macaques acquired at Yerkes Primate Research Center at Emory. Each brain was processed using the minimal preprocessing pipelines developed for the Human Connectome Project (HCP) (Glasser et al., 2013) to extract cortical surfaces and subcortical volumes from the structural MRI scans and align individual scans to the template.

The HCP pipelines (developed for human MRI data) were adapted to work with monkey MRI. For the in vivo scans used to generate the atlas, the PreFreeSurfer pipeline aligned T1w and T2w volumes to native anterior commissure–posterior commissure space, allowing brain extraction, cross-modal registration, bias field correction, and FMRIB Software Library (FSL) analysis (Smith et al., 2004) of nonlinear volume registration to atlas space (as is done in the human HCP pipelines). Aside from using macaque volume templates, this only required adjustment of the brain size parameter to 80 mm. A customized pipeline (FreeSurferNHP) adapted from the FreeSurfer pipeline included the following NHP-specific changes: (1) brain extraction and initial intensity nonuniformity correction were done outside of FreeSurfer, in this case using the PreFreeSurfer brain extraction and $\sqrt{T1w*T2w}$ bias field correction methods, and (2) the data were converted into a “fake” 1 mm isotropic 256³ space [in “RAS” (right anterior superior) orientation] to conform to FreeSurfer's requirements without interpolation (Fischl, 2012). FreeSurfer 12 parameter affine and nonlinear registrations used a species-specific volume template, as did subcortical segmentation. The standard HCP FreeSurfer pipeline was then used up to the point of surface registration, when a species-specific surface template was used. FreeSurfer stages after pial surface generation (e.g., cortical parcellation) were not done. Finally, the volume and surface data were transformed from the FreeSurfer “fake” 1 mm RAS space back into the right posterior inferior input space (0.5 mm rigidly aligned to the macaque volume template) and cortical thickness was recomputed. The PostFreeSurfer pipeline was run using multimodal surface matching (MSM) surface registration (Robinson et al., 2014) using FreeSurfer's “sulc” measure of cortical shape to drive the alignment (MSM-Sulc). This pipeline generates a high-resolution (“164k”) surface mesh (∼164,000 vertices per hemisphere). This was resampled to form two lower resolution meshes (32k and 10k) used for subsequent analyses. Interhemispheric alignment between the left and right hemispheres was based on landmark-based alignment analogous to that performed on the macaque F99 atlas surfaces (Van Essen et al., 2012a) using 45 geographically corresponding landmark contours in each hemisphere. For the two postmortem monkeys analyzed in this study, identical steps were performed for the structural preprocessing with the exception of the creation of T1w- and T2w-like images described in the next section.

Data were mapped from individual experimental hemispheres to the Yerkes19 atlas using surface-based registration, as described below. Visualization used Connectome Workbench software (http://www.humanconnectome.org/software/connectome-workbench.html).

dMRI preprocessing.

Because the diffusion data were not echo-planar imaging (EPI) based and were from fixed tissue, many typical preprocessing steps (motion correction, eddy current correction, and b0 inhomogeneity correction) were not required. Cortical surface models were derived directly from the high-resolution (≤0.5 mm) diffusion data using steps that yielded analogs of the T1w and T2w images needed for acceptable FreeSurfer segmentation. First, FSL's bedpostX algorithm (Jbabdi et al., 2012) was run using modeling of three fibers and the anisotropic volume fractions from each fiber were summed across fibers. This produces an image that highlights anisotropic WM and avoids decreased intensity in regions containing well behaved crossing fibers. A T1w-like image having contrast similar to a conventional T1-weighted image was generated by taking the fourth root of the sum of volume fractions image. A T2w-like image having contrast similar to conventional T2-weighted was obtained from the mean of the b = 0 images. These two high-resolution T1w-like and T2w-like images were fed into the PreFreeSurfer, FreeSurferNHP, and PostFreeSurfer pipelines described above. For the high-resolution tractography analysis, the 32k mesh was used (0.8 mm average vertex spacing).

Fiber orientation modeling was performed using a model-based deconvolution approach (Jbabdi et al., 2012) to estimate up to three crossing fibers per voxel. We used the RubiX framework (Sotiropoulos et al., 2013) to further regularize these orientations. RubiX jointly estimates orientations in neighborhoods of voxels. To apply RubiX on a single resolution of data, the data were downsampled by half (e.g., from 0.5 to 1 mm) and RubiX was applied to both resolutions (i.e., the original and downsampled data). When used in this way, some soft spatial constraints are imposed directly on the parameter space and the model acts as an edge-preserving spatial filter. Pilot analyses indicated that such an approach slightly increased precision of the orientation estimates and the incidence of WM voxels modeled by three crossing fiber bundles in regions where we expected complex fiber structure. It was therefore preferred in this study to the more standard voxelwise estimation approach. Importantly, none of the results depends heavily on or changes significantly due to this spatial filtering choice.

Probabilistic tractography.

Tractography was performed in native volume space using the WM/GM boundary surface registered to the same 32k mesh used for the Yerkes19 atlas. Probabilistic tractography was performed using FSL's probtrackx (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FDT/UserGuide; Behrens et al., 2007) using a [1/4] voxel step size constrained by a 90° threshold for maximal curvature (angle difference) between successive steps choosing the fiber orientation with least angular deviation from the previous tractography step. Recent versions of the tractography toolbox (probtrackx2 in FSL version 5.0 and higher) support tracking using surfaces and volumes simultaneously (Sotiropoulos et al., 2013). As a general inclusion criterion, streamlines were counted if they intersected the surface mesh representing the WM/GM boundary at a minimum of two locations. Such intersections are indicated at the level of tiles of the surface tessellation equivalent to small planar patches parallel to the local WM/GM boundary. To avoid artifactual loops, streamlines were terminated if they crossed the pial surface, traversed subcortical GM or a ventricle, or revisited a previously traversed voxel. Tractography was conducted separately for the left and right cerebral hemispheres to reduce computational time and storage requirements and because the retrograde tracer data were available only for intrahemispheric connectivity. The resulting data included (cortical GM) × (cortical GM) “dense connectomes” (cortical GM) × (WM) × (fiber orientation) “trajectory files” (to enable visualization of fiber trajectories), and (cortical GM) × (cortical GM) “streamline average distance matrices” (to enable computation of distances between areas along the tractography streamlines). In this study, tractography-derived connectivity was computed using two seeding strategies: unidirectional surface-to-surface and bidirectional voxel-to-surface (see Fig. 1C,D), each yielding a dense diffusion tractography matrix (dDT1 and dDT3, respectively).

WM/GM surface to WM/GM surface (dDT1).

dDT1 was generated with the probtrackx algorithm by seeding from every vertex on the WM/GM boundary surface. For each vertex, random locations were generated within a sphere with a diameter equal to the voxel edge length and centered on the vertex's coordinates. The voxel containing this random location was chosen as the origin of a streamline, the initial orientation of which was drawn from the underlying fiber distribution (based on the randfib and fibst options in probtrackx). Propagation through other voxels was as described above. A streamline that crossed a second tile of the WM/GM surface was assigned to that tile's nearest surface vertex. A streamline connecting a pair of vertices, beginning and ending at the WM/GM boundary surface, was considered a candidate anatomical connection and the streamline count at both vertices was incremented. The seeding process was repeated 5000 times per seed vertex (regardless of how many streamlines were successful), yielding a connectivity matrix (“dense connectome”) of cortical GM to GM structural connectivity, in which the number of streamlines between each pair of vertices was used as a surrogate for connection weight (see below).

The strategy of seeding at vertices along the WM/GM boundary surface and stopping streamlines when they encountered the WM/GM boundary at a different location was designed to estimate long-distance corticocortical connectivity comprehensively within the WM proper, given known anatomical and tractography constraints. We did not attempt to analyze trajectories within the cortical GM, for example, to/from the specific cellular layers in which axons originate and terminate (or to a surrogate single layer such as the cortical midthickness, as was done by Reveley et al., 2015). This is because using tractography to assess trajectories within GM introduces confounds that, in our view, compound rather than ameliorate the challenges of tractography through WM. One reason is that the dominant diffusion orientation within deep layers of GM is often tangential, especially in and near sulcal fundi (in our data and also in Fig. 1D,H of Reveley et al., 2015; see also Fig. 7 in Dyrby et al., 2011); this presumably reflects a strong tangential plexus of dendritic as well as axonal arborizations in the deep layers. Accordingly, tracking streamlines through deep cortical layers will frequently lead to misalignment between streamline start/stop locations in GM and the point at which streamlines cross into WM. This contrasts with anatomical observations that axons of cortical projection neurons generally descend radially until they reach WM and input axons tend to ascend radially before arborizing in their target layers (Rockland and Virga, 1989, 1990; Coogan and Burkhalter, 1993). Another consideration is that ascending and descending axons often take sharp turns (i.e., with a radius of curvature much smaller than a dMRI voxel) in the WM near the WM/GM boundary, particularly in and near the fundus of a sulcus (Figs. 16.12, 16.13 of Van Essen et al., 2014; Figs. 4, 5 of Reveley et al., 2015). In such regions, it is very difficult for current tractography algorithms to track streamlines associated with a high radius of curvature at or near the WM/GM boundary. Instead, our approach initiates streamlines associated with a seed vertex based on the modeled fiber orientation distribution in the nearest WM voxel. When such a voxel occupies a predominantly tangential fiber plexus in superficial WM under a sulcus (Reveley et al., 2015), it is expected that many streamlines will not accurately represent actual trajectories of axons crossing the nearby WM/GM boundary. Such cases will contribute to erroneous connectivity estimates, but represent a fair test of tractography performance and limitations given current methods.

Figure 4.

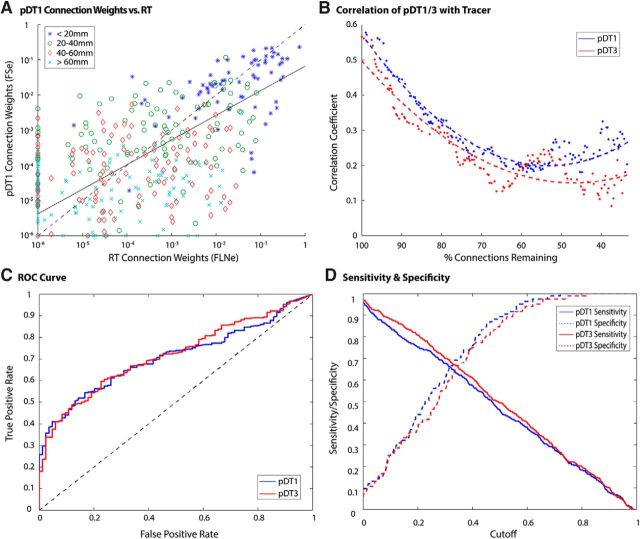
Tracer versus tractography performance comparison. A, Scatterplot of RT vs tractography (pDT1) log-scale connection weights in case PM1. Data points are depicted according to their corresponding path length bin (bin width = 20 mm; excluded path lengths > 80 mm, n = 10). The solid line denotes the least absolute residuals fit to data excluding points along either axis (false negatives: n = 13; false positives: n = 76). The dashed line (y = x) is for reference. B, Correlation between tractography and tracer connectivity weight in case PM1 for pDT1 and pDT3. Dotted lines represent second-order polynomial fits to the plotted data points. The horizontal axis depicts the number of connections remaining in tractography matrices. Only true positives were considered in this analysis. The final 10% of values were excluded due to low sample size. C, x-axis represents false positive rate (FPR); y-axis represents true positive rate (TPR). Results suggest similar performance for pDT1 and pDT3. D, Sensitivity and specificity were similar for pDT1/3. Cutoff refers to the experimental connection weight detection threshold.

Figure 5.

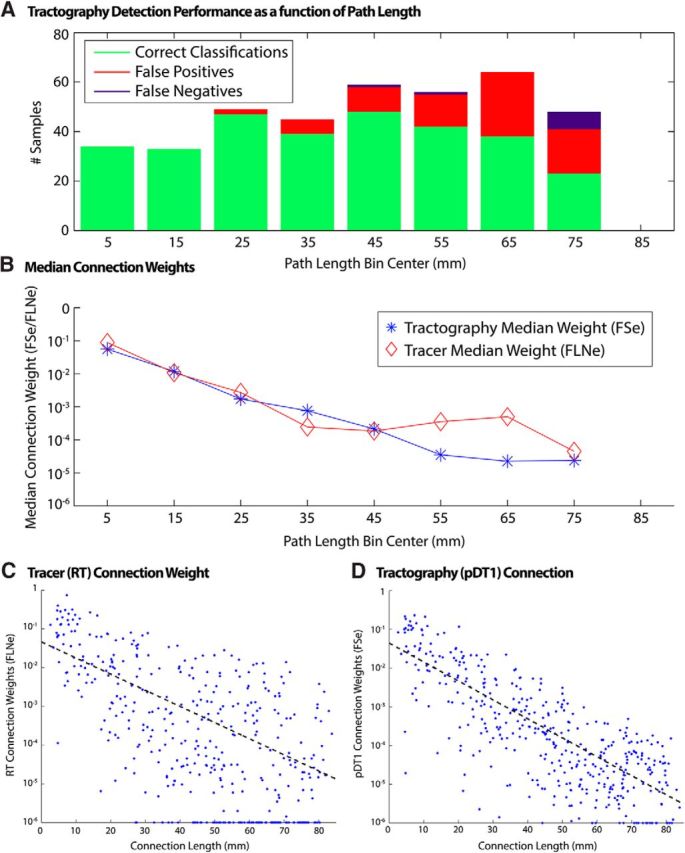
Tractography performance as a function of path length. A, Number of correct tractography detections, false positives, and false negatives (using tracer as ground truth). B, Median connection weights of correctly classified connections binned by tractography-measured connection path length. C, Tracer connection weights versus tractography-derived path length. D, Tractography connection weights versus tractography-derived path length. Solid lines correspond to least absolute residual fit to data excluding points along axes.

WM to WM/GM surface (dDT3).

dDT3 was designed to mitigate a probabilistic distance bias inherent to tractography, in which streamlines for short pathways are more likely to be identified than those for long pathways (Li et al., 2012; Liptrot et al., 2014). To reduce this bias, we initiated tractography from every WM voxel enclosed in the WM surface and seeded from fiber orientations in the seed voxel according to their anisotropic volume fraction. We tracked in both directions along the chosen seed orientation and counted connections that intersected the WM surface once in each direction. We seeded 100 times per seed voxel, reasoning that, because there are many more WM voxels than surface vertices at the WM boundary, the resulting computational time and average connection density should match that of dDT1. Our analysis should not be especially sensitive to the number of streamlines because relatively few are needed to achieve statistical sensitivity (Ambrosen et al., 2013; Liptrot et al., 2014). For each voxel, random locations were generated within a sphere with a diameter equal to the voxel edge length and centered on the voxel's center. Streamlines were seeded from these locations. This resulted in a GM-by-GM connectivity matrix in which the number of streamlines was again used as a surrogate for connection weight.

Evaluating biases in cortical connectivity.

One component of the gyral bias for tractography (see Introduction) is attributable to the geometry of cortical convolutions insofar as the wedge-like folding of cortex implies that a unit surface area of the WM/GM interface is associated with a different cortical volume and therefore predicts higher streamline density in gyral crowns and lower streamline density in sulcal fundi. This geometrically predicted bias was estimated using the ratio of cortical GM volume in a given wedge to the surface area of the WM under this wedge (Van Essen et al., 2014). The observed tractography bias was calculated by averaging streamline density across “source” vertices in dDT1/3. To compare the predicted and actual biases directly, each vertex value was divided by the mean value at zero curvature ± 0.025, thus normalizing the values of each. Values were converted to a logarithmic scale for easier comparison and visualization. Note that the appearance of the above patterns would be less easy to predict for tractography algorithms that count streamlines on the cortical surface using voxels rather than using surface tiles and vertices as performed here. This is due to the lower spatial specificity and a greater partial volume effect, as described above.

Parcellated tractography connectomes.

Dense tractography matrices were parcellated in two ways using command-line tools in the Connectome Workbench. Our primary analyses were based on an “injection-site-to-area” method, in which connectivity values were weighted in the vicinity of each of the 29 reported tracer injection sites (see Fig. 1B) using a circular Gaussian distribution on the cortical surface centered at the injection site, thereby generating an intermediate “(source-injection-zone) × (target-vertex)” connectivity matrix. The full width at half maximum used was 1.9 mm, based on the estimated spread of retrograde tracer uptake reported by Markov et al. (2011). Averaging across vertices in each parcel resulted in an injection-site-to-area 29 × 91 parcellated connectivity matrix. We also implemented an “area-to-area” method in which connectivity values were averaged across parcel vertices in each of the 91 cortical areas in the M132 parcellation to generate an intermediate “(source-area) × (target-vertex)” connectivity matrix (i.e., a 91 × 32k matrix). Identical averaging in the other direction resulted in a 91 × 91 parcellated connectivity matrix.

From both of these parcellated tractography connection matrices, the 29 × 29 area edge-complete subgraph from the tracer study was extracted, and used for all analyses comparing tractography and tracer data. We will refer to these as the pDT1_29×29 and pDT3_29×29 matrices (pDT1 and pDT3 for short), respectively.

Tractography-estimated interareal path lengths.

Tractography-based estimates of interareal pathway length were computed using probtrackx, which outputs a dense distance matrix of mean streamline length between connected vertices. This dense matrix was then parcellated using a weighted version of the “area-to-area” method described previously, in which the number of streamlines encountering each vertex was used to weight within-parcel average distances. This weighting makes the estimate a mean length of all the streamlines that reached the area, instead of being a mean of the lengths associated with each vertex within the area by emphasizing vertices having a larger number of streamlines.

Normalizing connection weights.

Comparisons between tracer and tractography data were facilitated by normalizing both measures of connection weights. As noted above, FLNe provides a quantitative and objective measure of tracer connection weights. For tractography, we estimated connection weights based on the number of streamlines between any pair of surface vertices. In particular, we implemented a method of FSe to describe connection weights in tractography-derived matrices.

Because the dDT1 connectivity matrix is by nature asymmetric, symmetry could not be assumed in computing fractionally scaled values. For this reason, it becomes important to define the index notation of connectivity values: DT_i,j denotes the number of streamlines initiated at area index i and terminated at area index j. Generally, the FSe value for a pathway originating in some area A and terminating in some area B is defined as the ratio of the number of streamlines originating at A and terminating at B to the total number of streamlines that either originate at A or terminate at B while excluding streamlines that represent self (within-area) connections. Therefore, for a connectivity matrix of N × N areas, DT, we computed the fractionally scaled value of FSe(DT) for each area pair as follows:

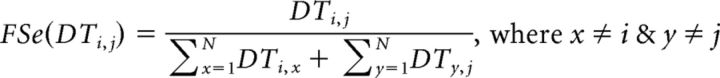In this study, fractional scaling was performed after averaging within either areas or injection site domains, thus using 91 × 91 and 29 × 91 parcellated connectome weight matrices. This makes all parcellated tractography matrices comparable to one another, as well as to the FLNe connection weight metric used to describe tracers. Within-area (area-to-self) connections were not considered in this analysis and their connection weights were set to the minimum threshold value for both tracer and tractography datasets. Symmetrization via arithmetic mean $\left(\frac{D{T}_{i,j}+D{T}_{j,i}}{2}\right)$ was performed after computing the fractionally scaled connection weights. Because connection weight values span many orders of magnitude, most analyses were performed in log-space using log₁₀ connection weights. Averaging of connection weights across hemispheres was performed for corresponding vertices of the dense connectome (dDT1/3) based on interhemispheric alignment of the Yerkes19 atlas mesh.

Correlation while excluding tractography and tracer weights.

Correlation coefficients were used to determine the degree to which pDT1/3 reflect those described by RT. The effect size η² was computed to quantify the variance shared between pDT1/3 and RT. Correlation coefficients were first computed for the full pDT1/3 and RT matrices. Subsequently, the strongest interareal connection in the tracer matrix was removed from both the tractography matrix being assessed and the RT matrix. The correlation coefficient of the resulting matrices was then computed and the process was repeated until all connections had been removed. Because the aim of this analysis was to quantify tractography's ability to characterize connection weights reliably, only nonzero weighted connections were considered (i.e., all false positives/negatives and true negatives were excluded from the analysis, effectively thresholding for connection strengths greater than zero). The impact of these false positives/negatives is described by the subsequent detection analyses.

Evaluating tractography detection performance.

The receiver operating characteristic (ROC), sensitivity and specificity were used to measure the capacity of tractography to predict the existence of a connection using tracer connection weights as an estimate of “ground truth.” Both correlation and detection performance are necessary in interpreting tractography's ability to estimate connectivity because both acceptable correlation and reliable detection are needed to consider results neurobiologically interpretable.

Relationship between tractography performance and path length.

Connections were allocated by their length into bins covering a range of 10 mm. In each bin, the median value of tracer and tractography connections was computed.

Results

Folding-related biases

Cortical folding introduces a geometric bias in which the amount of cortical GM per unit area of the WM/GM surface is elevated in a gyral crown and reduced in a sulcal fundus relative to that in a flat sulcal bank (Van Essen et al., 2014). If the number of axons entering and leaving the cortex depends on cortical volume, then there should be a gyral bias in axonal density crossing the WM/GM boundary. This in turn predicts a geometrically based gyral bias in tractography streamline density, which may be exacerbated by the observation that the dominant fiber bundles in diffusion imaging voxels within gyral blades tend to be oriented along the axis pointing toward gyral crowns (Van Essen et al., 2014). To examine this issue, we used two distinct tractography seeding methods to estimate connectivity matrices for dense (vertex-based, dDT) and for parcellated (area-based, pDT) representations. The seeding strategies (Fig. 1C,D), identified as either dDT1 (unidirectional surface-to-surface) or dDT3 (bidirectional white-matter-voxel-to-surface), yielded strikingly different patterns of overall streamline density. Figure 2 compares these patterns with that predicted by the aforementioned geometric cortical folding bias (Van Essen et al., 2014). The folding pattern for macaque postmortem 1 (PM1; Fig. 2A) predicts a geometric bias (Fig. 2B) in which the density of axonal connections should be elevated in gyral crowns and reduced in sulcal fundi relative to flat sulcal banks by a magnitude that is approximately symmetric across gyral and sulcal regions and has a range twice that of the average connection density. The relative density of observed tractography streamlines in dDT1 (Fig. 2C) shows modest regional differences that are not correlated with the folding-predicted bias (r = −0.08). In contrast, dDT3 (Fig. 2D) exhibits streamline densities that exceed the prediction in many regions (both gyral and sulcal), yet correlate with it modestly (r = 0.36). Further inspection of these biases suggest that streamlines may be particularly underrepresented in sulcal regions and somewhat overrepresented in gyral regions, consistent with observations of Reveley et al. (2015); this contrasts with the relatively unbiased distributions of retrogradely labeled neurons observed in tracer studies (Markov et al., 2011, 2014). Therefore, the overall fidelity of estimates of axonal densities using functions of the number of tractography streamlines will be affected by such biases. However, they should be ameliorated in a parcellated analysis to the degree that each cortical area spans a mixture of gyral and sulcal cortex.

Figure 2.

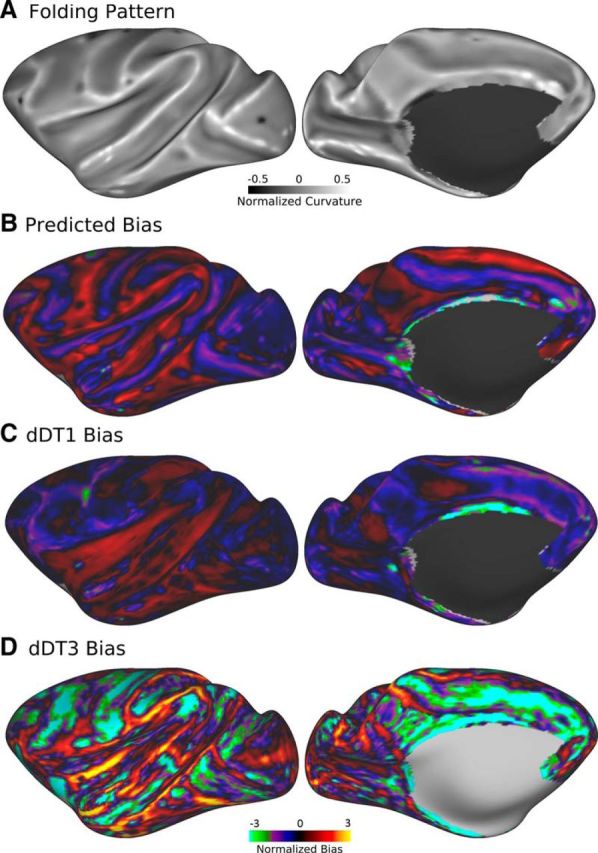
Geometry-predicted versus observed tractography streamline density biases for monkey PM1 normalized to the mean streamline density at flat regions (sulcal banks). A, Folding pattern. B, Geometric bias predicted via the ratio of cortical GM volume to WM surface area. C, D, Observed tractography bias of dDT1/3 computed via average streamline density at each surface vertex. Scale bars are in log2 units. Full data are available at https://balsa.wustl.edu/R7kj.

Parcellated connectivity analyses

The dense tractography matrices dDT1 and dDT3 were converted to initial hemisphere-specific parcellated matrices pDT1 and pDT3, respectively, using the 91-area cortical parcellation generated by Markov et al. (2014) and mapped to the Yerkes19 group average surface-based atlas. Tractography-based parcellated connectivity matrices (“parcellated connectomes”) were highly correlated between left and right hemispheres of individual brains (PM1: r = 0.86, PM2A: r = 0.92, PM2B: r = 0.93). Therefore, the tractography results reported here were averaged across hemispheres and displayed after registration to the left hemisphere of the atlas surface. Fractional scaling was then implemented to generate the final pDT1 and pDT3 connectivity matrices.

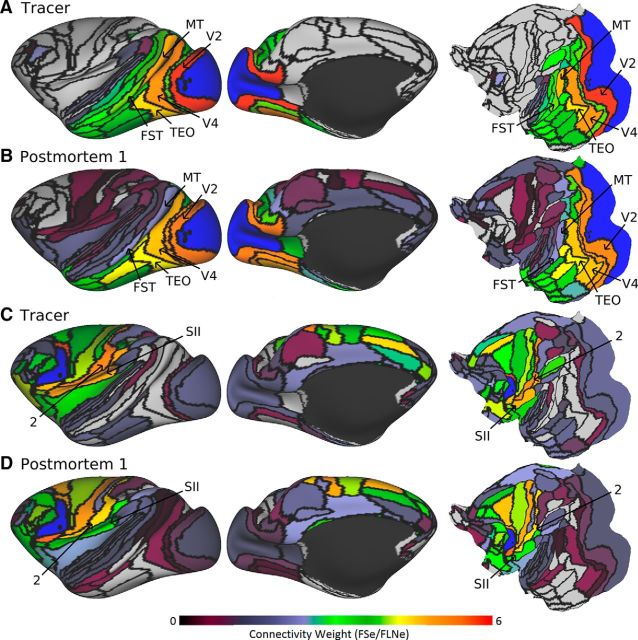
Figure 3A shows the tracer-based parcellated connectivity map (connection weights) averaged across multiple injections in foveal V1 (Markov et al., 2011, 2014), revealing notably strong connections with several extrastriate visual areas, including V2, V4, MT, and TEO. Also shown are pDT1 connectivity maps for monkey PM1 (Fig. 3B) using a seeding method restricted to the location of the tracer injection (injection-site-to-area or IS-A method; see Materials and Methods). Visual inspection suggests that tractography examples exhibit patterns similar to those produced by tracers, though with some important differences. For example, area MT is more weakly connected with V1 according to tractography than tracer. The tractography maps also show consistent false positives in medial parietal, insular, and somatomotor regions that are low to moderate in estimated weight. The false-positive medial pathways may reflect trajectories that run through the large cingulum bundle. In Figure 3C, the tracer injection in area F5 reveals connectivity with 72 cortical areas, including all areas of frontal cortex and areas 2 and SII of parietal cortex. The pDT1 map for PM1 (Fig. 3D) also shows connectivity with frontal regions and moderate connectivity with areas 2 and SII. Similar trends for both V1 and F5 connectivity were observed using pDT3.

Figure 3.

Tracer and tractography log-scale connection weights for area V1 (A, B) and F5 (C, D). Retrograde tracer connection weights were based on FLNe to each injected area from the full 91-area parcellation. Tractography brain postmortem 1 was FSe. Areas V1 and F5 are labeled in blue in A, B and C, D, respectively. Black spheres illustrate the corresponding tracer injection sites for each area. Full data are available at https://balsa.wustl.edu/R698 and https://balsa.wustl.edu/R1Xr.

Retrograde tracers identify unidirectional pathways, whereas tractography is inherently bidirectional given the physical nature of the water diffusion signal. Our primary comparisons with tractography used the symmetrized 29 × 29 subgraph of the full (29 × 91) tracer matrix. As performance metrics, we report the Pearson correlation coefficient (r) to describe linear dependences and η² to indicate the proportion of associated variance (which would differ from r² if there were a nonlinear dependence). Separate connectivity matrices were computed using tracer injection sites as seeds (IS-A) or by a whole area-to-area method (A-A). The fractionally scaled pDT1_29×29 IS-A matrices were reasonably correlated with tracer (PM1: r = 0.59, η² = 0.35; PM2A: r = 0.60, η² = 0.36 and PM2B: r = 0.55, η² = 0.31), with all subject A-A cases showing similar correlation values (same value for PM1 IS-A and A-A). The 29 × 29 IS-A matrices were highly correlated across brains and scans (PM1/2A: r = 0.89; P1/2B: r = 0.85 and PM2A/2B: r = 0.94).

In the following, we report results for PM1 parcellated using the IS-A method. PM1 was chosen to minimize species differences (tracer and PM1 were both macaques; PM2 was a vervet); the IS-A method was used to better emulate the focal nature of the tracer injections. PM2A and PM2B, scanned with b values of 4000 and 8000 s/mm², respectively, provide additional insight into how differences in scan parameters may affect tractography performance (see Supplemental Materials).

Compared with absolute streamline densities, fractional scaling and symmetrization improved tractography's correlations both with tracer (from r = 0.48 to r = 0.59 and from η² = 0.23 to η² = 0.35) and between pDT1 and pDT3 in the same animal (correlation between the 91 × 91 pDT1 and pDT3 matrices (log values, fractionally scaled) yielded r = 0.95, 0.96, 0.97 for PM1/2a/2b, respectively). Figure 4A illustrates fractionally scaled PM1 connection weights plotted against tracer, with data points labeled according to their tractography-based interareal path length. For high values of FLNe (tracer), the tractography weights (FSe) are slightly below the diagonal, indicating that tractography tends to underestimate connection weights by a modest amount for the most strongly connected pathways, which are generally fairly short (<20 mm). For moderately and weakly connected anatomical pathways, the degree of correlation is less evident visually.

Another measure of tractography's performance examined correlations while progressively removing connections from strongest to weakest as reported by tracer. We analyzed only true positives (connections detected by both tractography and tracer; n = 309) to avoid penalizing tractography for binary detection mistakes; that is, excluding false positives (n = 76), false negatives (n = 13), and true negatives (n = 8). As shown in Figure 4B, the correlation with tracer for both pDT1 and pDT3 becomes weaker as progressively more high-weight connections are excluded; therefore, pDT1 correlation was halved (r = 0.28) when the strongest 25% of connections had been removed. However, modest correlation remains even for weak connections (after the strongest half of connections had been removed, pDT1: r > 0.2 and pDT3: r > 0.1).

To assess tractography's ability to detect connections in a purely binary fashion, we performed a ROC analysis on the same data (Fig. 4C). This analysis produces a metric, the area under the curve (AUC), that quantifies the classifier's accuracy (1 signifies perfect prediction of tracer; 0.5 signifies no better than chance). The AUC was 0.71 for pDT1 and 0.72 for pDT3, suggesting that tractography is a fair but far from perfect predictor of connection presence. Sensitivity and specificity (Fig. 4D) also exhibit similar performance for pDT1 and pDT3. At a cutoff threshold of zero, sensitivity is almost unity (all but a few percent of tracer-based pathways are detected by unthresholded tractography), but specificity is about 0.1 (tractography correctly predicted only ∼10% of true negatives). The intersection of the sensitivity and specificity curves occurs at 0.65 for pDT1 and 0.67 for pDT3 (a value of 1 being a perfect test). The associated cutoff value (6.5E-5 FSe for pDT1 and 1.1E-4 FSe for pDT3) offers a balanced compromise between maximizing true positives and minimizing false positives for this particular analysis. When thresholding from weakest to progressively stronger connections, the correlation coefficient remains relatively flat and is above r = 0.5 at the threshold noted here.

Relationship between tractography accuracy and interareal path length

We estimated interareal path lengths based on the streamline trajectories generated by probabilistic tractography (see Materials and Methods). These estimates are likely more accurate than the piecewise-linear trajectories within WM used previously to estimate interareal distances (Ercsey-Ravasz et al., 2013) because observed anatomical trajectories can be curved or irregular (Schmahmann and Pandya, 2009; Jbabdi et al., 2013) as they navigate around subcortical nuclei (e.g., basal ganglia, thalamus). The pDT1/3-derived path lengths were highly correlated with those reported by the tracer study (r = 0.84; η² = 0.71).

Correct classifications, false positives, and false negatives were sorted by path length (Fig. 5A, 10 mm bins). False positives and false negatives were absent for path lengths <20 mm and their incidence increased with longer path lengths. Nevertheless, tractography performed reasonably well in identifying long connections (up to 60–70 mm). Median values were determined for both tracer and tractography within each bin (Fig. 5B) and showed that tractography correlated well with median tracer values at path lengths <50 mm, but their values diverged at longer path lengths. It is unsurprising that tractography is a stronger predictor of connection classification and characterization for shorter paths, but this analysis provides additional objective measures of performance as a function of connection path length.

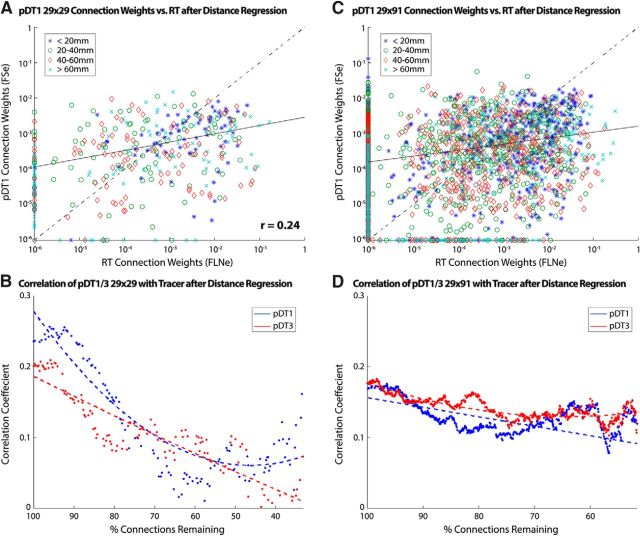
The relationship between a connection's logarithmic weight and its path length shows a quasilinear decline for both tracers (Fig. 5C) and tractography (Fig. 5D). This confirms a previously reported (Ercsey-Ravasz et al., 2013) exponential distance relationship for tracers and extends it to tractography, in both cases using the aforementioned tractography-derived path lengths as opposed to linear piecewise path length estimates computed in the tracer study (Markov et al., 2014). We used the slope (S) of this line along with path length (PL) to regress the relationship out of the data as follows: G_DR = G + S * PL. The result (Fig. 6A) shows that the correlation between tractography and replace is markedly reduced (r = 0.22, η² = 0.05).

Figure 6.

Comparison of tracer versus tractography log-scale connection weights with reduced path length dependency. A, Tracer and tractography log-scale connection weights after regression of estimated exponential relationship. Data points are depicted according to their corresponding path length bin (bin width = 20 mm; excluded path lengths >80 mm, 2.5% of all connections). The solid line denotes the LAR fit to data excluding points along either. The dashed line (y = x) is for reference. B, Correlation between tractography and tracer connectivity weight in case PM1 for pDT1 and pDT3 after regression of estimated exponential relationship. Dotted lines represent second-order polynomial fits to the plotted data points. Data inclusion is as described in Figure 3. C, D, Analyses from A and B applied to full 29 × 91 connectivity dataset. The increase in false negatives (n = 128) and false positives (n = 788) were proportional to sample size. The correlation between tracer and tractography connection weight was r = 0.43.

We applied our previous correlation analysis that involved progressive removal of connections strongest to weakest (Fig. 4B) after regressing out the estimated exponential path length relationship (Fig. 6B). This reduced the correlation over the whole range of remaining connections relative to that shown in Figure 4B, but, interestingly, the correlation remains positive even for weak connections (right half of plot). We then expanded the analysis from the 29 × 29 connectivity matrix to the full 29 × 91 tracer and tractography matrices (Fig. 6C,D). Inclusion of these additional samples (unidirectional for tracer; bidirectional for tractography) made the correlation curve less noisy and also strikingly flatter. Therefore, inclusion of unidirectional pathways degraded correlations for stronger pathways (left half of plot), but strengthened the correlations when a much larger number of weaker connections remain (right half). These observations suggest that tractography is modestly informative about anatomical connection weights over a wide range of connection weights and path lengths beyond what can be surmised simply from their exponential relationship with distance.

Discussion

By comparing tractography-created cortical connectomes systematically with published parcellated connectome data derived from neuroanatomical tracers, we have shown that current state-of-the-art tractography performs much better than chance, yet far from perfectly, in detecting neuroanatomical pathways and estimating weights corresponding to their connection strength. Our analysis benefitted from a fractional scaling normalization scheme to assess the correlation between connection weight metrics reported by these two modalities. We confirmed an exponential relationship between connection weight and interareal path length and showed that tractography remains modestly predictive after regressing out this relationship.

Of the two tractography seeding strategies used, the unidirectional surface-to-surface method, producing dDT1, had a slight performance advantage over the bidirectional voxel-to-surface (dDT3) method. Relative to a geometrically predicted streamline bias, dDT1 showed a bias similar in magnitude, but different in spatial pattern, whereas bias from dDT3 exceeded the predicted bias, especially in sulcal regions. When tracking out from the WM (dDT3), streamline density tends to be lower in sulci and higher in gyri (Van Essen et al., 2014). Our findings suggest that a strong negative sulcal bias predominates over a weaker positive gyral one. This is likely related to dense WM fiber bundles parallel to the WM/GM boundary (Reveley et al., 2015), which (1) impede tractography detection of weaker crossing fiber bundles entering/exiting GM in sulcal fundi and (2) include streamlines that run within these superficial WM bundles but fail to track accurately the relatively sparse fraction of axons within these bundles that branch or turn sharply to enter/exit the overlying GM.

We found that tractography became less correlated with tracer as strong connections were removed progressively. Importantly, each weak interareal pathway involves far fewer neurons and axons than each strong pathway. Therefore, in aggregate, weaker pathways account for a small fraction of overall connectivity at the level of cells and axons, though weak and strong pathways both contributed to our reported correlation coefficients.

Investigating tractography's ability to classify connection existence using a ROC analysis revealed performance that can be considered “fair” or “moderate” insofar as the AUC was 0.71 in the case of pDT1. In our data, the intersection of sensitivity and specificity curves corresponded to a plausible tractography threshold FSe of 6.5E-5 for pDT1 (1.1E-4 for pDT3). Although specific to this study, this threshold offers a starting point when considering possible thresholds for other datasets, including humans and other species in which connectivity “ground truth” is completely lacking.

The observed trend between connection weight and path length in both tracer and tractography is consistent with previous observations of a “noisy” exponential relationship (Ercsey-Ravasz et al., 2013). Regressing out this relationship indicates that, whereas path length is a major factor in estimating connection weights, tractography has useful explanatory power that transcends predictions based purely on connection path length. Algorithmic refinements that better model anatomically observed path length dependency may enhance tractography's utility in characterizing long-distance pathways (Liptrot et al., 2014).

The quality of postmortem dMRI imaging data used here surpasses typical spatial and angular resolutions used in conventional in vivo dMRI, though recent advances such as multiband acceleration (Feinberg et al., 2010; Setsompop et al., 2012) can reduce this gap (Sotiropoulos et al., 2013). A previous analysis of different fiber orientation modeling methods (Thomas et al., 2014) found that the original ball and stick model (Behrens et al., 2007) effectively balanced sensitivity and specificity when identifying connections and was robust to changes in angular threshold. We used an improved ball and stick model that accounts for non-mono-exponential decay (Jbabdi et al., 2012), enabling estimation of up to three crossing fibers per voxel. By making these datasets freely available, other investigators will be able to compare and contrast the performance of alternative fiber orientation and tractography models.

A recent study (van den Heuvel et al., 2015) reported low correlations (r = 0.26–0.31) between macaque in vivo tractography and two macaque tracer datasets, the CoCoMac database and the Markov et al. (2014) dataset analyzed in the present study. We attribute our twofold higher correlation (0.59) to differences in analysis methods as well as data acquisition. For dMRI acquisition, we used higher spatial resolution (0.43–0.5 vs 1.1 mm isotropic voxels), angular resolution (120 vs 60 diffusion directions), b values (8000 vs 1000 s/mm), and scan durations. Higher spatial and angular resolution may improve the fidelity of tractography modestly (Sotiropoulos et al., 2013; Thomas et al., 2014; Jbabdi et al., 2015; Wu and Zhang, 2016). Potentially important analysis differences include our finer-grained parcellation (the 91-area Markov parcellation vs their 39 area “WBB47” parcellation). van den Heuvel et al. (2015) attempted to reduce effects associated with tractography false positives by thresholding based on reproducibility of connections (>60% of the 10 monkeys scanned), but the resulting tractography connectivity matrix was notably sparse (their Fig. 1B). We instead performed separate analyses for correlating connectivity strength (using the full connectivity matrix) and ROC analysis to describe the effects of false positives and negatives. Finally, despite their low reported correlation coefficients (accounting for <10% of observed variance), they interpret their results more optimistically than we consider warranted for even our own data by stating that “in vivo DWI connectome reconstructions” “represent fairly realistic estimates of the wiring strength of WM projections” and this is a “valid methodology for robust description and interpretation of brain wiring” (van den Heuvel et al., 2015).

Although our approach aimed to compare tractography with tracers fairly, we also note limitations in the representation of “ground truth” using retrograde tracers. First, repeated tracer injections into the same portion of the same area vary approximately one order of magnitude around the group mean (Markov et al., 2011), presumably reflecting a combination of genuine individual variability in connection weight, statistical fluctuations, and methodological limitations. Second, most identified connections are reciprocal but exhibit weight asymmetry (0.2 log units on average). The incidence of nonreciprocal pathways reported (Markov et al., 2014) exceeds that from an older meta-analysis (Felleman and Van Essen, 1991), but is comparable to recent studies in the mouse (Oh et al., 2014; Zingg et al., 2014), suggesting commonality of interareal pathway asymmetry. Third, we used a 91-area parcellation (Markov et al., 2014) based mainly on architectonic boundaries in a single atlas hemisphere. Methodological factors limit the fidelity with which the M132 histology-based atlas parcellation was mapped to the individual hemispheres used for tracer injections and to the Yerkes19 atlas. Fourth, retrogradely labeled neuronal counts reflect only one aspect of connection weights. Anterograde tracers provide complementary information relating to axonal terminations, but results are harder to quantify accurately. Finally, there is substantial internal heterogeneity in the connectivity of a given area, especially those organized topographically (Markov et al., 2014). Because each retrograde tracer injection was restricted to one locus, observed profiles of connection weights may inadequately represent the area as a whole. For tractography, this can be addressed by applying our “injection-site-to-area” method to additional sites.

Our observations are relevant to human in vivo diffusion imaging studies, including the high-resolution dMRI data from the HCP (Sotiropoulos et al., 2013; Vu et al., 2015), but diverse differences make such comparisons challenging. Human neocortex is ∼10-fold larger than that of the macaque (Van Essen et al., 2012a, 2012b) and WM occupies a larger fraction of human brain volume. However, dMRI voxel sizes are larger (1.05 mm/1.25 mm for the HCP and conventionally 2 mm vs 0.43–0.5 mm in the present study), so the number of voxels spanning a gyral WM blade may be approximately comparable. Postmortem monkey scans were longer (>60 h non-EPI, nonaccelerated postmortem acquisitions vs 1 h for HCP and typically less for human in vivo using EPI, often accelerated) and used higher b values, compensating for reduced diffusivity ex vivo compared with in vivo (D'Arceuil et al., 2007). Given these anatomical and methodological differences, the correlation between tractography-based connectivity and a hypothetical “ground truth” connectivity in humans might in principle be either higher or lower than what we reported here for monkeys. Our evidence that monkey tractography connection weight estimates are accurate to within one or two orders of magnitude relative to tracer-based ground truth suggest that quantitative studies in humans may be limited to an approximately comparable degree using high-quality data such as that from the HCP and perhaps even more for many widely used protocols.

In summary, when using tracers as ground truth, diffusion tractography in postmortem NHPs is a fair detector of cortical interareal connections and a reasonably reliable predictor of weight for strong connections, but less so for longer pathways. Connectivity assessments may benefit from algorithmic refinements (e.g., fiber fanning models; Sotiropoulos et al., 2012). Tractography may also benefit robustly from anatomically informed priors using rules that depend on anatomical location in relation to identifiable landmarks or local features such as proximity to cortical GM. The quantitative findings (as well as freely shared data) reported here, whereas not directly translatable, may nonetheless aid in analyzing and interpreting human tractography data.

Notes

Supplemental material for this article is available via the BALSA database at https://balsa.wustl.edu/study/show/W336. Key anatomical and connectivity datasets associated with this study are provided (Van Essen et al., 2016). This material has not been peer reviewed.