Prediction of Growth Factor Dependent Cleft Formation During Branching Morphogenesis Using A Dynamic Graph-Based Growth Model

Abstract

This study considers the problem of describing and predicting cleft formation during the early stages of branching morphogenesis in mouse submandibular salivary glands (SMG) under the influence of varied concentrations of epidermal growth factors (EGF). Given a time-lapse video of a growing SMG, first we build a descriptive model that captures the underlying biological process and quantifies the ground truth. Tissue-scale (global) and morphological features related to regions of interest (local features) are used to characterize the biological ground truth. Second, we devise a predictive growth model that simulates EGF-modulated branching morphogenesis using a dynamic graph algorithm, which is driven by biological parameters such as EGF concentration, mitosis rate, and cleft progression rate. Given the initial configuration of the SMG, the evolution of the dynamic graph predicts the cleft formation, while maintaining the local structural characteristics of the SMG. We determined that higher EGF concentrations cause the formation of higher number of buds and comparatively shallow cleft depths. Third, we compared the prediction accuracy of our model to the Glazier-Graner-Hogeweg (GGH) model, an on-lattice Monte-Carlo simulation model, under a specific energy function parameter set that allows new rounds of de novo cleft formation. The results demonstrate that the dynamic graph model yields comparable simulations of gland growth to that of the GGH model with a significantly lower computational complexity. Fourth, we enhanced this model to predict the SMG morphology for an EGF concentration without the assistance of a ground truth time-lapse biological video data; this is a substantial benefit of our model over other similar models that are guided and terminated by information regarding the final SMG morphology. Hence, our model is suitable for testing the impact of different biological parameters involved with the process of branching morphogenesis in silico, while reducing the requirement of in vivo experiments.

1 Introduction

Branching morphogenesis is a developmentally conserved process occurring in many organs, including the lungs, pancreas, kidneys, salivary and mammary glands [1], [2]. Branching morphogenesis is a temporally regulated highly dynamic, multiscale process involving mRNA modifications, protein signaling pathways and reciprocal interactions between epithelial and mesenchymal cell types; leading to tissue level structural changes affecting organogenesis [2]. Although the branching structures in developing organs have been studied in detail, we are still far from comprehending the integrated process.

Since the early developmental processes in branching morphogenesis in several branched organs are conserved, we used mouse embryonic submandibular salivary gland (SMG) in our investigations [3]. The ability to produce saliva is important in maintaining oral health, and continued efforts are being targeted to identify methods to restore functionality or design artificial salivary glands. Computational modeling of the developing organ can not only add to the basic knowledge of developmental mechanisms but can also facilitate organ engineering efforts. Embryonic SMG organ explants have long been used as a biological model system to study pattern formation during the process of branching morphogenesis [3], [4]. The embryonic SMG explants undergo branching morphogenesis when grown on filters at the air/media interface in serum-free medium in a way that reproduces the branching pattern that occurs in vivo [5].

The SMG initiates as a thickening of the primitive oral cavity epithelium on embryonic day 11 (E11). At E12 the protrusion of the primitive oral epithelium into the surrounding condensed mesenchyme forms a single cellularized epithelial primary bud on an epithelial stalk, as shown in Fig. 1. By E12.5 clefts, or invaginations of the basement membrane begin to form on the epithelial surface of this initial bud, as seen in Fig. 1(a). These clefts are stabilized before they begin to progress deeper into the gland and separate the initial bud into multiple secondary buds, as shown in Fig. 1(b). Epithelial proliferation occurs during cleft progression aiding in tissue growth [5]. Clefts eventually stop progressing further into the tissue and begin to widen at their base during cleft termination, as seen in the left-most cleft in Fig. 1(c), and ultimately transition into newly forming ducts. The gland undergoes multiple rounds of cleft and bud formation, and duct elongation throughout development and, as a result, a progressively complex and highly arborized structure is formed. Detectable epithelial cellular differentiation starts by E15; thereafter creating functional ductal structures to transport saliva and secretory acinar units capable of saliva secretion.

Fig. 1.

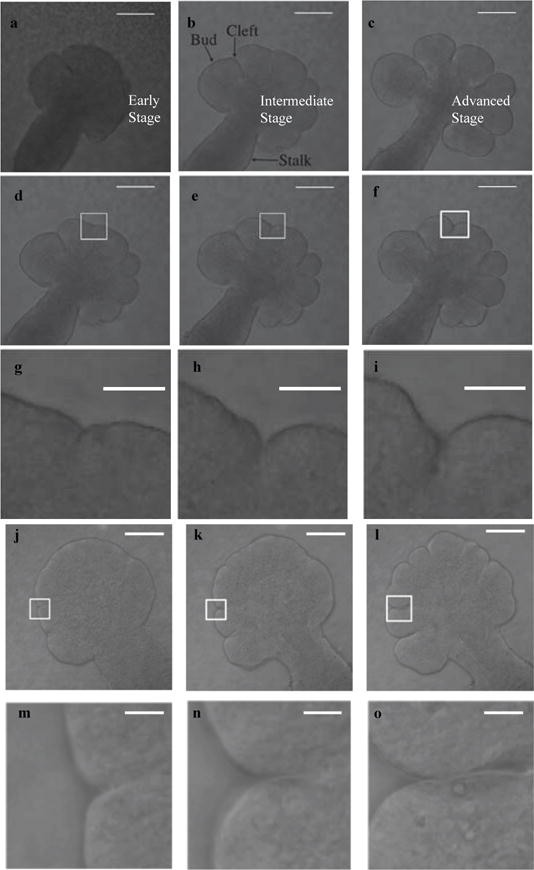
Three stages in cleft formation during early branching morphogenesis between embryonic days E12 and E13. Selected frames from the time-lapse confocal microscopy image sets demonstrate progressively deeper clefts and bud outgrowth. In (a), multiple nascent clefts are visible on a single large bud, which deepen in (b), and begin to form buds. By image (c), some clefts have terminated, and the gland has at least partially separated into distinct buds. Scale, 100 μm. Figures (d)–(o) show the progression of individual clefts in two data sets, with the upper rows ((d)–(f) and (j)–(l) Scale, 100 μm) displaying the entire gland and a white rectangle around the particular cleft, and the lower rows ((g)–(i) and (m)–(o) Scale, 50 μm) displaying the zoomed in version of this rectangle.

Branching of the salivary gland epithelial tissue is known to be dependent upon growth factors and exogenous basement membrane [6]–[8]. Epidermal growth factor (EGF) is one such growth factor, which is known to be involved in the morphogenesis and fetal development of several organs, including the lungs [9], kidney [10], mammary gland [11], and pancreas [12]. The role of several growth factors in SMG branching morphogenesis, including EGF, was previously investigated using mesenchyme-free epithelial rudiments cultured in a basement membrane extract in the presence of exogenously added growth factors [13]–[15]. Addition of EGF induced cleft formation and development of a highly lobed structure with little ductal elongation. The Epidermal Growth Factor Receptors (EGFR) family displays receptor tyrosine kinase activity and ligand binding induces several downstream signaling cascades that modulate EGFR activity affecting global growth patterns in a tissue [16]–[19]. EGF is known to activate several developmental processes including growth, survival, migration, and cell-fate determination [20]; however, the exact mechanism by which EGF regulates cleft formation has not yet been investigated.

Conventional cellular and molecular biological techniques are limited in their ability to explain complex biological phenomenon, and thus computational approaches have been introduced as a means to model branching morphogenesis [21]. Computational modeling of morphogenesis dates back to the mid 20th century with important mathematical models that advanced our understanding of fundamental properties of clusters of cells [22], [23]. These theories were followed by biochemical and mechanochemical models [24] that led to the use of continuum mechanics which considered a tissue to be composed of cells and extracellular matrix (ECM) and described the stress forces between the cells and the ECM [25]–[27]. Such models have also been used for modeling of epithelial morphogenesis in 3D breast culture acini [28], and lung [29]–[31] and kidney branching morphogenesis [32]. Each of these models was tailored to the particular biological process in question to account for the structurally different final branching patterns in these organs, even though mechanistic pathways are conserved across several branching organs.

The continuum mechanics models laid the foundation for utilizing computational approaches to model complex biological processes; however, they often made oversimplified assumptions regarding small deformations at the tissue-scale. Also, solutions for continuum mechanical problems have higher computational complexity, and require knowledge of the strength of bonds between cell types or the knowledge of various force fields, which are not known. Although recent studies have considered the tissue to behave as a viscous liquid under the assumption that the epithelium and mesenchyme are immiscible Stokes fluids; these models also fell short in reproducing actual salivary gland cleft shapes [33]–[35]. To overcome the shortcomings in these earlier modeling techniques and to better replicate the complicated dynamics governing biological processes, stochastic models were constructed based on Monte-Carlo (MC) methods. MC-based approaches can provide approximate solutions to complex, sometimes intractable mathematical problems when a large percentage of the possible configurations of the system have high energies and thus have a low probability of being attained [36]. The Glazier-Graner-Hogeweg model, an on-lattice MC model, was used to determine cellular parameters regulating cleft progression during branching morphogenesis in the epithelial tissue of an early embryonic SMG [37]. The disadvantages of on-lattice MC-based approaches include a time-consuming sampling step to reach desired solution, potential negative effects of lattice discretization, and the use of variance-reduction techniques [38].

Over the past 20 years, graph theoretical models [39] have become significantly important in analyzing large-scale networks with complex interactions between multiple participating entities. Biological networks have also commonly benefitted from the advent of network analysis tools and techniques [40] that have been used to model protein-protein interactions [41]–[45], metabolic networks [46]–[49], genetic and transcriptional regulatory networks [50], [51], disease progression [52], [53], and neuronal connectivity [54]. We previously developed a graph theoretical model called cell-graphs to study the structure of cellular networks [55]–[58]. A cell-graph is an unweighted and undirected graph where the topological organization of the cells within tissues is characterized by graph theoretic features. The graph vertices (nodes) represent the cellular nuclei within the tissue and graph edges (links) capture cell-to-cell interactions. Cell-graphs enable quantification of the spatial uniformity, connectedness, and compactness at multiple scales. Conventionally, graph models have been used to depict structural properties of tissues at fixed time-points enabling characterization and quantification of the spatial evolution of tissue shape and integrity, without explicitly addressing the temporal component.

1.0.1 Our Contributions

In this study, we utilize a novel approach towards quantifying the spatio-temporal evolution of tissue shape and growth pattern using a graph-based growth model. We utilized time-lapse confocal images of SMG grown for 12 hours under the influence of varying concentrations of EGF and constant concentration of Fibroblast Growth Factor 7 (FGF7). FGF7 is critical to the processes of mitosis and cell differentiation. The primary contributions of this study are as follows:

• Descriptive model: We extracted morphometric parameters from multiple time-lapse confocal images of mesenchyme-free epithelial rudiments. A dynamic graph-based growth model was constructed that simulated the first round of branching morphogenesis with elongation of existing clefts, tissue proliferation and de novo cleft formation. From this graph model, novel local cleft and bud-based features such as median cleft depth and median bud perimeter percentage, and global morphological features such as area and perimeter of the growing epithelial tissue, were analyzed for each concentration of EGF. We show that the dynamic graph-based growth model successfully characterized the developmental stages of the SMG growth pattern and simulated temporal changes of structural properties of the tissue.

• Predictive growth model: Given only the initial configuration of an SMG organ explant, the dynamic graph model predicts the time-evolving development of the SMG between E12 and E13 as a function of initial gland morphology, EGF concentration, and mitosis and cleft progression rates. Varying concentrations of EGF was used to adjust rates of epithelial proliferation in the model [59]–[61] that accounted for global tissue growth.

• Interpolation-driven prediction modeling: We enhanced the dynamic graph-based growth model to predict the time-evolving morphology and expected configuration of an SMG organ explant without (i) time-lapse data obtained from biological experiments, and (ii) apriori knowledge to determine the halting configuration, or cleft termination. Our approach is based on building a linear regression model of cleft deepening dependent on the perimeter of the adjoining buds and the EGF concentration; this dependency allows us to better modulate the growth of the gland. This approach is novel since it automatically calculates the target configuration to determine the halting condition. We present simulation results that demonstrate significant qualitative agreement between the target configuration predicted by our linear regression model and the biological insight.

We also show that while the dynamic graph model is nondeterministic, multiple executions of the model successfully produce the same number of clefts that vary in their individual depths and locations across the epithelial periphery. This observed variance in cleft depths and locations in the the dynamic graph model closely mimics the high degree of variability in cleft depths and place of initiation found in the ex vivo grown samples. This realistic modeling by the dynamic graph model is because it is driven by EGF concentration, and mitosis and cleft progression rates, and does not enforce assumptions regarding bonds between cell types; also leads to reduced computational complexity.

1.0.2 Organization of the paper

The rest of the paper is organized into four primary sections. Following this introduction (Section 1), Section 2 describes the biological data sets used for our experiments, preliminary image processing techniques applied on these biological data sets, algorithms for detection and development of clefts, and extraction of features including global morphological features, and local region of interest features. Section 3 describes the descriptive model based on dynamic graphs, the feature-based clustering of the biological data sets, comparison of the predictive growth model with a Monte-Carlo based on-lattice model, and the augmented prediction model based on dynamic graphs. Section 4 summarizes the findings of the study and alludes to potential future directions.

2 Materials and Methods

2.1 Data Acquisition: Ex Vivo submandibular salivary gland epithelial organ cultures

Timed-pregnant female mice (strain CD-1, Charles River Laboratories) at E12, with day of plug discovery designated as E0, were used to obtain SMG rudiments following protocols approved by the National Institute of Dental and Craniofacial Research IACUUC committee, as reported previously [13]. E12 SMGs that contain a single primary epithelial bud were microdissected, the mesenchyme was removed and the epithelial rudiments were cultured in presence of 100ng/ml FGF7, as described previously [13]. For three of the glands, the media was also supplemented with 20 ng/mL epidermal growth factor (EGF), while for the other three 1 ng/mL EGF (R&D Systems) was used. Images were collected as described in the next section A.1. Henceforth, we will refer to the image sets as EGF-20a, EGF-20b and EGF-20c (20 ng/mL EGF), and EGF-1a, EGF-1b and EGF-1c (1 ng/mL EGF). Description of the other data acquisition techniques can be found in the Appendix sections A.1 and A.2.

2.2 Quantification of ground truth: Image Processing and Segmentation

The first step in characterizing the SMG morphology consists of segmenting the SMG regions in the FN (via ImageJ) and GFP (manual segmentation due to noisy images) time-lapse data sets. The FN images were segmented via Otsu’s technique [62] by calculating an optimal threshold to separate the tissue (foreground) from the Matrigel medium (background). Biologists visually inspected this manual segmentation to ensure that it correctly captured the morphology. To obtain nuclear information regarding cell distribution and cell morphologies, we referred to the ex vivo data set (in Section 2.1).

2.3 Quantification of ground truth: Detection of cleft regions

The first important step in characterizing the SMG morphology is the detection of clefts as they form and deepen. The SMG is comprised of alternating buds and clefts, where clefts are narrow valley-shaped indentations that form in the basement membrane. Figures 1(d)–(o) illustrate the progression stages of typical clefts from shallow nascent clefts to narrow and deep progressive clefts in the EGF-1a and EGF-20a data sets. We characterize the cleft region using cleft center defined as the deepest point of the cleft, with the walls of the cleft extending on either side of the surface normal at the cleft center, and the corresponding left and right extrema points that determine the extent of the cleft; the buds are considered to be starting beyond the points marked as cleft extrema. The cleft center and cleft extrema are illustrated in Fig 2(a). Automated detection of these key points is carried out as follows:

1. We identify local extrema of the gradient along the SMG boundary by detecting angular variations greater than 35° at regular intervals of 14 successive (x,y) coordinate points measured via Euclidean distance on a rectangular Cartesian grid. This interval constituted by 14 successive boundary points was found to be optimal based on the successful identification of inflection points along the boundary. Angular thresholds lower than 35° identified multiple outliers. The extrema thus identified correspond to potential cleft centers or peaks of boundary irregularities.

2. These peaks are eliminated using the signed area of the triangle formed by the candidate point, t, and two of its immediate 8-connected neighbors, t−1 and t+1, along the boundary ordered in clock-wise direction. This is obtained as $\left(\begin{array}{ccc}{x}_{t-1}& y_{t-1}& 1\\ x_t& y_t& 1\\ x_{t+1}& y_{t+1}& 1\end{array}\right)$,where (x_t, y_t), (x_t−1, y_t−1), x_t+1 y_t+1 1 and (x_t+1, y_t+1) represent the horizontal and vertical coordinates of the candidate point and its previous and next neighbors along the boundary, respectively. This expression is positive for clefts and negative for peaks.

3. After the peaks are eliminated, we identify the cleft extrema points using the mean-squared error (MSE) between the best-fit line and SMG boundary points on either side of the potential cleft centers. As points from the curved buds are included in the best-fit line, a higher MSE is obtained in comparison to the steeper cleft walls. The algorithm progresses from the cleft center incrementally adding points on either side of the cleft center to the cleft region. When the MSE exceeds a threshold the boundary point is labeled as a cleft extrema. We set a dynamic threshold for the MSE that is computed as a function of depth of the cleft from the closest convex hull vertices obtained after fitting a convex hull around the SMG. For every cleft center detected by the algorithm, we identify the vertices lying on the convex hull to its immediate left and right. The depth is then calculated as the perpendicular distance from the cleft center to the mid-point of the line segment joining these closest vertices identified on the convex hull. We implement cleft tracking as part of the algorithm to track the progress of the cleft.

4. As a final filtering step to eliminate boundary irregularities or nascent clefts, we exploit the cleft depth and spanning angle as illustrated for a sample cleft in Fig. 2(a). Cleft depth is described as the shortest Euclidean distance from the cleft center to the line segment joining the two-extrema points, and the spanning angle is the angle formed by the two line segments joining the extrema points to the cleft center. Indentations that had a depth of less than 9μm and spanning angle greater than 150° were not considered since our analysis of time-lapse data indicated that such regions were boundary irregularities that might not form a stable cleft. These thresholds were decided based on discussions with biologists and measurements from empirical data. Figures 2(b)–(e) show original images from four data sets with detected clefts highlighted in green and their cleft centers marked in red (or maroon as in Fig. 2(c)).

Fig. 2.

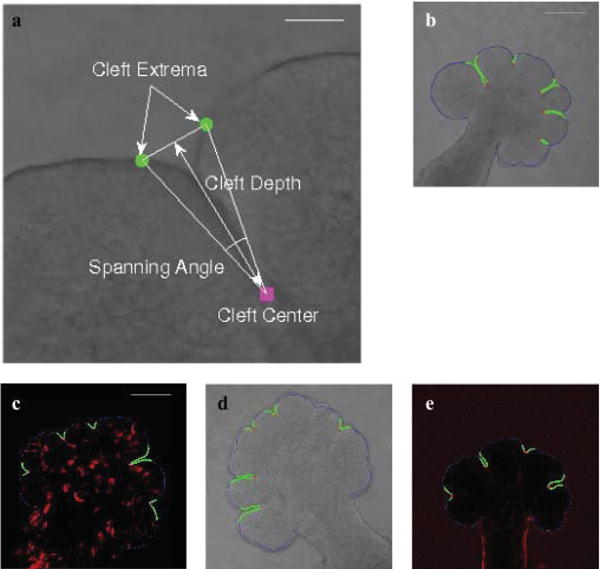
Characterization of clefts and sample results of the cleft detection algorithm. The figure shows cleft extrema (marked in green) and cleft center (marked in maroon) points that characterize the cleft in (a) (Scale, 50 μm). Spanning angle and cleft depth are calculated from these points as illustrated. In (b)–(e) (Scale, 100 μm), results of applying the cleft detection algorithm to four different data sets is shown. The cleft regions are highlighted in the DIC microscopy ((b) and (d)), GFP-labeled (c), and FN-labeled (e) images. The cleft centers are highlighted in red (or maroon in (c)) and the cleft regions are marked in green.

2.4 Quantification of ground truth: Extraction of global SMG morphological features

The morphology of the SMG undergoes quantifiable transformations as a consequence of creating the ramified structure. We capture these transformations by extracting seven morphological features, namely area, perimeter, eccentricity, elliptical variance, convexity, solidity, and box-count dimension. We label this data matrix of morphological features as $\mathbb{D}$. When referring to a feature matrix in subsequent text, we allude to the data matrix $\mathbb{D}\in {\mathbb{R}}^{M\times 7}$, consisting of the values of the seven morphological features over M time-steps. Appendix Table A1 lists the definitions of the various morphological features.

2.5 Quantification of ground truth: Extraction of novel local cleft and bud features

Early branching morphogenesis is characterized primarily by bud outgrowth and cleft deepening. Early clefts tend to get deeper and narrower with time, with the end result being that the initial buds are split into multiple secondary buds. We ascertained novel local cleft and bud-based features to analyze the effects of cleft deepening on early branching morphogenesis. Using QR factorization with column pivoting, we sorted these features in accordance with their ability to capture the variance within the data [63]. This factorization is performed when the feature matrix, A, is not of full rank. QR factorization with column pivoting is given as A = QRP^T, where Q is an orthogonal matrix, R is an upper triangular matrix, and P is a permutation matrix chosen such that the diagonal elements of R are non-increasing |r₁₁| ≥ |r₂₂| … ≥ |r_nn|. The selection of features (columns) from A is based on finding the feature with the maximum Euclidean norm, and successively finding the features maximally orthogonal to the subspace spanned by the previously such determined features. The sequence of selection of features is stored in P. Other algorithms including singular value decomposition (SVD) may also be used for feature selection (please refer http://featureselection.asu.edu/for other feature selection techniques). The lower computational cost of QR factorization as compared to SVD was the reason we chose it as the feature selection algorithm.

2.6 Modeling cleft progression as a function of EGF concentration and adjacent bud perimeters

We observed that although EGF stimulates branching, higher EGF concentrations produced quantitatively shallower clefts as compared to lower EGF concentrations. We thus determined that cleft depth is a function of the EGF concentration levels. We also found that cleft depth is a function of the perimeter of the adjacent buds. Larger adjacent buds allow the cleft to progress much deeper into the tissue, and higher EGF concentration levels create more buds but shallower clefts. Appendix Table A2 lists correlation coefficients, represented by ρ, between cleft depth and adjacent bud perimeters for three of the data sets. In all we identified 524 cleft segments, where a cleft segment is defined only for the sequence of images where its adjacent buds do not split. We collected information regarding cleft depth and adjacent bud perimeters from all the data sets to formulate cleft progression as a linear regression model with equations of the form c = BA + E, where c ∈ ℝ^524×1 is a vector of depths attained by the cleft before one of its adjacent bud splits creating a new cleft, B ∈ ℝ^524×3 is the matrix of adjacent bud perimeters (with a column of 1s for the intercept), A ∈ ℝ^3×1 is the vector of equation coefficients, and E ∈ ℝ^524×1 is the vector of errors. For our simulations, to determine the depth a cleft can achieve, we first calculate distances to every cleft in the database by comparing the adjacent bud perimeters in Euclidean space. We then apply two levels of weights to these Euclidean distances, one weight for the EGF concentration, and the other weight for each cleft in the database. For the EGF concentration, we calculate the absolute difference of the EGF concentration from 1 ng/mL and 20 ng/mL (our two sample EGF concentrations), calculate the inverse of these differences and normalize the inverse differences by dividing by their sum. We call these weights W1. We repeat this procedure for the distances of the bud perimeters adjacent to the cleft under investigation to the corresponding bud perimeters for each cleft in the database: calculate the inverse of the distances and normalize by dividing the inverse distances by their sum. We call these weights W2. We split the equation coefficients (B) into two groups for the two sample EGF concentrations, and weight the coefficients corresponding to each cleft in either group by the appropriate weight in W2. We then take the product of these new coefficients with W1 and sum the cleft depth values estimated by the two EGF concentrations. This gives us the final interpolated cleft depth. The simulated cleft is then assigned this cleft depth, which is updated when there is further splitting of its adjacent buds, or it exceeds the ascribed depth. We decrease the rate of growth of the cleft for higher EGF concentrations, and vice versa for lower EGF concentrations. This allows us to create shallow clefts for higher EGF concentrations, and deeper clefts for lower EGF concentrations.

2.7 Predictive dynamic graph growth model: Construction of a biologically data driven dynamic graph-based growth model of epithelial branching

This section details one of the most important contributions of this study – the development of a dynamic graph model to describe the first round of cleft formation and progression in SMG branching morphogenesis. The dynamic graph-based growth model advances our prior work on a graph-theoretical model called cell-graphs, which was used for histopathological image analysis [64], tissue modeling [55], and characterization of the response of E13 salivary glands to 24 hours of inhibition of the Rho kinase (ROCK) signaling pathway [56], [58]. A cell-graph G = (V, E) consists of a set of vertices V representing cell nuclei, and a set of edges E representing cell to cell interactions. An edge is present in the graph where the distance between two cell nuclei is less than a predetermined threshold. The model takes the initial gland morphology, nuclei locations, and EGF concentration as input. The initial image in each time-lapse image set was used for gland morphology. The EGF concentration levels determine the mitosis and cleft deepening rates. We assume cells to be circular in shape, and cell size is approximated by the diameter. We start with a uniform grid-graph where V is the intersection of the grid lines, and the grid lines themselves constitute E. The grid is continuously distorted on every iteration of the algorithm.

The outline of the dynamic graph-based growth model is given in Fig 3. The steps involved in the algorithm are listed below:

Fig. 3.

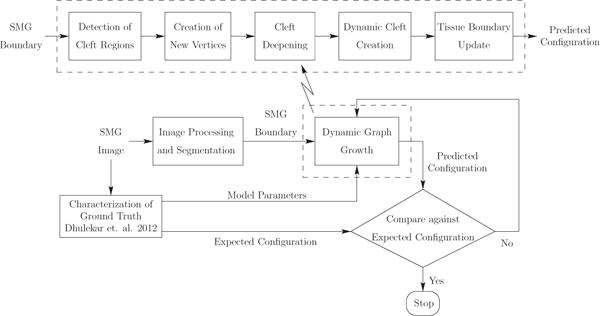
Overview of dynamic graph-based growth model. We start with acquisition of the biological data that gives us the SMG images. We then quantify the biological data by identifying clefts and computing global tissue-scale morphological features and local features. We run our dynamic graph-based growth model with the model parameters computed from the biological data as shown in the figure. Termination is based on reaching the optimal iteration that minimizes the distance to the target configuration.

1. Detection of cleft regions: The first step of the model involves identifying clefts. Please refer to Section 2.3 for details regarding the methodology of detecting clefts.

2. Creation of new vertices: Each iteration of the growth algorithm divides the cells into two populations based on the distance from the gland boundary, namely internal (I) and periphery (P). Subsets I′⊂ I and P′ ⊂ P are chosen to undergo a proliferation attempt. Cells in P′ that successfully undergo mitosis create new cells (or vertices) V′ that are added to V. For I′, we compute the shortest distance to the boundary of the gland (not including the cleft region) and find the cell in P closest to that boundary point; new cells $\widehat{V}$ thus created are added to V. New edges, E′ and $\widehat{E}$ for periphery and internal cells respectively, are also constructed based on the distances from the new cells to existing cells in G.

   $$\begin{array}{r}\forall I\prime \subset I:\mathit{\text{mitosis}}\left(I\prime \right)=\widehat{V}\text{then}\widehat{V}\in V,\widehat{E}\in E\\ \forall P\prime \subset P:\mathit{\text{mitosis}}\left(P\prime \right)=\widehat{V}\text{then}V\prime \in V,E\prime \in E\end{array}$$

   We measured average mitosis rates for EGF-1 and EGF-20 concentration levels as 4 cells/minute and 6 cells/minute, respectively. Additional assumptions that build upon the Eden model [23] were imposed to model mitosis. These assumptions included cells with identical topology and growth permitted only at the gland boundary where a hypothesized “nutrient medium” provided by the mesenchyme is accessible. In our dynamic graph-based growth model, this similarity is enforced via the local structural properties of cell-graphs that maintain consistency in the topology of the SMG throughout the development stages. When first created, potential daughter vertices are placed outside the initial gland boundary in a region within 20° of the surface normal from the parent vertex at a minimum distance of one cell diameter, but less than the specified maximum edge length. Five possible candidate daughter vertices satisfying these spatial and angular constraints are chosen, and the daughter vertex with the closest local cell-graph features to the parent vertex is selected as the optimal daughter vertex. These local structural features (refer to Appendix C) assess the spatial uniformity (clustering coefficient), connectedness (degree, closeness centrality, betweenness centrality), and compactness (edge length statistics) of the cell-graph. We distribute the extension distances to the neighbors of the parent vertex to model bud outgrowth in a local region and prevent spikes in the gland boundary. Figures 4(a–c) show a sample illustration of the configuration with creation of new vertices at different magnification levels. Supplementary Movie V1 shows mitosis events occurring over 3 hours (movie can be downloaded here: http://dsrc.rpi.edu/cellgraph/SMG_modeling/Supplementary_Video_V1.mp4). As described above, mitosis events are only allowed to occur on the SMG boundary; this was done primarily to reduce computational overload involving bookkeeping tasks.
3. Cleft deepening: To create dynamic clefts and to deepen existing clefts, we delete edges to vertices that would now lie in the cleft region (C).

   $$\begin{array}{r}\forall E\left(V_i,V_j\right):V_i\in C,V_j\in C\text{then}\\ E\left(V_i,V_j\right)\notin G,V_i\notin V,V_j\notin V\end{array}$$

   This edge deletion effectively isolates these vertices from the rest of the graph. All edges that have vertices lying on opposite sides of a cleft, i.e. edges go across the cleft, are also deleted. Figure 5 illustrates the cleft deepening algorithm. Once a cleft deepens, the cleft centers (marked in red) are removed from the cell-graph – the edges from these vertices to all other vertices are deleted. The deleted vertices are marked in brown in the second panel. Cleft progression is based on the linear regression model described previously in. The cleft deepening rate is modulated by the EGF concentration. For lower EGF concentrations, we use a higher cleft deepening rate, thereby producing deeper clefts, and we use a lower cleft deepening rate for higher EGF concentrations to produce shallower clefts. For a sample cleft we list the observed and estimated cleft depth values in Table 1, based on the growth coefficients computed earlier. We can see that the linear regression model estimates the cleft depth better for deeper clefts than for shallow clefts. We found that the coefficient of determination, R², was 0.9873, confirming our hypothesis that the cleft depths can be computed as a function of the adjacent bud perimeters. Restricting mitosis in the clefts as well as progressively increasing cleft depth causes the cleft to narrow and to deepen, both characteristics of progressive cleft formation.

4. Dynamic cleft creation: We first determined the smallest possible perimeter at which a bud splits, and the percent increase in the perimeter of buds before they split. These values were also found to be dependent on the EGF concentration. Since higher EGF concentrations stimulate branching morphogenesis and create more buds, we use progressively smaller increases in bud perimeter under increased EGF concentration levels. The position of the split is determined probabilistically. We select coordinate points along the boundary that lie in the vicinity of the center of the bud, and we randomly choose a point from this list as the cleft center for the dynamic cleft. We isolate the vertices that lie in the newly created cleft region from the rest of the graph by deleting edges incident to these vertices. All edges that go across the cleft are also deleted.

5. Maintaining boundary smoothness: We use the spatial orientation of vertices to create a smoother gland boundary. The smoothness algorithm is based on the hypothesis that if daughter vertices are aligned similarly to the parent vertices, then smoothness will be maintained when the daughter vertices are integrated into the boundary. This is accomplished by minimizing the quantity $|{\varphi }_i^{\prime }-{\varphi }_i|$, where ϕ_i is the angle ∠p_i−1p_ip_i+1, and ${\varphi }_i^{\prime }$ is the angle $\angle p_{i-1}{p}_i^{\prime }{p}_{i+1}$, as shown in Fig. 4(d). The previous and next vertices p_i−1 and p_i+1, respectively, are fixed, and the position of the daughter vertex $p_i^{\prime }$ is varied along the line segment $p_i{p}_i^{\prime }$. This process is repeated from the second till the (n − 1)th daughter vertex, keeping the first and nth daughter vertices fixed.

6. Updating the gland boundary: An interpolating cubic spline curve is used to insert the daughter vertices into the existing gland boundary. If the distance between the current and next daughter vertices is greater than a predetermined threshold, we connect the current daughter vertex to the +3 neighbor of the parent vertex along the SMG boundary.

7. Compare against expected target configuration: The simulation is run for 100 iterations, after which the optimal terminating iteration is selected via post-processing by determining the iteration number that minimizes the weighted Euclidean distance to the target configuration. From our analysis, we found that about 6 hours of experimental data translates to running 100 iterations of the model. We compute the morphological feature vectors for all the iterations, and project this data matrix into the reduced space (x_j) by post-multiplying by the right singular vectors of the particular ground truth data set. We then compare this projected feature matrix to the projected feature vector corresponding to the target configuration of the corresponding ground truth data set (y_j) using a weighted Euclidean distance given as:

   $$d_{xy}=\sqrt{{\displaystyle \sum _{j=1}^N{w}_j{\left(x_j-y_j\right)}^2}}$$

   Weights are computed as the square of the positive singular values of the projected ground truth data set divided by the sum of the squares of all positive singular values. We look for the global minima in the distance d_xy values and select this optimal iteration as the terminal configuration for our simulation. Table 2 lists biological processes and properties, and the corresponding mechanisms to handle them in the dynamic graph-based growth model.

Fig. 4.

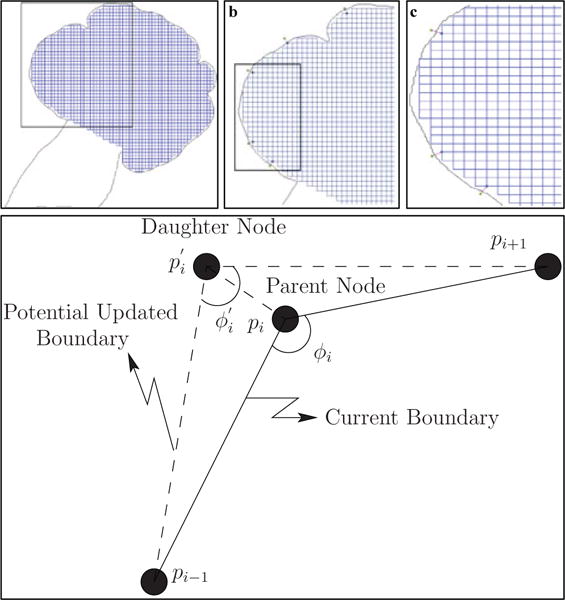
Creation of new vertices and maintaining boundary smoothness. The configuration of the cell-graph (initially a grid-graph where vertices are found at the intersection of the grid lines, and the grid lines are the edges of the graph) after a single iteration of creation of new vertices (step 2 of the dynamic graph-based growth algorithm) is shown in (a). The black rectangle in (a) represents the closer snapshot of the sub-graph viewed in (b). A further black rectangle in (b) represents a smaller sub-graph shown in (c). The spatial positions of parent vertices in the current boundary are used to identify the optimal location for daughter vertices, as shown in (d). The uniformity in the grid-graph is distorted with every iteration of the dynamic graph-based growth algorithm.

Fig. 5.

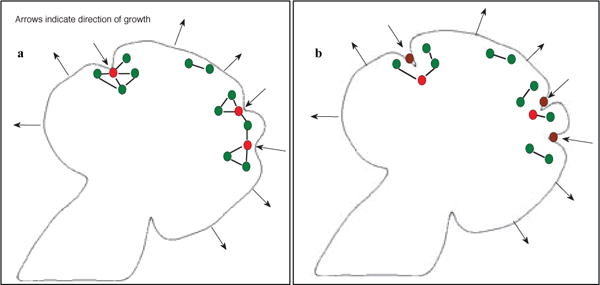
Illustration of the algorithm driving cleft deepening and dynamic cleft creation. The two panels show the initial (in a) and final (in b) conditions of the SMG before and after cleft deepening. In (a), vertices that are designated as cleft centers are marked in red. All other vertices are marked in green. After cleft deepening, all cleft centers lie in the cleft region (these original cleft centers are marked in brown) and are replaced by new vertices. The edges from these original cleft centers to other vertices are deleted. This effectively isolates these vertices from the graph. Supplementary Movie V1 shows mitosis events occurring over 3 hours.

TABLE 1.

Observed Cleft Depth Values as Calculated by the Cleft Detection Algorithm vs. the Cleft Depth Values Predicted by the Linear Regression Model. Cleft Depth is reported in μm.

Observed Cleft Depth	Estimated Cleft Depth from Linear Regression Model
17.475	20.296
15.878	21.514
21.808	20.333
22.097	21.935
22.443	21.603
22.550	21.597
22.903	20.931
22.505	20.919
22.654	21.626
22.229	22.732
22.094	22.218

TABLE 2.

Biological Processes and Properties, and their Corresponding Interpretations in the Dynamic Graph-Based Growth Model, and the State-of-art Monte-Carlo-Based-Simulation Model Used for Comparison.

Biology	Dynamic Graph Model	GGH Model
Gland Structure	Graph Geometry	Effective Energy
Mitosis Rate	New Vertex Creation Rate	Mitosis
Cell-cell Adhesion	Maximum Link Length	Contact Energy
Cell Volume	Cell Diameter, or Minimum Link Length	Cell Area
Cell Surface Area	Not Included	Cell Perimeter
Cleft Deepening	Edge Deletion	Manual Specification

3 Results

We present three different types of results in this section. First, we validate the accuracy of our representation of the ground truth. Next, we compare the prediction accuracy of the dynamic graph-based growth model with a Monte-Carlo-based simulation model. Finally, we present results for the interpolation-driven prediction modeling.

3.1 Time-Series Analysis of SMG structural features

Based on the features described in the Sections 2.4 and 2.5, we present in this section the growth trends of the respective features for two of the ground truth data sets. Figure A2 displays the trends for the global and local SMG morphological features for the EGF-1a and EGF-20b data sets. There are 29 images in the EGF-1a data set stretching over a period of about 3 hours. There are 47 images in the EGF-20b data set stretching over a period of about 8 hours. Area and perimeter (Appendix Figures A2(a) and (b)) display an increasing trend over time as the SMG matures. Eccentricity (Appendix Fig. A2(c)) is a measure of the circularity of the ellipse fitted to the SMG that has the same second-moments as the SMG, and quantifies the elongation of the SMG. Eccentricity increases as the SMG becomes more elongated with growth. The drop in eccentricity values for the EGF-20b data set can be attributed to the drop in perimeter values for the same range. Elliptical variance (Appendix Fig. A2(d)) displays an increasing trend as the clefts deepen since the error of fitting an ellipse to the SMG with deeper clefts would be higher than a SMG with shallow clefts. Convexity (Appendix Fig. A2(e)) displays a decreasing trend over the time-lapse images. As the clefts progress, the perimeter of the SMG increases, but there is only a minor increase in the perimeter of the convex hull. The perimeter of the convex hull is dependent on bud outgrowth, and this is a much slower process as compared to cleft progression [5]. Solidity (Appendix Fig. A2(f)) decreases over time since deepening of the clefts reduces the rate of growth of the SMG as compared to its convex hull. The box-count dimension (Appendix Fig. A2(g)) is a measure of a shape’s space-filling capacity. Cleft deepening is expected to increase the box-count dimension. Although the rates of change of the features differ for the EGF-1 and EGF-20 data sets, all the global morphological features follow similar trends, i.e. either the features increase for both data sets or the features decrease for both data sets.

From the feature analysis, we identified median cleft depth and median bud perimeter percentage as the most important local features. We considered median cleft depth since some clefts progress towards termination faster than other nascent clefts. Median bud perimeter percentage is the median of the percentage of the SMG perimeter belonging to individual buds. Appendix Fig. A2(h) shows the trend in median cleft depth. An increasing trend is seen for this feature since the clefts deepen with time. Sudden dips in the trends indicate formation of nascent clefts. The deeper clefts that are characteristic of EGF-1 data sets are the reason a higher slope is observed in the graph for EGF-1a as compared to the slope for the EGF-20b graph. Median bud perimeter percentage drops over time as more buds are created that are smaller in perimeter than the original buds.

3.2 Validation of the morphological features

To verify whether the set of global morphological and local features described in the previous section was sufficient to capture the tissue-scale and local changes in the SMG, we attempted to cluster the EGF-1 and EGF-20 biological data sets (ground truth). The hypothesis being that the two EGF concentrations give rise to different morphological changes, and thus would cluster separately. As an illustration, consider the area of the SMG. It is known that the mitosis rate is dependent on EGF concentration [60]. A higher EGF concentration increases mitosis rate as compared to a lower mitosis rate for lower EGF concentration. This in turn implies that the area values for the target configuration of the EGF-1 data sets will differ from the area values for the target configuration of the EGF-20 data sets.

We ran QR factorization with column pivoting to determine the importance of each of the nine morphological features, seven global and two local region of interest features (see Section 2.5). We ran the factorization for each of the six data sets and found that no feature was consistently ranked with the least important score indicating that we needed to consider all nine features for our analysis. We ran k-means clustering [65] in the full nine-dimensional space, with k equals to 2, to separate the sets into two classes as shown in Fig. 6 with the three EGF-1 data sets listed first, followed by the three EGF-20 data sets. All the data sets are ordered chronologically within themselves from the first frame in the set to the last frame in that set. The EGF-1 data sets are either completely contained in cluster C2, or transition fairly early from cluster C1 to cluster C2 as they develop deeper clefts and larger buds. The EGF-20 data sets are either completely contained in cluster C1 or transition comparatively late from cluster C1 to cluster C2 exhibiting behavior similar to advanced EGF-1 data sets. The majority presence of the EGF-1 data sets in cluster C2 supports our claim that this cluster signifies larger but fewer buds and deeper clefts, whereas the majority presence of EGF-20 data sets in cluster C1 verifies that this cluster is characteristic of smaller but more buds and shallower clefts. Thus, we verify that our features were able to represent the morphological changes that occur in the SMG during branching morphogenesis. An interesting observation that was revealed via this analysis was that although increased EGF concentration stimulates branching morphogenesis by creating more buds, the clefts are shallower than when compared to lower EGF concentrations. Table 3 shows multiple clustering measures including recall and precision, F-score, and entropy to validate that the clustering is able to sufficiently distinguish the two data sets [66].

Fig. 6.

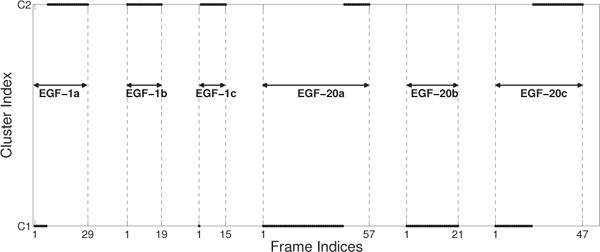
k-means clustering of EGF-1 and EGF-20 data sets based on morphological features. The markers represent the frames that belong to each data set. The EGF-1 data sets are listed first, followed by the EGF-20 data sets. All the data sets are ordered chronologically from the first image in the set to the last image in that set, where the frame indices for the initial and final image are indicated in the abscissa. We utilize the k-means clustering algorithm with k = 2 clusters. It is observed that cluster C1 is characteristic of smaller buds and shallows clefts, whereas cluster C2 is characteristic of larger buds and deeper clefts. The majority of EGF-1 data sets are present in cluster C2 indicating that this cluster represents larger but fewer buds with deep clefts. The majority of EGF-20 data sets are present in cluster C1 indicating that this cluster represents smaller but multiple buds with shallow clefts. Although, increased EGF stimulates branching morphogenesis by creating more buds, clefts are shallow in comparison to lower EGF concentrations.

TABLE 3.

Purity Measures for Evaluating the Effectiveness of Clustering

Cluster Numbers		Purity Measures
	Recall/Purity	Precision	F-score	Entropy
Cluster C1	0.87	0.57	0.69	0.98
Cluster C2	0.69	0.92	0.79	0.41

3.3 Performance Evaluation of the Predictive Growth Model on the basis of the Accuracy of Predicted SMG Morphology

To understand the efficacy of the predictive growth model, we compare it with a Monte-Carlo-based simulation model that works on the principle of energy minimization of the combined effective energy function (constructed as a Hamiltonian expression).

3.3.1 A Brief Overview of the GGH model

The Glazier-Graner-Hogeweg (GGH) model [67], [68] is built upon the energy minimization-based Ising model [69], using imposed fluctuations via a Monte Carlo (MC) approach. Previously, we performed an in-depth investigation where we constructed a local GGH-based model of epithelial cleft formation and analyzed the ranges of the cellular parameters [37]. In this study, we utilized similar values for each of the parameters in the simulation of cleft formation occurring on a tissue scale. Please refer to Appendix B for further details about implementation of the GGH model. The authors would also like to mention that they discussed the initial development of the specific GGH model parameter set with members of the Glazier Lab at Indiana University.

We compared the ability of the dynamic graph-based growth model to simulate EGF-stimulated cleft formation to that of the GGH model. To make a fair comparison between the dynamic graph-based growth model and the GGH model, we included the dynamic cleft creation module, described in the Section 2.7 to our implementation of the GGH model. This ability of the GGH model to generate de novo clefts is an improvement on our earlier work [37], [70].

3.3.2 Evaluation of the predictive growth model

The morphological feature-based comparison of the dynamic graph-based growth model with a quantitative analysis of the biological data set (ground truth) and the GGH model under the specific parameter set described above (and in Appendix B and [37]) for organ explants grown in the presence of low or high levels of EGF (EGF-1a and EGF-20b datasets, respectively) is shown in Fig. 7 and Appendix Fig. A3. For the sake of brevity and page restrictions, only the area feature for both EGF concentrations is shown in the figure. Please refer to Appendix Figs. A3 and A4 for further feature comparisons. Although, both models are constructed by very different modeling techniques, one is a graph-based model whereas the other minimizes a Hamiltonian formulation, our comparison is solely based on the final shape of the epithelial tissue produced by them. No comparison is done based on the outputs of the models in their original form. The ground truth trends are displayed in green, the dynamic graph-based-growth-model’s trends are displayed in red, and the GGH model’s trends are displayed in blue. As observed in the ground truth, an increase in area and perimeter is seen in both models. The dynamic graph-based growth model is able to replicate the increase in area and perimeter more effectively than GGH, and usually remains faithful to the increasing trend. Eccentricity increases for the ground truth as the gland becomes more elongated. This is a trend that the dynamic graph model is also able to replicate, whereas GGH fails to reproduce the appropriate trend. The GGH models inability to properly reproduce the eccentricity trend could be attributed to the fact that it tries to acquire a circular structure because of the anisotropic growth of the model. Both models are able to model the trends in median cleft depth that are observed in the ground truth, although GGH performs better in a few cases since it can exactly specify the number of clefts, location of the clefts, and the depth of each cleft. The sudden drops in the value of the median cleft depth in the ground truth as well as the models signify creation of new clefts.

Fig. 7.

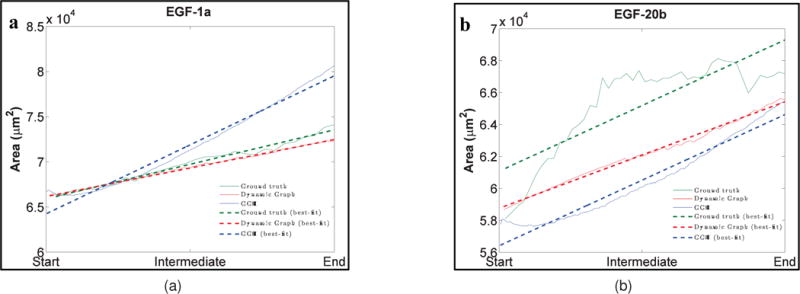
Comparison of SMG morphological features between ground truth (green), dynamic graph-based growth model (red), and the GGH simulation (blue) for EGF-1a and EGF-20b data sets. The features are area (a) and (b), perimeter (c) and (d), eccentricity (e) and (f), and median cleft depth (g) and (h). “Start” refers to cleft initiation, “Intermediate” refers to mid cleft progression stage, and “End” refers to beginning of cleft termination. Area and perimeter display increasing trends and similar trends are also seen for the dynamic graph model as well as the GGH simulation. GGH shows the opposite trend for eccentricity as it tries to create circular shapes. Increasing median cleft depth trends are shown by both dynamic graph model and the GGH simulation. For more detailed explanation of the feature trends, please refer to Section 3.3.

Although the range of values of elliptical variance is fairly small (10⁻²), both models show an increasing trend for this feature. Convexity drops as the rate of increase of perimeter of the SMG increases at a faster rate than the perimeter of its convex hull. In keeping with the ground truth, both models show the appropriate decreasing trend. Solidity decreases with deepening of the clefts. While the dynamic graph-based growth model reproduces the appropriate trend, since the GGH model tends to grow the gland more circular, solidity is also affected by this trait of the GGH model. Also, the clefts generated by GGH are in constant flux, appearing and disappearing from one MCS step to the next, and this may also be causing the solidity patterns to be modeled incorrectly. In general, the dynamic graph model has a higher box-count dimension than the GGH model. This could be because it tends to create more clefts than the GGH model, thereby creating more area of concavity. These plots illustrate that the dynamic graph-based growth model is able to predict the growth of the clefts during early branching morphogenesis. Figure 8 displays target ground truth configuration, and sample terminal configurations for both models for the EGF-1a and EGF-20b data sets. As can be noticed from the terminal configurations, the dynamic graph-based growth model is able to produce de novo clefts and the final configuration is comparable to that produced by the GGH model.

Fig. 8.

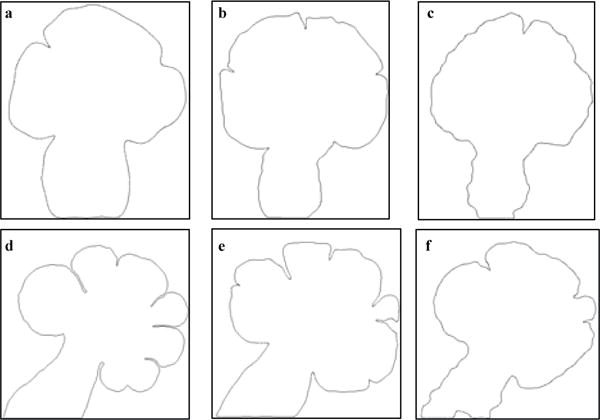
Target configuration of the ground truth data sets, and the final configurations reached by the simulations for the dynamic graph-based growth model and the GGH simulation. The target ground truth configuration is shown in (a) and (d), the dynamic graph model’s configurations are shown in (b) and (e), and the GGH model’s configurations are shown in (c) and (f). Dynamic graph-based growth model creates more clefts than the GGH model and this is one of the primary reasons that it has better quantitative agreement with the ground truth in regards to the morphological features.

3.3.3 Computational Complexity Comparison

We analyzed the time complexity of both approaches to illustrate the savings in time afforded by the dynamic graph model. The dynamic graph model has worst case time complexity of $\mathcal{O}\left(n^2\right)$, whereas the GGH model has worst case time complexity of $\mathcal{O}\left(n^3\right)$, omitting the constants that come from convergence criteria (or number of iterations). This is unsurprising given that the GGH model calculates an energy function between each pair of cells, and considers increased cellular-level detail thereby further increasing its complexity.

As an illustration, we compared the simulation times for both models. We ran 50 experiments on a 2.4 GHz Intel Core 2 Duo processor with 4GB RAM. The dynamic graph model was on average 10.24 times faster than the GGH model, taking an average of 4.83 min ± 1.41 sec to complete the experiment, whereas GGH took 49.47 min ± 34.21 sec.

3.4 Interpolation-driven prediction modeling: Prediction of growth factor dependent branching morphogenesis

For the majority of comparisons to biological data, both the time-lapse data set and the expected target configurations are available in advance. Our objective was to enhance our dynamic graph growth model such that when presented with an initial SMG boundary image and EGF concentration, the model could predict gland morphologies without the aid of a time-lapse data set, and thus no information regarding the target configuration.

We start by artificially creating ground truth morphological feature vectors from the initial SMG boundary image and EGF concentration, using as a first attempt, linear growth equations under the assumption that all features are uncorrelated. We computed two sets of average linear regression models for all features for EGF-1 and EGF-20 concentrations, given in Appendix Table A3. The linear growth rates follow the expected behavior as explained in Section 3.1. For any intermediate EGF concentration, we interpolate between these two sets of models, and apply a normalized inverse distance function for the EGF concentration as a weighting factor (similar to the function defined in 2.3). With these individual feature growth equations, we determine the values the features would attain after a certain time interval. For our experiments, we consider time intervals of 3, 4.5, and 6 hours. Since the GGH model requires apriori knowledge of expected target configurations (i.e. final cleft depth) it was not possible to make such predictions with this model.

Using the formula mentioned earlier in Section 2.2, we calculated average mitosis rates (MR) for EGF-1 and EGF-20 concentrations as 4 cells/minute and 6 cells/minute, respectively. Mitosis rates for intermediate EGF concentrations were predicted by interpolating between these two mitosis rates, weighted by a normalized inverse distance function. We also interpolated cleft deepening rates and maximum cleft depth using a linear interpolation scheme (described in Section 2.6), and ran our algorithm (Section 2.7) based on these interpolated mitosis and cleft deepening rates, and bud-splitting statistics for about 100 iterations, approximately the number of iterations required to simulate 6 hours of growth. For all iterations of the algorithm, we computed the morphological feature vector (y_j) and compared it to the expected target feature vector, or target configuration, as determined by the ground truth generated by the linear growth model (x_j). The comparison is done as following:

$$d_{xy}=\sqrt{{\displaystyle \sum _{j=1}^N{\left(\frac{y_j-x_j}{x_j}\right)}^2}}$$

The comparison was performed in the original feature space, since the rank of the matrix of the linearly generated ground truth is 1. We look for the iteration number that minimizes the distance d_xy, and use this iteration number as the terminal configuration for each of the three time-intervals mentioned above.

This interpolation-driven dynamic graph growth model was used to predict gland morphology at specific time points for different EGF concentrations. Figure 9 shows the same starting image grown under EGF-1, EGF-10, and EGF-20 concentrations with predicted outcomes using the dynamic graph-based growth model for 3, 4.5, and 6 hours. Table 4 lists the area, perimeter, number of clefts, and median cleft depth for the three configurations. We can observe that higher EGF concentrations stimulate branching morphogenesis by creating more buds. As time progresses, the lower EGF concentrations have deeper clefts. This can be observed at 6 hours where EGF-1 has a much higher median cleft depth, whereas EGF-20 has relatively shallower clefts that have hardly progressed beyond 3 hours. Supplementary Movie V2 shows a simulation time-lapse movie produced by the dynamic graph model of all three EGF concentrations together (movie can be downloaded from http://dsrc.rpi.edu/cellgraph/SMG_modeling/Supplementary_Video_V2.mp4).

Fig. 9.

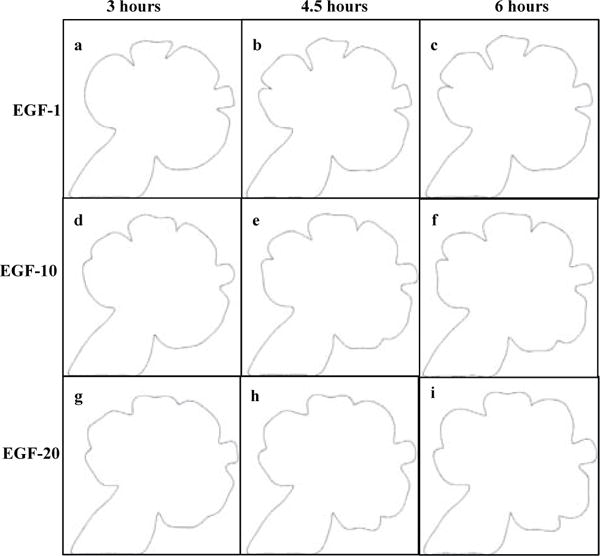
Dynamic graph-based prediction model results. Same starting image grown under different EGF concentrations for 3, 4.5, and 6 hours. The configuration of the salivary gland after 3 hours under EGF-1, EGF-10, and EGF-20 concentrations are shown in (a), (d), and (g), respectively. The configuration of the salivary gland after 4.5 hours under under the same concentrations are shown in (b), (e), and (h), respectively. The configuration of the salivary gland after 6 hours under the same concentrations are shown in (c), (f), and (i), respectively. The number of buds increases from EGF-1 to EGF-20, with clefting occurring more frequently in higher EGF concentrations. Buds are larger and clefts are deeper in lower EGF concentrations. Please recall that we do not compare the prediction model to a Monte-Carlo-based simulation (MCS) model. For further information about the prediction model, please refer to Section 3.4

TABLE 4.

Comparison of Final Configurations of the Three EGF Concentrations as Predicted by the Dynamic Graph-Based Growth Model.

	Area (μm2)	Perimeter (μm)	Number of clefts	Median cleft depth (μm)
EGF-1	74132.43	1057.03	5	36.42
EGF-10	77473.87	1041.53	6	23.11
EGF-20	80715.32	1067.93	6	17.09

4 Discussion

The objective of this study was to quantify and predict the core processes involved in the initial stages of branching morphogenesis to initiate the process of branching morphogenesis: cleft initiation, stabilization, and progression, under different concentrations of EGF. These cleft stages occur simultaneously with bud outgrowth and subsequently lead to cleft termination and duct formation. For this purpose, we extracted morphometric parameters from time-lapse mouse submandibular salivary gland (SMG) images. We developed a biological data driven descriptive model utilizing dynamic graphs. This dynamic graph model describes and predicts early branching morphogenesis in SMG. Given an initial SMG boundary image and EGF concentration level, the dynamic graph model is able to predict the growth of the SMG between embryonic days E12 and E13. The model probabilistically adds daughter cells and integrates these cells into the SMG by appropriately expanding its boundary. The model also creates new edges between the daughter cells and cells existing in the graph representing the initial gland. This augmented cell-graph (with the daughter cells) maintains the local structural properties of the original cell-graph. Cleft deepening and creation of dynamic clefts are crucial components of the model allowing it to produce more realistic branched structures and deeper clefts, and are based on the rules captured from the time-lapse data sets. The process of de novo cleft creation is modeled by first identifying the regions of initiation of the cleft, as well as the increase required in the perimeter of the buds. Given this information, we then use a probabilistic model to create de novo clefts.

Our results indicate that the dynamic graph model can correctly capture and represent the tissue-level morphological changes during cleft formation in the developmental stages of the SMG branching morphogenesis. We also showed that cleft progression is linearly dependent on the perimeters of the adjacent buds and is modulated by the EGF concentration. As was expected, higher EGF stimulated branching morphogenesis by producing more clefts, whereas lower EGF concentrations produced fewer clefts. Our analysis revealed an interesting observation regarding the depth of the clefts. Higher EGF concentrations produced shallower clefts, whereas lower EGF concentrations produced deeper clefts, for reasons that remain unclear. Future studies will be required to understand the cellular processes activated by EGF during cleft formation. Since this dynamic graph modeling approach can model cleft formation in response to modulation of EGF signaling, this approach could be employed to evaluate the contribution of other signaling pathways to cleft formation. Similar modeling approaches could be employed towards understanding other developmental processes in which large changes in shape occur.

Interestingly, the morphology of the epithelial buds tends to be slightly more circular than the buds produced by the dynamic graph-based growth model. It is not possible to capture this difference in the circularity of buds with the methods used here and would require a more complicated model. Currently, this level of detail in shape modeling is beyond the consideration of the dynamic graph-based growth model, and would be a potential direction of enhancement for the model. We compared our results against a well-known on-lattice Monte-Carlo-based simulation model, the Glazier-Graner-Hogeweg (GGH) model, under a specific parameter set consisting of energy functions that have biologically relevant equivalents, and demonstrated that our results are in a similar quantitative agreement with the biological data as those of the GGH model, but converge significantly faster to the target configuration. The authors would like to point out that the GGH model handles cellular-level changes at a higher resolution than the dynamic graph-based growth model. We also presented a method to introduce de novo clefts in the SMG using the GGH model thus adding to the dynamic nature of the GGH model.

We enhanced the dynamic graph-based growth model to predict the growth of the SMG at any specified time between embryonic days E12 and E13 without requiring a time-lapse data set. This is one of the primary benefits of the interpolation-driven prediction modeling approach – it does not require apriori knowledge of the target configuration – the initial configuration and growth rules determined from the biological data are sufficient for the algorithm to predict the gland morphology at a future time point. The predictive nature of the model reduces its dependence on in vivo experiments, allowing the biologists to view a simulation of the experiment prior to performing it. Most other computational biological techniques, including the GGH model, require information regarding the final configuration of the ground truth data in advance. Thus, it was not possible to compare our predictive model to other simulative models. We examined the growth trends in the biological data from the viewpoint of morphological features and discovered that individual linear growth models are able to predict the evolution of each feature. This allowed us to identify the expected configuration of the morphological features at different time points.

While analyzing the results of the dynamic-graph growth model, we observed that it has certain shortcomings. Since individual tissue-scale and cellular-scale models have their deficiencies with regards to modeling different aspects of cleft formation in branching morphogenesis, future efforts should be aimed at creating a multi-scale hybrid model that can achieve better tissue-scale modeling, and be able to more realistically capture cellular-level events such as mitosis and cellular reorganization in cleft regions. The dynamic graph model is a generic model and as such can be used in conjunction with other models to create this hybrid model. Another future direction for the dynamic graph-based growth model involves including dynamic cell movement information for accurate construction of cell graphs with a better estimation of the spatial distribution of cells [13].

Biographies

Nimit Dhulekar is an Application Support Engineer at MathWorks, Inc. He received his Ph. D. in Computer Science from Rensselaer Polytechnic Institute (RPI) in 2015. He received his B. E. degree in Computer Engineering from Mumbai University in 2006, and his M. S. degree in Computer Science from Dartmouth College in 2010. His research interests include analysis of time-series data for various complex systems, image informatics, computer vision, and computational modeling.

Shayoni Ray is a Post-Doctoral Research Scientist in the Antisense Drug Discovery, Cardiovascular Group at ISIS Pharmaceuticals, Inc. She received her Ph. D. in Cellular/Molecular and Computational Biology from SUNY Albany in 2014. She received her B. S. degree in Chemistry from Calcutta University in 2004, and her M. S. degree in Biotechnology and Bioinformatics from Jadavpur University in 2007. Her research interests include elucidating cellular and molecular mechanisms during organogenesis, tumor biology and skin fibrosis, and computational modeling of complex biological processes.

Daniel Yuan received his B. S. degree in Chemistry from Massachusetts Institute of Technology in 2008 and his M. S. degree in Cellular and Molecular Biology from University of Wisconsin – Madison in 2011. He studied Computer Science at RPI where he contributed to a computational model for mouse salivary gland development.

Abhirami Baskaran received her B. E. degree in Computer Science from People’s Education Society Institute of Technology in India in 2011, and her MS degree in Computer Science from RPI in 2013.

Basak Oztan is a Senior Image Processing Scientist with American Science and Engineering Inc., Billerica, MA. He received his B. S. degree in Electrical and Electronics Engineering from Middle East Technical University, Ankara, Turkey, in 2003 and his M. S. and Ph. D. degrees in Electrical and Computer Engineering from the University of Rochester, in 2004 and 2010, respectively. He was a Post-Doctoral Research Associate with the Department of Computer Science, RPI between 2010 and 2013. His research interests include image informatics, computer vision, and machine learning.

Melinda Larsen is as Associate Professor in the Department of Biological Sciences at the University at Albany, SUNY. Dr. Larsen obtained her B. S. degree from the University of Utah in 1993, and her Ph. D. from Baylor College of Medicine in 1999. She completed postdoctoral training at the NIH/NIDCR from 1999–2006. Her core research interests are in understanding the molecular mechanisms driving salivary gland organ formation and in deciphering the contribution of the extracellular environment to epithelial cell function for application in engineering artificial organs.

Bülent Yener is a Professor in the Department of Computer Science with joint appointments with the Department of Electrical, Computer and Systems Engineering, and with the Department of Mathematical Sciences at RPI in Troy, New York. He received his M. Sc. and Ph. D. degrees in Computer Science, both from Columbia University, in 1987 and 1994, respectively. He is the founding director of the Data Science Research Center at RPI. Dr. Yener is a Fellow of IEEE, and a senior member of ACM. His research focus is on various aspects of data science spanning from modeling of complex systems to data security.