Generalized LASSO with under-determined regularization matrices

Abstract

This paper studies the intrinsic connection between a generalized LASSO and a basic LASSO formulation. The former is the extended version of the latter by introducing a regularization matrix to the coefficients. We show that when the regularization matrix is even- or under-determined with full rank conditions, the generalized LASSO can be transformed into the LASSO form via the Lagrangian framework. In addition, we show that some published results of LASSO can be extended to the generalized LASSO, and some variants of LASSO, e.g., robust LASSO, can be rewritten into the generalized LASSO form and hence can be transformed into basic LASSO. Based on this connection, many existing results concerning LASSO, e.g., efficient LASSO solvers, can be used for generalized LASSO.

1. Introduction

The least absolute shrinkage and selection operator (LASSO) [1] is one of the most popular approaches for sparse linear regression in the last decade, which is usually formulated as

$${\mathit{x}}^{*}(\lambda )=\underset{\mathit{x}}{\text{arg min }}\{\frac{1}{2}{\Vert \mathit{y}-\mathit{A}\mathit{x}\Vert }^2+\lambda {\Vert \mathit{x}\Vert }_1\},\hspace{1em}(\mathrm{L}\mathrm{A}\mathrm{S}\mathrm{S}\mathrm{O})$$

where y ∈ ℝⁿ gathers n observed measurements; A ∈ ℝ^n×p contains p predictors of dimension n; x ∈ ℝ^p contains p coefficients; ‖ ․ ‖ and ‖ ․ ‖₁ stand for the ℓ₂- and ℓ₁-norm respectively; and λ > 0 is the regularization parameter, controlling the tradeoff between the data fidelity and the model complexity. The most attracting feature of LASSO is the use of ℓ₁-norm regularization, which yields sparse coefficients. The ℓ₁-norm regularization results in the piecewise linearity [2] of the solution path {x^* (λ)|λ ∈ (0, +∞)} (i.e., the set of solutions with respect to continuous change of the regularization parameter λ), allowing for efficient reconstruction of the whole solution path. Based on this property, famous path tracking algorithms such as the least angle regression (LARS) [3] and the homotopy [2, 4] have been developed. LARS is a greedy algorithm working with decreasing λ value. At each iteration, a dictionary atom is selected and appended to the set previously selected, and the next critical λ value is computed. Homotopy is an extension of LARS, performing both forward and backward selection of the atoms already selected.

The generalized LASSO [5] (or analysis [6, 7], least mixed norm [8]) extends the basic LASSO (or synthesis) by imposing a regularization matrix D ∈ ℝ^m×p on the coefficient vector x:

$${\mathit{x}}^{*}(\lambda )=\underset{\mathit{x}}{\text{arg min }}\{\frac{1}{2}{\Vert \mathit{y}-\mathit{A}\mathit{x}\Vert }^2+\lambda {\Vert \mathit{D}\mathit{x}\Vert }_1\},\hspace{1em}(\text{generalized }\mathrm{L}\mathrm{A}\mathrm{S}\mathrm{S}\mathrm{O})$$

where D typically contains the prior knowledge (e.g., structure information) [9] about x. For example, if x is expected to be a piecewise constant signal (i.e., implying that its first order derivative is sparse), then D is taken to be the first order derivative operator [10]. Some variants of LASSO can be regarded as the generalized LASSO by forming a structured matrix D. For example, the fused LASSO proposed by Tibshirani et al. [10] imposes the ℓ₁ regularization on both the coefficients and their first order derivatives to encourage the solution to be locally constant. When one of the two regularization parameters is fixed, a fused LASSO problem can be rewritten as a generalized LASSO by cascading a scaled identity matrix with a first order derivative matrix to form the D matrix. The graph-guided fused LASSO [11, 12] incorporates the network prior information into D for correlation structure. Application of generalized LASSO can be found in image restoration [8], visual recognition [13], electroencephalography (EEG) [14], bioinformatics [15], ultrosonics [16], etc.

Since the LASSO has been proposed, results concerning the recovery condition [3, 17], solution path property [18], degree of freedom [19], model selection consistency [20], efficient algorithms as well as software development [2, 4] have been widely studied. One may want to know whether these results can be applicable to a generalized LASSO problem, e.g., solving a generalized LASSO problem with a LASSO solver. An immediate example is when D is a full rank square (hence invertible) matrix. By a simple change of variables u = Dx, the original generalized LASSO problem can be transformed into the basic LASSO form with a predictor matrix AD⁻¹ and a coefficient vector u. Therefore it can be solved by calling the LASSO subroutine.

Although the generalized LASSO and LASSO have been studied from various aspects [5, 7, 21], their connections are not fully explored, which is the main focus of this paper. Elad et al. [6] showed that they are equivalent, but confined the discussion to the denoising case, where A is an identity matrix. Tibshirani and Taylor [5] showed that the former can be transformed to the latter; however, their method needs to introduce a matrix D₀ (see Appendices), which brings other potential questions as discussed in the conclusion.

The paper is organized as follows: in Section II, we show that when the regularization matrix is even- or under-determined with full rank conditions, the generalized LASSO can be transformed into the LASSO form via the Lagrangian framework. Based on this formula, in Section III we show that some published results of LASSO can be extended to the generalized LASSO. In Section IV, two variants of LASSO, namely the regularized deconvolution and the robust LASSO are analyzed under the generalized LASSO framework. We conclude the paper in Section IV.

2. Condition and formula of transformation

The simplification of the generalized LASSO depends on the setting of D [6]. For the even-determined case (m = p)¹, if D has full rank, by a simple change of variables u = Dx, the original generalized LASSO problem can be transformed into the basic LASSO with a predictor matrix AD⁻¹ and a coefficient vector u. Once the LASSO solution û(λ) is known, the original generalized LASSO solution is immediate: x̂(λ) = D⁻¹û(λ).

For the over-determined case (m > p), if we change the variable x to u, then u has a higher dimension than x, or higher degree of freedom. If only a solution û satisfies the constraint DD^†û = û where D^† is the Moore-Penrose pseudoinverse of D, the original solution is guaranteed to be found [6]. Therefore, the generalized LASSO under this case cannot be transformed into a basic LASSO but a LASSO with equality constraint [22].

We consider the under-determined case (m < p). The following Theorem 1 states that a generalized LASSO problem can be transformed into a basic LASSO form under some conditions.

Theorem 1

If matrix $\mathbf{\Phi }=\left[\begin{array}{c}\hfill \mathit{A}\hfill \\ \hfill \mathit{D}\hfill \end{array}\right]$ has full column rank (implying m + n ≥ p), and D has full row rank (implying m ≤ p), then the generalized LASSO problem can be transformed into the following LASSO form:

$${\mathit{u}}^{*}(\lambda )=\underset{\mathit{u}}{\text{arg min }}\{\frac{1}{2}{\Vert \mathit{z}-\mathit{H}\mathit{u}\Vert }^2+\lambda {\Vert \mathit{u}\Vert }_1\},$$ (1)

where

$$\mathit{H}\mathit{=}{\mathit{Q}}_1{\mathit{Q}}_2^{†}$$ (2)

$$\mathit{z}\mathit{=}({\mathit{I}}_n-{\mathit{Q}}_1({\mathit{I}}_p-{\mathit{Q}}_2^{†}{\mathit{Q}}_2){\mathit{Q}}_1^T)\mathit{y}$$

and Q₁ ∈ ℝ^n×p and Q₂ ∈ ℝ^m×p are defined from the (unique) QR decomposition

$$\mathbf{\Phi }=\mathit{Q}\mathit{R}=\left[\begin{array}{c}\hfill {\mathit{Q}}_1\hfill \\ \hfill {\mathit{Q}}_2\hfill \end{array}\right]\mathit{R}.$$ (3)

Proof

Since Φ has full column rank, its QR decomposition (3) is unique and the square matrix R ∈ ℝ^p×p is invertible. Moreover, Q₂ ∈ ℝ^m×p is full row rank because D is full row rank. (3) rereads:

$$\mathit{A}={\mathit{Q}}_1\mathit{R},$$ (4)

$$\mathit{D}={\mathit{Q}}_2\mathit{R}.$$ (5)

From Q^TQ = I_p, we have

$${\mathit{Q}}_1^T{\mathit{Q}}_1+{\mathit{Q}}_2^T{\mathit{Q}}_2={\mathit{I}}_p.$$ (6)

The generalized LASSO problem is equivalent to the following constrained optimization problem

$$({\mathit{x}}^{*}(\lambda ),{\mathit{u}}^{*}(\lambda ))=\underset{\mathit{x},\mathit{u}}{\text{arg min }}\{\frac{1}{2}{\Vert \mathit{y}-\mathit{A}\mathit{x}\Vert }^2+\lambda {\Vert \mathit{u}\Vert }_1\}$$

$$\text{subject to }\mathit{D}\mathit{x}=\mathit{u}.$$ (7)

The Lagrange function associated with (7) reads

$$L(\mathit{x},\mathit{u},\mathit{\mu })=\frac{1}{2}{\Vert \mathit{y}-\mathit{A}\mathit{x}\Vert }^2+\lambda {\Vert \mathit{u}\Vert }_1+{\mathit{\mu }}^T(\mathit{u}-\mathit{D}\mathit{x}),$$

where μ gathers m Lagrange multipliers. The optimality condition reads

$$\frac{\partial L(\mathit{x},\mathit{u},\mathit{\mu })}{\partial \mathit{x}}={\mathit{A}}^T(\mathit{A}\mathit{x}-\mathit{y})-{\mathit{D}}^T\mathit{\mu }=\mathbf{0},$$

$$\frac{\partial L(\mathit{x},\mathit{u},\mathit{\mu })}{\partial \mathit{\mu }}=\mathit{u}-\mathit{D}\mathit{x}=\mathbf{0}.$$

From these two equations, we have the following system

$$\left[\begin{array}{cc}\hfill {\mathit{A}}^T\mathit{A}\hfill & \hfill -{\mathit{D}}^T\hfill \\ \hfill \mathit{D}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \mathit{x}\hfill \\ \hfill \mathit{\mu }\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathit{A}}^T\mathit{y}\hfill \\ \hfill \mathit{u}\hfill \end{array}\right].$$ (8)

If matrix

$$\mathit{M}\triangleq \left[\begin{array}{cc}\hfill {\mathit{A}}^T\mathit{A}\hfill & \hfill -{\mathit{D}}^T\hfill \\ \hfill \mathit{D}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]$$ (9)

is invertible, we can find the equivalent form of the generalized LASSO problem. By substituting A and D with (4) and (5) respectively, we have

$$\mathit{M}=\left[\begin{array}{cc}\hfill {\mathit{R}}^T{\mathit{Q}}_1^T{\mathit{Q}}_1\mathit{R}\hfill & \hfill -{\mathit{R}}^T{\mathit{Q}}_2^T\hfill \\ \hfill {\mathit{Q}}_2\mathit{R}\hfill & \hfill \mathbf{0}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathit{R}}^T\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\mathit{Q}}_1^T{\mathit{Q}}_1\hfill & \hfill -{\mathit{Q}}_2^T\hfill \\ \hfill {\mathit{Q}}_2\hfill & \hfill \mathbf{0}\hfill \end{array}\right]\left[\begin{array}{cc}\hfill \mathit{R}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right],$$

where I_m ∈ ℝ^m×m is the identity matrix. Since R and I_m are full rank, the invertibility of M is equivalent to that of

$$\mathit{N}\triangleq \left[\begin{array}{cc}\hfill {\mathit{Q}}_1^T{\mathit{Q}}_1\hfill & \hfill -{\mathit{Q}}_2^T\hfill \\ \hfill {\mathit{Q}}_2\hfill & \hfill \mathbf{0}\hfill \end{array}\right].$$

From (6),

$$\mathit{N}=\left[\begin{array}{cc}\hfill {\mathit{I}}_p-{\mathit{Q}}_2^T{\mathit{Q}}_2\hfill & \hfill -{\mathit{Q}}_2^T\hfill \\ \hfill {\mathit{Q}}_2\hfill & \hfill \mathbf{0}\hfill \end{array}\right]={\mathit{I}}_{p+m}+\left[\begin{array}{cc}\hfill {\mathit{Q}}_2^T\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right]\left[\begin{array}{cc}\hfill -{\mathit{I}}_m\hfill & \hfill -{\mathit{I}}_m\hfill \\ \hfill {\mathit{I}}_m\hfill & \hfill -{\mathit{I}}_m\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\mathit{Q}}_2\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right].$$

From Woodbury’s matrix identity [23, p.141], N is invertible if and only if

$$\mathit{W}\triangleq {\left[\begin{array}{cc}\hfill -{\mathit{I}}_m\hfill & \hfill -{\mathit{I}}_m\hfill \\ \hfill {\mathit{I}}_m\hfill & \hfill -{\mathit{I}}_m\hfill \end{array}\right]}^{-1}+\left[\begin{array}{cc}\hfill {\mathit{Q}}_2\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\mathit{Q}}_2^T\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathit{Q}}_2{\mathit{Q}}_2^T-\frac{1}{2}{\mathit{I}}_m\hfill & \hfill \frac{1}{2}{\mathit{I}}_m\hfill \\ \hfill -\frac{1}{2}{\mathit{I}}_m\hfill & \hfill \frac{1}{2}{\mathit{I}}_m\hfill \end{array}\right]$$

is invertible. Since

$$\text{det}(\mathit{W})=\text{det}(\frac{1}{2}{\mathit{Q}}_2{\mathit{Q}}_2^T),$$

and $\text{det}({\mathit{Q}}_2{\mathit{Q}}_2^T)\ne 0$ (Q₂ is full rank), the invertibility of W is guaranteed, and therefore M is invertible.

From the block matrix inversion lemma [23, p.108], we have

$${\mathit{W}}^{-1}=\left[\begin{array}{cc}\hfill {({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}\hfill & \hfill -{({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}\hfill \\ \hfill {({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}\hfill & \hfill 2{\mathit{I}}_m-{({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}\hfill \end{array}\right].$$

Therefore,

$${\mathit{N}}^{-1}={\mathit{I}}_{p+m}-\left[\begin{array}{cc}\hfill {\mathit{Q}}_2^T\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right]{\mathit{W}}^{-1}\left[\begin{array}{cc}\hfill {\mathit{Q}}_2\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right],$$

and

$${\mathit{M}}^{-1}=\left[\begin{array}{cc}\hfill {\mathit{R}}^{-1}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right]{\mathit{N}}^{-1}\left[\begin{array}{cc}\hfill {\mathit{R}}^{-T}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{I}}_m\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathit{R}}^{-1}({\mathit{I}}_p-{\mathit{Q}}_2^T{({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}{\mathit{Q}}_2){\mathit{R}}^{-T}\hfill & \hfill {\mathit{R}}^{-1}{\mathit{Q}}_2^T{({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}\hfill \\ \hfill -{({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}{\mathit{Q}}_2{\mathit{R}}^{-T}\hfill & \hfill {({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}-{\mathit{I}}_m\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathit{R}}^{-1}({\mathit{I}}_p-{\mathit{Q}}_2^{†}{\mathit{Q}}_2){\mathit{R}}^{-T}\hfill & \hfill {\mathit{R}}^{-1}{\mathit{Q}}_2^{†}\hfill \\ \hfill -{({\mathit{Q}}_2^{†})}^T{\mathit{R}}^{-T}\hfill & \hfill {({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}-{\mathit{I}}_m\hfill \end{array}\right],$$

where ${\mathit{Q}}_2^{†}={\mathit{Q}}_2^T{({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}$. Finally, from (8) we have

$$\mathit{x}={\mathit{R}}^{-1}({\mathit{I}}_p-{\mathit{Q}}_2^{†}{\mathit{Q}}_2){\mathit{Q}}_1^T\mathit{y}+{\mathit{R}}^{-1}{\mathit{Q}}_2^{†}\mathit{u},$$ (10)

and

$$\mathit{\mu }=-{({\mathit{Q}}_2^{†})}^T{\mathit{Q}}_1^T\mathit{y}+({({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}-{\mathit{I}}_m)\mathit{u}.$$

By substituting (10) into (7), we obtain the results (1) and (2).

Once the solution path {û(λ)|λ ∈ (0, +∞)} is known, the corresponding solution path {x̂(λ)|λ ∈ (0, +∞)} can be calculated according to (10).

By substituting Q₁ = AR⁻¹ and Q₂ = DR⁻¹ into (2), and utilizing

$$\mathbf{\Psi }\triangleq {\mathbf{\Phi }}^T\mathbf{\Phi }={\mathit{A}}^T\mathit{A}+{\mathit{D}}^T\mathit{D}={\mathit{R}}^T\mathit{R},$$ (11)

up to a few manipulations, an useful equivalent form of (2) without QR decomposition is obtained as

$$\mathit{H}=\mathit{A}{\mathbf{\Psi }}^{-1}{\mathit{D}}^T{(\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{D}}^T)}^{-1}$$ (12)

$$\mathit{z}=({\mathit{I}}_n-\mathit{A}{\mathbf{\Psi }}^{-1}{\mathit{A}}^T+\mathit{H}\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{A}}^T)\mathit{y}$$

And from (10), x can be recovered as

$$\mathit{x}={\mathbf{\Psi }}^{-1}({\mathit{A}}^T-{\mathit{D}}^T{\mathit{H}}^T)\mathit{y}+{\mathbf{\Psi }}^{-1}{\mathit{D}}^T{(\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{D}}^T)}^{-1}\mathit{u}$$ (13)

Note that H has the same dimensionality as AD^†, but normally they are not equal unless Ψ is a diagonal matrix.

Remark 1

There are many real-world examples that satisfy this condition. e.g., the total variation denoising problem where A and D are an identity and a first order derivative matrix, respectively. By substituting A and D into M in (9), one can check that M is invertible, and hence satisfies the condition in Theorem 1. Another two examples are the regularized deconvolution problem and the robust LASSO, which will be presented in detail in Sec. 4.

Remark 2

Under the case m + n = p, Φ is a full rank (square) matrix. Therefore, the row vectors of Q are orthogonal, and ${\mathit{Q}}_1{\mathit{Q}}_2^T=\mathbf{0}$. From (1)–(2), we have H = 0 and the solution is obviously u = 0. According to (10), the original solution is $\mathit{x}={\mathit{R}}^{-1}{\mathit{Q}}_1^T\mathit{y}$. This solution does not depend on λ, and the solution path {x̂(λ)|λ ∈ (0, +∞)} is a singleton.

Another viewpoint is obtained by a change of variables. Defining υ = Rx, the generalized LASSO problem rereads

$${\mathit{\upsilon }}^{*}(\lambda )=\underset{\mathit{\upsilon }}{\text{arg min }}\{\frac{1}{2}{\Vert \mathit{y}-{\mathit{Q}}_1\mathit{\upsilon }\Vert }^2+\lambda {\Vert {\mathit{Q}}_2\mathit{\upsilon }\Vert }_1\}.$$ (14)

Since the rows of Q₁ and Q₂ form an orthonormal basis, it is obvious that the minimum ℓ₂-norm least square solution $\hat{\mathit{\upsilon }}={\mathit{Q}}_1^{†}\mathit{y}={\mathit{Q}}_1^T\mathit{y}$ satisfies Q₂υ̂ = 0. This means that υ̂ minimizes both the ℓ₂- and ℓ₁-term simultaneously. Therefore, the cost function in (14) is equal to 0 whatever λ > 0.

Remark 3

Under the case m + n < p, Null(Φ) ≠ ∅, therefore one can check that the generalized LASSO does not yield unique solution, and there are unlimited number of solutions $\{{\mathit{x}}^{*}|{\mathit{x}}^{*}={\mathbf{\Phi }}^{†}\left[\begin{array}{c}\hfill \mathit{y}\hfill \\ \hfill \mathbf{0}\hfill \end{array}\right]+{\mathit{x}}_0,{\mathit{x}}_0\in \mathit{\text{Null}}(\mathbf{\Phi })\}$ with Dx^* = 0 and Ax^* = y whatever λ > 0.

Note that this case does not satisfy the condition in Theorem 1 since Φ does not have full column rank. This case serves to complete the discussion.

3. Extension of existing LASSO results

Since the LASSO has been intensively studied during the last decade, many results concerning the computational issue have been published. In this section, we extend some of them into the generalized LASSO problem.

3.1. Monotonic solution path property

Our earlier result [18, Theorem 2] shows that if (H^TH)⁻¹ is diagonally dominant, then the solution path of the corresponding LASSO problem changes monotonically with respect to λ. In other words, the solution path has at most m segments. Therefore, the ‘forward’ algorithm, LARS, yields the same solution path as the ‘forward-backward’ algorithm, homotopy, and both of them can recover the complete solution path within m iterations. Based on this fact, the computational complexity can thus be reduced. The following corollaries extend this result to the generalized LASSO.

Corollary 1

If a generalized LASSO problem satisfying condition in Theorem 1 also satisfies that ((DΨ⁻¹ D^T)⁻¹ − I)⁻¹ is diagonally dominant, then the complete solution path can be recovered within m iterations of LARS and homotopy algorithm.

Proof

When a generalized LASSO problem satisfying condition in Theorem 1, it can be transformed into a LASSO problem with H and z being defined in (2). By utilizing equations (4), (5), (6) and (11), we have

$${\mathit{H}}^T\mathit{H}={({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}-\mathit{I}={(\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{D}}^T)}^{-1}-\mathit{I},$$

therefore, (H^TH)⁻¹ is diagonally dominant. From [18], this corollary is straightforward.

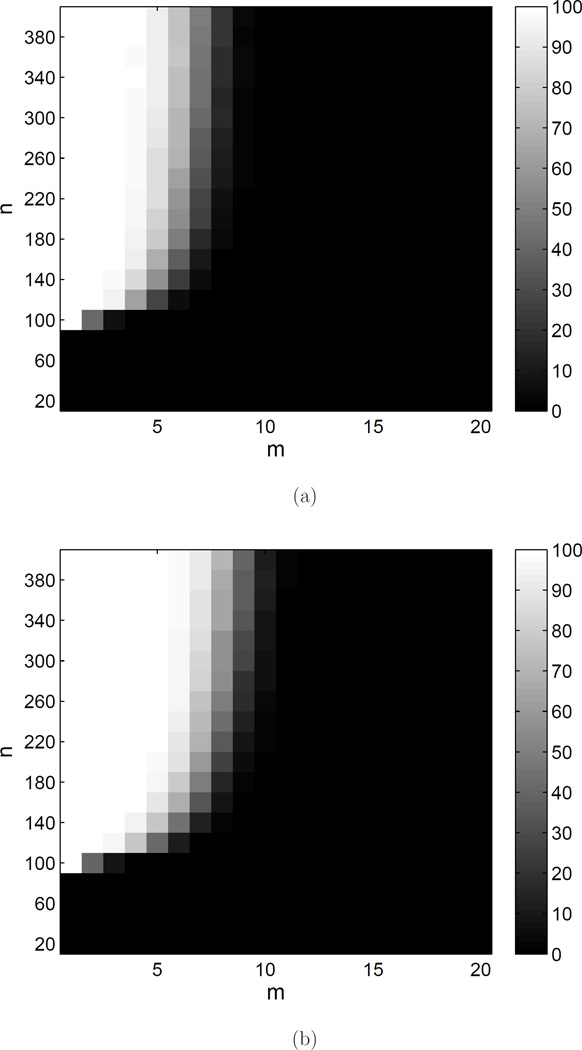
There exist many matrices satisfying above condition. Obvious examples are the orthogonal dictionaries like Dirac basis or Hadamard basis. By Monte Carlo simulation, we study the probability of random matrices to satisfy the condition. p is fixed to 100, and for each given configuration (n, m), 1000 trials A and D are generated, whose entries obey i.i.d. normal distribution or Bernoulli distribution with parameter b = 0.1 (the probability for 1 is b, for 0 is 1 − b). The frequency of A and D satisfying condition in Corollary 1 is shown in Fig. B.1. From the simulation results, it is shown that random matrices satisfy the condition when n ≫ m.

Figure B.1.

The frequency (in percentage) of random matrices A and D satisfying condition in Corrolary 1 with p = 100. (a) Entries in A and D obeys normal distribution and Bernoulli distribution with parameter b = 0.1, respectively. (b) The distributions of A and D are exchanged.

When A^TA forms an orthogonal design, i.e., A^TA = I, above condition can be further simplified to the following corollary.

Corollary 2

If a generalized LASSO problem satisfying condition in Theorem 1 also satisfies that A forms an orthogonal design, and DD^T is diagonally dominant, then the complete solution path can be recovered within m iterations of LARS and homotopy algorithm.

Proof

Since D has full row rank, DD^T is invertible. By utilizing Searle’s set of matrix identities [24, page 151], we can verify that

$$\mathit{D}{(\mathit{I}+{\mathit{D}}^T\mathit{D})}^{-1}{\mathit{D}}^T={(\mathit{I}+{(\mathit{D}{\mathit{D}}^T)}^{-1})}^{-1}.$$

When A^TA = I, we have

$${({\mathit{H}}^T\mathit{H})}^{-1}={((\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{D}}^T)-\mathit{I})}^{-1}={({(\mathit{D}{(\mathit{I}+{\mathit{D}}^T\mathit{D})}^{-1}{\mathit{D}}^T)}^{-1}-\mathit{I})}^{-1}=\mathit{D}{\mathit{D}}^T$$

Therefore, condition in Corollary 1 can be simplified into checking the diagonal dominance of DD^T.

Corollaries 1 and 2 show that in the best case, the computational complexity of homotopy can reach as low as m iterations to compute the complete regularization path on λ ∈ (0, +∞). It is shown [25] that in the worst case, the computation complexity can reach as high as (3^m − 1)/2. Therefore, the computation complexity highly varies depending on the specific problem. Instead of using a generic LASSO solver such as LARS, fast and efficient algorithms can be developed for some specific problems. e.g., the algorithm in [26] permits fast computation and low storage for the regularized deconvolution problem introduced later in Sec. 4.1 with α = 0 and β = − 1. The computational advantage is significant when the dimension is extremely large.

3.2. Decoupling into 1-dimensional subproblems

Efron et al. [3] and Friedman et al. [27] have shown that if the dictionary A forms an orthogonal design (or uncorrelated design), i.e., A^TA = I, a LASSO problem can be decoupled into a set of subproblems, and then solved separately.

To be more specific, when A^TA = I the LASSO criterion can be rewritten as

$$\frac{1}{2}{\Vert {\mathit{A}}^T\mathit{y}-\mathit{x}\Vert }^2+\lambda {\Vert \mathit{x}\Vert }_1+{\mathit{y}}^T\mathit{y}-{\mathit{y}}^T\mathit{A}{\mathit{A}}^T\mathit{y}.$$

This shows that the p-dimensional LASSO problem can be decoupled into p’ 1-dimensional subproblems, and each subproblem can be solved separately. The closed-form solution reads

$${\mathit{x}}^{*}={\eta }_{\lambda }({\mathit{A}}^T\mathit{y}),$$ (15)

where η_λ(·) is the componentwise soft thresholding function [28]:

$${\eta }_{\lambda }(x)=\{\begin{array}{cc}x-\lambda ,\hfill & x>\lambda ;\hfill \\ 0,\hfill & |x|\le \lambda ;\hfill \\ x+\lambda ,\hfill & x<-\lambda .\hfill \end{array}$$

Similarly, for generalized LASSO problem the following corollary provides a sufficient condition to guarantee decoupling.

Corollary 3

If a generalized LASSO problem satisfying condition in Theorem 1 also satisfies

$$\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{D}}^T=\frac{1}{2}\mathit{I},$$ (16)

then it can be decoupled into p 1-dimensional LASSO problems, with the following closed-form solution

$${\mathit{u}}^{*}={\eta }_{\lambda }(2\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{A}}^T\mathit{y}).$$ (17)

Proof

Since A and D satisfy condition in Theorem 1, this generalized LASSO problem can be transformed into a LASSO problem, with H, z being defined in (2), and matrices Q₁, Q₂ and R being defined in the proof of Theorem 1.

By substituting equations (4), (5) and (11) into (16), an equivalent condition reads

$${\mathit{Q}}_2{\mathit{Q}}_2^T=\frac{1}{2}\mathit{I}.$$ (18)

Therefore, ${\mathit{Q}}_2^{†}=2{\mathit{Q}}_2^T$.

From (2) and by utilizing (6), it is easy to prove that the Gramian matrix of H is an identity matrix, i.e., H^TH = I, so H forms an orthogonal design, indicating the transformed LASSO problem can be decoupled.

$$\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill \beta -\alpha \hfill & \hfill -\alpha \beta \hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill \beta -\alpha \hfill & \hfill 1+{(\beta -\alpha )}^2\hfill & \hfill (\beta -\alpha )(1-\alpha \beta )\hfill & \hfill -\alpha \beta \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill -\alpha \beta \hfill & \hfill (\beta -\alpha )(1-\alpha \beta )\hfill & \hfill 1+{\alpha }^2{\beta }^2+{(\beta -\alpha )}^2\hfill & \hfill (\beta -\alpha )(1-\alpha \beta )\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill -\alpha \beta \hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill -\alpha \beta \hfill & \hfill (\beta -\alpha )(1-\alpha \beta )\hfill & \hfill 1+{\alpha }^2{\beta }^2+{(\beta -\alpha )}^2\hfill & \hfill (\beta -\alpha )(1-\alpha \beta )\hfill \\ \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill -\alpha \beta \hfill & \hfill (\beta -\alpha )(1-\alpha \beta )\hfill & \hfill 1+{\alpha }^2{\beta }^2+{(\beta -\alpha )}^2\hfill \end{array}\right]$$ (20)

Further more, with the help of (18), we can also prove

$${\mathit{H}}^T\mathit{z}=2{\mathit{Q}}_2{\mathit{Q}}_1^T\mathit{y}=2\mathit{D}{\mathbf{\Psi }}^{-1}{\mathit{A}}^T\mathit{y}.$$ (19)

Finally, by replacing A and y in (15) with H and z respectively, and substituting (19), the closed-form solution reads in (17).

Remark 4

If A^TA is invertible, by utilizing Searle’s set of matrix identities [24, page 151], an alternative condition of (16) reads

$$\mathit{D}{({\mathit{A}}^T\mathit{A})}^{-1}{\mathit{D}}^T=\mathit{I}$$

Note that this condition is stronger than (16) since for under-determined A, A^TA is not invertible.

One can check that condition in Corollary 3 fulfills when D is a square matrix with full rank and A^TA = D^TD.

4. Two examples on the analysis of LASSO variants

Several variants of LASSO can be unified under the generalized LASSO framework, such as the total variation regularized deconvolution for signal and image recovery [29], the robust LASSO for face recognition and sensor network [30], the adaptive LASSO for variable selection [31], the fused LASSO for gene expression data analysis [10], the ℓ₁ trend filtering for time series analysis [32], and the adaptive generalized fused LASSO for road-safety data analysis [33]. In this section, the first two will be discussed.

4.1. Regularized deconvolution

Deconvolution is a challenging problem, which can be formulated as a LASSO problem with a Toeplitz predictor matrix. Total variation [34] is a regularization tool to restore piecewise constant signals. This leads to the generalized LASSO form in which A is a Toeplitz matrix containing the convolution kernel and D is also a Toeplitz matrix containing the total variation kernel. For high dimensional problems, the computation burden is a major factor. The following theorem sheds some lights on this issue.

Corollary 4

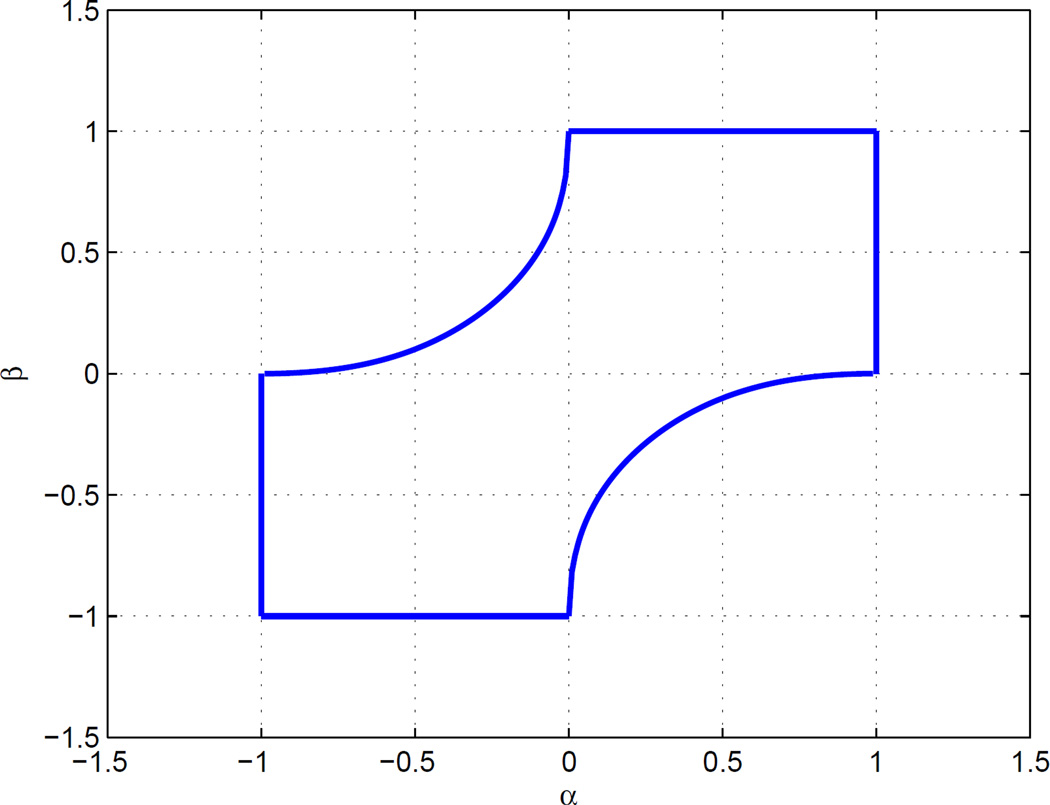
Let A and D be lower square triangle Toeplitz matrices with the first column [1, α, α², α³, …, αⁿ⁻¹]^T and [1, β, 0, 0, …, 0]^T, respectively. If α and β fall within the region displayed in Fig. B.2, then the generalized LASSO problem can be solved for all λ by the LARS and homotopy algorithms in at most n iterations.

Figure B.2.

The feasible region that admits matrix (12) to be diagonal dominant. The region is mirror symmetric with respect to line α = β, and the curve in the south-east quadrant has expression $\beta =\frac{-({\alpha }^2+1)+2\sqrt{\alpha ({\alpha }^2-\alpha +1)}}{{(\alpha -1)}^2}$.

The total variation regularization corresponds to the special case when β = − 1.

Proof

According to Theorem 1, since D is invertible, this generalized LASSO problem is equivalent to the basic LASSO problem (1) with H = AD⁻¹. Since A is squared and invertible, the Gramian matrix inverse reads (H^TH)⁻¹ = DA⁻¹ A^−T D^T. So in the following we will show that this matrix is diagonally dominant.

One can check that A⁻¹ is also a lower triangle Toeplitz matrix with the first column as [1, −α, 0, 0, …, 0]^T. Then the Gramian matrix DA⁻¹ A^−T D^T reads as (20). In order to have the diagonal dominance property, the following three inequalities are required, which correspond to the first three rows in matrix (20) (The conditions related to the other rows are obviously implied by the third inequality):

$$1\ge |\beta -\alpha |+|\alpha \beta |,$$

$$1+{(\beta -\alpha )}^2\ge |\beta -\alpha |+|\beta -\alpha ||1-\alpha \beta |+|\alpha \beta |,$$

$$1+{\alpha }^2{\beta }^2+{(\beta -\alpha )}^2\ge 2|\alpha \beta |+2|\beta -\alpha ||1-\alpha \beta |.$$

Those inequalities yield three regions in the 2D plane (α, β) whose intersection is displayed on Fig. B.2.

Corollary 4 in this paper, Theorem 2 in [18], Theorem 1 and Corollary 2 in [17] jointly show that for deconvolution problem with total variation regularization (β = −1), if the convolution kernel is high pass (−1 ≤ α < 0) or all pass (α = 0), but not low pass (0 < α ≤ 1), the true solution can be recovered via the generalized LASSO. If there is no total variation constraint (β = 0), then any convolution kernel having exponential attenuation ([1, α, α², α³, …, αⁿ⁻¹]^T, −1 ≤ α ≤ 1) admits the perfect recovery.

4.2. Robust LASSO

LASSO with the first order total variation method can recover piecewise constant signals. However, if there are outliers in the signal y, this approach tends to introduce false detections. A second component signal s ∈ ℝⁿ is introduced to cope with the outliers in the observation [30]. Since outliers are usually due to burst error, which are assumed to obey the Laplace distribution, a second ℓ₁ regression term is incorporated into the objective function, yielding the robust generalized LASSO as follows,

$$({\mathit{x}}^{*},{\mathit{s}}^{*})=\underset{\mathit{x},\mathit{s}}{\text{arg min }}\{\frac{1}{2}{\Vert \mathit{y}-\mathit{A}\mathit{x}-\mathit{s}\Vert }^2+{\lambda }_1{\Vert \mathit{D}\mathit{x}\Vert }_1+{\lambda }_2{\Vert \mathit{s}\Vert }_1\}.$$

This problem can be rewritten into a generalized LASSO form with ${\mathit{A}}_{\mathit{\text{robust}}}=[\mathit{A},\mathit{I}],{\mathit{D}}_{\mathit{\text{robust}}}=\left[\begin{array}{cc}\hfill \mathit{D}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \tau \mathit{I}\hfill \end{array}\right]$, and ${\mathit{x}}_{\mathit{\text{robust}}}=\left[\begin{array}{c}\hfill \mathit{x}\hfill \\ \hfill \mathit{s}\hfill \end{array}\right]$, where τ = λ₂/λ₁. When $\mathbf{\Phi }=\left[\begin{array}{c}\hfill \mathit{A}\hfill \\ \hfill \mathit{D}\hfill \end{array}\right]$ has full column rank, D has full column rank, and τ > 0, one can check that ${\mathbf{\Phi }}_{\mathit{\text{robust}}}=\left[\begin{array}{c}\hfill {\mathit{A}}_{\mathit{\text{robust}}}\hfill \\ \hfill {\mathit{D}}_{\mathit{\text{robust}}}\hfill \end{array}\right]$ has full column rank, D_robust has full row rank, and M is invertible. Therefore, from Theorem 1 the robust LASSO problem can be transformed into a basic LASSO form.

5. Conclusion

This paper discusses the simplification of a generalized LASSO problem into the basic LASSO form. When the regularization matrix D is even- or under-determined (m ≤ p), we showed that this simplification is possible. Otherwise, there is no guarantee that this simplification can be done. In the former case, optimization tools dedicated to LASSO can be straightforwardly applied to the generalized LASSO.

Tibshirani and Taylor [5] gave a simple way to transform a generalized LASSO to the basic LASSO form when D is not a square matrix (m < p). As shown in Appendix Appendix A, they introduced a matrix D₀ to form $\tilde{\mathit{D}}=\left[\begin{array}{c}\hfill \mathit{D}\hfill \\ \hfill {\mathit{D}}_0\hfill \end{array}\right]$, a square matrix D̃, which is invertible. This poses the question on whether their results depend on D₀ or not. Appendix Appendix B shows that their method yields the equivalent results as ours, and this indicates that H and z in their formula do not depend on D₀. In addition, an improperly introduced D₀ may incur potential numerical error.

The proposed formula reposes directly on A and D, therefore gives an insight into their interaction in the generalized LASSO problem. Based on the proposed formula, it is shown that existing results related to LASSO can be extended to the generalized LASSO. Since some variants of LASSO can be unified under the generalized LASSO framework, they can be transformed into the basic LASSO, and hence efficient LASSO solvers can be applied for the solution. Furthermore, under this framework, many different types of regression formulations such as the trend filtering in a recent study [35] can be unified.

Appendix A

Tibshirani and Taylor’s transformation method

Tibshirani and Taylor [5] proposed the following method to transform a generalized LASSO when rank(D) = m < p.

First a matrix D₀ ∈ ℝ(p − m) × p is found, whose rows are orthogonal to these in D. Then matrix $\tilde{\mathit{D}}=\left[\begin{array}{c}\hfill \mathit{D}\hfill \\ \hfill {\mathit{D}}_0\hfill \end{array}\right]\in {ℝ}^{p\times p}$ is a square matrix with full rank, and thus invertible.

For further use, let us define $\tilde{\mathit{D}}\mathit{x}=\left[\begin{array}{c}\hfill \mathit{D}\mathit{x}\hfill \\ \hfill {\mathit{D}}_0\mathit{x}\hfill \end{array}\right]\triangleq \left[\begin{array}{c}\hfill \mathit{u}\hfill \\ \hfill \mathit{\upsilon }\hfill \end{array}\right]$ with u and υ are column vectors of length m and p−m respectively, therefore $\mathit{x}={\tilde{\mathit{D}}}^{-1}\left[\begin{array}{c}\hfill \mathit{u}\hfill \\ \hfill \mathit{\upsilon }\hfill \end{array}\right]$, and the generalized LASSO criterion rereads

$$\frac{1}{2}{\Vert \mathit{y}-\mathit{A}{\tilde{\mathit{D}}}^{-1}\left[\begin{array}{c}\hfill \mathit{u}\hfill \\ \hfill \mathit{\upsilon }\hfill \end{array}\right]\Vert }^2+\lambda {\Vert \mathit{u}\Vert }_1.$$

Let’s also define

$$\mathit{A}{\tilde{\mathit{D}}}^{-1}=[{\mathit{A}}_1\hspace{1em}{\mathit{A}}_2],$$

where A₁ and A₂ are matrices of size n × m and n × (p − m) respectively. Above criterion rereads

$$\frac{1}{2}{\Vert \mathit{y}-{\mathit{A}}_1\mathit{u}-{\mathit{A}}_2\mathit{\upsilon }\Vert }^2+\lambda {\Vert \mathit{u}\Vert }_1.$$ (A.1)

which is a least sequare problem with respect to υ, and the solution is

$${\mathit{\upsilon }}^{*}={\mathit{A}}_2^{†}(\mathit{y}-{\mathit{A}}_1\mathit{u}),$$

where ${\mathit{A}}_2^{†}={({\mathit{A}}_2^T{\mathit{A}}_2)}^{-1}{\mathit{A}}_2^T$.

Finally, by substituting υ^* into (A.1), the generalized LASSO can be transformed into form (1) with

$$\mathit{H}={\mathit{A}}_1-{\mathit{A}}_2{\mathit{A}}_2^{†}{\mathit{A}}_1$$ (A.2)

$$\mathit{z}=({\mathit{I}}_n-{\mathit{A}}_2{\mathit{A}}_2^{†})\mathit{y}$$

Appendix B

The equivalence between Tibshirani and Taylor’s method and the proposed method in the current paper

In this appendix, we prove that H’s and z’s in form (2) and (A.2) are equal.

Appendix B.1. Equivalence of H’s

First, for further use let’s define Q₀ ≜ D₀R⁻¹ and

$${\left[\begin{array}{c}\hfill {\mathit{Q}}_2\hfill \\ \hfill {\mathit{Q}}_0\hfill \end{array}\right]}^{-1}\triangleq [{\mathit{P}}_2\hspace{1em}{\mathit{P}}_0],$$ (B.1)

where P₂ and P₀ are of size p × m and p × (p − m), respectively.

It is easy to verify that

$${\mathit{P}}_0^T{\mathit{Q}}_2^T=\mathbf{0},$$ (B.2)

$${\mathit{P}}_2{\mathit{Q}}_2+{\mathit{P}}_0{\mathit{Q}}_0=\mathit{I},$$ (B.3)

$${\mathit{Q}}_1{\mathit{P}}_2={\mathit{A}}_1,$$

$${\mathit{Q}}_1{\mathit{P}}_0={\mathit{A}}_2.$$ (B.4)

From (B.4), (6) and (B.2), we have

$${\mathit{A}}_2^T{\mathit{Q}}_1{\mathit{Q}}_2^T={\mathit{P}}_0^T{\mathit{Q}}_1^T{\mathit{Q}}_1{\mathit{Q}}_2^T={\mathit{P}}_0^T(\mathit{I}-{\mathit{Q}}_2^T{\mathit{Q}}_2){\mathit{Q}}_2^T=0.$$ (B.5)

Left multiply both sides of (B.3) with Q₁, and substitute resultant equation into (B.5), we have

$${\mathit{A}}_2^T({\mathit{A}}_1{\mathit{Q}}_2+{\mathit{A}}_2{\mathit{Q}}_0){\mathit{Q}}_2^T=\mathbf{0}.$$

Move the second part to the right side of equals sign, and left multiply both sides with ${({\mathit{A}}_2^T{\mathit{A}}_2)}^{-1}$, right multiply with ${({\mathit{Q}}_2{\mathit{Q}}_2^T)}^{-1}$, we have

$${\mathit{A}}_2^{†}{\mathit{A}}_1=-{\mathit{Q}}_0{\mathit{Q}}_2^{†}.$$

Left multiply both sides of above equation with −A₂, and add with A₁, we have

$${\mathit{A}}_1-{\mathit{A}}_2{\mathit{A}}_2^{†}{\mathit{A}}_1={\mathit{A}}_1+{\mathit{A}}_2{\mathit{Q}}_0{\mathit{Q}}_2^{†}.$$

The left side of above equation is H in (A.2), and the right side is equal to H in (2), since left multiply both sides of (B.3) with Q₁, and right multiply with ${\mathit{Q}}_2^{†}$ yields

$${\mathit{A}}_1+{\mathit{A}}_2{\mathit{Q}}_0{\mathit{Q}}_2^{†}={\mathit{Q}}_1{\mathit{Q}}_2^{†}.$$

Appendix B.2. Equivalence of z’s

To prove that z’s in (2) and (A.2) are equal, we have to prove

$${\mathit{Q}}_1{\mathit{Q}}_1^T-{\mathit{Q}}_1{\mathit{Q}}_2{\mathit{Q}}_2^{†}{\mathit{Q}}_1^T={\mathit{A}}_2{\mathit{A}}_2^{†}.$$

From (B.1), one can verify that

$$\mathit{I}-{\mathit{Q}}_2^{†}{\mathit{Q}}_2={\mathit{P}}_0{\mathit{P}}_0^{†}.$$

Left multiply both sides of above equation with Q₁, and right multiply with ${\mathit{Q}}_1^T$, we have

$${\mathit{Q}}_1{\mathit{Q}}_1^T-{\mathit{Q}}_1{\mathit{Q}}_2{\mathit{Q}}_2^{†}{\mathit{Q}}_1^T$$

$$={\mathit{Q}}_1{\mathit{P}}_0{\mathit{P}}_0^{†}{\mathit{Q}}_1^T$$

$$={\mathit{A}}_2{({\mathit{P}}_0^T{\mathit{P}}_0)}^{-1}{\mathit{A}}_2^T$$ using Eq. (B.4)

$$={\mathit{A}}_2{({\mathit{P}}_0^T{\mathit{P}}_0-{\mathit{P}}_0^T{\mathit{Q}}_2^T{\mathit{Q}}_2{\mathit{P}}_0)}^{-1}{\mathit{A}}_2^T$$ using Eq. (B.2)

$$={\mathit{A}}_2{({\mathit{P}}_0^T(\mathit{I}-{\mathit{Q}}_2^T{\mathit{Q}}_2){\mathit{P}}_0)}^{-1}{\mathit{A}}_2^T$$

$$={\mathit{A}}_2{({\mathit{P}}_0^T({\mathit{Q}}_1^T{\mathit{Q}}_1){\mathit{P}}_0)}^{-1}{\mathit{A}}_2^T$$ using Eq. (6)

$$={\mathit{A}}_2{\mathit{A}}_2^{†}$$ using Eq. (B.4)