Answering evolutionary questions: a guide for mechanistic biologists

Summary

The questions and methods of molecular biology and evolutionary biology are clearly distinct, yet a unified approach can lead to deep insights. Unfortunately, attempts to unify these approaches are fraught with pitfalls. In this informal series of questions and answers, we offer the mechanistically oriented biologist a set of steps to come up with evolutionarily reasonable and meaningful hypotheses. We emphasize the critical power and importance of carefully constructed null hypotheses, and we illustrate our ideas with examples representing a range of topics, from the biology of aging, to protein structure, to speciation, and more. We also stress the importance of mathematics as the lingua franca for biologists of all stripes, and encourage mechanistic biologists to seek out quantitative collaborators to build explicit mathematical models, making their assumptions explicit, and their logic clear and testable. Biologists in all realms of inquiry stand to gain from strong bridges between our disciplines.

Introduction: What is a “why” question?

There is a longstanding divide in biology [1]. Molecular, cellular and developmental biologists ask “how” questions about mechanisms, e.g. “How does X get built?” and “How does X operate?” [2]. Evolutionary biologists ask “why” questions, e.g. ‘Why is X prevalent?” and “Why will X continue to persist?” [2,3]. Unifying the two can lead to profound insights [4,5], but different questions require different approaches, and challenges often arise when one sort of biologist ventures into the territory of the other. This article is meant as a primer for biologists who have been trained to answer mechanistic “how” questions, but who also have an interest in and ideas about evolutionary “why” questions. We hope that reading this article will clarify how to think about evolution, while avoiding the most common pitfalls.

I think that Y is why X evolved. What do I need to do to convince people that I am right?

To do any kind of science, you need a null hypothesis. Your alternative hypothesis is that “Y is why X evolved”. Saying that “Y is not why X evolved” doesn’t count as a null hypothesis. You need a second, null explanation for why X could have evolved without Y. The null should be a really boring account of something necessarily true, as opposed to the more complex story that you are interested in. Of course, there may be multiple possible complex and interesting stories. But before you start trying to distinguish between those stories, you need to define a clear “null” story that has special status.

I can think of many alternative explanations, but they all seem equally complex. Which one deserves the special status of the null hypothesis?

In the classical statistical sense, a null model is a way of saying that X happened “by chance alone” [6]. In evolution, hypotheses about “chance alone” can be complicated, going beyond the usual statistical meaning of the term “null”, and it can take a lot of work to fully develop them. You need to do that work before you can even convince people that X is an observation that needs an evolutionary explanation that isn’t completely mundane and dull.

What do you mean? Of course X needs an explanation!

You still need to go through the process of proving the obvious. Let’s demonstrate this with an example. The fact that a protein must have a function (i.e., an evolutionary explanation for why it is there) is generally considered obvious, even when people disagree about what that function is. But even though nobody is advocating for a null model to explain the existence of proteins, the null model still exists, and can be clearly formulated and then formally rejected.

For this null model, we assume that we have a system in place capable of making proteins, including DNA, mRNA, and amino acids, and all the transcription and translation machinery. But according to the null model, our protein of interest is simply a product of random mutation, with no selection for any function. As you’ll see, this null is easy to reject. Three out of the 64 codons are stop codons. If we start translating at a random AUG, then by chance alone, we expect stop codons to arise, on average, every 64/3 ≈ 20 codons. The average open reading frame in a random transcript should be around 20 amino acids long. If our protein of interest were not much more than 20 amino acids long, we would accept our null hypothesis. Of course, far longer open reading frames are seen much more often than we would expect by chance alone. This is why we assume that proteins longer than about 100 amino acids require an evolutionary explanation [7]; we need to explain why they don’t disappear due to premature stop codon mutations.

For whatever observation X that you have in mind, try to construct an equally compelling case for why your observation X cannot be explained by a null model.

Could something interesting ever be explained by such a boring null model?

Sure. Let’s start with the question “Why do organisms senesce?” That is, why does physiological function and survival decline with age? Starting with Weismann [8], many people have argued that aging must have some direct, adaptive benefit, given that its high costs affect everyone over a certain age. Against this seemingly compelling logic, what might a null hypothesis of aging look like?

The answer dates back to early work on the genetics of Huntington’s Disease (HD) by the renowned evolutionary geneticist, J.B.S. Haldane [9]. Julia Bell had shown in the 1930s that HD was caused by a dominant mutation. But HD is lethal. Surely natural selection should have rid the population of this dominant lethal allele. So why was HD so prevalent in some populations? Rather than come up with an adaptive explanation, Haldane asked if it was possible that HD is as common as it is for non-adaptive reasons. He realized that if HD were expressed late enough in life, then by the time carriers of the HD mutation became sick, they could have already passed it on to their children, and their children could have passed it along, in turn, to their children. So HD might be as common as it is because HD mutations appear by chance, and natural selection at late age is too weak to remove them quickly. We consider this explanation a null hypothesis because it explains an evolutionary phenomenon—the persistence of a deleterious allele—without having to invoke selection or adaptation.

A few years later, in his ‘mutation accumulation’ (MA) model of aging, Peter Medawar [10] recognized that this null hypothesis could be extended to all late-acting mutations—not just lethal ones like HD, but also mutations with weak deleterious effects. We can understand the evolution of aging in terms of the lack of natural selection acting at late age. By default, things fall apart with age, because the ability of selection to purge the genome of deleterious mutations declines with age. Mutations tend to make things fall apart quicker, not slower. Natural selection has helped to weed out such mutations, and to slow down the process of falling apart. When organisms fall apart anyway, the default hypothesis is that there is not enough natural selection to perfect the organism, not that the aging we see must in some way be the best of all possible outcomes, chosen by natural selection.

How could I falsify the mutation accumulation theory of aging in favor of an adaptive one?

Deleterious mutations are inevitable, as is the age-related decline in the ability of selection to purge those mutations. As such, from an evolutionary perspective, MA is an intrinsic, or ‘null’, hypothesis. How might we falsify this hypothesis? This question leads us into the realm of mathematical models, which are critically important in evolutionary biology [11–13]. W.D. Hamilton developed a formal mathematical model of MA in 1966 [14]. Hamilton’s model starts from a set of premises, and through a process of deduction arrives at the conclusion that senescence (increasing mortality with age) will happen, because selection fails to weed out deleterious mutations if they act on older individuals.

Qualitatively, the only way to falsify this conclusion is to falsify at least one premise. That will be hard; for example, Hamilton assumes that mutations that make something function worse are more common that those that make things function better; the truth of this assumption seems self-evident. The other premises are that selection acts to make things function better, and that there exist mutations with age-dependent effects. From this, he is able to deduce that the strength of selection declines with age, leading to senescence. All the premises seem watertight, at least for organisms in which “age” has a clear definition with respect to the time since an “individual” was “born”.

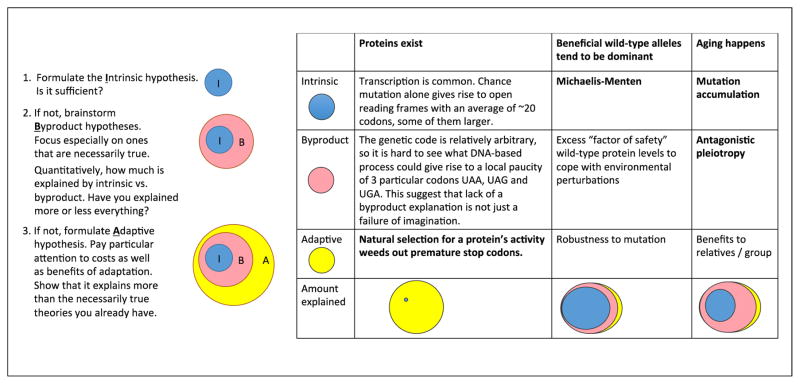
Quantitatively, your prospects for falsifying MA are brighter. You could try to argue that while some amount of aging follows inevitably from the uncontroversial premises of the MA theory, the aging we see in the real world is too fast, relative to how much selection still goes on in old organisms. In other words, there is too much aging; selection should have been strong enough to reduce it to a lower level. Then you propose a model that includes both MA (which must necessarily be happening all the time) and an additional component that describes your alternative theory. Then you could ask, in your combined model, what percentage of aging is explained by MA and what percentage by the additional component (Fig. 1; relative sizes of circles).

Figure 1.

A) Evolutionary biologists give intrinsic hypotheses priority over byproduct hypotheses, and adaptive hypotheses are considered only after all else fails. B) Three examples of the contrast between intrinsic vs. byproduct vs. adaptive explanations of a phenomenon. The consensus on how much of the phenomenon is explained by each level is shown by the relative sizes of the ellipses. The primary explanations are in bold.

You could also argue that some patterns in how aging works cannot be explained by MA alone. For example, eusocial ant queens can live up to three decades, while a female worker carrying the identical load of deleterious mutations lives just a few months.

What if there are multiple alternative theories?

Evolutionary biologists recognize three types of theories to explain some phenomenon X: null or ‘intrinsic’ theories such as MA, adaptive theories, and byproduct theories [15] (Fig. 1). We have already considered an intrinsic theory (MA to explain aging) and an adaptive one (selection on protein function to explain long ORFs). An adaptive hypothesis assumes that the reason why X evolved is because X is, in itself, a good thing from the perspective of natural selection. The danger of adaptive hypotheses is that they are too easy to come up with [16]. To guard against this temptation, evolutionary biologists set a higher bar for adaptive hypotheses than they do for other kinds of hypotheses, requiring scientists to find reasons to reject not only intrinsic theories, but also to reject a third type of theory known as a byproduct hypothesis.

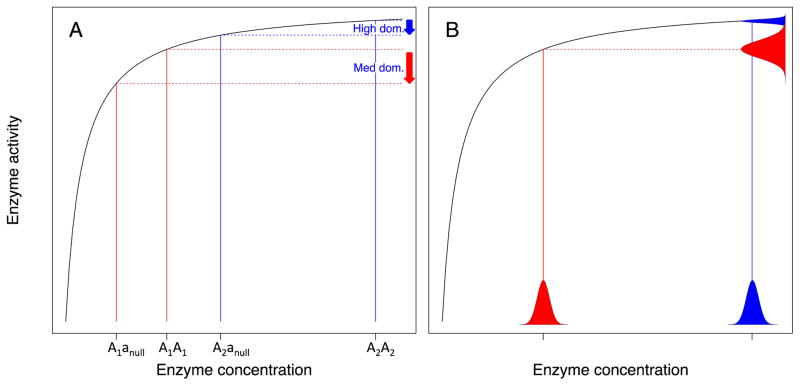
A byproduct hypothesis assumes that the trait of interest evolved due to selection not for the trait itself, but rather for some other related trait. Let’s consider the evolution of dominance. Most wild-type genes are dominant, and most deleterious mutations are recessive. The evolutionary geneticist and statistician R.A. Fisher believed that this was so because dominance provides an adaptive advantage, protecting carriers of single copies from the deleterious effects of the mutations that took away their other copy [17]. However, genes automatically exhibit some intrinsic level of dominance when enzyme activity follows Michaelis-Menten kinetics, where the activity increases initially with enzyme level, but then levels off at some asymptotic value of activity (Fig. 2A). While Fisher’s adaptive explanation requires that more genetic dominance than the intrinsic minimum is in itself useful, byproduct explanations posit an adaptive advantage to having an excess of enzyme as a precaution against environmental fluctuations (Fig. 2B), with increased robustness to heterozygous mutations (i.e., dominance) tagging along as a mere byproduct [18].

Figure 2.

A) Michaelis-Menten curves intrinsically give rise to dominance, i.e. when you halve the amount of enzyme in a heterozygous knockout, the amount of enzyme activity is reduced by less than a factor of two. However, different dominant alleles may reside in different portions of the curve, corresponding to more (A₂A₂ genotype, blue arrow) or less (A₁A₁ genotype, red arrow) dominance; this opens the way for adaptive or byproduct explanations for why we see high dominance rather than medium dominance. B) In one version of the byproduct explanation, genotypes with higher concentration (blue versus red) will show less variation in enzyme activity (blue and red histograms on vertical axis) in response to equivalent stochastic perturbations (blue and red histograms on horizontal axis). Thus, genetic dominance is a byproduct of selection for enzyme activity to be robust to environmental fluctuations in enzyme concentration.

How do these three types of hypotheses play out for aging?

MA is an intrinsic hypothesis: there is no adaptation going on, simply selection that is too weak to prevent aging. In his ‘Antagonistic Pleiotropy’ model, George Williams [19] took Medawar’s idea of MA and added a byproduct hypothesis. He posited a trade-off, whereby maximizing early-age fitness costs something—genes that increase fertility early in life are associated with higher mortality later in life. Just as high levels of dominance might be a byproduct of selection for environmental robustness, rapid rates of aging might be a byproduct of selection for high early-age fitness.

What about the final level—aging as an adaptation? Adaptive hypotheses of aging and death [20–22] tend to focus on the good of the group. Growing old and dying is obviously bad for you. According to an adaptive hypothesis, your younger relatives, who share some of your genes, benefit enough from your old age and death to make up for the loss.

Assuming you agree that the data are sufficient to reject MA, it may be difficult to distinguish between adaptive and byproduct hypotheses. Because adaptive hypotheses are so easy to come up with, some argue that we should, a priori, give byproduct hypotheses greater weight in cases of inconclusive evidence [16], yielding a priority system of intrinsic, then byproduct, then adaptive (Fig. 1). Alternatively, once the intrinsic hypothesis is found wanting, we could take byproduct and adaptive hypotheses equally seriously.

Mathematical models play a critical role in how evolutionary biologists decide between theories [13]. A mathematical model that starts from premises that everybody agrees are true, and that arrives at the phenomenon by deduction alone, earns the automatic right to be at least a component of future theories, irrespective of its position in the hierarchy of intrinsic vs. byproduct vs. adaptive hypotheses. A mathematical model that shows “proof of principle” that something can happen, depending on what the parameter values and other specific model assumptions are, is not as powerful, although it is still a good thing. Measuring parameters can sometimes help convert a proof of principle model into a model of what must necessarily be true.

These theories of aging don’t say anything about telomeres/oxidative damage/proteostasis/etc. Should I reject them for a theory that does?

This gets at the distinction between proximate “how” questions and evolutionary “why” questions. Telomeres etc. tell us something about how aging happens. Mutation accumulation and antagonistic pleiotropy tell us why. Often, exactly the same “why” model works for many different “how” theories. For example, a mathematical model of evolution under the disposable soma theory [23] assumes that it costs time and energy to prevent things falling apart; this assumption is true no matter which component of the organism you think is the most important/expensive to keep repairing. The core facts about molecular mechanisms appear only in an abstract, stylized form in the assumptions of the mathematical model of evolution. Often, many different molecular mechanisms can be described by the same equations.

How did evolutionary biology and mechanistic biology grow so far apart – aren’t they both biology, after all?

They didn’t grow apart – they were never together to begin with. Traditional biological disciplines such as zoology and botany made little contribution to the birth of modern mechanistic biology. Instead, many of the founders of molecular biology brought training, techniques and concepts from physics, chemistry and physical chemistry [24]. Genetics and microbiology were among the few points of contact between evolutionary biologists who went out in the world to study the diversity of living things that they found there, and mechanistic biologists who developed tools to delve deeper into a relatively small number of model systems.

Many early figures in molecular biology took an active philosophical interest in evolution, most prominently Monod [25] and Jacob [26]. However, relatively few contributed to concrete research questions in evolutionary biology, with Zuckerkandl and Pauling [27] and Luria and Delbrück [28] as prominent exceptions. Interestingly, the former pair founded the new field of molecular evolution [29], while the latter’s canonical experiment became fossilized in textbooks with limited follow-up research on microbial evolution for several decades [30].

What will it take to truly bring the fields together?

It is obviously no easy task to address questions that merge the tools and concepts of molecular biology with those of evolutionary biology, in a way that satisfies experts in both fields. Even among sub-disciplines that we consider as falling within the purview of evolution, such integration has not always been easy. To illustrate the challenges of expanding the (relatively) new disciplines of mechanistic biology in more evolutionary directions, it is useful to look historically at how the “old” pre-evolutionary disciplines of zoology, botany, paleontology, genetics etc. needed to change in order to arrive at modern evolutionary thought. This tumultuous process is known to historians as the “modern evolutionary synthesis”, in reference to the synthesis between what had previously seemed irreconcilable differences between Mendelian discontinuities (e.g., dwarf vs. normal plants) and the continuously distributed traits observed by naturalists (e.g., a full spectrum between tall and short). This true synthesis was accomplished by the mathematical models of population genetics [31], which showed how combinations of Mendelian genes could generate continuous traits.

Mendelian genetics and Darwinian theory were united, with the help of population genetics. However, the many other fields that participated in the so-called synthesis did not, in fact, undergo integration of their separate disciplines into one; their transformation during the 1930s and 1940s is more accurately described as the “modern evolutionary constriction” [32]. The modern evolutionary synthesis defined a set of factors capable of influencing evolution (natural selection, population structure, random genetic drift, mutation, recombination, assortative mating, etc.), and a mathematical language for describing those factors. Anything that didn’t fit within that framework was purged [32,33], such as the idea that ontogeny recapitulating phylogeny is an organizing principle of evolution. Non-Mendelian inheritance, especially the inheritance of acquired traits, was also constricted at this time, and what was previously ascribed to forces of progress or purpose became the purview of natural selection.

The use of mathematical language to describe evolutionary ideas gave rise to the claim, to rephrase Dobzhansky’s famous statement, that “nothing in evolution makes sense except in the light of population genetics” [34], and left the disciplines at least consistent, if not synthesized, with one another. Consensus was not part of the synthetic deal; indeed scientists continue to disagree forcefully about the relative importance of the various allowed factors, within a mutually compatible framework. A discipline effectively “joined” the synthesis when it purged incompatible ideas, while continuing to do good science.

Mechanistic biology has not yet undergone this painful purging process. Evolutionarily taboo language comparing “higher” and “lower” species is not uncommon within mechanistic fields, accompanied by an expectation that humans are somehow evolutionarily special. The “Panglossian Paradigm” [16], that everything in biology is exactly as it should be, is also strong. For example, biochemists talk freely about “structure-function relationships” as though function were the only reason for a structure, whereas in evolutionary biology, claims about the “function” of a structure or behavior require a considerable amount of evidence to exclude null hypotheses [34,35], as discussed above for aging, dominance, and protein-coding status. Because the modern evolutionary synthesis was actually a process of purging, in order to join, mechanistic biology must similarly purge itself of implicit concepts of progress and assumptions of perfect functionality.

How do you express mechanistic biology in the language of theoretical population genetics?

For those who want to discover the evolutionary causes for the phenomena that they observe, we have already suggested that one needs to start with an appropriate null hypothesis. To formulate null and other hypotheses, evolutionary biologists often turn to the classical language of population genetics—mathematics. When arguments are expressed in terms of equations, the assumptions and derivations can be rigorously evaluated and tested in a way often not possible with verbal models [11–13].

Mathematical models can describe the mapping of genotypes (together with the developmental environment) onto phenotypes, and the mapping of phenotypes (together with the selective environment) onto survival and reproduction (i.e., fitness). The mathematical foundations of the modern synthesis simplified this, by using simple direct maps of genotypes to fitness, in the process ignoring most of mechanistic biology.

Modern mechanistic biology can fill this gap, giving us information about the complex relationship between genotypes and phenotypes. This information can sometimes be stylized into simple models, for example, Michaelis-Menten enzyme kinetics, which played a prominent role in the arguments about the evolution of dominance discussed above. Mechanistic knowledge about the genotype-phenotype map can be integrated with reasonable assumptions about the phenotype-fitness map, leading to a much better description of evolution than would otherwise be possible [36].

Unfortunately, the need to express population genetics in precise mathematical language can become an obstacle for some mechanistic biologists. For those who want to integrate mechanistic and evolutionary biology, we strongly encourage them to pursue a high level of quantitative training.

How much overlap is going on already?

We already see many examples where the distinction between mechanistic and evolutionary biology blurs. For example, genetic screens using mutagenesis date back almost a hundred years to early work with the fruit fly, Drosophila melanogaster. This approach has enabled geneticists to ask which gene, if altered, would change a focal phenotype. Historically, mutations acted randomly throughout the genome. Today, we can knock out or overexpress target genes of interest.

In a tour de force of induced global mutagenesis in Drosophila, Nüsslein Volhard and colleagues found a large set of genes any one of which, when knocked out, led to embryonic lethality [37]. Close analysis of these mutations enabled this team to identify the cascade of interacting genes responsible for the transition from a relatively unformed egg to a highly differentiated, fully formed adult fly.

A recent evolutionary study used a similar approach, but reversed the concept. Rather than looking for genes that caused embryonic lethality, they sought genes that eliminated embryonic lethality. Two widely distributed and well-studied species of fruit fly, D. melanogaster and D. simulans, are phenotypically almost completely identical. However, when these two species mate, they only produce hybrid daughters. Male embryos are non-viable. The genetic basis of hybrid lethality is a topic of long-standing interest to evolutionary biologists [38–40]. Phadnis et al. [41] mutagenized thousands of D. simulans males, mated these males to D. melanogaster females, and asked which genes, when knocked out, led to viable hybrid sons. Thus, borrowing an approach from molecular biology, Phadnis and colleagues were able to identify a key piece of the puzzle in the genetics of speciation. They go on to ask why the particular gene they discovered might do what it does—a topic beyond the scope of our review. But it is important to keep in mind that molecular studies of embryo inviability are driven more by questions of exactly how changing a focal gene makes things go wrong, instead of the question of why changes to that particular gene are the ones that, historically speaking, did make things go wrong. The smooth transition in this example from how-it-hypothetically-would to why-it-actually-did illustrates the porous nature of the divide between the two disciplines.

There are two main approaches to create overlap among molecular and evolutionary approaches. The focus of the current article is how to use mechanistic insights to answer evolutionary questions. Lying outside the scope of this article are the various ways that evolutionary insights can answer mechanistic questions. For example, researchers have used co-evolutionary patterns between amino acid residues to predict protein structures [42]. In vitro evolution has been used to create novel proteins with new functions (e.g. [43]). And comparative evo-devo approaches are routinely used to identify genes that are mechanistically important in developmental processes.

How much of this overlap involves falsifying null hypotheses in favor of adaptive ones, and how much involves poking null-hypothesis-sized holes in things that used to be uncontroversial?

That depends on how much flawed evolutionary thinking needs to be purged from the relevant field of mechanistic biology. When purging is needed, the first step of the synthesis will usually entail poking holes in those weak ideas that have not been considered controversial, but perhaps should be. After the purging, new synthetic questions can open up. Let’s consider another example of how this plays out. Most proteins are only marginally thermostable, and biochemists used to think that this must be for adaptive reasons; too much stability was presumed to get in the way of the flexibility needed for function. But if destabilizing mutations are much more common than stabilizing ones, then mutation-selection balance—the process whereby mutation continually generates deleterious mutations, and selection later eliminates them—can lead to marginal protein stability, even if there is no selective advantage to the marginal nature of the stable fold [44]. This argument against casual assumptions of adaptation, expressed in the mathematical language of population genetics, was later confirmed by the construction of super-stable proteins that remained fully functional [45]. Mathematical models of mutation-selection balance explain why extant proteins aren’t super-stable, given their full functionality and additional robustness. Understanding protein evolution as a struggle to find adaptations among a sea of destabilizing mutations opened up new lines of research that blur the lines between evolutionary biology and mechanistic biology [46]; this is a great example of the true synthesis underway today.

So is showing that a phenomenon could be non-adaptive enough to win most of the battle?

It’s a start, but it still has to lead to a research program. Let’s look at another example: errors in gene expression. It has been crudely estimated that at least 15% of proteins have an amino acid misincorporated during translation, and of course many more proteins contain other kinds of errors too [47]. It isn’t plausible that such a high frequency of mistakes could be adaptive. It was also long ago demonstrated that there is no intrinsic limitation to lower rates of error; higher fidelity strains can be constructed, but they grow more slowly [48]. This evidence suggests that translational error rates are high as a byproduct of a cost of fidelity. In other words, a nonadaptive hypothesis can explain high error rates.

Interestingly, this knowledge had little effect on molecular biology for a long time. Molecular biologists continued to think of a one-to-one relationship between DNA sequence and protein, even in the face of evidence suggesting that a high proportion of proteins were flawed. Perhaps non-adaptive phenomena garner less attention than adaptive phenomena. But with recent renewed interest in non-adaptive hypotheses in molecular biology, scientists have started paying more attention to error rates. For example, recent studies by one of us used the ubiquity of errors to explain the puzzling phenomenon of the de novo birth of protein-coding genes from previously non-coding sequences [49]. When “non-coding” sequences are translated due to gene expression errors, this gives selection an opportunity to “pre-select” out the most deleterious options [50]; those that remain are more likely to persist as functional new coding genes after a mutation brings their expression to higher levels. Mathematical models show how this fortuitous pre-selection is an automatic consequence of the non-adaptive phenomenon of high error rates [50].

Conclusion: This was interesting, but you didn’t say anything about my favorite theory and my favorite evolutionary hypothesis about it. Where do I go from here?

Keep in mind that an evolutionarily plausible null model can require some careful thinking. Once you have figured out a null model, and have some intuition about why that null model can be rejected, try talking to someone who has trained as an evolutionary biologist. Great things can happen when people with complementary expertise talk to one another. You are the expert in X. The evolutionary biologist may know nothing about X, but is an expert in what sort of evidence is needed to answer “why” questions. We hope this primer will help that conversation go more smoothly, and lead to a wonderful collaboration.