Discerning the Catalytic Mechanism of Staphylococcus aureus Sortase A with QM/MM Free Energy Calculations

Abstract

Sortases are key virulence factors in Gram-positive bacteria. These enzymes embed surface proteins in the cell wall through a transpeptidation reaction that involves recognizing a penta-peptide “sorting signal” in a target protein, cleaving it, and covalently attaching it to a second substrate that is later inserted into the cell wall. Although well studied, several aspects of the mechanism by which sortases perform these functions remains unclear. In particular, experiments have revealed two potential sorting signal binding motifs: a “Threonine-Out” (Thr-Out) structure in which the catalytically critical threonine residues protrudes into solution, and a “Threonine-In” (Thr-In) configuration in which this residue inserts into the binding site. To determine which of these is the biologically relevant state, we have performed a series of conventional and hybrid quantum mechanics/molecular mechanics (QM/MM) molecular dynamics simulations of the Staphylococcus aureus Sortase A (SrtA) enzyme bound to a sorting signal substrate. Through the use of multi-dimensional metadynamics, our simulations were able to both map the acylation mechanism of SrtA in the Thr-In and Thr-Out states, as well as determine the free energy minima and barriers along these reactions. Results indicate that in both states the catalytic mechanisms are similar, however the free energy barriers are lower in the Thr-In configuration, suggesting that Thr-In is the catalytically relevant state. This has important implications for advancing our understanding of the mechanisms of sortase enzymes, as well we for future structure based drug design efforts aimed at inhibiting sortase function in vivo.

1. Introduction

Bacterial cell walls are decorated with surface proteins that play key roles in several pathogenic activities including cellular adhesion, host invasion, and evasion of the immune response [1, 2]. In Gram-positive bacteria, these proteins are covalently attached to the cell wall through a mechanism that is dependent on sortase enzymes [3, 4]. The functioning of sortases is therefore directly linked to bacterial virulence, and indeed knockout strains of Staphylococcus aureus, Streptococcus pneumonia, and Listeria monocytogenes have been shown to be less pathogenic than their wild type counterparts [5, 6, 7]. These observations have motivated recent drug-discovery efforts that focus on inhibiting sortases, as antimicrobial compounds that reduce pathogenicity may be more resistant to selective pressures than traditional therapeutics [8, 9, 10]. However, before the potential of these efforts can be fully realized, a more complete understanding of the structure/function relationship in sortases is required.

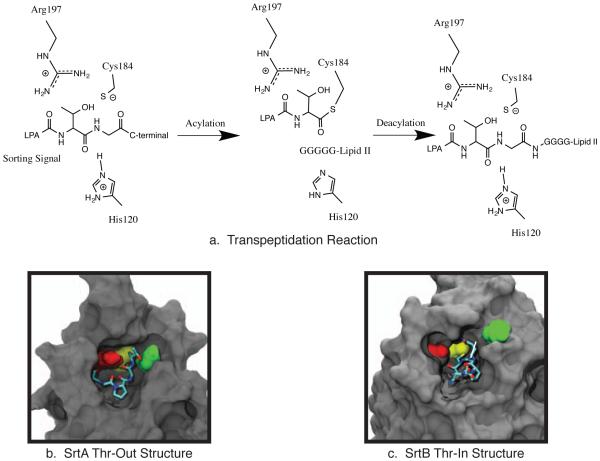
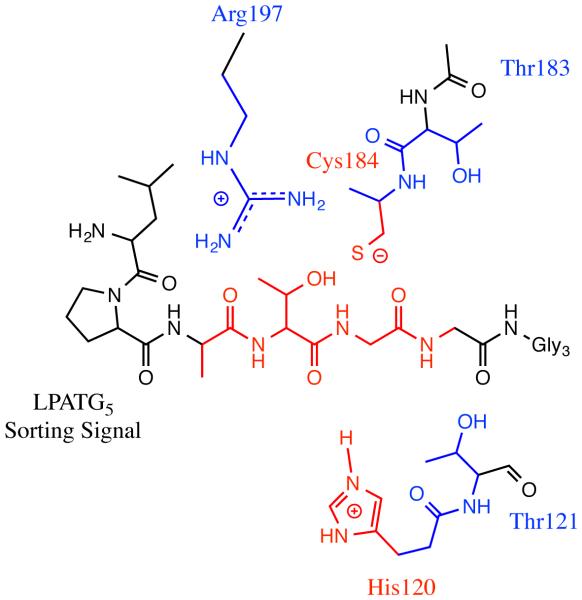
The prototypical sortase is the Staphylococcus aureus class A sortase (SrtA) enzyme. SrtA recognizes an LPXTG “sorting signal” (SS) motif in the protein destined to be embedded in the cell wall (the first substrate of catalysis) and then catalyzes a transpeptidation reaction that transfers the target protein to a lipid II molecule (the second substrate of catalysis) that is later incorporated into the cell wall [11, 12, 13]. The physical basis for this transpeptidation mechanism follows two steps. First, the target protein binds to the sortase through its sorting signal, and in the acylation step the SS is cleaved between the threonine and glycine residues and the target protein is covalently attached to SrtA. Second, a deacylation step occurs in which the target protein is transferred to the N-terminal glycine chain of a lipid II molecule (Figure 1a). Mutagenesis and biochemical experiments have indicated that SrtA uses the catalytic triad of His120, Cys184, and Arg197 in a reverse protonation mechanism to perform this function [11, 14, 15, 16, 17, 18]. In this mechanism, His120 and Cys184 typically exist in a neutrally charged/inactive state, however the system transiently samples an active configuration that has both a deprotonated/negatively charged Cys184 and a protonated/positively charged His120 residue [17, 18]. When this occurs, the cysteine thiolate anion attacks the carbonyl of the SS Thr-Gly bond, whereas the histidine protonates the SS leaving group.

Figure 1.

a. The transpeptidation reaction catalyzed by SrtA involves two steps: an acylation reaction in which the sorting signal is cleaved and covalently attached to Cys184, and a deacetylation reaction in which the surface protein is transferred to a lipid II molecule. b. The “threonine out” (Thr-Out) configuration observed in the SrtA NMR structure [19]. c. The “threonine in” (Thr-In) configuration observed in the SrtB crystal structure [20].

Significant insight into the structural basis for the SrtA transpeptidation mechanism was provided by Suree et al. when they reported the NMR-derived solution structure of SrtA covalently bound to a sorting signal analog [19]. By examining the acyl-enzyme intermediate, they were able to show that sortases function by an “induced fit” mechanism that involves an opening of the β7/β8 loop to accommodate the SS in the active site, along with a closing of the β6/β7 loop to form a hydrophobic pocket that recognizes the leucine and proline SS residues. This structure was the first reported sortase/substrate bound structure that could explain the roles of each residue in the catalytic triad. Molecular dynamics (MD) simulations based on this model demonstrated that the substrate bound states of the β6/β7 and β7/β8 loops are highly stable on the hundreds of nanoseconds timescale and do not sample conformations observed in the substrate free crystal structure [21], even when the sorting signal is removed [22].

More recently, Jacobitz et al. solved the crystal structure of a similar sortase enzyme, Staphylococcus aureus sortase B (SrtB), bound to an analog of its NPQTN sorting signal substrate [20]. Although many of the same induced fit characteristics were observed in SrtB as in SrtA, there was an intriguing difference in the SS conformation. In SrtA, the sidechain of the SS threonine residue protruded into solution, while the alanine sidechain was inserted into the active site pocket (see Figure 1b). However, in SrtB the threonine sidechain was inserted into the active site, whereas the sidechain of the third SS residue, which in SrtB is a glutamine, was pointed into solution (Figure 1c). Multiple lines of evidence lead to the hypothesis that the “Thr-In” state of SrtB is the more catalytically active configuration than the previously solved “Thr-Out” state observed in SrtA. First, the Thr-In configuration creates hydrogen bonds that help stabilize the position of the catalytically important arginine residue such that it creates an oxyanion hole. Second, insertion of the threonine sidechain into the sortase active site creates a mechanism for recognition of the threonine residue, which has been shown to be critical for substrate binding [23]. Finally, positioning the sidechain of the third SS residue in solution provides an explanation for the lack of specificity observed at this position in SS recognition by SrtA [23].

To address whether the Thr-In position is the catalytically active state in SrtA, we previously performed MD simulations using an umbrella sampling protocol to determine the free energy differences between Thr-In and Thr-Out in both SrtA and SrtB [20]. The results revealed that in the acyl-enzyme intermediate, SrtA can adopt both a Thr-In and Thr-Out state, however SrtB could only accommodate a SS in the Thr-In state. Furthermore, although the free energy barriers between the Thr-In and Thr-Out states were relatively low for a sorting signal substrate (on the order of a few kcal/mol), the path between these states suggested that these barriers would be significantly increased in a full-length protein substrate. Therefore, we expect the interconversion rate between these two states to be significantly slower than the transpeptidation reaction in vivo. Taken together, although it has not been experimentally observed, the evidence suggests that the Thr-In state is also present in SrtA and it may be the more biologically active SS configuration.

To test the hypothesis that the Thr-In state is more catalytically active than Thr-Out in SrtA, we performed a series of conventional and hybrid quantum mechanics/molecular mechanics (QM/MM) MD simulations of the SS/SrtA complex in both states. Our protocol involved multiple steps that were repeated for both states, including: (1) generating and equilibrating initial models of the non-covalently bound SS/SrtA complexes, (2) deriving several approximate reactant (noncovalently bound SS/SrtA complexes) and product (acyl-enzyme intermediate) configurations, (3) computing multiple approximate reaction pathways, and (4) performing extensive metadynamics calculations to compute the potentials of mean force (PMFs) for the acylation reaction with semiempirical QM calculations. Results indicate that the reaction mechanisms for Thr-In and Thr-Out are similar, however the free energy barriers are lower in Thr-In, suggesting this is the catalytically relevant state.

Methods

Model Generation

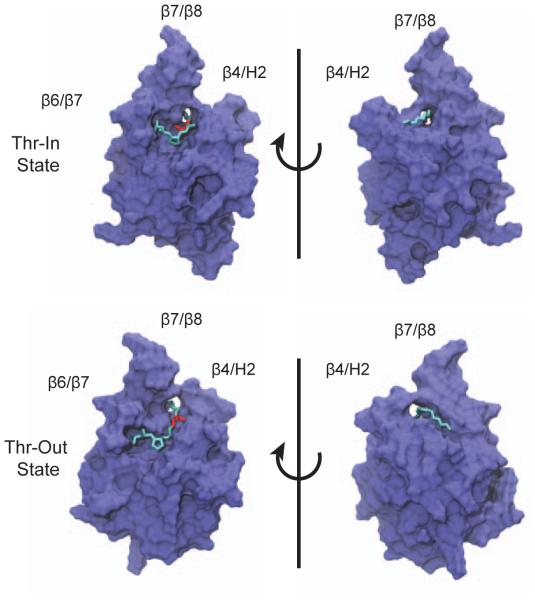
Initial coordinates for the SrtA protein and the catalytically important Ca²⁺ ion were taken from the first model in the 2KID NMR structure [19]. Although 20 models are in 2KID, they are highly similar to one another with an average backbone RMSD of 0.55 Å between structures. Therefore, the choice of an initial model likely has little effect on the simulations that follow. For both the Thr-In and Thr-Out structures, initial configurations of the SS were derived by aligning the LPAT sequence to the appropriate experimental structure, which in the case of Thr-Out is the 2KID SrtA structure and for Thr-In is the 4LFD SrtB structure [20]. The penta-glycine tail was constructed by iterative rounds of manual placement of a glycine residue and energy minimization of the structure using the Maestro modeling suite (version 10.0, Schrödinger, LLC, New York, NY, 2014). Refinement of these geometries was performed with the FlexPepDock Refinement protocol in the Rosetta protein modeling suite [24]. For both Thr-In and Thr-Out, 500 candidate structures were generated, and the diversity of conformations was increased through the use of a centroidmode optimization step for half of these structures. For each state, the top-scoring structure was used for further simulations. Similar calculations were performed for alternative initial configurations of the penta-glycine chain, however configurations similar to those depicted in Figure 2 were consistently the best-scoring with the Rosetta force field.

Figure 2.

Initial configurations for SrtA Thr-In (top) and Thr-Out (bottom) simulations. The sorting signal threonine is shown in red, whereas the rest of the sorting signal is in cyan.

Molecular Dynamics Simulations

Structures generated with Rosetta were solvated in a box of TIP3P water [25], with a minimum spacing of 10 Å between protein heavy atoms and the box edges using the tleap program in AmberTools [26]. Three chloride ions were added to neutralize the system. The FF99SB-ILDN force field was used for all protein parameters [27, 28]. A three stage minimization was used in which the restraints on the solute heavy atoms were gradually reduced, followed by a stage of unrestrained minimization. For each MD simulation, an initial 300 ps equilibration was performed in which the restraints on all solute heavy atoms were reduced, which was followed by an additional 700 ps of simulation in which the CA, C, and N atoms of the SS were restrained with a harmonic force constant of 0.1 kcal/mol/Ų. Simulations were then run for an additional 24 ns of unrestrained MD. All simulations were performed in the NPT ensemble with a Berendsen barostat with a time constant of 1 ps, and a collision frequency of 2 ps⁻¹ for Langevin dynamics [29]. Short range non-bonded interactions were truncated at 10 Å, while long-range electrostatics were treated with the particle mesh Ewald method [30]. SHAKE was used for constraining hydrogen containing bonds, and a 2 fs timestep was used for integration [31]. All simulations were run with the GPU accelerated version of PMEMD in the AMBER suite [32]. VMD, Gromacs, and CPPTRAJ were used for analysis [33, 34, 35].

To estimate the SS binding affinity, the final 20 ns of each trajectory was post-processed with a Molecular Mechanics/Poisson Boltzmann Surface Area (MM/PBSA) analysis [36]. Here, a “single trajectory” approach was used in which the difference in energy terms was computed based on separate analysis of the same trajectory file partitioned into “complex” (SrtA and SS), “receptor” (SrtA), and “ligand” (SS) molecules. For PB calculations, a solvent probe of 1.4 Å was used, and the molarity was set to 150 mM. The non-polar contribution to binding was based on a linear scaling of the solvent accessible surface area, with a scaling factor of .005 kcal/mol/Ų. To estimate the configurational entropy term, T ΔS_config , a quasi-harmonic (QH) analysis was performed for the complex, as well as the SrtA protein and SS [37]. To account for the sampling-dependence of quasi-harmonic analysis, a series of QH calculations were performed on progressively longer simulation segments, and the results were fit to:

$$S\left(t\right)=S_{inf}-\frac{\beta }{t^{\alpha }}$$ (1)

with β and α chosen to best fit the data [38, 39]. The value for infinitely long simulations, S_inf , was used for all reported entropy values. Error estimates are the standard error of the mean, with the number of independent data points computed by dividing the total number of simulation frames analyzed by the statistical inefficiency, as computed with the PyMBAR package [40].

QM/MM Simulations

Semiempirical QM/MM calculations were performed using the Density Functional Theorybased tight-binding (DFTB) Hamiltonian for atoms in the quantum region [41, 42]. Two quantum regions were used in this work, the “small” region which comprises the His120 and Cys184 sidechains, along with the ATG segment of the SS, and a “large” regions which included His120, Thr121, Thr183, Cys184, the sidechain of Arg197, and the ATG segment of the SS (see Figure 3). When the large region was used, dispersion effects were also included [43]. QM/MM simulations used similar parameters to the MD simulations described above, except SHAKE was not used for constraining bonds, the timestep was set to 1 fs, and simulations were performed with sander.

Figure 3.

QM/MM partitioning scheme used. The red region represents the “small” QM region, and the combined red and blue regions represent the “large” QM region.

Initial reaction pathways were generated from MD snapshots through a combination of steered MD, simulated annealing, and nudged elastic band (NEB) simulations [44]. First, reactant and product structures were setup with steered molecular dynamics (SMD) simulations. For each configuration, 5 ps of SMD was performed with the small QM region in which the reaction coordinate was the sum of the C_Thr-N_Gly and S_Cys-C_Thr distances, the harmonic force constant was set to 500 kcal/mol/Ų, and the target sum of distances was 7.5 and 2.8 Šfor reactant and product respectively. Following this, five independent simulated annealing runs were performed for both the product and reactant states. In each run, 56 ps of annealing was first performed with the small QM region in which the temperature was heated to 400 K and then slowly cooled to 0 K. This was followed by an additional 56 ps of annealing that was performed with the large QM region. The product and reactant state structures with the lowest QM energies following this procedure were chosen as end states for NEB calculations. In NEB simulations, the RMS alignment and NEB forces were performed on the four atoms involved in the acetylation reaction (the C_Thr , S_Cys, N_Gly , and H_His), a spring constant of 50 kcal/mol/Ų, and 24 windows were used. Coordinates were heated to 300 K over 15 ps, equilibrated for 25 ps, and then cooled to 0 K over 25 ps. This procedure was performed first for the small QM region, and then again for the large QM region. To improve sampling near the transition state, a third set of NEB calculations was performed with the large QM region and end structures taken from the two midpoints of the second NEB simulation.

Multiple-walker, well-tempered metadynamics calculations were performed using version 1.3 of the PLUMED plugin for sander [45, 46, 47]. Thirty-two NEB configurations were used, and from each one, four simulations were initiated for a total of 128 windows for each PMF. Four reaction coordinates were used: the C_Thr-N_Gly , H_His-N_His, S_Cys-C_Thr , and H_His-N_Gly distances. For each reaction coordinate, Gaussians of width 0.1 Å were deposited every 50 steps. The initial height of the hills was 1.5 kcal/mol, which was decreased following the welltempered protocol using a bias factor of 40 (corresponding to a CV temperature of 12000 K). To restrict the conformational space accessible to the system, half-quartic potentials with a bias of 250 kcal/mol/Å⁴ were applied above a CV value of 6.0 Å for the C_Thr-N_Gly and S_Cys-C_Thr reaction coordinates, and above 10.0 Å for the H_His-N_His and H_His-N_Gly reaction coordinates. Following minimization, windows were run for 600 ps with the small QM region, which was followed by another round of minimization and 400 ps of simulation with the large QM region. For each PMF, all windows were run concurrently to maximize the efficiency of the multiple-walker algorithm. Mean PMFs were computed by averaging the three PMFs generated in the Thr-In and Thr-Out states, and error bars represent the standard error of the mean at each location on the PMF. A Jacobian correction of 2kT · ln (r) was added to each dimension of the final PMF [48].

Zero temperature string (ZTS) calculations were run on the mean four-dimensional PMFs using a modified version of the maximum flux transition path python code available at https://www.cs.purdue.edu/homes/wolff1/bionum_www/transpath.html [49, 50]. Interpolation between points was performed with a second-order spline. Since ZTS only performs a local minimization of transition pathways, it was necessary to calculate a large number of pathways between the product and reactant state. For both the mean Thr-In and Thr-Out PMFs, 30,000 random pathways were calculated between the local minima in the product and reactant states. Redundant pathways were removed by measuring the Fr`echet distance between the curves that had a free energy barrier lower than 40 kcal/mol relative to the reactant state [51]. Hierarchical clustering was performed using code from scipy, and the representative pathways with the lowest free energy barriers are reported in Figure 7 and Tables 3-4.

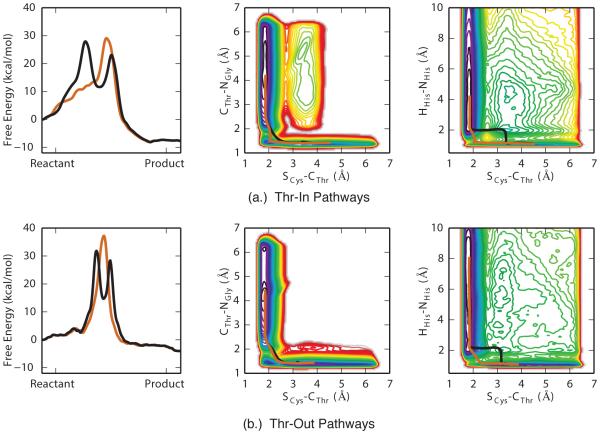
Figure 7.

Free energy profiles of the two pathways with the lowest barriers for (a.) Thr-In and (b.) Thr-Out simulations, as revealed by zero-temperature string calculations (left side). Overlay of these pathways on selected two-dimensional PMFs (middle and right). The sequential and concurrent pathways are shown in black and orange respectively.

Table 3.

The location and free energies of the critical points along pathways in the Thr-In PMF as determined with zero-temperature string calculations.

		SCys-CThr (Å)	CThr-NGly (Å)	HHis-NGly (Å)	HHis-NHis (Å)	Free Energy (kcal/mol)
Reactant		4.50	1.42	3.85	1.09	0.0±0.1
	Barrier 1	3.36	1.44	1.41	1.28	27.9±1.0
Pathway 1	Minimum	3.14	1.42	1.08	2.04	11.6±2.5
	Barrier 2	2.43	1.54	1.10	1.99	23.0±0.5
Pathway 2	Barrier	2.07	1.65	1.45	1.25	29.0±0.4
Product		1.85	3.91	1.08	2.26	−8.1±0.9

Table 4.

The location and free energies of the critical points along pathways in the Thr-Out PMF as determined with zero-temperature string calculations.

		SCys-CThr (Å)	CThr-NGly (Å)	HHis-NGly (Å)	HHis-NHis (Å)	Free Energy (kcal/mol)
Reactant		3.84	1.43	7.75	1.09	0.0±0.2
	Barrier 1	3.17	1.45	1.43	1.26	31.2±1.5
Pathway 1	Minima	3.11	1.42	1.09	2.07	14.7±2.1
	Barrier 2	2.37	1.62	1.09	2.14	28.4±1.3
Pathway 2	Barrier	2.21	1.72	1.33	1.36	37.2±1.5
Product		1.84	4.24	1.08	7.95	−4.0±1.1

Results

Modeling and MD Simulations of Sortase/Sorting Structure Complex

Initial models of the SrtA/LPATG₅ complexes were constructed with the “FlexPepDock” protocol in the Rosetta modeling suite (see Methods section). An alanine residue was used at the third SS position to maintain consistency with previous studies [52, 22, 20]. We initiated these calculations with the SS in both the Thr-In and Thr-Out states, which resulted in a pair of low-energy conformations (see Figure 2). In each of these configurations, Trp194 functions as a “lid” over the Thr-Gly linkage in the SS. In addition, these structures, as well as the other low-energy structures generated by Rosetta, indicate that the penta-glycine sequence binds in the groove between the β4/H2 and the β7/β8 loops, which is the same region that was identified by Suree et al. as a potential location for binding of the second substrate of catalysis. Therefore, although a structure of the non-covalently bound SrtA/LPATG₅ complex has yet to be solved, the agreement between Rosetta and chemical shift results strongly suggests that our starting configurations are close to the biologically active configuration. The LPATG₅ peptide was chosen to mimic the SS over an LPATG sequence to create a more “protein-like” region in the active site and to reduce potential effects of the SS C-terminal on the simulation results, especially the QM/MM results described below. In addition, the LPATG₅ peptide is similar to the SS/lipid II complex formed by SrtA at the end of its transpeptidation reaction.

To explore the conformational space around the Rosetta-generated structures, we performed ten independent 25 ns MD simulations for both the Thr-In and Thr-Out states. For both states, these ten simulations were initiated from the top scoring Rosetta configuration with different initial velocities. Each of these simulations were performed in the catalytically active state of a deprotonated and negatively charged Cys184 residue along with a doubly-protonated/positively charged His120 residue. Although simulations for the Thr-In and Thr-Out states were initiated from the same initial configuration, individual trajectories demonstrated multiple levels of stability of the SS/SrtA complex. Visual inspection indicated that nine of the ten Thr-In simulations exhibited stable SS conformations, whereas only five of the ten Thr-Out simulations had stable SS binding.

The stability of individual simulations was further analyzed with two root-mean-square deviation (RMSD) measurements, which are reported in Tables 1 and 2. In the first measurement, the average RMSD of the complete SS relative to its initial configuration is reported, whereas in the second, the average RMSD of the initial seven residues, the “core” of the SS, was computed. For both measurements, a structural alignment was performed on each simulation frame to minimize the RMSD to the initial structure of only the SrtA molecule, and the reported values are averaged over the final 20 ns of the simulation. In a majority of cases, in simulations where we observed stable binding the complete SS RMSDs were on the order of 3-4 Å, whereas the core RMSDs were lower (on the order of 2-3 Å). This indicates that even in stably bound conformations, the final three glycine residues are flexible and likely exist in an ensemble of states in vitro. For simulations that did not appear stably bound, significantly higher RMSD values were observed for both the complete and core SS measurements.

Table 1.

Results of Thr-In MD simulations. For each of the ten, 25 ns MD simulations, two RMSD measurements and the results of an MM-PBSA analysis are shown. Based on visual inspection, the RMSDs, and the energetics, nine of the 10 simulations exhibited stable SS binding.

#	Complete SS RMSD (Å)	Core SS RMSD (Å)	ΔEelec (kcal/mol)	ΔEvdw (kcal/mol)	ΔGpolar (kcal/mol)	ΔGnonpolar (kcal/mol)	–TΔSconfig (kcal/mol)	ΔGtotal (kcal/mol)
1	5.4 ± 0.4	2.1 ± 0.1	−53.7 ± 0.9	−172.2 ± 5.7	190.1 ± 5.2	−6.4 ± 0.1	29.1	−12.9 ± 1.2
2	3.3 ± 0.3	1.6 ± 0.1	−54.2 ± 1.7	−133.4 ± 11.9	154.7 ± 11.2	−6.3 ± 0.1	27.9	−11.2 ± 2.5
3	3.7 ± 0.2	2.1 ± 0.1	−57.0 ± 1.1	−142.3 ± 7.0	172.1 ± 6.9	−6.3 ± 0.1	30.4	−3.1 ± 1.7
4	4.1 ± 0.3	1.9 ± 0.1	−50.4 ± 1.5	−141.7 ± 14.3	164.9 ± 13.7	−6.0 ± 0.1	28.2	−5.0 ± 2.8
5	3.6 ± 0.1	1.7 ± 0.1	−51.2 ± 1.1	−141.5 ± 5.9	158.6 ± 5.5	−6.2 ± 0.1	28.5	−11.8 ± 1.4
6	3.1 ± 0.2	2.7 ± 0.2	−52.4 ± 0.9	−125.8 ± 6.0	145.4 ± 5.5	−6.2 ± 0.1	27.7	−11.4 ± 1.4
7	3.4 ± 0.1	1.7 ± 0.1	−53.5 ± 1.0	−201.2 ± 6.4	215.7 ± 5.9	−6.6 ± 0.1	26.7	−18.8 ± 1.4
8	3.4 ± 0.1	2.2 ± 0.1	−52.0 ± 1.1	−130.7 ± 5.8	158.2 ± 5.6	−6.2 ± 0.1	26.2	−4.4 ± 1.0
9	3.1 ± 0.1	2.6 ± 0.1	−54.1 ± 0.5	−150.8 ± 3.2	160.7 ± 3.0	−6.4 ± 0.1	27.0	−23.5 ± 0.6
10	9.9 ± 0.8	5.3 ± 0.4	−41.6 ± 1.3	−100.8 ± 9.1	125.0 ± 8.6	−5.3 ± 0.1	34.9	12.3 ± 1.8
Average ΔGtotal for SS bound states (simulations 1-9):								−11.3 ± 2.4

Table 2.

Results of Thr-Out MD simulations. For each of the ten, 25 ns MD simulations, two RMSD measurements and the results of an MM-PBSA analysis are shown. Based on visual inspection, the RMSDs, and the energetics, five of the 10 simulations exhibited stable SS binding.

#	Complete SS RMSD (Å)	Core SS RMSD (Å)	ΔEelec (kcal/mol)	ΔEvdw (kcal/mol)	ΔGpolar (kcal/mol)	ΔGnonpolar (kcal/mol)	–TΔSconfig (kcal/mol)	ΔGtotal (kcal/mol)
1	3.7 ± 0.3	2.2 ± 0.2	−58.7 ± 1.5	−86.7 ± 11.3	125.8 ± 10.2	−6.5 ± 0.1	26.9	0.8 ± 2.6
2	3.1 ± 0.1	2.0 ± 0.1	−50.8 ± 0.5	−124.5 ± 4.3	145.4 ± 4.0	−5.8 ± 0.1	28.5	−7.2 ± 0.7
3	4.2 ± 0.1	3.5 ± 0.1	−50.0 ± 0.8	−187.1 ± 6.2	210.3 ± 6.6	−6.4 ± 0.1	26.0	−7.3 ± 1.1
4	3.0 ± 0.1	2.6 ± 0.1	−54.3 ± 1.8	−191.8 ± 11.0	210.4 ± 10.2	−6.4 ± 0.1	26.1	−16.1 ± 2.8
5	2.7 ± 0.1	2.6 ± 0.1	−60.4 ± 0.6	−166.5 ± 3.2	196.3 ± 2.9	−6.1 ± 0.1	26.1	−10.5 ± 0.8
6	14.2 ± 0.8	9.7 ± 0.7	−30.4 ± 1.9	−94.8 ± 8.6	110.6 ± 7.9	−4.1 ± 0.2	34.0	15.2 ± 1.4
7	6.8 ± 0.3	4.5 ± 0.1	−50.4 ± 0.8	−112.8 ± 5.9	143.1 ± 5.5	−6.0 ± 0.1	28.8	2.8 ± 1.4
8	7.4 ± 1.1	4.5 ± 1.0	−45.7 ± 4.0	−82.6 ± 26.2	111.3 ± 24.7	−5.7 ± 0.2	34.2	11.5 ± 3.7
9	6.0 ± 1.3	4.1 ± 1.3	−44.1 ± 4.1	−81.4 ± 17.2	102.2 ± 18.3	−5.5 ± 0.4	30.2	1.4 ± 3.8
10	7.9 ± 0.9	4.6 ± 0.5	−40.6 ± 2.0	−95.2 ± 16.2	117.4 ± 15.5	−5.5 ± 0.2	35.8	11.9 ± 2.7
Average ΔGtotal for SS bound states (simulations 1-5):								−8.1 ± 2.5

To probe the energetics of SS binding, we performed a Molecular Mechanics/PoissonBoltzmann Surface Area (MM/PBSA) calculation on the final 20 ns of each simulation to approximate the binding free energy of the SS (see Tables 1 and 2) [53, 36]. Results show that simulations that visually appeared stable and that exhibited low RMSD values also had favorable binding energies. Furthermore, on average the Thr-In stably bound states had a slightly more favorable binding free energy (−11.3 ± 2.4 kcal/mol) than the Thr-Out state (−8.1 ± 2.5 kcal/mol), although the difference between these is within the overlapping error bars of the two sets of calculations. These values are a results of a delicate balance of favorable direct electrostatic and van der Waals (VDW) interactions between the SrtA and SS molecules, and an unfavorable polar solvation free energy difference upon binding. Finally, we note the expected trend that SS binding is stabilized by a large enthalpic energy gain and opposed by a significant entropic penalty, which is on the order of 26-40 kcal/mol.

Taken together, RMSD and MM-PBSA calculations suggest that the Thr-In state may be slightly more favorable to SS binding than the Thr-Out state, although both initial configurations result in stable binding. This is in agreement with previous umbrella sampling calculations we performed of the acyl-enzyme intermediate in which we observed small free energy differences between Thr-In and Thr-Out states in SrtA [20]. In addition, the glycine tail of the SS appears particularly flexible, although it preferentially samples the groove between the β4/H2 and the β7/β8 loops, which is the same region implicated in lipid II binding in previous NMR experiments [19].

QM/MM Free Energy Calculations

To determine the potentials of mean force (PMFs) for the catalytic mechanisms of SrtA in Thr-In and Thr-Out states requires the use of hybrid quantum mechanics/molecular mechanics (QM/MM) approaches. Although ab initio and DFT based methods have improved accuracy over semiempirical methods, their intense computational costs make them intractable for the large-scale calculations described below. Therefore, we have used the semiempirical Self-Consistent Charge Density Functional Tight Binding (SCC-DFTB) Hamiltonian to compute the QM energies and forces [41, 42]. The SCC-DFTB approach was chosen as it has been shown to have an acceptable tradeoff of computational efficiency and chemical accuracy in a wide-range of biologically relevant systems [54, 55, 56].

We used two QM/MM partitioning schemes, which are shown in Figure 3. The “small” region had 47 atoms and included the SrtA residues that directly participate in the transpeptidation reaction (His120 and Cys184), as well as the SS residues involved in the reaction (the ATG segment). The “large” QM region includes these residues as well as Thr121, Thr183, and the sidechain of Arg197, each of which are located in close proximity to the peptide bond cleaved by SrtA. The large region therefore has a total of 97 atoms. These QM regions were inspired by those used in the work by Tian & Eriksson [52], however we did not include surrounding solvent molecules as this would require the use of adaptive QM partitioning schemes and increase the computational cost of these calculations.

Initial Transition Pathway

To extract initial structures from our MD simulations for further analysis, we performed a clustering analysis with a cutoff of 1.2 Å with the gromos clustering algorithm that utilized the atoms in the large QM region for both the alignment and RMSD calculations [57]. These calculations were performed on the trajectories of the Thr-In and Thr-Out MD simulations that exhibited stable SS binding. For each state, we selected three unique structures from the largest cluster for further simulations. By selecting multiple conformations from the same cluster, we were able to account for the effects of different protein (MM) environments on the QM acetylation reaction.

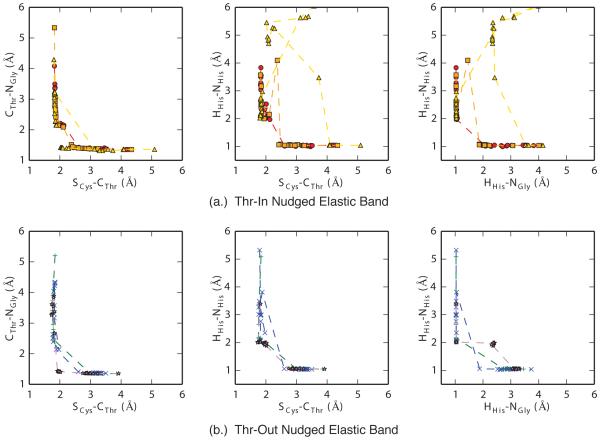
For each of these six structures (three Thr-In and three Thr-Out), reactant and product structures were generated through a combination of steered and simulated annealing QM/MM simulations (details are described in the methods section). No conventional MD simulations of the acyl-enzyme intermediate were performed here, although the interested reader is directed to previous simulations of the SrtA-acyl enzyme intermediate [20]. Using these structures as endpoints, we performed six sets of nudged elastic band (NEB) calculations to determine approximate transition pathways between the reactant and product configurations. As shown in Figure 4, most of the NEB pathways generated with the large QM region demonstrate that both the Thr-In and Thr-Out states have similar reaction mechanisms that include a direct transfer of the proton from His120 to the SS and a nucleophilic attack by Cys184, consistent with the reverse protonation mechanism, although in one ThrIn pathway the proton was shuttled along the SS backbone before covalently attaching to the SS nitrogen. However, while these pathways can suggest reaction mechanism, NEB results were not able to quantify the different energetics in the Thr-In and Thr-Out states or produce configurations close to the transition state.

Figure 4.

Results of three sets of nudged elastic band (NEB) calculations for the Thr-In (a.) and Thr-Out (b.) states. Overall, NEB results show that a reverse protonation mechanism is likely, however they did not produce configurations close to the transition state nor did they provide reliable energetics for the observed reactions.

Metadynamics Calculations

To explore and rigorously quantify the thermodynamics of the full acetylation mechanism, we performed multiple walker, well-tempered metadynamics calculations for each of the six NEB pathways [45, 46]. For each pathway, we simultaneously simulated 128 windows for 1 ns each, for a total of 384 ns of sampling for both the Thr-In and Thr-Out states. The first 600 ps of each window was performed with the small QM region, and the results were refined in the final 400 ps of each window with the large QM region. Biases were applied along four reaction coordinates: the C_Thr-N_Gly , H_His-N_His, S_Cys-C_Thr , and H_His-N_Gly distances. The first two dimensions correspond to bonds that are broken in the acetylation reaction, while the second two represent bonds that are formed in the product state.

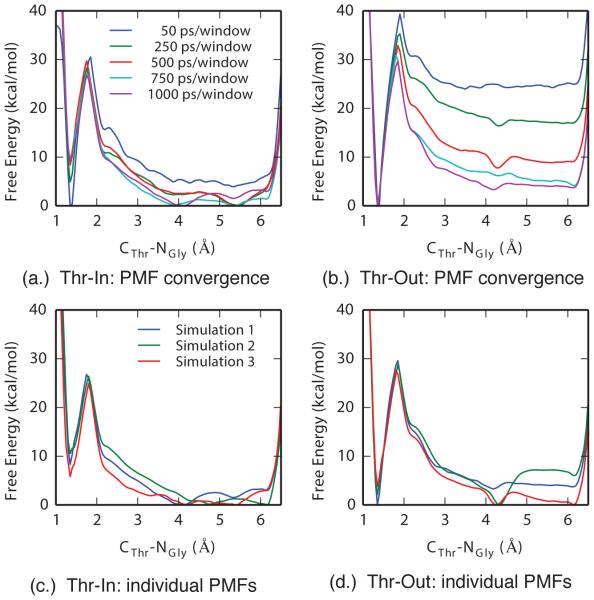
The computed potentials of mean force demonstrated good convergence, both within a single pathway and between the three pathways for each state. In Figure 5a-b, representative one-dimensional PMFs for the C_Thr-N_Gly reaction coordinate are shown as a function of simulation time for one set of Thr-In and Thr-Out calculations. These results demonstrate that the initial PMFs are poor approximations to the final results, however good convergence of the free energy minima and barriers can be reached with 750 ps of simulation per window, which was further refined with the additional 250 ps per window of sampling we performed. In addition, despite starting each set of metadynamics calculations from different configurations, the high degree of similarity between the PMFs after 1 ns of sampling per window further indicates that not only are the simulations well converged, but that they are not an artifact of the initial system configuration (Figure 5c-d).

Figure 5.

Projections of four-dimensional PMFs onto the C_Thr-N_Gly reaction coordinate demonstrate good convergence in both each simulation and between simulations. A comparison of Thr-In (a.) and Thr-Out (b.) PMFs as a function of simulation time show that the minima and barriers are largely converged after 750 ps/window. Comparison of each of the three final Thr-In (c.) and Thr-Out (d.) PMFs demonstrate that although small differences exist, the free energies and locations of the minima and barriers are consistent in each PMF.

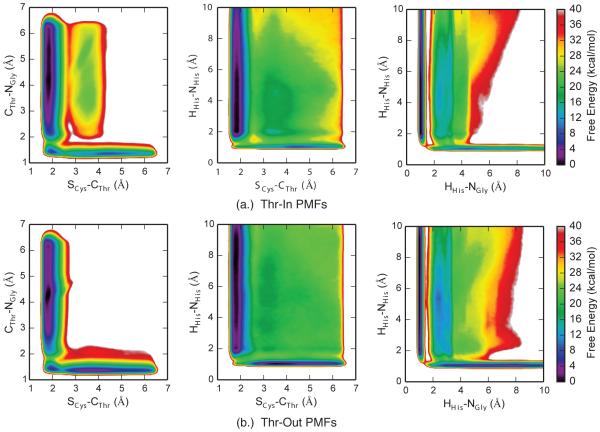
Projections of the mean four-dimensional PMFs for each state into two dimensions reveal several details about the catalytic process of SrtA. For example, the PMFs corresponding to the movement of the heavy atoms (first column of Figure 6) show that the S_Cys-C_Thr distance must go below 2.0 Å before the C_Thr-N_Gly distance significantly increases from its canonical value of ~1.4 Å, demonstrating that the S-C bond forms before the peptide bond is broken. Interestingly, we also observe metastable states that correspond to, potentially transient, tetrahedral intermediates in which both the S-C and peptide bonds are present. These states have longer peptide bonds, suggesting that the partial double-bond characteristics are converted into single bonds in this region of phase space.

Figure 6.

Projections of four-dimensional PMFs into two-dimensions for (a.) Thr-In and (b.) Thr-Out metadynamics calculations. Each PMF is the average of three independent sets of simulations.

Meanwhile, the S_Cys-C_Thr /H_His-N_His PMFs demonstrate no metastable states in the region corresponding to a formed S_Cys-C_Thr bond and a protonated histidine residue, suggesting that the proton transfer must happen before the S_Cys-C_Thr bond formation (middle column of Figure 6). Finally, the proton transfer between His120 and the SS appears to be direct, as the H_His-N_Gly /H_His-N_His PMFs shows two distinct free energy wells corresponding to the proton being bonded to either the histidine or SS, with a barrier between these states corresponding to the proton being ~1.4 Å between both sites (third column of Figure 6). We also note that there exist regions of relatively low free energy that correspond to the proton not bound to either His120 or SS (distances greater than 1.5 Å in both dimensions of the H_His-N_Gly /H_His-N_His PMFs). Configurations in this region of phase space correspond to reactant-like structures with an intact peptide bond and no bond between Cys184 and the SS, along with a proton that has transferred to one of the multiple oxygens in the SS backbone. This agrees with our visual observations of the simulation trajectories which demonstrated that the proton can move between the carboxyl groups on the peptide backbone. However, this process does not appear to be significant for the reaction under study here, as the free energy barrier for the proton to move from one of these states to the SS glycine backbone nitrogen is significantly higher than the barrier for a direct transfer of the proton from His120.

Although the Thr-In and Thr-Out PMFs in Figure 6 are qualitatively similar, we note two key differences between the sets of free energy profiles. First, the energy wells corresponding to the reactant state are both deeper and broader in the Thr-Out PMFs relative to Thr-In. Second, the S_Cys-C_Thr /C_Thr-N_Gly Thr-In PMF has a plateau around 25 kcal/mol that corresponds to configurations in which both the S-C and peptide bonds are broken, whereas in the Thr-Out state these configurations have energies greater than 40 kcal/mol. Although the additional stabilization of this state in Thr-In is of note, the barriers to reach that region of phase space from both the reactant and product states are significant. Therefore, this difference in PMFs is likely not biologically relevant.

Zero Temperature String

Projections of four-dimensional free energy profiles into two-dimensions illustrate important details about the reaction mechanism. However, a quantitative interpretation of these PMFs can be difficult due to the presence of “hidden barriers” in degrees of freedom orthogonal to the projection, and the fact that multiple free energy minima can be combined into a single state in these projections. Therefore, we performed zero temperature string calculations on the mean four-dimensional PMFs to determine the most likely pathways between product and reactant state. In Figure 7, the two pathways with the lowest free energy barriers are shown for both the Thr-In and Thr-Out simulations. The locations and free energy of the barriers and minima of these pathways are listed in Tables 3 and 4.

In the case of Thr-In, the pathway with the lowest free energy barrier corresponds to a mechanism in which the proton is initially transferred from His120 to the SS before the nucleophilic attack of the Cys184 thiolate anion. The same two events occur in the second pathway, however in this case they occur concurrently and there is therefore only a single barrier. Differences between the two pathways can be visualized by overlaying them on the two dimensional PMFs shown in Figure 6. In the S_Cys-C_Thr /H_His-N_His phase-space (Figure 7a right), the first pathway demonstrates that the H_His-N_His distance increases above 2 Å while the S_Cys-C_Thr distance is still greater than 3 Å, while in the second pathway the S_Cys-C_Thr distance decreases to 2.07 Å before the proton is separated from His120. Meanwhile, both pathways have similar projections in the S_Cys-C_Thr /C_Thr-N_Gly space (Figure 7a, middle). Relative to the reactant state, the barrier for the proton transfer step of the first pathway is 27.9±1.0 kcal/mol, while the nucleophilic attack step has a 23.0±0.5 kcal/mol barrier. A local minima of 11.6±2.6 kcal/mol exist between these barriers, which corresponds to a configuration of a protonated SS and a S_Cys-N_Gly distance of over 3 Å. In the second pathway, a single free energy barrier of 29.0±0.4 kcal/mol was observed that corresponds to a concurrent proton transfer and nucleophilic attack reaction. For both pathways there is a free energy gain of 8.1±0.9 kcal/mol as the reaction proceeds from reactant to product.

The Thr-Out state had similar low-energy pathways, but with higher free energy barriers. The pathway with the lowest barriers again corresponded to an initial direct proton transfer from His120 to the SS followed by nucleophilic attack of the Cys184 thiolate anion, however in this case the free energy barriers were 31.2±1.5 kcal/mol and 28.4±1.3 kcal/mol, while the local minimum between these barriers had a free energy of 14.7±2.1 kcal/mol. The pathway corresponding to the concurrent proton transfer and nucleophilic attack has a barrier height of 37.2±1.5 kcal/mol. Interestingly, in the Thr-Out state the free energy gained in the reaction is lower than in the Thr-In state, with a difference of only 4.0±1.1 kcal/mol.

Overall, these results show that catalysis in both the Thr-In and Thr-Out states follows two pathways: (1) a sequential reaction that is characterized by first a proton transfer from His120 to the SS and then nucleophilic attack of the Cys184 thiolate anion, and (2) a concurrent reaction in which the proton transfer and nucleophilic attack occur simultaneously. In the case of Thr-Out, there is a significant free energy difference between the sequential and concurrent reactions, whereas in the Thr-In state the difference is more minor. In addition, while acetylation reactions in both the Thr-In and Thr-Out states have an overall favorable free energy, the net free energy gain in Thr-In is more favorable than Thr-Out by ~4 kcal/mol.

Details of these results may be influenced by the semiempirical DFTB method used in this study. The choice of this method was motivated by the requirement for an efficient Hamiltonian that was capable of effectively and accurately sampling large amounts of conformational space, however the approximations inherent to semiempirical methods may introduce artifacts. For example, although the concurrent reaction mechanism is presented, it likely has a low probability in vitro. In contrast, the proton transfer followed by nucleophilic attack mechanism is similar to the mechanism observed by Tian & Eriksson in ONIOM(DFT:MM) calculations of Thr-Out [52]. Future studies may build on these results through the use of ab initio and density functional theory methods, which should provide more accurate results, albeit at significantly higher computational cost. Despite these limitations, the results presented here strongly suggest that Thr-In is the more catalytically active state than Thr-Out due to lower free energy barriers along the reaction pathway and not unique reaction mechanisms.

Conclusion

In this study, we tested the hypothesis that the Thr-In conformation observed in the crystal structure of SrtB by Jacobitz et al. is more catalytically active in SrtA than the Thr-Out conformation observed by Suree et al. We have done this with a series of conventional MD and enhanced sampling and free energy QM/MM simulations, which have allowed us to establish endstates for the reaction, map its mechanism, and quantify its thermodynamics.

Overall, our results indicate that the Thr-In state is the catalytically active configuration in SrtA. Similar to our previous studies of the acyl-enzyme intermediate [20], we found that the binding free energies of Thr-In and Thr-Out were comparable for the unbound SrtA/SS state. However, the free energy barriers in the catalysis pathways are lower in Thr-In than Thr-Out. This study therefore reinforces Thr-In as the catalytically relevant state for SrtA. Given that Thr-In has been observed crystallographically in SrtB and computationally in SrtA, and that all sortases have highly similar active sites, it is likely that these results extend to all members of the sortase family. In addition, by mapping the low free-energy pathways, our results lead further credence to the reverse protonation mechanism for sortase catalysis. Finally, our molecular modeling and MD simulations provide further evidence for the lipid II binding site being between the β4/H2 and β7/β8 loops, which has yet to be conclusively demonstrated by in vitro experiments. Taken together, our results not only extend our understanding of the sortase recognition and catalysis processes, but also provide a basis for future structure based drug design processes that seek to modulate sortase activity.

• The binding and catalysis of two substrate conformations by sortase A is explored.

• Conventional MD simulations show a slight preference for the “Threonine In” state.

• Also, QM/MM metadynamics calculations show lower free energy barriers in this state.