Population pharmacokinetic/pharmacodynamic modelling of the effects of axomadol and its O‐demethyl metabolite on pupil diameter and nociception in healthy subjects

Abstract

Aim

The aim of the present study was to characterize the pharmacokinetic/pharmacodynamic (PK/PD) properties of the active components of axomadol and to quantify their contribution to observed the pupillometric and analgesic (measured through the cold pressor test) effects linking the PD engagement biomarker with clinical response.

Methods

Healthy subjects (n = 74) received either placebo or axomadol orally at doses ranging from 66 mg to 225 mg following multiple dosing regimens in two separate clinical trials. Plasma concentrations of the two enantiomers of axomadol and their metabolites, and PD responses were measured at specific times. The population analysis was performed using NONMEM 7.2.

Results

The kinetics of the parent drug and its metabolite could be described simultaneously using an extra compartment mimicking the liver, where the metabolite is formed. The SS parent compound elicited a plasma concentration‐dependent increase in pupil diameter, with estimates (percentage relative standard errors) of maximal effect (E_max) and plasma concentration exerting a half‐maximal effect (C₅₀) of 0.79 (17.4) mm, and 90.7 (27) ng ml⁻¹, respectively. The predicted effect site concentrations of the RR O‐demethyl metabolite decreased the pupil diameter linearly, with an estimate of the slope of 0.00967 (18.7) mm·ml ng⁻¹. An additive model, integrating the net effect on pupil diameter, described adequately the reduction in pain with a linear function. The PK/PD model revealed that each 0.5 mm change in pupil diameter is associated with a 10% decrease in cold pressor area under the concentration–time curve effects.

Conclusions

The PK/PD analysis performed enabled the individual contributions of the active compounds to the observed effects to be identified and quantified. These effects were in accordance with the known mechanisms of action – namely, opioid agonism and noradrenaline reuptake inhibition.

What is Already Known about this Subject

• Analgesia is mediated by various pathways. Axomadol, an analgesic agent administered as racemic mixture, with opioid agonistic properties and inhibitory effects on the reuptake of monoamines, provides the framework to study the ‘in vivo’ contribution of these two components to the analgesic effects.

• Changes in pupil physiology are being used as pharmacodynamic biomarker for analgesic effects; however, to date, a quantitative relationship between the change in pupil parameters and analgesia has not yet been established.

• The present study aimed to identify and quantify the role of axomadol and its metabolite on the biomarker response, and link the latter to the analgesic effects.

What this Study Adds

• The net reduction in pupil diameter was described based on the plasma concentration of SS axomadol and the predicted effect‐site concentrations of the RR O‐demethyl metabolite.

• SS axomadol and the RR O‐demethyl metabolite induced mydriasis and meiosis, respectively, in accordance with known pharmacodynamic properties.

• Our pharmacokinetic/pharmacodynamic model revealed that each 0.5 mm change in pupil diameter is associated with a 10% decrease in the analgesia cold pressor test.

Introduction

The paradigm of discriminating drug vs. system‐dependent parameters by means of pharmacokinetic/pharmacodynamic (PK/PD) analysis has important translational relevance as it allows elements of the model to be reused and aids the development of additional compounds in the same therapeutic area. Establishing the quantitative relationship between drug exposure, PD biomarkers and clinical response in the early phases of drug development provides a highly valuable framework in which to evaluate untested dosing scenarios and optimize dose selection. This approach is of particular relevance for drugs with complex mechanisms of action, such as axomadol.

Axomadol is a centrally active analgesic agent with opioid agonistic properties and additional inhibitory effects on the reuptake of the monoamines noradrenaline (NA) and, to a lesser degree, serotonin [5‐hydroxytrypyamine (5‐HT)]. Axomadol is administered as a racemic mixture of the RR and SS enantiomers. It is metabolized to the active metabolite O‐demethyl‐axomadol primarily via the cytochrome P450 (CYP) enzyme 2D6. The opioid action component is generally attributed to the RR enantiomer of the O‐demethyl metabolite (referred to as the ‘RR metabolite’ hereafter), whereas the moderate monoamine reuptake inhibition is exerted by the SS enantiomers of the parent (SS parent) and of the metabolite. The inhibitory constant (Ki) values for the binding to the human recombinant μ‐opioid receptor are 22.7 μM for the RR parent, >10 μM for the SS parent, 0.14 μM for the RR metabolite and 3.8 μM for the SS metabolite. The Ki values for NA reuptake inhibition in rat brain synaptosomes are 3.16 μM for the RR parent, 0.12 μM for the SS parent, 27.2 μM for the RR metabolite and 0.13 μM for the SS metabolite. Finally, the Ki values for 5‐HT reuptake inhibition in rat brain synaptosomes are 2.36 μM for the RR parent, 0.56 for the SS parent, 23.5 μM for the RR metabolite and 7.49 μM for the SS metabolite (data on file).

The monitoring of pupil diameter changes in response to exteroceptive and/or nociceptive stimuli has proven to be a useful and non‐invasive technique in the investigation of autonomic nervous system reactivity 1. In line with this, pupil size has been found to correlate with clinical pain 2 and pupillometry can be used to estimate the level of analgesia in anesthetized patients 3. Reflex pupillary dilatation in response to noxious stimulation was found to be reduced by opioids during anesthesia in a concentration‐dependent manner 4, 5, 6. Recently, it was suggested that the pupillary dilatation reflex can be used as an objective pain assessment in the immediate postoperative setting and it was found to be significantly correlated with pain intensity and morphine requirements to obtain pain relief 7. Pupillary effects have been described as a valid PD marker for target engagement not only for opioids, but also for drugs exerting noradrenergic responses 8, 9. The cold pressor test is a well‐established test model for evaluating opioid‐induced analgesia 10, 11.

The aim of the present study was to characterize the PK/PD properties of the active components of axomadol by quantifying their contributions to the pupillometric and analgesic effects measured by pupil diameter and the cold pressor test, respectively.

Materials and methods

All patients provided written informed consent in accordance with International Conference on Harmonization of Technical Requirements for Registration of Pharmaceuticals for Human Use – Good Clinical Practice (ICH‐GCP) 12 and local legislation, once the nature and the intention of the investigation had been fully explained. The studies were performed in accordance with the Declaration of Helsinki and were approved by the institutional review board of the ethics committee at each study site.

Study designs

Data from two clinical phase I trials performed in healthy subjects were used in the current analysis. The healthy subjects received either placebo or axomadol (at doses ranging from 66 mg to 225 mg) orally (Table 1). Subjects who had used drugs that inhibit CYP2D6 within the previous 4 weeks were excluded from the trials. All subjects were CYP2D6 extensive metabolizers. In study A, all subjects were phenotyped and received a dose of dextromethorphan for a stratification of the subjects according to their metabolizer status with respect to CYP2D6 13. Subjects with a urinary metabolic ratio for dextromethorphan/dextrorphan of <0.3 were classified as extensive metabolizers and those with a metabolic ratio of >0.3 were classified as poor metabolizers. In study B, the CYP2D6 phenotype (metabolizer status) was predicted from CYP2D6 genotyping by assessing the presence or absence of the following CYP2D6 alleles: *3, *4, *5, *6, *7 and *8, using TaqMan® technology (Waltham, Massachusetts, United States) 14, 15, 16, 17.

Table 1.

Study design, and pharmacokinetic and pharmacodynamics measurements from both studies

	Dose administered [mg]	Dosing schedule	PK samples		Samples (pupil diameter)	Samples (cold pressorAUC)
Study A (n = 24)	66 (n = 12)	D1: 0 h	D1: –1 h, 0.33 h, 0.75 h, 1.5 h, 3 h, 4 h, 6 h, 8 h, 10 h, 12 h, 16 h	D7: 11.83 h, 23.83 h D8: 0.33 h, 0.75 h, 1.5 h, 3 h, 4 h, 6 h, 8 h, 10 h, 12 h, 16 h	D1–8: ‐1 h, 1 h, 4 h, 11 h, 23 h	D1–8: –1 h, 2 h, 5 h, 12 h, 24 h
	111 (n = 12)	D3–D7: 0 h, 12 h	D2: 0 h, 8 h, 16 h	D9: 0 h, 8 h, 16 h
		D8: 0 h	D3: 0, 11.83 h, 23.83 h	D10: 0, 12 h
			D6: 11.83 h, 23.83 h	D11: 0 h
Study B (n = 48)	100 (n = 11) 125 (n = 12) 150 (n = 13)	D1: 0 h, 12 h	D1: 5, 12 h	D5: 0 * , 8 * , 14 * , 22 * h	D1: 0 h, 4 h, 11 h, 23 h	D1: 0 h, 4 h, 11 h, 23 h
		D2–D4: 0 h, 8 h, 16 h
			D2: 0 h, 4 h * , 10 h, 12 h *	D6: 4 h * , 10 h * , 22 h *	D2: 23 h	D2: 11 h, 23 h
		D5: 0 h
	225 (n = 12)	D1: 0 h, 12 h † ,	D3‐D4: 0 h, 12 h *	D7: 22 h *	D5: 0 h	D5: 0 h, 1 h, 4 h, 11 h, 23 h, 35 h, 47 h
		D2–D4: 0 h, 12 h
		D5: 0 h

AUC, area under the curve; D, day; n, the number of individuals or observations included in the data analysis; PK, pharmacokinetic;

^* additional observations collected only from the highest dose (225 mg);

^† the dose on day 1 was only 150 mg b.i.d. in the 225 mg group.

Study A

Study A was a randomized, double‐blind, placebo‐controlled, two‐period crossover trial in 12 healthy male and 14 female Caucasian subjects. The mean age was 56.0 years (range 46–64 years), the mean height was 169.5 cm (range 156.0–185.0 cm), the mean weight was 74.9 kg (range 61.0–92.2 kg) and the mean body mass index (BMI) was 26.0 kg m⁻² (range 22.2–29.1 kg m⁻²). The trial was conducted with two consecutive dose groups. The designated number of subjects was 12 subjects per group, with six males and six females in each. Group 1 received 66 mg axomadol and placebo, and group 2 received 111 mg of axomadol and placebo in randomized order. On day 1 of every period, each subject received one single oral dose of axomadol or placebo in the morning. On days 3 to 7, the subjects received a b.i.d. dosing regimen, followed by the final single dose in the morning of day 8. On days 1 and 8, drugs were administered under fasting conditions – i.e. overnight fasting from 10:00 PM on the day prior to dosing. On days 3 to 7, dosing occurred without regard to food. PK profiles were performed on days 1 and 8 of each period. Periods were separated by at least 1 week but no more than 2 weeks.

Study B

This study was a randomized, double‐blind, placebo‐controlled, parallel group, dose escalation, two‐period crossover trial. Overall, four dose groups with 12 subjects each were planned. A total of 48 healthy subjects (24 males and 24 female) were enrolled into the trial. Their mean age was 54.9 years (range 40–65 years), mean height was 168.1 cm (range 150–195 cm), mean weight was 71.1 kg (range 48–100 kg) and mean BMI was 25.1 kg m⁻² (range 20–30 kg m⁻²). Within each dose group, the administration of the axomadol and placebo was randomized, multiple doses were administered for 5 subsequent days and a two‐way crossover was applied, with a washout period of 7–11 days. In groups 1 to 3, axomadol and placebo were administered b.i.d. on day 1 (titration day). On days 2 to 4, the dosage regimen was changed to t.i.d. and the daily dose was thus enhanced. On day 5, the final dose was administered in the morning. The doses administered in groups 1, 2 and 3 amounted to 100 mg, 125 mg and 150 mg of axomadol, respectively. After the end of the dose escalation, a maximum well‐tolerated daily dose was defined. This daily dose was then administered in group 4 following a b.i.d. regimen on days 2–4. Day 1 in group 4 corresponded to day 1 in group 3 regarding dose and dosing regimen. The final dosing in group 4 took place in the morning of day 5. The dosage regimen of axomadol applied in group 4 was 150 mg b.i.d. on day 1, 225 mg b.i.d. on days 2 to 4, and 225 mg in the morning of day 5. Table 1 shows the dosing schedules used in both clinical studies.

Blood sampling for pharmacokinetic determination

Blood samples (6 ml) were withdrawn during the course of the studies to quantify the plasma concentrations of the two enantiomers of either axomadol or its O‐demethyl metabolite at the selected times listed in Table 1.

Analytical methods

Study A

Both enantiomers of the parent compound and of the metabolite were analysed in the plasma using a chiral high‐performance liquid chromatography/fluorescence method; the lower limits of quantification (LLOQ) in the plasma were 0.96 ng ml⁻¹ for each of the parent compound enantiomers and 3.88 ng ml⁻¹ for each of the metabolite enantiomers [the coefficient of variation (CV%) at LLOQ ranged from 5.26 to 8.48]. The calibration range was 0.96–191 ng ml⁻¹ for the parent compound enantiomers and 3.88–777 ng ml⁻¹ for the metabolite enantiomers. The method was validated in accordance with the respective Food and Drug Administration guidance 18. Assays were conducted in the bioanalytical laboratories of Grünenthal GmbH, Aachen, Germany.

Study B

All quantitative analytical determinations were carried out for enantiomers of the parent drug and enantiomers of the O‐demethyl metabolite by means of a validated stereoselective liquid chromatography–mass spectrometry method. The LLOQ for each enantiomer was 0.5 ng ml⁻¹ plasma (CV% at LLOQ ranged from 4.27 to 7.61). The calibration range was 0.5–1000 ng ml⁻¹ for each enantiomer. Assays were conducted in the bioanalytical laboratories of Cephac, St Benoit, France.

PD measurements

Pupillometry

Each pupil diameter measurement was the average of at least five repetitions of single measurements. The pupil size was measured using a Compact Integrated Pupillograph (CIP) (AMTech GmbH, Dossenheim, Germany; Pupillography User Handbook, Version 10/00) according to a methodology described previously 19. The measurements were performed under standard low‐light conditions (10–15 lux). The subject adjusted to the low‐light conditions for 5 min prior to the measurements. Thereafter, the light intensity of the room was reduced to a maximum of 0.5 lux for 3 min prior to the measurement of the pupil diameter. During the measurement, the subject's eyes were exposed only to the light emitted by the CIP (~10 lux), and 30 s of adaptation to this light were allowed prior to any measurement. The same eye was assessed during all measurements in each subject. When optimal focusing of the pupil was attained, the CIP automatically captured and measured the pupil diameter.

Cold pressor test

In order to prevent any interference, the cold pressor test was performed after pupillometry; in cases where the sequence of events was incorrect, the pupillometry data were not included in the analysis. To start the test, the subject's dominant hand was immersed in a 37 °C circulating water quench for 2 min. Thereafter, the same hand was plunged into a 1–3 °C circulating water quench for another 2 min. By using a computer mouse with the other free hand, the subjects adjusted a visual analogue scale on a computer screen facing them. The scale was labelled ‘no pain’ at one end and ‘maximum pain’ at the other. The pointer was initially located at the ‘no pain’ end and the subjects moved the pointer across the line to rate their pain sensation. This pain intensity was registered automatically every second. At the end of the 2 min immersion period, the computer system automatically instructed the subjects to remove their hands. The pain intensity ratings were numerically read out on a 0–200 scale in study A and on a 0–100 scale in study B by the respective computer programs. From these numerical pain scores, the area under the pain intensity vs. 2 min curve (cold pressor AUC) was calculated and used as PD endpoint. If a subject withdrew their hand before the end of the 2‐min assessment period, the respective AUC for this period was not calculated. Nonresponders to the cold pressor test [i.e. subjects experiencing no pain at all and thus resulting in a cold pressor AUC of 0 (pain unit*s)] were not excluded from participation in the trial. The cold pressor test was performed according to standard operating procedures and user manuals for the respective clinical research organizations at which the trials were conducted.

Data analysis

The population analyses were performed using the software NONMEM version 7.2, using the first‐order conditional estimation (FOCE) method with the INTERACTION option 20. Parent and metabolite plasma concentration data for the two enantiomers, as well as cold pressor AUC data, were transformed logarithmically for the analysis. Pupil diameter data were not transformed for the analysis.

Interindividual variability was modelled exponentially, and residual variability was described using an additive model for the PK measurements and the two response variables. Nondiagonal elements of the Ω variance–covariance matrix and subject‐specific residual error were also evaluated for significance. The current analysis was performed in healthy volunteers and therefore covariate selection was limited to dose level.

Model selection

Selection between different model structures, and the significance of the elements of the Ω variance–covariance matrix and the potential effects of the dose level and the time after the start of dosing was performed on the basis of the log(likelihood) ratio test. For each model, the minimum value of the objective function value provided by NONMEM and approximately equal to –2 × log(likelihood) (−2LL) was assessed. Differences between two hierarchical (nested) models were compared using a χ² distribution in which a decrease of 3.84, 6.63, 7.88 or 11.87 points in −2LL was considered significant at the 5, 1, 0.5 and 0.1% levels for one extra parameter in the model, respectively. Non‐nested models were compared using the Akaike information criteria. Additional information used for model selection included visual inspection of the goodness‐of‐fit (GOF) plots, and calculations of the percentage relative standard errors [RSE(%)], as the ratio multiplied by 100 between the standard errors provided by NONMEM and the estimate of the corresponding parameter (the variance, in the case of the random effects).

Model development and evaluation

The first step (i) involved describing the PK data (PK model; Figure 1). In the second step (ii), the pupil diameter measurements were modelled as a function of the predicted active concentrations of parent and metabolite (see below) (biomarker model; Figure 1). In the final step (iii), the cold pressor AUC data were fitted as a function of the changes in pupil diameter (model for analgesia; Figure 1). In (ii) the individual predicted parameters obtained from the PK analysis were incorporated into the dataset used to fit the pupil diameter observations, and in (iii) both the individual parameters of the PK and biomarker models were incorporated into the dataset used to fit the cold pressor AUC measurements.

Figure 1.

Schematic representation of the selected population pharmacokinetic, biomarker and analgesia models. AUC, area under the curve; C_RR‐p, RR‐parent concentration; C_SS‐p, plasma concentration of the RR and SS parent compounds, respectively; C_RR‐m, RR‐metabolite concentration; C_SS‐m, plasma concentration of the RR and SS metabolite, respectively; Ce_RR‐m, effect site concentrations of the RR metabolite; PK, pharmacokinetic; *the estimation of parameter k_1e, defined as the first‐order rate constant of distribution between the central and the effect site compartments, is not required 24. Arrows represent connections between entities. The structure of the biomarker and analgesia models are represented in detail in equations (1)–(4) in the text

Prediction‐corrected visual predictive checks (pc‐VPC) 21 were used to evaluate the performance of the model. One thousand simulated datasets were generated for each type of measurement (parent and metabolite levels in the plasma, for each of the two enantiomers; pupil diameter and cold pressor AUC) and stratified by dose level. Additionally, parameter precision was evaluated from the analysis of 500 bootstrap datasets.

For graphical and statistical analysis, the R software (http://cran.r‐project.org, version 2.6.0) was used. Pc‐VPC and bootstrap analyses were performed using Perl‐speaks‐NONMEM (PsN) 22 and Xpose version 4 23.

PK modelling

Data for each enantiomer were modelled separately. Parent and metabolite disposition were described using compartmental models parameterized in apparent volumes of distribution, and first‐order distribution and elimination rate constants. To avoid non‐identifiability issues, the apparent volume of distribution of the central compartments of the parent (V_P) and metabolite (V_M) were assumed to be equal. The models tested to describe drug absorption included first‐order rate models with or without latency times (t_lag). In the absence of plasma concentration data after intravenous administration, the typical (unknown) absolute bioavailability (F) was assumed to be complete, and interindividual variability in F was allowed. To allow for the rapid formation of the metabolite owing to the first‐pass effect, a compartment mimicking the liver was included between the depot and the parent central compartment. Covariate effects of the dose level and time after the start of the study were tested for significance in all parameters in the model. Different magnitudes of the residual error were allowed between the parent and metabolite.

Pupil diameter modelling

The SS enantiomer of the parent compound and the RR enantiomer of the metabolite were considered as the active components of axomadol, based on the results from in vitro and in vivo preclinical experiments (data on file). The SS parent is a moderate inhibitor of monoamine reuptake, and therefore is expected to exert a mydriatic effect, whereas, being the RR metabolite a μ‐opioid agonist, it is expected to exert a miotic response. The general form of the model for the dual effects of axomadol on pupil diameter is represented by the following equation:

$$P_{\mathit{\text{Diameter}}\left(t\right)}=P_{\mathit{\text{Diameter}}\left(0\right)}\pm f\left(\mathit{\text{Placeb}}{o}_{\left(t\right)}\right)+E_{\mathit{SS}\_p\left(t\right)}–E_{\mathit{RR}\_m\left(t\right)}$$ (1)

where P_Diameter(t) and P_Diameter(0) are the pupil diameter at any time (t) during the course of the study and at baseline, respectively. Placebo effects are represented by the function f(Placebo_{(t )}), which can take a linear or nonlinear form [i.e. maximal effect (E_max)‐type model, Bateman function] for the time after (i) the start of the study or (ii) dosing. The PD relationships are represented by the functions E_{SS_p(t)} and E_{RR_m(t)}, which correspond to linear and nonlinear (i.e. sigmoidal E_max model) forms of the concentrations of SS parent and RR metabolite in the plasma (C _SS‐p, C_RR‐m, respectively) or at the effect site (Ce_SS‐p, Ce_RR‐m, respectively) 24 predicted at time t. The development of tolerance for the effects of the SS parent or RR metabolite was also evaluated by incorporating a tolerance compartment 25.

Cold pressor AUC modelling

With respect to analgesia, both the SS parent and RR metabolite contribute to a decrease in the cold pressor AUC value. The general form of the model is represented by equation (2):

$$\mathit{\text{Cold Pressor}}\mathit{AU}{C}_{\left(t\right)}=\mathit{\text{Cold pressor}}\mathit{AU}{C}_{\left(0\right)}\pm g\left(\mathit{\text{Placeb}}{o}_{\left(t\right)}\right)-h\left(E_{\mathit{SS}\_p\left(t\right)}\right)–i\left(E_{\mathit{RR}\_m\left(t\right)}\right)$$ (2)

where cold pressor AUC_(t) and cold pressor AUC₍₀₎ are the cold pressor AUC values at any time during the course of the study and at baseline, respectively. As in the case of pupil diameter, placebo effects were also considered for cold pressor AUC [g(Placebo_(t)]. The functions h(E_{SS_parent(t)}) and i(E_{RR_metabolite(t)}) can be linear or nonlinear forms of their corresponding element, and quantify the individual contributions of parent and metabolite concentrations to the assessment of analgesia at any given time t.

Results

Data

PK

A total of 3144 samples (1542 SS and 1602 RR enantiomers) for the parent compound were used for the analysis. The total number of samples for the metabolite was 3014 (1512 SS and 1502 RR enantiomers).

Pupil diameter

For studies A and B, there were 465 and 701 assessments, respectively.

Cold pressor

For AUC measurements, studies A and B contributed 460 and 809 measurements, respectively. A comparative exercise across the placebo groups revealed that the cold pressor AUC responses were similar between the two studies. No data below the LLOQ were reported.

Population PK modelling

The absorption process of both the RR and SS enantiomers was described by a first‐order rate model. The incorporation of t_lag, as well as a compartment mimicking the liver, in the absorption process resulted in a significantly better fit (P < 0.001). With respect to drug disposition, a one‐compartment model was adequate to fit the data. An additional elimination pathway, besides the formation of the O‐demethyl metabolite, resulted in statistically significant concentrations of the two enantiomers of the parent compound (P < 0.01).

The PK properties of the RR and SS enantiomers for both parent and metabolite were not affected by the dose level or time after the start of the study. Interindividual variability was supported in all model parameters except the first‐order distribution rate constants between the liver and central compartments of the parent compounds, and Relative Bioavailability parameter (F₁). The contribution of the nondiagonal elements of the Ω matrix was found to be negligible. The residual variability was found to be greater in study B than study A.

The upper section of Figure 1 represents the structure of the final population PK model and Table 2 lists the estimates of the population parameters. Typical population parameters differ between the RR and SS enantiomers. Figure S1 shows the typical simulated profiles for the parent and metabolite enantiomers, reflecting the differences in parameters between the two enantiomers shown in Table 2. By contrast, estimates of interindividual variability were fairly similar between the enantiomers, ranging from 18% for the first‐order elimination rate constant of the metabolite (k_MO) and 70% for the first‐order absorption rate constant (k_GL). In general, model parameters were estimated precisely. Values of η‐shrinkage 26 were lower than 10%, with the exception of k_GL and t_lag (~ 45%).

Table 2.

Population pharmacokinetic estimates of axomadol and O‐demethyl metabolite SS and RR enantiomers after multiple oral dosing in healthy volunteers

Parameters	RR enantiomer	Bootstrap RR enantiomer	SS enantiomer	Bootstrap SS enantiomer
k GL ( h −1 )	1.68 (22.4)	1.74 [1.08–2.65]	2.81 (27.4)	2.74 [1.82–4.21]
k LP ( h −1 )	18.8 (35.3)	20.0 [10.9–55.9]	18.0 (29.2)	19.6 [12.0–66.7]
k PL ( h −1 )	4.69 × 10−2 (11.4)	4.7 × 10−2 [3.8–6.0] × 10−2	9.97 × 10−2 (10.5)	10.0 × 10−2 [8.1–12.2] × 10−2
k P0 |k M0 ( h −1 ) *	7.93 × 10−2 (3.9)	8.0 × 10−2 [7.3–8.7] × 10−2	8.94 × 10−2 (4.1)	9.0 × 10−2 [8.3–10.1] × 10−2
k LM ( h −1 )	1.15 × 10−2 (37.0)	1.2 × 10−2 [0.6–3.3] × 10−2	1.57 × 10−2 (30.6)	1.7 × 10−2 [1.0–5.9] × 10−2
V P /F (L)	424 (3.2)	423 [398–455]	528 (4.3)	528 [489–582]
t lag (h)	0.26 (5.7)	0.26 [0.23–0.30]	0.27 (4.8)	0.27 [0.24–0.30]
IIV kGL (%)	77 (13.8)	76 [34–101]	66 (46.4)	68 [33–111]
IIV kP0 (%)	37 (19.7)	35 [20–50]	40 (17.5)	39 [21–52]
IIV kM0 (%)	20 (21.2)	19 [12‐28]	18 (19.2)	17 [12‐25]
IIV kLM (%)	48 (15.6)	46 [32–61]	35 (12.0)	34 [26–43]
IIV VP (%)	24 (9.7)	24 [19‐29]	31 (12.6)	31 [23–38]
IIV tlag (%)	32 (34.8)	31 [7–53]	27 (33.6)	26 [5–43]
Residual variability
Parent Study A [log(ng ml −1 )]	0.20 (9.2)	0.20 [0.17–0.24]	0.26 (13.5)	0.26 [0.20–0.34]
Parent Study B [log(ng ml −1 )]	0.33 (16.7)	0.33 [0.22–0.43]	0.49 (15.2)	0.48 [0.34–0.62]
Metabolite Study A [log(ng ml −1 )]	0.17 (8.3)	0.17 [0.14–0.20]	0.14 (11.4)	0.14 [0.11–0.17]
Metabolite Study B [log(ng ml −1 )]	0.24 (15.7)	0.23 [0.16–0.30]	0.27 (19.7)	0.26 [0.16–0.36]

Parameters are listed as estimates with relative standard error (RSE%) in parenthesis. Bootstrap results show the median parameter estimate, with the 2.5th–97.5th confidence interval in brackets. IIV, interindividual variability, expressed as the coefficient of variation; k_GL, first‐order absorption rate constant; k_LP, first‐order distribution rate constant of parent compound; k_PL, first‐order distribution rate constant of parent compound; k_P0, first‐order elimination rate constant of parent compound; k_M0, first‐order elimination rate constant of metabolite compound; k_LM, first‐order absorption rate constants (k_GL), for distribution from the liver to the central parent compartments and vice versa (k_LP and k_PL), parent elimination (k_P0), metabolite elimination (k_M0) and metabolite formation (k_LM), respectively; V_P, apparent volume of distribution of the parent and metabolite; F, unknown bioavailability (arbitrarily set to 1); t_lag, lag time;

^* different estimates for the k_P0 and k_M0 parameters did not improve the fit significantly (P > 0.05).

The pc‐VPCs for the active components SS parent and RR metabolite are displayed in Figure 2 and show that the typical tendency and dispersion of the data were well captured by the model, except in the case of the upper percentiles of the simulations, where the data variability is overpredicted. Figure S2 shows the pc‐VPCs for the RR parent and SS metabolite.

Figure 2.

Visual predictive check obtained from 1000 simulated studies using the selected population pharmacokinetic model and its corresponding model parameters (Table 2). Shaded areas represent the 95% prediction intervals of the 2.5th, 50th and 97.5th percentiles of the simulated studies, respectively. The points represent the observed plasma drug concentrations; the solid and dashed lines represent the median and 2.5th and 97.5th percentiles of the raw data, respectively

Population PK/PD modelling of the pupil diameter

Table 3 shows the main results obtained during the model‐building process. No placebo effects were found during the analysis (P < 0.05). Both the SS parent and RR metabolite exerted significant effects. The concentration of the SS parent (C_SS‐p) induced an increment in the initial pupil diameter which was best described by an E_max model. The reduction in the initial pupil diameter elicited by the RR metabolite was described as a linear function of Ce_RR‐M. Lindauer et al. identified the development of tolerance for the pupillometric effects of venlafaxine, a monoamine reuptake inhibitor 27. However, incorporation of a model for tolerance was not supported by the data analysed in the current evaluation (P < 0.05). The following equation represents the structure of the final model for the effects of axomadol on pupil diameter:

$$P_{\mathit{\text{Diameter}}\left(t\right)}=P_{\mathit{\text{Diameter}}\left(0\right)}+E_{\mathit{MAX}}\times \frac{C_{\mathit{SS}-p\left(t\right)}}{C_{\mathit{SS}-p\left(t\right)}+E{C}_{50}}-\mathit{SL}{P}_2\times C{e}_{\mathit{RR}-m\left(t\right)}$$ (3)

Table 3.

Summary of results from the pharmacokinetic/pharmacodynamic model‐building process

Pharmacokinetic–biomarker analysis	−2LL
P Diameter(0)	42.3
P Diameter(0) – SLP × C RR‐m	−2.6
P Diameter(0) – SLP 1 × C SS‐p	22.7
P Diameter(0) – SLP 2 × Ce RR‐m	−50.4
P Diameter(0) – SLP 2 × Ce RR‐m + SLP 1 × C SS‐p	−110.5
P Diameter(0) – SLP 2 × Ce RR‐m + E max × C SS‐p /(C 50 × C SS‐p )	−174.2
Biomarker–cold pressor AUC analysis
Cold pressor AUC(0)	−493.5
Cold pressor AUC(0) – SLP 3 × E RR‐m	−563.8
Cold pressor AUC(0) – SLP 3 × E RR‐m ‐ SLP 4 × E SS‐p	−593.2
Cold pressor AUC(0) – SLP 3 × E RR‐m ‐ SLP 4 × E SS‐p – α × E RR‐m × E SS‐p	−593.2

α, interaction parameter; AUC, area under the curve; C₅₀, plasma concentration of SS parent exerting a half‐maximal effect on initial pupil diameter; Cold pressor_AUC(0), cold pressor AUC at baseline; E_max, maximum increment in the initial pupil diameter that can be elicited by the SS parent; P_Diameter(0), initial pupil diameter at baseline; SLP, SLP₁, SLP₂, slope of the linear relationship between pupil diameter and (i) C_RR‐m, is the concentration of the RR‐metabolite (ii) C_SS‐p, is the concentration of the RR‐parent and (iii) Ce_RR‐m, is the concentration in the effect compartment of the RR‐metabolite; SLP₃, SLP₄, slope of the linear relationship between cold pressor AUC and (i) E_RR‐m, the absolute effect of the RR metabolite on the initial pupil diameter (SLP₂ × Ce_RR‐m), and (ii) E_SS‐p, the absolute effect of the SS parent on the initial pupil diameter [E_max × C_SS‐p/(C₅₀ × C_SS‐p)]; ‐2LL, ‐2‐Log‐likelihood.

where EC₅₀ is the value of C_SS‐p eliciting a half‐maximal effect (E_max) and SLP₂ is a parameter governing the linear relationship between P_Diameter and Ce_RR‐m. Interindividual variability was estimated for P_Diameter(0), EC₅₀ and SLP₂. The contribution of the nondiagonal elements of the Ω matrix was found to be negligible. Table 4 shows the estimates of the model parameters. Parameters were estimated precisely, as indicated by the fact that RES% values were below 30%. Estimates of interindividual variability were low for P_Diameter(0) (18%) and high for SLP₂ and EC₅₀ (84% and 257%, respectively). Values of η‐shrinkage were 1.2%, 28% and 36% for P_Diameter(0), SLP₂ and EC₅₀, respectively.

Table 4.

Population pharmacodynamic estimates of the effects of axomadol on pupil diameter

Parameters	Estimate	Bootstrap (n = 500)
P Diameter(0) (mm)	5.45 (1.9)	5.45 [5.26–5.65]
k e0 ( h −1 )	1.24 × 10−2 (2.7)	1.32 × 10−2 [0.44–9.33] × 10−2
SLP 2 (mm × ml ng −1 )	9.67 × 10−3 (18.7)	9.76 × 10−3 [4.44–19.91] × 10−3
C 50 (ng ml −1 )	90.7 (27.0)	93.21 [26.89–335.64]
E max (mm)	0.79 (17.4)	0.82 [0.49–1.37]
IIV PDiameter(0) (%)	16 (9.0)	16 [13‐19]
IIV SLP2 (%)	84 (13.1)	86 [62–114]
IIV C50 (%)	257 (22.4)	250 [150–432]
Residual error (mm)	0.46 (5.1)	0.46 [0.41–0.51]

Parameters are listed as estimates with RSE% in parenthesis. Bootstrap results show the median parameter estimate, with the 2.5th–97.5th confidence interval in brackets. C₅₀, plasma concentration of SS parent exerting a half‐maximal effect on initial pupil diameter; E_max, maximum increment in the initial pupil diameter that SS parent can elicit; IIV, interindividual variability, expressed as the coefficient of variation; k_e0, first order rate constant governing the distribution equilibrium between the central and biophase compartments of the RR metabolite; P_Diameter(0), initial pupil diameter at baseline; SLP₂, slope of the linear relationship between pupil diameter and predicted metabolite concentration in plasma.

The results of the pc‐VPCs represented in the left‐hand panels of Figure 3 indicate good model performance, describing the typical tendency and the dispersion of the data. Figure S3 shows the overall model performance through the GOF plots of the biomarker model at the population and individual level.

Figure 3.

Visual predictive check obtained from 1000 simulated studies using the selected population biomarker (left‐hand panels) and analgesia (right‐hand panels) models and their corresponding model parameters (Tables 3, 4, respectively). Shaded areas represent the 95% prediction intervals of the 2.5th, 50th and 97.5th percentiles of the simulated studies, respectively. The points represent observations; the solid and dashed lines represent the median and 2.5th and 97.5th percentiles of the raw data, respectively

Population PK/PD modelling of the cold pressor AUC

The results listed in the lower section of Table 3 indicate that the effect of the SS parent and RR metabolite on the pain response can be related to the changes in pupil diameter through E_RR‐m and E_SS‐p, which take the form SLP₂ × Ce_RR‐m, and E_max × C_SS‐p/(EC₅₀ + C_SS‐p), respectively (see Equation (3)). Neither placebo effects nor the interaction between E_RR‐m and E_SS‐p were found during the analysis (P < 0.05). The following equation represents the structure of the selected model for the effects of axomadol on the cold pressor AUC:

$$\mathit{\text{Cold pressor}}\mathit{AUC}=\mathit{\text{Cold pressor}}\mathit{AU}{C}_{\left(0\right)}-\left[\mathit{SL}{P}_3\times E_{\mathit{RR}-m\left(t\right)}+\mathit{SL}{P}_4\times E_{P-\mathit{SS}-p\left(t\right)}\right]$$ (4)

where SLP₃ and SLP₄ represent the linear relationship between the cold pressor AUC and E_M‐RR(t) and E_P‐SS(t), respectively. A model estimating a single slope parameter for E_RR‐m(t) and E_{P‐SS‐p(t)} resulted in a worse fit. Table 5 represents the estimates for the model parameters. In general, parameters were estimated precisely, as indicated by the fact that %RES values were below 25%, except for SLP₃, which had a value of 43.8%. Intersubject variability was estimated for the cold pressor AUC₍₀₎ and for [SLP₃ × E_M‐RR(t) + SLP₄ × E_P‐SS(t)], with estimates of 68% and 93%, respectively, and associated values of η‐shrinkage of 0.7% and 32.7%.

Table 5.

Population pharmacodynamic estimates of cold pressor AUC effects of axomadol

Parameters	Estimate	Bootstrap (n = 500)
Cold pressor AUC (0) (pain units)	3760 (8.2)	3653 [3115–4154]
SLP 3 (pain units mm −1 )	9.39 × 10−2 (43.8)	3.85 × 10−2 [0.24–16.29] × 10−2
SLP 4 (pain units mm −1 )	0.23 (23.3)	0.28 [0.15–0.42]
IIV cold pressor AUC(0) (%)	68 (10)	68 [55–80]
IIV Total effect (%)	93 (21)	101 [65–140]
Residual error [log(pain units)]	0.42 (9.4)	0.44 [0.37–0.53]

Parameters are listed as estimates with %RSE value in parenthesis. Bootstrap results show the median parameter estimate, with the 2.5th–97.5th confidence interval in brackets. AUC, area under the curve; IIV, interindividual variability, expressed as coefficient of variation; Cold pressor AUC₍₀₎, cold pressor AUC at baseline; E_max, maximum increment in the initial pupil diameter that can be elicited by the SS parent; SLP₃, SLP₄, slope of the linear relationship between cold pressor AUC and (i) E_RR‐m, the absolute effect of RR metabolite on the pupil diameter, and (ii) E_SS‐p, the absolute effect of SS parent on the pupil diameter, respectively. E_RR‐m and E_SS‐p take the form SLP₂ × Ce_RR‐m and E_max × C_SS‐p/(EC₅₀ × C_SS‐p), respectively. SLP₂, slope of the linear relationship between pupil diameter and predicted metabolite concentration in plasma; E_max, maximum increment in the initial pupil diameter that SS parent can elicit; EC₅₀, plasma concentration of SS parent exerting a half‐maximal effect on initial pupil diameter.

The results of the pc‐VPC are represented in the right‐hand panels of Figure 3. As in the case of the pupil diameter response, the results indicate good model performance, describing the typical tendency and the dispersion of the data. GOF plots of the model for analgesia (Figure S4) illustrate an adequate performance by the model, based on the experimental data available. Figure 4 represents the individual fitting of the biomarker model (pupil diameter) and the model for analgesia (cold pressor AUC) for a selection of individuals.

Figure 4.

Individual predicted and experimental profiles of pupil diameter and log cold pressor AUC vs. time for a group of individuals. Green circles (pupil diameter) and orange triangles (log cold pressor AUC) represent experimental observations. Individual predictions are show as a green line (pupil diameter) and orange line (log cold pressor AUC). AUC, area under the curve; ID, Individual number

Model exploration

Figure 5 illustrates the typical PK and response profiles of the active enantiomers, as predicted by the selected models, assuming b.i.d. administration of 225 mg axomadol during 3 weeks of treatment. Steady‐state conditions in the plasma were achieved after the 5th and 7th administrations of the SS parent and RR metabolite, respectively (Figure 5A). The estimate of the first‐order rate constant governing the distribution equilibrium between the central and biophase compartments of the RR metabolite (k_e0) listed in Table 4 corresponds to a t½_ke0 value of 55.9 h, indicating that steady state would be almost achieved after approximately after 10–12 days of continuous administration. Figure 5B shows the dual effects of the active components of axomadol on pupil diameter. Firstly, the direct effect of the increase in SS parent levels in the plasma elicits an increase in the initial pupil diameter. Over time, this increase is neutralized by the increasing levels of the concentrations of the RR metabolite at the effect site. Once the distribution equilibrium is established, the overall net effect of axomadol results in a reduction in the pupil diameter.

Figure 5.

Typical predicted population profiles vs. time obtained assuming multiple 225 mg oral administration b.i.d. during 3 weeks of treatment. (A) pharmacokinetic profiles corresponding to the SS parent and RR metabolite in the plasma, and the RR metabolite at the effect site. (B) pupil diameter, showing the contribution of SS parent and RR metabolite effects. (C) cold pressor AUC, showing the contribution of SS parent and RR metabolite effects. AUC, area under the curve

Although the effects on the pupil diameter occur on different time scales, the SS parent and RR metabolite both contribute to the analgesic effect: at a dose of 225 mg administered b.i.d. over 3 weeks, the parent and metabolite contributed to a maximum decrease of 12% and 10% in the cold pressor AUC value, respectively (Figure 5C).

In Figure S5, the typical profiles of initial pupil diameter and cold pressor AUC over time, simulated at b.i.d. doses of 66 mg, 111 mg and 225 mg axomadol given over 3 weeks, are presented. The typical PD relationships between initial pupil diameter and cold pressor AUC vs. steady‐state concentrations are shown in Figure 6.

Figure 6.

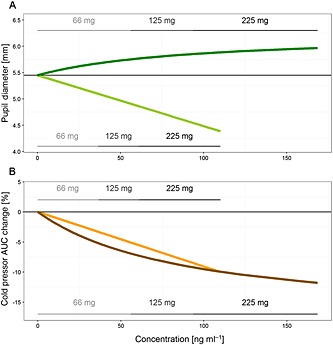
(A) Pharmacodynamic relationship between initial pupil diameter and concentrations of the SS parent in the plasma and RR metabolite at the effect site. (B) Pharmacodynamic relationship between cold pressor AUC and concentrations of the SS parent in the plasma and the RR metabolite at the effect site. The thin horizontal lines in each panel represent the baseline condition for each pharmacodynamic measurement. Note that the relationship between pupil diameter and SS axomadol is nonlinear but the link between the net change in pupil diameter caused by SS axomadol and the cold pressor AUC is linear. AUC, area under the curve. Dark and light lines represent the net effect on pupil diameter (green) or cold pressor AUC (brown) of the SS axomadol or RR metabolite, respectively

Lastly, Figure 7 represents the relationship at steady state between the cold pressor AUC expressed as the percentage reduction from baseline, and the absolute change in the initial pupil diameter, including the degree of intersubject variability. Typically, each 0.5 mm change in initial pupil diameter is associated with a 10% decrease in cold pressor AUCs (Figure 7B).

Figure 7.

(A) Stochastic simulated profiles representing the relationship at steady state between the relative cold pressor AUC change vs. the absolute change in pupil diameter of the RR metabolite (grey) and SS parent (black) achieved at 66 mg, 125 mg and 225 mg. (B) Stochastic simulated profile representing the overall contribution of both active isoforms between the relative cold pressor AUC change vs. the absolute change in pupil diameter obtained at 66 mg, 125 mg and 225 mg. AUC, area under the curve

Discussion

In the present analysis, we have developed a population PK/PD model to elucidate the relationship between changes in pupillometry and the analgesic effects of axomadol. We should emphasize that changes in pupil diameter and analgesic effects in the current model occur in parallel, rather than one causing the other. In fact, there is no causal connection between pupil size and e.g. pain intensity.

The PK properties of the SS and RR enantiomers of axomadol and its O‐demethyl metabolite could be well described by a one‐compartment model for both parent and metabolite, and a first‐order absorption model. Neither the dose nor the time after the start of the administration showed an effect on the PK parameters under the current design characteristics. The results listed in Table 2 indicate that although the PK profiles of the enantiomers for both the parent and the metabolite are quantitatively different, plasma levels after multiple dosing appear to increase over time, in a similar fashion to that indicated in the Figure S1.

Our analysis confirmed that the observed effects on pupil diameter were mediated by the axomadol SS parent and RR O‐demethyl metabolite, the enantiomers which are expected to have an effect, based on in vitro data. As discussed above, owing to the similarity of the temporal evolution of the exposure profiles, it was not possible to ascertain which enantiomer for the parent and which for the metabolite contributed to the effects evaluated here, based on concentrations alone.

Ultimately, a study design including administration of each enantiomer alone would be required to validate whether the RR parent and/or SS metabolite contribute to the effects of axomadol. This type of experiment has been performed for tramadol, a drug with a similarly complex mechanism of action as axomadol, in an experiment performed in rats. In that experiment, it was found that RR tramadol was inactive and that the SS metabolite showed a potency four times lower that the SS parent 28. These in vivo results are in line with the in vitro data for axomadol (data on file).

The resting pupil diameter and dynamic pupillary light reflex are considered a valid PD test for the effects of opioids and noradrenergic drugs 27. The effector organ of the pupil is the iris, a smooth muscle diaphragm, which receives both sympathetic and parasympathetic innervation 9. Inhibitors of noradrenaline reuptake such as reboxetine potentiate sympathetic innervation and have been shown to increase the resting pupil diameter – i.e. induce a mydriasis 9. By contrast, μ‐opioid receptor agonists such as morphine lead to a constriction of the pupil – i.e. a meiosis – by an excitatory action on the parasympathetic innervation of the iris. This opioid‐related meiosis is a sensitive, dose‐dependent and objective measure of the μ‐receptor agonistic effect 8.

Other authors have used meiosis to characterize the PK/PD properties of tested compounds. Dershwitz et al. described the effects of morphine in healthy volunteers after intravenous or inhaled administration 29. As in the present analysis, these authors described the meiotic effects as a function of the effect site concentration. Their estimate of the slope parameter for morphine (0.23 mm × ml ng⁻¹) is a factor of approximately 20 higher than the 9.7 × 10⁻³ mm × ml ng⁻¹ value obtained for the RR metabolite in the current analysis, indicating that the active RR metabolite of axomadol has a lower potency than morphine. The estimate of k_e0 obtained in the current analysis was low and implies a slow distribution of the RR metabolite to the biophase (t½_ke0 = 55.9 h) compared with the values for morphine (t½_ke0 = 3.5 h) and O‐demethyl tramadol (t½_ke0 = 1.65 h) obtained in a study performed in a paediatric population 30. However, other phenomena might have taken place in addition to slow distribution to the biophase, such as slow drug–receptor complex dissociation, or signal transduction processes 31, which are not distinguishable in the current experimental setting.

Lindauer et al. characterized the PK/PD effects of the noradrenergic drug venlafaxine using the pupillary light reflex 27. As in the present study, they used the plasma concentrations to describe drug effects, and no placebo effects could be identified. However, their data showed rapid development of tolerance, which was not detected in the present study.

Axomadol caused a significant reduction in the cold pressor AUC, which in principle could have been analysed as a function of SS parent and RR metabolite exposure as was done for the initial pupil diameter response. With such an approach, however, it would not have been possible to identify and quantify the contribution of the two active components to analgesia. In the case of axomadol, an absolute change of 0.5 mm and 1.0 mm in the initial pupil diameter caused by the noradrenergic and the μ‐opioid components were associated with a 12% and 10% decrease in the cold pressor AUC, respectively (Figure 7A).

A natural expansion of the model framework presented here would be to test the analgesia predicted by the cold pressor test to other pain‐related situations, such as extraction of the third molar (as has been carried out in phase II studies), bunionectomy (typically in phase II studies) and in neuropathic pain.

In summary, the effects of axomadol on pupil diameter were mediated by SS axomadol and RR O‐demethyl axomadol. Both components contributed significantly to the effects on this PD marker. After b.i.d. administration of a 225 mg oral dose over 3 weeks, RR O‐demethyl axomadol reduced the pupil diameter by 1 mm, while SS axomadol increased pupil diameter by 0.5 mm. The total effect resulted into an overall maximum reduction in pupil diameter of 0.5 mm at the end of the 3 weeks of treatment.

Our rationale for developing a model in which the cold pressor test AUC data were described as a function of (and not driven by) the net change in pupil diameter was that the analgesic response alone does not allow the contribution of the different active components to nociception to be differentiated, whereas the pupil diameter response does, through meiotic and mydriatic effects. The current approach showed that the use of model‐based simulation makes it possible to explore different scenarios – e.g. the potential impact of CYP2D6 polymorphism (which may decrease the concentrations of the O‐demethyl metabolite) on the analgesic profile. The present study on axomadol paves the way for similar analyses for other analgesic compounds.

Conclusion

The analgesia represented by pain AUC in the cold pressor test was associated with the pupil diameter effects elicited by SS axomadol and RR O‐demethyl axomadol. The contributions of the two active components on the pain AUC effects in the cold pressor test were comparable. After b.i.d. administration of a 225 mg oral dose and at steady‐state conditions, the overall effect was a 20% reduction in pain AUC in the cold pressor test from its baseline value.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: JMP and IFT had support from Grünenthal GmbH for the submitted work; and JR and RB are employed by Grünenthal GmbH.

VM‐S received a predoctoral grant from the Ministry of Education and Science of Spain and Miguel Hernandez University [FPU AP2010–2372]. The authors thank Werner Englberger and Tieno Germann from Grünenthal GmbH for providing the molecular inhibition data for the enantiomers of axomadol and its metabolite.

Supporting information

Figure S1 Typical model‐predicted pharmacokinetic profiles for the two enantiomers of axomadol and O‐demethyl metabolite, assuming b.i.d. administration over 3 weeks at a dose of 225 mg. The blue lines represent the RR enantiomers, and the red lines the SS enantiomers

Figure S2 Visual predictive check obtained from 1000 simulated studies using the selected population pharmacokinetic model and its corresponding model parameters. Shaded areas represent the 95% prediction intervals of the 2.5th, 50th, and 97.5th percentiles of the simulated studies. The points represent the observed plasma drug concentrations; the solid and dashed lines represent the median and 2.5th and 97.5th percentiles of the raw data, respectively

Figure S3 Goodness‐of‐fit plots of the biomarker model. CWRES, conditional weighted residuals; DV, experimental concentration; IPRED, individual predicted concentration; IWRES, individual weighted residuals; PRED, population‐predicted concentration. The blue dotted line represents the identity line, and the red solid line the linear regression fitting

Figure S4 Goodness‐of‐fit plots of the model for analgesia. CWRES, conditional weighted residuals; DV, experimental concentration; IPRED, individual predicted concentration; IWRES, individual weighted residuals; PRED, population‐predicted concentration. The blue dotted line represents the identity line, and the red solid line the linear regression fitting

Figure S5 Typical population response vs. time profiles corresponding to initial pupil diameter (A) and the area under the curve in the cold pressor test (B), assuming b.i.d. administration over 3 weeks at doses of 66 mg, 125 mg and 225 mg.

Mangas‐Sanjuan, V. , Pastor, J. M. , Rengelshausen, J. , Bursi, R. , and Troconiz, I. F. (2016) Population pharmacokinetic/pharmacodynamic modelling of the effects of axomadol and its O‐demethyl metabolite on pupil diameter and nociception in healthy subjects. Br J Clin Pharmacol, 82: 92–107. doi: 10.1111/bcp.12921.