Development of a population pharmacokinetic–pharmacodynamic model of a single bolus dose of unfractionated heparin in paediatric patients

Abstract

Background

Unfractionated heparin (UFH) is the anticoagulant of choice in paediatric patients undergoing a variety of cardiac procedures. There are currently no population pharmacokinetic–pharmacodynamic (PKPD) models for UFH in paediatrics.

Objective

The aim of the present study was to develop and evaluate a PKPD model of UFH in paediatrics.

Methods

Data from 64 children who received 75–100 IU kg⁻¹ of UFH during cardiac angiography were analysed. Five blood samples were collected at baseline and at 15, 30, 45 and 120 min postdose. The UFH concentration was quantified using a protamine titration assay. The UFH effect was quantified using activated partial thromboplastin time (aPTT). A PKPD model was fitted using nonlinear mixed‐effects modelling. Patient covariates such as gender, weight (WT) and fat‐free mass (FFM) were tested. The final model was evaluated using the likelihood ratio test and visual predictive checks (VPCs).

Results

A one‐compartment model with linear elimination provided the best fit for the dose–concentration data. FFM was a significant covariate on clearance. A linear model provided the best fit for the concentration–effect data using aPTT as a biomarker for effect. The models performed well using VPCs. However, when used to simulate UFH infusion (at a much lower dose), the model overpredicted target aPTT responses.

Conclusions

A PKPD model to describe the time course of the UFH effect was developed in a paediatric population. FFM was shown to describe drug disposition well. However, when applied to smaller UFH infusion doses, the model overpredicted target aPTT responses. This unsuccessful extrapolation may be attributed to a possible nonlinear relationship for heparin PKPD.

What is Already Known about this Subject

• Current dosing and monitoring guidelines for heparin in children are largely extrapolated from adult studies.

• There is evidence to suggest that the dose–response relationship for heparin in children is different to that in adults, even when pharmacokinetic (PK) and pharmacodynamic (PD) parameters are scaled to size; this can potentially result in over‐ or under‐dosing.

• There are currently no PKPD models of heparin in children. Such models could potentially improve dose selection in this patient group.

What this Study Adds

• A heparin PKPD model for children was developed and evaluated, and could potentially be used to improve dosing guidelines.

• Fat‐free mass as a covariate on the clearance parameter was shown to improve model fit.

• The model was derived on data that were based on a single high dose of heparin, so could not be extrapolated to the smaller infusion doses more commonly used in clinical practice; data in that region of the dose–response curve are needed in order to for the model to be used clinically.

Background

Unfractionated heparin (UFH) is an anticoagulant used for the treatment and prevention of thromboembolism (TE). UFH comprises a heterogeneous mixture of glycosaminoglycans of various chain lengths (average molecular weight of 15 kDa) normally derived from porcine or bovine intestines 1. UFH binds to antithrombin (AT) via a pentasaccharide sequence and induces a conformational change which enhances AT binding to activated clotting factors such as Xa. Additionally, long UFH molecules (≥ 18 saccharide units, molecular weight > 5 kDa) serve as a catalytic template to which both AT and factor IIa bind, effectively inhibiting IIa 2.

UFH is widely used in paediatric patients, principally because of its long history of clinical use and ease of reversibility 3, 4. Its relatively short half‐life makes it an ideal anticoagulant for use in critically ill children, who may be at a greater risk of bleeding. Current guidelines on the use of antithrombotic agents in children recommend that UFH be used as a first‐line intervention to treat arterial and venous TE 5. UFH is also recommended for primary thromboprophylaxis (e.g. cardiac angiography, cardiopulmonary bypass and haemodialysis).

Compared with the prevalence of TE in adult populations, TE in infancy and childhood is a relatively infrequent occurrence. This fact has hindered the conduct of robust clinical trials of anticoagulant therapies within this age group. As a result, the majority of anticoagulant therapy recommendations are based on cohort studies and extrapolation from adult data 5. However, there is evidence that extrapolation of adult‐derived data may be inappropriate due to significant pharmacokinetic and pharmacodynamic differences between neonates, infants, children and adults 6, 7, 8, 9, 10, 11.

There are standard dosing nomograms for UFH in children 12. The current recommendation is for a UFH bolus to be no greater than 100 units kg⁻¹, with bolus doses to be withheld or reduced in the presence of significant bleeding risks 5. Given the between‐ and within‐subject variability of dose requirements for UFH, blood monitoring is advocated. However, applying the activated partial thromboplastin time (aPTT) target range from adults to paediatric patients is not appropriate 13, 14, 15, 16. Instead, a heparin concentration (determined by protamine titration) of 0.2–0.4 units ml⁻¹ or an anti‐Xa concentration of 0.35–0.7 units ml⁻¹ is advocated 17.

Variability in the dose–response relationship of UFH necessitates consideration of the individual risk factors for bleeding and the perceived risk of thrombosis 5. Accounting for the sources of this variability could potentially optimize treatment. One possible source is variability in body size and composition. Evidence from the literature in adult patients gives credence to the use of fat‐free mass (FFM) as a suitable body size descriptor of drug clearance, and, hence, is potentially optimal for drug dosing. FFM, when compared with total body weight (WT), correlates well with metabolism and drug clearance 18. The aim of the present study was to develop and evaluate a pharmacokinetic –pharmacodynamic (PKPD) model to predict the dose–response relationship of UFH in paediatric patients. A further aim was to explore the use of FFM to guide dose individualization of UFH in this population.

Methods

Data

The data used in the present analysis have been described previously by Newall et al. 10. Briefly, 64 children requiring cardiac angiography who received a single intravenous bolus dose of UFH participated in the study (Table 1). Patients received no antiplatelet or anticoagulant therapy in the 10 days preceding the scheduled procedure. Blood samples were collected at baseline and at 15, 30, 45 and 120 min post‐UFH administration. UFH concentration (231 measurements) was determined using a modified protamine titration method 19. The aPTT was measured (290 measurements with 43% above the upper limit of quantification) using the PTT‐A® kit (Diagnostica Stago; Parsippany, NJ, USA) with the upper limit of clot detection modified to measure up to 999 s on the STA‐R analyser (Diagnostica Stago; Parsippany, NJ, USA). This was to accommodate the high single dose used in the present study.

Table 1.

Demographic characteristics of the study population. Values are expressed as mean (range)

N	64
Gender (M : F)	30:34
Age (years)	6.7 (0.5–15.5)
– age < 2 years (n)	8
Weight (kg)	23.6 (6.7–68.6)
Height (cm)	115.7 (65–176)
BMI ( kg m −2 )	16.1 (11.5–24.7)
UFH dose (IU)	2020 (600–5000)
UFH dose per weight (IU kg −1 )	91 (47.9–105.4)

BMI, body mass index; F, female; M, male; UFH, unfractionated heparin

Model building

Data from all 64 patients were included in the model‐building process. Two patients had no recorded value of height, and their height was imputed using multivariate linear regression using the distribution of age, gender and weight in the dataset.

Linear and nonlinear elimination one‐ and two‐compartment disposition models were considered to describe the concentrations of UFH. Maximum response (E _max), sigmoid E _max, linear and log‐linear models were considered to describe the concentration–effect relationship. PD parameters were estimated sequentially using the population pharmacokinetic parameters and data (PPP & D) estimation method 20. A sequential estimation method was chosen in order to avoid introducing bias to the PK model estimation 21.

Censored PD data (above the upper limit of quantification) were accounted for using Beal's M3 likelihood estimation (modified to account for right‐censoring of data) 22. This was implemented in NONMEM using the F‐Flag variable, where the likelihood of an observation being above the upper limit of quantification is calculated and maximized with respect to model parameters.

Covariate selection

Age, gender, WT, allometric weight with a fixed exponent 23, allometric weight with the exponent estimated, body surface area 24 and FFM were considered as covariates on model parameters. The covariates were added to the model using forward inclusion/backward elimination.

FFM and WT were standardized to their median values in the population (15 kg for FFM and 20 kg for WT).

Model selection

The analysis was performed in NONMEM v7.2 26 (with Wings for NONMEM v720 27) using the first‐order conditional estimation method with interaction and the combined residual error (RUV) model. Between‐subject variability (BSV) was implemented using exponential models. Model selection was guided by: (i) the decrease in the objective function value (OFV, the minimization criterion in NONMEM); (ii) visual goodness‐of‐fit analysis; and (iii) the estimated uncertainty in parameter estimates, as reported by the 95% confidence interval (CI) of parameter estimates based on nonparametric bootstrapping.

Model selection was based on the likelihood ratio test. The OFV of NONMEM is proportional to minus twice the log‐likelihood (−2LL). The difference in the OFV between two nested models is χ²‐distributed, meaning that a difference of 3.84 corresponds to P = 0.05 for one degree of freedom.

Evaluation of model performance

The final PK and PKPD models were evaluated using visual predictive checks (VPCs). 28 One thousand datasets were simulated and the 5th, 50th and 95th percentiles from the simulated response data were plotted against time with the same percentiles of the observed data (and the 95% CIs around the percentiles) superimposed. Additionally, the 95% CIs of parameter estimates in the final model were calculated using nonparametric bootstraps. One thousand bootstrap samples were simulated and used to estimate model parameters. Runs with terminated minimization were excluded and replaced with additional successful runs.

Simulation of current dosing guidelines

Current dosing guidelines for UFH infusion for the treatment of thromboses were used to simulate the dose–response relationship, and the success rate in attaining the therapeutic target (defined as aPTT between 50and 90 s) was calculated using FFM‐, WT‐, and age‐ and‐WT‐based dosing. Ten thousand virtual patients were simulated in MATLAB (version 2013b, MathWorks, Natick, MA, USA) using parametric resampling based on a large dataset of children 25. A joint multivariate normal distribution 29, 30 of gender, age, weight and height was constructed and randomly sampled. The covariates were then used as a part of the covariate model to generate the population parameters. The fixed and random parameters of the final heparin PKPD model were used for the simulation.

The current guidelines for UFH infusion in children recommend a bolus dose based on a patient's weight followed by a continuous infusion of 20 IU kg⁻¹ for children aged 1–12 years and 18 IU kg⁻¹ for children aged 12–18 years 5. As the model was developed using a single high (mean = 91 IU kg⁻¹) interventional prophylactic dose of UFH, the dosing guidelines were simulated at steady state, where the influence of a bolus dose is negligible.

The success rates for achieving a target aPTT of 50–80 s at steady state were calculated with the assumption that no subsequent dose adjustments occurred. Additionally, the dose rate based on the PKPD model was explored further by calculating a FFM‐based dose through a regression of the target biomarker vs. dose curve.

Results

Sixty‐four paediatric patients provided PK and PD data following a single high dose of UFH during a cardiac catheterization procedure. None of the patients were being treated for thromboses at the time of the study.

Population PK

A one‐compartment model with linear elimination, with a combined (additive and exponential) residual error model provided the best fit for the dose–concentration data (Table 2). Size (WT and FFM) and both clearance (CL) and volume of distribution (V) had a significant influence on model performance and resulted in a 90‐point reduction in the OFV. FFM as a covariate of CL, and WT as a covariate of V, as well as allowing the CL and V to co‐vary using a block covariance matrix, resulted in the lowest variance of CL and V, lowest additive error (without increasing the proportional error) and lowest OFV (see Appendix S1 for covariate model building steps). Bootstrap estimates of final model parameters were similar to model estimates, and the precision (95% CI) was reasonable except for the additive error bootstrap estimate, which had a wide 95% CI (Table 2). Diagnostic plots in the form of VPC showed that the model performed well when 1000 datasets were parametrically bootstrapped (Figure 1).

Table 2.

Final pharmacokinetic model parameter estimates. Bootstrap results are presented as mean and 95% confidence interval (CI)

Parameter	Covariate model	Parameter estimate	Bootstrap (95% CI)
θ CL (l h −1 15 kg −1 )	CL = θCL × FFM/15	0.603	0.601 (0.528, 0.684)
ωCL(%)		50	50 (40, 61)
θV (l 20 kg −1 )	V = θV × WT/20	0.751	0.745 (0.656, 0.840)
ωV(%)		40	39 (29, 48)
Corr(CL, V)		0.75	0.74 (0.40, 0.99)
θD1(h)		0.1 *
σprop(%)		17	16 (11, 22)
σadd (U l −1)		90	93 (1, 204)

Corr_(CL, V), correlation between heparin clearance and volume of distribution; Θ, mean value of the fixed effect parameter; ω, between‐subject variability (presented as coefficient of variation percentage, CV%); σ_prop, proportional component of the residual variability (presented as CV%); σ_add, additive component of the residual variability (presented as standard deviation).

^* The infusion rate parameter D1 was fixed.

Figure 1.

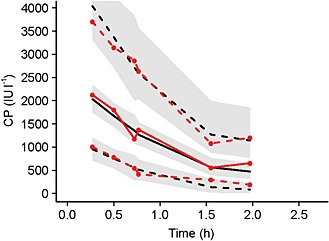
Visual predictive check plot for the final pharmacokinetic model. Median of observed (unbroken red line, closed circles) and predicted (unbroken black line) date are depicted. Also, 5th and 95th percentiles of observed (dashed red lines, closed circles and predicted (dashed black lines) data are shown. Grey bands are the 95% confidence intervals. CP, the plasma concentration of heparin in IU/L

Population PKPD

A linear model provided the best fit for the concentration–effect data using the PPP & D sequential estimation method 20 (Table 3). When asymptotic models (such as E _max and sigmoid E _max) were attempted, the estimates for E _max and the drug concentration associated with 50% of peak drug effect became large and implausible, and the correlation between these two parameters was high. Between‐subject and residual variability were also estimated. The PKPD model performed well using VPCs (Figure 2), especially once censored data had been accounted for.

Table 3.

Final pharmacokinetic–pharmacodynamic model parameter estimates. Bootstrap results are presented as mean and 95% confidence interval (CI)

Parameter	Covariate model	Parameter estimate	Bootstrap (95% CI)
θCL (l h −1 15 kg −1 )	CL = θCL × FFM/15	0.603*
ωCL(%)		50*
θV (l 20 kg −1 )	V = θV × WT/20	0.751*
ωV(%)		40*
Corr(CL, V)		0.745*
θD1(h)		0.1*
θE0(s)		35.6	35.6 (34.6, 36.7)
ωE0(%)		0.43	0.44 (0.38, 0.51)
θSLP		0.67	0.67 (0.58, 0.78)
ωSLP(%)		64	63 (50, 76)
σprop(%)		30	30 (26, 33)
σadd (U l −1)		0.005	0.005 (0.001, 0.012)

aPTT, activated partial thromboplastin time; Corr_(CL, V) , correlation between heparin clearance and volume of distribution; E0, baseline aPTT in s; SLP, slope of the linear model; θ, mean value of the fixed‐effect parameter; ω, between‐subject variability (presented as coefficient of variation percentage, CV%); σ_prop proportional component of the residual variability (presented as CV%); σ_add , additive component of the residual variability (presented as standard deviation).

^* Values fixed.

Figure 2.

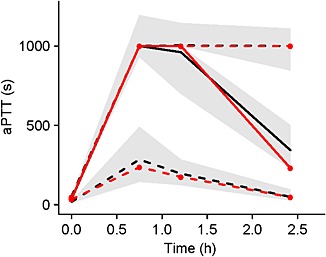
Visual predictive check plot for the final pharmacokinetic–pharmacodynamic model using activated partial thromboplastin time (aPTT) response. Median of observed (unbroken red line, closed circles) and predicted (unbroken black line) date are depicted. Also, 5th and 95th percentiles of observed (dashed red lines, closed circles and predicted (dashed black lines) data are shown. Grey bands are the 95% confidence intervals

Simulation of UFH infusion

The simulation showed that the majority of patients had aPTT above 80 s, with a mean aPTT of 380 s. An optimal dose that would result in approximately 57% success in attaining a target aPTT of 65 s at steady state was found to be 2.4 IU kg⁻¹. This dose, however, is much smaller than that observed in clinical practice, which suggests that the model cannot be extrapolated to the smaller infusion doses.

Discussion

The present study is the first to describe a PKPD model of UFH in children. The model described the data well, even though a third of the aPTT data were above the upper limit of quantification (> 999 s). To account for these censored values, a modified version of Beal's M3 method was used 22. The method improves the model fit by calculating the likelihood that a datum falls outside the limit of quantification 31. This is in line with good population modelling practice as censoring data have been known and shown to cause bias in model parameter estimation 32, 33.

The covariate model which provided the best fit to the data included WT in the V parameter and FFM in the CL parameter. No measures of hepatic or renal function were included in the covariate model because none of the patients suffered from hepatic or renal impairment. The model showed FFM to be a better measure of the influence of size on CL. WT has often been used to scale drug doses but this has been found to overpredict CL in obese adults 18. Finding a more suitable size descriptor is particularly important, given the rise in obesity in both developed and developing countries, including in children.

The PKPD model was based on data collected from 64 children who received a large (~ 92 IU kg⁻¹) single bolus dose during cardiac catheterization. The model was found to be linear, which is inconsistent with evidence in the literature on UFH pharmacology. Previously reported evidence suggests that UFH is cleared through a mixture of a saturable mechanism (through binding to endothelial cells and macrophages) and a first‐order mechanism (through the kidneys) 34. As a result, the dose–response relationship for UFH is considered nonlinear, with the half‐life increasing from ~30 min after a single dose of 25 IU kg⁻¹ to ~60 min after a dose of 100 U kg⁻¹ 35, 36, 37.

In the PKPD model, the average CL was found to be 0.6 l h⁻¹ (per 15 kg FFM) and the average V was 0.75 l (per 20 kg WT). This results in a half‐life of approximately 52 min. It is likely that the model describes an incomplete segment of the heparin dose–response relationship and would overpredict aPTT when a small dose is given. This became evident when the model was applied to the infusion dosing guidelines, which utilize doses of 18–28 IU kg⁻¹. In clinical practice, aPTT is measured frequently during heparin infusion and the infusion rate is adjusted accordingly in order to reach target aPTT. The average aPTT predicted by the model was 380 s instead of the 50–80 s observed in clinical practice. Data covering a larger range of doses and concentrations would have made this model more clinically applicable.

Conclusion

A PKPD model to describe the time course of the UFH effect was developed in a paediatric population that received a high single prophylactic bolus dose. FFM was shown to describe drug disposition well and could potentially be used in dose calculation after appropriate evaluation. However, the PKPD model was linear and resulted in overprediction of aPTT when smaller UFH infusion doses were simulated.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: no support from any organization for the submitted work; no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years; no other relationships or activities that could appear to have influenced the submitted work.

We would like to acknowledge the contribution of Professor Linda Johnston (Dean of Faculty of Nursing, University of Toronto, Toronto, ON, Canada) to the original data collection study.

Supporting information

Appendix S1 Noteworthy steps in heparin pharmacokinetic–pharmacodynamic model development

Supporting info item

Al‐Sallami, H. , Newall, F. , Monagle, P. , Ignjatovic, V. , Cranswick, N. , and Duffull, S. (2016) Development of a population pharmacokinetic–pharmacodynamic model of a single bolus dose of unfractionated heparin in paediatric patients. Br J Clin Pharmacol, 82: 178–184. doi: 10.1111/bcp.12930.