Genome-Wide Estimates of Heritability for Social Demographic Outcomes

Abstract

An increasing number of studies that are widely used in the demographic research community have collected genome-wide data from their respondents. It is therefore important that demographers have a proper understanding of some of the methodological tools needed to analyze such data. Our paper details the underlying methodology behind one of the most common techniques for analyzing genome-wide data, Genome-Wide Complex Trait Analysis (GCTA). GCTA models provide heritability estimates for health, health behaviors, or indicators of attainment using data from unrelated persons.. Our goal is to describe this model, to highlight the utility of the model for biodemographic research, and to demonstrate the performance of this approach under modifications of the underlying assumptions. The first set of modifications involves changing the nature of the genetic data used to compute genetic similarities between individuals (the genetic relationship matrix). We then explore the sensitivity of the model to heteroscedastic errors. In general, GCTA estimates are robust to the modifications proposed here but we also highlight potential limitations of GCTA estimates.

1. Introduction

Demographic research often describes the factors responsible for variation in population health (Majer et al. 2013;Masters et al. 2014), health behaviors (Pampel and Denney 2011), birth outcomes (Fuller 2014), and mortality (Ross et al. 2012). Importantly, each of these outcomes has evidenced moderately sized heritability estimates (e.g., Rice et al. 2014; Daw et al. 2013). Not only are most physical health morbidities influenced by genetic factors common to family members (Pilia et al. 2006) but so are health-related lifestyles such as smoking (Boardman et al, 2011), exercise (Bartels et al. 2012; Mustelin et al. 2012) and birth outcomes including birth weight and gestational age (Clausson et al. 2000) and even mortality (Wienke et al. 2001). Given that genes influence nearly all of the outcomes of interest to demographers, characterizing the relative contribution of genetic influences to health, health behaviors, birth outcomes, and mortality is critical for demographic researchers.

Heritability is the traditional approach for quantifying genetic influence on a trait. Heritability studies date back to Galton’s work in the 19^th century (e.g., Galton 1869). The workhorse during the pre-genomic era for estimating heritability had been the twin study, which utilizes family pedigrees. Currently there is a proliferation of genome-wide data from unrelated individuals in large, representative, longitudinal data sources such as the Health and Retirement Study, the National Longitudinal Study of Adolescent to Adult Health (McQueen et al., 2014), and many other, more targeted, datasets (e.g., Framingham Heart Study; Splansky et al., 2007). These studies have begun genotyping respondents and providing information on single nucleotide polymorphisms (SNPs) across the entire human genome. SNPs are common genetic variants and are the most convenient form of genome-wide data available for use by non-geneticists (Guo and Adkins 2008).

Initially, SNP data were the backbone of genome-wide association studies (GWAS) in which specific positions on the human genome are correlated with health phenotypes. This technique generates hundreds of thousands (and now several million) of regression estimates comparing genotype (e.g., 0, 1, or 2 copies of the minor allele of the SNP) to phenotype (e.g., height) for each SNP. Novel genetic associations with many diseases have been found (Welter et al., 2014) but these individual loci only predict a small amount of observed phenotypic variation. For example, the associations identified in a GWAS for educational attainment (Rietveld et al., 2013b) explain only 0.02% of the observed variation.

It is also possible to utilize genetic similarity, based on information from the entire genome, among unrelated persons to decompose overall phenotypic variation into genetic and environmental components. The most common maximum likelihood methods used in these analyses are bundled in GCTA, a suite of software for Genome-wide Complex Trait Analysis (Yang et al., 2010, 2011). Although alternative techniques exist for computing such heritabilities (e.g., Ge et al., 2015), GCTA has been widely used and is relatively straightforward.

The key insight embedded in the GCTA approach is that measured SNP-level variation can be used to estimate the genetic similarity between two unrelated individuals, and this estimated genetic similarity can be compared to phenotypic similarity to produce a heritability estimate. A number of scholars are beginning to utilize these techniques. Table 1 contains a range of heritability estimates produced using GCTA that may be of interest to demographers. This is not intended as a comprehensive list of papers published using GCTA but is rather meant to provide a description of the types of GCTA outcomes that may be of interest to demographers and to illustrate the range of the associated heritability estimates. The estimates are grouped into different categories of phenotypes. One possible expectation might be for anthropometric phenotypes such as height to evince larger heritabilities than behavioral traits such as nicotine use and alcohol consumption. Height, for example, is driven largely by biology (outside of extreme nutritional environments) whereas decisions about nicotine and alcohol use are clearly influenced by peers and broader society. Yet, heritability estimates between the two sets of outcomes are frequently quite similar. We also emphasize that heritabilities do not capture fundamental unchanging biological mechanisms but are instead highly contextual. Dating back to at least Feldman & Lewontin’s characterization of heritability estimation as “local perturbation analyses” (1975, p. 1163) it has been understood that heritabilities are not fixed, immutable quantities but are contingent upon the social world in which the relevant actors are embedded.

Table 1.

Heritability estimates from applications of GCTA.

Outcome	h2(SE)	Sample Size	Reference
Anthropometric Phenotypes
Height	0.44 (0.09)	2,000	Speed et al. 2012
Height	0.35 (0.12)	3,154	Plomin et al. 2012
Height	0.32 (0.06)	6,379	Conley et al. 2014
Weight	0.42 (0.12)	3,154	Plomin et al. 2012
BMI	0.43 (0.10)	4,233	Boardman et al. 2014
BMI	0.31 (0.07)	6,320	Conley et al. 2014
Medical/Clinical Phenotypes
Type 1 Diabetes	0.73 (0.06)	2,000	Speed et al. 2012
Type 1 Diabetes	0.28 (0.04)	2,599	Lee et al. 2011
Type 2 Diabetes	0.35 (0.06)	2,000	Speed et al. 2012
Rheumatoid Arthritis	0.57 (0.06)	2,000	Speed et al. 2012
Crohn Disease	0.61 (0.08)	2,599	Lee et al. 2011
Crohn Disease	0.54 (0.06)	2,000	Speed et al. 2012
Coronary Artery Disease	0.39 (0.06)	2,000	Speed et al. 2012
Pediatric Obesity	0.37 (0.15)	3,152	Llewellyn et al. 2013
Hypertension	0.42 (0.06)	2,000	Speed et al. 2012
Parkinson's Disease (Early-Onset)	0.15 (0.14)	7,096	Keller et al. 2012
Parkinson's Disease (Late-Onset)	0.31 (0.07)	7,096	Keller et al. 2012
Parkinson's Disease (All Types)	0.27 (0.05)	7,096	Keller et al. 2012
Parkinson's Disease	0.22 (0.02)	3,426	Do et al, 2011
Multiple Sclerosis	0.3 (0.02)	1,854	Watson et al. 2012
Cognitive Phenotypes
General Cognitive Ability	0.35 (0.12)	3,154	Plomin et al. 2012
General Cognitive Ability	0.29 (0.05)	6,609	Marioni et al. 2014
Nonverbal Cognitive Ability	0.20 (0.11)	3,154	Plomin et al. 2012
Verbal Cognitive Ability	0.26 (0.11)	3,154	Plomin et al. 2012
Language Ability	0.29 (0.12)	3,154	Plomin et al. 2012
Intelligence (age 7–12)	0.60 (0.26)	2,875	Trzaskowski et al. 2014
Intelligence	0.51 (0.02)	3,511	Davies et al. 2011
Intelligence from Childhood to Old Age	0.24 (0.20)	1,940	Deary et al. 2012
IQ (Age 12)	0.32 (0.14)	3,000	Trzaskowski et al. 2014
IQ (Age 7)	0.28 (0.17)	3,000	Trzaskowski et al. 2014
Psychological Phenotypes
Bipolar Disorder	0.59 (0.06)	2,000	Speed et al. 2012
Bipolar Disorder	0.37 (0.04)	2,599	Lee et al. 2011
ADHD	0.42 (0.13)	1,040	Yang et al. 2013
Adult Anti-Social Behavior	0.55 (0.41)	2,172	Tielbeek et al. 2012
Depression	0.19 (0.10)	4,233	Boardman et al. 2014
Major Depressive Disorder	0.32 (0.09)	4,605	Lubke et al. 2012
Behavioral Disinhibition	0.19 (0.16)	3,452	Vrieze et al. 2013
Neuroticism	0.06 (0.03)	12,000	Vinkhuyzen et al. 2012
Borderline Personality Features	0.23 (0.09)	7, 125	Lubke et al. 2014
Callous-Emotional Behavior	0.07 (0.12)	2,930	Viding et al. 2013
Extraversion	0.12 (0.03)	12,000	Vinkhuyzen et al. 2012
Anxiety Related Behaviors	0.01–0.12 (0.12)	2,810	Trzaskowski et al. 2013
Substance Dependency Phenotypes
Drug Use	0.22 (0.16)	3,452	Vrieze et al. 2013
Drug Dependence	0.36 (0.13)	2,596	Palmer et al. 2014
Dependence Vulnerability	0.33 (0.13)	2,596	Palmer et al. 2014
Problematic Drug Use	0.25 (0.13)	2,596	Palmer et al. 2014
Alcohol Consumption	0.16 (0.16)	3,452	Vrieze et al. 2013
Alcohol Dependence	0.12 (0.16)	3,452	Vrieze et al. 2013
Nicotine Use/Dependence	0.18 (0.16)	3,452	Vrieze et al. 2013
Sociological/Health Behavior/Educational Phenotypes
Socioeconomic Background	0.18 (0.05)	6,533	Marioni et al. 2014
Socioeconomic Status (age 2)	0.18 (0.12)	3,000	Trzaskowski et al. 2014
Socioeconomic Status (age 7)	0.19 (0.12)	3,000	Trzaskowski et al. 2014
Subjective Well-Being	0.05–0.10 (0.05–0.10)	11,500	Rietveld et al. 2013a
Reporting Stressful Life Events	0.3 (0.15)	2,578	Power et al. 2013
Self-Rated Health	0.18 (0.10)	4,233	Boardman et al. 2014
Moderate to Vigorous Activity	0.17 (0.09)	4,244	Richmond et al. 2014
Sedentary Time	0.25 (0.09)	4,244	Richmond et al. 2014
Total Physical Activity	0.21 (0.10)	4,244	Richmond et al. 2014
Education	0.21 (0.05)	6,578	Marioni et al. 2014
Education	0.33 (0.10)	4,233	Boardman et al. 2014
Education	0.17 (0.07)	6,414	Conley et al. 2014

Although GCTA holds promise, great care needs to be used in the application of these methods to obtain credible results. This paper is meant, in part, to act as a guide for demographers who are potentially new to genetic analyses and are interested in conducting a heritability study. It builds on the work of the GCTA development team (e.g., Visscher et al., 2010; Yang et al., 2010; Yang et al., 2011) and others (Conley et al., 2014) who are well aware of the need for caution in the application of these methods. We begin by describing the method for an audience with minimal training in genetics. We then present three empirical examples demonstrating the sensitivity of GCTA estimates to certain “twists” in the typical approach to using this model. This work is not meant as a critique of the model but is meant to illuminate how the method works and its potential limitations.

2. The method

The core insight underlying the estimation of heritability in both twin studies and with GCTA is that if genetic variation accounts for some measure of phenotypic variation then more genetically similar pairs should be more phenotypically similar. Clearly, this depends upon being able to measure genetic similarity. In twin, extended twin, or family studies, the estimation of genetic similarity occurs only between family members and is trivial since the family relationships are known and pairs receive their expected identity by descent (IBD) value (e.g, .5 for full siblings and dizygotic twins, .25 for half-siblings, etc.). With GCTA, we estimate genetic similarity between all pairs of unrelated individuals (with n unrelated individuals, there are $\frac{n^2-n}{2}$ possible pairs) on the set of genetic markers in question.¹ We emphasize that the metric for similarity used in GCTA is just one of many possible metrics (Speed and Balding, 2014 describe alternatives). Second, a restricted maximum likelihood (REML) estimate of heritability is computed by comparing phenotypic similarity to genetic similarity. We describe these steps in more detail below.

2a. Estimating Genetic similarity

The genetic similarity A_jk between individual j and individual k is estimated as (Equation 3, Yang et al., 2011; Equation 5, Yang et al., 2010)

$$A_{jk}=\frac{1}{N}{\sum }_i\frac{(x_{ij}-2p_i)(x_{ik}-2p_i)}{2p_i(1-p_i)}$$ (Eqn1)

where N is the number of available genetic markers, i indexes these markers, x_ij and x_ik are the number of minor alleles at SNP i for individuals j and k respectively, and p_i is the minor allele frequency.² Genotypes are effectively standardized so that the sample variance is independent of allele frequency. At this stage, we pause to discuss consequences of the fact that the genetic similarity is estimated based on the full set of N markers and not the subset of causal variants that would, ideally, be of interest. The dilemma is that one does not know the set of true causal variants. The causal variants are unlikely to be a random sample of markers. In particular, they are likely to be a sample with relatively low minor allele frequencies (see Yang et al., 2011). This has implications as the quality of the heritability estimate based on A_jk will only be as good as the approximation of A_jk to the genetic similarity on the causal variants. For polygenic traits based on many common variants, heritability estimates based on A_jk should be accurate. However, traits associated with rare variants are not a good target for GCTA analyses (see Zuk et al., 2014 on working with rare variants).

2b. Estimating heritability

The model for decomposing phenotypic variation is

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{g}+\mathit{\epsilon }$$ (Eqn2)

where X is an optional matrix of covariates, g is a vector of random effects, and ε is a vector of errors each with variance ${\sigma }_{\epsilon }^2$. Standard assumptions regarding ε apply, namely that it is independent of X and g. The genetic similarity matrix A enters here through the assumption that

$$\mathit{g}~\text{Normal}[0,{\sigma }_g^{2}A]$$ (Eqn 3)

where A is the matrix of similarity estimates. Heritability is defined as a ratio of the variance of genetic effects to the total variance:

$$\frac{{\sigma }_g^2}{{\sigma }_g^2+{\sigma }_{\epsilon }^2}$$ (Eqn 4)

Heritability is intuitive in Eqn 4 in the sense that we see it is the fraction of total variance accounted for by genetic random effects.

Eqn (2) is estimated via REML. REML is preferred to normal maximum likelihood (ML) estimation, since it leads to improved estimation of variance components (Harville, 1977). In contrast to ML estimation, REML focuses on a likelihood function that is independent of nuisance parameters and should, therefore, provide more reliable variance parameter estimates. Additional details on the estimation technique used here can be found in Gilmour et al. (1995).

2c. Key data requirements

GCTA should only be applied to a sample that has already been through a quality control (QC) process including: pruning for missingness, minor allele frequency (MAF) thresholds (e.g. a MAF below 0.05, a common threshold for identifying a SNP as a “common” rather than a “rare” variant), and Hardy-Weinberg equilibrium³. Dichotomous traits may require even stricter controls (Lee et al., 2011). Statistical power is an important aspect of GCTA (Visscher et al., 2014) and while an online tool⁴ is available, a rule of thumb is that at least 5,000 respondents are needed to detect heritability less than 0.2 (see Figure 3 of Visscher et al., 2014). It is also important that the data be comprised of genetically homogeneous respondents. This is due to the sensitivity of Eqn 1 to population stratification in which allele frequencies may differ across socially defined racial and ethnic groups (i.e., p_i in Eqn 1 changes substantially across groups). The significance of this issue is shown quite clearly in Figure S5 of Domingue et al. (2014) which demonstrates that black spouses from the Health and Retirement Study are estimated to have extreme genetic similarities due to the fact that the majority of the sample is made up of non-Hispanic whites. That is, small and typically meaningless differences in minor allele frequencies among non-Hispanic black and white populations for certain portions of the human genome translate to excessive levels of similarity among same race-groups that may have important implications for the interpretation of heritability estimates.

Even amongst a racially homogeneous groups of respondents, there may still be a concern that population stratification is biasing the results. Figure 2 of Nelis et al. (2009) suggests that even amongst racially homogenous groups, there is remaining population stratification. One standard technique for adjusting for such population stratification is through the inclusion of principal components (Price et al., 2006). Such an approach was taken in the original study of height (Yang et al., 2010) and it is probably prudent to consider such adjustments. However, principal components may also adjust for meaningful differences (in terms of the trait in question) between individuals and thus may lead to under-estimated heritabilities. We would thus encourage users to report adjusted and unadjusted estimates of heritability when appropriate (i.e., when the values differ).

2d. Caveats

The GCTA approach bypasses our lack of knowledge regarding the true causal variants by assuming that these causal variants are distributed throughout the genome in such a way that an estimate of genome-wide similarity is a suitable proxy for similarity on the causal SNPs. It is important to note that this logic only applies to certain traits. Alzheimer’s is an interesting counterexample. The e4 allele of APOE is well known to be a strong genetic risk for developing Alzheimer’s (Genin et al., 2011). For carriers of e4, their probability of developing the disease is substantially elevated compared to non-carriers, regardless of their overall genetic similarity to fellow carriers. For complex traits that are completely polygenic (e.g., the causal variants are large in number but weak in effect size), it is reasonable to inquire how consistent estimates of genetic similarity are over different sets of markers which might be used to compute heritability. This is the empirical focus of Example 1.

Although we still have only limited knowledge about the variants which underlie complex traits, over the last 10 years there has been a large-scale hunt for the genetic variants which underlie specific diseases, traits, and other attributes such as education (Rietveld et al., 2013b). The key technique in linking phenotype and genotype is the previously discussed GWAS approach. Given that we now have a large number of GWAS results it is natural to inquire about potential changes in GCTA estimates if estimates were computed based on genetic similarities from SNPs known to be associated with the relevant outcome. We use information from a GWAS on height to inquire about the sensitivity of GCTA estimates to causal variants which are known to underlie a trait in Example 2.

Estimation of Eqn 2 is premised with additional assumptions that one might question. Just as in the case of a simple linear model, one key assumption underlying estimation is that the errors are of constant variance (homoscedastic). Heteroscedasticity is a common problem in applied settings typically leading to incorrect estimates of standard errors. Given that GCTA is focusing on a ratio containing the estimated error variance, heteroscestasticity could have important implications here. We examine the consequences for heritability estimates if the error term is heteroscedastic in Example 3.

3. Examples

The below examples rely upon data from non-Hispanic white adults (born between 1900 and 1970, but with the majority born between 1930 and 1940) in the Health and Retirement Study.⁵ DNA samples were collected via buccal swabs in 2006 and via saliva samples in 2008. Genotype calls were then made based on a clustering of both data sets using the Illumina HumanOmni2.5-4v1 array. Details on this process can be found online at the HRS website. After standard quality control procedures (e.g., removing SNPs that were missing in more than 5% of samples, MAF below 1%, failure to meet Hardy-Weinberg equilibrium; complete details are available upon request), we retained 1,698,845 SNPs. From this sample of SNPs, the main genetic similarity estimates are computed based on 1,473,658 SNPs (only autosomal SNPs which are also pruned slightly due to a second MAF filter imposed by GCTA) for 4,950 non-Hispanic whites (those from the full sample of non-Hispanic whites who had no missing data on several key variables). With this sample, we obtain reasonable heritability estimates: cognition 0.23, height 0.40, weight 0.25, educational attainment 0.33 (all standard errors are 0.09 which is to be expected given Figure 1 of Visscher et al., 2014).⁶

3a. Example 1: Sensitivity of genetic similarity to the set of SNPs

Heritability estimates rely upon genetic similarity which may be sensitive to the choice of markers. We first choose SNPs that are pruned from the full set to ensure that they are in linkage equilibria (for different thresholds). Linkage disequilibrium arises when genetic markers at nearby locations are correlated due to the fact that large segments of DNA are inherited together. Although genetic similarity is frequently computed via sets of markers which have not been pruned for LD (linkage disequilibria), Speed & Balding (2014, p. 8) note that the use of multiple SNPs in regions of high LD can have consequences for heritability estimates. We also consider randomly chosen sets of markers that are 10%, 30%, and 50% of the full sample of SNPs. Given the underlying philosophy of GCTA, heritability estimates based on reasonably large subsamples of markers should be similar to those based on the full sample of markers. This requires that the different samples of markers produce similarity estimates that are highly correlated.

Table 2 presents the correlations between the genetic similarity estimates (greater than 0.025, as might be used in a heritability analysis) based on the various sets of markers. We focus on the correlations between the similarity estimates from the full set of markers and the similarity estimates from the various subsets (the bolded column). To begin, consider that the genetic relationship values for all persons i and j are correlated at 0.57 when we examine their genetic similarity based all SNPs compared to their genetic similarity using only SNPs that are not in LD using the most conservative threshold. However, when we increase the r² threshold from 0.01 to 0.2 the correlation jumps from 0.57 to 0.75. Increasing the threshold again to 0.5, the correlation is at 0.88. These values can be interpreted via a comparison to correlations between the full set of markers and a random subset of markers. When we compute genetic similarities based on random subsets of SNPs, the correlations are generally high (>0.9) except for the 10% sample. Nevertheless, even when we only use 10% of the SNPs, we present relationship estimates that are correlated with the overall GRM at a value of 0.83.

Table 2.

Correlations between similarity estimates based on different sets of markers and their resulting heritability estimates for height.

	r=0.01	r=0.2	r=0.5	10% Sample	30% Sample	50% Sample	Full	h2	se
r=0.01	1.00	0.52	0.53	0.47	0.54	0.56	0.57	0.10	0.06
r=0.2	0.52	1.00	0.88	0.63	0.71	0.73	0.75	0.44	0.10
r=0.5	0.53	0.88	1.00	0.73	0.83	0.86	0.88	0.42	0.11
10% Sample	0.47	0.63	0.73	1.00	0.79	0.81	0.83	0.31	0.07
30% Sample	0.54	0.71	0.83	0.79	1.00	0.93	0.95	0.39	0.08
50% Sample	0.56	0.73	0.86	0.81	0.93	1.00	0.98	0.38	0.08
Full	0.57	0.75	0.88	0.83	0.95	0.98	1.00	0.40	0.09
N SNPs	61,904	331,433	626,182	169,884	509,654	849,422	1,698,845

We now turn to the impact the differences in the estimates of genetic similarity have on the estimated heritability. To address this, we computed heritability estimates for height based on the various sets of SNPs (italicized column of Table 2). We drop any pair with a relationship greater than 0.025 since these are typically excluded in the calculation of heritability. The full set of markers produces an estimate of 0.40 which, it should be noted, is identical to the estimate in the original GCTA paper (Yang et al., 2010). The 10% random sample of SNPs produced a substantially lower estimate of 0.31, but the 30% and 50% samples produced estimates much closer to 40%. Interestingly, the sets of markers pruned only modestly for LD produced slightly higher estimates of heritability with the exception of the rather extreme case of r²=0.01. Although the rise isn’t large, this effect has also been observed (Vilhjalmsson et al., 2015) in the context of genetic risk scores (indices derived from GWAS studies meant to predict a given phenotype; see Belsky et al., 2013 for a review of this method). When the LD pruning threshold is quite stringent (0.01), the heritability estimate is only 0.1. Thus, calculating genetic similarity using only SNPs that are independent of one another, we reduce the heritability estimate by roughly three-quarters. However, this estimate is based on a relatively small number of SNPs (N=61,904). The next example continues to examine the sensitivity of heritability results to the choice of SNPs, but in Example 2 the subsample of SNPs is chosen in a different manner.

3b. Example 2: Incorporation of GWAS Information

For some traits, such as height, there is now high-quality information available about which SNPs “matter.” Thus, we can use published GWAS results to decide which SNPs to include in the GRM and heritability estimates can be limited to markers with significant p-values (Wood et al., 2014). To use the results from this GWAS, we first selected a set of 842,889 SNPs which are in the GWAS and also in our genetic database of SNPs. Based on these SNPs, we estimate a GCTA heritability for height of 0.34, which is reduced from the original estimate of 0.40 using the full set of markers, but still significant (SE=0.077).⁷ This is an important observation (consistent with Example 1) because we eliminated ~50% of the SNPs yet the heritability was only reduced by roughly 20%. This bolsters support for the GWAS results but also highlights that much of the information across the genome is not necessary for reliable indicators of heritability.

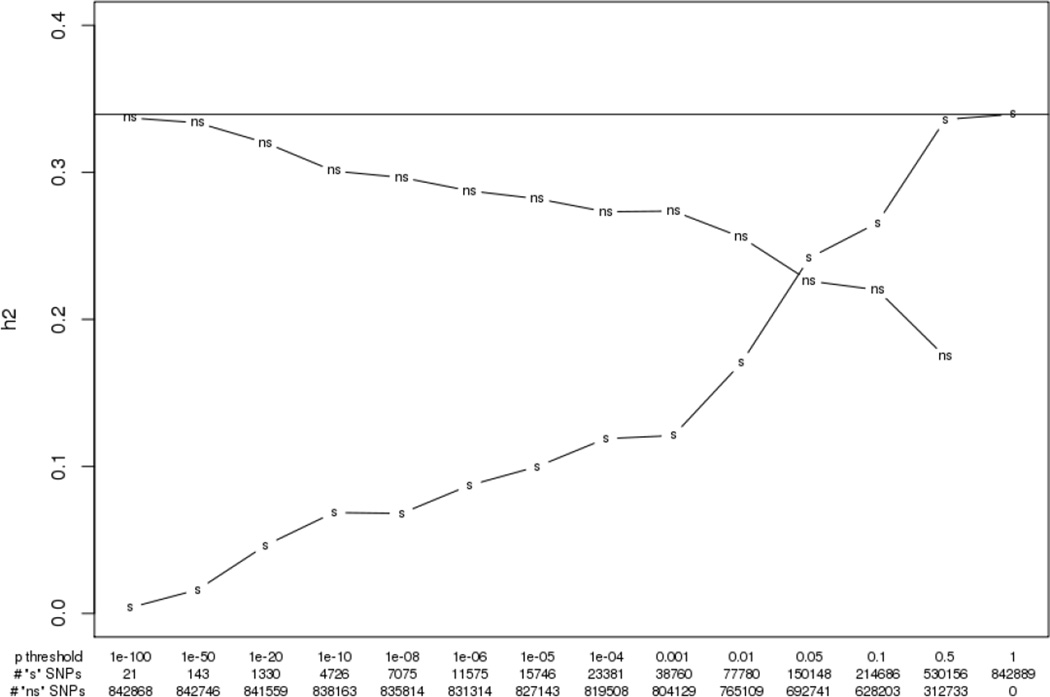
For a given p-value threshold, we designate two sets of markers. The first set of markers, those with a p-value greater than the threshold, are designated by “ns” (for not significant). These are the markers that are unassociated with height as judged by the p-value threshold from the height GWAS (Wood et al. 2014). The second set of markers, those markers with p-values less than the threshold (e.g., those SNPs that are deemed to be associated with height), are designated by “s” (for significant). Consider Figure 1. The horizontal line shows the GCTA heritability of 0.34. The other two lines show the GCTA estimates for the “ns” and “s” SNPs using a range of thresholds (the p-value threshold and the number of markers for each set of SNPs are shown on the x-axis). At the far left, we start with a threshold of 1e-100. This is an extreme threshold (only 21 SNPs reach such a level of significance) and the heritability computed for the 842,868 “ns” markers is very nearly the original estimate. The estimate of the heritability from the “ns” markers above the threshold stays above 0.25 until the 0.05 threshold. Even after the removal of 312,733 SNPs at the 0.5 threshold, there is a still statistically significant heritability “ns” estimate of 0.17. This is noteworthy since we have removed any marker remotely associated with height. The fact that GCTA does not explicitly utilize information related to causal SNPs is very clear.

Figure 1.

GWAS informed GCTA heritability results for height. The heritabilities are computed for different sets of markers. The “ns” lines are based on only those markers with a p-value above the given p-value threshold (not significant markers) while the “s” lines are based on only those markers with a p-value below the given p-value threshold (significant markers) where the p-value for each marker is taken from a large GWAS on height (Wood et al. 2014). Confidence intervals are omitted since they are consistent. Standard errors for “ns” estimates are less than 0.02 for p-value thresholds of 1e-04 and below and under 0.07 for larger thresholds. The standard GRM pruning threshold of 0.025 is not included since it led to the exclusion of large numbers of sample participants in the cases using relatively small (e.g., fewer than 100,000) markers.

Now let’s consider the curve associated with heritability estimates from the “s” markers. The 21 markers that are the most predictive of height produce genetic similarity estimates that lead to a heritability estimate of 0.004. This is not surprising since collectively these markers predict only a very small amount of variability of height. One can observe a slow rise in the estimated heritability of height as the p-value threshold is relaxed (so that increasing numbers of SNPs are in the “s” category. The curves cross around the 0.05 threshold, meaning that similarities in height are better explained by similarities on the 150,148 SNPs below this threshold rather than the 692,741 SNPs above this threshold.

3c. Example 3: Heteroscedastic Outcome

In many empirical settings, the assumption of a constant error variance is questionable. To probe the performance of GCTA in such cases, we simulate an outcome where the variance of the errors is a function of an individual’s height. We generate data using

$$\mathit{y}=0.5*\text{height}+\mathit{g}+\mathit{\epsilon }$$ (Eqn 8)

where ε_i is normally distributed with variance $e^{\alpha •\text{height}}{\sigma }_e^2$ (where height is standardized). The degree of heteroscedasticity is controlled via α (note that when α = 0 the errors are homoscedastic) such that there is a greater variance in the ε_i for tall individuals. This has clear implications for the definition of heritability since Eqn 4 depends on ${\sigma }_e^2$. We fix ${\sigma }_g^2=1$ and control the level of heritability via ${\sigma }_e^2$ (increasing this variance decreases heritability and vice-versa). In our simulation, we use the observed ratio of the variability of the genetic component to the total observed variability (these quantities are available only due to the fact that the data is simulated and thus completely known) as a metric for heritability, but advise the reader that this ratio is not identical to the GCTA definition. Indeed, the quantity of interest in GCTA is poorly defined due to the non-constant error variance. Thus, instead of exact recovery, we focus on the relevant patterns.

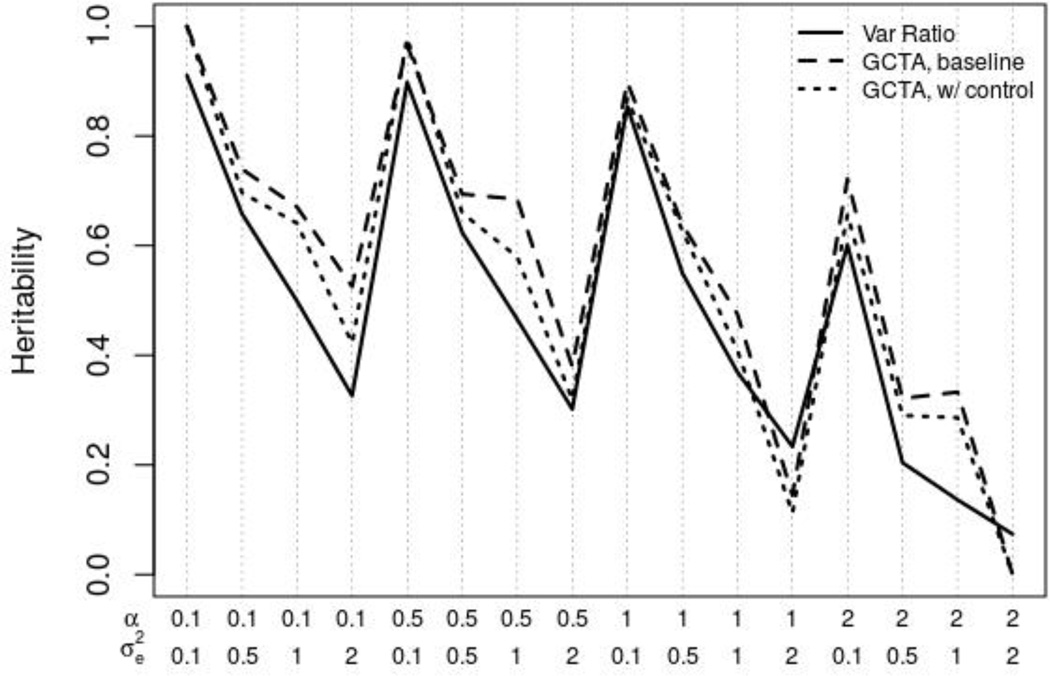
Figure 2 compares the variance ratio discussed above (solid line) and compares it to GCTA estimates that do not (dashed line) and do include height as a covariate (dotted line). The three sets of estimates consistently move together. The GCTA estimate when the control is included tends to be closer to the observed ratio of variances than the estimate without the control, but again we caution that the observed variance here is a somewhat amorphous quantity since the error variance is non-constant. Importantly, the baseline estimates of heritability from GCTA (estimates that do not include height as a predictor) are robust to heteroscedasticity. There may not always be an identifiable correlate of the error variance so it is reassuring to know that relatively reliable information regarding heritability can still be recovered in such cases.

Figure 2.

Comparison of true ratio of genetic to total variance to GCTA estimates (with and without control for the variable associated with the heteroscedastic error) in presence of heteroscedastic errors.

4. Discussion

The examples considered here help to illustrate two key points about GCTA. First, examples 1 and 2 illustrate the fact that GCTA is a method for computing heritability based on genome-wide similarity. Example 1 illustrates the relative consistency of results as long as sufficient samples of SNPs are used. Example 2 illustrates the fact that one does not need to include SNPs thought to be causal for GCTA to estimate heritability. Of course, if too many of these SNPs are removed, the estimate may start to suffer (note the decline in the “ns” line to the right of Figure 2). Second, example 3 suggests that GCTA estimates are relatively robust to heteroscedasticity. Intuitively, there is reason to be concerned about heteroscedasticity since GCTA is based on estimates of variance components. While GCTA estimates are likely to overestimate heritability in the presence of heteroscedasticity, the bias does not seem extreme and relevant information regarding heritability may still be obtained.

This paper adds to the evidentiary base regarding GCTA’s performance in the face of violations of the underlying assumptions. An additional concern is that genetic similarity may be associated with environmental similarities. If that was the case, then these environmental similarities could be the true cause of phenotypic similarities between respondents rather than the genetic similarities studied via GCTA. Other research (Conley et al., 2014) has considered this fact. The environments studied in that research (e.g., childhood urbanicity and parental education) did not seem to bias GCTA estimates for other, putatively heritable outcomes such as height. Later research (Conley et al., 2015) tries to explore this issue further in a more nuanced manner by decomposing the correlation between parent and offspring education levels into genetic and environmental components but focuses on genetic predisposition towards educational attainment (as determined by an educational polygenic risk score) rather than GCTA heritability.

There are several additional applications of GCTA that this paper does not explore. We focus here on two: heritability by environment and bivariate analyses. There is ample reason to think that the relative influence of genotype on phenotype varies across environmental context. GCTA allows one to model the effect of environment on heritability but the ability to adjust for environmental differences is not a cure all. The relevant environments may be unknown, unobserved, or poorly measured. Even when there is a promising candidate for the appropriate environment, GCTA analyses suggesting environmental differences must be interpreted with caution. For example, if environmental differences are associated with, say, ethnic differences, then population stratification could be an issue. In such a case, LD patterns between the causal SNPs and other markers across the two ethnic groups may be different. It could also be the case that genetic or phenotypic variation may be constrained in one environment relative to the other. For that matter, the phenotype could be measured with less fidelity in certain environments. All of these scenarios could potentially lead to HxE findings via GCTA and yet would not necessarily indicate that there is truly a difference in the influence of genotype across environment.

Finally, bivariate GCTA models (Lee et al. 2012) are an interesting method for engaging in genetically informed demographic research. This method yields an estimate of genetic correlation (rG) between two traits which indicates whether an observed correlation between traits, such as height and weight, is due to common genetic factors. For example, Boardman et al. (2015) used this method to show that a non-negligible proportion of the correlation between education and self-rated health appears to be confounded with genes that influence both traits. Such genetic associations may underlie many variables frequently considered in demographic inquiry and a failure to account for these associations may lead to forms of omitted variable bias.