Selection on protein structure, interaction, and sequence

Abstract

Characterizing the probabilities of observing amino acid substitutions at specific sites in a protein over evolutionary time is a major goal in the field of molecular evolution. While purely statistical approaches at different levels of complexity exist, approaches rooted in underlying biological processes are necessary to characterize both the context‐dependence of sequence changes (epistasis) and to extrapolate to sequences not observed in biological databases. To develop such approaches, an understanding of the different selective forces that act on amino acid substitution is necessary. Here, an overview of selection on and corresponding modeling of folding stability, folding specificity, binding affinity and specificity for ligands, the evolution of new binding sites on protein surfaces, protein dynamics, intrinsic disorder, and protein aggregation as well as the interplay with protein expression level (concentration) and biased mutational processes are presented.

Introduction

The biochemistry and biophysics that underlie selection on amino acid sequences in proteins is complex. A growing field aims to model substitution in proteins, building on a now classic framework that independently models the probability of a mutation occurring and the probability of that mutation going to fixation based on its selective effects.1 However, specifying this framework with an aim toward uncovering lineage‐specific functional change requires characterizing what the selective pressures are (overviewed in Fig. 1), including those that do not affect protein function, and describing them in mathematical terms. This review will aim to begin this synthesis conceptually, to enable future theoretical work in describing the processes.

Figure 1.

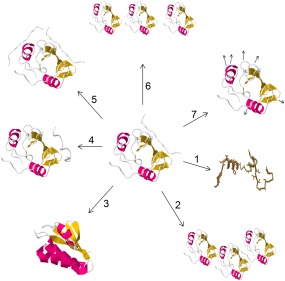
Aspects of protein biochemistry/biophysics on which selective pressures may act are depicted. (1) Stability of the folded state; (2) protein aggregation; (3) misfolding and kinetic traps; (4) nonspecific binding or change in the binding partner at the native site; (5) binding at a new site; (6) concentration levels of the protein; (7) kinetic motions of the protein. Images obtained from the RSCB PDB (www.rscb.org)2 of PDB ID 2MRK,3 PDB ID 1KA5,4 and Foldit.5

The Role of Protein Structure

One of the key aspects of a protein is its structure. A functioning protein relies on being folded into a stable conformation. This simple objective, however, has many elements to it, on which selection can act without directly affecting the protein's function (e.g., binding to a ligand or catalyzing a reaction by stabilizing a transition state). Structure itself is important in maintaining the orientation of functional residues in high local effective concentration about each other. This contribution to the structure of vast fractions of the sequence is hard to quantify. It is clear that a global ΔG is not a great metric to quantify this important aspect of function. However, it is not clear what the right measure would be. Many studies in molecular evolution that treat structure and function (where function is binding) treat them independently.6, 7 Different metrics that quantify the contribution of residues that contribute to stability in a positive sense are needed and conceptual thinking on computationally fast methods to do this is needed. Models to describe protein sequences that are commonly used in the molecular evolution community rely on site independent likelihood calculations. Simulating under such models over long branches will result in a sampling of the equilibrium frequencies of the model at every site, sequences that are all but guaranteed not to fold into the specific structure. So, in the end, both a global ΔG _folding and a site independent likelihood appear to be poor metrics to evaluate selection on amino acid mutations within a protein sequence/structure because they do not adequately describe selection on the interactions between residues.

What Properties Do Folded Structures Have?

Marginal stability is a property of proteins that arises simply due to the large and complex state space of amino acid sequences and conformations, of which the vast majority of folded proteins will result in marginally stable proteins (proteins not far from the unfolding transition); via simulation studies, it has been shown that marginally stable proteins will dominate even if marginal stability is not a property under positive selection, due to mutation‐selection balance.6, 8 The Boltzmann Distribution is often used to model the probability that an amino acid sequence is in any given conformation; accordingly, the fraction of a protein in the folded state can be under selection. Selection is of course weak near the top of an asymptotic function, where increases in stability do not have a large effect on the fraction folded.9, 10, 11 In this regime, where the distribution of fitness effects is linked to the stability of the protein, mutation‐selection balance will dominate and amino acid substitution will be more permissible as the asymptote is reduced.12 Goldstein11 has suggested that changes in the value of this asymptote lead to temporally relaxed selection when the value is reduced and temporal positive selection when the value is increased. While we have indicated that global ΔG may not properly capture the role of selection in maintaining the orientation of functional residues, it is still expected that these general properties will still apply to the effective local concentration of functional residues about each other and changes in selection to this.

In addition to the large number of possible conformations, it is also important to consider the environment of the protein, including solvent effects. That is, molecules in the surrounding solvent will interact with atoms of the protein in many ways, such as by forming hydrogen‐bonds and van der Waals interactions, but also through strong hydrophobic interactions. This is because most proteins contain a high proportion of amino acids with nonpolar side chains, which will thus tend to fold inside the protein structure if possible.13 Thus, hydrophobic interactions are highly influential on what the native state of a protein will be. For example, proteins have been evolved to function in organic solvents, with different amino acid composition patterns.14

Accordingly, it is important to model these effects together with other interactions when studying the effect of selection on protein structure. One approach is to incorporate solvent effects by incorporating them into inter‐residue contact energies.7, 15, 16 Essentially, proteins can be represented as a contact matrix C, where C_ij is equal to one if residues i and j are in contact with each other, and zero otherwise. The amino acid residues are of course linked linearly (as they are in an actual protein), so although adjacent residues are in fact in contact with each other, these do not contribute to any energy difference between a folded protein and an unfolded protein. This is likewise true for residues that are two spaces apart, so in this representation, C_ij is set to zero if $|i‐j|\le 2$. Otherwise, only residues/effective solvent molecules that are close enough to each other in the folded state are assumed to have any interaction. Through this representation of the protein and its environment, contact energies are estimated by considering residues that come into contact with each other, and regarding them as statistical averages over distance and relative orientation. While this representation is a simplification of reality, it has been a useful step toward modeling the effects of selection on structural stability. In addition to the large state space of conformations, interactions, and solvent effects, an additional consideration in modeling structure is that proteins have an enormous number of atoms, each of which has a specific location in the folded structure of the protein. To model each atom would be extremely computationally expensive, so models have been formulated to simplify this. At a first level, hydrogens can be ignored. At deeper levels of coarse graining, amino acid side chains can be averaged. Specifically, we focus on the two‐bead model, first described by Levitt,17 and used by Grahnen et al.,7 among others. In the two‐bead model, each residue is represented by two beads, one of which resides on the backbone of the protein, and the other at the center of the atoms of the residue. This simplification reduces the number of degrees of freedom from the order of magnitude of the number of atoms down to two angles and a radius, per residue. Using this model, it may be possible to study the effects of selection on structure in a realistic manner. The original model did not explain extant sequences particularly well, but more parameter‐rich variants that model constraints on individual sites show promise.18 In general, a theory of how to coarse grain peptides and amino acids has been developed, with some powerful applications19 and it may also be that the Grahnen et al.7 model is too simple. Aromatic residues are particularly poorly modeled in the Grahnen et al.7 approach. Additionally, approaches to move the backbone during mutation to fit residues of different types need further exploration.

Grahnen et al.7 is one of several attempts to incorporate structural information in evolutionary models. As an earlier approach, Robinson et al.20 propose a model with the primary aim of capturing dependencies that arise due to protein structure. Their statistical framework is quite general, by simply modifying the usual instantaneous substitution rate matrix. In their case, being interested in site‐dependencies due to protein structure, they propose a new substitution rate matrix that accounts for whether the substitution is beneficial for the stability of the protein. This model did provide substantial improvements in terms of model fit. Furthermore, using this model, Choi et al.21 showed that tertiary structure is indeed an important component in models of protein evolution and that ignoring it is detrimental. However, the model of Robinson et al.20 falls short of models that account for structure more explicitly. Kleinman et al.22, 23 build on the model of Robinson et al.,20 adding parameters for energy potentials of the protein, to account for structure in a similar way to Grahnen et al.7 The Kleinman et al. model23 has different strengths and weaknesses compared to the Grahnen et al. model,7 but neither offers a sufficiently accurate characterization of protein biophysics to account for the amino acid substitution process.

Selection against Alternate States Being More Stable

While proteins need only marginal stability in their native state, it is generally the case for a typical protein that the native state is indeed the most stable form for that protein's amino acid sequence. If alternate states were to become more stable, if kinetically accessible, this would then become the native state, thus having likely implications for proper function. Therefore, it should be the case that negative selection is acting to reduce the stability of alternate states for a typical protein. One study has suggested this using directed evolution of a de novo protein binding pair, which resulted in an increase in the energy gap of alternative conformations.24 This evolutionary trajectory will depend of course on the nature of the selective pressure applied.

Under simplified representations of proteins (like a lattice model), it was shown that proteins in which stabilizing interactions between residues are also present in non‐native states will tend to utilize selection against the stability of alternate states, or “negative design.”25 This work relied on an assumption that stabilization of long‐range interactions is an indication of negative design, which is true in lattice models because calculation of energies accounts only for residues that are in contact with each other; therefore, stabilization due to long‐range interactions must result from a destabilization of non‐native states. Although this assumption is not necessarily correct in real proteins, Noivirt‐Brik et al.25 also examined real proteins, and found evidence that negative design is acting on proteins in similar patterns to their computer‐generated proteins. With the use of an explicit statistical mechanical model with intrinsic decoys (described below), Minning et al.26 also detect selective pressures associated with negative design on protein structure.

Use of Decoys to Characterize Alternative States

Scoring functions are commonly used to evaluate the effect of substitutions on the conformation of the protein. As substitutions accumulate within a fold, the scoring function simply indicates if the sequence fits better in the native state than in an unfolded state. However, sequence change can lead to fold transitions, where alternatively folded structures do not necessarily carry out the same function. Therefore, it is necessary to make sure that mutations do not cause a sequence to prefer an alternative conformation. This is usually done with sets of decoy structures that are either explicit or implicit.

Decoy structures are alternate conformations of a particular amino acid sequence, which can then be used to test any scoring function of protein conformations. Generally, any scoring function is based on the free energy of the conformation, since the native state should have the lowest energy among all possible conformations for a given sequence. However, formulation of a scoring function is a non‐trivial task, with many possible considerations, such as whether to use a statistics‐based or a physics‐based model,27 or whether to use an all‐atom model or a coarse‐grained model such as in the aforementioned Grahnen et al.7 model.

Thus, scoring functions need to be evaluated to determine whether their predictions are accurate. By testing any potential scoring function on decoys against known correct conformations, one can then determine how frequently the scoring function correctly assigns the best score to the correct conformation. For example, consider a decoy set with one correct and many incorrect conformations. The scoring function can then be calculated on each decoy, and then this can be compared to some measure of how far each decoy is from the native state, such as root‐mean‐square deviation (RMSD) of the C_α atoms from their placement in the native state.28 The correlation with RMSD has been used to evaluate scoring functions; however, it is important to note that good scoring functions should also be able to recognize situations that may lower their correspondence with RMSD, such as structures whose C_α atoms are close to the native state but have large clashes between other atoms, or structures that are quite different from the native state but also are of low energy.

To study selective pressures as they pertain to the structure of a protein, the development of accurate scoring functions is crucial. Thus, decoys are an important contribution to this body of knowledge. Additionally, decoys may be used to study selection directly, which will be mentioned briefly below.

Explicit decoys can be used that are similar in length to the protein (without a model for indels) to evaluate the fit of sequences into explicit alternative structures. Databases of such decoys exist.29 Alternatively, native structures that are similar in size from PDB can be utilized, where the most information will come from those that are close to fold transitions in sequence space. Using a limited number of explicit decoys may poorly reflect the actual distribution of the fold space that exerts a selective pressure on the sequence.

Implicit decoys can be made by resampling contacts from the native structure.30 Doing this blindly will consider structures that are physically impossible. It is unclear if that is a problem, as these structures are used to sample the background distribution and it is the nature of the distribution rather than the specific contacts that are critical. If it is a problem, implicit decoys that are consistent with a self‐avoiding walk can be used. One important aspect of proteins is the greater importance of short range contacts to long range contacts due to conformational entropy. Consideration of primary sequence distance in sampling contacts can account for this.

Another potential mechanism for generating implicit decoys is to sample substructures from longer structures in PDB. These would not be expected to fold into these conformations independently from the rest of the structure, but might also generate a realistic set of contacts that are reflective of the background distribution. Further research on the performance of different approaches for generating implicit decoys is needed.

Selection against Kinetic Traps in Folding

Reactions in chemistry are typically thermodynamically or kinetically controlled and protein folding is no different. It is commonly assumed that proteins fold into their most thermodynamically stable structure. However, to the extent that they do so, this is likely the product of selection against amino acid transitions that would enable non‐native contacts in the folding process that might lead to kinetic traps (kinetically rather than thermodynamically controlled folding processes). However, with respect to the possibility that kinetic traps may be selected against, only indirect evidence for this exists. The question of how to detect this directly from sequence data still remain. One idea is to use intrinsic decoys that come from resampling the sequence contacts. If this procedure is carried out to identify background contacts a priori, it only has to be done once in an analysis and need not be computationally prohibitive, even if based on self‐avoiding walks. However, a second point to consider is that proteins seem to only make contacts that remain present in the active conformation during the folding process.31 These would then not be largely reflected in the background intrinsic decoy distribution, but would be partially unfolded versions of the native state with small numbers of non‐native contacts. They would not be reflected at all if the sampled set were controlled to have the same number of contacts as the native state and would need explicit addition. A further complication is the potential role of chaperones in refolding proteins that are not natively folded, perhaps toward thermodynamic minima.

Another aspect of the folding process is the speed of folding. It may be essential for proteins to fold quickly. Kinetic traps would slow down the folding process, or even cause the polypeptide chain to fold into an alternate state. The possible detrimental effects of a kinetic trap have been explored in the Multidrug Resistance 1 (MDR1) gene, in which a synonymous single‐nucleotide polymorphism (SNP) was seen to be associated with the presence of altered conformations of the protein product P‐glycoprotein (P‐gp).32 This is remarkable because synonymous substitutions do not change the resulting amino acid, so they are generally not expected to change the function or structure of the final protein product. In this case, however, the substitution produces a rare codon. This may slow down the translation from mRNA to amino acid. Specifically, Kimchi‐Sarfaty et al.32 hypothesize that this affects the speed of co‐translational folding, thereby causing the presence of alternate conformations.

To begin to address the question of whether the folding rate is selected against, a couple of approaches have been explored. These approaches have attempted to compare the folding speed between proteins resulting from laboratory‐generated polypeptides and actual proteins.33, 34, 35, 36 Each of these studies found that these laboratory‐generated proteins have as fast or faster rates of folding than naturally occurring proteins, suggesting that evolution has not optimized proteins for fast folding.

Conformational Ensembles and IDPs

Despite the fact that selection should be acting against the stability of alternate states to the extent that they affect function (see above), proteins with multiple stable states do exist and are quite prevalent in some organisms. At the extreme end, these are known as intrinsically disordered proteins (IDPs); these polypeptides lack a single native state, and instead exist as a collection of conformations. For any given IDP, its collection of conformations may cover a range from fully unfolded to partially structured to fully structured on binding. Selective pressures for function on this class of proteins seem to depend on the functional requirements of the protein. In the case of a limited number of specific conformations, this can be modeled as selection on pleiotropic structural constraint.37, 38 The selective pressures are more complex with regard to true IDPs.

It has been observed in genome comparisons that there is a positive correlation between IDP prevalence and decreasing effective population size (with organismal complexity as a proxy).39 As smaller population size organisms tend to have decreased selective power acting on them in general (as fixation probabilities depend on the selective coefficient scaled by the effective population size), a possible null hypothesis for the evolution of IDPs is simply that IDPs have not been selected against as strongly in the organisms in which they tend to be prevalent.40 In other words, this null hypothesis would imply that there is no reason why organisms should have IDPs other than by chance. However, IDPs have particular functions that are crucial to the cell.41, 42 If these functions cannot be performed by ordered proteins and are under negative selection, then this would be evidence against the null hypothesis above. Such an analysis would of course need to account for the reduced selective pressures in organisms where IDPs are more prevalent.43 One possible selective pressure against IDPs would be against nonspecific interaction. However, IDPs are enriched for polar residues, which might be less likely to generally associate with protein surfaces nonspecifically and might be evolutionarily tunable in small population size regimes. Further sequence‐structure‐function work is needed to understand the selective pressures acting on IDPs. The explicit Markov model generated by Szalkowski and Anisimova44 is a start to understanding the selective pressures associated with order to disorder transitions and when sequences are evolutionarily stable as ordered or disordered. Clearly there is variance in evolutionary rates for both ordered and disordered regions.

From Static Structures to Protein Dynamics

All proteins have some degree of disorder, including flexible motions about a mostly stable state. Protein dynamics describe the flexibility of a protein in terms of the motions that individual atoms undertake about the structure. Proteins naturally have some movement between different conformations. It is unclear when this flexibility is vital for a protein and when it evolves neutrally. Flexibility can be essential for proper folding, catalysis and interactions with ligands. As such, it may be a trait that is under selection.

Modeling protein flexibility, however, is not a straight forward problem. One strategy is to quantify flexibility by its energetic response to a force. Specifically, a flexible protein will respond to an applied force with large‐amplitude low frequency motions, whereas a rigid protein will respond to an applied force with small‐amplitude high‐frequency motions. Jimenez et al.45 developed a method utilizing photon echo spectroscopy to measure both the amplitude and time scale of these motions of a protein after being subject to an applied force.

This approach was used to investigate evolutionary dynamics of flexibility in an anti‐fluorescein antibody.46 Antibodies tend to be promiscuous during initial stages of an immune response and then highly specific during later stages. Furthermore, antibodies that are isolated at later stages of an immune response are usually highly mutated in comparison to their germ‐line gene sequences.47 Jimenez et al.46 demonstrate that antibody dynamics are under strong selection as the mutations during the immune response appear to be responsible for increased rigidity of the protein, thus leading to the requisite increased specificity.

Normal mode analysis (NMA) is another approach to studying flexibility. It is an approach for studying protein dynamics, which dates back to the 1980s,48, 49 but it has gained renewed interest more recently as it may be successful in predicting protein dynamics that are relevant to function.50 Typical usage of NMA in the study of protein dynamics assumes that the potential energy function of each atom is at most quadratic, and thus can be estimated by a Taylor series expansion. The entire system of movements of atoms can then be represented by a 3N by 3N Hessian matrix, where N is the number of atoms. Alternatively, one can consider only the C_α backbone atoms, which reduces the computational burden tremendously. On the other side, a fuller treatment of the motions of a protein can be gained by molecular dynamics, but this is not tractable for evaluating the evolutionary trajectories of proteins probabilistically. Some balance between accounting for physical reality and computational speed is necessary in this area, as in others.

Additionally, NMA has been used within a phylogenetic approach to study protein dynamics.31 In this manner, a comparison of changes in dynamics to the expected rates of change under selection is able to be made, throughout the evolutionary history of a protein family. Two strategies were proposed to account for phylogenetic structure. One strategy reconstructed the vectors of motions of extant proteins over the tree with an end point constrained diffusion model. The other strategy built ancestral sequences at internal nodes of the tree computationally, built homology models for these sequences, and then measured the normal modes directly on the homology models. These strategies of reconstructing genotypes and molecular phenotypes both are approximate, with statistical disadvantages compared with an integrated model for normal mode evolution, but gave similar conclusions. In the end, neither was powerful enough to predict a priori which enzymes in a family will have changed functions. Conversely, not accounting for the background rate of change of normal modes with amino acid substitution is a problem, so better methods that work in a phylogenetic context are in fact needed.

The Null Model of Normal Modes Evolution under Negative Selection

Much work up to this point has focused on identifying and characterizing negative selection on protein dynamics. Because fluctuations in a protein are generally necessary for it to function, one biological hypothesis is that there will be negative selection against changes in these fluctuations. A comparison of backbone flexibilities across 2087 proteins found that flexibility profiles are indeed conserved at the family and superfamily levels.51 However, backbone flexibility is only a proxy for internal protein dynamics; that is, investigating the normal modes via NMA or Elastic Network Models provides a more direct understanding of protein dynamics. Specifically, it is typically observed that the lowest energy modes are the ones that are functionally relevant.50, 52, 53 Several studies have demonstrated evolutionary conservation of these low‐energy large‐amplitude normal modes;54, 55, 56, 57, 58, 59 however, these were case studies that only investigated small sets of proteins, and are thus not immediately generalizable to all proteins.

A comprehensive study of the normal modes of a large set of proteins utilized a Gaussian Network Model, finding that the lowest modes are the most conserved.60 This implies that the previous finding regarding the conservation of backbone flexibility is due to the conservation of the lowest modes. Further, as the proteins in this study were representative of all structural classes and folds, this result is generalizable to all proteins.

While these findings are consistent with the biological hypothesis that dynamics are conserved because fluctuations are functionally important, they do not specifically address whether that is actually the case. Indeed, Maguid et al.60 point out that this is an unlikely explanation given their finding that functionally important normal modes are conserved at the superfamily level; that is, conservation at the family level is consistent with the hypothesis that fluctuations are functionally important, but at the superfamily level, one would expect higher functional diversification, which suggests that we should also expect higher normal mode diversification if this hypothesis is true.

An alternate hypothesis is that the low energy modes are simply more robust to mutations. The rationale for this is that lower modes are averages across more sites than higher modes; thus, mutating one site will have little effect on a lower mode. Thus, if one wants to investigate the potential effect of selection, the null model must account for the effect of random mutations on lower modes. Such a null model was formulated using a variation of an Elastic Network Model,61 under which proteins were simulated with random mutations, and compared to a dataset of evolved proteins. The variability in normal modes were found to be similar between the simulated proteins and the evolved proteins, suggesting that random mutations were adequate to explain the apparent evolutionary conservation of low energy normal modes. Against a background of neutral evolution, a priori knowledge of specific modes critical for conserved or altered function could potentially be utilized in evolutionary models.

Allostery

Allostery involves regulation over a distance in a protein governed by nonphysically interacting residues (see Nussinov and Tsai62 for a recent review). A question arises of when allosteric regulation changes in evolution, can this be detected computationally. Allosteric regulation can involve explicit conformational change on binding to an external partner and/or changes in dynamics that affect function (both including changes in the conformational ensemble). Predicting such changes requires both an accurate model for sequence‐based kinetic motions (described above) and for changes to a structure that are induced by binding. Models for protein‐protein interaction are described below, although the molecular evolution field does not have appropriate models to predict conformational changes on binding when there are not solved homologous structures in bound and unbound states.

Selection against Nonspecific Binding in Functional Pockets

The binding interface of a protein is under selective pressure to maintain the contacts necessary for interacting with native ligands. It is also under selective pressure to not bind to ligands that might bind at high affinity that would be deleterious to bind to. Examples of this are known in SH3 domains and in alcohol dehydrogenase.63 When such selective pressures are known to exist, there is selection on the amino acid content of the binding pocket/interface to both maintain tight binding to the native ligand and to prevent tight binding to deleterious ligands.63, 64 To model this, one would need explicit knowledge of the subset of potential binding partners that bind at high affinity and that cause deleterious fitness effects when bound. Such knowledge is currently very limited.

Within a particular organism, proteins may interact with specificity for one or a few partners, or with numerous partners.65 The evolutionary mechanisms that have produced this specificity divergence are not yet well understood. For proteins that have high specificity, it is generally assumed that they evolved from more promiscuous forms, and that selection has driven their transformation into monogamous or highly specific forms. However, we are only beginning to uncover evidence that contributes to our actual understanding of the evolutionary processes.

Another approach is the phylogenetic reconstruction of ancestral protein sequences, to infer the evolutionary history of ligand recognition.66, 67 Using this approach, an investigation of steroid hormone receptors (SRs) has found that SRs evolve according to a so‐called principle of minimal specificity: at any given evolutionary time point, proteins have enough specificity to distinguish between the substances in their current environment, but not more.68 The studies do not explicitly consider the full range of substrates that a particular substrate is likely to encounter in a cell.

Selection against Nonspecific Binding in Other Surface Regions (and for Specific Binding in New Locations)

Detecting the emergence of new binding interfaces is difficult. One example that has been detected through the emergence of negative selection in patches on the surface is leptin in humans.69 Another approach to do this is to use a docking engine to systematically screen the surface of a protein.70 To integrate such an approach in a phylogenetic context would not be tractable at present. Further, selection would only act against non‐specific interactions that might be deleterious. A starting point, related to detecting aggregation, might be examination of the emergence of hydrophobic patches on protein surfaces, where selection emerged on specific amino acids or on non‐specific hydrophobic content.

Selection against Aggregation

In addition to nonspecific binding among properly folded proteins, misfolding can also contribute to another form of nonspecific binding known as aggregation, in which misfolded proteins will clump together. Protein aggregation is potentially lethal, as it is the cause of several diseases such as Alzheimer's disease, Parkinson's disease and Type 2 diabetes. This suggests that selective pressures should be acting against aggregation. While there is a general consensus that this is true in most cases, the characterization of selective pressures on aggregation is still developing.

It has been believed that there are so‐called gatekeeper residues, which encourage the proper folding of the protein and thus help the protein avoid misfolded states that might lead to aggregation.71, 72, 73 Thus, these residues would be natural targets for selection to act on. However, most of the early studies demonstrating this were case studies on particular proteins, and thus not generalizable to all proteins. One approach to study this more globally is to use a statistical mechanics algorithm called TANGO, to predict how sequence and mutation affects aggregation.74, 75, 76

The model employed by the TANGO algorithm considers four possible structural states for each peptide to be in: α‐helix, β‐turn, α‐helical aggregation, and β‐sheet aggregation. For each peptide, the probability that it resides in each of these states is modeled with the Boltzmann distribution. Using this model, it was demonstrated across 28 full proteomes from all kingdoms of life that selection is acting against substitutions that would cause aggregation.77 Additionally, in the proteomes of Saccharomyces cerevisiae, Drosophila melanogaster, and Caenorhabditis elegans, the TANGO algorithm was used to demonstrate evidence that selection acts more strongly against aggregation in “essential” proteins as compared to “nonessential” proteins, where the classification of essential versus nonessential was made based on the protein's contribution to the organism's fitness.78

However, although some simplifications are employed in the calculation of the partition function, the TANGO algorithm is likely too computationally intensive to be used in evolutionary simulations for further study. A possible alternative would be to replace the actual energies with an approximation that considers only solvent‐accessible surface area (SASA), and calculate the potential due to solvation of the protein based on this.7

Under this modification, for example, it may be possible to explore the relationship between aggregation and surface hydrophobicity of the protein. It is well‐established that a protein's propensity to form aggregates is positively correlated with its surface hydrophobicity.79, 80 However, a further exploration of this relationship would lead to a better understanding of the mechanisms of aggregation, and consequently the selective pressures that act on aggregation. Simulation studies under this model could be useful in characterizing the evolutionary history of surface regions that would prefer to be intermolecularly buried rather than exposed to the solvent. That is, what were the selective pressures that resulted in these residues being on the surface of the protein? Are there selective pressures that act against the presence of hydrophobic residues on the surface of the protein? How large of a hydrophobic patch is necessary for aggregation to occur and how does it relate to other physical characterizations of a protein (like the size and energy required to prevent diffusion)? Answers to these questions will be important in forming a model that detects regions on protein surfaces likely to generate selective regimes that prevent aggregation.

The Role of Protein Concentration (Expression Level) in Determining Selective Pressures

Expression level (typically measured at the mRNA level) is thought to be a critical determinant of evolutionary rate and selective pressures placed on a protein sequence.81, 82 One straight forward interaction is that the fractional occupancy of all binding sites on a protein (specific and non‐specific) will depend on its concentration. Any deleterious binding interactions at low affinity will occur more often when a protein is at higher concentration. This is a classic argument that follows naturally from chemical understanding, and has recently been further characterized by Levy et al.,83 while also addressing ideas related to selection against non‐specific binding (above). In particular, Levy et al. find that non‐specific binding is inversely related to concentration, and together these impose constraints on the evolutionary trajectory of the protein.

Additionally, it is known that the error rate in translation is relatively high. As a protein is expressed at high levels, the number of mutant proteins (through translational error) will increase. As most mutations are destabilizing, this is mostly a negative effect. The negative effect has been hypothesized to generate selection on translational robustness, especially in larger population size species.84 However, a positive variant of this preceding adaptation has been termed, “The Look Ahead Effect.”85

Overall, increasing the concentration of a protein is therefore expected to increase both the fraction of non‐specific interactions as well as the number of translational errors leading to mis‐folded proteins. For example, it has been suggested that there is selective pressure for robustness against translational errors in bacterial β‐lactamase.86 Expression level might then be viewed as a modulator of selective strength, in a different way than effective population size is.

Selection and Mutational Bias at the DNA Level

Mutational bias is a process that changes the nucleotide and corresponding codon frequencies independently from any selection at the protein level. Selection for codon usage or for GC content can also affect amino acid usage. For example, intergenic GC content in bacterial lineages has been shown to affect coding sequence amino acid content.87 Together these processes can shape amino acid sequences and should be considered. Repeat Induced Polymorphism in filamentous fungi88 systematically introduces G to A and C to T mutations to repeated sequences. Those that survive this process without the introduction of stop codons end up with an increased hydrophobic content in their proteins simply due to the structure of the genetic code. A number of mutational processes are known to affect GC content in bacterial lineages (see e.g., Lasselle et al.89). GC content in some thermophilic bacterial and archaeal lineages may also be under direct selection.90 This also influences protein sequences before selection at the protein level is accounted for. Codon usage in general can also affect amino acid sequences, as different codons have different single mutation neighbors in the genetic code that are more easily sampled.91 Further, viruses are known to have overlapping reading frames.92, 93 The overlapping reading frames place selective pleiotropic constraints on codon usage and amino acid content in any single lineage. This can explicitly be considered by accounting for the different reading frames and their selective pressures individually.

Halpern and Bruno1 shaped an early variation of the mutation‐selection model that allows for treating mutational probabilities and fixation probabilities independently. This mechanistic separation allows for more explicit treatment of processes like biased mutation than is easily available in standard amino acid transition rate models.

Linkage

Sites that are linked on chromosomes can affect the probabilities of fixation of individual amino acid changes. In a positive sense, this is known as a selective sweep. In a negative sense, this is known as background selection. Linkage can lead to rapid fixation of deleterious changes or elimination of adaptive changes based on co‐segregating variants. The effect is expected to be stronger in more gene dense regions of genomes. Population geneticists typically model this effect through modulation of effective population size as a parameter, although more mechanistic approaches are envisionable (Weber et al., manuscript in preparation).

Conclusions

Mechanistically modeling protein sequence evolution is a hard problem. It is inherently linked to the protein folding and inverse folding problems, as well as to population genetic and phylogenetic processes.94 A number of phenomena at the DNA and protein levels affect protein sequence evolution. Determination of the relative importance of different effects and mathematical/computational treatment of the influence of important processes on selective coefficients will keep researchers in this field busy for many years to come.