Improved illumination system of laparoscopes using an aspherical lens array

Abstract

The current fiber-based illumination systems of laparoscopes are unable to uniformly illuminate a large enough area in abdomen due to the limited numerical aperture (NA) of the fiber bundle. Most energy is concentrated in a small region at the center of the illumination area. This limitation becomes problematic in laparoscopes which require capturing a wide field of view. In this paper, we propose an aspherical lens array which is used to direct the outgoing rays from the fiber bundle of laparoscope to produce a more uniformly illuminated, substantially larger field coverage than standalone fiber source. An intensity feedback method is developed to design the aspherical lens unit for extended non-Lambertian sources, which is the key to the design of this lens array. By this method, the lens unit is obtained after only one iteration, and the lens array is constructed by Boolean operation. Then, the ray-tracing technique is used to verify the design. Further, the lens array is fabricated and experimental tests are performed. The results clearly show that the well-illuminated area is increased to about 0.107m² from 0.02m² (about 5x larger than a standard fiber illumination source). More details of the internal organs can be clearly observed under this improved illumination condition, which also reflects the significant improvement in the optical performance of the laparoscope.

1. Introduction

Laparoscopes, which have unparalleled ability to visualize lesions within internal organs with high resolution, allow doctors to perform both minor and complex surgeries with a few small cuts in the abdomen. Usually, a laparoscope consists of an imaging system and an illumination system [1]. In the illumination system, the light beam emitted from a source is first coupled into a fiber bundle, and subsequently cast onto organs in the abdomen after its propagation along the fiber bundle. Then, the illuminated organs are captured by the imaging system and their images are displayed on a screen. Figure 1 shows three laparoscopes, along with the illumination patterns produced by the three laparoscopes on an acrylic sheet at a lighting distance of 150mm. The spatial energy distributions of these three laparoscopes have one thing in common: most energy is concentrated in a small region at the center of illumination area and the illuminance dramatically decreases from the center to the edge of the illumination pattern. In standard laparoscopes that typically image a field of view about 50mmx50mm across at a close working distance of about 50mm, the overly concentrated illumination pattern does not seem to present a significant problem in laparoscopic image as the well-illuminated area is adequate for the field coverage. However, the concentrated non-uniform illumination problem present a severe challenge in laparoscopes whose imaging systems are designed to capture a large surgical area or the objectives of the laparoscopes have large numerical aperture for higher light efficiency. For instance, we developed a multi-resolution foveated laparoscope (MRFL) technology [2,3] that is capable of capturing both wide-angle and high-magnification views simultaneously for improved situational awareness. At a working distance of 150mm, the MRFL system captures a surgical field of approximately 300mm by 300mm. The numerical aperture of its objective is about 3 times of a standard laparoscope. The conventional illumination system not only limits the utility of the wide-angle view due to the poor illumination at large field angles, but also leads to over exposure in the central region. As shown later in this paper [see Fig. 9(c)], most part of the organ cannot be clearly observed due to the poor performance of such an illumination system, especially at the center and the edge of the organ. Besides, with such an illumination system, any attempt to improve the optical performance of laparoscopes by increasing the resolution of the imaging system might be in vain.

Fig. 1.

Examples of the illumination patterns produced by the current laparoscopes: (a) three laparoscopes with fiber-based illumination systems and three illumination patterns produced by (b) laparoscope 1, (c) laparoscope 2 and (d) laparoscope 3, respectively. The illumination patterns are recorded on an acrylic sheet with the size of 500mm × 500mm at a lighting distance of 150mm. The Stryker X-6000 Xenon Light Source is used here.

In this paper, we present a novel method for overcoming the illumination challenge in laparoscopes offering wide field coverage. An aspherical lens array is placed adjacent to the end surface of the laparoscope, to direct the outgoing rays from the fiber bundle to improve the performance of the illumination system. The aspherical lens array works for an extended non-Lambertian source here, and an efficient intensity feedback method is presented to design the aspherical lens unit. As the experimental tests will show, the performance of the illumination system is significantly improved by the aspherical lens array, and the organs can be well illuminated under this new illumination method, which allows the imaging system of the laparoscope to capture more details of internal organs. The rest of the paper is organized as follows. In Section 2, we will first explain how an aspherical lens can be used here to improve the illumination condition of the laparoscope, and then develop an intensity feedback method to design the aspherical lens unit for a non-Lambertian source. After that, the prescribed design of the aspherical lens array will be achieved in Section 3. Also in this section, experimental tests will be performed and comparisons will be made to demonstrate the significant improvement in the illumination condition of laparoscopes. Then, we will conclude our work in Section 4.

2. Design strategy and design approach

2.1. Design strategy

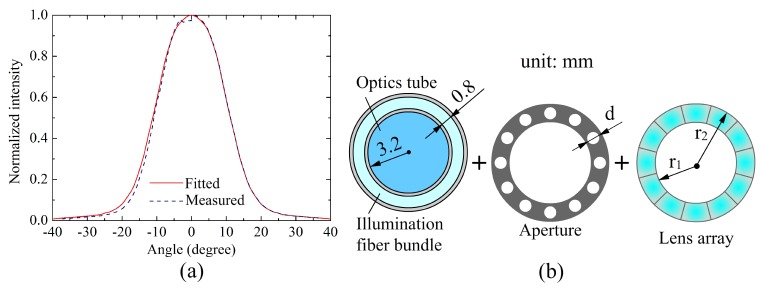
In a typical laparoscope illumination system, the light rays from a light source are coupled into a fiber bundle and produce a uniform annular illumination pattern at the end surface of the fiber bundle after their propagation along the fiber bundle. From the illumination engineering point of view, we consider the end surface of the fiber bundle as a secondary light source. Figure 2(a) shows the normalized intensity distribution of the outgoing beam of the fiber bundle experimentally measured from the laparoscope 1 shown in Fig. 1(a). The distribution clearly shows the intensity dramatically decreases with the increase of the emission angle of the outgoing ray, which clearly suggests that the secondary light source is a non-Lambertian source. On the other hand, we can consider the secondary source to be space-invariant given the nature of the fiber bundle.

Fig. 2.

(a) The normalized intensity distribution of the outgoing beam from the laparoscope 1. The blue dash line represents the measured intensity distribution and the red solid line represents the one obtained from data fitting, which will be used in the lens unit design. (b) Design strategy: an aspherical lens array is placed adjacent to the end surface of the laparoscope to produce a uniform illumination. The dimensions of the end surface of the laparoscope just indicate the limited degree of design freedom left for the subsequent lens design.

Based on the space-invariant non-Lambetian property of the secondary source produced by the fiber bundle, Fig. 2(b) illustrates our proposed method to improve the illumination condition of the laparoscopes. An aspherical lens array along with an aperture array is placed adjacent to the end surface of the laparoscope, which redistributes the outgoing beam from the fiber bundle of the laparoscope to produce a uniform illumination over an extended area. In this illumination system, one key element is the aperture array. By the use of the aperture array shown in Fig. 2(b), the annular non-Lambertian source can be divided into several non-Lambertian disk sources which have the same diameter, d. The choice of parameter d is determined by the energy efficiency and the packaging requirements of the illumination system. A smaller value of d means that the lens array can be very compact, but the energy efficiency cannot be high. Thus, trade-offs should be made between the energy efficiency and the compactness of the illumination system. To facilitate our design, we suppose all these non-Lambertian disk sources are the same. Then, the spatial energy distribution of each disk source is redistributed by a corresponding lens unit to generate the given uniform illumination. Once the lens unit is obtained, the number of lens units in the lens array can be calculated and the lens array can be constructed. The final illumination produced by the lens array is simply the sum of all those outputs produced by the lens units. Thus, the key to achieving the prescribed illumination is to design the aspherical lens unit that can produce the given uniform illumination.

2.2. Design approach

A major challenge for designing the aspherical lens array is the very limited space of the laparoscope, as clearly shown by the dimensions of the laparoscope given in Fig. 2(b). In this limited space, we should make the lens array as compact as possible, while maximizing the number of rays passing through the aperture to achieve a high energy efficiency. Based on the method shown in Fig. 2(b), the unit lens design to be addressed here is actually a prescribed illumination design for an extended non-Lambertian source in three-dimensional (3D) rotational geometry. Usually, those zero-étendue methods [4–8], which rely on point source or parallel beam assumption, are not able to generate good designs when the influence of the source size or angular extent on the performance of an illumination system cannot be ignored. A few illuminance compensation approaches have been developed for 3D rotational (or freeform) designs of extended source [9–12]. Since the design during each iteration is created by a zero-étendue method, these methods are less effective in compact designs where the ratio of the distance between the lens and the source to the size of the source is less than 3 [13]. Thus, these methods mentioned above may not be the best choice in our design.

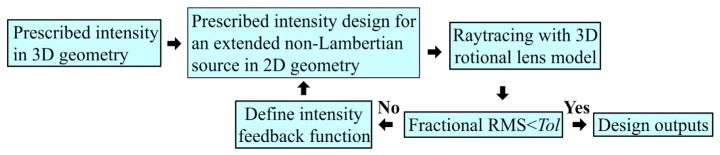
In our previous work [14], we developed a feedback method for extended Lambertian sources in 3D rotational geometry. This method can generate very compact designs (the ratio of the distance between the lens and the source to the size of the source can be less than 3.) with good optical performance. To address the design problem described above, we develop a feedback method for extended non-Lambertian sources in 3D rotational geometry and the flowchart of the extended method is shown in Fig. 3. Given a prescribed intensity distribution, first we perform a two-dimensional (2D) design for the extended non-Lambertian source with the prescribed intensity. We then generate the 3D model of the aspherical lens by applying the rotation to the 2D lens profile and analyze the 3D performance of the aspherical lens by ray-tracing technique. Finally, a feedback strategy will be employed to further improve the optical performance until the predefined stopping criterion is met.

Fig. 3.

A feedback method for extended non-Lambertian sources in 3D rotational geometry.

One of the keys to this feedback method shown in Fig. 3 is to achieve the prescribed design for the extended non-Lambertian source in 2D geometry. In our previous work [15], we already developed a direct method for the prescribed intensity design for extended non-Lambertian sources in 2D geometry. Here we directly apply this method to the 2D design stage shown in Fig. 3. The only difference is that the light source was immersed in the lens in Ref [15], and in this design the light source is immersed in the air and attached to the planar entrance surface of the lens.

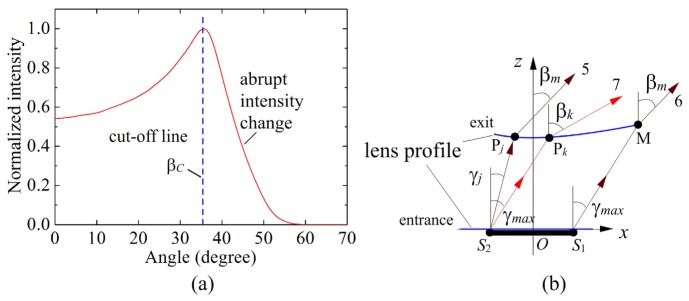
In 3D geometry, the prescribed intensity distribution I_t(β) which can produce uniform far field illuminance should satisfy I_t(β) = cos⁻³β (0≤β≤β_max) [16], where β_max is the desired maximum direction angle of the outgoing ray from the lens unit. Following the step of the 2D design in a meridian plane of the aspherical lens, the 3D model of the aspherical lens is generated by applying the rotation to the lens profile. Usually, a good agreement cannot be achieved between the prescribed intensity and the actual one produced by the 3D model due to skew rays which are not considered in the 2D design. Thus, an intensity feedback strategy [14], which is another key to this feedback method, is employed here to improve the performance of the aspherical lens. Let β_C denotes the maximum effective angle of the 3D design, as shown in Fig. 4(a). Then, the feedback function is calculated on the region [0,β_C]. Let I_i(β) be the actual 3D intensity distribution obtained from the i-th iteration. The feedback function is defined by [14]

$${\eta }_i\left(\beta \right)=I_t\left(\beta \right)/I_i\left(\beta \right),\hspace{0.17em}0\le \beta \le {\beta }_C$$ (1)

Then, the target intensity distribution used for the (i + 1)th iteration to design the lens profile is given by

$$I_{t\left(i+1\right)}\left(\beta \right)=I_t\left(\beta \right)\times {\displaystyle \prod _{j=0}^i{\eta }_j}\left(\beta \right),\hspace{0.17em}0\le \beta \le {\beta }_C$$ (2)

Since the target intensity distribution is not that complex, here we can use the polynomial fitting technique to calculate the target intensity distribution on [0,β_max] after the intensity distribution on [0,β_C] is obtained by Eq. (2), which can be expressed as

Fig. 4.

(a) Due to the limitation of one single aspherical surface and the Monte Carlo raytracing, there will be a region of abrupt intensity change near β_C. (b) γ_max represents the maximum direction angle of the ray from point S₁ after the refraction of the entrance surface (That is, γ_max satisfies nsinγ_max = sinθ_max.) and β_m is the direction angle of ray 6. The direction angle of ray 5 also equals β_m. Due to the limitation of one single aspherical surface, we have the fact that γ_j<γ_max, and β_m<β_max. Plus, an arbitrary ray emitted from S₂ with a direction angle between γ_j<θ<γ_max will take a resulting direction angle between β_m<β<β_k (β_k is the direction angle of the ray 7. Usually, β_k>β_max) [14].

$$I_{t\left(i+1\right)}\left(\beta \right)=a_2{\beta }^4+a_1{\beta }^2+a_0,\hspace{0.17em}0\le \beta \le {\beta }_{\max }$$ (3)

With this new target intensity on [0,β_max], we can update the 2D design and perform the subsequent operations till the stopping criterion is met. Here, we employ the fractional RMS to quantify the difference between the actual intensity and the prescribed one:

$$RMS=\sqrt{\frac{1}{N}{\displaystyle \sum _{k1=1}^N{\left(\frac{I_{ak1}-I_{tk1}}{I_{tk1}}\right)}^2}}$$ (4)

where, N is the number of the sample points, I_tk1 is the target intensity of the k1-th point defined by the prescribed intensity and I_ak1 is the actual intensity of the k1-th point. A smaller value of RMS represents less difference (i.e. a better agreement) between the actual intensity and the prescribed one. Suppose the iteration stops when RMS<Tol, where Tol is a predefined value measuring the tolerance for the difference between the prescribed and obtained intensity distributions. Since the region of abrupt intensity change shown in Fig. 4(a) cannot be eliminated due to the limitation of one single ashperical surface, a design can be considered acceptable as long as good agreement is achieved for the region within [0,β_C]. In the next section, we will use this feedback method to design the aspherical lens unit, and show the significant improvement in the optical performance of the laparoscope that we achieved by using the aspherical lens.

3. Aspherical lens array and experimental tests

Although the illumination design method described in Section. 2 is not limited to a particular type of fiber illumination source used in laparoscopes, the design of the lens unit and the resulted array depends on the intensity profile produced by the fiber bundle. Without loss of generality of this method, we use the laparoscope 1 shown in Fig. 1(a) as an example and aim to design a lens array which yields more uniform illumination in a much larger area. We therefore assume that each of the disk sources produced by the aperture array have the same intensity distribution as the one shown in Fig. 2(a).

Figure 2(b) gives the measured dimensions of the laparoscope 1, which just indicates the huge challenge that we might face in the subsequent design. In order to obtain high energy efficiency, we let the diameter, d, of the circular hole on the aperture equal 0.8mm, which is also the diameter of the non-Lambertian disk source used in the subsequent design. The interior radius, r₁, of the lens array is equal to 3.2mm, which is defined by the clear aperture of the laparoscope imaging system, while the exterior radius of the lens array should be less than 5.5mm which is limited by the packaging requirements of typical laparoscopes. The half field of view of the imaging system of the laparoscope 1 equals 40°. It is required the aspherical lens array should be able to produce a good illumination on the region [-40°, 40°]. Due to the limitation of one single aspherical surface used in the lens design, both the maximum effective angle β_m obtained from the 2D design and the maximum effective angle β_C obtained from the 3D raytracing simulation will be less than the prescribed maximum angle β_max, as shown in Fig. 4(b). Thus, we let β_max = 50° so as to get a good illumination on the region [-40°, 40°], and suppose the refractive index of the lens unit equals 1.4935. The design parameters are summarized in Table 1.

Table 1. Design parameters.

d	r1	r2	n	Tol	θmax	βmax
0.8mm	3.2mm	<5.5mm	1.4935	0.01	40°	50°

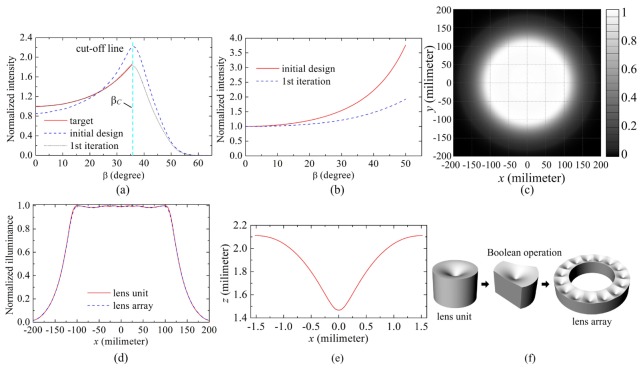
Figure 5(a) gives the intensity distribution produced by the initial design, which is represented by the blue dash line. From this figure we can see the actual intensity deviates significantly from the prescribed one. The RMS of the initial design equals 0.1054 on [0,β_C] (β_C = 35.54°), which just reflects this significant difference. Then, the feedback strategy described in Section 2.2 is employed here to improve the performance. Five millions rays are traced during each iteration. The feedback design converges quite fast with the stopping criterion being met after the 1st iteration. The intensity distribution obtained from the 1st iteration is also given in Fig. 5(a) with RMS = 0.0053. It clearly shows that good agreement is achieved on the region [0,β_C]. The updated target intensity used in the 1st iteration is given in Fig. 5(b) (a₂ = 0.8927, a₁ = 0.5350 and a₀ = 1). From this figure we observe significant difference between the target intensity which is used in the 1st iteration and the one used in the initial design. The illumination pattern obtained from simulation at a lighting distance of 150mm is given in Fig. 5(c) and the illuminance distribution along the line y = 0mm is depicted in Fig. 5(d). From Figs. 5(c) and 5(d), we can see the illuminance almost keeps unchanged with the radius of the illumination pattern changing from 0mm to 100mm, which means an excellent uniformity over the field of view within ± 40°. Although the illuminance decreases a little bit with the radius of the pattern increasing from 100mm to 125mm, the overall illumination condition on the region [0mm,125mm] is still very good, which, of course, just meets our requirement that a good illumination should be achieved on the region [0°, 40°]. Besides, the 2D lens profile is depicted in Fig. 5(e). Let H denote the z-coordinate of the vertex of the lens unit. From Fig. 5(e), we know H = 1.4673mm. That means the ratio of the distance between the lens and the source to the size of the source (d = 0.8mm), H/d = 1.8341. Obviously, the lens unit is very compact. As a final step, the lens array is constructed by Boolean operation, as shown in Fig. 5(f). The exterior radius of the lens array equals 5.3mm and the height of the lens array equals 2.1052mm. The illuminance distribution produced by the lens array along the line y = 0mm is given in Fig. 5(d), which is represented by the blue dash line. It shows clearly that the performance of the lens array is almost the same with that of the lens unit.

Fig. 5.

(a) Normalized intensity distribution. (b) The target intensity distribution used in the initial design and the 1st iteration. (c) The illumination pattern obtained from Monte Carlo ray-tracing. (d) The illuminance distribution along the line y = 0mm. (e) The profile of the lens unit which is a spline curve passing through a set of discrete data points and (f) the Boolean operation. 15 lens units are used here.

To further demonstrate the effectiveness of the proposed lens array, the lens array along with the aperture is replaced by a diffuser element which is assumed to be a perfect Lambertian transmitter with no losses. Figure 6 shows the illuminance distribution produced by the diffuser (blue dashed line). From this figure we can see that although the incoming light rays from the fiber bundle is scattered by the diffuser, most energy is still concentrated in a small region at the center of the illumination area. We also simulate the effect of utilizing an annular aspherical lens which is constructed by rotating the profile of the lens unit around the optical axis of the annular fiber bundle. Since only those meridional rays can be well controlled, the target illumination cannot be achieved by such an annular lens. As shown in Fig. 6, the illuminance produced the annular lens still dramatically decreases from the center to the edge of the illumination pattern (green dotted line). Based on these comparisons, we can see the proposed lens array is very effective in redistributing the spatial energy distribution of the incoming light rays from the fiber bundle. Since some incoming rays are blocked by the aperture, those light rays passing through the aperture array account for 34.1% of the total energy of all the incoming rays from the fiber bundle.

Fig. 6.

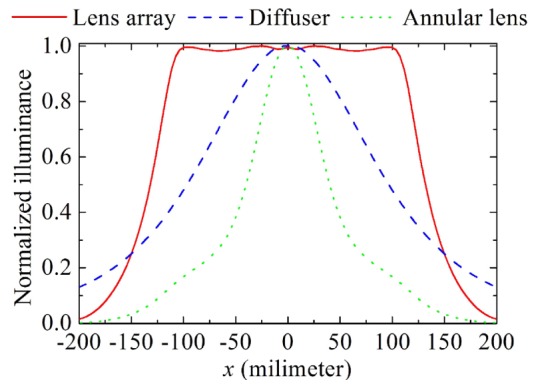
The illuminance distributions along the line y = 0 mm on the target plane at a lighting distance of 150 mm produced by the lens array, the diffuser element and the annular lens, respectively.

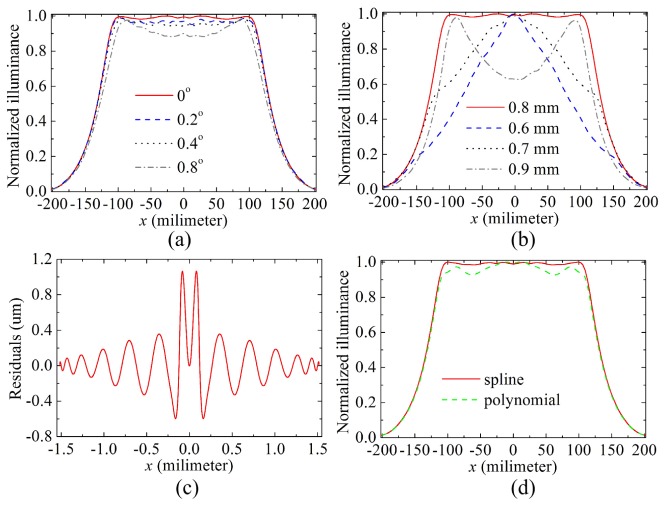
As mentioned above, the aperture array is a key element in the improved illumination system. Thus, it is necessary to explore the influence of the aperture array on the performance of the illumination system. We first analyzed the influence of alignment errors which may be present in aligning the aperture and the lens array. Keeping the position of the aperture array unchanged, we rotated the aspherical lens array around the optical axis of the fiber bundle by a small angle, which resulted in a small center displacement between the aperture and lens arrays. Note that the distance between the center of the aperture and the optical axis of the fiber bundle is equal to 4.4mm. Figure 7(a) gives the illuminance distributions when the rotation angle equals 0.2°, 0.4° and 0.8°, respectively. From this figure we can see the illuminance at the center of the illumination pattern decreases slightly from 0.9942 to 0.8995 when the rotation angle increases from 0° to 0.8°. Next, the influence of the fabrication errors of the aperture was analyzed, as shown in Fig. 7(b). The lens array shown in Fig. 5(f) is designed for an aperture array with the diameter d of 0.8 mm. With the same lens array, we changed the diameter d of the aperture from 0.6 mm to 0.9 mm. Figure 7(b) clearly shows that the performance of the illumination system is very sensitive to the change of the diameter of the aperture.

Fig. 7.

Misalignment and tolerancing analyses. (a) The influence of misalignment between the aperture and the lens unit on the performance of the illumination system. (b) The influence of fabrication errors of the aperture array on the performance of the illumination system. (c) The fitting deviation is used to simulate the fabrication errors which may be present in fabricating the lens array. (d) The influence of fabrication errors of the lens unit on the performance of the illumination system.

Finally, we performed a sensitivity analysis of the lens profile design to fabrication errors. A 26th order even polynomials was used to fit the aspherical surface of the lens unit shown in Fig. 5(e), and the residuals (fitting deviation) are considered as the fabrication errors, as shown in Fig. 7(c). The maximum residual equals 1.065 um (The wavelength of the light ray during simulation is 520 nm.). The green dashed line depicted in Fig. 7(d) represents the illuminance distribution produced by the fitted polynomial surface, and the red solid line represents the illumination distribution produced by the lens unit shown in Fig. 5(f) whose profile is a spline curve passing through a set of discrete data point. The minor differences between these two illuminance distributions suggest that the relatively small departure from the nominal design due to those fabrication errors can be neglected.

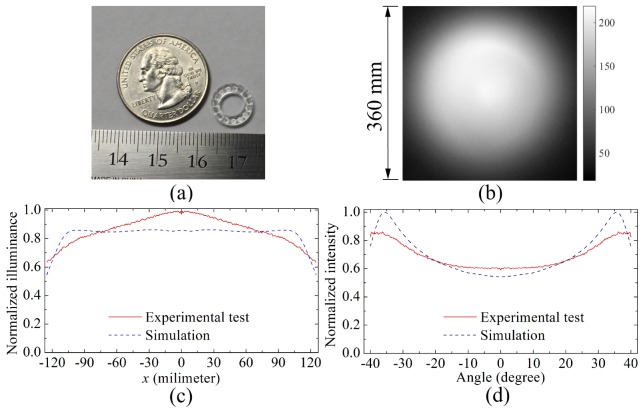
The aspherical lens array was fabricated by a diamond turning machine with a slow tool servo. The prototype of the lens array is given in Fig. 8(a) and the material of the lens array is PMMA. This lens array along with an aperture array was attached to the front end of the illumination system of the laparoscope 1 with the Stryker X-6000 Xenon Light Source. Figure 8(b) shows the illumination pattern produced by the updated illumination system on an acrylic sheet at a lighting distance of 150mm. Figure 8(c) gives the normalized illuminance distribution along the line passing through the center of the pattern in the horizontal direction, and Fig. 8(d) shows the intensity distribution of the output of the updated illumination system. From Figs. 8(c) and 8(d) only small differences between the experimental tests and the simulation results were observed. RMS = 0.0881 The normalized illuminance distribution on the target region [-125mm,125mm] has an RMS difference of 0.0881, while the normalized intensity distribution on the target region [-40°,40°] has an RMS difference of 0.0801. Based on the analysis of the misalignment and fabrication errors presented above, the size error of the aperture array is likely the major factor that contributed to the differences.

Fig. 8.

(a) The fabricated lens, and (b) the illumination pattern produced by the updated illumination system on an acrylic sheet at a lighting distance of 150mm. (c) The normalized illuminance distribution and (d) the normalized intensity distribution produced by the updated illumination system.

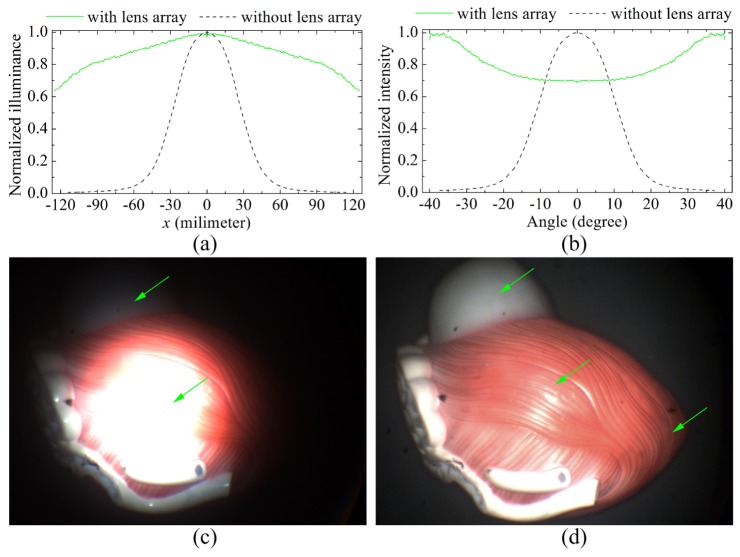
Further comparisons were made between the output of the original fiber-bundle based illumination system built for our MRFL prototype and that of the updated one which was integrated with the lens arrays. Figures 9(a) and 9(b) shows the normalized illuminance and intensity, respectively, without (black dashed line) and with lens array (green solid line), both of which were experimentally measured. Although the actual illuminance distribution deviates a little bit from the target uniform distribution, we still can see the energy concentrated at the center of the illumination pattern produced by the fiber bundle alone without lens array is spread out substantially within much a larger illumination area by the use of the lens array, and the illuminance decreased more slowly from the center to the edge of the illumination pattern. With such an illumination condition, the optical performance of the laparoscope was significantly improved, as shown in Figs. 9(c) and 9(d). Both images were captured by the wide-angle imaging probe of our MRFL system at a working distance of 150mm. In Fig. 9(c), without the lens array, most part of the organ model cannot be clearly observed either due to the over exposure caused by the highly concentrated light distribution in the center or due to very dim lighting near the edge of the model. Figure 9(d), on the other hand, shows clear improvements on detail visibility when the designed aspherical lens array is applied. The whole organ model is well illuminated so that it can be clearly observed due to the excellent performance of the updated illumination system.

Fig. 9.

Comparisons between the optical performance of the initial laparoscope and that of the updated laparoscope. (a) The normalized illuminance distribution and (b) the normalized intensity distribution. (c) The organ model cannot be well illuminated by the initial illumination system, and most part of the organ model cannot be clearly observed, especially at the center and the edge of the model. (d) The organ model is well illuminated by the updated illumination system, and the whole model can be clearly observed.

4. Conclusion

The fiber-based illumination systems of current laparoscope systems fail to produce uniform energy distribution over a large field of view and therefore impose significantly limitations and challenges for effective laparoscopic procedures. In this paper, an aspherical lens array is designed to improve the illumination system to produce a better illumination condition for surgeries. The lens array is placed adjacent to the end surface of the laparoscope, and the outgoing rays from the fiber bundle of the laparoscope are directed by the lens array to produce a prescribed uniform illumination. To achieve this goal, an intensity feedback method is developed to design the lens unit for extended non-Lambertian sources. The fast convergence of this method is illustrated by the fact that the lens unit is obtained after only one iteration, and the effectiveness of this method is also proved by the good simulation results of the lens array. Further, the aspherical lens array is fabricated and the illumination system of the laparoscope is updated with this lens array. By making detailed comparisons between the illumination system without and with the lens array, substantial improvements on the performance of the laparoscope imaging system is demonstrated when the lens array method is utilized.