Abstract
Purpose
Cone-beam CT (CBCT) of the extremities provides high spatial resolution, but its quantitative accuracy may be challenged by involuntary sub-mm patient motion that cannot be eliminated with simple means of external immobilization. We investigate a two-step iterative motion compensation based on a multi-component metric of image sharpness.
Methods
Motion is considered with respect to locally rigid motion within a particular region of interest, and the method supports application to multiple locally rigid regions. Motion is estimated by maximizing a cost function with three components: a gradient metric encouraging image sharpness, an entropy term that favors high contrast and penalizes streaks, and a penalty term encouraging smooth motion. Motion compensation involved initial coarse estimation of gross motion followed by estimation of fine-scale displacements using high resolution reconstructions. The method was evaluated in simulations with synthetic motion (1–4 mm) applied to a wrist volume obtained on a CMOS-based CBCT testbench. Structural similarity index (SSIM) quantified the agreement between motion-compensated and static data. The algorithm was also tested on a motion contaminated patient scan from dedicated extremities CBCT.
Results
Excellent correction was achieved for the investigated range of displacements, indicated by good visual agreement with the static data. 10–15% improvement in SSIM was attained for 2–4 mm motions. The compensation was robust against increasing motion (4% decrease in SSIM across the investigated range, compared to 14% with no compensation). Consistent performance was achieved across a range of noise levels. Significant mitigation of artifacts was shown in patient data.
Conclusion
The results indicate feasibility of image-based motion correction in extremities CBCT without the need for a priori motion models, external trackers, or fiducials.
Keywords: motion correction, cone-beam CT, extremities imaging, statistical reconstruction
1. INTRODUCTION
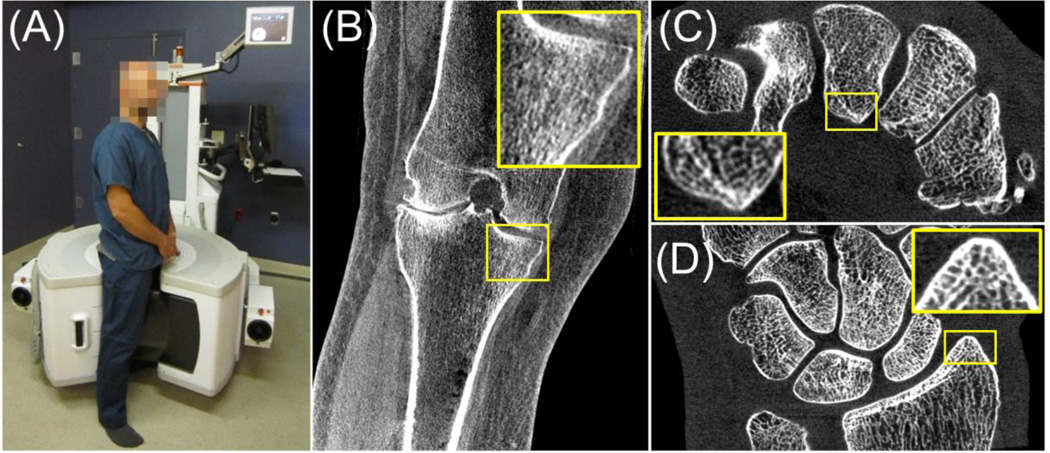
Recently developed dedicated flat-panel detector (FPD) cone-beam CT (CBCT) systems for extremities imaging (Fig. 1 A) offer capability for weight-bearing imaging, simplified workflow, modest patient dose, and high spatial resolution (typically surpassing conventional CT1). Further improvements in spatial resolution of extremities CBCT could enable in-vivo quantitative assessment of bone morphology using metrics of trabecular and cortical microarchitecture typically accessible only to ex-vivo micro-CT. Such ability to evaluate bone microstructure directly in patients would be valuable in early detection of osteoporosis and osteoarthritis, prediction of insufficiency fractures (e.g. due to diabetes or radiation therapy) and in monitoring of treatment response. Development of the next generation ultra-high-resolution extremities CBCT based on a large-area CMOS x-ray detector that offers smaller pixel size and reduced electronic noise compared to current FPDs is currently pursued at our institution.
Figure 1.
(A) Dedicated extremities CBCT scanner with a clinical reconstruction (B) illustrating image quality of the current system. Image of a cadaveric wrist obtained on a testbench with a CMOS detector is shown in (C) and (D) illustrating the improved delineation of trabecular detail and demonstrating the potential for enhanced spatial resolution in the next generation extremities CBCT based on CMOS technology.
The new detector technology, along with other technical upgrades (including a compact small focal spot x-ray source), is likely to improve the baseline system resolution from the current ~300 µm to ~150 µm, consistent with the size of the trabeculae and thus enabling accurate characterization of bone microstructure. One of the challenges in maintaining this very high spatial resolution in clinical practice may be the motion of the extremity during the scan. Despite the relatively long acquisition time (~20–30 s) of current extremities CBCT, effective patient immobilization via cushions or air bladders largely mitigates any impact on the diagnostic performance from blur and artifacts caused by motion (see Fig. 1 B for a representative reconstruction of a knee from an ongoing clinical study). In imaging of bone microstructure, however, quantitative accuracy will be diminished even for slight, sub-mm motion that cannot be easily controlled with immobilization. This creates the need for robust motion compensation algorithms.
Estimation and compensation of motion in CBCT has been previously achieved using fiducial-based techniques2,3 and although such approaches have shown promising performance, they may introduce undesired complexity in the imaging workflow. Fiducial-free motion correction based on 2D–3D registration has been proposed; however, such methods sometimes do not outperform the approaches relying on fiducials5, and they may require prior information that might not always be available6. In cardiac and lung imaging, image-based, fiducial- and tracker-free motion correction has been performed using parametric models of breathing and the beating heart7. In the extremities, however, a predictable, periodic displacement pattern is rarely present, necessitating correction algorithms that do not rely on a priori motion models.
One promising, purely image-based solution involves estimating the motion by optimizing a metric of image sharpness. In CBCT, such approaches (often referred to as “auto-focus” methods) have been primarily investigated in the context of geometrical misalignment estimation in CBCT8. Compared to using 2D–3D registration, motion estimation in the image-based framework can be easily restricted to a region-of-interest (ROI), since no forward projection of the volume is needed. The correction can then be limited to a local neighborhood within which rigid motion can be assumed, even if the extremity as a whole follows a complex motion pattern (e.g. distal femur and proximal tibia moving independently).
In this work, we assume that the system geometry is accurately calibrated and employ the “auto-focus” methodology to develop an automatic, multi-scale image-based motion compensation approach optimized for high-resolution CBCT of the extremities. We propose a novel, two-step iterative estimation of the motion field with a penalized multi-component image sharpness cost function and evaluate its performance in simulation studies and real patient data.
2. METHODS
2.1. Motion compensation framework
The motion compensation framework relies on maximizing a metric of image sharpness to estimate the motion trajectory of the volume. To simplify the problem, we limit the correction to an ROI within which all voxels are assumed to be undergoing the same rigid motion (recognizing that the extremity as a whole may exhibit a more complex deformation). The motion is assumed to consist of a sequence of rigid transformations (one per projection), characterized by 6 degree-of-freedom (DoF) transformation matrices. The full set of motion parameters (three translations and three rotations per projection) is denoted T and estimated through maximization of the following, penalized multi-component cost function:
| (1) |
| (2) |
| (3) |
where μ is the reconstructed volume, ∇x, ∇y and ∇z are the components of its gradient, and hi(μ) is the value of the i-th bin of a histogram of voxel values (i = 0, … N). The term G is the Tenengrad gradient that favors sharp images9. To reduce the impact of noise, the summation in G involves only gradient magnitudes above a user defined threshold. The second term in the cost function, E, is the entropy of image voxel values. Minimizing the entropy encourages high contrast structures8 and mitigates streak artifacts that may be reinforced by the gradient metric G. A penalty R (L2 norm of the first order difference) is included to discourage large changes of motion parameters between consecutive projections. Parameters α and β control the tradeoff between the gradient, entropy, and penalty.
The optimization problem in Eq. 1 is non-convex and thus challenging to solve with conventional gradient-based methods. In this work, the Covariance Matrix Adaptation Evolution Strategy (CMA-ES)10 was used as to solve for a global optimum in a non-convex space. At each iteration of CMA-ES, a population of reconstructed volumes for a set of candidate motions T is obtained with the Feldkamp (FDK) algorithm. The reconstructions for all members of the population are executed in parallel using a GPU-accelerated implementation.
The framework involves a multi-scale optimization divided in two stages. In the first stage, a coarse estimation of the motion trajectory is obtained by maximizing Eq. 1 in a sub-volume containing air-soft tissue and soft tissue-bone interfaces. This stage corrects for gross motion (e.g. due to insufficient immobilization), where air-soft tissue boundaries were found to be particularly important in driving the optimization process. Coarse object discretization and smooth reconstruction kernel (to reduce the impact of streaks) are used. Motion is estimated for a subset of the projections and extended to the complete orbit by spline interpolation. This initial motion estimate is used in the second stage that accounts for fine motions in a local neighborhood of interest. This second stage is performed in a ROI including only soft tissue-bone interfaces and uses a sharp reconstruction kernel and small voxels to maximize image sharpness. The multi-scale approach yields significant performance gains by using high-resolution reconstructions only for fine tuning the motion estimate around an initial guess obtained with coarse reconstruction.
2.2. Experimental Studies
A numerical study was performed using a digital phantom obtained from a CBCT volume of a cadaveric hand (Fig. 1 C and D) acquired on a high-resolution CMOS-based x-ray imaging testbench. The system geometry was the same as in the extremities CBCT prototype. The CMOS detector was a Dalsa Xineos 3030 (Eindhoven, NL) with a pixel size of 100 µm and 600 µm-thick CsI columnar scintillator. A rotating anode x-ray source was operated at 90 kV (+2 mm Al, +0.2 mm Cu), 0.4 focal spot and 0.25 mAs per projection; 720 projections were acquired over 360°. A high-resolution, motion free volume was obtained with FDK (Hann apodization, cutoff at the Nyquist frequency) on an 800×1300×400 grid (0.075 mm voxels).
Motion-contaminated projections were simulated by applying a 6 DoF rigid transformation to the static volume at each view angle and forward projecting the transformed volume using an in-house implementation of a separable footprint projector11. The performance of the compensation algorithm was evaluated for two types of motion patterns. The first experiment involved low frequency periodic motions (“drifts”), where each of the six degrees of freedom followed a sinusoidal function of the view angle with a period of 360°. A range of motions with different magnitudes was simulated by changing the amplitude of the sinusoid for one of the horizontal translation components between 0.2 mm and 2.0 mm. The amplitude of the two remaining translations was fixed at 0.2 mm. The rotational components of the transformation had amplitudes of 0.1° and 0.05° for the in-plane and the two out-of-plane rotations, respectively.
The second numerical experiment emulated a “jitter” motion with much shorter period than in the previous experiment (set at 20°) and small amplitude (1 mm). The high frequency of this motion posed an additional challenge for compensation. The fast sinusoidal pattern was applied to one of the horizontal translation components; other components followed the same pattern as in the previous motion design.
Motion compensation involved 100 iterations of each of the stages of the image-based framework. The first stage used a 150×200×70 voxels centered ROI with 0.5 mm voxels and FDK reconstruction with Hann apodizer and filter cutoff at 20% of the Nyquist frequency. Motion parameters were estimated in 10° steps. The cost function weights were α = 5×105 and β = 10−3. The second stage used a 150×200×70 voxels ROI with 0.075 mm voxels, centered at the center of the volume, and FDK reconstruction with a sharp filter (Hann apodizer, cutoff at 80% of the Nyquist frequency). The regularization weights were α = 5×105 and β = 2×10−4. The threshold for gradient estimation in G was 5×10−4 mm−1 for both stages, selected to preserve strong gradients from bones, but ignore gradients from noise and soft tissue interfaces.
Structural similarity index (SSIM)12 was used to quantitatively compare the motion-compensated reconstructions with the original static reconstruction:
| (4) |
where is the average attenuation and σi is the variance of the attenuation values in image i. The index sta denotes the static image, while MC denotes the motion compensated image, and σsta-MC is the covariance between the two images. The regularization terms c1 (= 10−4) and c2 (= 3×10−4) stabilize the measurement in regions of very low attenuation. Higher values of SSIM indicate improved fidelity of the motion-corrected reconstruction.
In addition to the numerical studies, experimental validation was performed using a motion-contaminated CBCT patient scan of a knee obtained on the extremities FPD-CBCT. A total of 200 projections over a short scan trajectory (240°) were acquired. Motion compensation used 100 iterations of each stage of the algorithm with a 230×230×100 voxels ROI (0.75 mm voxel) employed in the first stage, and a 230×230×100 voxels ROI (0.3 mm voxel) employed in the second stage. Reconstruction parameters were as in the first experiment. The projection data suggested relatively smooth motion, so the regularization strength was increased to β = 0.1 in the second stage. The values of α and gradient threshold were as in the first experiment.
3. RESULTS AND BREAKTHROUGH WORK
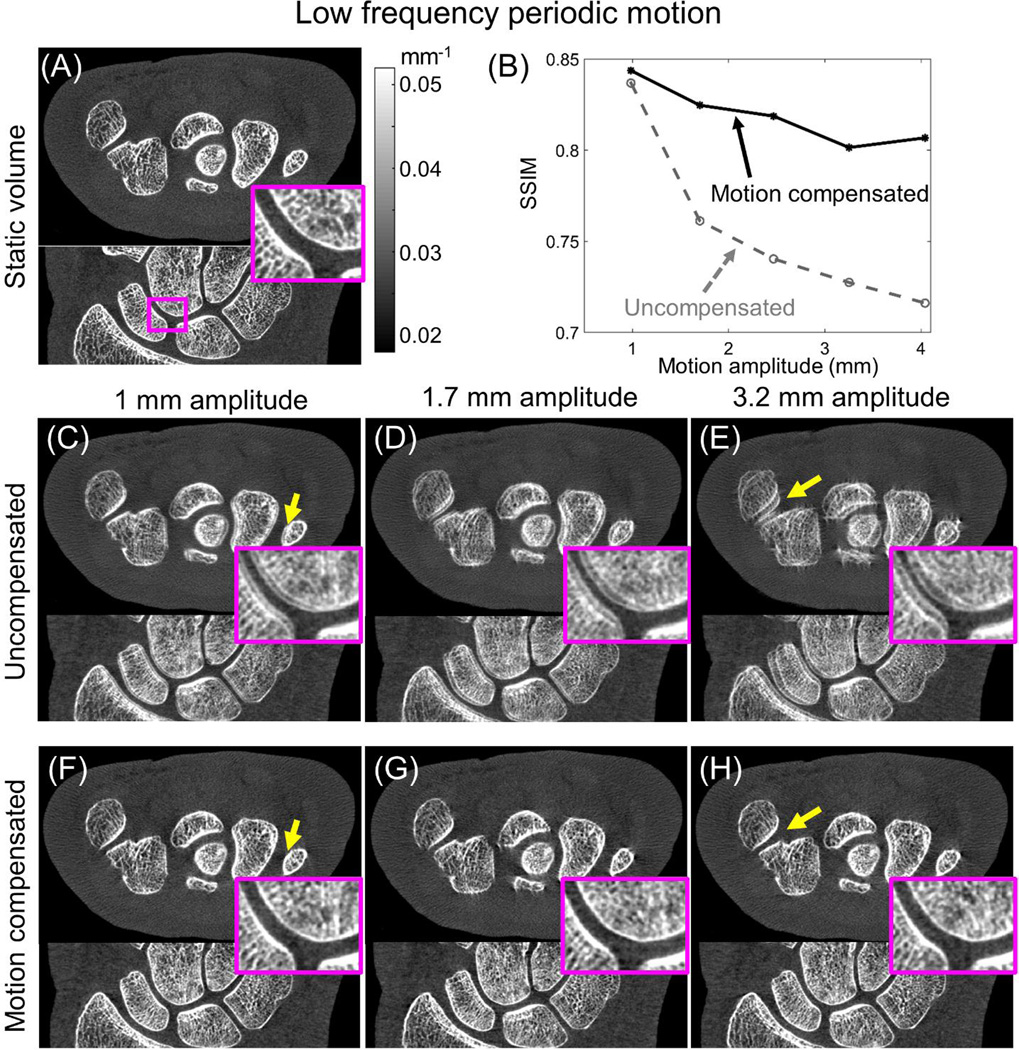
Figure 2 illustrates the performance of the motion compensation framework as a function of motion amplitude for the low frequency periodic motion pattern (“drift”). Motion amplitude was calculated as the average maximum displacement of a set of voxels evenly distributed in the volume. SSIM as a function of motion magnitude (Fig. 2 B) indicates robust performance of the correction method for up to 4 mm motion. For small motion amplitudes, the gain in SSIM is modest due to the relatively low level of motion artifacts in the contaminated image. Approximately 15% increase in SSIM was achieved at larger motions (2–4 mm), where artifacts in the uncompensated reconstruction were more pronounced. SSIM for motion corrected data does not show a significant decrease with increasing motion, indicating consistent performance of the compensation method.
Figure 2.
Performance assessment of the motion compensation algorithm for low frequency periodic motion (“drift”). The baseline static reconstruction is shown in (A). Significant improvement in SSIM [measured against the static image in (A)] is achieved after motion compensation, as illustrated in (B) for a broad range of motion magnitudes. Visual comparison between the data before (C, D, and E) and after motion compensation (F, G, and H) demonstrate reduction of artifacts and improved visualization of trabecular detail (emphasized in the zoom insets) with motion compensation.
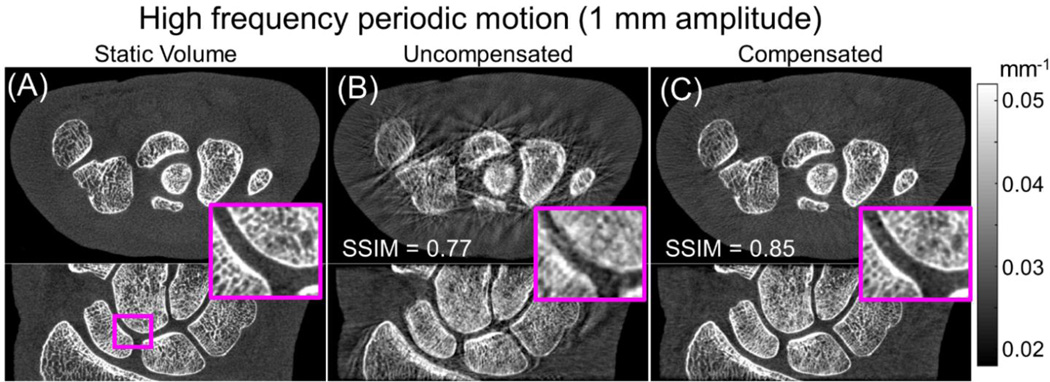
The result of motion compensation for the fast periodic motion (“jitter”) is shown in Fig. 3. In this case, the SSIM of the motion contaminated dataset was 0.77, lower than for the low frequency motion with the same amplitude. The lower SSIM reflects the larger conspicuity of the artifacts (streaks and blurring of trabecular structures). Motion compensation was able to increase the SSIM to 0.85, obtaining a value comparable to the one achieved for the slow motion. The results of the simulation studies indicate robust performance of the compensation method across a wide range of motion frequencies.
Figure 3.
Motion compensation results for the fast periodic motion (“jitter”). Comparison of static images (A) with reconstructed images before compensation (B) show conspicuous streak artifacts and blurring of the bone trabecular structures, resulting in low SSIM. Application of the motion compensation (C) yielded marked reduction of motion artifacts and resolution recovery, resulting in 10% increase in SSIM.
The impact of noise was studied by generating Poisson noise in the original projection dataset. The motion amplitude was fixed at 1.7 mm and standard deviation in the reconstructed data varied between 0.003 and 0.0045 mm−1. The motion correction strategy was found to be robust against noise, yielding similar relative improvement in SSIM independently of the noise level.
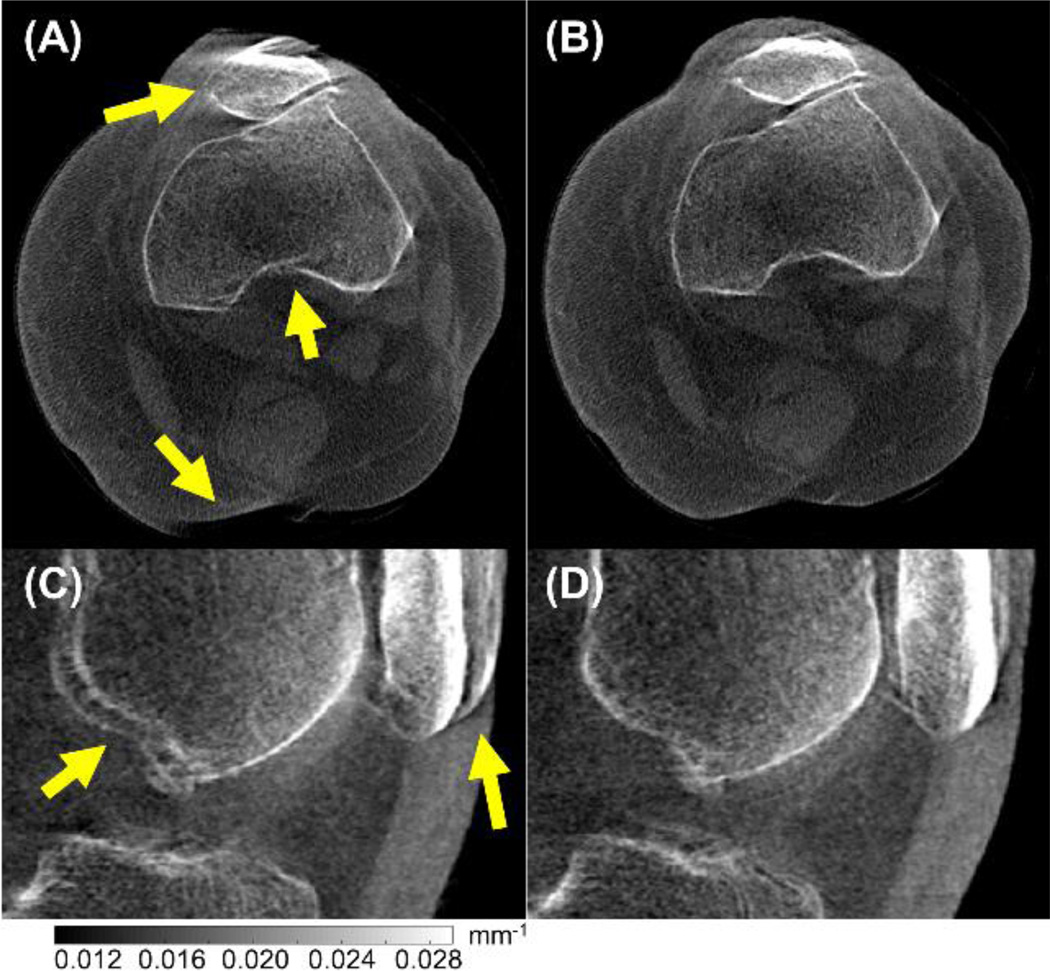
Results of motion compensation in real patient data are shown in Fig. 4. The dataset shown here was obtained on the current extremities CBCT system and represents a case of relatively large motion, likely due to insufficient immobilization. Major image quality improvement and reduction of image artifacts is achieved using the proposed motion compensation method.
Figure 4.
Results of motion compensation in real patient data showing motion artifacts in CBCT images of the standing (weight-bearing) knee. Before compensation (A, C), motion artifacts are evident as discontinuities at the edge of bone structures and double contours (arrows). Those artifacts are clearly reduced after motion compensation (B, D).
4. CONCLUSIONS
We developed and evaluated an image-based motion compensation algorithm for high-resolution extremities CBCT imaging. The algorithm employs a multi-component image sharpness criterion combining image gradient, image entropy, and a penalty that encourages smooth motion trajectories. The framework requires only ROI reconstructions, so the method is applicable to complex trajectories of the extremity as long as the motion is rigid within the ROI. Accordinlgy, the method is directly scalable / parallelizable to multiple ROIs for region-wise correction of complex motion of multiple rigid bodies - e.g., the femur, patella, and tibia. Artifact reduction and improved visualization of bone microarchitecture was demonstrated. In simulations, excellent correction was achieved for displacements of up to ~4 mm, consistent with residual motion occurring despite patient immobilization in extremities CBCT. The proposed compensation method was also successful in significantly reducing artifacts in a clinical case representing larger displacement due to insufficient immobilization. Current work involves optimization of the framework and evaluation in simulations and experiments using realistic motion patterns measured in human subjects using external trackers. The robust motion correction framework developed here will be essential to fully realize the potential gains in spatial resolution of extremities CBCT that are expected with new imaging hardware.
Acknowledgments
The authors thank Dr. Shadpour Demehri and Dr. Gaurav Thawait (Department of Radiology, Johns Hopkins University) for acquisition and interpretation of clinical image data in an ongoing study of extremity CBCT imaging performance. This work was supported in part by NIH Grant R01-EB-018896 and R21-AR-062293 with thanks for ongoing collaboration with scientists at Carestream Health (Rochester NY).
REFERENCES
- 1.Zbijewski W, De Jean P, Prakash P, Ding Y, Stayman JW, Packard N, Senn R, Yang D, Yorkston J, et al. A dedicated cone-beam CT system for musculoskeletal extremities imaging: Design, optimization, and initial performance characterization. Med. Phys. 2011;38(8):4700. doi: 10.1118/1.3611039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Choi J-H, Maier A, Keil A, Pal S, McWalter EJ, Beaupré GS, Gold GE, Fahrig R. Fiducial marker-based correction for involuntary motion in weight-bearing C-arm CT scanning of knees. II. Experiment. Med. Phys. 2014;41(6):061902. doi: 10.1118/1.4873675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jacobson MW, Stayman JW. Compensating for head motion in slowly-rotating cone beam CT systems with optimization transfer based motion estimation; IEEE Nucl. Sci. Symp. Conf. Rec; 2008. pp. 5240–5245. [Google Scholar]
- 4.Kim J-H, Nuyts J, Kyme A, Kuncic Z, Fulton R. A rigid motion correction method for helical computed tomography (CT) Phys. Med. Biol. 2015;60(5):2047–2073. doi: 10.1088/0031-9155/60/5/2047. [DOI] [PubMed] [Google Scholar]
- 5.Unberath M, Choi J-H, Berger M, Maier A, Fahrig R. Image-based compensation for involuntary motion in weight-bearing C-arm cone-beam CT scanning of knees. Proc. SPIE 9413, Med. Imaging 2015 Image Process. 2015;9413:94130D. [Google Scholar]
- 6.Berger M, Müller K, Aichert A, Unberath M, Thies J, Choi J-H, Fahrig R, Maier A. Marker-free motion correction in weight-bearing cone-beam CT of the knee joint. Med. Phys. 2016;43(3):1235–1248. doi: 10.1118/1.4941012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brehm M, Paysan P, Oelhafen M, Kachelrieß M. Artifact-resistant motion estimation with a patient-specific artifact model for motion-compensated cone-beam CT. Med. Phys. 2013;40(10):101913. doi: 10.1118/1.4820537. [DOI] [PubMed] [Google Scholar]
- 8.Wicklein J, Kunze H, Kalender WA, Kyriakou Y. Image features for misalignment correction in medical flat-detector CT. Med. Phys. 2012;39(8):4918–4931. doi: 10.1118/1.4736532. [DOI] [PubMed] [Google Scholar]
- 9.Kingston A, Sakellariou A, Varslot T, Myers G, Sheppard A. Reliable automatic alignment of tomographic projection data by passive auto-focus. Med. Phys. 2011;38(9):4934. doi: 10.1118/1.3609096. [DOI] [PubMed] [Google Scholar]
- 10.Hansen N, Kern S. Evaluating the CMA Evolution Strategy on Multimodal Test Functions. Proc. 8th Int. Conf. Parallel Probl. Solving from Nat. - PPSN VIII. 2004;3242/2004:282–291. [Google Scholar]
- 11.Long Y, Fessler JA, Balter JM. 3D forward and back-projection for X-ray CT using separable footprints. IEEE Trans Med Imaging. 2010;29(11):1839–1850. doi: 10.1109/TMI.2010.2050898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004;13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]