A finite element head and neck model as a supportive tool for deformable image registration

Abstract

Purpose

A finite element (FE) head and neck model was developed as a tool to aid investigations and development of deformable image registration and patient modeling in radiation oncology. Useful aspects of a FE model for these purposes include ability to produce realistic deformations (similar to those seen in patients over the course of treatment) and a rational means of generating new configurations, e.g., via the application of force and/or displacement boundary conditions.

Methods

The model was constructed based on a cone-beam computed tomography image of a head and neck cancer patient. The three-node triangular surface meshes created for the bony elements (skull, mandible, and cervical spine) and joint elements were integrated into a skeletal system and combined with the exterior surface. Nodes were additionally created inside the surface structures which were composed of the three-node triangular surface meshes, so that four-node tetrahedral FE elements were created over the whole region of the model. The bony elements were modeled as a homogeneous linear elastic material connected by intervertebral disks. The surrounding tissues were modeled as a homogeneous linear elastic material. Under force or displacement boundary conditions, FE analysis on the model calculates approximate solutions of the displacement vector field.

Results

A FE head and neck model was constructed that skull, mandible, and cervical vertebrae were mechanically connected by disks. The developed FE model is capable of generating realistic deformations that are strain-free for the bony elements and of creating new configurations of the skeletal system with the surrounding tissues reasonably deformed.

Conclusions

The FE model can generate realistic deformations for skeletal elements. In addition, the model provides a way of evaluating the accuracy of image alignment methods by producing a ground truth deformation and correspondingly simulated images. The ability to combine force and displacement conditions provides flexibility for simulating realistic anatomic configurations.

Introduction

In recent years, there has been considerable progress in head and neck cancer intensity-modulated radiation therapy [1]. Despite daily corrections of patient position with treatment imaging modalities such as cone-beam computed tomography (CBCT), local shape and position variations persist [2–4]. Deformable image registration (DIR) therefore is essential for monitoring the changing geometric configurations of tumor and normal tissues [5]. However, existing DIR methods, generally intensity-based, have failed to provide transformations that accurately encompass the complex changes present in local neck anatomy due to lack of physiologically realistic constraints [6]. Furthermore, the accuracy of the existing DIR algorithms has not been rigorously evaluated due to lack of ground truth deformation for a given set of image data.

Quantitative measures, which have been frequently used in many previous investigations, may misinterpret the registration accuracy. First, a volume overlap index has been frequently used in order to evaluate the registration accuracy [7,8]. Although the volume overlap index is a good predictor of auto-contouring accuracy, a high score of the index is not necessarily related to accurate voxel-by-voxel deformation which is required for dose accumulation. Second, image similarity metrics such as normalized correlation coefficient, used in previous works [9,10], may not be robust surrogates of the registration accuracy as reported in [11]. Finally, target registration error [7–10,12–14], which is defined as the difference between the distance of a landmark pairs and the displacement obtained by DIR, is one of the most popular measures. However, the target registration error was calculated with a limited number of landmark pairs, with which the accuracy of the volumetric deformation cannot be rigorously evaluated.

Finite element (FE) models and related analysis methods hold significant promise for improving the veracity of evaluating the registration accuracy. This is because analysis using FE models can generate realistic deformations describing anatomic changes during radiation treatment, which thus can serve as ground truth deformations. FE analysis (FEA) is a numerical method to find an approximate solution of system governing equations. In FEA, a system is geometrically discretized into small elements, called “finite elements,” having several points (“nodes”) shared by neighboring elements. For instance, FEA can be used for a structural analysis, in which resultant deformation under external loading is calculated. For the structural FEA, a set of constraints on force/displacement, called “boundary conditions,” is applied to some of the nodes. Theoretically, FE models having extremely detailed representations of anatomic segments with mechanical properties assigned can simulate anatomic changes in a cancer patient who undergoes radiotherapy. It is noted that the accuracy of the analysis is largely affected by how the boundary conditions applied to the model are similar to those that acted on the patient.

Schnabel et al. [15] first introduced a FE-based evaluation framework for DIR accuracy. The basic idea of the evaluation framework is to compare the resultant deformation by DIR with the ground truth deformation simulated by a FE analysis. The FE-based evaluation method was used for the DIR of breast magnetic resonance images. In the FE-based evaluation framework, reference images were synthetically generated by deforming target images with the deformations by the FE analysis. Provided that DIRs are performed between synthetic reference images and target images, the FE-computed deformations can serve as ground truths. Zhong et al. [16] applied the FE-based evaluation method to evaluate the accuracy of demons and B-spline DIR of prostate and lung CT images. Given the displacement boundary conditions to the bottom of bladder for the prostate model and to the diaphragm for the lung model, the FE models were used to generate the ground truth deformation maps, to which the resultant deformations were compared.

For head and neck radiation therapy, Al-Mayah et al. [8] first introduced a FE-based DIR method, in which a FE head and neck model consisted of cervical vertebrae (C1–C7, first to seventh cervical vertebrae), mandible, and body surface. Specifically, deformations were estimated by testing the FE model under boundary conditions obtained by rigid alignments for bony components and by a surface projection for body surface. While clearly showing the value of FE method in patient modeling, this phantom lacked appropriate physical connections between bony elements (i.e., intervertebral disks were not present), and their implementation of image registration as the direct result of surface fitting could lead to physically unrealistic transformations.

Instead of directly using FE models for the DIR purpose, this investigation aims at using FE models to aid in evaluating the accuracy of DIR. In this work, a FE model is developed that has an interconnected skeletal system which can quickly generate realistic skeletal deformations through FE analysis with boundary conditions on local displacements or force vectors. The developed model has potential to support image registration research and development.

Methods

Model construction

A FE head and neck model was constructed based on a head and neck CBCT scan with an image dimension of 384× 384 × 72 (0.651 × 0.651 × 2.5 mm³ pixel dimension). First, voxels belonging to bony elements were classified into seven subsets of voxels, which are corresponding to five cervical vertebrae (C1–C5), mandible, and skull. For the segmentation of each bony structure, a simple thresholding was performed by setting up lower and upper bounds of intensity values. After the thresholding, manual modification (usually done in an hour for each scan) was followed in order to mainly remove misclassified voxels and to refine the segmentation to obtain smooth three-dimensional geometries. Second, intervertebral disks, which connect bony elements together, were manually segmented based on a published study [17]. Last, surrounding soft tissues including fat and muscle were classified into one group by excluding the voxels classified for bony structures, intervertebral disks, and air from the entire set of voxels.

These classified and refined voxel groups were converted to surface models with three-node triangular elements, each of which has three points forming a triangle. For the segmentation and surface model creation, a commercial software package (Mimics 14, Materialise Inc., Ann Arbor, MI) was used. Each space between the surfaces was filled with additional points where displacements will be calculated, and then, each set of four points was connected so that all structures are composed of three-dimensional four-node tetrahedral elements. During this volumetric mesh generation, all the surface models were connected; any two surfaces share all the nodes at the interface (HyperMesh 10.0, Altair Engineering Inc., Troy, MI). In other words, continuity conditions of the displacement vector field at the interfaces are imposed.

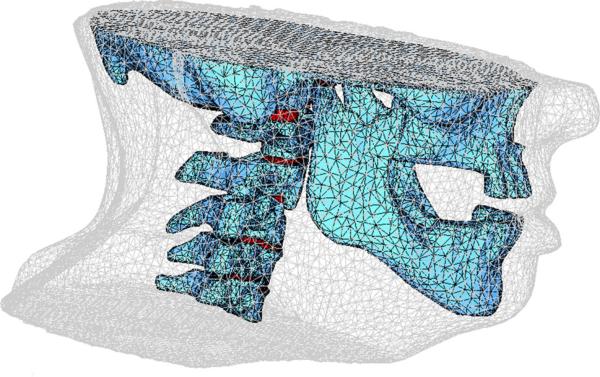
Figure 1 shows a rendering of a FE model, consisting of 49,731 nodes and 270,382 elements. The bones, disks, and surrounding tissue were modeled as homogeneous linear elastic materials. Values of Young's modulus and Poisson's ratio (Table 1) were taken from previous studies [18,19]. Young's modulus is a mechanical property that measures of the stiffness of a material. Young's modulus is the ratio of the stress along a direction to the strain along the direction, analogous to the spring constant (ratio of force to displacement) in Hooke's law. Poisson's ratio, another mechanical property necessary to model a linear elastic material, is defined as the ratio of the displacement in the lateral direction to the displacement in the direction to which a force is applied. To simulate rigidity of bony structures, relatively large values of Young's modulus were assigned to the cervical vertebrae, mandible, and skull. With smaller Young's modulus assigned than bony structures, soft tissue regions can be deformed under boundary conditions.

Fig. 1.

Illustration of volumetric meshes for the finite element head and neck model, including the intervertebral disks

Table 1.

Mechanical properties used for bone, disk, and soft tissue in the FE head and neck model

Material	Young's modulus (MPa)	Poisson's ratio
Bone	12,000.0	0.29
Disk	3.4	0.40
Soft tissue	1.8	0.49

FE analysis under displacement boundary conditions

As an example of the possible applications of the FE head and neck model, a deformation analysis was performed on the model under a set of displacement boundary conditions. For this analysis, individual displacement boundary conditions were extracted from each of the surface pairs of the skull, mandible, and cervical vertebrae on two cone-beam CT scans, which were taken at different treatment sessions. Specifically, 4 × 4 transformation matrices were obtained by using a surface registration algorithm (STL Registration, Mimics 14, Materialise Inc., Ann Arbor, MI), indicating translation and rotation of each bony structure. These transformation matrices were then used to calculate displacement vectors. Given these displacements as boundary conditions, a displacement vector field was calculated by FE analysis using a commercial software package (ABAQUS 6.10, Simulia Corp, Northville, MI).

It was assessed how the resultant deformation was close to the deformation occurred between two different treatment fractions. For this evaluation, eight corresponding landmark pairs were manually located on both images; these landmark points were located at the midpoint of the bilateral foramina of the cervical vertebrae. Differences between measured displacements of the landmarks and those generated by the FE analysis were calculated.

FE analysis under force boundary conditions

As the skeletal elements in the FE model are interconnected, a simple means of phantom reconfiguration can be achieved via application of a small number of force vectors. This method may be more efficient than finding displacement boundary conditions by using surface registrations for each bony element as long as the resultant deformation is similar to that seen from patients.

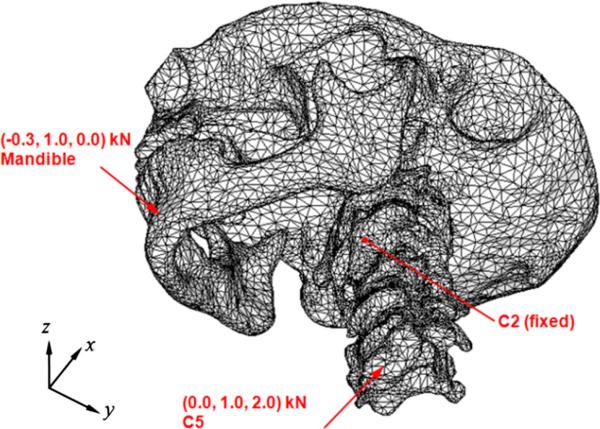
As an example, a set of forces was found to mimic patient deformation by testing several magnitudes of force: (−0.3, 1.0, 0.0) kN to the mandible and (0.0, 1.0, 2.0) kN to the C5 vertebra as shown in Fig. 2. Rotation of the vertebrae about the inferior–superior axis and translation of lower cervical vertebrae relative to C2 vertebra in the anterior–posterior direction are examples of the motions that can be observed from head and neck patients during the course of radiation treatment as reported in a previous study. The direction and location of the forces were determined to simulate these motions. To reflect the condition of patient positioning at treatment (i.e., to restrict the transformation to the deformation about the treated configuration of the patient), zero displacement on four points on the C2 vertebral body was imposed as displacement boundary conditions. By combining the aforementioned force/displacement boundary conditions, a new phantom configuration was obtained by FE analysis (ABAQUS 6.10, Simulia Corp, Northville, MI).

Fig. 2.

Illustration of the force boundary conditions applied to the mandible and fifth cervical vertebra

Results

FE analysis under displacement boundary conditions

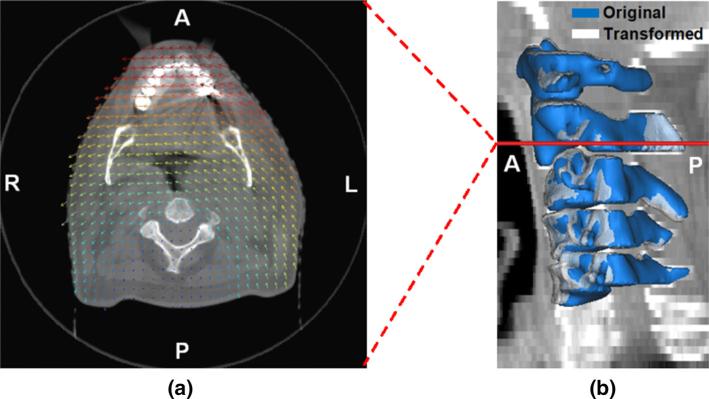
Figure 3a shows the resultant displacement vector field overlaid on an axial cut of the cone-beam CT image volume that the construction of the FE model was based on. The displacement vector field demonstrates that the transformation, with which the original configuration was transformed, was mainly associated with translation and rotation. The deformation in the soft tissue region surrounding the cervical vertebra resulted from the rigid motions (i.e., translation and rotation) of the bony structures, which were applied as the displacement boundary conditions.

Fig. 3.

Results of the FE analysis under displacement boundary conditions: a the displacement vector field overlaid on an axial plane of the cone-beam CT image volume on which the model was constructed (scaled), b the original and deformed geometries of the cervical vertebrae (C1–C5) with the level of the CT slice shown in a annotated (A anterior, P posterior, L left, R right)

In addition, Fig. 3b shows the transformed configuration (shown as white) of the five cervical vertebra bodies overlaid with the original configuration (shown as blue) on the reference CBCT image. While the original configuration coincided with the geometries of the vertebrae visible in the CBCT image, the transformed configuration was mismatched with the image, demonstrating how the vertebral bodies were transformed by the FEA. This comparison also shows the boundary conditions applied to the vertebrae for the FEA. The maximum displacement magnitude of all nodal points was 7.0mm.

The examination with eight landmark pairs showed discrepancies of (0.2 ± 0.3, −0.2 ± 0.4, −0.1 ± 1.0) (mm) between the measured displacement and the FE-computed displacement in the left–right, anterior–posterior, and inferior–superior directions, respectively. This result shows that the FE analysis correctly transformed the original configuration into the target configuration. The strain components calculated on the bony elements were close to zero, indicating a realistic skeletal deformation was resulted.

FE analysis under force boundary conditions

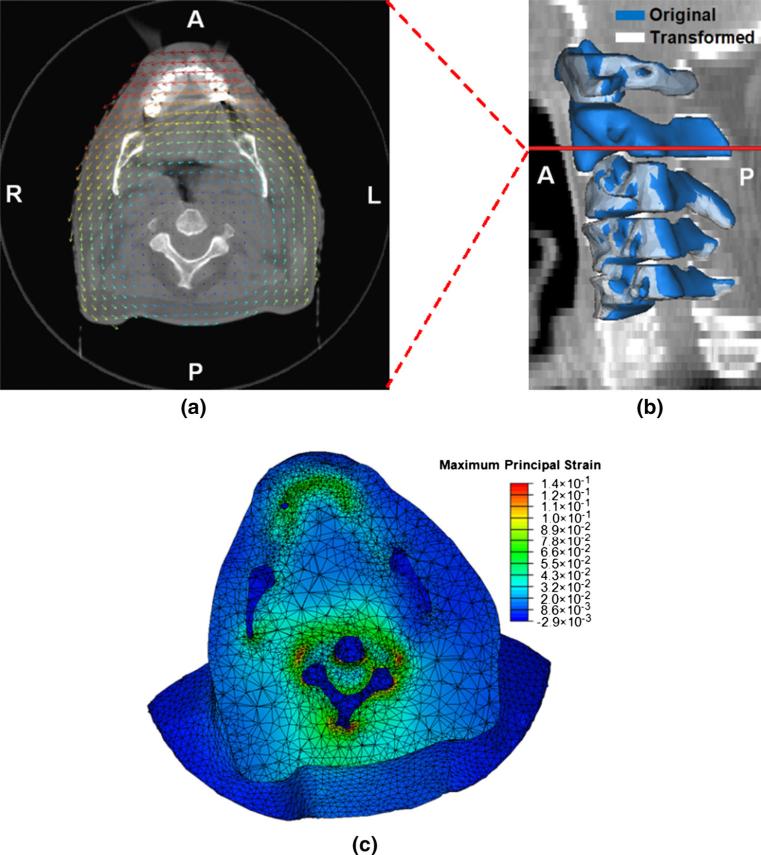
Figure 4 shows an example of force-based model reconfiguration with forces applied to the mandible and C5 and with the C2 vertebra fixed. Applying two forces caused the entire model to transform via the mechanics implemented therein. The resultant displacement vector field is overlaid on an axial plane of the cone-beam CT scan in Fig. 4a. Comparing with the displacement vector field obtained with the displacement boundary conditions in Fig. 3a, a similar displacement vector field was obtained with the force boundary conditions as intended. This finding supports the use of equivalent force boundary conditions instead of displacement boundary conditions.

Fig. 4.

Results of the FE analysis under a combined set of force and displacement boundary conditions: a the displacement vector field overlaid on an axial plane of the cone-beam CT image volume on which the model was constructed (scaled), b the original and transformed geometries of the cervical vertebrae (C1–C5) with the level of the CT slice shown in a annotated, c the maximum principal strain field shown on the deformed geometry (A anterior, P posterior, L left, R right)

The original (blue) and deformed (white) surfaces of the cervical vertebrae are overlaid on the sagittal plane of the reference CBCT image in Fig. 4b. The rigid motions of the vertebral bodies in Fig. 4b are similar to those in Fig. 3b. Translations of lower cervical vertebrae (C3–C5) toward the anterior direction were observed on both cases. A difference between the cases is on the motions of the C2. While the C2 vertebra was fixed for the FEA under the force boundary conditions, it was transformed by the FEA under the displacement boundary conditions.

The values of the maximum principal strain are plotted on the deformed geometry in Fig. 4c. Nearly zero strains induced in the regions of the mandible and C4 clearly show that the FE model is able to produce skeletal deformations via FEA under force boundary conditions. Nonzero strains were observed surrounding the bony elements, clearly showing that the FE model is not merely translated or rotated, but rather deformed. In other words, the finite elements in the regions surrounding the bony structures could be compressed or expanded depending on the boundary conditions applied to the model even though the bony structures are translated or rotated.

Discussion

The objective of this work was to develop a FE head and neck model as a supportive tool for DIR research in radiation therapy. By connecting skeletal elements appropriately, the FE model can provide realistic deformations in the neck region under force boundary conditions as well as under displacement boundary conditions.

As a computational head and neck phantom, the model provides a tool for the evaluation of image registration accuracy. The deformations obtained by the FE model can be used to simulate images with the effects of realistic variations in neck translocation and articulation. These ground truth deformations and corresponding image volumes provide a set of tools to examine the accuracy of image alignment methods.

In addition, the FE head and neck model has the potential to improve image registration accuracy when it is incorporated into existing image alignment methods. For instance, when penalty terms are combined to an image registration method in order to regularize deformation in specific regions such as rigidity penalty term for bones, the model can be used for obtaining the segmentations of the regions for other patients. Since the segmentation processes are time-consuming, it is beneficial to automatically generate classified voxel groups by aligning the reference patient image with another patient image and deforming the configuration.

There is a possibility that the current FE model will become more realistic as other soft tissues such as muscles in the neck are specified. With the use of hyperelastic material properties, deformation in the surrounding tissues may be more reasonably produced. Therefore, the current model provides a fundamental framework for further development of realistic human head and neck model.

Segmenting bony structures is time-consuming and labor-intensive because it requires manual modification (an hour for each data set as mentioned in Section II. A.) following automatic thresholding. However, as long as the FE model is used for the evaluation purpose only instead of being used for DIR, no further effort to construct models is required, justifying the feasibility of the FE model as an evaluation tool for DIR. One of the challenging tasks for the construction of the FE model was to segment the disks which are, in general, not visually distinguishable in CT images. The geometries of the disks in the model may have an influence on the value of the elastic stiffness of the disks. However, this may not remarkably degrade the ability of the model to generate realistic deformations; assigning large values of Young's modulus to the skull, mandible, and cervical vertebrae (Table 1) guarantees the rigid body motions of those components.

Another limitation of the current model is that the geometry of the skull is simplified for the sake of convenience in volumetric meshing. While increasing the potential for nonphysical deformations, the overall rigidity of the skull as a unit suggests that simplifying its shape somewhat may have minimal influence on the propagation of forces and displacements to surrounding anatomy.

Furthermore, physiological changes such as weight loss, tumor growth, and tumor response to radiation have not been taken into consideration. Incorporating a mathematical model of tumor growth and response may further aid the utility of this model for enhancing and investigating image registration accuracy.